
Нейросети в трейдинге: Оптимизация LSTM для целей прогнозирования многомерных временных рядов (DA-CG-LSTM)
Введение
Финансовые рынки — это не просто цифры на экранах. Это динамичная среда, в которой каждый тик, каждая свеча, каждое изменение объёма торгов являются отражением человеческих эмоций, ожиданий, страхов и надежд. Понять этот ритм, научиться прогнозировать, куда пойдёт цена, — задача, над которой бьются трейдеры.
В центре внимания — многомерные временные ряды. Классическая форма представления рыночных данных: цена актива во времени, объём торгов, индикаторы, новости. Это всё данные, которые можно анализировать, моделировать и использовать для прогнозирования.
Ещё недавно рынок опирался на проверенные временем классические методы ARIMA, SARIMA и прочие. Эти модели удобны, понятны и не требовали колоссальных вычислительных ресурсов. Они неплохо справлялись с задачами сезонности и линейных зависимостей, особенно в спокойных рыночных условиях. Но финансовый рынок не стационарен. Здесь всё перемешано: новости влияют на ожидания, настроения инвесторов меняются за секунды, алгоритмические сделки создают эффекты резонанса, и всё это порождает сложные, нелинейные, часто хаотические зависимости. Традиционные модели могут указать направление, но не покажут детали.
С приходом методов глубокого обучения, ситуация резко изменилась. Рекуррентные нейронные сети (RNN) дали возможность учитывать историю изменений, однако они тоже не были панацеей. Их фундаментальное ограничение — так называемая "короткая память". Иными словами, такие модели могут обрабатывать только ограниченный временной контекст. С увеличением длины исходной последовательности, они быстро забывают важную информацию из начала временного ряда.
Для решения этой проблемы были разработаны улучшенные архитектуры — такие, как LSTM (Long Short-Term Memory) и GRU (Gated Recurrent Unit). Эти модели дали нейросетям память — возможность удерживать важную информацию на протяжении более длинных временных промежутков.
Однако, и у них оказались свои ограничения. Несмотря на способность улавливать зависимости на более длинном временном интервале, они по-прежнему чувствительны к качеству исходных данных. Особенно тяжело им даются ситуации, где краткосрочные рыночные всплески имеют ключевое значение. Такие мутации зачастую не фиксируются в долгой памяти модели, особенно если они не сопровождаются заметными изменениями в долгосрочном контексте.
С целью преодоления этих ограничений был предложен механизм внимания (attention). Он позволил моделям эффективно фокусироваться на ключевых участках временного ряда, независимо от их удалённости от текущего момента. В отличие от LSTM, механизмы внимания не требуют последовательной обработки всех временных шагов и могут сразу сосредоточиться на действительно важной информации. Это резко улучшило способность нейросетей улавливать долгосрочные зависимости, особенно в сложных, многомерных временных рядах.
Но и здесь есть подводный камень: такие модели хорошо ловят долгосрочные зависимости, но игнорируют краткосрочные сигналы, которые могут быть критически важны. Финансовый рынок не прощает промедления — один новостной заголовок, и цена может взлететь или рухнуть. Если модель не реагирует на подобные мутации, она упускает шанс вовремя изменить позицию.
Авторы работы "A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction" попытались объединить лучшее из двух подходов и предложили новый фреймворк Dual-Staged Attention Conversion-Gated LSTM (DA-CG-LSTM). Модель использует двойной механизм внимания. На первом этапе она оценивает значимость признаков и временных интервалов, а затем, после обработки в специальном блоке CG-LSTM, — повторно анализирует временные зависимости, усиливая важные сигналы и ослабляя незначительные.
Дополнительным преимуществом модели стала продуманная работа с функциями активации, что помогло удерживать долгосрочную информацию и реагировать на кратковременные всплески.
Алгоритм DA-CG-LSTM
Фреймворк DA-CG-LSTM представляет собой модель, способную выделять суть из многомерных временных рядов. Его архитектура сочетает два уровня внимания и модифицированный рекуррентный блок в виде Conversion-Gated LSTM. Это делает модель особенно эффективной в задачах прогнозирования динамических многомерных процессов.
Всё начинается с подачи на вход модели многомерной временной последовательности исходных данных. Эта последовательность представляет собой матрицу X = [x1, x2, ..., xT] ∈ RT*n, где каждая строка xt — это вектор из n признаков на момент времени t. Но модель не обрабатывает эту информацию вслепую. Сначала она учится понимать, какие признаки и какие временные шаги в этой истории действительно важны. Так начинается первый этап — входное внимание.
Сначала анализируются признаки внутри каждого момента времени. Модель вычисляет степень важности каждого признака xkt на временном шаге t по формуле:
![]()
Здесь We и be представляют собой обучаемые веса и смещения линейного слоя, применяемого к каждому вектору признаков исходных данных xt. Этот слой позволяет трансформировать исходные данные в более информативное скрытое представление, удобное для оценки значимости. Кроме того, вектор ve, также обучаемый, играет роль интерпретируемой маски внимания — он используется для вычисления скалярной оценки важности. Такая конструкция даёт модели возможность гибко ранжировать признаки по их вкладу, что особенно важно при работе с шумными и многомерными временными рядами.
Полученные коэффициенты важности нормализуются функцией SoftMax, превращая набор оценок в вероятностное распределение по признакам:
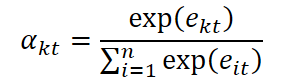
С их помощью корректируется вектор исходных данных x ̃t, в котором каждый признак масштабируется своей значимостью.
![]()
Но на этом не останавливаемся. Следующим этапом, модель анализирует значимость каждого временного шага, определяя, какие временные точки стоит усилить при обработке. Для этого используется аналогичная структура:
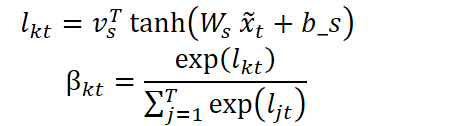
Итоговая последовательность — это взвешенные по времени представления:
![]()
Таким образом, ещё до начала рекуррентной обработки, модель фокусируется на информации, которая, по её мнению, действительно важна.
Далее последовательность попадает в модифицированный рекуррентный блок CG-LSTM. Здесь происходит второй уровень магии. В стандартном механизме LSTM авторы фреймворка поработали с функциями активации врат исходных данных и забвения. Это сделано для увеличения чувствительности модели к всплескам, сопровождающим краткосрочные мутации, и одновременного усиления способности к запоминанию долгосрочной информации.
В классическом LSTM-блоке врата исходных данных используют сигмоидальную функцию для принятия решений о том, какая информация должна быть сохранена. Однако, сигмоида склонна к насыщению: при малых или больших значениях входа, её производная становится близкой к нулю, что снижает эффективность обучения. Авторы фреймворка DA-CG-LSTM предложили использовать комбинацию сигмоиды и гиперболического тангенса, что выражается следующей формулой:
![]()
Такая конструкция позволяет избежать насыщения на ранних этапах обучения и сохранить чувствительность к слабым, но значимым колебаниям. В условиях финансовых временных рядов это особенно важно — например, резкое изменение объёма торгов или всплеск волатильности могут указывать на смену рыночного режима, и своевременное обнаружение таких паттернов даёт модели преимущество в прогнозировании.
Врата забвения CG-LSTM также модифицированы. В отличие от стандартного LSTM-блока, здесь применена функция, сочетающая сигмоиду с обратным гиперболическим тангенсом:
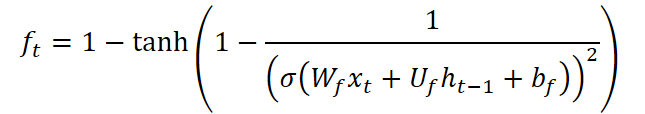
Эта формула обладает уникальным свойством: производная функции принимает значения в диапазоне от 0 до примерно 2.89, создавая эффект рассеивания данных. То есть, модель становится способной более агрессивно забывать нерелевантную или устаревшую информацию, тем самым фокусируясь на свежих изменениях. Это особенно ценно в рыночных условиях, когда прошлые события быстро теряют актуальность, и успех зависит от реакции на текущие сигналы.
На выходе CG-LSTM блока получаем последовательность (h1, h2, ..., hT), где каждый ht несёт в себе кратко- и долгосрочную информацию. Однако важно не просто сохранить, а и правильно вспомнить. Это задача второго уровня внимания — временного.
Здесь модель как бы заново смотрит на свою память. Она вычисляет значимость каждого скрытого состояния hj для текущего момента времени. Полученные значения нормализуются через SoftMax. И на их основе создаётся контекстный вектор — квинтэссенция всей временной истории, который обрабатывается вторым CG-LSTM блоком.
Имея актуальное скрытое состояние ht и богатый контекст ct, модель выдаёт финальный прогноз:
![]()
Где f — это, как правило, полносвязный слой или другая выходная структура модели.
Архитектура DA-CG-LCTM не просто умна, она рассудительна. Модель не запоминает всё подряд, а делает осознанный выбор. Она не реагирует на каждый шум, а учится отличать вспышки от закономерностей. В задачах финансового прогнозирования это особенно важно. Система способна уловить сигналы, аналогичные прошлым, распознать их силу и скорректировать прогноз.
Таким образом, DA-CG-LSTM представляет собой живой, динамичный организм, который учится, адаптируется и делает выводы, опираясь на структурированный анализ информации. Её сила не только в формальных уравнениях, но и в концептуальной ясности:
Внимание + Память + Интерпретация = Осмысленный Прогноз
Авторская визуализация фреймворка DA-CG-LSTM представлена ниже.
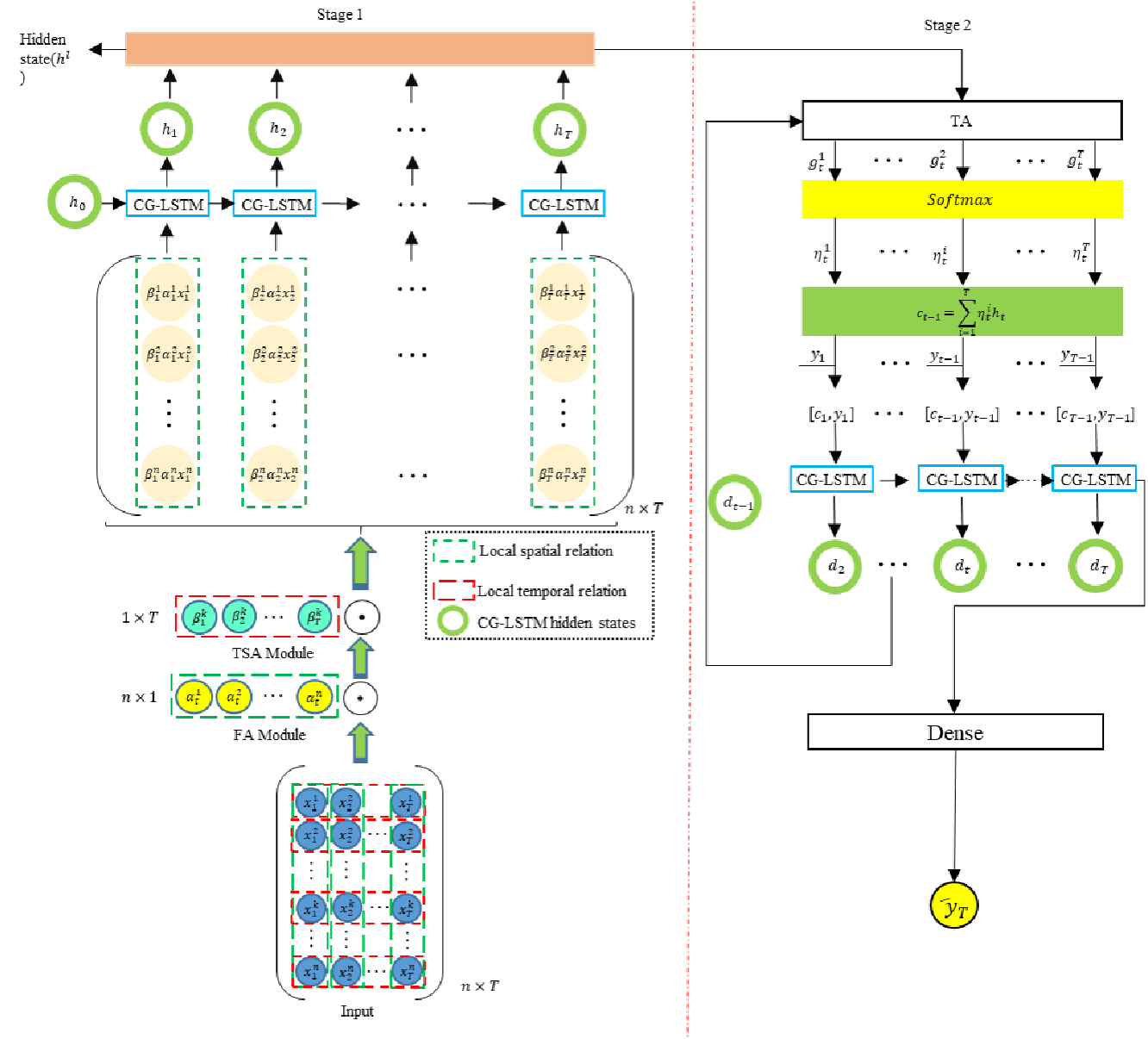
Реализация средствами MQL5
После рассмотрения теоретических аспектов фреймворка DA-CG-LSTM, мы переходим к практической части нашей работы, в которой рассмотрим вариант реализации собственного видения предложенных подходов средствами MQL5.
Свою работу мы начнем с построения модифицированного CG-LSTM блока, авторская визуализация которого представлена ниже.
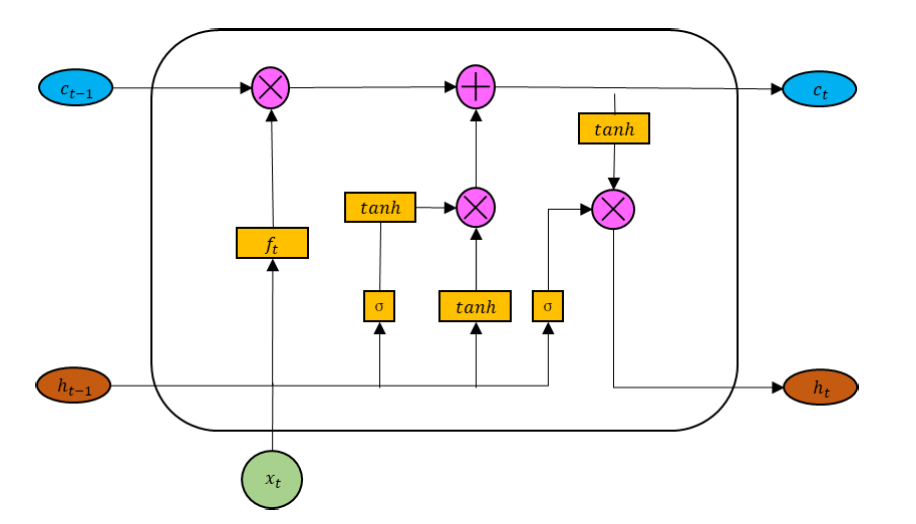
Здесь стоит обратить внимание, что аналогично классическому LSTM-блоку, тензор исходных данных конкатенируется со скрытым состоянием блока, сформированным на предыдущем временном шаге. Полученный тензор используется для формирования 4 сущностей: трех врат и представления нового контекста. Для формирования каждой из указанных сущностей используется линейный слой. Однако, результатам работы линейных слоев придается нелинейность путем использования различных функций активации.
Использование 4 различных функций активации при формировании отдельных сущностей приводит нас к необходимости создания 4 полносвязных слоев, вызов которых будет осуществляться последовательно. Согласитесь, это не лучший вариант. В своих работах мы стремимся найти пути максимальной параллелизации операций, что позволит ускорить процесс обучения моделей и принятия решений в условиях эксплуатации.
Для этого, при построении классического LSTM-блока, мы организовали весь процесс прямого прохода блока в рамках единого кернела. При этом, формирование значений каждой сущности осуществлялось в параллельных потоках рабочей группы с последующей передачей значений между путем сохранения данных в локальной памяти. Такая реализация подтвердила свою эффективность. Однако, при использовании более сложных последовательностей функций активации, предложенных авторами фреймворка DA-CG-LSTM, мы сталкиваемся с необходимостью создания дополнительных буферов данных для хранения промежуточных значений и общим усложнением алгоритма.
Поэтому, в рамках данной реализации, было принято решение использовать альтернативный подход. Для этого мы разделим процесс прямого прохода на 2 этапа. Вначале осуществим формирование данных всех 4 сущностей без функций активации. Здесь мы можем воспользоваться простым полносвязным или сверточным слоем, тензор результатов которого кратен количеству формируемых сущностей. В случае работы с многомерными исходными данными, использование сверточного слоя является предпочтительным, так как позволяет организовать независимые операции для отдельных унитарных последовательностей.
На втором этапе организовываем непосредственно работу CG-LSTM блока, применяя необходимые функции активации к полученным данным и выстраивая процессы внутри блока.
Думаю, очевидно, что работу мы начнем с реализации второго этапа на стороне OpenCL-контекста.
Изменение OpenCL-программы
Вначале мы организуем процесс прямого прохода нашего видения CG-LSTM блока в рамках кернела CSLSTM_FeedForward. В параметрах данного кернела мы получаем лишь указатели на 3 буфера данных.
Один из них содержит исходные данные (concatenated), в котором собраны значения четырёх компонент до применения функций активации. С целью минимизации задержки при обращении к глобальной памяти и ускорения чтения значений, данные в этом буфере представлены в формате float4 — векторном типе, позволяющем считывать сразу четыре последовательных элемента одним обращением. Такая организация обеспечивает более эффективное использование пропускной способности памяти и позволяет ускорить вычисления, особенно при обработке больших массивов исходных данных.
Два других буфера предназначены для сохранения контекста и результатов.
__kernel void CSLSTM_FeedForward(__global const float4* __attribute__((aligned(16))) concatenated, __global float *memory, __global float *output) { uint id = (uint)get_global_id(0); uint total = (uint)get_global_size(0); // hidden size uint idv = (uint)get_global_id(1); uint total_v = (uint)get_global_size(1); // variables
Функционирование данного керенела предполагается в двухмерном пространстве задач без создания рабочих групп. Первое измерение указывает размерность скрытого состояния ячейки, а второе — количество унитарных последовательностей в исходных данных. В теле кернела мы сразу идентифицируем поток во всех измерениях пространства задач.
На основании полученных данных определяем смещение в буферах данных и сразу считываем в локальную переменную соответсвующий блок исходных данных.
uint shift = id + total * idv;
float4 concat = concatenated[shift];
Затем, мы добавим необходимые функции активации ко всем сущностям.
float fg = 1 - Activation(1 - 1 / pow(Activation(concat.s0, ActFunc_SIGMOID), 2), ActFunc_TANH); float ig = Activation(Activation(concat.s1, ActFunc_SIGMOID), ActFunc_TANH); float nc = Activation(concat.s2, ActFunc_TANH); float og = Activation(concat.s3, ActFunc_SIGMOID);
После чего, обновим значения контекста и скрытого состояния.
float mem = IsNaNOrInf(memory[shift] * fg + ig * nc, 0); float out = IsNaNOrInf(og * Activation(mem, ActFunc_TANH), 0);
Полученные значения сохраним в соответствующие элементы глобальных буферов данных и завершаем работу кернела.
memory[shift] = mem;
output[shift] = out;
} Код кернела получился компактным и легко читаемым — во многом благодаря использованию вспомогательного метода выбора функции активации. Такое решение не только упрощает логику основного тела кернела, но и делает код более модульным и расширяемым. Кроме того, внедрение механизма проверки корректности получаемых значений повышает надёжность всей вычислительной цепочки.
После завершения работы с кернелом прямого прохода, мы переходим к построению процессов обратного прохода. Легко заметить, что в процессе прямого прохода не использовались обучаемые параметры. Все они вынесены в нейронный слой, используемый на первом этапе. Поэтому, для реализации операций обратного прохода, нам достаточно корректно распределить градиент ошибки между участниками процесса. Данные операции выполняются в кернеле CSLSTM_CalcHiddenGradient.
Параметры кернела распределения градиента ошибки дополняются соответствующими буферами, при этом сохраняем прежним пространство задач.
__kernel void CSLSTM_CalcHiddenGradient(__global const float4* __attribute__((aligned(16))) concatenated, __global float4* __attribute__((aligned(16))) grad_concat, __global const float* memory, __global const float* grad_output ) { uint id = get_global_id(0); uint total = get_global_size(0); uint idv = get_global_id(1); uint shift = id + total * idv;
В теле кернела идентифицируем текущий поток во всех измерениях пространства задач и сразу определяем смещение в буферах данных до соответствующих элементов.
Стоит обратить внимание, что вычисление производных сложных функций активации, предложенных авторами фреймворка DA-CG-LSTM, требует ряда промежуточных значений, которые мы не стали сохранять при выполнении операций прямого прохода. Очевидно, что их сохранение потребовало бы значительных ресурсов памяти. Да и обращение к глобальным буферам данных — довольно дорогая операция. Однако, благодаря тому, что основной объем матричных операций был вынесен во внутренний нейронный слой первого этапа, мы легко и довольно быстро можем вычислить необходимые значения на основании значений сущностей до функции активации.
С этой целью, мы считываем исходные данные до активации в локальную переменную и повторно вычисляем функции с сохранением промежуточных результатов в локальных переменных.
float4 concat = concatenated[shift]; // Pre-activation values for all 4 gates // --- Forward reconstruction of gates --- float fg_s = Activation(concat.s0, ActFunc_SIGMOID); float fg = 1.0f - Activation(1.0f - 1.0f / pow(fg_s, 2), ActFunc_TANH); // Forget gate (ft) float ig_s = Activation(concat.s1, ActFunc_SIGMOID); float ig = Activation(ig_s, ActFunc_TANH); // Input gate (it) float nc = Activation(concat.s2, ActFunc_TANH); // New content (ct~) float og = Activation(concat.s3, ActFunc_SIGMOID); // Output gate (ot) float mem = memory[shift]; // New memory state (ct) float mem_t = Activation(mem, ActFunc_TANH); // tanh(ct)
Тут же обратным счетом вычисляем значение памяти на предыдущем временном шаге.
// --- Reconstruct previous memory state (t-1) --- float prev_mem = IsNaNOrInf((mem - ig * nc) / fg, 0);
После завершения подготовительной работы, мы переходим непосредственно к операциям распределения градиента ошибки. Здесь мы сначала считаем значение градиента на выходе модуля из глобального буфера в локальную переменную.
// --- Gradients computation --- float out_g = grad_output[shift];
И распределим полученное значение между вратами результатов и памятью контекста с использованием производных соответствующих функций активации.
float og_g = Deactivation(out_g * mem_t, og, ActFunc_SIGMOID); float mem_g = Deactivation(out_g * og, mem_t, ActFunc_TANH);
Далее, мы распределим градиент ошибки памяти контекста между проекцией нового контекста и вратами исходных данных.
float nc_g = Deactivation(mem_g * ig, nc, ActFunc_TANH); float ig_g = Deactivation(Deactivation(mem_g * nc, ig, ActFunc_TANH), ig_s, ActFunc_SIGMOID);
Обратите внимание на этапы применения производных соответствующих функций активации при последовательном корректировании градиента ошибки врат исходных данных.
В завершении, нам остается спустить градиент ошибки до значения врат забвения до применения функции активации. Как было сказано выше, здесь авторы фреймворка DA-CG-LSTM предложили использовать довольно сложную функцию активации. Соответственно, распределять градиент ошибки мы будем в несколько этапов.
Вначале определим погрешность значения врат забвения, исходя из градиента ошибки памяти контекста и её предыдущего значения.
// ∂L/∂fg = ∂L/∂ct * mem_(t-1) float fg_g = mem_g * prev_mem;
Полученное значение скорректируем на производную функцию активации гиперболического тангенса и сложного внутреннего выражения.
// Derivative of the complex forget gate: // f(z) = 1 - tanh(1 - 1 / σ(z)^2) float fg_s_g = 2 / pow(fg_s, 3) * Deactivation(-fg_g, fg, ActFunc_TANH); fg_g = Deactivation(fg_s_g, fg_s, ActFunc_SIGMOID);
А затем, скорректируем на производную сигмоиды.
Полученные значения сохраним в соответствующие элементы глобального буфера данных.
// --- Write back gradients ---
grad_concat[shift] = (float4)(fg_g, ig_g, nc_g, og_g);
}
На этом мы завершаем работу на стороне OpenCL-программы. С полным её кодом вы можете самостоятельно ознакомиться во вложении.
Создание объекта CG-LSTM
Далее мы переходим к работе на стороне основной программы. Здесь создадим новый объект CNeuronCGLSTMOCL, в рамках которого и организуем работу нашего CG-LSTM блока. Структура нового объекта представлена ниже.
class CNeuronCGLSTMOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL cConcatenateInputs; CNeuronConvOCL cProjection; //--- virtual bool CSLSTM_feedForward(void); virtual bool CSLSTM_CalcHiddenGradient(void); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronCGLSTMOCL(void) {}; ~CNeuronCGLSTMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) override; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint count, uint window, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual int Type(void) override const { return defNeuronCGLSTMOCL; } virtual bool Clear(void) override; virtual CBufferFloat *getLSTMWeights(void) { return cProjection.GetWeightsConv(); } virtual void SetOpenCL(COpenCLMy *obj) override; virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; };
В представленной структуре нового класса мы видим привычный набор переопределяемых методов и 2 внутренних объекта, с функционалом которых познакомимся ближе в процессе реализации методов класса. Все внутренние объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Непосредственно инициализация объявленных и унаследованных объектов осуществляется в методе Init.
В параметрах метода инициализации мы получаем ряд констант, которые позволяют однозначно интерпретировать архитектуру создаваемого объекта.
bool CNeuronCGLSTMOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint count, uint window, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, count * variables, optimization_type, batch)) return false; SetActivationFunction(None);
Часть из полученных значений сразу передаем в одноименный метод родительского класса, где уже организованы процессы проверки полученных значений и инициализации унаследованных объектов.
Обратите внимание, что здесь же мы явным образом указываем отсутствие функции для создаваемого объекта.
После успешного выполнения операций метода родительского класса, переходим к подготовке работоспособности объявленных объектов. В данном случае, их всего 2. Один из них — полносвязный слой для записи конкатенированного тензора исходных данных и скрытого состояния последних операций прямого прохода.
if(!cConcatenateInputs.Init(0, 0, OpenCL, (count + window) * variables, optimization, iBatch)) return false; cConcatenateInputs.SetActivationFunction(None);
И здесь мы так же явным образом указываем отсутствие функции активации.
Вторым является сверточный слой проекции конкатенированного тензора на 4 сущности.
if(!cProjection.Init(0, 1, OpenCL, count + window, count + window, count * 4, 1, variables, optimization, iBatch)) return false; cProjection.SetActivationFunction(None);
Как обсуждалось ранее, данный слой не использует функцию активации, на что мы указываем явным образом.
Особого внимания заслуживает инициализация свёрточного слоя. При его создании, мы явно задаём длину последовательности равной единице. На первый взгляд это может показаться ограничением, однако, за этим решением стоит чёткая архитектурная идея: одновременно с этим мы указываем количество унитарных (независимых) последовательностей, которые будут обрабатываться параллельно.
Такой подход позволяет задать для каждой унитарной последовательности свой собственный набор обучаемых параметров — отдельную матрицу весов. Это обеспечивает полную независимость в их анализе и обучении. Каждая последовательность может обучаться в своём контексте, реагируя на специфические шаблоны и закономерности, не разделяя параметров с другими. В результате, мы получаем более выразительное, адаптивное и структурно гибкое представление исходных данных, особенно в задачах, где разные временные подпоследовательности несут различные смысловые функции или отражают поведение отдельных рыночных факторов.
Подобная изоляция параметров играет важную роль и в процессе обучения. Во-первых, она снижает взаимное влияние между каналами, что уменьшает переобучение на доминирующих паттернах. Во-вторых, каждая унитарная последовательность может сфокусироваться на собственных свойствах данных. Такой тип дифференцированного обучения делает модель не только точнее в конкретных задачах, но и гораздо более устойчивой к изменению рыночных условий.
Кроме того, независимое обучение унитарных фильтров способствует лучшему обобщению — модель реже запоминает данные и чаще — извлекает общие закономерности. Это особенно важно в финансовых временных рядах, где исторические данные могут содержать уникальные, нерепрезентативные события. За счёт декомпозиции процесса обучения на множественные изолированные ветви, модель становится способной распознавать типовые рыночные сигналы даже в новых, ранее не встречавшихся ситуациях.
И конечно, особенностью рекуррентных моделей является использование собственных данных предыдущего прямого прохода. Поэтому мы очистим все буферы данных и, лишь затем, завершаем работу метода инициализации.
if(!Clear()) return false; //--- return true; }
Следующим этапом нашей работы является построение процессов прямого прохода, которые мы организуем в рамках метода feedForward. Должен сказать, что здесь все довольно просто. В параметрах метода получаем указатель на объект исходных данных, актуальность которого мы сразу проверяем.
bool CNeuronCGLSTMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Затем, из параметров слоя проекции извлекаем размерности тензора исходных данных и скрытого состояния.
int hidden = (int)cProjection.GetFilters() / 4; int inputs = (int)cProjection.GetWindow() - hidden; int variables = (int)cProjection.GetVariables();
После чего, конкатенируем исходные данные с результатами предыдущего прямого прохода в разрезе унитарных последовательностей.
if(!Concat(NeuronOCL.getOutput(), getOutput(), cConcatenateInputs.getOutput(), inputs, hidden, variables)) return false;
Полученные значения проецируем на 4 сущности.
if(!cProjection.FeedForward(cConcatenateInputs.AsObject())) return false;
И теперь остается лишь вызвать метод-обертку постановки вышесозданного кернела прямого прохода в очередь выполнения CSLSTM_feedForward.
return CSLSTM_feedForward();
}
Методы постановки кернелов в очередь выполнения созданы по уже знакомой вам схеме. Поэтому, в рамках данной статьи, мы не будем останавливаться на детальном рассмотрении их алгоритма.
После завершения построения метода прямого прохода, переходим к реализации процессов обратного прохода. Как вы знаете, здесь процесс разделяется на 2 этапа: распределении градиента ошибки и оптимизации обучаемых параметров.
В данном случае, обучаемые параметры содержатся только в слое проекции конкатенированных данных. Следовательно, процесс оптимизации обучаемых параметров модели вырождается в вызов одноимённого метода проекции.
bool CNeuronCGLSTMOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return cProjection.UpdateInputWeights(cConcatenateInputs.AsObject()); }
Немного сложнее выглядит алгоритм метода распределения градиента ошибки между участниками процесса calcInputGradients. В параметрах метода получаем указатель на объект исходных данных. Это тот же объект, который мы анализировали в рамках прямого прохода. Только на этот раз, нам необходимо передать в него градиент ошибки в соответствии с влиянием исходных данных на итоговый результат работы модели.
bool CNeuronCGLSTMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
В теле метода сразу проверяем актуальность полученного указателя. Необходимость выполнения данной точки контроля уже много раз обсуждалась в предыдущих статьях.
Далее, аналогично методу прямого прохода, определяем размерности исходных данных и скрытого состояния.
int hidden = (int)cProjection.GetFilters() / 4; int inputs = (int)cProjection.GetWindow() - hidden; int variables = (int)cProjection.GetVariables();
Вначале мы распределим градиент ошибки между сущностями, путем вызова метода-обертки добавления в очередь выполнения соответствующего кернела.
if(!CSLSTM_CalcHiddenGradient()) return false;
Затем, опустим градиент ошибки до уровня конкатенированного тензора исходных данных.
if(!cConcatenateInputs.calcHiddenGradients(cProjection.AsObject())) return false;
И путем обратной конкатенации выделим градиент ошибки исходных данных.
if(!DeConcat(NeuronOCL.getGradient(), getPrevOutput(), cConcatenateInputs.getGradient(), inputs, hidden, variables)) return false;
Здесь стоит обратить внимание, что в процессе инициализации внутренних объектов мы намеренно отключили функции активации. Однако, это не исключает использование таковой для исходных данных. Поэтому мы проверяем наличие функции активации исходных данных и, при необходимости, корректируем полученные градиенты ошибки на производные соответствующих функций активации.
if(NeuronOCL.Activation() != None) if(!DeActivation(NeuronOCL.getOutput(), NeuronOCL.getGradient(), NeuronOCL.getGradient(), NeuronOCL.Activation())) return false; //--- return true; }
После чего, завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.
На этом мы завершаем рассмотрение алгоритмов построения метода нашего нового класса CNeuronCGLSTMOCL. С полным кодом данного класса и всех его методов можно ознакомиться во вложении.
Постепенно, незаметно даже для нас самих, мы подошли к пределу объёма текущей статьи. Однако, логическая завершённость этого исследования требует продолжения. Сделаем небольшую паузу. Продолжение следует — и оно будет не менее содержательным.
Заключение
В данной статье мы познакомились с теоретическими аспектами фреймворка DA-CG-LSTM. В отличие от традиционных моделей, его архитектура включает в себя несколько инновационных механизмов, таких как CG-LSTM и двойной механизм внимания, которые обеспечивают более глубокое и точное извлечение зависимостей в данных. Эти компоненты позволяют эффективно обрабатывать сложные временные зависимости и учитывать как долгосрочные, так и краткосрочные паттерны.
В практической части статьи мы представили свое видение реализации блока CG-LSTM средствами MQL5. Однако, наша работа ещё не завершена, и мы продолжим её в следующей статье, доведя до логического завершения.
Ссылки
- A Dual-Staged Attention Based Conversion-Gated Long Short Term Memory for Multivariable Time Series Prediction
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник офлайн обучения моделей |
| 4 | StudyOnline.mq5 | Советник | Советник онлайн обучения моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
 Разрабатываем мультивалютный советник (Часть 26): Информер для торговых инструментов
Разрабатываем мультивалютный советник (Часть 26): Информер для торговых инструментов
 Переосмысливаем классические стратегии в MQL5 (Часть III): Прогнозирование индекса FTSE 100
Переосмысливаем классические стратегии в MQL5 (Часть III): Прогнозирование индекса FTSE 100
 Реализация торговой стратегии на основе полос Боллинджера с помощью MQL5: Пошаговое руководство
Реализация торговой стратегии на основе полос Боллинджера с помощью MQL5: Пошаговое руководство
 Парный трейдинг: Алготорговля с автооптимизацией на разнице Z-оценки
Парный трейдинг: Алготорговля с автооптимизацией на разнице Z-оценки
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
И каковы точные параметры модели (размеры входных данных, число нейронов, оптимизатор)?