MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
Статистические распределения вероятностей в MQL5

Статистические распределения вероятностей в MQL5

MetaTrader 5 — Примеры | 25 марта 2011, 18:42
8 606 6
Denis Kirichenko
Denis Kirichenko

Вся теория вероятности зиждется на практике нежелательности.
(Леонид Сухоруков)

Введение

По роду своей деятельности трейдер вынужден очень часто сталкиваться с такими категориями, как вероятность и случайность. На другом полюсе относительно случайности находится такое понятие, как "закономерность". Удивительно, но в силу общефилософских законов, случайность, как правило, перерастает в закономерность. Об обратном пока говорить не будем. В общем, соотношение случайность-закономерность является ключевым, так как оно, в контексте рынка, непосредственно влияет на размер получаемой трейдером прибыли.

В данной статье я попытаюсь рассказать о теоретических базовых инструментах, которые в дальнейшем помогут находить некоторые рыночные закономерности.


1. Распределения, сущность, виды

Итак, для описания некоторой случайной величины нам потребуется одномерное статистическое распределение вероятностей. Оно будет описывать некоторую выборку случайных величин по определенному закону, т.е., чтобы применить какой-либо закон распределения, нам потребуется некоторое множество случайных величин.

Зачем нам анализировать [теоретические] распределения? С их помощью несложно выявлять закономерности изменения частот в зависимости от значений варьирующего признака. Кроме того, можно получить некоторые статистические параметры нужного распределения.

Что касается видов вероятностных распределений, то в специализированной литературе чаще всего принято разделять семейство распределений на непрерывные и дискретные, в зависимости от типа множества случайных величин. Однако, существуют и другие классификации, например, по таким критериям, как: симметричность кривой распределения f(x) относительно прямой x=x0, параметр сдвига, количество мод, интервал случайной величины и пр.

Есть несколько способов, позволяющих задать нам закон распределения. Среди них нужно отметить наиболее популярные:


2.  Теоретические распределения вероятностей

Итак, давайте в рамках MQL5 попробуем создать классы, описывающие статистические распределения. Кроме того, я хотел добавить, что в специализированной литературе есть много примеров кода, написанного на С++, который можно успешно применить для MQL5 кодирования. В общем, я не стал изобретать колесо, в некоторых случаях пользовался наработками С++ кода.

Самая большая сложность, с которой столкнулся, заключалась в отсутствии множественного наследования в MQL5. Поэтому сложные классовые иерархии использовать не удалось. Самым оптимальным источником в плане С++ кода стала книга Numerical Recipes: The Art of Scientific Computing [2], откуда было заимствовано мною большинство функций. Чаще всего, их приходилось дорабатывать под нужды MQL5.

2.1.1 Нормальное распределение

Традиционно, начнем с нормального распределения.

Нормальное распределение, также называемое гауссовским распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:


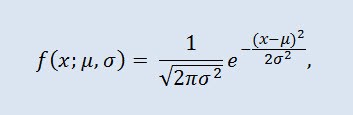
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.


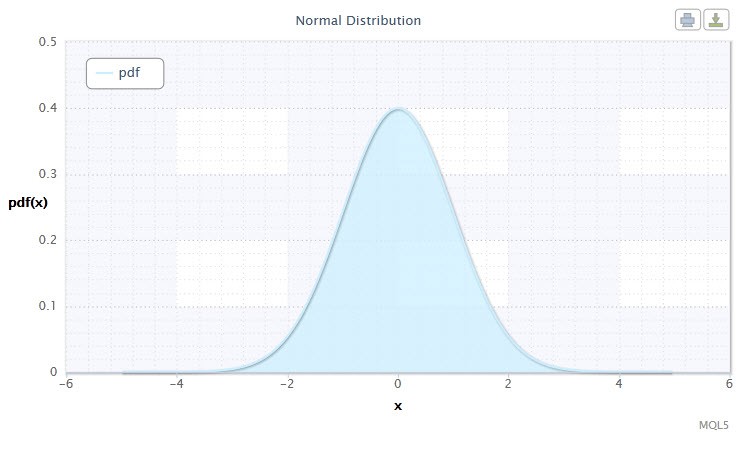
Рисунок 1. Плотность нормального распределения Nor(0,1)

Оно имеет следующую нотацию: X ~ Nor(μ, σ2), где:

  • X - это случайная величина, выбранная из нормального распределения Nor;
  • μ - параметр среднего (-∞ ≤ μ ≤ +∞);
  • σ - параметр дисперсии (0<σ).

Допустимый диапазон случайной величины X:  -∞ ≤ X ≤ +∞.

Формулы, использованные в статье, могут отличаться от аналогичных из прочих источников. Иногда такое различие математически непринципиально. В некоторых случаях оно обусловлено различной параметризацией.

Нормальное распределение играет большую роль в статистике, т.к. оно отражает закономерность, возникающую при взаимодействии множества случайных причин, ни одна из которых не имеет превалирующего влияния. И хотя нормальное распределение - это большая редкость на финансовых рынках, тем не менее, важно сравнивать с ним эмпирические распределения для выяснения меры и характера отклонения их от нормального.

Определим класс CNormaldist для нормального распределения следующим образом:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // наследование от класса Erf
  {
public:
   double            mu, //параметр среднего (μ)
   sig;                 //параметр дисперсии (σ)
   //+------------------------------------------------------------------+
   //| Конструктор класса CNormaldist                                   |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //параметры μ и σ по умолчанию
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Как можно заметить, класс CNormaldist является производным классом от базового класса СErf, который определяет в свою очередь класс функции ошибок. Он нам понадобится при расчете некоторых методов класса CNormaldist. Сам класс СErf и вспомогательная функция erfcc выглядят примерно так:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    //размер массива коэффициентов
   double            cof[28]; //массив коэффициентов Чебышева
   //+------------------------------------------------------------------+
   //| Конструктор класса CErf                                          |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//коэффициенты Чебышева
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-метод для ncof                                               |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Деструктор класса CErf                                           |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Функция ошибок                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Дополнительная функция ошибок                                    |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Аппроксимация функции ошибок по методам Чебышева                 |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Обратная дополнительная функция ошибок                           |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция ошибок                                          |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 дополнительная функция ошибок erfc(x) c
 относительной погрешностью 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+


2.1.2 Логнормальное распределение

Теперь давайте рассмотрим логнормальное распределение.

Логнормальное распределение в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то ее логарифм имеет нормальное распределение.


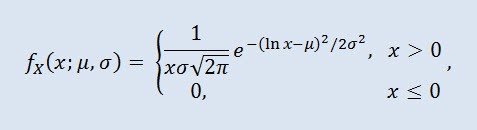
где μ - параметр сдвига (0<μ ), а σ - масштабный параметр (0<σ).


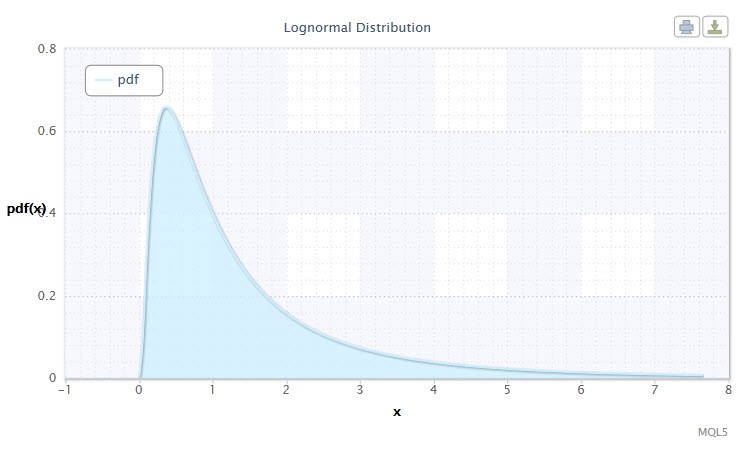
Рисунок 2. Плотность логнормального распределения  Logn(0,1)

Оно имеет следующую нотацию: X ~ Logn(μ, σ2), где:

  • X - это случайная величина, выбранная из логнормального распределения Logn;
  • μ - параметр сдвига (0<μ );
  • σ - масштабный параметр (0<σ).

Допустимый диапазон случайной величины X:  0 ≤ X ≤ +∞.

Создадим класс CLognormaldist, описывающий логнормальное распределение. Он будет представлен следующим образом:

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // наследование от класса Erf
  {
public:
   double            mu, //параметр сдвига (μ)
   sig;                 //масштабный параметр (σ)
   //+------------------------------------------------------------------+
   //| Конструктор класса CLognormaldist                                |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //параметры μ и σ по умолчанию
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Как можно заметить, логнормальное распределение мало чем отличается от нормального. Разница в том, что параметр x заменен на log(x). 


2.1.3 Распределение Коши

Распределе́ние Коши́ в теории вероятностей (также называемое в физике распределе́нием Ло́ренца и распределе́нием Бре́йта — Ви́гнера) — класс абсолютно непрерывных распределений. Случайная величина, имеющая распределение Коши, является стандартным примером величины, не имеющей математического ожидания и дисперсии. Плотность имеет вид:


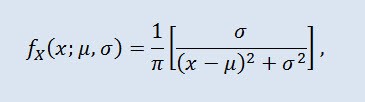
где μ - параметр сдвига (-∞ ≤ μ ≤ +∞ ), а σ - масштабный параметр (0<σ).

Распределение Коши имеет следующую нотацию: X ~ Cau(μ, σ), где:

  • X - это случайная величина, выбранная из распределения Коши Cau;
  • μ - параметр сдвига (-∞ ≤ μ ≤ +∞ );
  • σ - масштабный параметр (0<σ).

Допустимый диапазон случайной величины X:  -∞ ≤ X ≤ +∞.


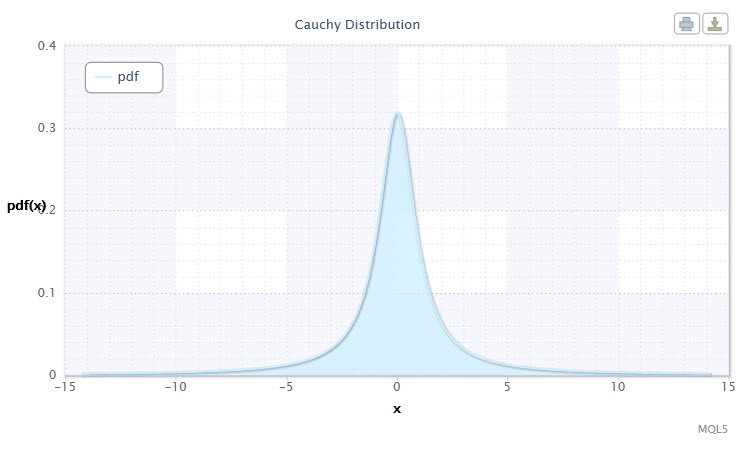
Рисунок 3. Плотность распределения Коши Cau(0,1)

В MQL5 формате, созданное с помощью класса CCauchydist, оно выглядит таким образом:

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//параметр сдвига (μ)
   sig;                 //параметр масштаба (σ)
   //+------------------------------------------------------------------+
   //| Конструктор класса CCauchydist                                   |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //параметры μ и σ по умолчанию
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Здесь нужно отметить, что используется функция atan2(), которая возвращает главное значение арктангенса, выраженное в радианах:

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function 
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }


2.1.4 Гиперболическое секанс распределение

Гиперболическое секанс распределение заинтересует тех, кто анализирует финансовые ряды.

Гиперболическое секанс распределение в теории вероятностей и статистике является непрерывным вероятностным распределением, чья функция плотности вероятности и характеристическая функция пропорциональны функции гиперболического секанса. Плотность задаётся согласно формуле:


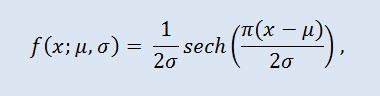
где μ - параметр сдвига (-∞ ≤ μ ≤ +∞ ), а σ - масштабный параметр (0<σ).



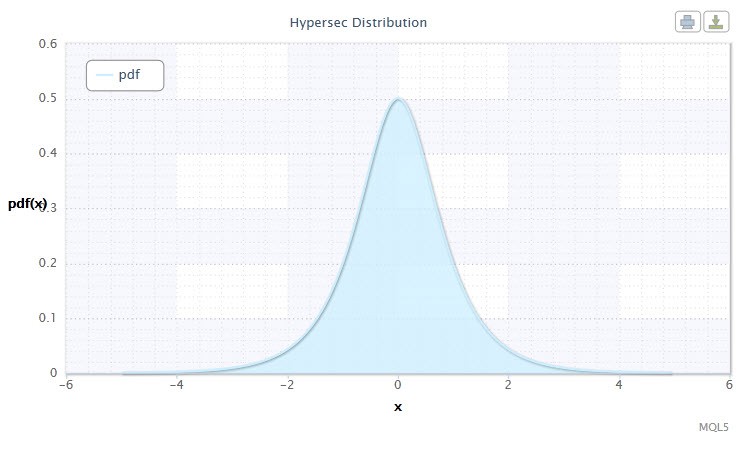
Рисунок 4. Плотность гиперболического секанс распределения HS(0,1)

Оно имеет следующую нотацию: X ~ HS(μ, σ), где:

  • X - это случайная величина;
  • μ - параметр сдвига (-∞ ≤ μ ≤ +∞ );
  • σ - масштабный параметр (0<σ).

Допустимый диапазон случайной величины X:  -∞ ≤ X ≤ +∞.

Опишем его следующим образом посредством класса CHypersecdist:

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| Конструктор класса CHypersecdist                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //параметры μ и σ по умолчанию
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Нетрудно заметить, что это распределение получило свое название от функции гиперболического секанса, функция плотности вероятности которого пропорциональна первой.

Функция гиперболического секанса sech выглядит так:

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }


2.1.5 Распределение Стьюдента

Важным распределением в статистике является распределение Стьюдента.

Распределе́ние Стью́дента в теории вероятностей — это чаще всего однопараметрическое семейство абсолютно непрерывных распределений. Однако, можно считать его и трёхпараметрическим распределением, которое задаётся функцией плотности распределения:


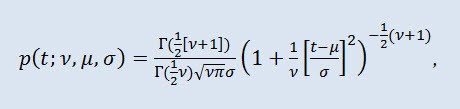
где Г - гамма-функция Эйлера, ν - это параметр формы (ν>0), μ - параметр сдвига (-∞ ≤ μ ≤ +∞ ), σ - масштабный параметр (0<σ).


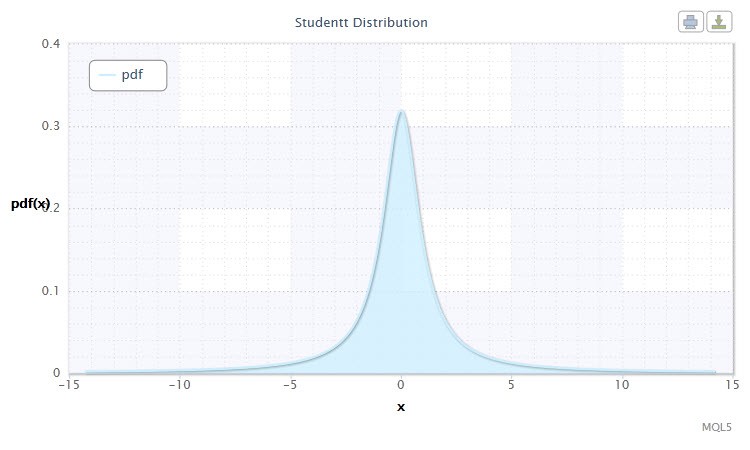
Рисунок 5. Плотность распределения Стьюдента Stt(1,0,1)

Оно имеет следующую нотацию: t ~ Stt(ν,μ,σ), где:

  • t - это случайная величина, выбранная из распределения Стьюдента Stt;
  • ν - это параметр формы (ν>0)
  • μ - параметр сдвига (-∞ ≤ μ ≤ +∞ );
  • σ - масштабный параметр (0<σ).

Допустимый диапазон случайной величины X:  -∞ ≤ X ≤ +∞.

Часто, особенно при тестировании гипотез, используется стандартизированное распределение Стьюдента, с параметрами μ=0 и  σ=1. Таким образом, оно превращается в однопараметрическое распределение с параметром ν.

Это распределение  используют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.

Представим его классом CStudenttdist:

//+------------------------------------------------------------------+
//|                Student-t Distribution class definition           |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // наследование от класса CBeta
  {
public:
   int               nu;     // параметр формы(ν)
   double            mu,     // параметр сдвига (μ)
   sig,                     // параметр масштаба (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| Конструктор класса CStudenttdist                                 |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //параметры ν, μ и σ по умолчанию
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Двусторонняя (интегральная) функция распределения                |
   //| The two-tailed cumulative distribution function (aa) A(t|ν)      |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Обратная двусторонняя (интегральная) функция распределения       |
   //| The inverse two-tailed cumulative distribution function (invaa)  |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

Из листинга класса CStudenttdist следует, что для него базовым классом является CBeta, который описывает неполную бета-функцию.

Класс CBeta представим следующим образом:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //когда использовать метод квадратур
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| Конструктор класса CBeta                                         |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| Set-метод класса CBeta                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

У класса так же есть свой базовый класс CGauleg18, который предоставляет коэффициенты для такого метода численного интегрирования, как квадратура Гаусса - Лежандра.


2.1.6 Логистическое распределение

Следующим для изучения распределением предлагаю считать логистическое.

В теории вероятностей и статистике логистическое распределение является непрерывным вероятностным распределением. Его функция распределения представляет собой логистическую функцию. По форме оно напоминает нормальное распределение, но имеет более тяжёлые хвосты. Плотность распределения:

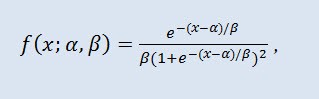
где α - параметр сдвига (-∞ ≤ α ≤ +∞ ), β - масштабный параметр (0<β).


Рисунок 6. Плотность логистического распределения Logi(0,1)

Оно имеет следующую нотацию: X ~ Logi(α,β), где:

  • X - это случайная величина;
  • α - параметр сдвига (-∞ ≤ α ≤ +∞ );
  • β - масштабный параметр (0<β).

Допустимый диапазон случайной величины X:  -∞ ≤ X ≤ +∞.

Класс CLogisticdist является реализацией описанного распределения:

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//параметр расположения (α)
   bet;                   //параметр масштаба (β)
   //+------------------------------------------------------------------+
   //| Конструктор класса CLogisticdist                                 |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //параметры μ и σ по умолчанию
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.7 Экспоненциальное распределение

Давайте также посмотрим на экспоненциальное распределение случайной величины.

Случайная величина X имеет экспоненциальное распределение с параметром λ > 0, если её плотность имеет вид:


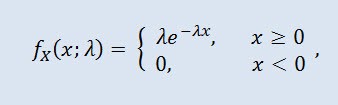
где λ - параметр масштаба (λ>0).


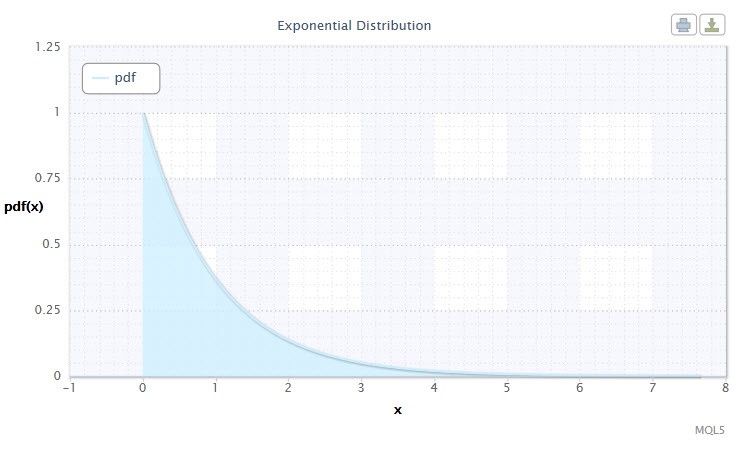
Рисунок 7. Плотность экспоненциального распределения Exp(1)

Оно имеет следующую нотацию: X ~ Exp(λ), где:

  • X - это случайная величина;
  • λ - параметр масштаба (λ>0).

Допустимый диапазон случайной величины X:  0 ≤ X ≤ +∞.

Это распределение интересно тем, что описывает последовательность событий, происходящих одно за другим в какие-то моменты времени. Так, с помощью этого распределения трейдер может анализировать убыточную серию сделок и пр.

В MQL5 коде распределение оформлено классом CExpondist:

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //параметр масштаба (λ)
   //+------------------------------------------------------------------+
   //| Конструктор класса CExpondist                                    |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //параметр λ по умолчанию
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.8 Гамма-распределение

Следующим видом непрерывного распределения случайной величины я избрал гамма-распределение. 

Га́мма распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр α принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга. Плотность имеет вид:

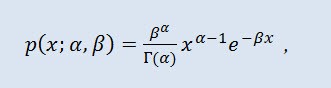
где Г - гамма-функция Эйлера, α - параметр формы (0<α), β - масштабный параметр (0<β).


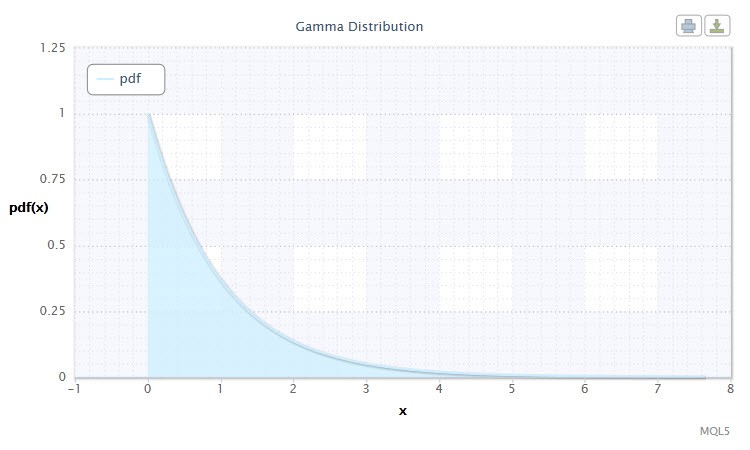
Рисунок 8. Плотность гамма-распределения Gam(1,1).

Его нотация выглядит следующим образом: X ~ Gam(α,β), где:

  • X - это случайная величина;
  • α - параметр формы (0<α);
  • β - масштабный параметр (0<β).

Допустимый диапазон случайной величины X:  0 ≤ X ≤ +∞.

В классовом варианте CGammadist оно представлено так:

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // наследование от класса CGamma
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| Конструктор класса CGammaldist                                   |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//параметры α и β по умолчанию
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Класс гамма-распределения является производным от класса CGamma, который , который описывает неполную гамма-функцию.

Класс CGamma представим следующим образом:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| Конструктор класса CGamma                                        |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //set-метод для CGamma
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Класс CGamma, как и класс CBeta, имеет базовым классом класс CGauleg18.


2.1.9 Бета-распределение

Ну и давайте также представим  бета-распределение.

Бе́та распределе́ние в теории вероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений. Используется для описания случайных величин, значения которых ограничены конечным интервалом. Плотность представлена таким образом:

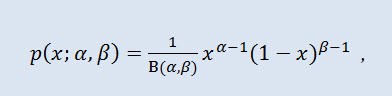
где B - бета-функция, α - 1-ый параметр формы (0<α), β - 2-ой параметр формы (0<β).


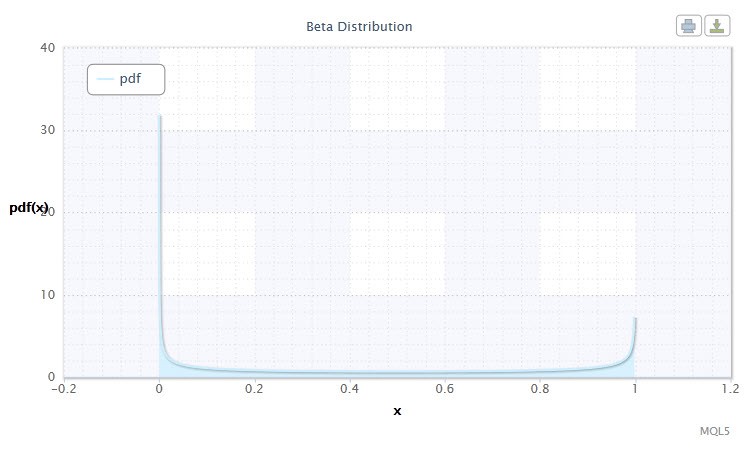
Рисунок 9. Плотность бета-распределения Beta(0.5,0.5)

Его нотация выглядит следующим образом: X ~ Beta(α,β), где:

  • X - это случайная величина;
  • α - 1-ый параметр формы (0<α);
  • β - 2-ой параметр формы (0<β).

Допустимый диапазон случайной величины X:  0 ≤ X ≤ 1.

Класс CBetadist характеризует это распределение так:

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // наследование от класса CBeta
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| Конструктор класса CBetadist                                     |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//параметры α и β по умолчанию
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.10 Распределение Лапласа

Еще одним интересным непрерывным распределением является распределение Лапласа (двойное экспоненциальное). 

Распределе́ние Лапла́са (двойно́е экспоненциа́льное) — в теории вероятностей это непрерывное распределение случайной величины, при котором плотность вероятности есть:

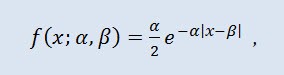
где α - параметр сдвига (-∞ ≤ α ≤ +∞ ), β - параметр масштаба (0<β).


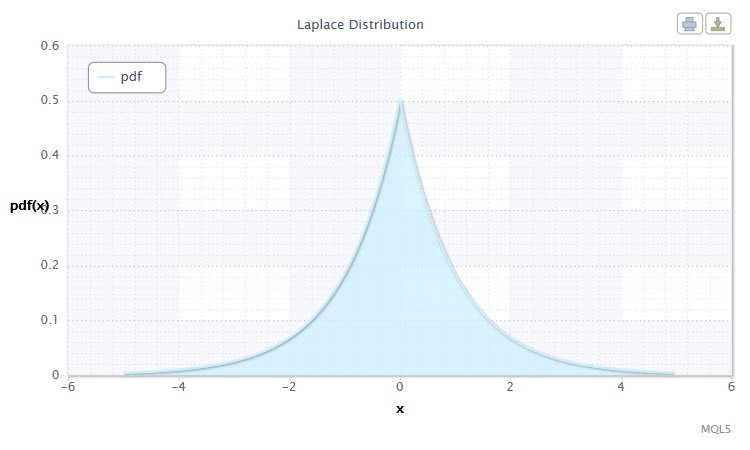
Рисунок 10. Плотность распределения Лапласа Lap(0,1)

Оно имеет такую нотацию: X ~ Lap(α,β), где:

  • X - это случайная величина;
  • α - параметр сдвига (-∞ ≤ α ≤ +∞ );
  • β - параметр масштаба (0<β).

Допустимый диапазон случайной величины X:  -∞ ≤ X ≤ +∞.

Класс CLaplacedist для распределения представим так:

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //параметр сдвига (α)
   double            bet;    //параметр масштаба (β)
   //+------------------------------------------------------------------+
   //| Конструктор класса CLaplacedist                                  |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //параметр α по умолчанию
      bet=1.;                //параметр β по умолчанию
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Итак, мы создали с помощью MQL5 кода 10 классов для десяти непрерывных распределений. Помимо этого, были созданы еще классы, которые, можно сказать, явились дополнительными, т.к. возникала необходимость в специфических функциях и методах (например, CBeta и CGamma).

Теперь я предлагаю заняться дискретными распределениями и создать несколько классов для этой категории распределений.


2.2.1 Биномиальное распределение

Давайте начнем с биномиального распределения.

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна . Плотность вероятности задаётся формулой:

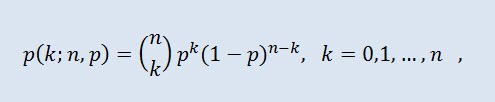
где  (n k) - биномиальный коэффициент, n - число испытаний (0 ≤ n), p - вероятность успеха (0 ≤ p ≤1).


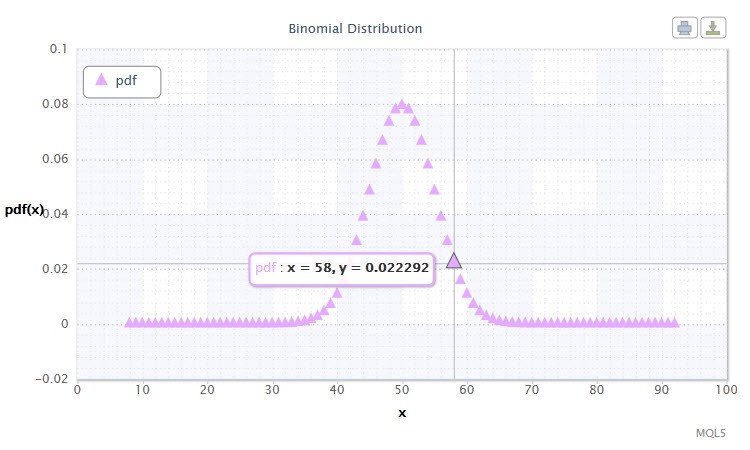
Рисунок 11. Плотность биномиального распределения Bin(100,0.5).

Его нотация выглядит следующим образом: k ~ Bin(n,p), где:

  • k - это случайная величина;
  • n - число испытаний (0 ≤ n);
  • p - вероятность успеха (0 ≤ p ≤1).

Допустимый диапазон случайной величины X:  0 или 1.

Не наводит вас на мысль диапазон возможных значений случайной величины X? Ведь совокупность выигрышных (1) и проигрышных сделок (0) торговой системы тоже можно анализировать с помощью этого распределения.

Создадим класс СBinomialdist следующим образом:

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // наследование от класса CBeta
  {
public:
   int               n;      //число испытаний
   double            pe,     //вероятность успеха
   fac;                      //множитель
   //+------------------------------------------------------------------+
   //| Конструктор класса CBinomialdist                                 |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//параметры n и pe по умолчанию
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+


2.2.2 Распределение Пуассона

Следующим станет распределение Пуассона.

Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Плотность имеет вид:

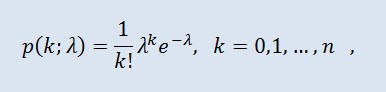
где k! - факториал, λ - параметр положения (0 < λ).


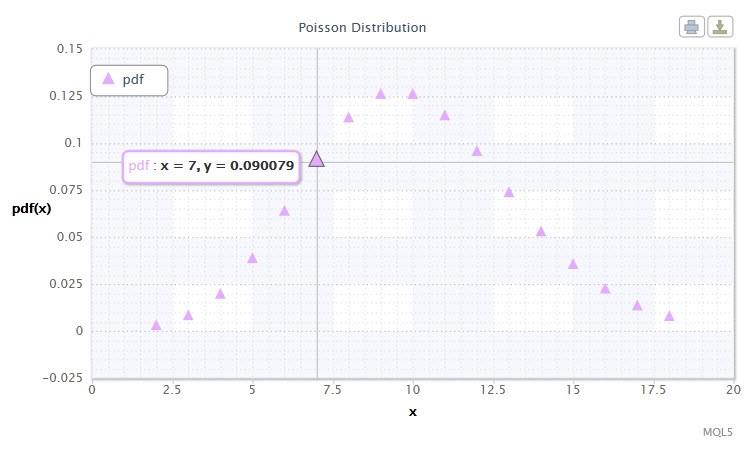
Рисунок 12. Плотность распределения Пуассона Pois(10).

Его нотация выглядит следующим образом: k ~ Pois(λ), где:

  • k - это случайная величина;
  • λ - параметр положения (0 < λ).

Допустимый диапазон случайной величины X:  0 ≤ X ≤ +∞.

Распределение Пуассона описывает "закон редких событий", что является важным моментом при определении степени риска.

Классом для распределения послужит CPoissondist:

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // наследование от класса CGamma
  {
public:
   double            lambda;   //параметр положения (λ)
   //+------------------------------------------------------------------+
   //| Конструктор класса CPoissondist                                  |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Функция плотности вероятности                                    |
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| (Интегральная) функция распределения                             |
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Обратная функция распределения(функция квантилей)                |
   //| Inverse cumulative distribution function (invcdf)                |
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Функция надежности (выживания)                                   |
   //| Survival function (sf)                                           |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

Естественно, в рамках одной статьи невозможно рассмотреть все статистические распределения, да и наверное, в этом нет необходимости. По желанию пользователь может расширить представленную галерею распределений. Созданные распределения находятся в файле Distribution_class.mqh.


3. Создание графиков распределений

Теперь предлагаю посмотреть, как мы можем использовать для дальнейшей работы наши созданные для распределений классы.

Тут я снова обратился к ООП и написал класс CDistributionFigure, который обрабатывает распределения определенных пользователем параметров и выводит его на экран средствами, описанными в статье "Графики и диаграммы в формате HTML". 

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //тип распределения
   Dist_mode         mode;  //вид распределения
   double            x;     //начало шага
   double            x11;   //левый предел
   double            x12;   //правый предел
   int               d;     //число точек
   double            st;    //шаг

public:
   double            xAr[]; //массив случайных величин
   double            p1[];  //массив вероятностей
   void              CDistributionFigure();  //конструктор 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-метод
   void              calculateDistribution(double nn,double mm,double ss); //расчет параметров распределения
   void              filesave(); //сохранение параметров распределения
  };
//+------------------------------------------------------------------+

Реализацию пропускаю. Отмечу, что в классе есть такие члены-данные, как type и mode, относящиеся к типам Dist_type и Dist_mode соответственно. Эти типы являются перечислениями изучаемых распределений и их видов.

Итак, попробуем наконец-то создать график какого-нибудь распределения.

Для непрерывных распределений я написал скрипт continuousDistribution.mq5, основные строки которого выглядят так:

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //левый предел
          Xx2,     //правый предел          
          st=0.05; //шаг
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //создание экземпляра класса CDistributionFigure 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Для дискретных распределений написан скрипт discreteDistribution.mq5.

Я запустил скрипт со стандартными параметрами для распределения Cauchy и получил следующий график, представленный на ролике ниже.




Заключение

В статье были представлены и закодированы в формате MQL5 некоторые теоретические распределения случайной величины. Считаю, что сама рыночная торговля, а значит, и работа торговой системы должна быть основана на фундаментальных вероятностных законах.

Надеюсь, что статья принесет практическую пользу для заинтересованных читателей. Я, со своей стороны, собираюсь развить эту тему и на практических примерах продемонстрировать, каким образом можно использовать статистические распределения вероятностей при анализе вероятностных моделей.


Расположение файлов:

 #  
Файл
 Путь
 Описание
 1
  Distribution_class.mqh
  %MetaTrader%\MQL5\Include  Галлерея классов распределений
 2  DistributionFigure_class.mqh            
 %MetaTrader%\MQL5\Include                           
 Классы графического отображения распределений            
 3  continuousDistribution.mq5   %MetaTrader%\MQL5\Scripts  Скрипт для создания непрерывного распределения     
 4
  discreteDistribution.mq5
   %MetaTrader%\MQL5\Scripts  Скрипт для создания дискретного распределения          
 5
  dataDist.txt
   %MetaTrader%\MQL5\Files  Данные для отображения распределения
 6
  Distribution_function.htm
   %MetaTrader%\MQL5\Files  HTML-график непрерывного распределения         
 7  Distribution_function_discr.htm          
  %MetaTrader%\MQL5\Files  HTML-график дискретного распределения                
 8  exporting.js
   %MetaTrader%\MQL5\Files  Java-скрипт для экспорта графика
 9  highcharts.js
   %MetaTrader%\MQL5\Files  JavaScript-библиотека
 10  jquery.min.js   %MetaTrader%\MQL5\Files  JavaScript-библиотека


Литература:

  1. K. Krishnamoorthy. Handbook of Statistical Distributions with Applications, Chapman and Hall/CRC 2006.
  2. W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing, Third Edition, Cambridge University Press: 2007. - 1256 pp.
  3. Булашев С.В. Статистика для трейдеров. - М.: Компания Спутник +, 2003. - 245 с.
  4. Гайдышев И. Анализ и обработка данных: специальный справочник - СПб: Питер, 2001. - 752 с.: ил.
  5. Кибзун А.И., Горяинова Е.Р. — Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами
  6. Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: Юнити-Дана, 2004. — 573 с.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (6)
Denis Kirichenko
Denis Kirichenko | 25 мар. 2011 в 19:40
Urain:

Очень интересно, спасибо, хрошая работа.

Спасибо за мнение.

Если не трудно добавьте вычисление распределения функции заданной таблично, чтоб было с чем сравнивать...

Уточните пожалуйста. Лучше на примере :-))

Ну и прицепом к нему, метод определения наибольшего подобия с теоретическими распределениями (это можно через коэф. корреляции).
В смысле?  В какой степени эмпирическое распределение отличается от теоретического?
Mykola Demko
Mykola Demko | 25 мар. 2011 в 19:46
denkir:

Спасибо за мнение.

1) Уточните пожалуйста. Лучше на примере :-))

2) В смысле?  В какой степени эмпирическое распределение отличается от теоретического?

1) Функция заданная таблично, значит что есть набор данных (например массив) где каждому x соответствует y, но не известна формула зависимости.

Такой функцией по сути есть котировки. И вот о вычислении распределения вероятностей таких данных я и говорю.

2) Да. На какое из теоретических распределений больше похоже эмпирическое. Или просто коэф корреляции эмпирического и теоретического.

Denis Kirichenko
Denis Kirichenko | 25 мар. 2011 в 23:30
Urain:

1) Функция заданная таблично, значит что есть набор данных (например массив) где каждому x соответствует y, но не известна формула зависимости.

Такой функцией по сути есть котировки. И вот о вычислении распределения вероятностей таких данных я и говорю.

Или я что-то недопонимаю или... обычно в табличной форме задаются уже известные теоретические распределения. Лично мне таблицы не очень нравятся. Мне на графике, так сказать, виднее... и форма распределения видна... В ролике, который приведён в статье, можно посмотреть, как меняются значения при перемещении курсора. И это только один из вариантов представления закона распределения... много нужно иметь таблиц, чтобы всё охватить... а график может...

2) Да. На какое из теоретических распределений больше похоже эмпирическое. Или просто коэф корреляции эмпирического и теоретического.

В заключении статьи я написал так:

Я, со своей стороны, собираюсь развить эту тему и на практических примерах продемонстрировать, каким образом можно использовать статистические распределения вероятностей при анализе вероятностных моделей.

Подробнее чуть позже.

Mykola Demko
Mykola Demko | 25 мар. 2011 в 23:41
denkir:

Или я что-то недопонимаю или... обычно в табличной форме задаются уже известные теоретические распределения. Лично мне таблицы не очень нравятся. Мне на графике, так сказать, виднее... и форма распределения видна... В ролике, который приведён в статье, можно посмотреть, как меняются значения при перемещении курсора. И это только один из вариантов представления закона распределения... много нужно иметь таблиц, чтобы всё охватить... а график может...

В заключении статьи я написал так:

Я, со своей стороны, собираюсь развить эту тему и на практических примерах продемонстрировать, каким образом можно использовать статистические распределения вероятностей при анализе вероятностных моделей.

Подробнее чуть позже.

Нет нет, рисовать аналитические (заданные в виде формулы) функции  как таблицу не нужно, я имел в виду создать метод(программную функцию) для расчёта распределения вероятности котировок. Котировки - это функция заданная таблично, те без знания формулы по которой происходит преобразование x в y.

ОК дождёмся продолжения.

Denis Kirichenko
Denis Kirichenko | 25 мар. 2011 в 23:58
Urain:

Нет нет, рисовать аналитические (заданные в виде формулы) функции  как таблицу не нужно, я имел в виду создать метод(программную функцию) для расчёта распределения вероятности котировок. Котировки - это функция заданная таблично, те без знания формулы по которой происходит преобразование x в y.

ОК дождёмся продолжения.

А, ну это называется подгонка под теоретическое распределение, если я точно уловил Вашу мысль... об этом в подробностях попозже... на практике по нескольким примерам... тем более, что при обсуждении моей статьи была жаркая полемика насчёт распределений :-)
Основы тестирования в MetaTrader 5 Основы тестирования в MetaTrader 5
В чем различия между тремя режимами тестирования в MetaTrader 5 и на что обратить внимание? Как происходит тестирование эксперта, торгующего одновременно на нескольких инструментах? Когда и как вычисляются значения индикаторов при тестировании и как обрабатываются события? Как синхронизировать бары с разных инструментов при тестировании в режиме "Только цены открытия"? Статья призвана дать ответы на эти и многие другие вопросы.
Индикаторы малой, промежуточной и основной тенденции Индикаторы малой, промежуточной и основной тенденции
Предметом статьи является исследование возможности автоматизации торговли и анализа на основании некоторых идей из книги Джеймса Хьержика "Модель, Цена и Время. Применение теории Ганна в системах торговли" в виде индикаторов и эксперта. Не претендуя на исчерпывающую полноту, здесь исследуется только первая часть теории Ганна - Модель.
Как заказать написание советника и получить желаемый результат Как заказать написание советника и получить желаемый результат
Как правильно написать Техническое Задание? Что можно и чего нельзя ожидать от программиста при заказе советника или индикатора? Как нужно вести диалог, на какие моменты обратить внимание? Статья дает ответы на эти и многие другие вопросы, которые зачастую неочевидны для многих без самостоятельного набивания шишек.
Уменьшаем расход памяти на вспомогательные индикаторы Уменьшаем расход памяти на вспомогательные индикаторы
Если индикатор для своих расчетов задействует значения множества других индикаторов, то такая система расходует много памяти. В статье рассмотрены несколько способов снижения расхода памяти при использовании вспомогательных индикаторов. Сэкономленная память позволит вам увеличить число одновременно используемых в терминале валютных пар, индикаторов и стратегий, что повысит надежность вашего торгового портфеля. Вот так простая забота о технических ресурсах вашего компьютера способна превратиться в материальные ресурсы на вашем депозите.