
Busca com restrições — Tabu Search (TS)
Conteúdo
Introdução
O algoritmo opera da seguinte forma: começa com a escolha de uma solução inicial e a exploração das soluções vizinhas, priorizando aquelas que melhoram o resultado atual. Para evitar retornar a soluções já exploradas sem sucesso, utiliza-se uma lista de restrições, que é uma estrutura que registra os movimentos "proibidos". Isso impede processos cíclicos e permite uma exploração mais eficiente do espaço de busca. No problema da mochila, por exemplo, o algoritmo pode alternar entre adicionar e remover itens para maximizar o valor total, evitando retornar a combinações já analisadas.
A base da busca tabu é a memória adaptativa, que não apenas impede retornos a soluções já encontradas, mas também orienta o processo de busca considerando os passos anteriores. Posteriormente, outros pesquisadores, como Manuel Laguna e Rafael Martí, expandiram significativamente sua aplicação em diversas áreas, como o planejamento de produção, a análise financeira e as telecomunicações. A busca tabu continua sendo uma ferramenta relevante para a solução de problemas combinatórios complexos que exigem análise profunda e cálculos intensivos.
Assim, a busca tabu é um excelente exemplo de como ideias inovadoras podem transformar métodos de otimização de busca, abrindo novas possibilidades para a ciência e a tecnologia. Embora o algoritmo tenha sido inicialmente projetado para resolver problemas combinatórios específicos, como o problema do caixeiro viajante e o problema da mochila, este artigo analisa uma modificação do algoritmo clássico que o torna capaz de resolver problemas de otimização mais gerais, incluindo aqueles em espaços contínuos de busca.
Implementação do algoritmo
Vamos analisar as fórmulas gerais e os mecanismos usados no algoritmo de busca tabu para resolver problemas de otimização combinatória (versão clássica do algoritmo):
1. Formulação geral do problema de otimização:
- Otimização de f(x) - função objetivo.
- x ∈ X, onde X é o conjunto de restrições sobre o vetor de variáveis x.
2. Vizinhança das soluções:
- N(x) - conjunto de soluções acessíveis a partir da solução atual x por meio de um único "movimento".
- N(x) - vizinhança modificada, que considera o histórico da busca (memória de curto e longo prazo).
3. Memória de curto prazo:
- Acompanhamento de atributos (características das soluções) que mudaram recentemente.
- Restrição para evitar visitar soluções que contenham atributos "tabu ativos".
4. Memória de longo prazo:
- Contagem da frequência de modificação/presença de atributos nas soluções visitadas.
- Uso dessas frequências para guiar a diversificação da busca.
5. Intensificação:
- Escolha do melhor movimento dentro da vizinhança modificada N(x).
- Retorno a regiões promissoras do espaço de soluções.
6. Diversificação:
- Escolha de movimentos que introduzam novos atributos não encontrados anteriormente.
- Exploração de regiões do espaço de busca diferentes das já analisadas.
7. Oscilações estratégicas:
- Alteração das regras de escolha de movimentos ao se aproximar de um "nível crítico".
- Transição através desse nível, seguida de um retorno subsequente.
8. Encadeamento de trajetórias:
- Geração de trajetórias que conectam soluções de alta qualidade.
- Escolha de movimentos que aproximem a solução atual das soluções-guia.
Para resolver problemas de otimização, deixaremos de lado o item 8 e focaremos na ideia central do algoritmo, tentando implementar uma modificação da busca tabu mantendo, sempre que possível, os itens 1-7. O algoritmo original opera com soluções discretas, buscando o caminho mais curto entre os nós. Para adaptá-lo a problemas em um espaço de busca contínuo, é necessário discretizar de alguma forma as regiões permitidas para cada parâmetro a ser otimizado. O problema é que não podemos marcar todas as soluções possíveis, pois a quantidade de marcas seria colossal, tornando a abordagem inviável.
Em vez da lista tabu, introduziremos os conceitos de "lista branca" e "lista negra" para cada parâmetro, dividindo seus intervalos em setores (um número pré-definido de setores para cada parâmetro a ser otimizado). Assim, poderemos adicionar uma "marca" à lista branca quando uma solução for bem-sucedida e marcar na lista negra se a solução não apresentar melhoria em relação ao passo anterior. Setores com soluções promissoras acumularão marcas, permitindo uma investigação mais detalhada da região e refinamento da solução. No entanto, um setor bem-sucedido pode conter também soluções extremamente ruins e, nesse caso, a marcação desse setor será incluída na lista negra. Isso significa que um mesmo setor pode conter tanto marcas na lista branca quanto na lista negra.
A seleção dos setores para gerar a próxima solução deve ocorrer de maneira que a probabilidade seja proporcional ao número de marcas na lista branca. Após gerar uma nova solução, verificamos o setor correspondente na lista negra e calculamos uma probabilidade proporcional à soma das marcas da lista negra em relação ao total de marcas das listas branca e negra. Se essa probabilidade for atendida, escolhemos outro setor selecionado aleatoriamente.
Dessa forma, considerando as características da superfície da função a ser otimizada, o algoritmo forma dinamicamente as probabilidades para explorar todas as áreas disponíveis no espaço de busca, sem se prender a um setor específico. Mesmo que o algoritmo esteja próximo da solução ótima global, ele não poderá melhorar os resultados indefinidamente. Isso, por sua vez, levará ao aumento das marcas na lista negra desse setor, forçando o algoritmo a mudar de setor e continuar a busca em outras áreas do hiperespaço.
A ideia desse método é garantir a diversificação no refinamento das soluções encontradas e uma ampla exploração do problema. Além disso, deve minimizar o número de parâmetros externos do algoritmo, proporcionando-lhe propriedades de autoadaptação à função do problema em questão.
Destacamos os principais pontos da ideia da implementação modificada da busca tabu clássica:
1. Discretização. A divisão do espaço de busca em setores permite uma exploração mais eficiente das regiões.
2. Listas branca e negra. Soluções bem-sucedidas e malsucedidas são registradas separadamente, garantindo um rastreamento dinâmico da viabilidade dos setores.
3. Exploração dinâmica. O algoritmo forma probabilidades para explorar todas as áreas disponíveis, evitando ficar preso em setores ineficientes.
4. Adaptabilidade. O algoritmo responde ao acúmulo de marcas na lista negra, o que o força a mudar de direção na busca e a garantir diversificação.
Assim, nossa versão do algoritmo combina elementos da busca tabu e de algoritmos evolucionários. Ele utiliza um mecanismo de memória, na forma de listas negras e brancas, para direcionar a busca para áreas promissoras do espaço de soluções e evitar regiões que resultaram em um pior desempenho.
Para maior clareza, vamos representar esquematicamente as listas branca e negra de setores para cada coordenada. Consideremos, por exemplo, três coordenadas, cada uma dividida em quatro setores. As listas branca e negra são registradas separadamente para cada coordenada.
Por exemplo, para a coordenada "0", o setor "3" na lista branca contém cinco marcas, o maior número entre todos os setores dessa coordenada. Isso significa que esse setor será escolhido com maior probabilidade na próxima iteração. No entanto, o mesmo setor possui seis marcas na lista negra, o que aumenta a probabilidade de ser substituído ao gerar uma nova solução, apesar de ser considerado o mais promissor. Assim, pode ocorrer uma situação em que um setor com menor potencial tenha menos chance de ser substituído por outro durante a seleção (o que pode não ser óbvio à primeira vista).
Como podemos ver, há um reequilíbrio constante das probabilidades ao longo da exploração do espaço de busca, o que permite levar em conta as características da superfície. Essa abordagem parece bastante promissora, pois depende minimamente dos parâmetros externos do algoritmo, tornando-o verdadeiramente autoadaptável.
0: |0)____VVV_____|1)____VV______|2)_____V______|3)____VVVVV____| 1: |0)_____VV_____|1)_____V______|2)____VVV_____|3)_____VVV_____| 2: |0)______V_____|1)____VVV_____|2)_____V______|3)_____VVV_____| 0: |0)_____ХХХ____|1)_____ХХ_____|2)_____XX_____|3)____XXXXXX___| 1: |0)______X_____|1)_____XXX____|2)____XXXXX___|3)______X______| 2: |0)_____XX_____|1)_____XXXX___|2)______X_____|3)____XXXXX____|
Agora podemos apresentar o pseudocódigo da versão modificada do algoritmo, que chamaremos de TSm:
1. Inicialização da população:
Para cada agente na população:
Atribuímos coordenadas aleatórias dentro do intervalo especificado.
Definimos o valor inicial da aptidão anterior como o mínimo possível.
2. Laço principal do algoritmo:
Enquanto a condição de término não for atingida, repetimos:
a) Se for a primeira iteração:
Executamos a inicialização da população.
b) Caso contrário:
Geramos novas coordenadas para os agentes:
Para cada agente e cada coordenada:
Com uma determinada probabilidade, copiamos a coordenada da melhor solução conhecida.
Caso contrário:
Selecionamos um setor da lista branca do agente.
Geramos uma nova coordenada dentro desse setor.
Se o setor escolhido estiver na lista negra, selecionamos um setor aleatório e geramos uma coordenada nele.
Garantimos que a nova coordenada não ultrapasse os limites do intervalo permitido.
c) Avaliamos a aptidão de cada agente com as novas coordenadas.
d) Atualizamos as listas branca e negra:
Para cada agente:
Comparamos a aptidão atual com a anterior.
Se a aptidão tiver melhorado, aumentamos o contador na lista branca para o setor correspondente.
Se a aptidão piorar, aumentamos o contador na lista negra.
Armazenamos a aptidão atual como a anterior para a próxima iteração.
d) Atualizamos a melhor solução encontrada caso um agente com aptidão superior seja identificado.
3. Ao final do ciclo, retornamos a melhor solução encontrada.
Agora, passamos à implementação do código. Descreveremos duas estruturas: S_TSmSector e S_TSmAgent, que são utilizadas para gerenciar setores e agentes na estratégia de busca.
1. S_TSmSector - essa estrutura contém um array de números inteiros sector [], que armazenará as marcas correspondentes ao setor (basicamente, um array de contadores).
2. S_TSmAgent - essa estrutura é mais complexa e representa um agente de busca no algoritmo.
- blacklist [] – array das listas negras organizadas por setor para cada coordenada.
- whitelist [] – array das listas brancas organizadas por setor para cada coordenada.
- fPrev – variável que armazena o valor da aptidão anterior do agente.
O método Init inicializa uma instância de S_TSmAgent. Parâmetros:
- coords – número de coordenadas.
- sectorsPerCord – número de setores por coordenada.
Lógica:
1. Redimensionamos os arrays blacklist e whitelist para corresponder ao número de coordenadas.
2. Inicializamos cada setor em um laço para todas as coordenadas:
- Redimensionamos o array sector para a lista negra da coordenada atual.
- Fazemos o mesmo para a lista branca.
- Inicializamos todos os elementos das listas branca e negra com zeros (são contadores que serão incrementados posteriormente).
3. Inicialização de fPrev – define fPrev como -DBL_MAX, representando o menor valor possível. Isso indica que o agente ainda não possui uma aptidão definida.
Esse código cria a estrutura de um agente capaz de gerenciar as listas negra e branca para setores em diferentes dimensões do espaço de busca, rastreando os setores permitidos e proibidos para os agentes visitarem.
//—————————————————————————————————————————————————————————————————————————————— struct S_TSmSector { int sector []; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— struct S_TSmAgent { S_TSmSector blacklist []; //black list by sectors of each coordinate S_TSmSector whitelist []; //white list by sectors of each coordinate double fPrev; //previous fitness void Init (int coords, int sectorsPerCord) { ArrayResize (blacklist, coords); ArrayResize (whitelist, coords); for (int i = 0; i < coords; i++) { ArrayResize (blacklist [i].sector, sectorsPerCord); ArrayResize (whitelist [i].sector, sectorsPerCord); ArrayInitialize (blacklist [i].sector, 0); ArrayInitialize (whitelist [i].sector, 0); } fPrev = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Agora, descreveremos a classe C_AO_TSm, que herda da classe base C_AO.
1. O construtor define os valores iniciais das variáveis:
- popSize (tamanho da população) é definido como 50.
- sectorsPerCoord (número de setores por coordenada) é definido como 100.
- bestProbab (probabilidade de escolha da melhor solução) é definida como 0.8.
- Cria e inicializa o array params com três parâmetros que correspondem às variáveis mencionadas acima.
2. O método SetParams define os valores dos parâmetros do array params de volta às variáveis correspondentes da classe.
3. O método Init inicializa o algoritmo com os intervalos e os passos de busca especificados.
4. Moving() – este método é responsável por movimentar os agentes no espaço de busca, enquanto Revision() executa a verificação e atualização das soluções atuais, utilizando a lógica da busca tabu.
5. Membros da classe:
- S_Agent agents [] – array de agentes que representam as soluções do problema durante o processo de busca.
6. Métodos privados:
- InitializePopulation() – método para inicializar a população de agentes.
- UpdateLists() – método para atualizar as listas negra e branca dos setores para os agentes.
- GenerateNewCoordinates() – método para gerar novas coordenadas durante a busca.
- GetSectorIndex() – método para obter o índice do setor com base na coordenada e dimensão.
- ChooseSectorFromWhiteList() – método para selecionar um setor da lista branca para um determinado agente e dimensão.
- GenerateCoordInSector() – método para gerar uma coordenada dentro de um setor especificado.
- IsInBlackList() – método para verificar a execução da probabilidade de escolha de outro setor, considerando a influência das listas branca e negra.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_TSm : public C_AO { public: //-------------------------------------------------------------------- C_AO_TSm () { ao_name = "TSm"; ao_desc = "Tabu Search M"; ao_link = "https://www.mql5.com/en/articles/15654"; popSize = 50; sectorsPerCoord = 100; bestProbab = 0.8; ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "sectorsPerCoord"; params [1].val = sectorsPerCoord; params [2].name = "bestProbab"; params [2].val = bestProbab; } void SetParams () { popSize = (int)params [0].val; sectorsPerCoord = (int)params [1].val; bestProbab = params [2].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- int sectorsPerCoord; double bestProbab; S_TSmAgent agents []; private: //------------------------------------------------------------------- void InitializePopulation (); void UpdateLists (); void GenerateNewCoordinates (); int GetSectorIndex (double coord, int dimension); int ChooseSectorFromWhiteList (int agentIndex, int dimension); double GenerateCoordInSector (int sectorIndex, int dimension); bool IsInBlackList (int agentIndex, int dimension, int sectorIndex); }; //——————————————————————————————————————————————————————————————————————————————
Agora, vamos analisar o método Init da classe C_AO_TSm, que é responsável por inicializar o algoritmo de busca tabu. Vamos detalhá-lo por partes:
1. O método primeiro chama StandardInit, passando arrays de valores mínimos, máximos e passos. Essa inicialização padrão define os parâmetros do algoritmo. Em seguida, o tamanho do array agents é ajustado com base no valor de popSize, que determina o número de agentes na população. Depois, um laço percorre cada agente no array agents. Para cada agente, o método Init é chamado, inicializando seus parâmetros, como as coordenadas (coords) e o número de setores por coordenada (sectorsPerCoord).
2. Se todas as etapas de inicialização forem concluídas com sucesso, o método retorna true, indicando que a inicialização do algoritmo foi bem-sucedida.
O método Init é fundamental para preparar o algoritmo de busca tabu para a execução. Ele define os intervalos de busca, inicializa o array de agentes e os prepara para a busca de soluções. Se ocorrer um erro em qualquer etapa da inicialização, o método interrompe a execução e retorna false.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSm::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agents, popSize); for (int i = 0; i < popSize; i++) agents [i].Init (coords, sectorsPerCoord); return true; } //——————————————————————————————————————————————————————————————————————————————
Agora, vejamos o método Moving da classe C_AO_TSm. A lógica do método é a seguinte:
- if (!revision) – verifica a variável lógica revision. Se for false (ou seja, a inicialização ainda não foi concluída), o próximo bloco de código será executado.
- InitializePopulation() – inicializa a população de agentes.
Nas iterações subsequentes do algoritmo, o método GenerateNewCoordinates() é chamado, gerando novas coordenadas (novas soluções) para os agentes durante o processo de busca.
O método Moving gerencia o processo de movimentação dos agentes no algoritmo de busca tabu. Primeiro, ele verifica se a população foi inicializada. Caso contrário, inicializa a população; caso contrário, o método gera novas coordenadas para os agentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::Moving () { //---------------------------------------------------------------------------- if (!revision) { InitializePopulation (); revision = true; return; } //---------------------------------------------------------------------------- GenerateNewCoordinates (); } //——————————————————————————————————————————————————————————————————————————————
O método Revision é responsável por atualizar a melhor solução encontrada durante a busca tabu. Ele percorre todas as soluções na população, compara suas avaliações com o melhor valor encontrado até o momento e, caso encontre uma solução melhor, atualiza as variáveis correspondentes. Ao final do método, as listas branca e negra são atualizadas, o que é essencial para a continuidade do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::Revision () { //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c); } } //---------------------------------------------------------------------------- UpdateLists (); } //——————————————————————————————————————————————————————————————————————————————
O próximo método, InitializePopulation, é responsável por inicializar a população de agentes da busca tabu. Ele gera valores aleatórios para cada coordenada dos agentes dentro dos intervalos especificados e define um valor inicial para a avaliação anterior de cada um. Isso é fundamental para as iterações subsiguientes do algoritmo, nas quais ocorrerá a avaliação e a atualização das soluções.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::InitializePopulation () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } agents [i].fPrev = -DBL_MAX; } } //——————————————————————————————————————————————————————————————————————————————
Agora, vejamos o método UpdateLists da classe C_AO_TSm. A lógica do método é a seguinte:
- O laço externo percorre todos os agentes da população, onde popSize representa o tamanho da população.
- O laço interno percorre todas as coordenadas de cada agente.
- Para cada coordenada c do agente a[i], o índice do setor é calculado utilizando o método GetSectorIndex. Isso é necessário para classificar os valores em setores específicos para análise posterior.
- Se a avaliação atual do agente a[i].f for maior que sua avaliação anterior agents[i].fPrev, significa que o agente melhorou sua solução. Nesse caso, o contador correspondente na lista branca (whitelist) é incrementado para esse setor.
- Se a avaliação atual for menor que a anterior, significa que a solução piorou, e o contador correspondente na lista negra (blacklist) para esse setor é incrementado.
- Após processar todas as coordenadas do agente, sua avaliação anterior é atualizada para o valor atual, para que na próxima iteração possa ser comparada com o novo valor.
O método UpdateLists é responsável por atualizar as listas branca e negra para cada agente da população, com base em suas avaliações atuais e anteriores. Isso permite que o algoritmo de busca tabu rastreie quais setores foram bem-sucedidos (lista branca) e quais foram ineficazes (lista negra). Assim, esse método auxilia no gerenciamento do processo de busca de soluções, evitando a revisitação de áreas ineficientes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::UpdateLists () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { int sectorIndex = GetSectorIndex (a [i].c [c], c); if (a [i].f > agents [i].fPrev) { agents [i].whitelist [c].sector [sectorIndex]++; } else if (a [i].f < agents [i].fPrev) { agents [i].blacklist [c].sector [sectorIndex]++; } } agents [i].fPrev = a [i].f; } } //——————————————————————————————————————————————————————————————————————————————
Agora, analisemos o método GenerateNewCoordinates da classe C_AO_TSm. A lógica do método é a seguinte:
- O laço externo percorre todos os agentes da população, onde popSize representa o tamanho da população.
- O laço interno percorre todas as coordenadas de cada agente.
- Primeiro, a probabilidade é verificada utilizando o método RNDprobab. Se a probabilidade for satisfeita, o agente recebe a coordenada do melhor resultado global conhecido cB[c].
- Se a probabilidade não for satisfeita, um setor é escolhido a partir da lista branca usando o método ChooseSectorFromWhiteList().
- Em seguida, uma nova coordenada é gerada dentro desse setor utilizando o método GenerateCoordInSector().
- Se o setor selecionado estiver na lista negra, um novo setor é escolhido aleatoriamente utilizando u.RNDminusOne(), e nele é gerada uma nova coordenada.
- Por fim, verifica-se se a nova coordenada está dentro dos limites especificados e segue o passo requerido.
O método GenerateNewCoordinates é responsável por gerar novas coordenadas para cada agente da população. Ele usa um método probabilístico para escolher as melhores coordenadas conhecidas entre todas e gerá-las aleatoriamente em setores, com base nas listas branca e negra. Além disso, o método garante a correção das coordenadas, verificando se elas estão dentro dos limites estabelecidos.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_TSm::GenerateNewCoordinates () { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < bestProbab) { a [i].c [c] = cB [c]; } else { int sectorIndex = ChooseSectorFromWhiteList (i, c); double newCoord = GenerateCoordInSector (sectorIndex, c); if (IsInBlackList (i, c, sectorIndex)) { sectorIndex = u.RNDminusOne (sectorsPerCoord); newCoord = GenerateCoordInSector (sectorIndex, c); } newCoord = u.SeInDiSp (newCoord, rangeMin [c], rangeMax [c], rangeStep [c]); a [i].c [c] = newCoord; } } } } //——————————————————————————————————————————————————————————————————————————————
Agora, analisemos a função GetSectorIndex, que determina o índice do setor para uma coordenada específica em um determinado eixo. A lógica da função é a seguinte:
- Se os valores máximo e mínimo do intervalo para esse eixo forem iguais, significa que o intervalo não tem comprimento. Nesse caso, a função retorna imediatamente o valor 0, pois não é possível dividir o intervalo em setores.
- Em seguida, calcula-se o comprimento de um setor sL, obtido ao dividir o comprimento do intervalo pelo número de setores sectorsPerCoord.
- O índice do setor ind é determinado por uma fórmula que calcula em qual setor a coordenada está localizada. Primeiro, subtrai-se o valor mínimo do intervalo da coordenada; depois, o resultado é dividido pelo comprimento do setor, e o valor obtido é arredondado para o número inteiro mais próximo.
- Se a coordenada for igual ao valor máximo do intervalo, a função retorna o índice do último setor.
- Por fim, verificações garantem que o índice não ultrapasse os valores permitidos. Se o índice for maior ou igual ao número de setores, o último setor é retornado. Se o índice for menor que 0, o valor retornado é 0.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_TSm::GetSectorIndex (double coord, int dimension) { if (rangeMax [dimension] == rangeMin [dimension]) return 0; double sL = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord; int ind = (int)MathFloor ((coord - rangeMin [dimension]) / sL); // Special handling for max value if (coord == rangeMax [dimension]) return sectorsPerCoord - 1; if (ind >= sectorsPerCoord) return sectorsPerCoord - 1; if (ind < 0) return 0; return ind; } //——————————————————————————————————————————————————————————————————————————————
Agora passamos ao método ChooseSectorFromWhiteList, que seleciona um setor da lista branca de setores para um determinado agente e dimensão. O método retorna o índice do setor escolhido. A lógica do método é a seguinte:
- A variável totalCount é inicializada com o valor zero. Ela é utilizada para contar o número total de marcas nos setores da lista branca.
- Se totalCount for igual a zero, significa que os setores ainda não contêm marcas e todos são equivalentes. Nesse caso, o método escolhe aleatoriamente um setor entre todos os disponíveis e o retorna.
- Em seguida, dentro de um laço, ocorre a contagem acumulativa das marcas. Se o valor aleatório randomValue for menor ou igual ao valor acumulado atual, o método retorna o índice do setor atual, s, o que permite que a escolha do setor seja proporcional ao seu peso na lista branca.
O método ChooseSectorFromWhiteList permite que o agente selecione um setor da lista branca com base em uma distribuição probabilística, simulando um processo de seleção por roleta.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_TSm::ChooseSectorFromWhiteList (int agentIndex, int dimension) { int totalCount = 0; for (int s = 0; s < sectorsPerCoord; s++) { totalCount += agents [agentIndex].whitelist [dimension].sector [s]; } if (totalCount == 0) { int randomSector = u.RNDminusOne (sectorsPerCoord); return randomSector; } int randomValue = u.RNDminusOne (totalCount); int cumulativeCount = 0; for (int s = 0; s < sectorsPerCoord; s++) { cumulativeCount += agents [agentIndex].whitelist [dimension].sector [s]; if (randomValue <= cumulativeCount) { return s; } } return sectorsPerCoord - 1; } //——————————————————————————————————————————————————————————————————————————————
Agora, analisemos o método GenerateCoordInSector, que gera uma coordenada aleatória dentro de um setor específico para uma dimensão determinada. A lógica do método é a seguinte:
- O tamanho do setor para a dimensão especificada é calculado.
- sectorStart é determinado como o valor mínimo do intervalo para a dimensão mais um deslocamento, que corresponde ao índice do setor multiplicado pelo tamanho do setor. sectorEnd é calculado como sectorStart mais sectorSize, definindo os limites do setor.
- Em seguida, a função RNDfromCI é chamada para gerar um valor aleatório dentro do intervalo de sectorStart até sectorEnd. Esse valor representa a coordenada gerada dentro do setor especificado.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_TSm::GenerateCoordInSector (int sectorIndex, int dimension) { double sectorSize = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord; double sectorStart = rangeMin [dimension] + sectorIndex * sectorSize; double sectorEnd = sectorStart + sectorSize; double newCoord = u.RNDfromCI (sectorStart, sectorEnd); return newCoord; } //——————————————————————————————————————————————————————————————————————————————
Por fim, analisemos o método IsInBlackList, que verifica se um agente está na lista negra para um determinado setor e dimensão. Parâmetros:
- agentIndex – índice do agente a ser verificado.
- dimension – índice da dimensão.
- sectorIndex – índice do setor que está sendo avaliado.
O método retorna true se o agente estiver na lista negra e se a probabilidade de troca de setor, considerando o "histórico" do setor na lista branca, for satisfeita.
- blackCount e whiteCount armazenam a quantidade de registros na lista negra e na lista branca, respectivamente, para o agente, dimensão e setor especificados.
- O total de registros totalCount é calculado como a soma dos registros das listas negra e branca.
- Se totalCount for igual a zero, o método retorna imediatamente false, indicando que o agente não pode estar na lista negra, pois não há registros disponíveis.
- Em seguida, a probabilidade de que o setor deva ser considerado como pertencente à lista negra é calculada dividindo-se o número de registros na lista negra pelo total de registros.
- O método RNDprobab() gera um número aleatório entre 0 e 1. Se esse número for menor do que a probabilidade calculada para a lista negra (blackProbability), o método retorna true.
O método IsInBlackList considera tanto os registros na lista negra quanto na lista branca para determinar a probabilidade de um setor estar na lista negra e precisar ser alterado. Quanto maior o número de registros na lista negra em relação aos registros na lista branca, maior será a probabilidade de o setor ser substituído aleatoriamente no futuro.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_TSm::IsInBlackList (int agentIndex, int dimension, int sectorIndex) { int blackCount = agents [agentIndex].blacklist [dimension].sector [sectorIndex]; int whiteCount = agents [agentIndex].whitelist [dimension].sector [sectorIndex]; int totalCount = blackCount + whiteCount; if (totalCount == 0) return false; double blackProbability = (double)blackCount / totalCount; return u.RNDprobab () < blackProbability; } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Saída da execução do algoritmo TSm em funções de teste:
TSm|Tabu Search M|50.0|100.0|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.8779456463913048
25 Hilly's; Func runs: 10000; result: 0.6143121517195806
500 Hilly's; Func runs: 10000; result: 0.2910412462428753
=============================
5 Forest's; Func runs: 10000; result: 0.9288481105123887
25 Forest's; Func runs: 10000; result: 0.5184350456698835
500 Forest's; Func runs: 10000; result: 0.19054478009120634
=============================
5 Megacity's; Func runs: 10000; result: 0.6107692307692308
25 Megacity's; Func runs: 10000; result: 0.3821538461538462
500 Megacity's; Func runs: 10000; result: 0.1215692307692319
=============================
All score: 4.53562 (50.40%)
O algoritmo TSm apresenta um desempenho bastante satisfatório, com bons resultados tanto na execução sobre funções de teste quanto na visualização dos dados. Naturalmente, há uma certa dispersão nos testes em funções de baixa dimensionalidade, mas esse fenômeno já havia sido notado e é comum entre muitos algoritmos. Destaca-se a capacidade do algoritmo de identificar a maioria das regiões significativas da superfície da função analisada.
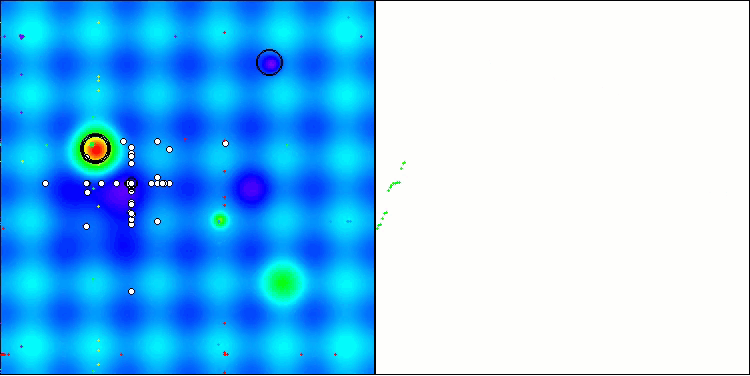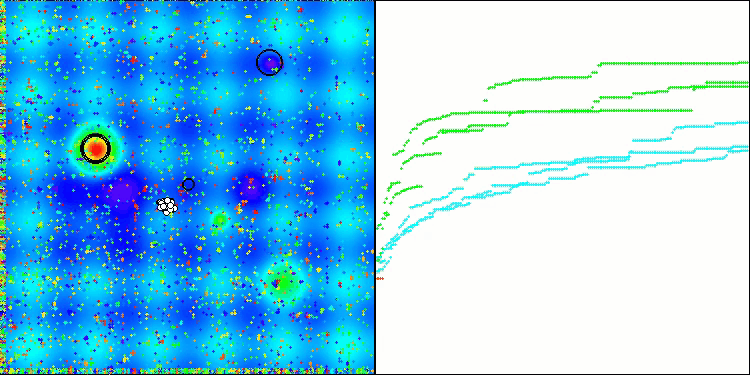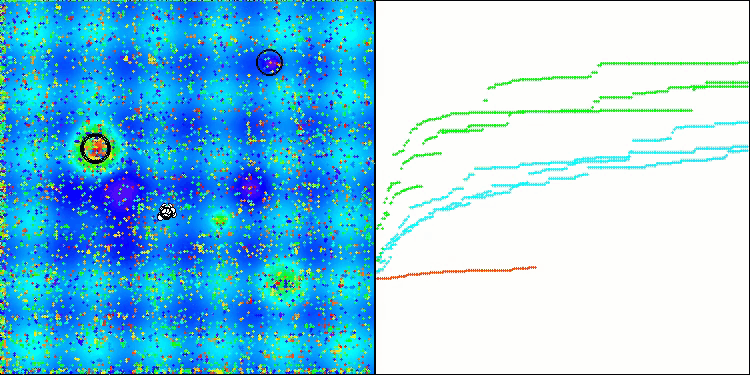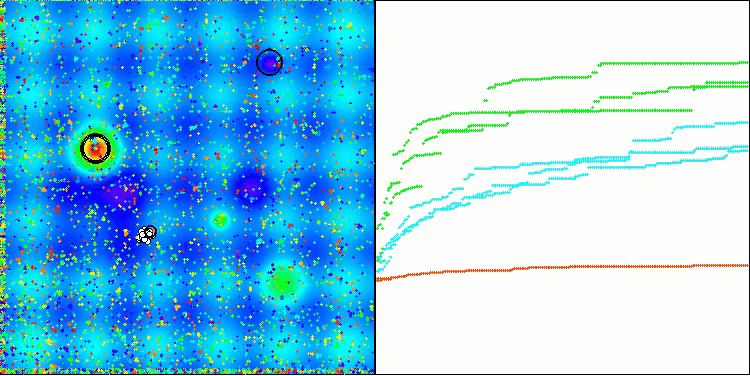
TSm na função de teste Hilly
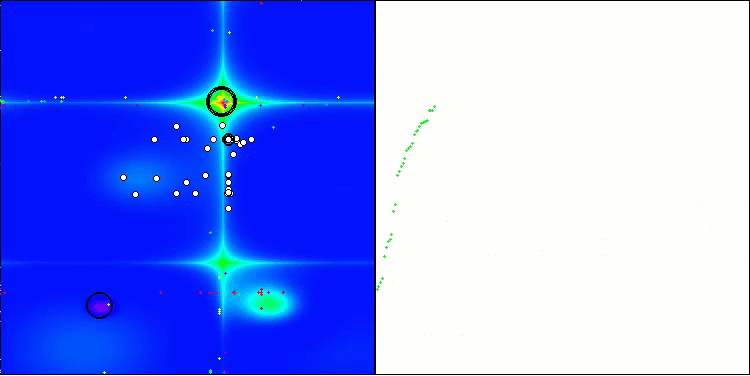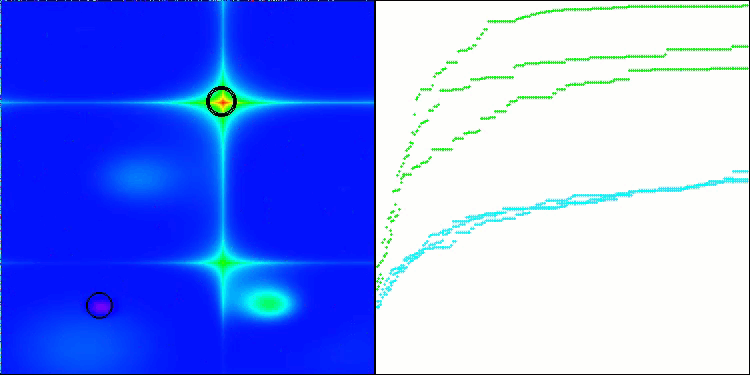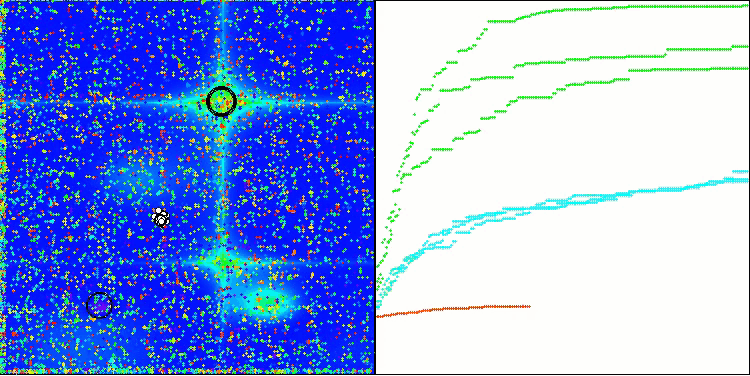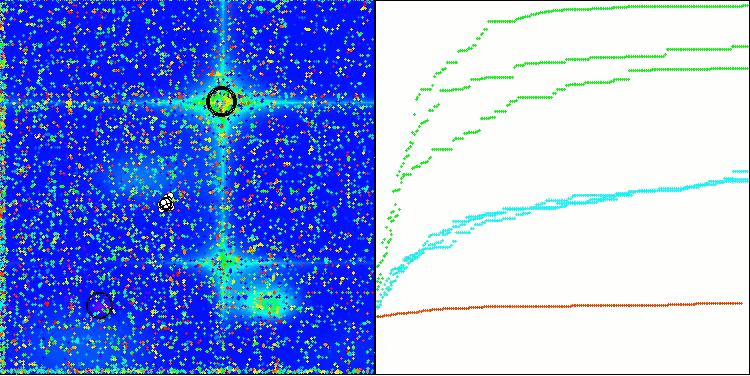
TSm na função de teste Forest
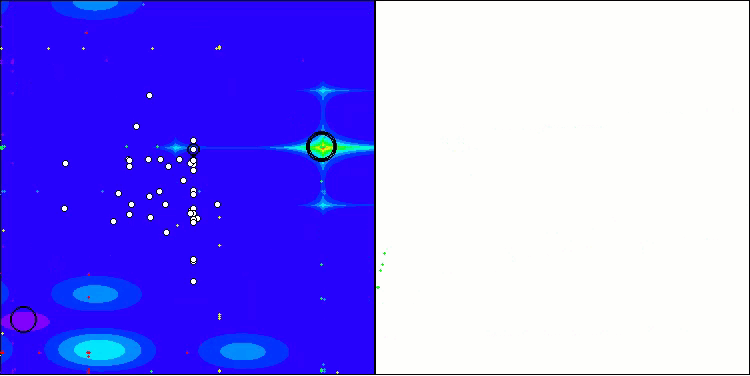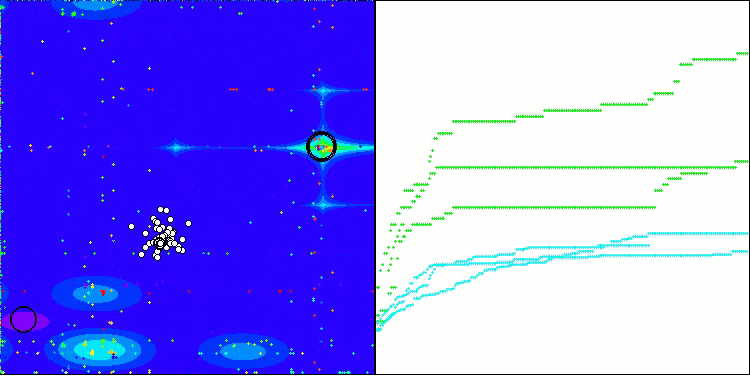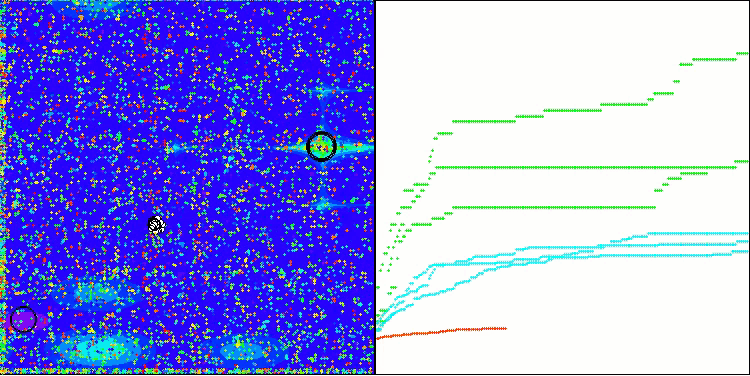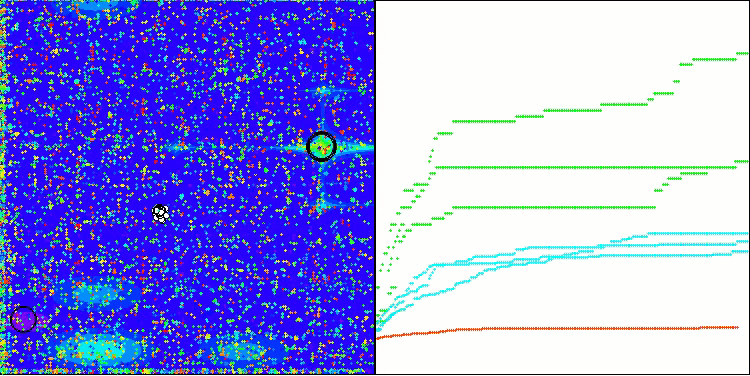
TSm na função de teste do Megacity
Os testes mostram que o algoritmo TSm ocupa a 18ª posição no ranking de algoritmos de otimização, um resultado acima da média.
№ | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 8 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 9 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 10 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 11 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 12 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 13 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 14 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 15 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 16 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 17 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 18 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 19 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 20 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 21 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 22 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 23 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 24 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 25 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 26 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 27 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 28 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 29 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 30 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 31 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 32 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 33 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 34 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 35 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 36 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 37 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 38 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 39 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 40 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 41 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 42 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 43 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 44 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 45 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
Considerações finais
Analisando o desempenho do algoritmo em funções de teste de diferentes dimensões, percebe-se que ele tem mais dificuldade em lidar com problemas de alta dimensionalidade em funções suaves, como a função Hilly. Nos demais testes, no entanto, o algoritmo demonstra resultados consistentes e satisfatórios.
A modificação proposta do algoritmo Tabu Search, ao contrário da versão original, pode ser aplicada a qualquer tipo de problema de otimização em espaços contínuos de busca, abrangendo tanto funções suaves quanto problemas discretos. O algoritmo pode servir como base promissora para o desenvolvimento de novos algoritmos. Para melhorar a precisão da convergência, podem ser utilizadas técnicas empregadas em algoritmos já estudados. No entanto, neste estágio, apresentamos a modificação do Tabu Search como está.
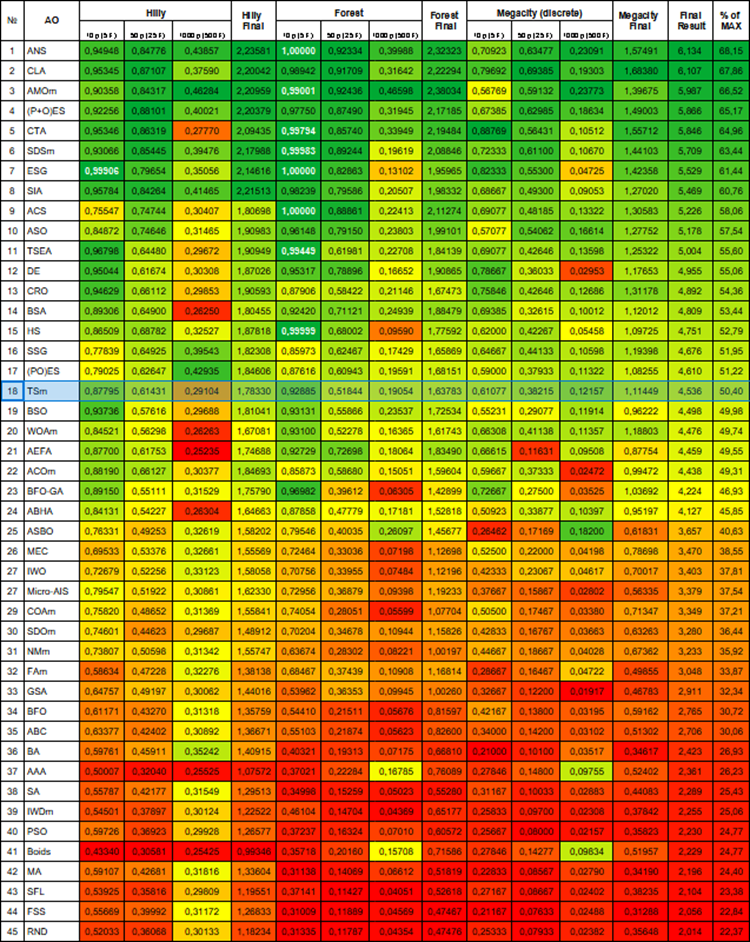
Figura 1. Graduação de cores dos algoritmos para os respectivos testes. Os resultados maiores ou iguais a 0,99 são destacados em branco.
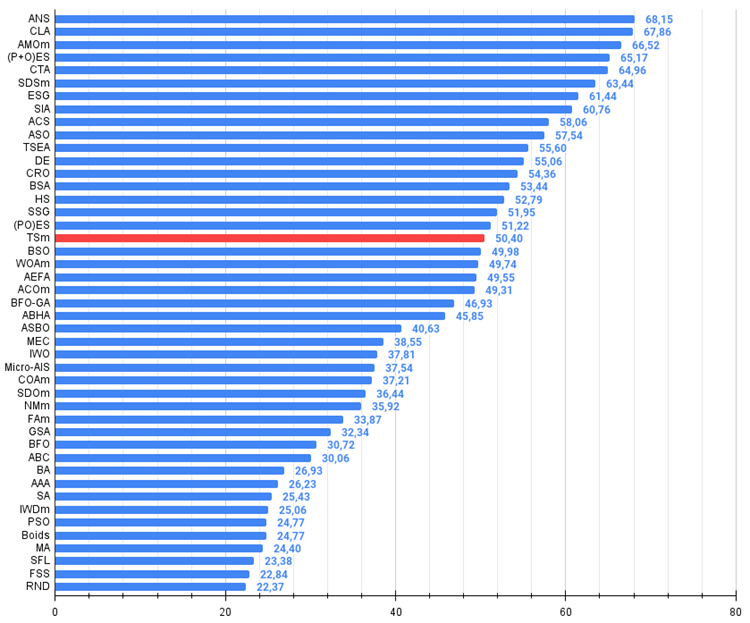
Figura 2. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, e o arquivo contém um script para cálculo da tabela de classificação)
Prós e contras do algoritmo TSm
Prós:
- Ideia promissora para futuras melhorias e como base para novos algoritmos.
- Boa escalabilidade.
- Poucos parâmetros a serem ajustados (apenas dois, excluindo o tamanho da população).
Contras:
- A precisão da convergência poderia ser maior.
O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15654
 Redes neurais em trading: Análise de nuvem de pontos (PointNet)
Redes neurais em trading: Análise de nuvem de pontos (PointNet)
 Redes neurais em trading: Transformer vetorial hierárquico (Conclusão)
Redes neurais em trading: Transformer vetorial hierárquico (Conclusão)
 Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 6): Integração Completa
Construindo um Modelo de Restrição de Tendência de Candlestick (Parte 6): Integração Completa
 Gráficos do índice do dólar e do índice do euro — exemplo de serviço no MetaTrader 5
Gráficos do índice do dólar e do índice do euro — exemplo de serviço no MetaTrader 5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso