MetaTrader 5 / 测试者
English Русский Español Português
preview
禁忌搜索（TS）

禁忌搜索（TS）

MetaTrader 5 — 测试者 | 14 四月 2025, 14:15
165 0
Andrey Dik
Andrey Dik

内容

  1. 概述
  2. 算法实现
  3. 测试结果

    概述

    禁忌搜索算法是最早的且最为人熟知的元启发式方法之一，它在20世纪80年代被开发出来，是组合优化领域的一个真正的突破。该方法由弗雷德·格洛弗（Fred Glover）提出，由于其创新性地使用记忆来禁止重复移动的策略，立即吸引了研究人员的注意。当时还有其他方法，如遗传算法，但禁忌搜索因其独特的方法而脱颖而出。

    禁忌搜索算法从选择一个初始解开始，然后探索邻近选项，其中优先考虑那些改善当前结果的选项。为了避免返回到以前探索过的不成功解，该算法采用了禁忌表——一个记录“禁止”移动的结构。这使我们能够避免循环过程，并更有效地探索搜索空间。例如，在背包问题中，算法可能会逐个添加或删除物品，寻求避免返回到以前考虑过的组合，同时最大化它们的价值。

    禁忌搜索的基础是自适应记忆，它不仅防止返回已经找到的解，还能控制搜索过程，考虑之前的步骤。其他研究人员，如曼努埃尔·拉古纳（Manuel Laguna）和拉斐尔·马蒂（Rafael Marti），随后进一步开发了该算法，极大地扩展了其在从生产计划到财务分析和电信等领域的应用。禁忌搜索仍然是解决需要深入分析和复合计算的复杂组合问题的相关工具。

    禁忌搜索是创新思想如何转变搜索优化方法的一个很好的例子，它在科学和技术领域开辟了新的可能性。尽管该算法最初是为了解决特定的组合问题（如旅行商问题和背包问题）而开发的，但本文探讨了对经典算法的一种修改，使其能够解决更一般的优化问题，包括连续搜索空间中的问题。


    算法实现

    让我们考虑用于解决组合优化问题（传统算法）的禁忌搜索算法中使用的一般方程和机制：

    1. 优化问题的一般表述：

    • f (x) 优化— 目标函数。
    • x ∈ X，其中X是对变量向量x的约束集合。

    2. 解的邻域：

    • N (x) 是从当前解x出发，通过一次“移动”可以到达的解的集合。
    • N (x)* 是考虑修改后的搜索历史（短期和长期记忆）的邻域。

    3. 短期记忆：

    • 跟踪近期变化的属性（决策的特征）。
    • 禁止访问包含“禁忌激活”属性的解。

    4. 长期记忆：

    • 统计访问过的解的属性变化/存在频率。
    • 利用这些频率管理搜索的多样化。

    5. 强化：

    • 从修改后的邻域N* (x) 中选择最佳移动。
    • 返回到有希望的解空间区域。

    6. 多样化： 

    • 选择移动那些此前从未出现过的属性。
    • 在与已探索区域不同的方向上搜索。

    7. 战略波动：

    • 在接近“临界水平”时改变选择移动的规则。
    • 通过该水平后返回。

    8. 连接路径：

    • 生成轨迹，连接高质量解。
    • 选择移动将当前解，使其尽可能靠近引导解。

      为了解决优化问题，我们将跳过第8点，专注于算法的核心思想，尝试实现禁忌搜索的修改版本，同时尽可能保留第1-7点。原始算法处理离散决策，试图找到节点之间的最短路径。为了将其适配到连续搜索空间中的问题，有必要以某种方式对每个正在优化的参数的可行区域进行离散化处理。问题是，我们不能标记每一个可能的解，因为标签的数量会是巨大的，导致解决方案几乎不可能实现。

      为了替代禁忌表，我们将引入“白名单”和“黑名单”的概念，将每个参数的范围划分为区域（每个优化参数指定数量的区域）。这样，当解决方案成功时，我们可以在白名单上添加一个标记，如果与前一步相比解决方案没有改进，则在黑名单上做一个标记。有希望的解决方案的区域将积累标记，这将允许更彻底地探索该区域并完善解决方案。然而，一个成功的区域也可能包含极其不成功的决策，在这种情况下，该区域将被列入黑名单。这意味着同一个区域可能同时包含白名单和黑名单的标记。

      应当按照白名单中的标记数量的概率比例，选择用于生成下一个解决方案的区域。在生成新解决方案后，我们检查相应的区域是否在黑名单上，并计算与黑名单标记的概率比例，作为白名单标记总和的分数。如果概率满足，我们挑出另一个随机选择的区域。

      因此，考虑到正在优化的函数表面的特征，该算法动态地为搜索空间中所有可用区域的探索生成概率，而不停留在任何特定区域。即使算法接近全局最优解，它也不能无限期地改进其结果。这样反过来又会导致该区域的黑名单标记增加，从而迫使算法改变区域，并继续在超空间的其他区域中搜索。

      这种方法的理念是确保找到的解决方案能够从多方面得到优化完善，并且能够广泛研究问题。这也应该最小化算法的外部参数数量，为其提供对正在研究的问题函数的自适应特性。

      让我们突出修改后的经典禁忌搜索实现的主要思想：

      1. 离散化。将搜索空间划分为区域，可以更高效地探索各个区域。
      2.白名单和黑名单。 成功和不成功的决策分别记录，提供对区域前景的动态跟踪。
      3. 动态探索。该算法用于探索所有可用区域生成概率，避免陷入低效区域。
      4. 适应性。该算法对黑名单标记的积累做出反应，迫使其改变搜索方向并提供多样性。

      因此，我们的算法版本结合了禁忌搜索和进化算法的元素。使用黑白名单形式的记忆机制，将搜索引导到有希望的解空间区域，并避免导致更差解的区域。

      为了清晰起见，我们将为每个坐标示意性地绘制区域的白名单和黑名单。例如，我们取三个坐标，每个坐标都分为4个区域。每个坐标分别设置白名单和黑名单。

      例如，“3)”区域的“0”坐标在白名单上有五个“标记”，这是该坐标所有区域中最多的。这意味着在下一次迭代中，该区域将有最高的概率被选中。另一方面，这个区域在黑名单上有六个“标签”，这将在生成新解决方案时增加其被替换的可能性，尽管它被认为是最有希望的区域。因此，可能会出现一种情况，在选择区域时，一个潜力较小的区域被另一个区域替换的概率较低（尽管第一眼并不明显）。

      由此可以看出，在探索搜索空间的过程中，概率不断地重新平衡，这使得算法能够考虑到表面的特征。这个方向似乎非常有前景，因为它几乎不依赖算法的外部参数，使其真正地具有自适应性。

       0: |0)____VVV_____|1)____VV______|2)_____V______|3)____VVVVV____| 

1: |0)_____VV_____|1)_____V______|2)____VVV_____|3)_____VVV_____|

2: |0)______V_____|1)____VVV_____|2)_____V______|3)_____VVV_____|



0: |0)_____ХХХ____|1)_____ХХ_____|2)_____XX_____|3)____XXXXXX___|

1: |0)______X_____|1)_____XXX____|2)____XXXXX___|3)______X______|

2: |0)_____XX_____|1)_____XXXX___|2)______X_____|3)____XXXXX____|

      现在我们可以为算法的修订版本编写伪代码，我们将这个版本称为TSm。

      1. 种群初始化：

          对于种群中的每个个体：

            在指定范围内设置随机坐标。

            将初始适应度值设置为可能的最小值。

      2. 算法的主循环：

          直到达到终止条件，重复以下步骤：

           a) 如果是第一次迭代：

               开始执行种群的初始化。

           b) 否则：

               为智能体生成新坐标：

               对于每个智能体及其每个坐标：

                   以一定概率，复制已知最优解的坐标。

                   否则：

                       从智能体的白名单中选择一个区域。

                       在此区域内生成一个新坐标。

                   如果所选区域在黑名单上，则选择一个随机区域并在其中生成一个坐标。

                   检查新坐标是否超出了可接受范围。

           c) 评估每个拥有新坐标的智能体的适应度。

           d) 更新黑白名单：

               对于每个智能体：

                   比较当前适应度与之前的适应度。

                   如果适应度有所提高，那么在白名单中的相应区域增加计数器。

                   如果适应度变差，在黑名单中增加计数器。

               将当前适应度保存为下一次迭代的前一次适应度。

           e) 如果找到适应度更好的智能体，则更新找到的最优解。

      3. 循环完成后，返回找到的最优解。

      现在我们开始编写代码。让我们描述两个结构：S_TSmSector和S_TSmAgent，用于在搜索策略中处理区域和智能体。

      1. S_TSmSector - 该结构包含一个整数数组sector[]，用于存储相应区域的“标记”（实际上，这是一个计数器数组）。

      2. S_TSmAgent - 此结构更加复杂。它描述了算法中的搜索智能体，包括：

      • blacklist [] - 每个坐标的区域黑名单数组。
      • whitelist [] - 每个坐标的区域白名单数组。
      • fPrev - 智能体之前的适应度值。

      Init方法用于初始化S_TSmAgent实例。参数：

      • coords - 坐标数量。
      • sectorsPerCord - 每个坐标的区域数量。

      逻辑如下 ：

      1. 将blacklist和whitelist数组大小调整为与坐标数量相匹配。

      2. 通过循环初始化所有坐标的每个区域：

      • 调整当前坐标的黑名单sector数组大小。
      • 白名单同理。
      • 将白名单和黑名单的所有元素初始化为零（这些是后续将逐一增加的计数器）。

      3. fPrev 初始化 - 将fPrev值设置为**-DBL_MAX**，代表可能的最小值。这表明该智能体尚未获得适应度值。

      该代码创建了一个智能体结构，能够管理搜索空间不同维度的区域的黑名单和白名单，其中有必要跟踪智能体被允许和被禁止访问的区域。

      //——————————————————————————————————————————————————————————————————————————————
struct S_TSmSector
{
    int sector [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
struct S_TSmAgent
{
    S_TSmSector blacklist []; //black list by sectors of each coordinate
    S_TSmSector whitelist []; //white list by sectors of each coordinate

    double fPrev;             //previous fitness

    void Init (int coords, int sectorsPerCord)
    {
      ArrayResize (blacklist, coords);
      ArrayResize (whitelist, coords);

      for (int i = 0; i < coords; i++)
      {
        ArrayResize (blacklist [i].sector, sectorsPerCord);
        ArrayResize (whitelist [i].sector, sectorsPerCord);

        ArrayInitialize (blacklist [i].sector, 0);
        ArrayInitialize (whitelist [i].sector, 0);
      }

      fPrev = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

      描述从C_AO基类继承而来的C_AO_TSm类。

      1. 构造函数为变量设置初始值：

      • popSize - 种群大小为50。
      • sectorsPerCoord - 每个坐标的区域数量为100。
      • bestProbab - 选择最优解的概率为0.8。
      • 创建并初始化了params数组，其中包含三个参数，分别对应上述变量。

      2. SetParams方法从params数组中将参数值重新设置到相应的类变量中。

      3. Init方法使用指定的范围和搜索步长初始化算法。

      4. Moving ()Moving () - 该方法负责在搜索空间中移动智能体，而Revision ()则使用禁忌搜索逻辑检查并更新当前解。

      5. 类成员：

      • S_Agent agents [] - 智能体数组表示搜索过程中问题的解。

      6. 私有方法：

      • InitializePopulation () - 用于初始化智能体种群的方法。
      • UpdateLists () - 用于更新智能体的区域黑名单和白名单的方法。
      • GenerateNewCoordinates () - 在搜索过程中生成新坐标的方法。
      • GetSectorIndex () - 基于坐标和维度获取区域索引的方法。
      • ChooseSectorFromWhiteList () - 为给定的智能体和维度从白名单中选择区域的方法。
      • GenerateCoordInSector () - 在给定区域内生成坐标的方法。
      • IsInBlackList () - 选择另一个区域的概率测试性能的方法，该方法对白名单和黑名单的选择有影响。

      //——————————————————————————————————————————————————————————————————————————————
class C_AO_TSm : public C_AO
{
  public: //--------------------------------------------------------------------
  C_AO_TSm ()
  {
    ao_name = "TSm";
    ao_desc = "Tabu Search M";
    ao_link = "https://www.mql5.com/en/articles/15654";

    popSize         = 50;
    sectorsPerCoord = 100;
    bestProbab      = 0.8;

    ArrayResize (params, 3);

    params [0].name = "popSize";         params [0].val = popSize;
    params [1].name = "sectorsPerCoord"; params [1].val = sectorsPerCoord;
    params [2].name = "bestProbab";      params [2].val = bestProbab;
  }

  void SetParams ()
  {
    popSize         = (int)params [0].val;
    sectorsPerCoord = (int)params [1].val;
    bestProbab      = params      [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int    sectorsPerCoord;
  double bestProbab;

  S_TSmAgent agents [];

  private: //-------------------------------------------------------------------
  void   InitializePopulation      ();
  void   UpdateLists               ();
  void   GenerateNewCoordinates    ();
  int    GetSectorIndex            (double coord, int dimension);
  int    ChooseSectorFromWhiteList (int agentIndex, int dimension);
  double GenerateCoordInSector     (int sectorIndex, int dimension);
  bool   IsInBlackList             (int agentIndex, int dimension, int sectorIndex);

};
//——————————————————————————————————————————————————————————————————————————————

      现在轮到考虑负责初始化禁忌搜索算法C_AO_TSm类的Init方法了。让我们逐步分析：

      1. 该方法首先通过传递最小值、最大值和步长数组来调用StandardInit。这是一种标准初始化，用于设置算法参数。接下来，基于popSize调整agents数组的大小，并定义种群中的智能体数量。接下来是一个循环，遍历agents数组中的每个智能体。为每个智能体调用Init方法。该方法初始化其参数，包括坐标（coords）和每个坐标的区域数量（sectorsPerCoord）。

      2. 如果所有初始化步骤都成功，该方法返回true，表示算法初始化成功。

      Init方法是为禁忌搜索算法做好准备的关键。它设置了搜索范围，初始化了智能体数组，并为它们进一步寻找解决方案做好准备。如果在初始化的任何阶段发生错误，该方法将终止并返回false。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSm::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agents, popSize);

  for (int i = 0; i < popSize; i++) agents [i].Init (coords, sectorsPerCoord);

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

      让我们来考虑一下C_AO_TSm类的Moving方法。方法逻辑：

      • if (!revision) - 在这里检查逻辑变量revision。如果是false（尚未进行初始化），则执行下一个代码块。
      • InitializePopulation () - 负责初始化智能体种群。

      在算法的第二次及以后的迭代中，调用GenerateNewCoordinates ()方法。该方法为搜索过程中的智能体生成新坐标（新解）。

      Moving方法管理禁忌搜索算法中智能体的移动。它首先检查种群是否已经初始化。如果还未初始化，那么将初始化种群，否则该方法为智能体生成新坐标。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    InitializePopulation ();
    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  GenerateNewCoordinates ();
}
//——————————————————————————————————————————————————————————————————————————————

      Revision方法负责在禁忌搜索过程中更新当前最佳解。它遍历种群中的所有解，将它们的得分与当前最佳值进行比较，如果找到更好的解，则更新相应的变量。在方法的最后，更新白名单和黑名单，这对于算法的进一步执行是必要的。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::Revision ()
{
  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c);
    }
  }

  //----------------------------------------------------------------------------
  UpdateLists ();
}
//——————————————————————————————————————————————————————————————————————————————

      接下来的InitializePopulation方法负责初始化禁忌搜索智能体的种群。它在给定范围内为每个智能体的每个坐标生成随机值，并且还为每个智能体的前一次得分设置初始值。这为算法的后续迭代是必要的，在后续迭代中将进行解的评估和更新。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::InitializePopulation ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
      a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
    agents [i].fPrev = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

      接下来是C_AO_TSm类的UpdateLists方法。方法逻辑：

      • 外层循环遍历种群中的所有智能体，其中popSize指的是种群大小。
      • 内层循环遍历每个智能体的所有坐标。
      • 对于智能体a [i]的每个c坐标，使用GetSectorIndex方法计算区域索引。这有助于将值分类到特定区域，以便进行进一步分析。
      • 如果智能体的当前得分a [i].f超过了其之前的得分agents [i].fPrev，这意味着该智能体改进了其决策。在这种情况下，相应区域的whitelist计数器会增加。
      • 如果当前得分低于之前的得分，则意味着该智能体的决策变差了，相应区域的blacklist计数器会增加。
      • 在处理完所有坐标后，智能体的前一次估计值会更新为当前值，以便在下一次迭代中与新值进行比较。

      UpdateLists方法负责根据每个智能体的当前得分和之前的得分更新种群列表（白名单和黑名单）。这使得禁忌搜索算法能够跟踪哪些区域是成功的（白名单）以及哪些区域是不成功的（黑名单）。因此，该方法有助于进一步管理解决方案的搜索，避免重新访问解空间中低效的区域。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::UpdateLists ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      int sectorIndex = GetSectorIndex (a [i].c [c], c);

      if (a [i].f > agents [i].fPrev)
      {
        agents [i].whitelist [c].sector [sectorIndex]++;
      }
      else
        if (a [i].f < agents [i].fPrev)
        {
          agents [i].blacklist [c].sector [sectorIndex]++;
        }
    }
    agents [i].fPrev = a [i].f;
  }
}
//——————————————————————————————————————————————————————————————————————————————

      现在我们来看一下C_AO_TSm类的GenerateNewCoordinates方法。方法逻辑：

      • 外层循环遍历种群中的所有智能体，其中popSize指的是种群大小。
      • 内层循环遍历每个智能体的所有坐标。
      • 首先，使用RNDprobab方法检查概率。如果概率满足条件，智能体将从cB [c]全局最优解中获得一个坐标。
      • 如果概率未满足条件，则使用ChooseSectorFromWhiteList()方法从白名单中选择一个区域。
      • 然后使用GenerateCoordInSector ()方法在该区域内生成一个新坐标。
      • 如果所选区域在黑名单中，则使用u.RNDminusOne ()随机选择一个新的区域，并在其中生成一个新坐标。
      • 检查新坐标是否在给定范围内，并符合所需的步长。

      GenerateNewCoordinates方法负责为种群中的每个智能体生成新坐标。采用概率方法，依据白名单和黑名单，在已知的最佳坐标和区域内随机生成的结果之间进行选择。该方法还通过检查坐标是否符合指定范围来确保其有效性。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_TSm::GenerateNewCoordinates ()
{
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      if (u.RNDprobab () < bestProbab)
      {
        a [i].c [c] = cB [c];
      }
      else
      {
        int sectorIndex = ChooseSectorFromWhiteList (i, c);
        double newCoord = GenerateCoordInSector (sectorIndex, c);

        if (IsInBlackList (i, c, sectorIndex))
        {
          sectorIndex = u.RNDminusOne (sectorsPerCoord);
          newCoord = GenerateCoordInSector (sectorIndex, c);
        }

        newCoord = u.SeInDiSp (newCoord, rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = newCoord;
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

      让我们来分析一下GetSectorIndex函数的代码，该函数为指定维度中的给定坐标指定区域索引。函数逻辑：

      • 如果给定维度范围的最大值和最小值相等，这意味着该范围没有长度。在此情况下，函数立即返回0，因为无法将范围划分为区域。
      • 接下来，通过将范围的长度除以区域数量sectorsPerCoord来计算一个区域的长度sL。
      • 使用一个方程计算ind区域索引，该方程确定给定坐标落在哪个区域中。首先，从坐标中减去范围的最小值，然后将结果除以区域的长度，并将得到的值向下取整到最接近的整数值。
      • 如果坐标等于范围的最大值，函数返回最后一个区域的索引。
      • 进一步的检查确保索引不会超出可接受的值。如果索引大于或等于区域数量，则返回最后一个区域。如果索引小于0，则返回0。

      //——————————————————————————————————————————————————————————————————————————————
int C_AO_TSm::GetSectorIndex (double coord, int dimension)
{
  if (rangeMax [dimension] == rangeMin [dimension]) return 0;

  double sL =  (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord;

  int ind = (int)MathFloor ((coord - rangeMin [dimension]) / sL);

  // Special handling for max value
  if (coord == rangeMax [dimension]) return sectorsPerCoord - 1;

  if (ind >= sectorsPerCoord) return sectorsPerCoord - 1;
  if (ind < 0) return 0;

  return ind;
}
//——————————————————————————————————————————————————————————————————————————————

      让我们继续分析ChooseSectorFromWhiteList方法，该方法从给定智能体和维度的“白名单”区域中选择一个区域。其返回所选区域的索引。方法逻辑：

      • 将变量totalCount初始化为0。其用于统计白名单区域中的“标记”总数。
      • 如果totalCount等于零，这意味着区域中尚未包含“标记”，所有区域都是等效的。在这种情况下，该方法从所有可用区域中随机选择一个区域并返回。
      • 接下来，在循环中累积统计“标记”的数量。如果randomValue小于或等于当前累积值，该方法返回当前区域s的索引。这样可以根据白名单中的权重比例选择区域。

      ChooseSectorFromWhiteList方法允许根据模拟轮盘选择的概率分布，为某个智能体从白名单中选择一个区域。 

      //——————————————————————————————————————————————————————————————————————————————
int C_AO_TSm::ChooseSectorFromWhiteList (int agentIndex, int dimension)
{
  int totalCount = 0;

  for (int s = 0; s < sectorsPerCoord; s++)
  {
    totalCount += agents [agentIndex].whitelist [dimension].sector [s];
  }

  if (totalCount == 0)
  {
    int randomSector = u.RNDminusOne (sectorsPerCoord);
    return randomSector;
  }

  int randomValue = u.RNDminusOne (totalCount);
  int cumulativeCount = 0;

  for (int s = 0; s < sectorsPerCoord; s++)
  {
    cumulativeCount += agents [agentIndex].whitelist [dimension].sector [s];

    if (randomValue <= cumulativeCount)
    {
      return s;
    }
  }

  return sectorsPerCoord - 1;
}
//——————————————————————————————————————————————————————————————————————————————

      我们来分析一下GenerateCoordInSector方法，该方法用于为给定维度在指定区域中生成一个随机坐标。方法逻辑：

      • 计算给定维度的区域大小。
      • sectorStart的计算方式为：用给定维度的范围最小值加上一个偏移量，该偏移量等于区域索引乘以区域大小。sectorEnd定义为sectorStart加上sectorSize（区域大小）。这样就定义了区域的边界。
      • 接下来调用RNDfromCI函数。该函数从sectorStart到sectorEnd的范围内生成一个随机值。此值表示在指定区域内生成的一个坐标。

      //——————————————————————————————————————————————————————————————————————————————
double C_AO_TSm::GenerateCoordInSector (int sectorIndex, int dimension)
{
  double sectorSize  = (rangeMax [dimension] - rangeMin [dimension]) / sectorsPerCoord;
  double sectorStart = rangeMin [dimension] + sectorIndex * sectorSize;
  double sectorEnd   = sectorStart + sectorSize;

  double newCoord = u.RNDfromCI (sectorStart, sectorEnd);

  return newCoord;
}
//——————————————————————————————————————————————————————————————————————————————

      最后，我们来分析一下IsInBlackList方法，该方法检查给定的智能体是否在特定维度和区域的“黑名单”中。参数：

      • agentIndex - 要检查的智能体的索引。
      • dimension - 维度索引。
      • sectorIndex - 要检查的区域索引。

      如果智能体在黑名单中，并且根据白名单中该区域的“表现”满足改变区域的概率，则该方法返回true。

      • blackCount和whiteCount分别获取指定智能体、维度和区域在黑名单和白名单中的条目数量。
      • 总条目数totalCount是黑名单和白名单条目数的总和。
      • 如果总条目数为0，该方法立即返回false，这意味着该智能体不能被列入黑名单，因为没有黑或白的条目。
      • 接下来，给定区域应被视为计算在黑名单中的概率。这是通过将黑名单中的条目数除以总条目数来完成的。
      • RNDprobab ()方法生成一个介于0和1之间的随机数。如果这个随机数小于计算出的blackProbability黑名单概率，则该方法返回true。

      IsInBlackList方法综合考虑黑名单和白名单中的条目，以确定一个区域被黑名单化的概率，并决定是否需要将其更改为另一个随机区域。与白名单中的条目相比，黑名单中的条目越多，将该区域更改为另一个随机区域的概率就越高。

      //——————————————————————————————————————————————————————————————————————————————
bool C_AO_TSm::IsInBlackList (int agentIndex, int dimension, int sectorIndex)
{
  int blackCount = agents [agentIndex].blacklist [dimension].sector [sectorIndex];
  int whiteCount = agents [agentIndex].whitelist [dimension].sector [sectorIndex];
  int totalCount = blackCount + whiteCount;

  if (totalCount == 0) return false;

  double blackProbability = (double)blackCount / totalCount;
  return u.RNDprobab () < blackProbability;
}
//——————————————————————————————————————————————————————————————————————————————


      测试结果

      TSm测试台结果：

      TSm|Tabu Search M|50.0|100.0|0.8|
      =============================
      5 Hilly's; Func runs: 10000; result: 0.8779456463913048
      25 Hilly's; Func runs: 10000; result: 0.6143121517195806
      500 Hilly's; Func runs: 10000; result: 0.2910412462428753
      =============================
      5 Forest's; Func runs: 10000; result: 0.9288481105123887
      25 Forest's; Func runs: 10000; result: 0.5184350456698835
      500 Forest's; Func runs: 10000; result: 0.19054478009120634
      =============================
      5 Megacity's; Func runs: 10000; result: 0.6107692307692308
      25 Megacity's; Func runs: 10000; result: 0.3821538461538462
      500 Megacity's; Func runs: 10000; result: 0.1215692307692319
      =============================
      总分: 4.53562 (50.40%)

      正如我们所见，该算法的表现相当出色。在测试函数和可视化方面都取得了不错的结果。当然，在小维度的函数上存在一定的分散性，但正如您所注意到的，许多算法都存在这种现象。值得注意的是，在突出显示所研究函数的大部分重要表面区域方面，该算法表现出色。

      Hilly值

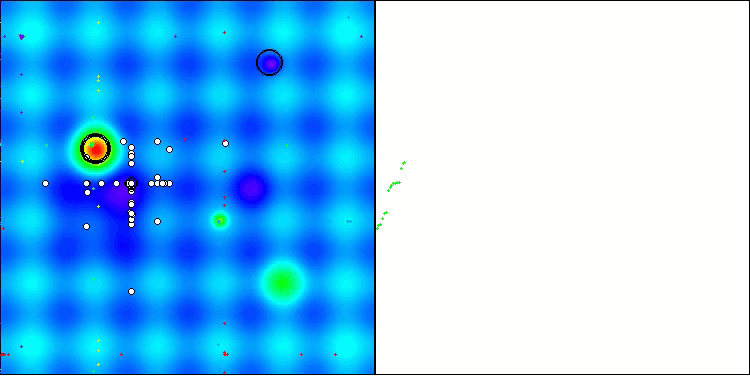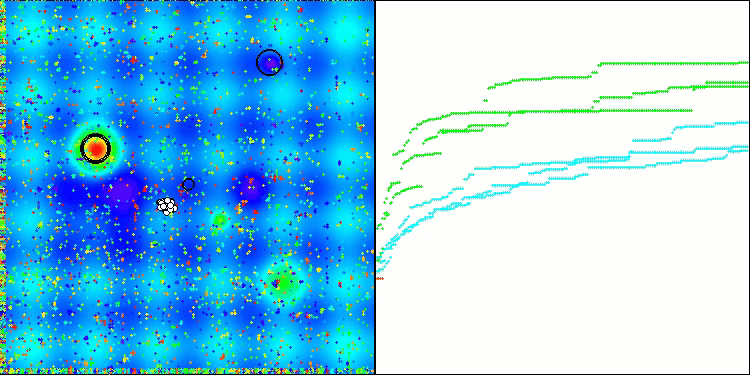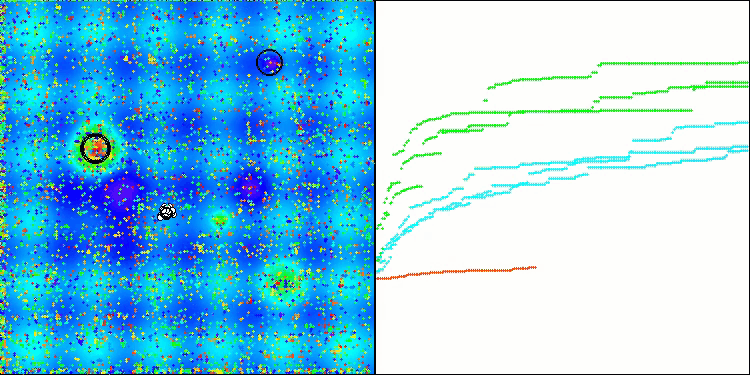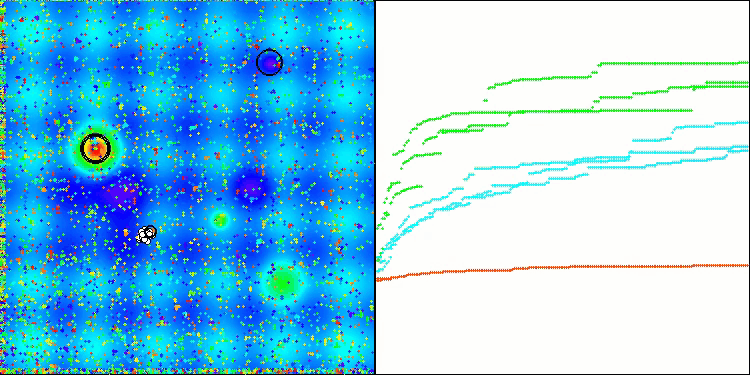
      TSm在Hilly测试函数上

      Forest值

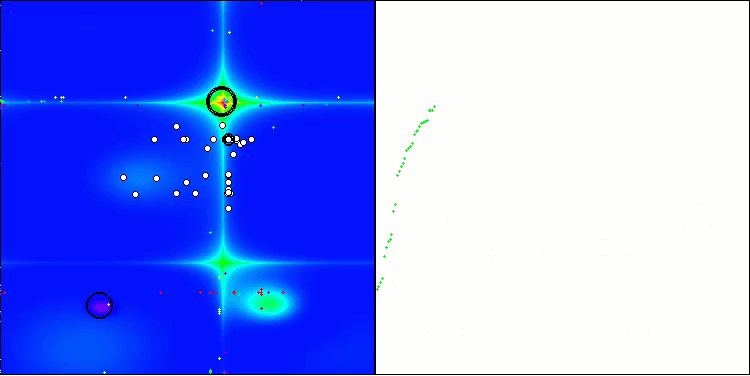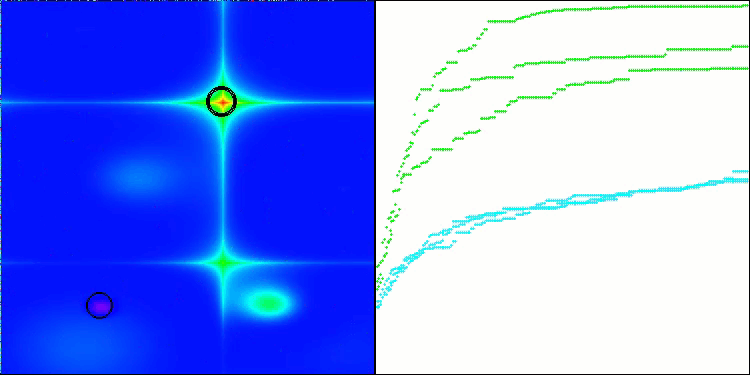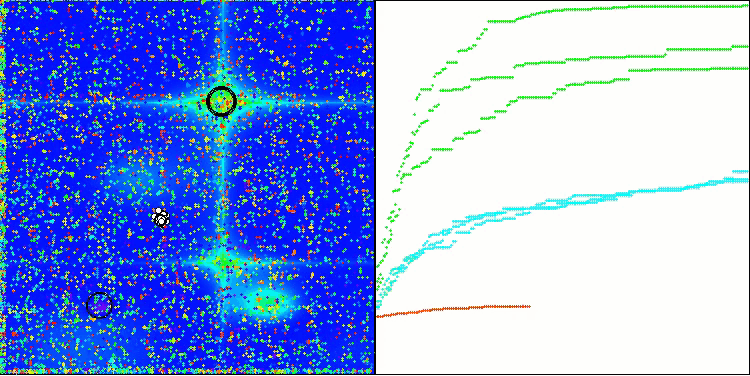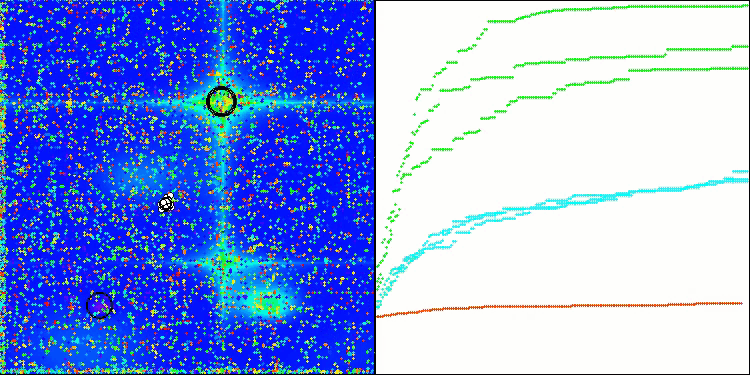
      TSm在Forest测试函数上

      Megacity

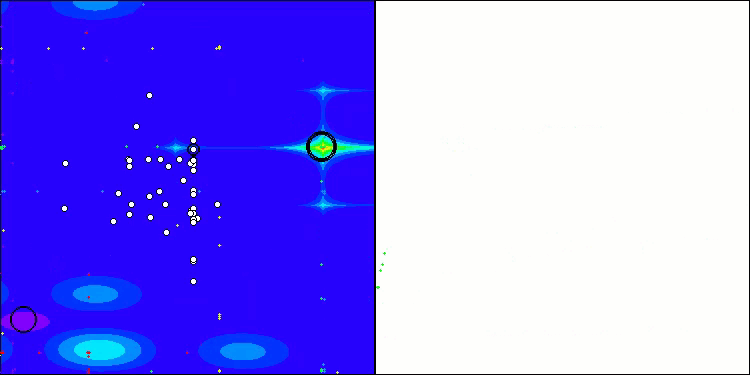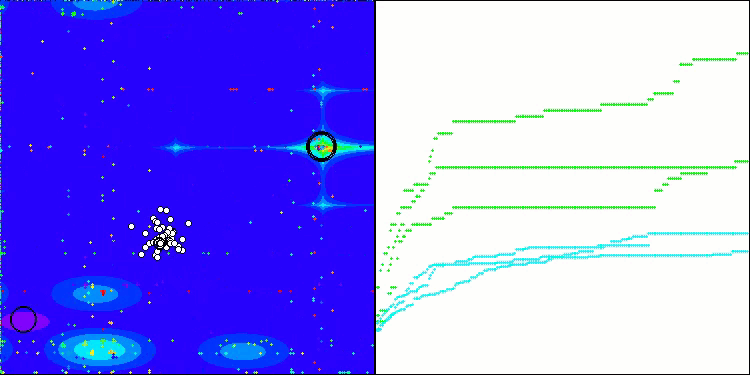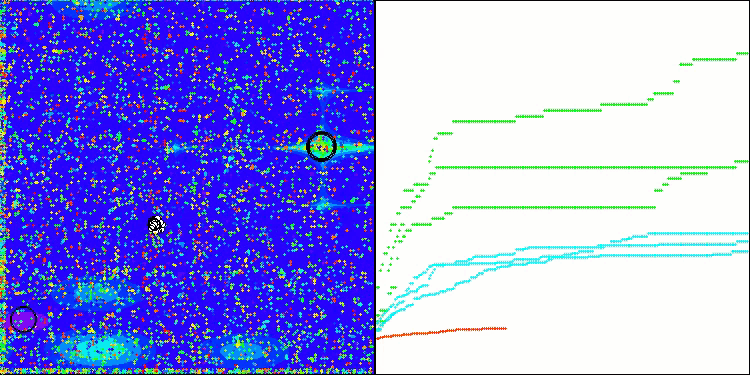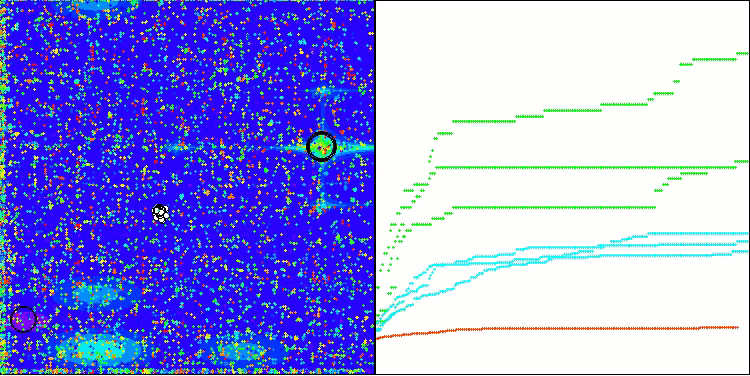
      TSm在Megacity测试函数上

      根据测试结果，该算法在评分表中排名第18位。这是一个高于平均水平的结果。

      #
      AO
      说明
      		Hilly值
      Hilly最终值
      		Forest值
      Forest最终值
      		Megacity (离散)
      Megacity最终值
      最终结果
      最大百分比
      10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
      1 ANS 跨邻域搜索 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA 密码锁算法 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 AMOm 动物迁徙优化M 0.90358 0.84317 0.46284 2.20959 0.99001 0.92436 0.46598 2.38034 0.56769 0.59132 0.23773 1.39675 5.987 66.52
      4 (P+O)ES (P+O) 进化策略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      5 CTA 彗星尾算法 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      6 SDSm 随机扩散搜索 M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      7 ESG 社会群体的进化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      8 SIA 模拟各向同性退火 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      9 ACS 人工协同搜索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      10 ASO 无序社会优化 0.84872 0.74646 0.31465 1.90983 0.96148 0.79150 0.23803 1.99101 0.57077 0.54062 0.16614 1.27752 5.178 57.54
      11 TSEA 龟壳演化算法 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      12 DE 差分进化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      13 CRO 化学反应优化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      14 BSA 鸟群算法 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      15 HS 和声搜索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      16 SSG 树苗播种和生长 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      17 (PO)ES (PO) 进化策略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      18 TSm 禁忌搜索M 0.87795 0.61431 0.29104 1.78330 0.92885 0.51844 0.19054 1.63783 0.61077 0.38215 0.12157 1.11449 4.536 50.40
      19 BSO 头脑风暴优化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      20 WOAm 鲸鱼优化算法M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      21 AEFA 人工电场算法 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      22 ACOm 蚁群优化 M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      23 BFO-GA 细菌觅食优化 - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      24 ABHA 人工蜂巢算法 0.84131 0.54227 0.26304 1.64663 0.87858 0.47779 0.17181 1.52818 0.50923 0.33877 0.10397 0.95197 4.127 45.85
      25 ASBO 适应性社会行为优化 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      26 MEC 思维进化计算 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      27 IWO 入侵杂草优化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      28 Micro-AIS 微型人工免疫系统 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      29 COAm 布谷鸟优化算法 M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      30 SDOm 螺旋动力学优化 M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      31 NMm Nelder-Mead方法 M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      32 FAm 萤火虫算法 M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
      33 GSA 引力搜索算法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
      34 BFO 细菌觅食优化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
      35 ABC 人工蜂群 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
      36 BA 蝙蝠算法 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
      37 AAA 人工藻类算法 0.50007 0.32040 0.25525 1.07572 0.37021 0.22284 0.16785 0.76089 0.27846 0.14800 0.09755 0.52402 2.361 26.23
      38 SA 模拟退火 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
      39 IWDm 智能水滴 M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
      40 PSO 粒子群优化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
      41 Boids算法 虚拟生物算法 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
      42 MA 猴群算法 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
      43 SFL 混合蛙跳算法 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
      44 FSS 鱼群搜索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
      45 RND 随机 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37


      总结

      考虑到该算法在不同维度的测试函数上的表现，可以注意到其在处理平滑的Hilly函数的高维问题时较为困难。在其他测试中，该算法表现出持续的良好结果。

      与原始版本不同，所提出的基于著名的禁忌搜索算法的修改版可以用于连续搜索空间中的任何一般优化问题，包括平滑和离散问题。该算法可以作为在其他算法中应用底层思想的强大基础。为了提高收敛的准确性，我们可以使用在之前探讨算法时应用的方法，但在现阶段，我仍以“原样”呈现这种修改。

      标签

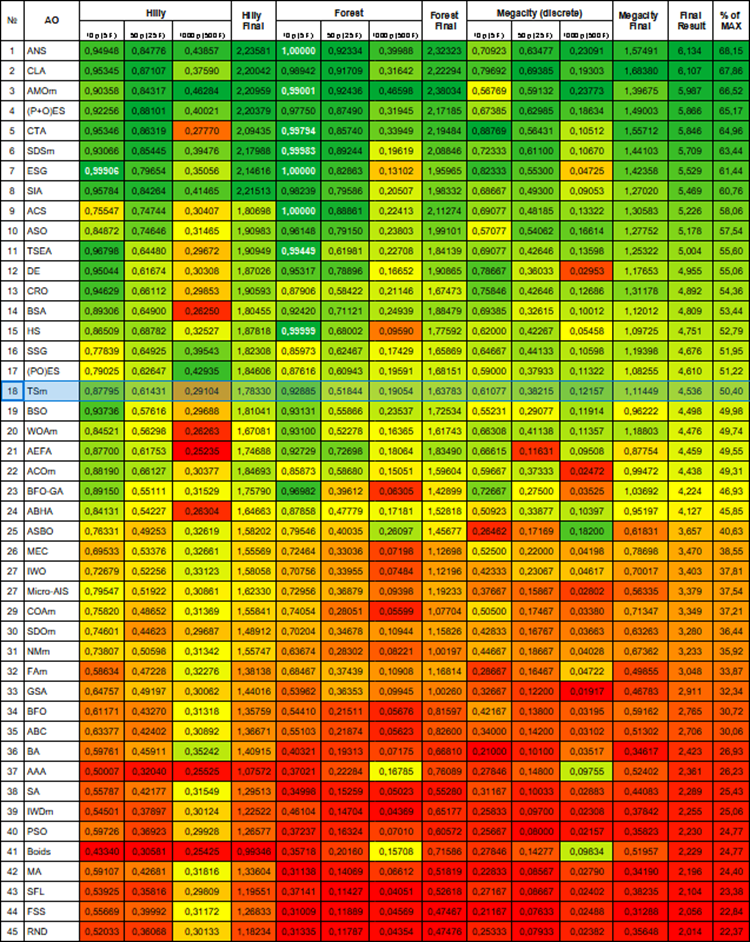
      图1. 根据相关测试，将算法的颜色等级大于或等于0.99的结果以白色突出显示。

      图表

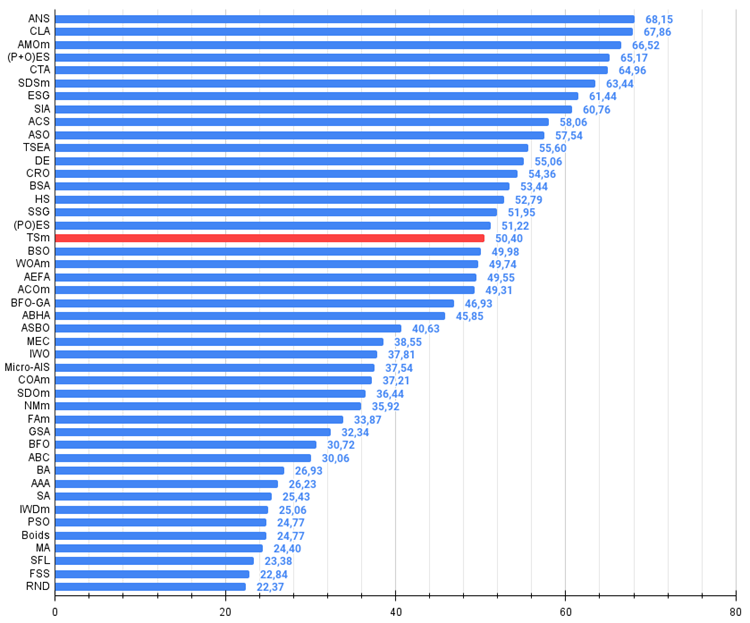
      图例2. 算法测试结果的直方图（标尺从 0 到 100，数字越大结果越好，

      其中 100 是理论上的最大可能结果，将计算评级表格的脚本存档）


      TSm的优缺点：

      优势：

      1. 一个有进一步改进前景的观点，并且可以作为新算法的基础。
      2. 良好的扩展性。
      3. 少量直观的参数（只有两个，不包括种群大小）。

      缺点：

      1. 收敛精度可以更高一些。

      文章附有一个包含当前版本算法代码的归档文件。本文作者对标准算法描述的绝对准确性不承担责任。为提升搜索能力，已经对其中的许多算法进行了修改。文章中表述的结论和论断都是基于实验的结果。

      本文由MetaQuotes Ltd译自俄文
      原文地址： https://www.mql5.com/ru/articles/15654

      附加的文件 |
      下载ZIP
      TSm.zip (35.52 KB)
      注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

      该作者的其他文章

      前往讨论
      开发回放系统（第 60 部分）：玩转服务（一） 开发回放系统（第 60 部分）：玩转服务（一）
      很长一段时间以来，我们一直在研究指标，但现在是时候让服务重新工作了，看看图表是如何根据提供的数据构建的。然而，由于整个事情并没有那么简单，我们必须注意了解前方等待我们的是什么。
      将您自己的 LLM 集成到 EA 中（第 4 部分）：使用 GPU 训练自己的 LLM 将您自己的 LLM 集成到 EA 中（第 4 部分）：使用 GPU 训练自己的 LLM
      随着当今人工智能的快速发展，语言模型（LLMs）是人工智能的重要组成部分，因此我们应该考虑如何将强大的 LLMs 整合到我们的算法交易中。对于大多数人来说，很难根据他们的需求微调这些强大的模型，在本地部署它们，然后将它们应用于算法交易。本系列文章将采取循序渐进的方法来实现这一目标。
      重构经典策略（第七部分）：基于USDJPY的外汇市场与主权债务分析 重构经典策略（第七部分）：基于USDJPY的外汇市场与主权债务分析
      在今天的文章中，我们将分析汇率走势与政府债券之间的关系。债券是固定收益证券中最受欢迎的形式之一，将成为我们讨论的重点。加入我们，一起探索是否可以利用人工智能技术改进一种经典策略。
      数据科学和机器学习（第 28 部分）：使用 AI 预测 EURUSD 的多个期货 数据科学和机器学习（第 28 部分）：使用 AI 预测 EURUSD 的多个期货
      众多人工智能模型的惯常做法是预测单一未来值。不过，在本文中，我们将钻研运用机器学习模型的更强大技术，即预测多个未来值。这种方式被称为多步预测，它令我们不仅能够预测明天的收盘价，还可以预测后天、及更久的收盘价。通过掌握多步骤预测，交易者和数据科学家能够获得更深入的见解，并制定更明智的决策，从而显著增强他们的预测能力和策略计划。