Ciência de dados e aprendizado de máquina (Parte 18): Comparando a eficácia do TruncatedSVD e NMF no tratamento de dados complexos de mercado

MetaTrader 5 — Negociação | 20 junho 2024, 14:59

Omega J Msigwa

-- Quanto mais você tem, menos percebe.

Conteúdo:

O que é NMF?

TruncatedSVD ou NMF - comparação

Redução de dimensionalidade

Segundo a Wikipédia a redução de dimensionalidade é a transformação de dados que consiste na diminuição do número de variáveis ao obter variáveis principais.

Trabalhar em espaços multidimensionais traz muitas complexidades, pois dados não processados frequentemente são esparsos e, consequentemente, sujeitos à chamada maldição da dimensionalidade. Além disso, a análise de dados geralmente é quase impossível do ponto de vista computacional (devido à complexidade de controle e processamento). A redução de dimensionalidade é frequentemente aplicada em áreas que lidam com um grande número de observações e/ou um grande número de variáveis, como processamento de sinais, reconhecimento de voz, neuroinformática e bioinformática (link).

Vamos examinar o conceito de redução de dimensionalidade e sua aplicação.

Dados de alta dimensionalidade

Sejamos honestos: na maioria das aplicações reais, muitos conjuntos de dados usados para construir modelos de aprendizado de máquina têm um número muito grande de funções ou variáveis (dimensões). Dados de alta dimensionalidade podem levar a vários problemas, como aumento da complexidade computacional, risco de ajuste excessivo e dificuldades de visualização. Normalmente, os conjuntos de dados com os quais lidamos contêm 5 variáveis independentes!

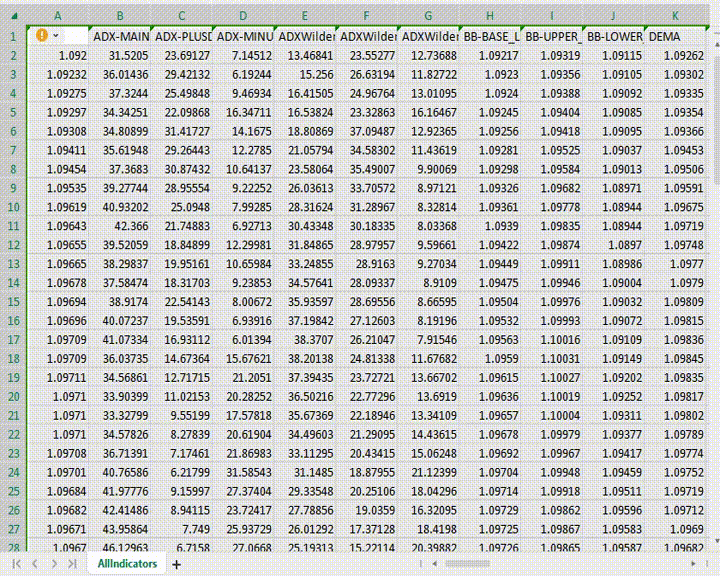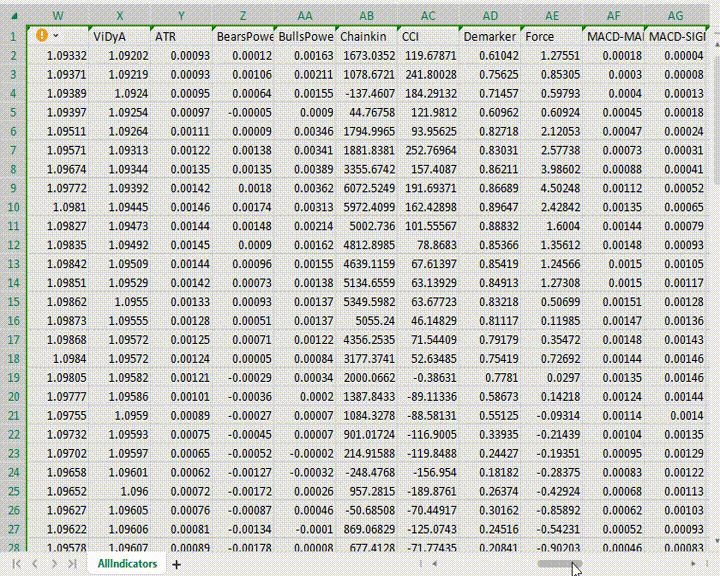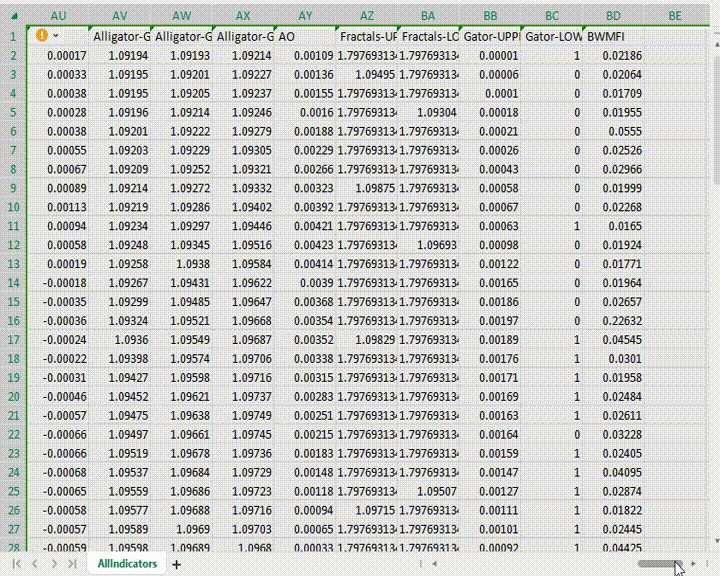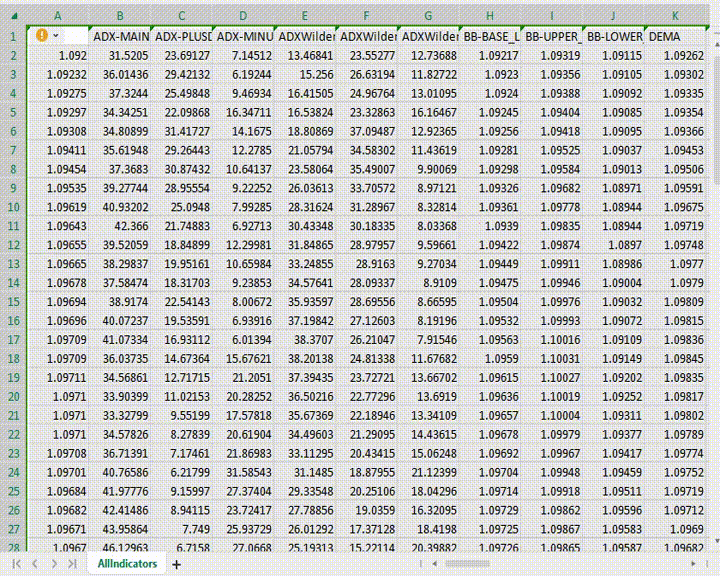
Vamos supor que pegamos todos os 38 buffers de indicadores padrão da plataforma MetaTrader 5. Assim, teríamos dados para 56 buffers. Isso é uma amostra muito grande.

A maldição da dimensionalidade

Essa maldição é real, e para aqueles que não acreditam, tentem implementar um modelo de regressão linear com um grande número de variáveis independentes correlacionadas.

A presença de funções fortemente correlacionadas pode fazer com que os modelos de aprendizado de máquina capturem ruídos e padrões específicos presentes nos dados de treinamento, que podem não se generalizar bem para novos dados desconhecidos.

Maldição da dimensionalidade refere-se a problemas que surgem ao trabalhar com dados multidimensionais, incluindo distribuição esparsa de dados, exigências computacionais elevadas e risco de ajuste excessivo do modelo (link).

Vamos demonstrar isso claramente com um exemplo de modelo de regressão linear:

Como os primeiros 13 indicadores no arquivo CSV são de tendência, é provável que eles se correlacionem entre si, bem como com o mercado, apesar de terem diferentes magnitudes de medição.

Ao usar apenas 10 indicadores de tendência para prever os preços de fechamento em 100 barras usando nosso modelo de regressão linear:

 matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y);
      
 lr.fit(train_x, train_y, NORM_MIN_MAX_SCALER);
   
 vector preds = lr.predict(train_x);
   
 Print("Train acc = ",metrics.r_squared(train_y, preds));

o modelo mostrou uma precisão de 92,2% na fase de treinamento.

IH      0       16:02:57.760    dimension reduction test (EURUSD,H1)    Train acc = 0.9222314640780123

Até as previsões foram tão precisas.

KE      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       Actuals
GS      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       [1.100686090182938,1.092937381937508,1.092258894809645,1.092946246629209,1.092958015748051,1.093392517797872,1.091850551839335,1.093040013995282,1.10067748979471,1.09836069904319,1.100275794247118,1.09882067865937,1.098572498565924,1.100543446136921,1.093174625248424,1.092435707204331,1.094128601953777,1.094192935809526,1.100305866167228,1.098452358470866,1.093010702771546,1.098612431849777,1.100827466038129,1.092880150279397,1.092600810699407,1.098722104612313,1.100707460497776,1.09582736814953,1.093765475161778,1.098767398966827,1.099091982657956,1.1006214183736,1.100698195592653,1.092047903797313,1.098661598784805,1.098489471676998,1.0997812203466,1.091954251247136,1.095870956581002,1.09306319770129,1.092915244023817,1.09488564050598,1.094171202526975,1.092523345374652,1.100564904733422,1.094200831112628,1.094001716368673,1.098530017588284,1.094081896433971,1.099230887219729,1.092892028948739,1.093709694144579,1.092862170694582,1.09148709705318,1.098520929394599,1.095105152264984,1.094272325978734,1.098468177450342,1.095849714911251,1.097952718476183,1.100746388049607,1.100114369109941,1.10052138086191,1.096938196194811,1.099992890418429,1.093106549957034,1.095523586088275,1.092801661288758,1.095956895328893,1.100419992807803]
PO      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       Preds
DH      0       07:10:55.652    GetAllIndicators Data (EURUSD,H1)       [1.10068609018278,1.092937381937492,1.092258894809631,1.09294624662921,1.092958015748061,1.093392517797765,1.091850551839298,1.093040013995258,1.100677489794526,1.098360699043097,1.100275794246983,1.098820678659222,1.09857249856584,1.1005434461368,1.093174625248397,1.09243570720428,1.094128601953754,1.094192935809492,1.100305866167089,1.098452358470756,1.09301070277155,1.098612431849647,1.100827466038003,1.092880150279385,1.092600810699346,1.098722104612175,1.100707460497622,1.095827368149497,1.093765475161723,1.098767398966682,1.099091982657809,1.100621418373435,1.100698195592473,1.092047903797267,1.098661598784675,1.098489471676911,1.099781220346472,1.091954251247108,1.095870956580967,1.09306319770119,1.092915244023811,1.094885640505868,1.094171202526922,1.092523345374596,1.100564904733304,1.094200831112605,1.094001716368644,1.098530017588172,1.094081896433954,1.099230887219588,1.092892028948737,1.093709694144468,1.092862170694582,1.091487097053125,1.098520929394468,1.09510515226494,1.094272325978626,1.098468177450255,1.095849714911142,1.097952718476091,1.100746388049438,1.100114369109807,1.100521380861786,1.096938196194706,1.099992890418299,1.093106549956975,1.09552358608823,1.092801661288665,1.095956895328861,1.100419992807666]

Acho que podemos concordar que isso é bom demais para ser verdade. Apesar de o modelo ter mostrado uma precisão impressionante de 87,5%, na amostra de teste a precisão caiu cerca de 5%.

IJ      0       16:02:57.760    dimension reduction test (EURUSD,H1)    Test acc = 0.8758590697252272

Podemos usar o método de redução de dimensionalidade mais popular, a análise de componentes principais (Principal Component Analysis, PCA), para diminuir as dimensões do nosso conjunto de dados, que agora contém 10 colunas.

//--- Reduce dimension
   
pca = new CPCA(8); //Reduce the dimensions of the data to 8 columns
data = pca.fit_transform(data);
pca.extract_components(data, CRITERION_SCREE_PLOT);

Como resultado, obtivemos um modelo de regressão linear com uma precisão de 88,98% durante o treinamento e 89,991% durante o teste. A precisão não diminuiu.

DJ      0       16:03:23.890    dimension reduction test (EURUSD,H1)    Train acc = 0.8898608919375138
RH      0       16:03:23.890    dimension reduction test (EURUSD,H1)    Test acc = 0.8991693574000851

Ainda é um modelo sobreajustado, mas é muito melhor do que o modelo com 92% de precisão quando se trata de capacidade de generalização, o que é extremamente importante para um modelo de ML. Você pode reduzir ainda mais a dimensionalidade para ver quais medições de dados produziram os melhores resultados fora da amostra.

Objetivos da redução de dimensionalidade

Eficiência computacional — a redução da dimensionalidade pode acelerar o treinamento e a execução de algoritmos de aprendizado de máquina.
Melhoria da capacidade de generalização — ao reduzir a dimensionalidade, o modelo pode generalizar melhor novos dados desconhecidos, como vimos no exemplo do modelo de regressão linear.
Visualização — dados com menos dimensões são mais fáceis de visualizar e interpretar, o que facilita o entendimento humano.

O que é TruncatedSVD?

A decomposição em valores singulares truncada (TruncatedSVD) é um método de redução de dimensionalidade que pode preservar grande parte da informação original. Este método é especialmente útil em casos onde os dados têm um grande número de funções, dificultando a execução de cálculos eficientes ou a visualização dos dados.

É uma variação da decomposição em valores singulares (SVD), que aproxima a matriz original preservando apenas os k maiores valores singulares e seus vetores singulares correspondentes.

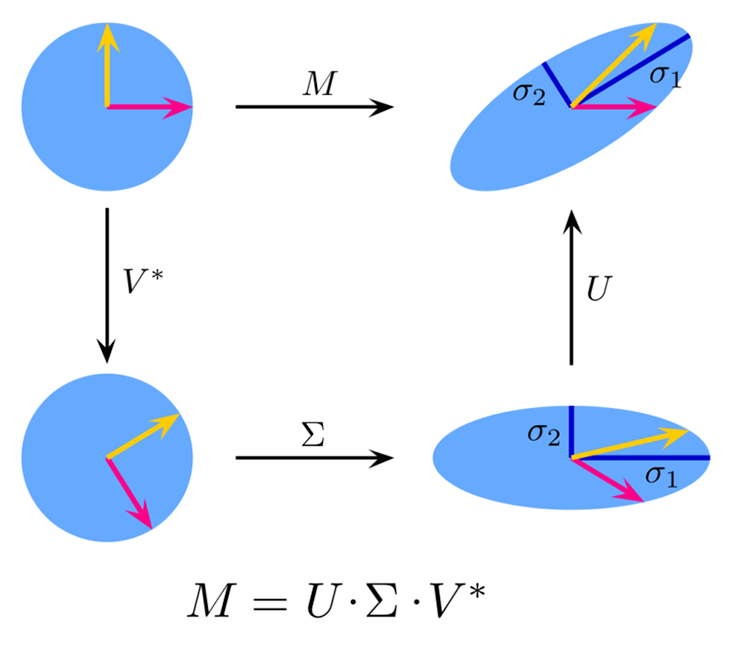
Teoria:

Fonte da imagem: Wikipedia

Para uma matriz com dimensão x , a decomposição singular é dada pela fórmula:

Onde:

— matriz ortogonal × (vetores singulares esquerdos),

— matriz diagonal × com valores singulares na diagonal,

— matriz ortogonal × (vetores singulares direitos).

O SVD truncado preserva apenas os k maiores valores singulares e os vetores correspondentes:

Onde:

— matriz ×

— matriz diagonal ×

matriz ×

Implementação:

matrix CTruncatedSVD::fit_transform(matrix &X)
 {
  n_features = X.Cols();
  
   if (m_components>n_features)
     {
       printf("%s Number of dimensions K[%d] is supposed to be <= number of features %d",__FUNCTION__,m_components,n_features);
       this.m_components = (uint)n_features;
     }
   
    // Center the data (subtract mean)
    matrix X_centered = CDimensionReductionHelpers::subtract(X, X.Mean(0));
        
   // Compute the covariance matrix
    matrix cov_matrix = X_centered.Cov(false);
    
   // Perform SVD on the covariance matrix
    matrix U, Vt;
    vector Sigma;
    
    if (!X_centered.SVD(U,Vt,Sigma))
       Print(__FUNCTION__," Line ",__LINE__," Failed to calculate SVD Err=",GetLastError());    
        
    this.components_ = CDimensionReductionHelpers::Slice(Vt, this.m_components).Transpose();
    
    if (MQLInfoInteger(MQL_DEBUG))
      Print("components\n",CDimensionReductionHelpers::Slice(Vt, this.m_components),"\ncomponents_T\n",this.components_);
    
    this.explained_variance_ = MathPow(CDimensionReductionHelpers::Slice(Sigma, this.m_components), 2) / (X.Rows() - 1);
    
    return X_centered.MatMul(components_);
 }

No MQL5, existe um método embutido para calcular a decomposição de matriz por valores singulares.

// Singular Value Decomposition.

bool matrix::SVD(
  matrix&  U,                   // unitary matrix 
  matrix&  V,                   // unitary matrix 
  vector&  singular_values      // singular values vector
   );

A função fit_transform faz o seguinte:

Centraliza os dados, subtraindo o valor médio.
Calcula a matriz de covariância dos dados centralizados (não importa).
Executa a decomposição SVD na matriz de covariância.
Preserva os k maiores valores singulares e seus vetores.
Constrói a representação da matriz original com dimensões reduzidas.

Isso realmente funciona, mas a verdadeira questão é como encontrar o melhor número de componentes k para reduzir os dados?

Cálculo da função de variância explicada

A função calcula a variância total somando os quadrados de todos os valores singulares.

ulong CTruncatedSVD::_select_n_components(vector &singular_values)
 {
    double total_variance = MathPow(singular_values.Sum(), 2);
    
    vector explained_variance_ratio = MathPow(singular_values, 2).CumSum() / total_variance;
    
    if (MQLInfoInteger(MQL_DEBUG))
      Print(__FUNCTION__," Explained variance ratio ",explained_variance_ratio);
    
    vector k(explained_variance_ratio.Size());
    
    for (uint i=0; i<k.Size(); i++)
      k[i] = i+1;
    
    plt.ScatterCurvePlots("Explained variance plot",k,explained_variance_ratio,"variance","components","Variance");
    
   return explained_variance_ratio.ArgMax() + 1;  //Choose k for maximum explained variance
 }

A função recebe como entrada uma matriz de valores singulares (singular_values). Esses valores singulares são obtidos como resultado da decomposição de matriz por valores singulares (SVD).

Em seguida, a função seleciona o número de componentes (k), encontrando o número de componentes k com a maior variância. Isso é feito na seguinte linha de código:

explained_variance_ratio.ArgMax() + 1;

Precisamos modificar a função fit_transform, permitindo a descoberta do melhor número de componentes(quando não especificado) para reduzir a dimensionalidade dos dados e aplicar o número de componentes para a decomposição Truncated SVD.

matrix CTruncatedSVD::fit_transform(matrix &X)
 {
  n_features = X.Cols();
  
   if (m_components>n_features)
     {
       printf("%s Number of dimensions K[%d] is supposed to be <= number of features %d",__FUNCTION__,m_components,n_features);
       this.m_components = (uint)n_features;
     }
   
    // Center the data (subtract mean)
    matrix X_centered = CDimensionReductionHelpers::subtract(X, X.Mean(0));
        
   // Compute the covariance matrix
    matrix cov_matrix = X_centered.Cov(false);
    
   // Perform SVD on the covariance matrix
    matrix U, Vt;
    vector Sigma;
    
    if (!cov_matrix.SVD(U,Vt,Sigma))
       Print(__FUNCTION__," Line ",__LINE__," Failed to calculate SVD Err=",GetLastError());    
        
     if (m_components == 0)
       {
         m_components = (uint)this._select_n_components(Sigma);
         Print(__FUNCTION__," Best value of K = ",m_components);
       }
            
    this.components_ = CDimensionReductionHelpers::Slice(Vt, this.m_components).Transpose();
    
    if (MQLInfoInteger(MQL_DEBUG))
      Print("components\n",CDimensionReductionHelpers::Slice(Vt, this.m_components),"\ncomponents_T\n",this.components_);
    
    this.explained_variance_ = MathPow(CDimensionReductionHelpers::Slice(Sigma, this.m_components), 2) / (X.Rows() - 1);
    
    return X_centered.MatMul(components_);
 }

O valor de k padrão é zero.

CTruncatedSVD::CTruncatedSVD(uint k=0)
:m_components(k)
 {
 
 }

Redução de dimensionalidade usando TruncatedSVD

Agora, vamos ver como os dados se comportam quando reduzidos em dimensão usando a decomposição Truncated SVD:

   truncated_svd = new CTruncatedSVD();
   
   data = truncated_svd.fit_transform(data);
   Print("Reduced matrix\n",data);

//--- 

   matrix train_x, test_x;
   vector train_y, test_y;
   
   data = matrix_utils.concatenate(data, target); //add the target variable to the dataset that is either normalized or not
   
   matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y, 0.7, 42);
     
   lr.fit(train_x, train_y, NORM_STANDARDIZATION); //training Linear regression model
   
   vector preds = lr.predict(train_x); //Predicting the training data
   
   Print("Train acc = ",metrics.r_squared(train_y, preds)); //Measuring the performance
  
   
   preds = lr.predict(test_x); //predicting the test data 
   
   Print("Test acc = ",metrics.r_squared(test_y, preds)); //measuring the performance

Resultado

LH      0       20:13:41.385    dimension reduction test (EURUSD,H1)    CTruncatedSVD::_select_n_components Explained variance ratio [0.2399955100411572,0.3875113031818686,0.3903532427910986,0.3929609228375971,0.3932960517565894,0.3933072531960168,0.3933072531960282,0.3933072531960282,0.3933072531960282,0.3933072531960282]
EH      0       20:13:41.406    dimension reduction test (EURUSD,H1)    CTruncatedSVD::fit_transform Best value of K = 7
...
...
...
MR      0       20:13:41.407    dimension reduction test (EURUSD,H1)    Train acc = 0.8934645199970468
HP      0       20:13:41.407    dimension reduction test (EURUSD,H1)    Test acc = 0.8988671205298875

Resultados surpreendentes e estáveis: 89,3% de precisão no treinamento e 89,8% no teste. E quanto ao NMF?

O que é NMF?

NMF significa fatoração de matriz não negativa. É um método de redução de dimensionalidade que fatoriza uma matriz em duas matrizes não negativas. O objetivo do NMF é representar a matriz original como o produto de duas matrizes de menor dimensão, onde todos os elementos são não negativos.

Dada uma matriz de entrada X com dimensão m×n, o método NMF a fatoriza em duas matrizes — W e H. Então:

Onde:

é uma matriz × , onde k é o número de componentes ou características.

representa uma matriz × .

Ambas e têm entradas não negativas, e essa restrição de não negatividade torna o NMF especialmente adequado para trabalhar com dados naturalmente não negativos: imagens, dados de texto, espectrogramas.

A fatoração é alcançada minimizando a norma de Frobenius da diferença entre a matriz original e sua aproximação × . Matematicamente, isso pode ser expresso assim:

onde significa a norma de Frobenius.

Implementação:

Método de transformação

matrix CNMF::transform(matrix &X)
 {
  n_features = X.Cols();
  if (m_components>n_features)
     {
       printf("%s Number of dimensions K[%d] is supposed to be <= number of features %d",__FUNCTION__,m_components,n_features);
       this.m_components = (uint)n_features;
     }
     
  if (this.W.Rows()==0 || this.H.Rows()==0)
    {
      Print(__FUNCTION__," Model not fitted. Call fit method first.");
      matrix mat={};
      return mat;
    }
  
  return X.MatMul(this.H.Transpose());
 }

A função transform transforma novos dados X, usando os componentes NMF já estabelecidos.

Método fit-transform

matrix CNMF::fit_transform(matrix &X, uint k=2)
 {
  ulong m = X.Rows(), n = X.Cols();
  double best_frobenius_norm = DBL_MIN;
  
   m_components = m_components == 0 ? (uint)n : k;      
   
//--- Initialize Random values 

   this.W = CMatrixutils::Random(0,1, m, this.m_components, this.m_randseed);  
   this.H = CMatrixutils::Random(0,1,this.m_components, n, this.m_randseed);
   
//--- Update factors
      
   vector loss(this.m_max_iter);
    for (uint i=0; i<this.m_max_iter; i++)
      {
        // Update W
         this.W *= MathAbs((X.MatMul(this.H.Transpose())) / (this.W.MatMul(this.H.MatMul(this.H.Transpose()))+ 1e-10));
         
        // Update H
         this.H *= MathAbs((this.W.Transpose().MatMul(X)) / (this.W.Transpose().MatMul(this.W.MatMul(this.H))+ 1e-10));
         
         loss[i] = MathPow((X - W.MatMul(H)).Flat(1), 2);
                    
         // Calculate Frobenius norm of the difference
        double frobenius_norm = (X - W.MatMul(H)).Norm(MATRIX_NORM_FROBENIUS);

         if (MQLInfoInteger(MQL_DEBUG))
           printf("%s [%d/%d] Loss = %.5f frobenius norm %.5f",__FUNCTION__,i+1,m_max_iter,loss[i],frobenius_norm);
         
          // Check convergence
          if (frobenius_norm < this.m_tol)
              break;
      }
  
  return this.W.MatMul(this.H); 
 }

O método fit_transform realiza a fatoração NMF na matriz de entrada X e retorna o produto das matrizes W e H.

Diferentemente do Truncated SVD, para o qual conseguimos escrever código para determinar o número de componentes e aplicá-lo a nós mesmos, facilitando o uso da biblioteca, o algoritmo de aprendizado NMF funciona de outra maneira. Ele requer repetições de n iterações para encontrar os melhores valores para o algoritmo. Durante esse ciclo, o número de componentes k deve permanecer o mesmo, portanto, a função fit_transform aceita o valor k dos componentes como um de seus argumentos.

Podemos obter o melhor número de componentes para o algoritmo de fatoração de matriz não negativa usando a função select_best_components:

uint CNMF::select_best_components(matrix &X)
{
    uint best_components = 1;
    this.m_components = (uint)X.Cols();
    
    vector explained_ratio(X.Cols());    
    for (uint k = 1; k <= X.Cols(); k++)
    {
       // Calculate explained variance or other criterion 
       matrix X_reduced = fit_transform(X, k);
   
       // Calculate explained variance as the ratio of squared Frobenius norms
       double explained_variance = 1.0 - (X-X_reduced).Norm(MATRIX_NORM_FROBENIUS) / (X.Norm(MATRIX_NORM_FROBENIUS));
        
        if (MQLInfoInteger(MQL_DEBUG))
            printf("k %d Explained Var %.5f",k,explained_variance);
       
       explained_ratio[k-1] = explained_variance;       
    }
    return uint(explained_ratio.ArgMax()+1);
}

Devido à natureza randômica de ambas as matrizes — Basic e Coefficient — os resultados do algoritmo iterativo multiplicativo também serão valores aleatórios, então o resultado deve ser imprevisível, a menos que o estado aleatório seja definido como um valor maior que zero.

class CNMF
  {
protected:
   uint m_components;
   uint m_max_iter;
   int m_randseed;
   ulong n_features;
   matrix W; //Basic matrix
   matrix H; //coefficient matrix
   double m_tol; //loss tolerance
   
public:
                     CNMF(uint max_iter=100, double tol=1e-4, int random_state=-1);
                    ~CNMF(void);
                    
                    matrix fit_transform(matrix &X, uint k=2);
                    matrix transform(matrix &X);
                    uint select_best_components(matrix &X);
                    
  };

Redução de dimensionalidade usando NMF

Agora, vamos ver como os dados se comportam quando reduzidos em dimensão usando a fatoração de matriz não negativa:

   nmf = new CNMF(30);
   
   data = nmf.fit_transform(data, 10);
   Print("Reduced matrix\n",data);

//--- 

   matrix train_x, test_x;
   vector train_y, test_y;
   
   data = matrix_utils.concatenate(data, target); //add the target variable to the dataset that is either normalized or not
      
   matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y, 0.7, 42);
      
   lr.fit(train_x, train_y, NORM_STANDARDIZATION); //training Linear regression model
   
   vector preds = lr.predict(train_x); //Predicting the training data
   
   Print("Train acc = ",metrics.r_squared(train_y, preds)); //Measuring the performance
   
   preds = lr.predict(test_x); //predicting the test data 
   
   Print("Test acc = ",metrics.r_squared(test_y, preds)); //measuring the performance

Resultados:

DG      0       11:51:07.197    dimension reduction test (EURUSD,H1)    Best k components = 10
LG      0       11:51:07.197    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [1/30] Loss = 187.40949 frobenius norm 141.12462
EG      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [2/30] Loss = 106.49597 frobenius norm 130.94039
KS      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [3/30] Loss = 84.38553 frobenius norm 125.05413
OS      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [4/30] Loss = 67.07345 frobenius norm 118.96900
OR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [5/30] Loss = 52.50290 frobenius norm 112.46587
LR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [6/30] Loss = 40.14937 frobenius norm 105.48081
RR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [7/30] Loss = 29.79307 frobenius norm 98.11626
IR      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [8/30] Loss = 21.32224 frobenius norm 90.63011
NS      0       11:51:07.198    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [9/30] Loss = 14.63453 frobenius norm 83.36462
HL      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [10/30] Loss = 9.58168 frobenius norm 76.62838
NL      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [11/30] Loss = 5.95040 frobenius norm 70.60136
DM      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [12/30] Loss = 3.47775 frobenius norm 65.31931
LM      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [13/30] Loss = 1.88772 frobenius norm 60.72185
EN      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [14/30] Loss = 0.92792 frobenius norm 56.71242
RO      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [15/30] Loss = 0.39182 frobenius norm 53.19791
NO      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [16/30] Loss = 0.12468 frobenius norm 50.10411
NH      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [17/30] Loss = 0.01834 frobenius norm 47.37568
KI      0       11:51:07.199    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [18/30] Loss = 0.00129 frobenius norm 44.96962
KI      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [19/30] Loss = 0.02849 frobenius norm 42.84850
MJ      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [20/30] Loss = 0.07289 frobenius norm 40.97668
RJ      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [21/30] Loss = 0.11920 frobenius norm 39.31975
QK      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [22/30] Loss = 0.15954 frobenius norm 37.84549
FD      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [23/30] Loss = 0.19054 frobenius norm 36.52515
RD      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [24/30] Loss = 0.21142 frobenius norm 35.33409
KE      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [25/30] Loss = 0.22283 frobenius norm 34.25183
PF      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [26/30] Loss = 0.22607 frobenius norm 33.26170
GF      0       11:51:07.200    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [27/30] Loss = 0.22268 frobenius norm 32.35028
NG      0       11:51:07.201    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [28/30] Loss = 0.21417 frobenius norm 31.50679
CG      0       11:51:07.201    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [29/30] Loss = 0.20196 frobenius norm 30.72260
CP      0       11:51:07.201    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [30/30] Loss = 0.18724 frobenius norm 29.99074
...
...
FS      0       11:51:07.201    dimension reduction test (EURUSD,H1)    Train acc = 0.604329883526616
IR      0       11:51:07.202    dimension reduction test (EURUSD,H1)    Test acc = 0.5115967009955317

A função select_best_components encontrou que o melhor número de componentes é 10, o mesmo número de colunas no conjunto de dados que fornecemos. Para ser justo, a precisão dos dados obtidos pelo NMF ao ser aplicada ao modelo de regressão linear produziu resultados medianos: 61% durante o treinamento e 51% durante o teste. Antes de concluirmos que o TruncatedSVD é o claro vencedor nesta situação, devemos reconhecer que a fatoração de matriz não negativa (NMF) requer um grande volume de programação. Com a implementação correta e utilizando um melhor algoritmo de aprendizado, como o gradiente descendente estocástico (SGD) ou qualquer outro algoritmo de aprendizado inteligente, ele pode criar um melhor conjunto de dados, mas para implementações básicas de ambos os algoritmos! O vencedor é o Truncated SVD (no papel)

Vamos ver como ambos os métodos funcionam com grandes volumes de dados:

Aplicaremos todos os dados aos nossos algoritmos e mediremos como eles funcionam em todo o conjunto de dados. Isso dará uma ideia de qual método deve ser aplicado para obter os dados mais compactos para nosso modelo de regressão linear.

Truncated SVD vs NMF - comparação

Desta vez, nenhum dado foi filtrado, mas sim todos os indicadores ao usar o Truncated SVD.

void TrainTestLR(int start_bar=1)
 {
   string names;
   matrix data = indicators.GetAllBuffers(names, start_bar, buffer_size);   
   
//--- Getting close values

   MqlRates rates[];
   ArraySetAsSeries(rates, true);
   CopyRates(Symbol(), PERIOD_CURRENT, start_bar, buffer_size, rates);
   
   double targ_Arr[];
   ArrayResize(targ_Arr, buffer_size);
   
   for (int i=0; i<buffer_size; i++)
     targ_Arr[i] = rates[i].close;
   
   vector target = matrix_utils.ArrayToVector(targ_Arr);
      
//--- Dimension reduction process 
   
   switch(dimension_redux)
     {
      case  NMF:
        {
          nmf = new CNMF(nmf_iterations);
         
          uint k = nmf.select_best_components(data);
          //Print("Best k components = ",k);
          data = nmf.fit_transform(data, k);    
        }
        break;
      case TRUNC_SVD:
      
         truncated_svd = new CTruncatedSVD();
         data = truncated_svd.fit_transform(data);  
         
        break;
      case None:
        break;
     }
     
//---

  Print(EnumToString(dimension_redux)," Reduced matrix[",data.Rows(),"x",data.Cols(),"]\n",data);
  
//--- 

   matrix train_x, test_x;
   vector train_y, test_y;
   
   data = matrix_utils.concatenate(data, target); //add the target variable to the dimension reduced data
      
   matrix_utils.TrainTestSplitMatrices(data, train_x, train_y, test_x, test_y, 0.7, 42);
      
   lr.fit(train_x, train_y, NORM_STANDARDIZATION); //training Linear regression model
   
   vector preds = lr.predict(train_x); //Predicting the training data
   
   Print("Train acc = ",metrics.r_squared(train_y, preds)); //Measuring the performance
   
   preds = lr.predict(test_x); //predicting the test data 
   
   Print("Test acc = ",metrics.r_squared(test_y, preds)); //measuring the performance

 }

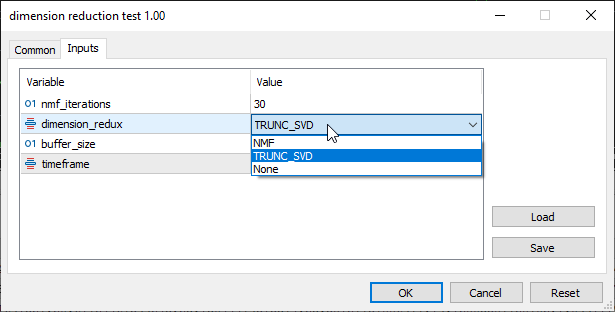
Nos parâmetros de entrada, escolhemos TRUNC_SVD:

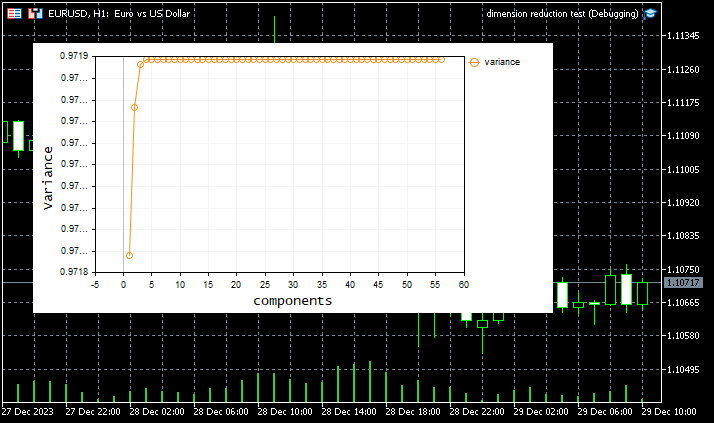
Os resultados foram impressionantes, como esperado para o método Truncated SVD. Os dados foram comprimidos em 11 componentes úteis no ponto central do gráfico abaixo.

Resultado

KI      0       13:35:07.262    dimension reduction test (EURUSD,H1)    [56x56] Covariance
HS      0       13:35:07.262    dimension reduction test (EURUSD,H1)    [[1.659883222775595e-05,0.03248108864728622,0.002260592127494286,0.002331226815118805,0.0473802958063898,0.009411152185446843,-0.0007144995075063451,1.553267567351765e-05,1.94117385500497e-05,1.165361279698562e-05,1.596183979153003e-05,1.56892102141789e-05,1.565786314082391e-05,1.750827764889262e-05,1.568797564383075e-05,1.542116504856457e-05,1.305965012072059e-05,1.184306318548672e-05,0,1.578309112710041e-05,1.620880130984106e-05,3.200794587841053e-07,1.541769717649654e-05,1.582152318930163e-05,5.986572608120619e-07,-7.489818958341503e-07,-1.347949386573036e-07,1.358668593395908,-0.0551110816439555,7.279528408421348e-05,-0.0001838813666139953,5.310112938097826e-07,6.759105066381161e-07,1.755806692036581e-05,-1.448992128283333e-07,0.003656398187537544,-2.423948560741599e-05,1.65581437719033e-05,-0.01251289868226832,-0.007951606834421109,8.315844054428887e-08,-0.02211745766272421,58.3452835083685,-0.004138620879652527,115.0719348800515,0.7113815226449098,-3.467421230325816e-07,1.456828920113124e-05,1.536603660063518e-05,1.576222466715787e-05,6.85495465028602e-07,0,0,1.264184887739262e-06,-8.035590653384948e-05,-6.948836688267333e-07]
DG      0       13:35:07.262    dimension reduction test (EURUSD,H1)     [0.03248108864728622,197.2946284096305,47.5593359902222,-70.84984591299812,113.00968468357,80.50832448214619,-85.73100643892406,0.01887146397983594,0.03089371802428824,0.006849209935383654,0.03467670330041064,0.02416916876582018,0.02412087871833598,0.0345064443900023,0.03070601018237932,0.02036445858890056,0.009641324468627534,0.006973716378187099,0,0.02839705603036633,0.02546230398502955,0.000344615196142723,0.04030780408653764,0.02543558488321825,0.0003508232190957864,0.00918131954773614,0.009950700238139187,18501.50888551419,578.0227911644578,1.963532857377992,7.661630153435527,0.006966837168084083,0.004556433245004339,2.562261625497797,0.002410403923079745,118.382177007498,1.555763207775421,1.620640369180333,97.88352837129584,116.7606184094667,0.0006817870698682788,163.5401896749969,108055.4673427991,140.7005993870342,173684.2642498043,3567.96895955429,0.0026091195479834,0.01088219157686945,0.01632411390047346,0.02372834986595739,0.02071124643451263,0,0,0.003953688163493562,-1.360529605248643,-0.04542261766857811]
IL      0       13:35:07.262    dimension reduction test (EURUSD,H1)     [0.002260592127494286,47.5593359902222,39.19958980374253,-35.49971367926001,7.967839162735706,33.38887983973432,-33.90876164339727,-0.001453063639065681,-0.000297822858867019,-0.002608304419264346,0.002816269112655834,-0.0006711791217058063,-0.0006698381044796457,0.002120545460717355,0.002300146098203005,0.0001826452994732207,-0.0003768483866125172,-0.002445364564315893,0,0.0003665645439668078,-0.003400376924338417,-1.141907378821958e-06,0.006568498854351883,0.0006581929826678372,-0.0005502523415197902,0.00579179204268979,0.006348707171855972,7967.929705662135,452.5996105540225,0.7520153701277594,4.211592829265125,0.001461149548206051,0.0001367863805269901,0.8802824558924612,0.001324363167679062,50.70542641656378,0.6826775813408293,0.5131585731076505,116.3828090044126,97.64469627257866,5.244397974811099e-05,113.6246589165999,13312.60086575102,66.02007474397942,15745.06353439358,3879.735235353455,0.002648988695504766,-0.00244724050922883,-0.00263645588222185,-0.001438073133818628,0.005654239425742305,0,0,-0.000119694862927093,-0.3588916052856576,-0.1059287487094797]
EM      0       13:35:07.262    dimension reduction test (EURUSD,H1)     [0.002331226815118805,-70.84984591299812,-35.49971367926001,60.69058251292376,1.049456584665883,-42.35184208285295,60.90812761343581,0.008675881760275542,0.008620685402656748,0.008731078117894331,-0.000667294720674837,0.005845080481159768,0.005833401998679988,0.002539790385479495,0.001675796458760079,0.00792229604709134,0.01072137357191657,0.01189054942647922,0,0.003518070782066417,0.00809138574827074,0.0002045106345618818,-0.005848319055742076,0.005549764528898804,0.00103946798619902,-0.008604821519805591,-0.007960056731330659,-10509.62154107038,-607.7276555152829,-1.225906326607001,-5.179537786920108,-0.003656220590983723,-0.001714862736227047,-1.657652278786164,-0.001941357854756676,-80.61630801951124,-1.158614351229071,-1.010395372975761,-137.5151461158883,-129.0146405010356,…]
DK      0       13:35:07.264    dimension reduction test (EURUSD,H1)    CTruncatedSVD::_select_n_components Explained variance ratio [0.9718079496976207,0.971876424055512,0.9718966593387935,0.971898669685807,0.9718986697080317,0.9718986697081728,0.9718986697082533,0.9718986697082695,0.9718986697082731,0.9718986697082754,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757,0.9718986697082757]
JJ      0       13:35:07.282    dimension reduction test (EURUSD,H1)    CTruncatedSVD::fit_transform Best value of K = 11
FE      0       13:35:07.282    dimension reduction test (EURUSD,H1)    components
GP      0       13:35:07.282    dimension reduction test (EURUSD,H1)    [[1.187125882554785e-07,1.707109381366902e-07,-2.162493440707256e-08,-3.212808990986057e-07,1.871672229653978e-07,-1.333159242305641e-05,-1.709658791626167e-05,5.106786021196193e-05,2.160157948893384e-05,-1.302989528292599e-06,4.973487699412528e-06,2.354866764130305e-06,0.0001127065022780296,-0.0001141032171988836,-7.674973628685988e-05,4.318893830956814e-06,-8.017085790662858e-05,1.258581118770149e-05,0.001793756756130711,0.0002550931459979332,0.0005154637372606566,0.001801147973070216,0.0001081777898713252,0.1803191282351903,-0.0971245889819613,0.1677985300894154,0.1116153850447159,0.6136670152098842,0.022810600805461,-0.4096528016535661,-0.04163009420605639,-6.077467743293966e-06,-0.01526638316446551,-0.5288520838909793,-0.03965140358106178,-0.1758179670991415,-0.003645717072725773,-0.0587633049540756,0.004124498383003558,-0.1172419838852104,0.06762215235985558,-0.04328191674666172,0.002573659612267772,0.003811049362514162,-0.0659455961610354,-0.02792883463906511,0.008647163802477509,-0.05514899696636823,0.008017364204121686,2.516946811168054e-06,-0.1623798112317545,6.339565837779877e-07,-9.103773865679859e-08,0,0,0]
CH      0       13:35:07.282    dimension reduction test (EURUSD,H1)     [0.000187434605818864,0.002812180913638008,0.000925532096115269,0.003073325320378009,0.009404433538995808,-0.1105512584754667,-0.2590049789665196,0.4726584971639716,0.1447383637844528,-0.05374370025421956,-0.752572111353205,0.04852191253671465,-0.1154729372340165,-0.2700032006603445,0.1267147455792905,-0.04806661586591762,-0.0004106947202907203,-0.001517506503982104,-0.003502569576390078,-0.002616630851275089,-0.0003258690084512006,-1.313122566421376e-05,-0.0009386837340425192,7.909925585103072e-05,-7.798476572374581e-05,-8.126463184191059e-05,5.556082790448295e-05,-2.687039190421141e-05,-6.540787996573879e-06,1.330764390715927e-05,-4.491635420079414e-05,-8.144156726118825e-06,-8.508538790002811e-07,5.307068574641107e-05,8.482440778162809e-06,-2.9724306932086e-05,2.843845070244019e-05,1.220433778827776e-05,4.206331251218703e-06,1.256512854012554e-05,7.365925693883173e-06,-1.116338606511276e-05,-2.071419560390051e-06,-3.218285979262829e-06,-1.138651025910271e-05,-7.728111919788928e-06,-4.653652137908648e-06,-9.580813709785919e-06,-1.028740118967147e-05,-6.979591632948435e-06,8.116615752437345e-06,1.763108270729631e-06,-4.348070304093866e-07,0,0,0]
JR      0       13:35:07.282    dimension reduction test (EURUSD,H1)     [1.848792316776081e-05,0.0008588118715707877,0.001008311173244842,0.002376194713912998,0.03118554398340165,0.07889519945845663,-0.07568381470451135,0.0286506682781276,-0.09873220604411656,-0.09161678196011247,-0.06574722506621368,-0.8477734032486133,-0.2533539865405071,0.01738574140899809,-0.2520128661222155,0.338533576002899,0.03018091859501061,0.03802772499047165,-0.001646103636389454,-0.00230341248842314,0.007310099460075021,-0.006012419384786831,-0.001413152018214914,2.142238614111051e-05,2.944210407515316e-05,-6.521097350129076e-05,4.95794487446122e-05,-8.706533732190571e-06,3.322659358695792e-05,-8.146689287415223e-07,7.338661273889888e-06,6.605547217087068e-06,9.447199984574336e-06,-5.17902002055696e-05,2.513872334761899e-06,-2.256988836110105e-05,-1.911456753589991e-05,-3.264899090321399e-05,-5.800966034108816e-06,1.84157480007614e-05,5.356185659483905e-06,-1.722849771456492e-05,1.407694486288703e-05,-7.853816348797691e-06,-1.555432680785718e-05,1.323568644672602e-05,-6.760913172750632e-06,-1.302135272406512e-05,-3.211793238456227e-06,5.802687671843603e-07,-4.280158053673846e-06,1.549960937140237e-06,-4.919157307518426e-07,0,0,0]
ND      0       13:35:07.282    dimension reduction test (EURUSD,H1)     [4.113935038265459e-05,-0.00163116425762962,-0.0006793200544509552,-0.002550542034446345,-0.0360619764220519,-0.05083503039040507,0.1457232134777539,-0.1319534223026893,-0.1000465688426969,0.03066773678926198,0.211126338548004,0.02610057183969087,-0.4621259104920466,-0.5881871797892803,0.5329599008633419,0.2326293789423069,-0.004192622153062945,-0.05839467173045784,0.002320319216461524,0.007699098543144081,-0.007658991162669676,-0.003166005488782055,-0.002283364895801648,0.0001978857108759482,9.652410400630472e-05,5.391765247424044e-05,-2.114027852314159e-05,-3.571496353187668e-06,6.919610375993553e-06,-2.388732546126286e-05,-1.795211964869842e-05,-4.375012411627235e-05,-6.279526099805299e-05,2.71361750709131e-06,-2.519904126359203e-05,-3.154274545518064e-05,-4.95034356619025e-05,4.982607182957078e-05,2.91223664932767e-05,7.266298957499022e-06,-5.27732883601878e-0…]
QD      0       13:35:07.283    dimension reduction test (EURUSD,H1)    TRUNC_SVD Reduced matrix[100x11]
FJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)    [[3032.510155721446,0.6797958296629614,0.3147476036369294,-1.879105115460979,2.342311343896795,-1.444862488231156,1.72748820545895,9003.45453268309,6583.0037062413,11248.15180107277,7664.89601210886]
QF      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2613.746957390415,0.8994353272147151,0.2278876639409569,-1.833173521667439,2.422820504229084,-1.194855144516288,1.619766862896731,8730.428168136412,6321.389560496657,10843.26327739175,7319.502533761807]
PE      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2290.391536977857,0.8379176898463352,0.123448650655239,-1.79572777997295,2.553555290053082,-1.261720012039457,1.872612496522998,9359.431555011421,6628.023623123124,11573.90347441899,7725.564567458286]
MG      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1793.638587775052,0.8840827856664026,-0.009259140368535656,-1.812929578463889,2.752934946133839,-1.194132624145421,2.137669035967074,10045.24774931484,6958.660329797975,12319.85906895874,8090.242616080116]
IG      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1067.248927502046,0.9361386848947133,0.2824462001532311,-2.094258230827017,2.302295904768048,-0.9859566963069195,1.849760818059724,8852.426567434784,5936.081092995532,10850.91447636461,7048.244994007338]
NK      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [875.831228770905,1.10630868463423,0.3875078994082357,-2.07189694520072,2.003365098290179,-0.8110375102176066,1.363090061871958,7086.981018896034,4689.12320342304,8755.082428498208,5718.774787652458]
GK      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [750.5105412678478,1.58876151742295,0.4277968820488219,-2.495434492237099,2.546292376170158,-0.5828893757361142,1.468026541982692,8457.543559890122,5579.75159746014,10352.91442474459,6691.476688344664]
EK      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1028.864261893481,1.737564309663063,0.6859148896559381,-2.576387294650619,2.22158096752311,-0.3483142589026745,0.9424367352835165,7447.770506698205,5028.271311988544,9145.898159310427,5970.749558054185]
MJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1315.206321750198,1.599230058650526,1.006274380327883,-2.7208483981554,1.702262719567507,-0.3336344655640055,0.5851633683692923,6123.681144041253,4208.879528858515,7625.280231352584,5091.190116446857]
PI      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1040.359603039049,2.015870643904685,1.297584348509677,-3.422661750068991,2.051984203691556,-0.1752179554187868,0.625382499042994,7446.846626605789,4973.286352001192,9200.911151239434,6040.469516939555]
MJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2056.827104147074,0.6969653180001977,0.5026500071613408,-1.539526411095017,1.333168361525386,-1.205142789226661,0.6457357287148752,4362.936467349854,3118.514061447938,5739.541487386377,4094.4444510553]
KI      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2595.720157415741,0.5163475309230526,0.7707831677360033,-1.609464385287863,0.6391376890497206,-1.091660522613616,0.2434028653397404,2245.471581325966,1932.755290423922,3219.551710692477,2600.234934440349]
FJ      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [2000.813854424802,-0.1645196557230545,0.0271698872028618,-1.136148599089293,1.199419424319289,-1.596267278271581,1.616290624329739,4340.908808342276,3155.426978423527,5643.263654816839,4006.305187235153]
GN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [714.201770611258,0.3322650152566928,-0.128924730742915,-1.497052055771412,1.889908667964611,-1.18328154703613,2.040965402442796,6411.664479403819,4214.549479233159,7917.864243044486,5153.2871400763]
PN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [676.7845833423586,0.1119963611895549,-0.4614956061196153,-0.7783442013329294,1.680735950870798,-1.110059082233565,1.926793017792492,5379.745050208609,3591.380424598063,6620.153862582291,4307.434978894435]
GL      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [766.9657214036708,0.3283061830008722,-0.3885600107901345,-1.031650548898253,1.912288786544761,-1.036499883901753,2.01321049032323,6312.725946828255,4249.957068368147,7723.98867795246,5012.0279192467]
LN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1272.697206108888,-0.3546159778199272,-0.7521309963906442,-0.1806331494361637,1.527697751794935,-1.486437217294949,2.136800392269752,5073.89079322631,3559.651506707118,6317.965379534476,4229.397904810504]
RM      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1869.479624807111,-0.0175694426730242,-0.7678796689175619,-0.2643173159395689,1.862033543014759,-1.44967470564508,2.028361828380722,5639.625182760593,4124.447639836587,7033.466549718048,4777.911629224665]
GN      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1936.02506453734,0.0845940044872068,-0.8282752540396139,-0.2824304083282199,1.982789807497455,-1.350085518779075,2.085883725566998,5911.195073473721,4372.189044548059,7316.534104301676,4945.624347822407]
CR      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1844.238763352675,-0.4606751585910102,-1.187448989349241,0.2320045292554417,1.900279565663612,-1.62110507361112,2.534343850099422,5907.730651516376,4364.59879103891,7282.962351393813,4893.24121551531]
ER      0       13:35:07.283    dimension reduction test (EURUSD,H1)     [1716.303347926322,-0.2450617860724134,-0.9482067759826802,-0.03979477150523128,1.79416546386642,-1.453641927846228,2.284520496569503,5710.722665215339,4183.828568899002,7048.670774203967,4734.907606214866…]
GP      0       13:35:07.283    dimension reduction test (EURUSD,H1)    Train acc = 0.8087284075835584
ER      0       13:35:07.283    dimension reduction test (EURUSD,H1)    Test acc = 0.7286157353628964

A precisão foi de 80% na fase de treinamento e 72% na fase de teste.

Fatoração de matriz não negativa (NMF)

O método NMF não conseguiu mostrar resultados valiosos, pois tudo o que produziu foram valores nan, e, no momento, ele não é mais um concorrente.

LK      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [1/100] Loss = nan frobenius norm nan
II      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [2/100] Loss = nan frobenius norm nan
FG      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [3/100] Loss = nan frobenius norm nan
KF      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [4/100] Loss = nan frobenius norm nan
PD      0       13:43:09.997    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [5/100] Loss = nan frobenius norm nan
PR      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [6/100] Loss = nan frobenius norm nan
KP      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [7/100] Loss = nan frobenius norm nan
NO      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [8/100] Loss = nan frobenius norm nan
QM      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [9/100] Loss = nan frobenius norm nan
MH      0       13:43:09.998    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [10/100] Loss = nan frobenius norm nan
....
....
LM      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [97/100] Loss = nan frobenius norm nan
OO      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [98/100] Loss = nan frobenius norm nan
NI      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [99/100] Loss = nan frobenius norm nan
CI      0       13:43:10.006    dimension reduction test (EURUSD,H1)    CNMF::fit_transform [100/100] Loss = nan frobenius norm nan
MI      0       13:43:10.008    dimension reduction test (EURUSD,H1)    NMF Reduced matrix[100x56]
FN      0       13:43:10.008    dimension reduction test (EURUSD,H1)    [[nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
EF      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
GK      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
QO      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan]
CL      0       13:43:10.008    dimension reduction test (EURUSD,H1)     
...
....
EO      0       13:43:10.008    dimension reduction test (EURUSD,H1)     [nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan…]
EL      0       13:43:10.010    dimension reduction test (EURUSD,H1)    Train acc = nan
GJ      0       13:43:10.010    dimension reduction test (EURUSD,H1)    Test acc = nan

Vamos tentar construir um modelo de regressão linear sem usar o método TruncatedSVD, aplicando todos os dados e vendo seu desempenho.

GM      0       13:53:03.686    dimension reduction test (EURUSD,H1)    None Reduced matrix[100x56]
MG      0       13:53:03.686    dimension reduction test (EURUSD,H1)    [[1.099900334222465,28.09636760954466,23.62682944559725,20.05254468697356,24.9034642580335,25.12500390358301,19.04617822178984,1.098553499999958,1.102834674021181,1.094272325978734,1.100734208567449,1.100855469999989,1.098655958571417,1.100133799959087,1.09983,1.097395,1.0950725,1.094895,1.10265,1.100030000000004,1.09944087984,0.03659425270713104,1.100626095746222,1.098825209694279,0.001265714285714323,1.705459946510501e-05,0.0009170545994650059,1655.083284093067,24.54629344924639,0.4388379204892836,0.1040346153847089,0.001226921314023466,0.0012463900886654,100.1775875415509,-1.946877464193406e-05,63.53135141907871,0.1040413928121892,0.1171616554839711,43.66576819407196,56.26437671196908,0.000170982627085528,-39.78494623655773,-2966278.270646845,59.66122501825306,-426422,2459,-0.0002127529411762598,1.096805768175659,1.098423909197834,1.099767192241293,0.00330055882353042,1.797693134862316e+308,1.797693134862316e+308,0.001618141022174502,0,0.03660024400162265]
DH      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.099895090784212,25.44125240854614,20.47658551951762,17.37887206204375,24.10764337690182,24.31185250851098,18.42976333679036,1.098807999999958,1.102730359493936,1.09488564050598,1.100648597660533,1.100904089999989,1.09870448142856,1.100085345856641,1.09983,1.097395,1.0949775,1.09511,1.10237,1.100145000000004,1.09954,0.03659633771631932,1.100539015261062,1.098860393123325,0.001167857142857174,0.000137475370969975,0.0006774753709699599,1151.094538712408,-2.654176423441059,0.4388379204892836,0.1582615384614039,0.001148578761165142,0.001262448000841409,100.0618688017469,-0.0001138692396762668,61.34588689321424,0.1137518684603838,0.1082289779011129,39.39899833055219,47.44710420521373,0.000170240277350424,-32.25806451612595,-2966207.715091289,53.52331983100873,-424517,1905,-0.0003920588235292355,1.097045324469839,1.098718420548105,1.099909753793035,0.003008823529412785,1.797693134862316e+308,1.797693134862316e+308,0.001673096078265379,0,0.0283464566929126]
LG      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.099896454740888,23.0468607955726,17.74637411691527,20.61724467599245,23.13044479515374,23.58127757886977,19.12803587728702,1.099111999999958,1.102374285088665,1.095849714911251,1.100636052620929,1.100962719999989,1.098762994285703,1.100079584777576,1.09983,1.097395,1.0949025,1.09511,1.10224,1.100252000000004,1.10126,0.03659849012444888,1.10032475011848,1.098869304036258,0.001062857142857168,-6.787825345444531e-05,0.0004021217465455251,385.6853260090575,21.57900929644156,0.4735973597359621,0.1358284615387142,0.001095648513071756,0.001261794377734486,100.0745976729165,-0.00016614586466273,63.02688593246703,0.1054308010829696,0.1073759442661703,21.12676056338241,34.73050902933566,0.000167907541851923,-45.79710144927351,-2967636.417218948,63.24364017027852,-427004,2487,-0.0004969529411762387,1.097296453356775,1.098949867979591,1.099885803034428,0.002709058823530563,1.797693134862316e+308,1.797693134862316e+308,0.001653414622816651,1,0.0188982710092469]
OH      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.09988711983821,22.27698129412946,15.38019090132657,21.80270494870316,22.00511532835773,22.64977536234809,19.53807060936342,1.099376999999958,1.101815803805105,1.096938196194811,1.100524122300143,1.101012769999989,1.098812944285703,1.100014455800224,1.099825,1.097395,1.09474,1.09511,1.10151,1.100228000000004,1.1012264,0.03660061924403133,1.100053014395182,1.098898955035223,0.0009950000000000245,-0.0002124670743897106,0.0003975329256102889,-665.9989270069636,-29.795012402167,0.4599358974358811,0.1292584615385153,0.001012177253020718,0.001241318811166551,100.0636954266684,-0.000229141558145832,59.22581938383797,0.05654610290371272,0.09982547246710144,18.13186813187058,26.21920900860187,0.0001634553208976355,-53.91304347826081,-2969847.417218948,53.21227207754287,-429215,2211,-0.000519241176470371,1.097569033867792,1.099141134482142,1.099908642427543,0.002445970588236479,1.797693134862316e+308,1.797693134862316e+308,0.001572100614350314,1,0.02758932609678876]
HJ      0       13:53:03.687    dimension reduction test (EURUSD,H1)     [1.099803229128606,19.89136498265082,20.62876885414336,18.89567762220941,21.68993269258447,25.44873831711815,17.83416777391867,1.099577499999958,1.101202281523733,1.097952718476183,…]
EK      0       13:53:03.689    dimension reduction test (EURUSD,H1)    Train acc = -nan
MR      0       13:53:03.689    dimension reduction test (EURUSD,H1)    Test acc = -nan

O modelo de regressão linear não conseguiu por si só gerar resultados para esse enorme conjunto de dados. Há algumas medidas que podem ser tomadas para resolver os problemas, como a normalização dos dados de entrada, a eliminação da instabilidade numérica e muito mais, que discutiremos em artigos futuros. Você sempre pode acompanhar as atualizações e mudanças futuras nas bibliotecas discutidas neste artigo no repositório GitHub:

Vamos analisar as vantagens e desvantagens de cada método de redução de dimensionalidade:

Vantagens do método TruncatedSVD

Preservação da variância:

O método SVD busca preservar o máximo de variação possível dos dados originais. Ele fornece uma maneira de representar os dados em um espaço de menor dimensão, mantendo as informações mais importantes.

Ortogonalidade dos componentes:

Os componentes (vetores singulares) obtidos pelo SVD são ortogonais, o que pode ser útil em certas aplicações. A ortogonalidade simplifica a interpretação dos componentes.

Estabilidade numérica:

Uma das vantagens do método SVD é sua estabilidade numérica. Ele lida bem com dados esparsos e ruidosos. A decomposição é baseada na decomposição de valores próprios da matriz de covariância.

Aplicações para compressão de imagens e redução de ruído:

O SVD é frequentemente usado para compressão de imagens e redução de ruído. Os valores singulares determinam a importância das medidas, e seu truncamento permite compressão, minimizando a perda de informações.

Vantagens da fatoração de matriz não negativa (NMF)

Representação baseada em partes:

O NMF aplica restrições de não negatividade tanto à matriz básica quanto à matriz de coeficientes. Isso resulta em uma representação baseada em partes, o que pode ser útil, por exemplo, na modelagem de tópicos ou na análise de imagens.

Interpretabilidade:

A restrição de não negatividade muitas vezes leva a fatores mais interpretáveis. Por exemplo, nos tópicos extraídos de dados textuais, cada tópico é representado como uma combinação linear não negativa de palavras, tornando os tópicos mais interpretáveis.

Aplicação na análise de documentos e processamento de imagens:

O método NMF é frequentemente usado na análise de documentos (modelagem de tópicos) e no processamento de imagens. Ele pode revelar padrões subjacentes nos dados e é especialmente útil quando os dados contêm naturalmente componentes não negativos.

Representações esparsas:

O NMF cria representações esparsas, onde apenas um subconjeto de componentes é usado para representar cada ponto de dados. Isso pode ser útil ao lidar com dados multidimensionais.

Vantagens gerais

Redução de dimensionalidade:

Tanto o SVD quanto o NMF fornecem métodos eficazes para reduzir a dimensionalidade dos dados, o que pode ser crucial para lidar com conjuntos de dados multidimensionais e extrair recursos significativos.

Extração de características:

Ambos os métodos são úteis para a extração de características, que pode melhorar o desempenho dos modelos de aprendizado de máquina e ajudar na interpretação dos dados.

Redução de ruído:

Ambos os métodos podem ajudar a reduzir o ruído nos dados, coletando informações importantes e filtrando o ruído.

Desvantagens do método TruncatedSVD

Sensibilidade a valores atípicos:

O método SVD pode ser sensível a valores atípicos nos dados, pois busca minimizar a soma dos erros quadráticos médios. Valores atípicos podem ter um impacto significativo na decomposição.

Complexidade computacional:

Calcular o método SVD completo pode ser computacionalmente caro, especialmente para grandes conjuntos de dados. O método TruncatedSVD usa uma aproximação, mas ainda pode exigir dados multidimensionais.

Aplicabilidade limitada a dados esparsos:

A eficiência do SVD é menor ao trabalhar com dados muito esparsos, pois a presença de muitos valores zero pode afetar a precisão da decomposição.

Complexidade de interpretação:

Embora os componentes obtidos pelo SVD sejam ortogonais, a interpretação desses componentes pode ser complexa, especialmente em comparação com o NMF, que impõe restrições de não negatividade.

Desvantagens do método de fatoração de matriz não negativa (NMF)

Não unicidade das soluções:

As soluções NMF não são únicas, o que significa que diferentes inicializações podem levar a diferentes fatorações. A falta de unicidade pode dificultar a comparação de resultados de diferentes execuções.

Dificuldade com entradas nulas:

O NMF enfrenta dificuldades ao lidar com entradas nulas na matriz de dados. Trabalhar com dados ausentes ou valores nulos requer atenção especial, como a remoção de valores Nan e Infinity.
void CDimensionReductionHelpers::ReplaceNaN(matrix &mat)
 {
   for (ulong i = 0; i < mat.Rows(); i++) 
     for (ulong j = 0; j < mat.Cols(); j++) 
       if (!MathIsValidNumber(mat[i][j]))
          mat[i][j] = 0.0;
 }

Escolha do rank (número de componentes):

Determinar o rank adequado (número de componentes) para o NMF pode ser uma tarefa desafiadora. A escolha incorreta pode levar ao sobreajuste ou subajuste dos dados.

Aplicabilidade limitada a valores negativos:

O NMF impõe a restrição de não negatividade, o que significa que o método não é adequado para conjuntos de dados em que valores negativos fazem sentido. Essa limitação restringe os tipos de dados que podem ser modelados efetivamente.

Considerações gerais

Interpretabilidade e precisão da reconstrução:

O método NMF pode fornecer componentes mais interpretáveis, mas isso frequentemente é alcançado à custa da precisão da reconstrução em comparação com o SVD. A escolha entre interpretabilidade e precisão depende dos objetivos específicos da análise.

Compromissos na redução de dimensionalidade

Ambos os métodos envolvem um compromisso entre a redução de dimensionalidade e a perda de informação. O desafio é encontrar o equilíbrio ideal que preserve as principais características e minimize a perda de informação.

Hiperparâmetros algorítmicos:

Para obter resultados ótimos, tanto o SVD quanto o NMF podem exigir ajustes de hiperparâmetros, como o número de componentes ou a força da regularização. A sensibilidade a esses hiperparâmetros deve ser considerada.

Perguntas frequentes sobre redução de dimensionalidade

Pergunta. Como funcionam os métodos de redução de dimensionalidade?

Resposta. Eles transformam os dados em um novo conjunto de componentes de variáveis não correlacionadas, que refletem a máxima variação dos dados originais. Eles determinam as direções ao longo das quais os dados variam mais.

Pergunta. Quando se deve usar a redução de dimensionalidade?

Resposta. A redução de dimensionalidade é útil ao trabalhar com dados multidimensionais, como em aprendizado de máquina, processamento de imagens e bioinformática. É muito valiosa quando há funções redundantes ou desnecessárias, e a eficiência computacional, interpretabilidade ou visualização são prioridades.

Pergunta. A redução de dimensionalidade pode ser usada com qualquer tipo de dados?

Resposta. A redução de dimensionalidade pode ser aplicada a diversos tipos de dados, incluindo dados numéricos, categóricos e textuais. No entanto, a escolha do método pode variar dependendo da natureza dos dados.

Pergunta. Existem alternativas aos métodos de redução linear de dimensionalidade?

Resposta. Sim, existem métodos não lineares, como Kernel PCA, t-SNE e autocodificadores, que capturam relações complexas nos dados além das transformações lineares.

Pergunta. A redução de dimensionalidade é sempre benéfica no aprendizado de máquina?

Resposta. Nem sempre. Embora a redução de dimensionalidade possa oferecer vantagens em termos de eficiência computacional, interpretabilidade e visualização, ela nem sempre melhora o desempenho do modelo. Tudo depende das características específicas do conjunto de dados e da tarefa de aprendizado de máquina.

Pergunta. A redução de dimensionalidade pode levar à perda de informação?

Resposta. Sim, a redução de dimensionalidade pode levar à perda de informação, especialmente se a representação reduzida descartar características relevantes. O objetivo é encontrar um equilíbrio entre a redução de dimensionalidade e a preservação de informações importantes.

Pergunta. Quais problemas podem surgir ao usar métodos de redução de dimensionalidade?

Resposta. Os problemas incluem a possibilidade de sobreajuste, sensibilidade a valores atípicos, não unicidade das soluções (especialmente no NMF) e a necessidade de ajuste cuidadoso dos hiperparâmetros.

Conteúdo do anexo:

Arquivo	Descrição/propósito
helpers.mqh	Contém código que auxilia na execução de operações de redução de dimensionalidade para NMF.mqh e TruncatedSVD.mqh.
Linear Regression.mqh	Contém código do modelo de regressão linear.
matrix_utils.mqh	Operações adicionais de matriz
metrics.mqh	Biblioteca contendo código para medir o desempenho de modelos de aprendizado de máquina.
NMF	Contém a classe de Fatoração de Matriz Não Negativa (NMF)
plots.mqh	Biblioteca para construção de gráficos no símbolo atual
preprocessing.mqh	Classe contendo funções para pré-processamento de dados e preparação para aprendizado de máquina
TruncatedSVD.mqh	Classe Truncated SVD
dimension reduction test.mq5	Script para testar todo o código discutido no artigo

Peace out.

Traduzido do Inglês pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/en/articles/13968

Arquivos anexados |

Baixar como ZIP

CODE.zip (26.25 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Negociação algorítmica com MetaTrader 5 e R para iniciantes

Neste artigo, vamos combinar análise financeira com negociação algorítmica, além de ver como integrar R e MetaTrader 5. Este artigo é um guia para unir a flexibilidade analítica do R com as enormes possibilidades de negociação do MetaTrader 5.

Desenvolvimento de um Cliente MQTT para o MetaTrader 5: Metodologia TDD (Parte 5)

Este artigo é a quinta parte de uma série que descreve as etapas de desenvolvimento de um cliente MQL5 nativo para o protocolo MQTT 5.0. Nesta parte, vamos detalhar a estrutura dos pacotes PUBLISH, configuraremos seus flags de publicação, codificaremos os nomes dos tópicos e estabeleceremos identificadores de pacotes quando necessário.

Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 10): RBM não convencional

As máquinas de Boltzmann restritas (Restrictive Boltzmann Machines, RBM) são, em um nível básico, uma rede neural de duas camadas capaz de realizar classificação não supervisionada através da redução de dimensionalidade. Vamos usar seus princípios básicos e ver o que acontece se a desenharmos e a treinarmos de forma não convencional. Será que conseguiremos obter um filtro de sinais útil?

Anotação de dados na análise de série temporal (Parte 5): Aplicação e teste de um EA usando Socket

Nesta série de artigos, apresentamos vários métodos de anotação de séries temporais que podem criar dados compatíveis com a maioria dos modelos de inteligência artificial (IA). A anotação precisa dos dados pode tornar o modelo de IA treinado mais alinhado com os objetivos e tarefas dos usuários, aumentar a precisão do modelo e até ajudar a alcançar uma melhoria significativa na qualidade!