Affittuario

Nuovo commento
 

Ciao a tutti!

Mi è stato permesso di usare un deposito di X0 rubli per t mesi. Ogni mese viene depositata una percentuale fissa q del valore attuale del deposito X. Sono autorizzato a prelevare ogni mese una percentuale k dal conto, ma non può superare il valore di q.

Quindi il compito è quello di massimizzare la quantità di denaro prelevato in un periodo di t mesi. Sembra ovvio che ritirare l'intero interesse maturato q ogni mese non è l'opzione migliore, perché in questo caso il deposito non cresce e con meno carico sul conto, l'importo eventualmente ritirato può essere maggiore... D'altra parte, il valore di k non dovrebbe andare a zero, perché in questo caso anche l'importo prelevato andrebbe a zero. A quanto pare, la verità è da qualche parte nel mezzo. Ma dove esattamente?

Aiutami a risolvere analiticamente questo problema in modo generale.

P.S. Non ha postato in un ramo di zadacha non legato al commercio, perché l'argomento proposto è legato a quest'ultimo.

 
Sembra che le equazioni dovrebbero essere uguali, e poi le equazioni dovrebbero essere differenziate (il problema ricorda un'ambulanza, quando si può prendere una scorciatoia a bassa velocità attraverso un campo, o guidare su asfalto ad una velocità più alta, ma su un percorso più lungo - dove si esce dall'asfalto e si entra in un campo?)
 

Quindi la domanda è: come si fa a comporli? Finora funziona solo in forma iterativa:


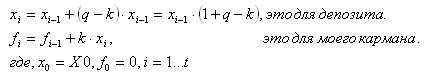
Dobbiamo presentarlo in forma analitica (come dipendenza funzionale dal tempo t).

 
Espandere ulteriormente la formula di f, cioè portarla a fi = fi(x0).
 

Allora si scopre così:

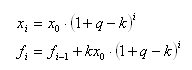
E l'espressione per la quantità di denaro prelevata in un periodo di t mesi può essere scritta come:

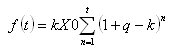
Se è così, è meglio. E poi? Dovete sbarazzarvi della quantità...

 

avrebbe un aspetto simile a questo.

 

Impossibile!...

Puoi essere più specifico? Intendo sotto forma di formula.

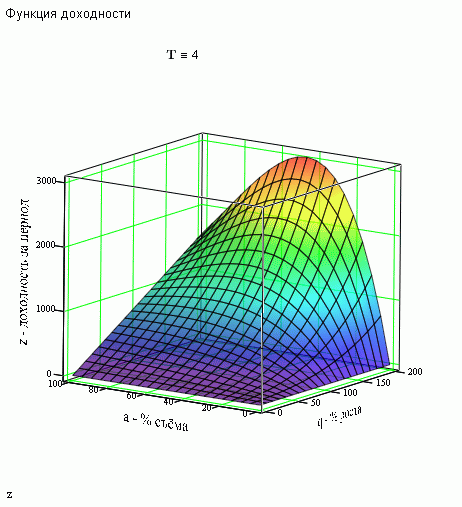
Così si può davvero vedere l'optimum in termini di percentuale di rimozione!

 
Neutron:

Se è così, è meglio. Cosa c'è dopo? Dobbiamo sbarazzarci della somma...

Ricorda la formula per la somma dei primi n termini di una progressione geometrica


 
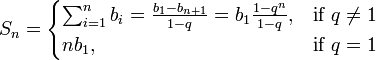
dove q è il denominatore del GP, b1 è il primo termine
 
alsu:

ricordare la formula per la somma degli n primi termini di una progressione geometrica



Shaitan! Infatti, .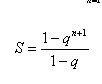

Quindi, alla fine, l'espressione per la somma dei fondi prelevati sarà data come:

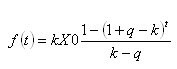
Non resta che prendere la derivata del tempo ed equipararla a zero... Sì...

 
Neutron:

Ciao a tutti!

Mi è stato permesso di usare un deposito di X0 rubli per t mesi. Ogni mese il deposito riceve una percentuale fissa q del valore attuale del deposito X. Sono autorizzato a prelevare ogni mese una percentuale k dal conto che non supera il valore di q.

Quindi il problema è quello di massimizzare la quantità di denaro prelevato in un periodo di t mesi.

È ovvio che l'importo da ritirare è q e solo alla fine del periodo t. In tutti gli altri casi l'importo prelevato sarà inferiore.
12345678910111213141516171819202122232425262728293031
Nuovo commento