Affittuario - pagina 7

Nuovo commento
 

Sono arrivato al punto in cui ho bisogno di una formula per la somma di una serie di potenze :(

Ho bisogno di questa soluzione generale, se la risposta è una singola cifra che non dipende da nessuna condizione? Scrivi un programma e lascia che una macchina di ferro faccia il lavoro.

 
Integer:

Sono arrivato al punto in cui ho bisogno di una formula per la somma di una serie di potenze :(


Beh, è un po' un non-problema! Disegna una vista generale di una serie di potenze.

 

La formula del profitto prelevabile per ogni mese:

fp = (d * (1 + pp) ^ (m - 1)) * ps

d è il deposito iniziale.

Il tasso bancario (rapporto) è pp+ps. pp - lo teniamo, ps - lo ritiriamo. All'inizio facciamo il deposito (pp+ps), e poi ne ritiriamo una parte (ps), e teniamo l'altra parte (pp). Forse sarebbe meglio inserire il coefficiente di prelievo dal maturato, poi nella formula sarà interesse bancario e coefficiente di prelievo dal maturato).

m è il numero del mese.

 
Neutron:

Sergei,

Ti suggerisco di integrare il problema con il tasso d'inflazione, cioè ritirare il massimo possibile k = q - inflazione. (cioè il deposito non rimane inferiore all'importo iniziale in termini reali / naturalmente, per semplicità consideriamo l'inflazione come un valore costante/).

Mi chiedo quanto cambierà la soluzione.

 
alsu:



Alexei, che differenza fa?

Che il tasso d'inflazione mensile sia I per cento. Quindi, per l'equazione dell'importo del prelievo per il periodo t , possiamo scrivere: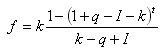

Per la derivata di k: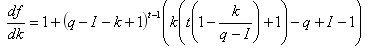 cioè sostituendo le variabili q-I con Q arriviamo automaticamente alle stesse espressioni di cui sopra e quindi non ci faciliteremo la vita in termini di ottenimento di una soluzione analitica per df/dk=0.

Cosa intendeva dire con questo? Semplicemente aggiungendo all'espressione un ulteriore termine responsabile dell'inflazione? È certamente interessante, ma non è il modo migliore per complicare il modello senza la soluzione dello scenario più semplice.

Intero:

La formula di ritiro dei profitti per ogni mese:

fp = (d * (1 + pp) ^ (m - 1)) * ps

d è il deposito iniziale.

Il tasso bancario (rapporto) è pp+ps. pp - lo teniamo, ps - lo ritiriamo. Iniziamo con pp+ps, poi ritiriamo (ps) e teniamo (pp). Forse sarebbe meglio inserire il coefficiente di prelievo dal maturato, poi nella formula sarà interesse bancario e coefficiente di prelievo dal maturato).

m - numero di sequenza del mese.

Integer, il tuo fp e il mio f sono la stessa cosa? Se è così, perché non hai 1 nel numeratore, che è preso dalla somma di una serie di potenze, e perché non hai un denominatore, che è preso dalla stessa.

 

Per prima cosa, guardiamo il riempimento del solo primo recipiente - il secondo recipiente è spento, la valvola è chiusa - non c'è prelievo dal deposito.

.


.

e ricordate che per la versione discreta utilizzata il fattore di crescita = 0,2

beh queste sono sottigliezze...

.

.

al secondo passo apriamo la valvola ;)

.

zy.

qui non introdurremo un ritardo - per non complicare le cose

 

Penso che sia utile ricordare la formula della rendita e come si ricava...

;)

 
rendita -- mi sono sempre piaciute queste parole divertenti :)))
 
Sorento:

Penso che sia utile ricordare la formula della rendita e come si ricava...

;)

È stato ricavato dai banchieri per estorcere più interessi ai clienti con la scusa di prendersi cura di loro...)
 

Beh, i banchieri non sono al sicuro!

quindi questa rendita spiega come accendere la valvola?

:)))

1234567891011121314...31
Nuovo commento