Distributions de Probabilités Statistiques dans MQL5

MetaTrader 5 — Exemples | 12 janvier 2022, 14:41

144

Denis Kirichenko

Toute la théorie des probabilités repose sur la philosophie de l'inopportunité.
(Leonid Sukhorukov)

Introduction

De par la nature de son activité, un trader doit très souvent faire face à des catégories telles que la probabilité et le hasard. L'antipode du hasard est une notion de « régularité ». Il est remarquable qu'en vertu des lois philosophiques générales, le hasard en règle générale se transforme en régularité. Nous ne discuterons pas l’opposé à ce stade. Fondamentalement, la corrélation hasard-régularité est un rapport clé car, si elle est prise dans le contexte du marché, elle affecte directement le montant du bénéfice reçu par un trader.

Dans cet article, je présenterai les instruments théoriques sous-jacents qui nous aideront à l'avenir à déceler des régularités de marché.

1.Distributions, Essence, Types

Ainsi, afin de décrire une variable aléatoire, nous aurons besoin d'une distribution statistique probability distribution Il décrira un échantillon de variables aléatoires par une certaine loi, c'est-à-dire que l'application de toute loi de distribution exigera un ensemble de variables aléatoires.

Pourquoi analyser des distributions [théoriques] ? Elles facilitent l'identification des modèles de changement de fréquence en fonction des valeurs d'attributs variables. En outre, nous pouvons obtenir quelques paramètres statistiques de la distribution requise.

En ce qui concerne les types de distributions de probabilité, il est d'usage dans les ouvrages spécialisés de diviser la famille de distribution en continue et discrète en fonction du type d'ensemble de variables aléatoires. Il existe cependant d'autres classifications, par exemple, selon des critères tels que la symétrie de la courbe de distribution f(x) par rapport à la ligne x=x0, le paramètre d'emplacement, le nombre de modes, l'intervalle variable aléatoire et autres.

Il existe plusieurs manières de définir la loi de distribution. Nous devons Souligner les plus populaires parmi elles :

2. Distributions de Probabilités Théoriques

Tentons,à présent,de créer des classes qui décrivent des distributions statistiques dans le contexte de MQL5. De plus, je voudrais ajouter que les ouvrages spécialisés fournissent de nombreux exemples de code écrit en C++ qui peuvent être appliqués avec succès au codage MQL5. Je n'ai donc pas réinventé la roue et, dans certains cas, j'ai utilisé les meilleures pratiques du code C++.

Le plus grand défi auquel j'ai été confronté était le manque de prise en charge de l'héritage multiple dans MQL5. C'est pourquoi je n'ai pas réussi à utiliser des hiérarchies de classes complexes. Le livre intitulé Numerical Recipes : The Art of Scientific Computing [2] est devenu pour moi la source la plus optimale de code C++ à laquelle j'ai emprunté la majorité des fonctions. Le plus souvent, elles ont dû être affinées en fonction des besoins du MQL5.

2.1.1 Distribution Normale

Traditionnellement, nous commençons par la distribution normale

La distribution normale, également appelée distribution gaussienne est une distribution de probabilité fournie par la fonction de densité de probabilité :

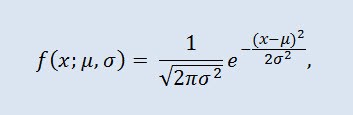
où le paramètre μ — est la moyenne (espérance) d'une variable aléatoire et indique la coordonnée maximale de la courbe de densité de distribution, et σ² est la variance.

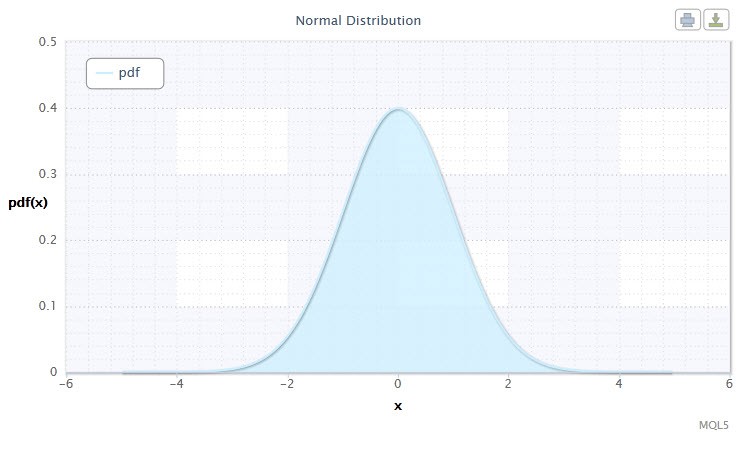
Figure 1. Densité de distribution normale Nor(0,1)

Sa notation se présente sous le format suivant : X ~ Nor(μ, σ²),où :

X est une variable aléatoire sélectionnée dans la distribution normale Nor ;
μ est le paramètre moyen (-∞ ≤ μ ≤ +∞) ;
σ est le paramètre de variance (0<σ).

Plage valide de la variable aléatoire X : -∞ ≤ X ≤ +∞.

Les formules utilisées dans cet article peuvent différer de celles fournies dans d'autres sources. Une telle différence n'est parfois pas mathématiquement capitale. Dans certains cas, elle est conditionnée à des différences de paramétrage.

La distribution normale joue un rôle important dans les statistiques car elle reflète la régularité découlant de l'interaction entre un grand nombre de causes aléatoires, dont aucune n'a de pouvoir dominant. Et bien que la distribution normale soit un cas rare sur les marchés financiers, il est néanmoins important de la comparer à des distributions empiriques afin de déterminer l'étendue et la nature de leur anomalie.

Définissons la classeCNormaldist pour la distribution normale comme suit:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

Comme vous pouvez le constater, la classe CNormaldist dérive depuis la СErf classe de base qui à son tour définit la classe defonction d’erreur. Il sera nécessaire lors du calcul de certaines méthodes de classe CNormaldist. La classe et la fonction auxiliaireСErf erfccont l’air plus au moins comme ceci:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+

2.1.2 Distribution Lognormale

Jetons à présent un coup d’ œil àlog-distribution normale.

La distribution log-normale en théorie des probabilités est une famille à deux paramètres de distributions absolument continues. Si une variable aléatoire est log-normalement distribuée, son logarithme a une distribution normale.

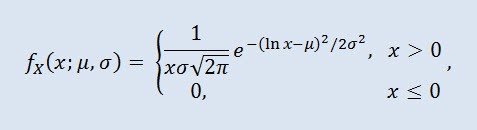
où μ est le paramètre d'emplacement (0<μ ) et σ est le paramètre d'échelle (0<σ).

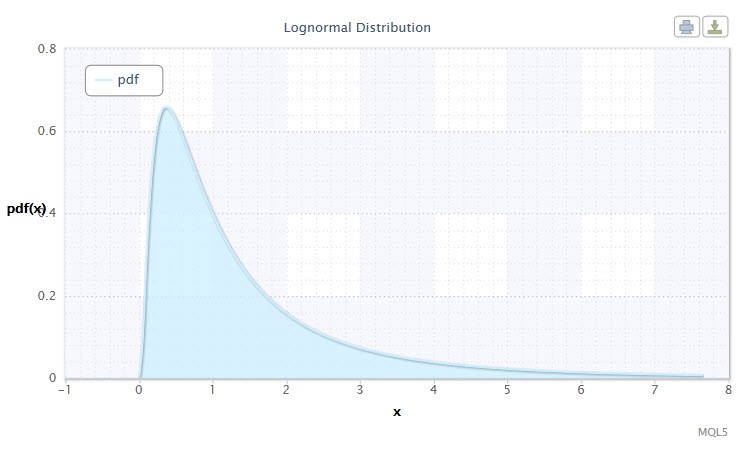
Figure 2. Densité de distribution log-normale Logn(0,1)

Sa notation se présente sous le format suivant : X ~ Logn(μ, σ²),où :

X est une variable aléatoire sélectionnée dans la distribution log-normale Logn ;
μ est le paramètre d’emplacement (0<μ );
σ est le paramètre d'échelle (0<σ).

Plage valide de la variable aléatoire X : 0 ≤ X ≤ +∞.

Créons la classe CLognormaldist décrivant la la distribution normale-log. EIle se présentera comme suit :

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Comme on peut le constater, la distribution log-normale n'est pas très différente de la distribution normale. La différence étant que le paramètre x est remplacé par le paramètre log(x).

2.1.3 Distribution de Cauchy

La distribution de Cauchy en théorie des probabilités (en physique également appelée distribution de Lorentz ou distribution de Breit-Wigner) est une classe de distributions totalement continues. Une variable aléatoire distribuée de Cauchy est un exemple courant d’une variable sans espérance et sans variance. La densité prend la forme suivante :

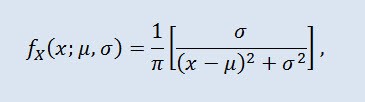
où μ est le paramètre d'emplacement (-∞ ≤ μ ≤ +∞ ), et σ est le paramètre d'échelle (0<σ).

La notation de la distribution de Cauchy distributiondispose du format suivant : X ~ Cau(μ, σ),où :

X est une variable aléatoire choisie dans la distribution de Cauchy Cau ;
μ est le paramètre d’emplacement (-∞ ≤ μ ≤ +∞ );
σ est le paramètre d'échelle (0<σ).

Plage valide de la variable aléatoire X : -∞ ≤ X ≤ +∞.

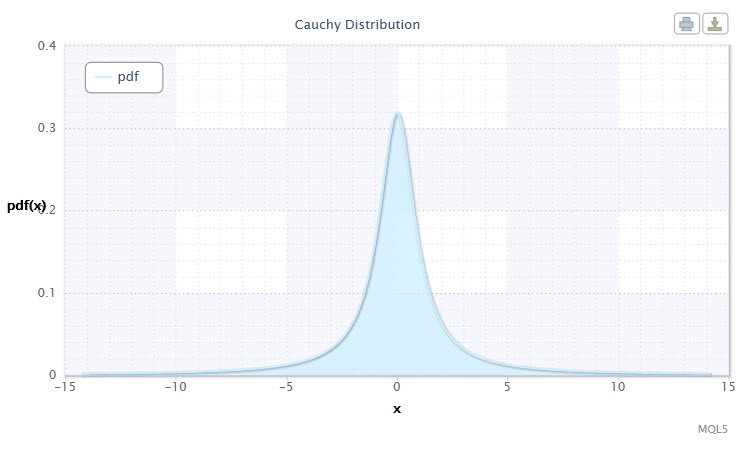
Figure 3. Distribution Cauchy densité Cau(0,1)

Créé à l'aide de la classe CCauchydist, au format MQL5, il se présente comme suit :

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Il convient de noter ici que la fonction atan2() est utilisée, qui renvoie la valeur principale de l'arc tangent en radians :

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function 
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }

2.1.4 Distribution sécante hyperbolique

Distribution hyperbolique sécante sera d’un intérêt à ceux qui traitent avec le rang de l’analyse financière.

En théorie des probabilités et statistique, la distribution sécante hyperbolique est une distribution de probabilité continue dont la fonction de densité de probabilité et la fonction caractéristique sont proportionnelles à la fonction sécante hyperbolique. La densité est donnée par la formule :

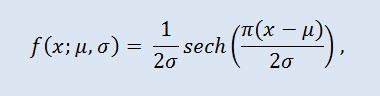
où μ est le paramètre d'emplacement (-∞ ≤ μ ≤ +∞ ), et σ est le paramètre d'échelle (0<σ).

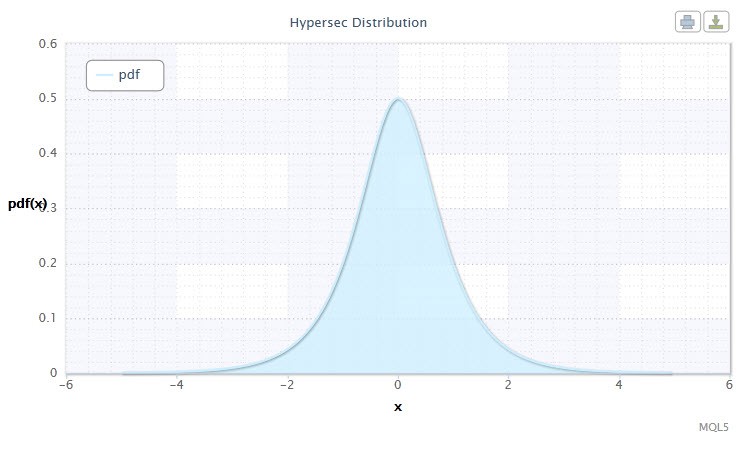
Figure 4. Hyperbolique distribution sécante densité HS(0,1)

sa notation dispose du format suivant: X ~ HS(μ, σ), où :

X est une variable aléatoire ;
μ est le paramètre d’emplacement (-∞ ≤ μ ≤ +∞ );
σ est le paramètre d'échelle (0<σ).

Plage valide de la variable aléatoire X : -∞ ≤ X ≤ +∞.

Décrivons-le en utilisant la classe CHypersecdist class comme suit:

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Il n'est pas difficile de constater que cette distribution tire son nom de la fonction sécante hyperbolique dont la fonction de densité de probabilité est proportionnelle à la fonction sécante hyperbolique.

La fonction sécante hyperbolique sech est la suivante :

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }

2.1.5 Student's t-Distribution

Student's t-distribution est une distribution importante dans les statistiques.

En théorie des probabilités, la distribution t de Student est le plus souvent une famille à un paramètre de distributions complètement continues. Cependant, elle peut également être considérée comme une distribution à trois paramètres donnée par la fonction de densité de distribution :

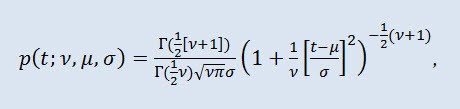
où Г est la fonction Gamma d'Euler, ν est le paramètre de forme (ν>0), μ est le paramètre d’emplacement (-∞ ≤ μ ≤ +∞ ), σ est le paramètre d'échelle (0<σ).

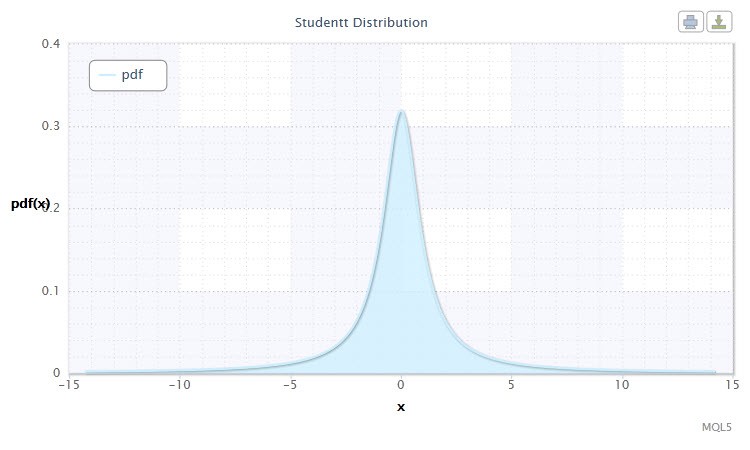
Figure 5. Student's t-distribution density Stt(1,0,1)

sa notation a le format suivant : t ~ Stt(ν,μ,σ), où:

t est une variable aléatoire sélectionnée à partir de t de Student'st-distribution Stt;
ν est le paramètre de forme (ν>0)
μ est le paramètre d’emplacement (-∞ ≤ μ ≤ +∞ );
σ est le paramètre d'échelle (0<σ).

Plage valide de la variable aléatoire X : -∞ ≤ X ≤ +∞.

Souvent, en particulier dans les tests d'hypothèses, une t-distribution standard est utilisée avec μ=0 et σ=1. Ainsi, il se transforme en une distribution à un paramètre avec le paramètre ν.

Cette distribution est souvent utilisée dans l’estimation de l'espérance, les valeurs projetées et d'autres caractéristiques au moyen d'intervalles de confiance, lors du test d'hypothèses de valeur d'espérance, de coefficients de rapport de régression, d'hypothèses d'homogénéité, etc.

Décrivons la distribution à travers la classe CStudenttdist :

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

la liste de la classe CStudenttdist montre que CBeta est une classe de base qui décrit la fonction incomplète beta .

La classe CBeta apparait comme suit:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

Cette classe dispose également de la classe de baseCGauleg18qui fournit des coefficients pour une telle méthode d’intégration numériqueGauss-Legendre quadrature.

2.1.6 Logistic Distribution

Je suggère d’examiner ladistribution logistique prochainement dans notre étude.

En théorie des probabilités et statistique, la distribution logistique est une distribution de probabilité continue. Sa fonction de distribution cumulative est la fonction logistique. EIle ressemble à la distribution normale en forme mais dispose de queues plus lourdes. Densité de distribution :

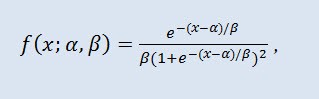
où α est le paramètre de localisation (-∞ ≤ α ≤ α ≤ +∞ ), β est le paramètre d’échelle (0<β).).

Figure 6. Logistic distribution density Logi(0,1)

Its notation dispose du format suivant : X ~ Logi(α,β), où :

X est une variable aléatoire ;
α est le paramètre de localisation (-∞ ≤ α ≤ +∞ );
βest le paramètre d'échelle (0<β).

Plage valide de la variable aléatoire X : -∞ ≤ X ≤ +∞.

La classeCLogisticdist est l'implémentation de la distribution décrite ci-dessus :

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.7 Exponential Distribution

Jetons également un coup d'œil à la distribution exponentielle d'une variable aléatoire.

Une variable aléatoire X a la distribution exponentielle de paramètre λ > 0 si sa densité est donnée par :

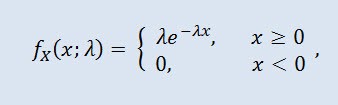
où λ est le paramètre d’échelle (λ>0).

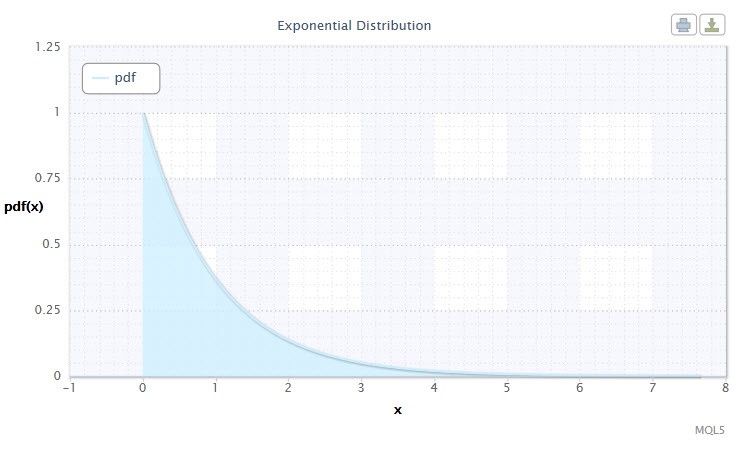
Figure 7. Exponential distribution density Exp(1)

Its notation dispose du format suivant : X ~ Exp(λ), où :

X est une variable aléatoire ;
λ est la paramètre d’échelle (λ>0).

Plage valide de la variable aléatoire X : 0 ≤ X ≤ +∞.

Cette distribution est remarquable par le fait qu'elle décrit une séquence d'événements intervenant un par un à certains moments. Ainsi, en utilisant cette distribution, un trader peut analyser une série de deals à perte et autres.

Dans le code MQL5, la distribution est décrite à travers la classe :CExpondist

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.8 Gamma Distribution

J'ai choisi la distributiongamma comme prochain type de distribution continue de variables aléatoires.

En théorie des probabilités, la distribution gamma est une famille à deux paramètres de distributions de probabilité complètement continues. Si le paramètre α est un entier, une telle distribution gamma est également appelée la distribution Erlang. La densité prend la forme suivante :

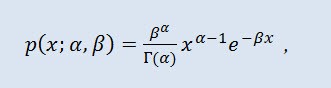
où Г est la fonction Gamma d'Euler, α est le paramètre de forme (0<α), β est le paramètre d’échelle (0<β).

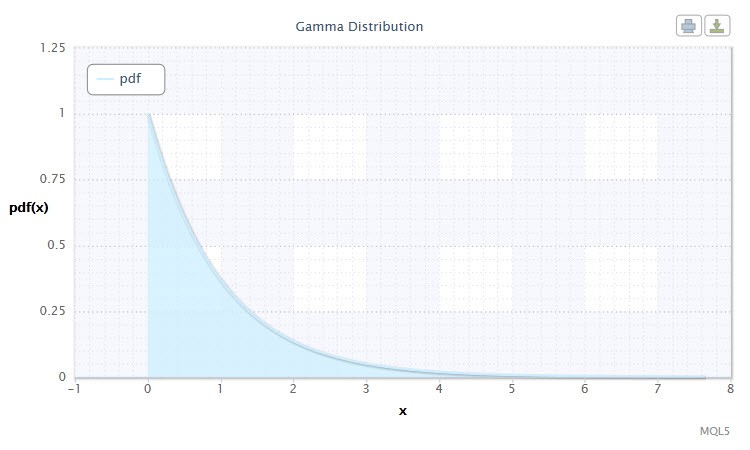
Figure 8. Gamma distribution density Gam(1,1).

Sa notation se présente sous le format suivant : X ~ Gam(α,β), où :

X est une variable aléatoire ;
α est le paramètre de forme (0<α);
βest le paramètre d'échelle (0<β).

Plage valide de la variable aléatoire X : 0 ≤ X ≤ +∞.

Dans la variante définie par la classeCGammadist , cela ressemble à ceci :

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

La classe de distribution gamma dérive de la classe CGamma qui décrit la fonction incomplète de gamma.

La classe CGamma est définie comme suit:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Les deux classes CGamma et CBeta disposent de CGauleg18comme classe de base

2.1.9 Beta Distribution

Eh bien, examinons maintenant la distribution beta..

En théorie des probabilités et statistique, la distribution bêta est une famille à deux paramètres de distributions complètement continues. Il est utilisé pour décrire les variables aléatoires dont les valeurs sont définies sur un intervalle fini. La densité est définie comme suit :

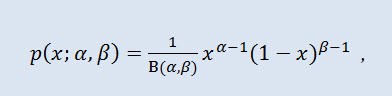
où B est la fonctionfonction beta f, α est le premier paramètre de forme (0<α), β est le deuxième paramètre de forme (0<β).

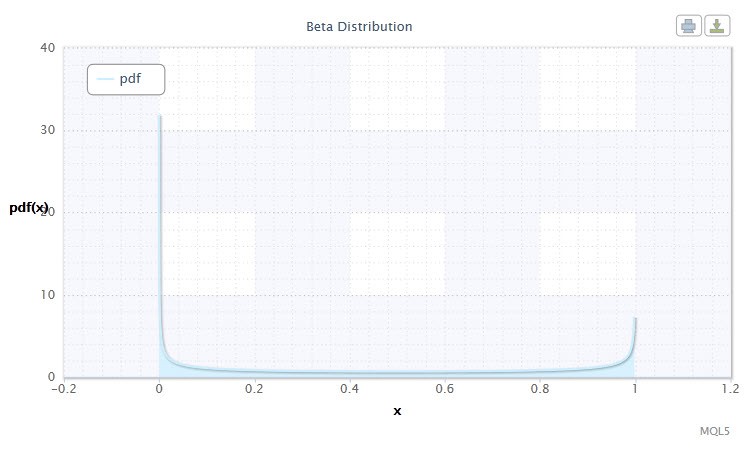
Figure 9. Beta distribution density Beta(0.5,0.5)

Sa notation se présente sous le format suivant : X ~ Beta(α,β), où :

X est une variable aléatoire ;
α est le 1er paramètre de forme (0<α) ;
β est la deuxième forme du paramètre (0<β).

Plage valide de la variable aléatoire X : 0 ≤ X ≤ 1.

La classe CBetadist décrit cette distribution de la manière suivante :

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.10 Répartition de Laplace

Une autre distribution continue remarquable est la distributionLaplace (distribution exponentielle double).

La distribution de Laplace (distribution exponentielle double) en théorie des probabilités est une distribution continue d'une variable aléatoire dans laquelle la densité de probabilité est :

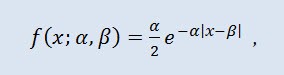
où α est le paramètre de localisation (-∞ ≤ α ≤ α ≤ +∞ ), β est le paramètre d’échelle (0<β).).

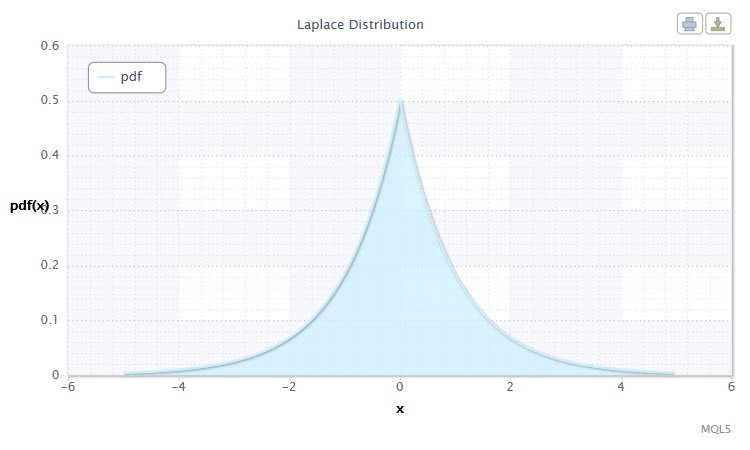
Figure 10. Laplace distribution density Lap(0,1)

Sa notation a le format suivant : X ~ Lap(α,β), où :

X est une variable aléatoire ;
α est le paramètre d’emplacement (-∞ ≤ α ≤ +∞ );
βest le paramètre d'échelle (0<β).

Plage valide de la variable aléatoire X : -∞ ≤ X ≤ +∞.

La classe CLaplacedist aux fins de cette distribution est définie comme suit :

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Ainsi, en utilisant le code MQL5, nous avons créé 10 classes pour les dix distributions continues. En dehors de celles-ci, d'autres classes ont été créées qui étaient, pour ainsi dire, complémentaires car il y avait un besoin de fonctions et de méthodes spécifiques (par exemple,CBeta and CGamma).

Passons maintenant aux distributions discrètes et créons quelques classes pour cette catégorie de distribution.

2.2.1 Distribution Binomiale

Commençons par la binomial..

En théorie des probabilités, la distribution binomiale est une distribution du nombre de réussites dans une séquence d'expériences aléatoires indépendantes où la probabilité de réussite dans chacune d'entre elles est égale. La densité de probabilité est donnée par la formule suivante :

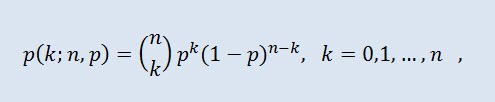
Où (n k) est le coefficient binomial , n est le nombre d’essais (0 ≤ n), p est la probabilité de succès (0 ≤ p ≤1).

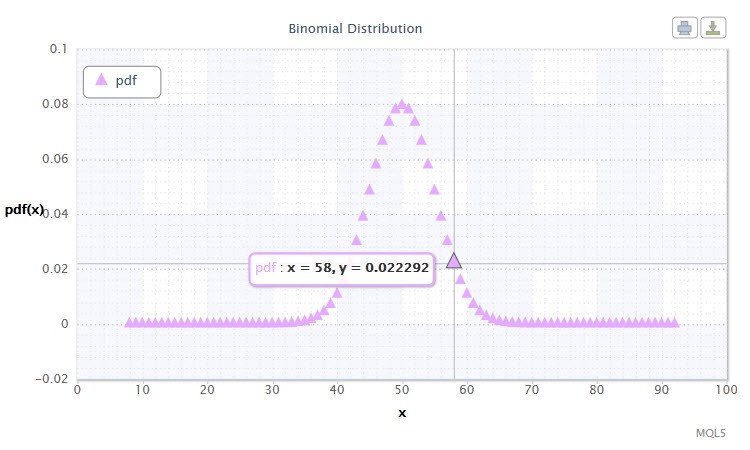
Figure 11. Binomial distribution density Bin(100,0.5).

Sa notation dispose du format suivant : k ~ Bin(n,p), où :

k est une variable aléatoire ;
n est le nombre d'essais (0 ≤ n);
p est la probabilité de succès (0 ≤ p ≤1).

Plage valide de la variable aléatoire X : 0 ou 1.

L'éventail des valeurs possibles de la variable aléatoire X vous suggère-t-il quelque chose ? En effet, cette distribution peut nous aider à analyser l'agrégat des deals gagnants (1) et perdants (0) dans le système de trading.

Créons la classeСBinomialdist comme suit :

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+

2.2.2 Distribution Poisson

La prochaine distribution à l'étude est la distribution distribution Poisson..

La distribution de Poisson modélise une variable aléatoire représentée par un nombre d'événements intervenant sur une période de temps fixe, à condition que ces événements interviennent avec une intensité moyenne fixe et indépendamment les uns des autres. La densité prend la forme suivante :

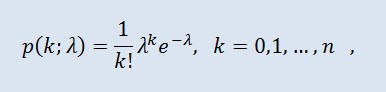
où k! est le factoriel, λ est le paramètre d’emplacement (0 < λ).

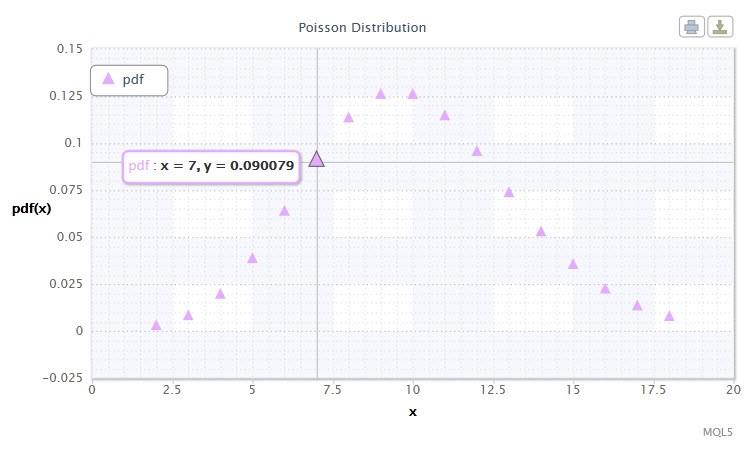
Figure 12. .Poisson distribution density Pois(10).

Sa notation a le format suivant : k ~ Pois(λ), où :

k est une variable aléatoire ;
λ est le paramètre de localisation (0 < λ).

Plage valide de la variable aléatoire X : 0 ≤ X ≤ +∞.

La distribution de Poisson décrit la "loi des événements rares" essentielle dans l’estimation du degré de risque.

La classeCPoissondist servira aux fins de cette distribution :

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

Il est évidemment impossible d’évoquer toutes les distributions statistiques au sein d'un même article et probablement même pas nécessaire. L'utilisateur, s'il le souhaite, peut étendre la galerie de distribution présentée ci-dessus. Les distributions créées peuvent être trouvées dans le fichier Distribution_class.mqh.

3. Création de Graphiques de Distribution

Maintenant, je suggère que nous voyions comment les classes que nous avons créées pour les distributions peuvent être utilisées dans nos travaux futurs.

À ce stade, en utilisant à nouveau la POO, j'ai créé la classe CDistributionFigure qui traite les distributions de paramètres définies par l'utilisateur et les affiche à l'écran par les moyens décrits dans l'article"Graphiques et Diagrammes in HTML".

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

Omission de l’implémentation. Notez que cette classe a des données de membres comme type et mode en rapport avec Dist_type et Dist_modeproportionnellement. Ces types sont desénumérations des distributions étudiées et de leurs types.

Tentons donc de créer enfin un graphique d'une certaine distribution.

J'ai écrit le scriptcontinuousDistribution.mq5 pour les distributions continues, ses lignes clés étant les suivantes :

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Pour les distributions discrètes, le script discreteDistribution.mq5 a été écrit.

J'ai exécuté le script avec des paramètres standard pour la distribution Cauchy et j'ai obtenu le graphique suivant, tel que indiqué dans la vidéo ci-dessous.

Conclusion

Cet article a introduit quelques distributions théoriques d'une variable aléatoire, également codées en MQL5. Je crois que le marché du trade par lui-même et par conséquent le travail d'un système de trading devrait être axé sur les lois fondamentales de la probabilité.

Et j'espère que cet article sera d'une valeur pratique pour les lecteurs intéressés. Pour ma part, je vais élaborer ce sujet et donner des exemples pratiques pour démontrer comment les distributions de probabilité statistiques peuvent être utilisées dans l'analyse des modèles de probabilité.

Emplacement du fichier:

#	Fichier	Chemin :	Description
1	Distribution_class.mqh	%MetaTrader%\MQL5\Include	Galerie des cours de distribution
2	DistributionFigure_class.mqh	%MetaTrader%\MQL5\Include	Classes d'affichage graphique des distributions
3	continuousDistribution.mq5	%MetaTrader%\MQL5\Scripts	Script pour la création d'une distribution continue
4	discreteDistribution.mq5	%MetaTrader%\MQL5\Scripts	Script de création d'une distribution discrète
5	dataDist.txt	%MetaTrader%\MQL5\Files	Données d'affichage de la distribution
6	Distribution_function.htm	%MetaTrader%\MQL5\Files	Graphe HTML de distribution continue
7	Distribution_function_discr.htm	%MetaTrader%\MQL5\Files	Graphique HTML de distribution discrète
8	exportation.js	%MetaTrader%\MQL5\Files	Script Java pour exporter un graphique
9	highcharts.js	%MetaTrader%\MQL5\Files	bibliothèque JavaScript
10	jquery.min.js	%MetaTrader%\MQL5\Files	bibliothèque JavaScript

Bibliographie:

K. Krishnamoorthy. Guide de Distributions Statistiques avec Applications, Chapman and Hall/CRC 2006.
W.H. Press, et al. Numerical Recipes : L'art de l'informatique scientifique, troisième édition, Cambridge University Press : 2007. - 1256 pp.
S.V. Bulashev Statistique pour les Traders. - M. Kompania Spoutnik +, 2003. - 245 p.
I. Gaidyshev Analyse et traitement des données : Guide de Référence Spécial - SPb : Piter, 2001. - 752 p. : ill.
A.I. Kibzun, E.R. Goryainova — Théorie des Probabilités et Statistiques Mathématiques. Cours de Base avec Exemples et Problèmes
N.Sh. Kremer Théorie de la Probabilité et les Statistiques Mathématiques. M.: Unité-Dana, 2004. — 573 p.

Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/271

Fichiers joints |

Télécharger ZIP

distribution_class.mqh (108.26 KB)

continuousdistribution.mq5 (2.45 KB)

discretedistribution.mq5 (2.01 KB)

distribution_function.zip (59.99 KB)

distributionfigure_class.mqh (19.68 KB)

Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.

Autres articles par cet auteur

Aller à la discussion

Traçage, Débogage et Analyse Structurelle du Code Source

L'ensemble complexe des problèmes de création d'une structure d'un code exécuté et de son traçage peut être réglé sans difficultés majeures. Cette possibilité est apparue dans MetaTrader 5 en raison de la nouvelle fonctionnalité du langage MQL5 - la création automatique de variables dont les données sont de type complexe (structures et classes) et leur élimination au moment de quitter le périmètre local. L'article comporte la description de la méthodologie et de l'outil prêt à l'emploi.

3 Méthodes d'Accélération des Indicateurs par l'Exemple de la Régression Linéaire

L'article traite des méthodes d'optimisation des algorithmes de calcul des indicateurs. Chacun trouvera une méthode qui correspond le mieux à ses besoins. Trois méthodes sont décrites ici. L'une d'elles est assez simple, la suivante exige de solides connaissances en mathématiques et la dernière un peu d'esprit. Des indicateurs ou des caractéristiques de conception de terminal MetaTrader5 sont utilisés pour réaliser la plupart des méthodes décrites. Les méthodes sont assez universelles et peuvent être utilisées non seulement pour accélérer le calcul de la régression linéaire, mais aussi pour de nombreux autres indicateurs.

Estimations Statistiques

L'estimation des paramètres statistiques d'une séquence est très importante, car la plupart des modèles et méthodes mathématiques sont axés sur des hypothèses différentes. Par exemple, la normalité de la loi de distribution ou la valeur de dispersion, ou d'autres paramètres. Ainsi, lors de l'analyse et de la prévision de séries chronologiques, nous avons besoin d'un outil simple et pratique qui permette d'estimer rapidement et clairement les principaux paramètres statistiques. L'article décrit brièvement les paramètres statistiques les plus simples d'une séquence aléatoire et plusieurs méthodes de son analyse visuelle. Il propose l’implémentation de ces méthodes en MQL5 et les méthodes de visualisation du résultat des calculs à l'aide de l'application Gnuplot.

Filtrage des Signaux en Fonction des Données Statistiques de la Corrélation des Prix.

Existe-t-il une corrélation entre le comportement passé des prix et ses tendances futures ? Pourquoi le prix répète-t-il aujourd'hui le caractère de son mouvement de la veille ? Les statistiques peuvent-elles être utilisées pour prévoir la dynamique des prix ? Il y a une réponse, et elle est positive. En cas de doute, cet article est fait pour vous. Je vais vous expliquer comment créer un filtre fonctionnel pour un système de trading dans MQL5, révélant une tendance intéressante dans les fluctuations de prix.