Algorithmes d'optimisation de la population : Semis et Croissance des Jeunes Arbres, ou Saplings Sowing and Growing up en anglais (SSG)

Sommaire :

1. Introduction
2. Algorithme
3. Résultats des tests

1. Introduction

Tous les organismes vivants dans la nature sont soumis à certaines lois. Cela leur permet de survivre dans des conditions environnementales changeantes. Il existe plusieurs possibilités d'adaptation des plantes à l'environnement. Certaines d'entre elles sont capables de tolérer les changements de saison, d'autres peuvent s'adapter au manque d'humidité, aux températures élevées ou basses et à l'absence de pollinisateurs. L'un des organismes les plus stables parmi les plantes est l'arbre, dont certains sont capables de vivre pendant plus de 50 000 ans en formant des colonies.

La nature est un champ d'inspiration inépuisable pour de nombreuses idées efficaces dans le développement et l'invention de méthodes informatiques. En fait, l'informatique évolutive est une projection de l'évolution dans des simulations informatiques. Il existe de nombreuses méthodes d'optimisation inspirées par des processus naturels, comme le calcul évolutif, l'immunologie artificielle, les méthodes démographiques, etc. Le SSG est essentiellement défini comme un processus itératif de génération et de combinaison travaillant avec un jardin de solutions potentielles appelées "jeunes pousses". L'algorithme Saplings Sowing and Growing (SSG) a été proposé par A. Karci et ses co-auteurs en 2002. L'algorithme s'inspire de l'évolution des arbres en croissance et modélise la croissance et la ramification des arbres.

2. Algorithme

L'algorithme est l'un des rares à ne pas faire l'objet d'une description claire de la part des auteurs (seules des dispositions et des idées générales sont fournies). Les opérateurs algorithmiques présentés par les auteurs ne sont pas non plus des instructions toutes faites pour la mise en œuvre algorithmique du programme. Il n'y a pas d'instructions claires concernant les arbres des enfants et des parents et leur interaction. Il n'y a aucune exigence quant à l'ordre dans lequel les opérateurs sont exécutés, et tout utilisateur peut modifier son ordre pour obtenir un meilleur semis.

Au sens large, le SSG n'est pas un algorithme d'optimisation, mais un ensemble général de règles conçu pour compléter d'autres algorithmes afin d'améliorer la qualité de l'optimisation. En d'autres termes, SSG est un complément pour tout algorithme de population évolutionnaire, ce qui me permet de faire preuve d'imagination et d'expérimenter une mise en œuvre spécifique de l'algorithme d'optimisation. J'ai appliqué certaines de mes réflexions et de mes expériences lors de l'écriture des algorithmes précédents et je les ai utilisées pour travailler avec SSG. Les résultats des expériences sont présentés ci-dessous à l'intention du lecteur.

Pour commencer à comprendre l'algorithme, nous devons considérer un arbre comme un agent d'optimisation. Un arbre est une solution à un problème d'optimisation, où chaque branche est un paramètre optimisé du problème. La figure 1 présente une illustration abstraite et artistique des arbres parents et enfants. Le tronc de l'arbre est un ensemble de paramètres à optimiser. Chaque branche est un paramètre optimisé distinct, la longueur de la branche étant limitée par la fourchette de valeurs autorisée pour le paramètre correspondant. La direction des branches n'a pas d'importance et n'est indiquée dans la figure que pour mettre en évidence leur différence.

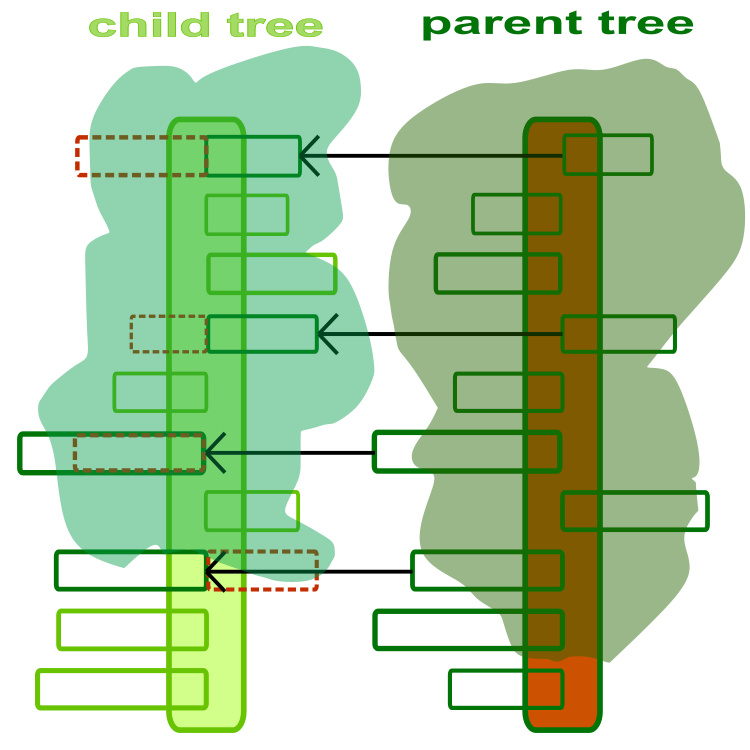
Figure 1. Arbre parent et enfant. La ligne en pointillé indique les branches enfantines remplacées par les branches parentales.

Les branches des arbres sont ainsi les coordonnées des arbres dans l'espace de recherche.

L'algorithme SSG se compose d'opérateurs de variation qui génèrent de nouvelles solutions - des candidats pour l’ensemble commun de solutions. Les principaux opérateurs de variation sont le croisement, la ramification et la vaccination. La plantation des semis doit être effectuée à une distance équidistante dans chaque direction (ouest, est, nord, sud). C'est l'étape initiale de la méthode. Lorsque le nombre de coordonnées (paramètres optimisés) est supérieur à 3, la plantation "uniforme" est une simple distribution aléatoire des semis dans l'espace de recherche. Ensuite, les plants grandissent, se croisent, se ramifient et le processus de vaccination se met en place.

Examinons les étapes et les opérateurs de l'algorithme SSG :

1) Planter des semis.

L'espace de recherche peut être considéré comme un jardin de semis, et tous les semis doivent donc être répartis uniformément dans le jardin. Lorsqu'il sème des graines, l'agriculteur les place à égale distance les unes des autres afin qu'elles poussent plus vite sans se gêner mutuellement. Pour résoudre le problème en simulant la culture de semis, les solutions arbitraires à générer initialement doivent être réparties uniformément dans l'espace de recherche valide.

Lorsqu'il y a 2 ou 3 coordonnées, il n'y a pas de problème pour répartir uniformément les semis. Mais lorsqu'il y en plus de 3, il est plus facile d'utiliser une distribution aléatoire. Dans la pratique, avec un petit nombre de coordonnées, il n'est pas nécessaire de s'occuper de la distribution uniforme des semis, puisque la tâche n'est pas un gros problème et que l'on sait que la solution sera obtenue avec une grande précision. Donc, quel que soit le nombre de coordonnées dans l'algorithme, nous utiliserons une distribution aléatoire des semis dans le jardin.

2) Culture de jeunes plants (arbres), 3 opérateurs exécutés en séquence.

2.1) Croisement.

L'objectif de l'opérateur "croisement" est de créer une nouvelle plantule à partir de plantules existantes en échangeant des informations entre elles. Le croisement est essentiellement la transplantation d'une copie d'une branche de l'arbre parent vers l'arbre enfant (figure 1). Pour chaque paire de plantules, on utilise un coefficient de croisement différent, qui est la probabilité de croisement. La probabilité de croisement dépend de la distance entre les plantules d'une paire. Plus la distance est grande, plus la probabilité de croisement est faible. L'opérateur de croisement est une méthode très importante de l'algorithme qui fournit des mécanismes combinatoires. La combinaison d'informations entre les agents peut améliorer de manière significative la qualité globale de l'algorithme d'optimisation.

2.2) Ramification.

L'opérateur modélise la croissance des branches. La croissance peut être positive (allongement) ou négative (dessèchement). « Pour qu'une branche pousse en un point quelconque du corps de la plantule, il ne faut pas qu'une branche voisine ait déjà poussé à cet endroit. » Il s'agit de la description approximative de l'opérateur par les auteurs de l'algorithme. En fait, ce processus est plus simple et plus clair qu'il n'y paraît à première vue. Il s'agit d'une modification des branches existantes de l'arbre enfant (la méthode spécifique de modification n'est pas spécifiée).

La modification de chaque branche individuelle est d'autant plus probable que le nombre d'itérations écoulées entre l'itération en cours et celle au cours de laquelle la dernière modification de la branche a été effectuée est élevé. Mes expériences ont montré l'inefficacité de cet opérateur. Par ailleurs, il n'y a pas d'indications directes de l'utilisation de la méthode de modification. J'ai pris l'initiative dans ce domaine en appliquant la modification de la longueur de la branche selon la loi de distribution des vols de Levy. La modification sera effectuée avec la probabilité et l'intensité spécifiées comme paramètres externes de l'algorithme.

2.3) Vaccination.

Le processus de vaccination a lieu entre deux semis différents en cas de similitude des semis. La similarité des semis influe sur le succès du processus de vaccination et est proportionnelle à la moyenne arithmétique de la distance pondérée. L'opérateur est similaire à l'opérateur de croisement et consiste en l'échange de branches, fournissant à l'algorithme un moyen supplémentaire de combiner les informations entre les agents. L'opérateur sera mis en évidence dans l'article, mais il est commenté dans les codes sources. Les résultats des tests sont présentés sans lui, puisque la vaccination aggrave les résultats.

3) Calculer l'aptitude des arbres.

4) Planter de nouveaux semis dans le jardin.

Les plants obtenus à l'aide des opérateurs de croisement, de ramification et de vaccination sont des solutions temporaires (jardin fille). À ce stade, il est nécessaire de sélectionner les n meilleurs semis (un paramètre externe de l'algorithme) et de les placer dans le jardin en remplacement des n pires arbres du jardin. Il convient de noter que le remplacement par des jeunes plants se fera dans tous les cas, même s'ils sont pires que les plus mauvais arbres du jardin.

C'est le bon moment pour examiner le code de l'algorithme de l'arbre croissant, ce qui nous rapproche de plus en plus du point culminant de cette étude : l'examen des résultats des tests.

Il est donc pratique de représenter chaque arbre comme une structure de jardin, qui servira de base à la création d'un jardin fleuri. Rien n'est plus simple dans cet algorithme que l'entité "tree" (ou arbre), qui ne nécessite que 2 composants : un tableau de coordonnées et la valeur d'aptitude f.

//——————————————————————————————————————————————————————————————————————————————
struct S_Garden
{
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

La classe C_AO_SSG de l'algorithme SSG n'a rien de particulier. Tout ici nous est très familier grâce aux algorithmes examinés précédemment. Dans la classe, nous déclarerons des membres et des méthodes pour opérer sur les jardins parents et enfants. Un jardin temporaire est nécessaire pour que la méthode de tri fonctionne, car nous devons trier à la fois le jardin enfant et le jardin parent. Déclarons un tableau des meilleures coordonnées de la solution dans son ensemble et de la meilleure valeur d'aptitude, ainsi que des constantes pour stocker les paramètres externes de l'algorithme.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SSG
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Garden pGarden []; //parent's garden
  public: S_Garden cGarden []; //child's garden
  public: S_Garden gardenT []; //temp garden
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP); //Power branching operator

  public: void Sowing      (int iter);
  public: void Germination ();


  //============================================================================
  private: void   Sorting        (S_Garden &garden []);
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];               //Vector
  private: int    ind [];
  private: double val [];
  private: double r;

  private: bool   sowing;               //Sowing
  private: int    coordinates;          //Coordinates number
  private: int    numberTrees;          //Number of trees
  private: int    seedlingsReplacement; //Seedlings replacement
  private: double probabMatingOperator; //Probability mating operator
  private: double probabBranchOperator; //Probability branching operator
  private: double powerBranchOperator;  //Power branching operator
};
//——————————————————————————————————————————————————————————————————————————————

Dans la méthode d'initialisation Init(), allouez de la mémoire aux tableaux et attribuez des valeurs aux paramètres constants. Étant donné que le paramètre seedlingsReplacementP est défini en fractions de la taille du jardin (de 0,0 à 1,0), ce qui détermine le nombre de jeunes plants à planter dans le jardin parent, il doit être converti en une représentation entière de la taille du jardin. Remettons à zéro le drapeau de semis initial et initialisons la variable de décision globale avec la plus petite valeur double possible.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SSG::Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP)  //Power branching operator
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberTrees    = numberTreesP;

  if (seedlingsReplacementP >= 1.0)
  {
    seedlingsReplacement = numberTreesP;
  }
  else
  {
    if (seedlingsReplacementP <= 0.0)
    {
      seedlingsReplacement = 1;
    }
    else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP);
  }

  probabMatingOperator = probabMatingOperatorP;
  probabBranchOperator = probabBranchOperatorP;
  powerBranchOperator  = powerBranchOperatorP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);


  ArrayResize (pGarden,  numberTrees);
  ArrayResize (cGarden,  numberTrees);
  ArrayResize (gardenT,  numberTrees);
  ArrayResize (ind,      numberTrees);
  ArrayResize (val,      numberTrees);

  for (int i = 0; i < numberTrees; i++)
  {
    ArrayResize (pGarden  [i].c, coordinates);
    ArrayResize (cGarden  [i].c, coordinates);
    ArrayResize (gardenT  [i].c, coordinates);
    cGarden [i].f = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

La première méthode publique appelée à chaque itération, Sowing(), est la plantation des semis. Lors de la première itération, lorsque l'algorithme est en cours d'exécution, nous dispersons les semis dans le jardin (espace de recherche) de manière aléatoire avec une distribution uniforme. Ici, nous voyons que les coordonnées sont générées aléatoirement dans la plage autorisée entre le min et le max des paramètres optimisés. Nous vérifions qu'il n'y a pas de sortie de la plage autorisée, puis nous ramenons les valeurs des coordonnées conformément à l'étape d'optimisation.

À ce stade, la capacité d'adaptation des semis est minimale. Nous définissons le vecteur vec[]. Nous en aurons besoin pour mettre à l'échelle les incréments des branches dans l'opérateur de branchement et pour calculer la distance euclidienne maximale possible r dans l'espace de recherche. Il sera utile à l'opérateur de croisement de déterminer la probabilité en fonction de la distance entre les paires d'arbres.

//the first planting of trees-------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;
  r = 0.0;

  for (int t = 0; t < numberTrees; t++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cGarden [t].f = -DBL_MAX;
  }

  for (int c = 0; c < coordinates; c++)
  {
    vec [c] = rangeMax [c] - rangeMin [c];
    r += vec [c] * vec [c];
  }

  r = sqrt (r);

  return;
}

Ensuite, dans la méthode Sowing(), les opérateurs de croisement, de ramification et de vaccination sont exécutés à la deuxième itération et aux itérations suivantes. Les opérateurs sont exécutés séquentiellement dans la boucle principale :

//tree growth-----------------------------------------------------------------
int child, parent;
double rnd;
double ed; //euclidean distance
double eM;
double u;
double temp;

for (int t = 0; t < numberTrees; t++)

Lors de l'exécution d'opérateurs, les concepts d'« enfant » et de « parent » sont très arbitraires. En fait, il s'agit simplement de sources d'informations de base pour la création d'un nouveau plant. La nouvelle plantule copie toutes les branches (comme vous vous en souvenez peut-être, les branches sont les paramètres à optimiser) de l'arbre enfant et en reçoit de nouvelles de l'arbre parent.

Pour chaque nouveau plant, deux arbres sont sélectionnés individuellement dans le jardin, un enfant et un parent au hasard, avec une probabilité égale pour tous les arbres du jardin. En d'autres termes, tous les arbres peuvent participer à la création d'un nouveau semis avec la même probabilité et indépendamment de leur aptitude. Ainsi, "child" et "parent" sont simplement les indices des deux arbres d'origine dans le tableau du jardin parent.

ed = 0.0;

rnd = RNDfromCI (0.0, numberTrees - 1);
child = (int)MathRound (rnd);
if (child < 0) child = 0;
if (child > numberTrees - 1) child = numberTrees - 1;

rnd = RNDfromCI (0.0, numberTrees - 1);
parent = (int)MathRound (rnd);
if (parent < 0) parent = 0;
if (parent > numberTrees - 1) parent = numberTrees - 1;

if (child == parent) parent++;
if (parent > numberTrees - 1) parent = 0;

ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);

Le premier opérateur est le croisement, ou conjugaison (accouplement). Pour exécuter l'opérateur de croisement sur une plantule d'indice t, il est nécessaire de calculer l'espace euclidien entre l'arbre fils et l'arbre parent avec les indices "child" et "parent" :

//mating operator-----------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  temp = pGarden [child].c [c] - pGarden [parent].c [c];
  ed += temp * temp;
}

ed = sqrt (ed);

La distance euclidienne intervient dans l'équation de calcul de la probabilité de croisement par normalisation à la distance euclidienne maximale possible r dans l'espace de recherche :

eM = 1.0 - (ed / r);

Générer un nombre aléatoire dans l'intervalle [0.0 ; 1.0]. Si le nombre obtenu se situe dans la limite de la probabilité calculée eM, nous procédons alors à un croisement - en copiant les branches de l'arbre parent avec la probabilité probabMatingOperator pour chaque branche. Si la probabilité eM n'est pas satisfaite, la plantule passe à l'exécution de la déclaration suivante avec toutes les branches originales de l'arbre enfant.

rnd = RNDfromCI (0.0, 1.0);

if (rnd <= eM)
{
  for (int c = 0; c < coordinates; c++)
  {
    rnd = RNDfromCI (0.0, 1.0);

    if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

L'opérateur de ramification est ensuite exécuté. Le branchement, ou ramification, permet de varier les branches - en les allongeant ou en les raccourcissant. Il s'agit de l'opérateur principal qui crée des branches d'une nouvelle longueur. Les autres opérateurs ne jouent qu'un rôle combinatoire et ne créent pas de nouvelles branches uniques. Pour chaque branche, nous générons un nombre aléatoire dans l'intervalle [0,0 ; 1,0]. Si la probabilité de probabBranchOperator est remplie, nous effectuons une ramification en modifiant la longueur de la branche conformément à la loi de distribution des vols de Levy considérée ici.

Comme vous pouvez le constater, toutes les branches de la plantule ne seront pas modifiées. Elles seront modifiées indépendamment du fait que la branche ait été copiée à partir de l'arbre parent dans la déclaration précédente ou qu'il s'agisse de la branche enfant originale. Après avoir modifié la branche, nous vérifions si les valeurs sont hors limites et nous les alignons sur l'étape d'optimisation.

//branching operator--------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  rnd = RNDfromCI (0.0, 1.0);

  if (rnd < probabBranchOperator)
  {
    double r1 = RNDfromCI (0.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);

    cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0);
    cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Le troisième opérateur est la vaccination. L'opérateur de vaccination a été conçu par les auteurs, apparemment, comme un opérateur combinatoire, et devrait être exécuté pour copier les branches de l'arbre parent dans le cas où les branches de l'arbre enfant et de l'arbre parent diffèrent de plus que la différence moyenne entre toutes les branches de la paire. Cela semble très compliqué, mais cet opérateur n'est guère utilisé, et il est donc commenté dans les fichiers sources. Dans ce cas, je ne peux pas agir en tant qu'expert et j'admets donc qu'il se peut que je n'aie pas une compréhension correcte de cet opérateur.

//vaccinating operator------------------------------------------------------
u = 0.0;
    
for (int c = 0; c < coordinates; c++)
{
  u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c];
}

u /= coordinates;

for (int c = 0; c < coordinates; c++)
{
  if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u)
  {
    cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

Le moment est venu de procéder à la dernière opération de l'algorithme, mais non la moins importante : la germination. Nous exécutons la deuxième méthode publique Germination() dont l'exécution est obligatoire à chaque itération.

Si la première itération touche à sa fin (nous le saurons certainement grâce à l'indicateur 'sowing'), cela signifie que le jardin parent est vide. Nous plantons tous les jeunes plants du jardin enfant dans le jardin parent en copiant simplement tous les jeunes arbres un par un. Ensuite, triez le jardin parent par valeur d'aptitude à l'aide de la méthode Sorting(). Si les arbres sont triés, l'arbre à l'index 0 aura la meilleure aptitude, et nous pouvons mettre à jour la meilleure solution globale si elle n'est pas déjà la meilleure.

if (!sowing)
{
  for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t];

  Sorting (pGarden);

  if (pGarden [0].f > fB)
  {
    fB = pGarden [0].f;

    ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY);
  }
  
  sowing = true;
  return;
}

Plus loin dans le code, nous n'arriverons qu'à la deuxième itération et aux itérations suivantes de l'algorithme, puisque l'indicateur "sowing" a été prudemment fixé à "true". Lors de la deuxième itération et des suivantes, le jardin enfant doit être trié avant que les jeunes plants ne soient transférés dans le jardin parent et que les arbres les plus mauvais ne soient remplacés. Vérifions si la solution globale s'est améliorée, puis copions les n meilleurs semis à l'extrémité du jardin parent.

En conclusion, il ne reste plus qu'à trier le jardin parent. Les nouveaux membres de la société de jardinage pourront remplacer les arbres des générations précédentes pour nous faire plaisir avec les résultats de la résolution de problèmes d'optimisation des fleurs.

//planting some part from all child trees-------------------------------------
Sorting (cGarden);

if (cGarden [0].f > fB)
{
  fB = cGarden [0].f;

  ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY);
}

for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t];

Sorting (pGarden);

3. Résultats des tests

Résultats du banc d'essai SSG :

2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    5 Rastrigin's ; Func runs 10000 result : 80,7052793572295
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    Score : 0,99998
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    25 Rastrigin's ; Func runs 10000 result : 77,3972262608643
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    Score : 0,95900
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    500 Rastrigin's ; Func runs 10000 result : 52,24518909141432
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    Score : 0,64735
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    5 Forest's ; Func runs 10000 result : 1,331178589711503
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    Score : 0,75298
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    25 Forest's ; Func runs 10000 result : 1,019329018074209
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    Score : 0,57658
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    500 Forest's ; Func runs 10000 result : 0,25410121872226443
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    Score : 0,14373
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    5 Megacity's ; Func runs 10000 result : 6,4
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    Score : 0,53333
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    25 Megacity's ; Func runs 10000 result : 4,504
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    Score : 0,37533
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    500 Megacity's ; Func runs 10000 result : 1,2336
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    Score : 0,10280
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    All score: 5,09109

Le SSG n'a pas trop de paramètres, bien que ce soit une conséquence de l'adaptation de l'algorithme (le SSG original a encore moins de paramètres). Mais tous les paramètres méritent une attention particulière. Les paramètres suivants ont été utilisés dans les tests. Comme vous vous en souvenez peut-être, dans chaque article, je fournis les meilleurs paramètres d'algorithme permettant d'obtenir les meilleurs résultats possibles lors des tests.

C_AO_SSG:50 ; 0.3 ; 0.5 ; 0.4 ; 0.1

input int NumberTrees_P = 50 ; - le nombre d'arbres dans le jardin. Je n'ai pas expérimenté ce paramètre en laissant la valeur par défaut (la valeur par défaut dans mes expériences). Dans le cas de la valeur 100, l'algorithme produit des résultats agrégés encore meilleurs, mais la capacité d'adaptation diminue en raison d'une baisse du nombre d'itérations autorisées par jardin, compte tenu de la taille de ce dernier. Un jardin avec un grand nombre de branches n'a pas le temps d'évoluer.

input double SeedlingsReplacement_P = 0.3 ; - la proportion de plants du jardin enfant à transférer dans le jardin parent.
input double ProbabMatingOperator_P = 0.5 ; - la probabilité de croisement (copie de branches de l'arbre parent) si la probabilité tenant compte de la distance entre une paire d'arbres est remplie.
input double ProbabBranchOperator_P = 0.4 ; - la probabilité de ramification (croissance/rétrécissement des branches). Il s'agit d'un paramètre important qui affecte de manière significative les performances de l'algorithme (en général, tous les paramètres sont importants).
input double PowerBranchOperator_P = 0.1 ; - la force de ramification. Il s'agit d'un facteur d'échelle dans la dimension des paramètres optimisés : 1,0 ou plus signifiera la croissance des branches jusqu'aux limites du jardin, 0,0 - aucune croissance des branches, c'est-à-dire que de nouvelles tailles de branches n'apparaîtront pas et que l'algorithme dégénère en un simple outil combinatoire (ce qui est probablement une excellente idée pour l'utilisation de SSG, mais des recherches plus approfondies sont nécessaires à cet égard).

Si vous observez attentivement l'animation de l'algorithme SSG sur les fonctions de test, vous remarquerez l'absence de tout modèle de mouvement d'arbre dans le jardin, seul un certain "regroupement" dans les extrema locaux est perceptible. Cependant, la qualité élevée de la convergence est immédiatement perceptible par rapport aux algorithmes considérés précédemment. La reproductibilité stable des résultats est également remarquable.

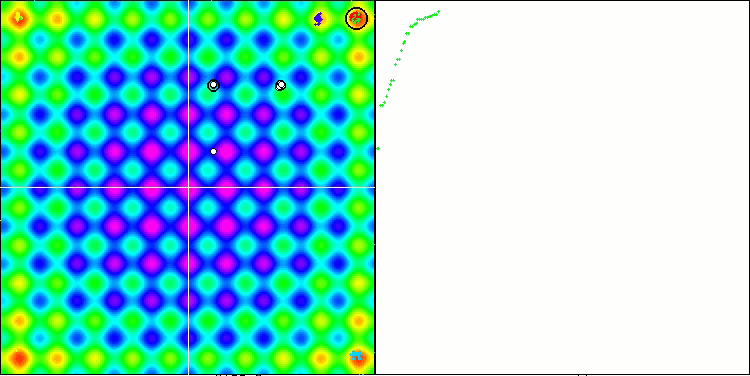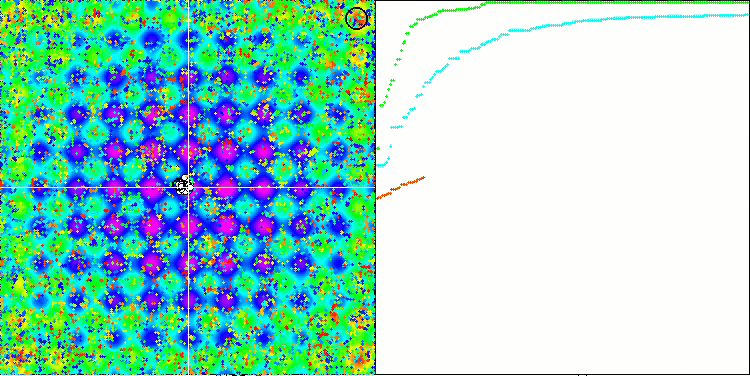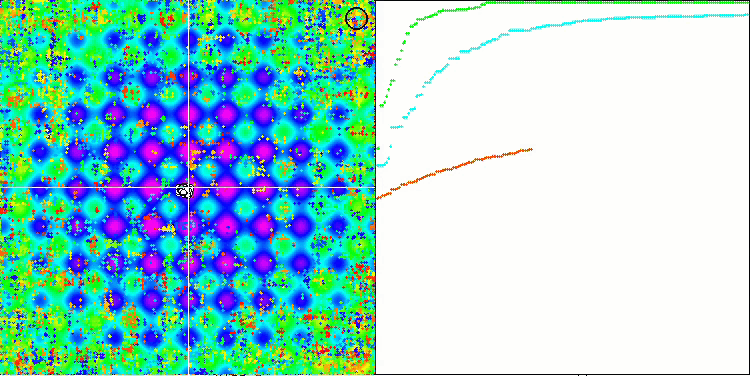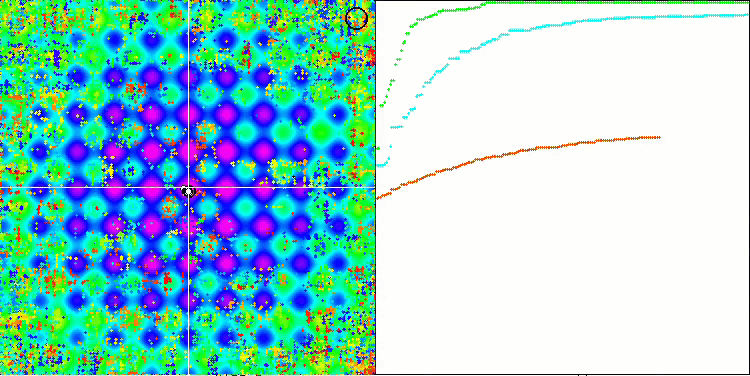
  SSG sur la fonction de test de Rastrigin.

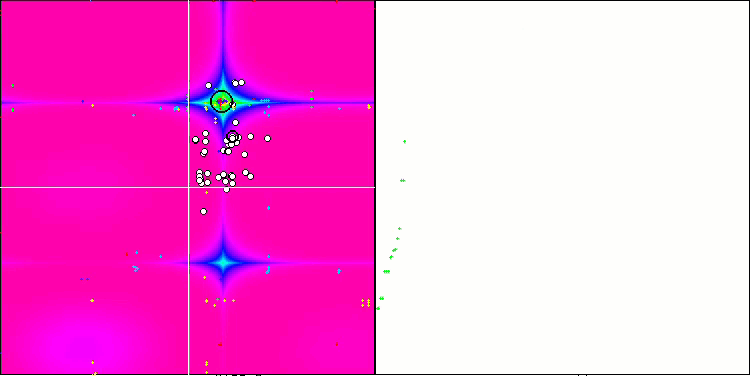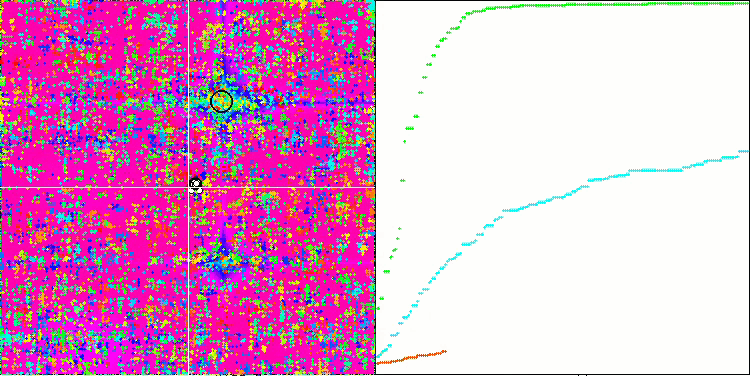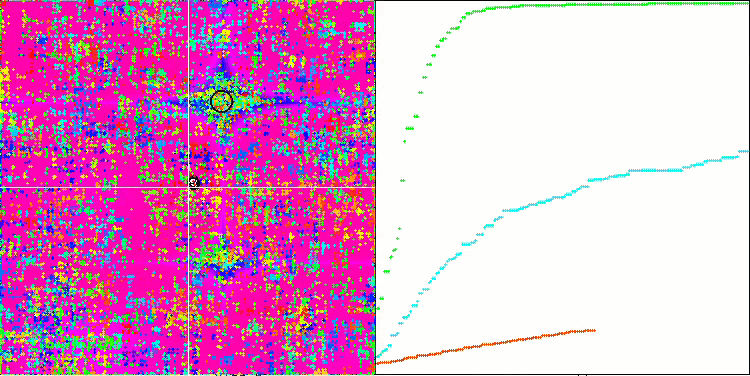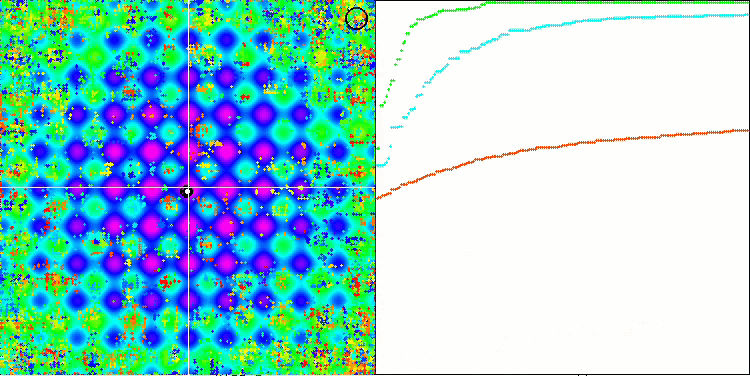
  SSG sur la fonction de test forest.

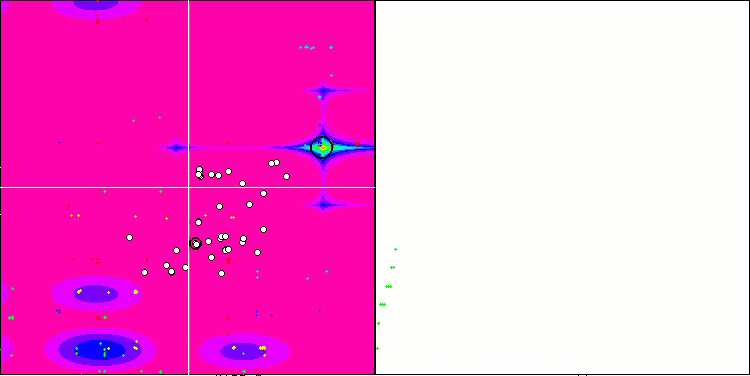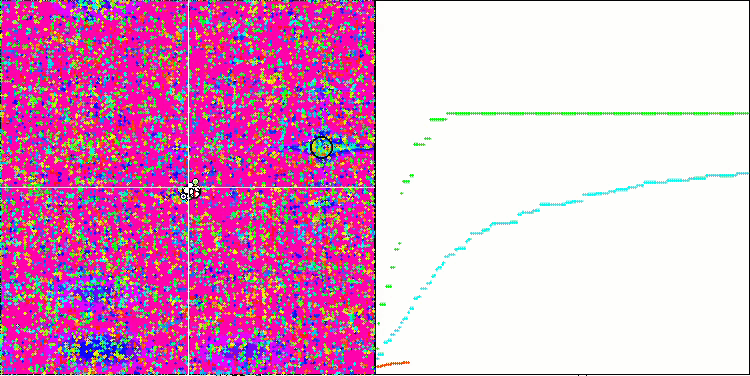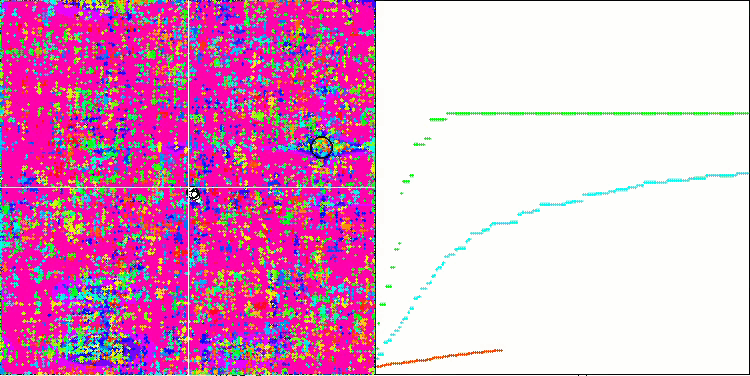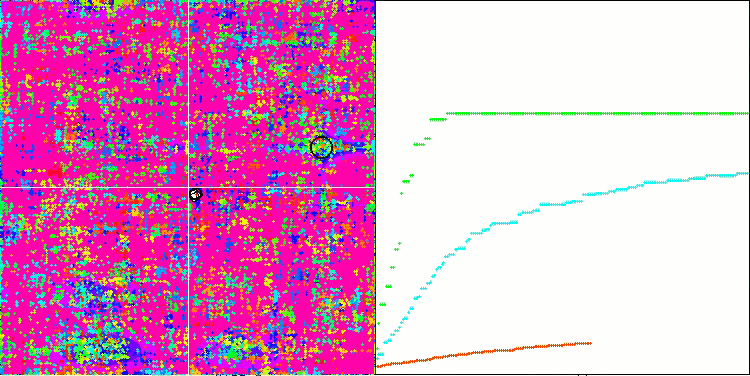
  SSG sur la fonction de test Megacity.

Passons maintenant à l'examen des résultats de l'algorithme SSG. Il y a vraiment matière à discussion. L'algorithme a triomphalement fait irruption à la première place du classement, laissant ses rivaux derrière lui ! L'algorithme n'utilise pas directement les connaissances en matière d'aptitude pour modifier les arbres de décision. L'aptitude n'est nécessaire que pour trier le jardin enfant et le jardin parent. Il est donc d'autant plus surprenant que l'algorithme ait pu obtenir des résultats aussi remarquables lors des tests.

C'est comme si l'équipe des aveugles battait l'équipe des voyants dans une course d'orientation. L'algorithme a devancé les participants du tableau dans 4 tests sur 6, tout en restant proche dans les tests où il n'était pas leader. SSG a montré l'avance la plus impressionnante par rapport à ses rivaux sur la fonction discrète Megacity, surpassant son concurrent le plus proche HS de près de 60% ! Cela démontre l'excellente évolutivité de l'algorithme. Le meilleur résultat en matière d'évolutivité a également été observé pour la fonction d'essai "sharp" de Forest. SSG a surpassé le meilleur concurrent de ce test (ACOm) de près de 30%.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)
SSG	saplings sowing and growing	1,00000	1,00000	0,65914	2,65914	0,70823	0,94522	1,00000	2,65345	0,71532	0,85412	1,00000	2,56944	100,000
HS	recherche d'harmonie	0,99676	0,95282	0,57048	2,52006	1,00000	0,98931	0,44806	2,43736	1,00000	1,00000	0,41537	2,41537	93,370
ACOm	optimisation par colonies de fourmis M	0,34611	0,17985	0,20182	0,72778	0,85966	1,00000	0,77362	2,63327	1,00000	0,88484	0,05606	1,94090	66,407
IWO	Optimisation des mauvaises herbes envahissantes	0,95828	0,67083	0,35295	1,98207	0,68718	0,46349	0,31773	1,46840	0,75912	0,39732	0,33289	1,48933	61,691
COAm	algorithme d'optimisation coucou M	0,92400	0,46794	0,30792	1,69987	0,55451	0,34034	0,16526	1,06012	0,67153	0,30326	0,17083	1,14561	48,226
FAm	algorithme firefly M	0,59825	0,33980	0,20290	1,14095	0,47632	0,42299	0,49790	1,39721	0,21167	0,25143	0,35258	0,81568	41,042
ABC	colonie d'abeilles artificielles	0,78170	0,32715	0,24656	1,35541	0,50591	0,21455	0,13344	0,85390	0,47444	0,23609	0,13926	0,84979	37,204
BA	algorithme des chauves-souris	0,40526	0,63761	1,00000	2,04287	0,15275	0,17477	0,25989	0,58741	0,15329	0,06334	0,17371	0,39034	36,703
GSA	algorithme de recherche gravitationnelle	0,70167	0,45217	0,00000	1,15384	0,26854	0,36416	0,33204	0,96475	0,51095	0,32436	0,00000	0,83531	35,834
BFO	optimisation du butinage bactérien	0,67203	0,30963	0,13988	1,12154	0,35462	0,26623	0,20652	0,82736	0,42336	0,30519	0,18932	0,91786	34,700
MA	algorithme du singe	0,33192	0,33451	0,17340	0,83983	0,03684	0,07891	0,08932	0,20508	0,05838	0,00383	0,10720	0,16941	13,185
FSS	recherche d'un banc de poissons	0,46812	0,25337	0,13383	0,85532	0,06711	0,05013	0,06516	0,18240	0,00000	0,00959	0,08283	0,09242	12,089
PSO	optimisation par essaims de particules	0,20449	0,08200	0,08478	0,37127	0,13192	0,10486	0,21738	0,45415	0,08028	0,02110	0,01957	0,12095	9,696
RND	aléatoire	0,16826	0,09743	0,09495	0,36065	0,07413	0,04810	0,04715	0,16938	0,00000	0,00000	0,04922	0,04922	4,916
GWO	optimiseur du loup gris	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,03645	0,02557	0,25179	1,000

Résumé

Caractéristiques du SSG : aucune exigence de différentiabilité et de continuité de la fonction optimisée, aucune restriction sur le type de représentation et d'encodage appliqués. L'algorithme n'utilise pas les informations relatives à l'aptitude des agents individuels et à la meilleure solution dans son ensemble. Grâce à ces caractéristiques, le SSG peut être facilement appliqué à divers problèmes d'optimisation, y compris des problèmes très complexes. SSG peut être définitivement recommandé pour une utilisation dans le cadre des problèmes des traders et de l'apprentissage automatique. À l'heure où nous écrivons ces lignes, l'algorithme Saplings Sowing and Growing up est le leader incontesté en termes de qualité de convergence, de stabilité des résultats et d'évolutivité.

La figure 2 montre les résultats du test de l'algorithme.

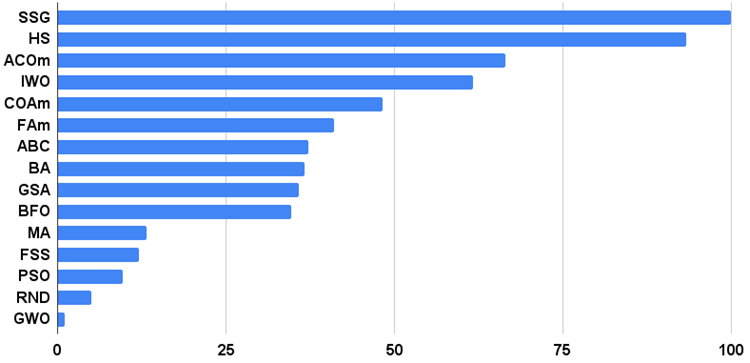
Figure 2. Histogramme des résultats des tests des algorithmes

Avantages et inconvénients des algorithmes SSG :

Avantages :
1. Mise en œuvre facile
2. Excellente convergence sur tous les types de fonctions sans exception
3. Evolutivité impressionnante

Inconvénients :
1. Nombreuses options de personnalisation, bien qu'elles soient intuitivement claires.

Chaque article présente une archive contenant les versions actuelles mises à jour des codes algorithmiques de tous les articles précédents. L'article est basé sur l'expérience accumulée par l'auteur et représente son opinion personnelle. Les conclusions et les jugements sont basés sur les expériences.