MetaTrader 5 / Ejemplos
English Русский 中文 Deutsch 日本語 Português 한국어 Français Italiano Türkçe
Distribuciones de Probabilidad Estadística en MQL5

Distribuciones de Probabilidad Estadística en MQL5

MetaTrader 5 — Ejemplos | 31 marzo 2014, 12:48
4 673 0
Denis Kirichenko
Denis Kirichenko

La teoría de probabilidad entera depende de la filosofía de indeseabilidad.
(Leonid Sukhorukov)

Introducción

Por la naturaleza de su trabajo, un trader tiene que tratar muy a menudo con categorías como probabilidad y aleatoriedad. La antípoda de aleatoriedad es una noción de "regularidad". Es notable que, en virtud de leyes filosóficas generales, la aleatoriedad por lo general evoluciona a regularidad. No discutiremos lo contrario por ahora. Básicamente, la correlación entre aleatoriedad y regularidad es una relación clave, puesto que si la ponemos en el contexto del mercado, afecta directamente al beneficio que recibe el trader.

En este artículo estableceré instrumentos teóricos subyacentes que nos ayudarán a encontrar algunas regularidades en el mercado en el futuro.


1.Distribuciones, Esencia, Tipos

De modo que, para describir una variable aleatoria necesitaré una distribución de probabilidad estadística unidimensional. Describirá una muestra de variables aleatorias por una ley determinada, es decir, la aplicación de cualquier ley de distribución requerirá un conjunto de variables aleatorias.

¿Por qué analizar distribuciones [teóricas]? Hacen más fácil identificar patrones de cambio de frecuencia dependiendo de los valores de atributo de la variable. Además, permiten obtener parámetros estadísticos de la distribución requerida.

En lo que respecta a los tipos de distribuciones de probabilidad, es habitual en la literatura profesional dividir la familia de distribución en continuo y discreto dependiendo del tipo de conjunto de variables aleatorias. Pero también hay otras clasificaciones; por ejemplo, por criterios como simetría de la curva de distribución f(x) con respecto a la línea x=x0, parámetro de localización, número de modos, intervalo de variable aleatorio y otras.

Hay varias formas de definir la ley de distribución. Deberíamos señalar que las más populares entre ellas son:


2. Distribuciones de Probabilidad Teóricas

Ahora tratemos de crear clases que describan distribuciones estadísticas en el contexto de MQL5. Además, me gustaría añadir que la literatura profesional ofrece muchos ejemplos de código escrito en C++ que se puede aplicar con éxito a la codificación MQL5. De modo que yo no he hecho ningún descubrimiento extraordinario, y en algunos casos usé las mejores prácticas de código C++.

El mayor reto al que me he enfrentado fue la falta de soporte de herencias múltiples en MQL5. Por esta razón no conseguí usar jerarquías de clase complejas. El libro titulado Numerical Recipes: The Art of Scientific Computing (Recetas Numéricas: El Arte de la Computación Científica) [2] se ha convertido para mí en la fuente óptima de código C++, del que he tomado la mayoría de funciones. A menudo las tuve que refinar de acuerdo a las necesidades de MQL5.

2.1.1 Distribución Normal

Tradicionalmente, comenzamos con la distribución normal.

La distribución normal, también llamada distribución Gaussian, es una distribución de probabilidad facilitada por la función de densidad de probabilidad:


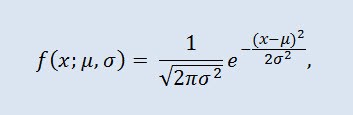
donde el parámetro μ — es la expectativa de una variable aleatoria e indica la coordenada máxima de la curva de densidad de distribución, y σ² es la diferencia.


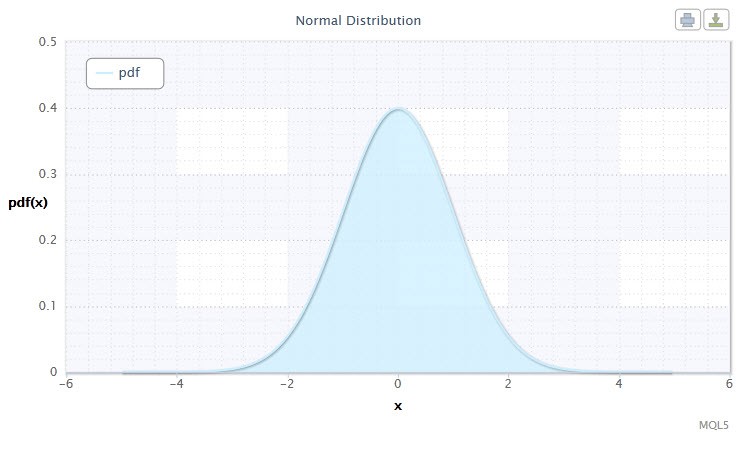
Figura 1. Densidad de distribución normal Nor(0,1)

Su notación tiene el siguiente formato: X ~ Nor(μ, σ2), donde:

  • X es una variable aleatoria seleccionada de la distribución normal Nor;
  • μ es el parámetro principal (-∞ ≤ μ ≤ +∞);
  • σ es el parámetro de diferencia (0<σ).

Alcance válido de la variable aleatoria X:  -∞ ≤ X ≤ +∞.

Las fórmulas usadas en este artículo pueden ser diferentes de las facilitadas en otras fuentes. Estas diferencias a veces no son matemáticamente cruciales. En algunos casos, es algo condicional para diferencias en parametrización.

La distribución normal juega un papel importante en estadística, ya que refleja la regularidad resultante de la interacción entre un gran número de causas aleatorias, de las cuales ninguna tiene un poder predominante. Y aunque la distribución normal es un caso inusual en mercados financieros, también es importante compararla con distribuciones empíricas para determinar el alcance y naturaleza de su abnormalidad.

Definamos la clase CNormaldist para la distribución normal de la siguiente manera:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

Como puede ver, la clase CNormaldist deriva de la clase base СErf, que a su vez define la clase de función de error. Se requerirá con el cálculo de algunos métodos de clase CNormaldist. La clase СErf y la función auxiliar erfcc tienen aproximadamente el siguiente aspecto:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+


2.1.2 Log-Normal Distribution

Ahora echemos un vistazo a la distribución log-normal.

La distribución Log-normal en teoría de probabilidad es una familia de dos parámetros de distribuciones continuas absolutas. Si una variable aleatoria se distribuye de forma log-normal, su logaritmo tendrá una distribución normal.


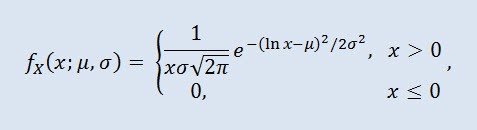
donde μ es el parámetro de localización (0<μ ), y σ es el parámetro de escala (0<σ).


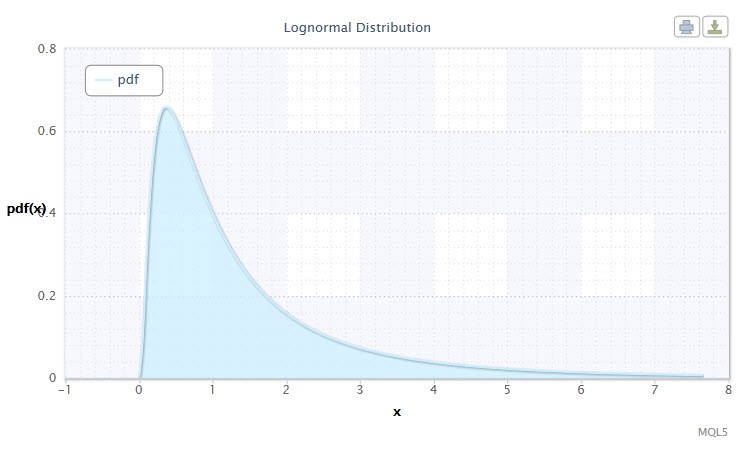
Figura 2. Densidad de distribución log-normal Logn(0,1)

Su anotación tiene el siguiente formato: X ~ Logn(μ, σ2), donde:

  • X es una variable aleatoria seleccionada de la distribución log-normal Logn;
  • μ es el parámetro de localización (0<μ );
  • σ es el parámetro de escala (0<σ).

Alcance válido de la variable aleatoria X:  0 ≤ X ≤ +∞.

Creemos la clase CLognormaldist para describir la distribución log-normal. Aparecerá de la siguiente manera:

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Como puede ver, la distribución log-normal no es muy diferente de la distribución normal. La diferencia es que el parámetro x se sustituye con el parámetro log(x). 


2.1.3 Distribución Cauchy

La distribución Cauchy en teoría de probabilidad (en física también se llama distribución de Lorentz o distribución de Breit-Wigner) es una clase de distribuciones continuas absolutas. Una variable aleatoria distribuida Cauchy es un ejemplo común de variable sin expectativas o diferencia. La densidad toma la siguiente forma:


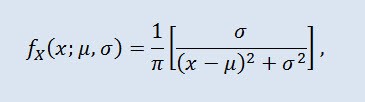
donde μ es el parámetro de localización (-∞ ≤ μ ≤ +∞ ), y σ es el parámetro de escala (0<σ).

La anotación de la distribución Cauchy tiene el siguiente formato: X ~ Cau(μ, σ), donde:

  • X es una variable aleatoria seleccionada de la distribución Cauchy Cau;
  • μ es el parámetro de localización (-∞ ≤ μ ≤ +∞ );
  • σ es el parámetro de escala (0<σ).

Alcance válido de la variable aleatoria X:  -∞ ≤ X ≤ +∞.


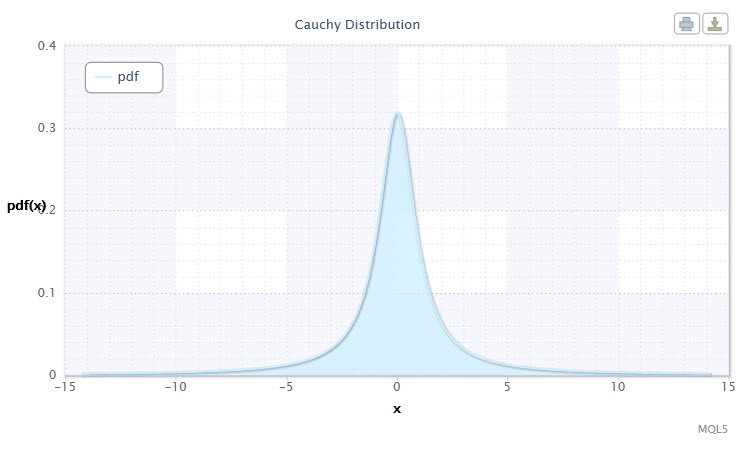
Figura 3. Densidad de la distribución Cauchy Cau(0,1)

Creada con la ayuda de la clase CCauchydist, en formato MQL5 tiene el siguiente aspecto:

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Debemos señalar aquí que se utiliza la función atan2(), que devuelve el principal valor del arco tangente en radianes:

double atan2(double y,double x)
/*
 Devuelve el valor principal del arco tangente y/x,
 expresado en radianes. Para computar el valor, la función 
 usa el signo de ambos argumentos para determinar el cuadrante.
 y - valor doble que representa una coordinada y.
 x - valor doble que representa una coordinada x. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }


2.1.4 Distribución de Secante Hiperbólico

La distribución de secante hiperbólico será interesante para aquellos que trabajan con análisis de ranking financiero.

En teoría de probabilidad y estadística, la distribución de secante hiperbólico es una distribución de probabilidad cuya función de densidad de probabilidad y función de característica son proporcionales a la función de secante hiperbólica. La densidad se consigue con la fórmula:


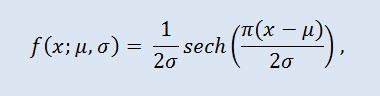
donde μ es el parámetro de localización (-∞ ≤ μ ≤ +∞ ), y σ es el parámetro de escala (0<σ).



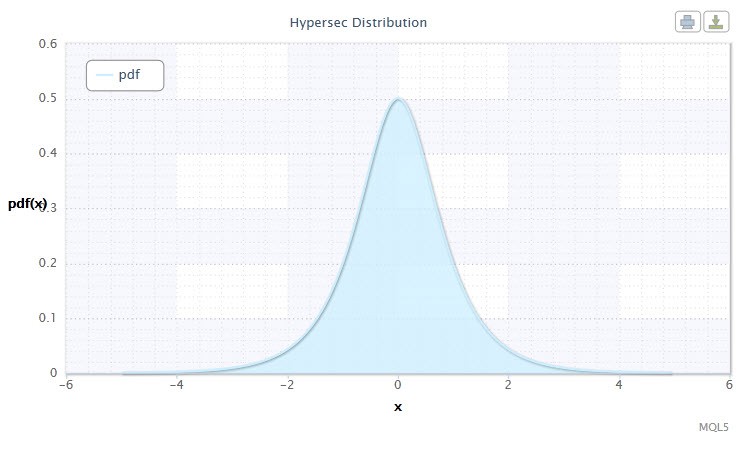
Figura 4. Densidad de distribución de secante hiperbólico HS(0,1)

Su anotación tiene el siguiente formato: X ~ HS(μ, σ), donde:

  • X es una variable aleatoria;
  • μ es el parámetro de localización (-∞ ≤ μ ≤ +∞ );
  • σ es el parámetro de escala (0<σ).

Alcance válido de la variable aleatoria X:  -∞ ≤ X ≤ +∞.

Describámosla utilizado la clase CHypersecdist de la siguiente manera:

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

No es difícil ver que esta distribución tomó su nombre de la función de secante hiperbólica cuya función de densidad de probabilidad es proporcional a la función de secante hiperbólica.

La función de secante hiperbólica tiene el siguiente aspecto:

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }


2.1.5 Student's t-Distribution

La distribución Student t es una distribución importante en estadística.

En teoría de probabilidad, la distribución Student t es en la mayoría de los casos una familia de un parámetro de distribuciones continuas absolutas. No obstante, también se puede considerar una distribución de tres parámetros que se consigue con la función de densidad de distribución:


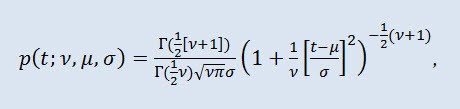
donde Г es la función Gamma de Euler, ν es el parámetro de forma (ν>0), μ es el parámetro de localización (-∞ ≤ μ ≤ +∞ ), σ es el parámetro de escala (0<σ).


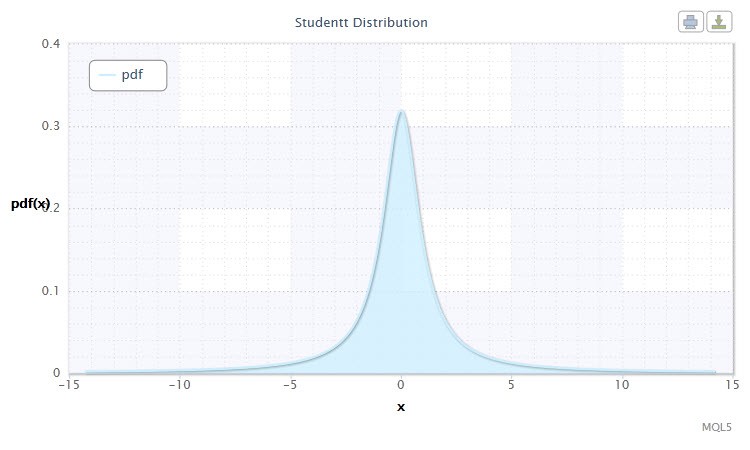
Figura 5. Densidad de la distribución Student Stt(1,0,1)

Su anotación tiene el siguiente formato: t ~ Stt(ν,μ,σ), donde:

  • t es una variable aleatoria seleccionada de la distribución Student t Stt;
  • ν es el parámetro de forma (ν>0)
  • μ es el parámetro de localización (-∞ ≤ μ ≤ +∞ );
  • σ es el parámetro de escala (0<σ).

Alcance válido de la variable aleatoria X:  -∞ ≤ X ≤ +∞.

A menudo, especialmente en hipótesis que ponen a prueban una distribución t, se usa con μ=0 y σ=1. Por tanto, se convierte en una distribución de un parámetro con parámetro v.

Esta distribución se usa a menudo en el cálculo de la expectativa, valores proyectados y otras características por medio de intervalos de confianza, cuando las expectativas de prueba valoran hipótesis, coeficientes de relación de regresión, hipótesis de homogeneidad, etc.

Describamos la distribución a través de la clase CStudenttdist:

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

El listado de la clase CStudenttdist muestra que CBeta es una clase base que describe la función beta incompleta.

La clase CBeta tiene el siguiente aspecto:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

Esta clase también tiene la clase base CGauleg18, que facilita coeficientes para métodos de integración numérica tales como la cuadratura Gauss-Legendre.


2.1.6 Distribución Logística

A continuación propongo considerar la distribución logística en nuestro estudio.

En teoría de probabilidad y estadística, la distribución logística es una distribución de probabilidad continua. Su función de distribución acumulativa es la función logística. Se parece a la distribución normal en su forma, pero tiene colas más pesadas. Densidad de distribución:

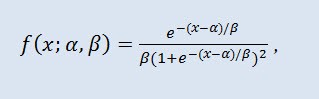
donde α es el parámetro de localización (-∞ ≤ α ≤ +∞ ), y β es el parámetro de escala (0<β).


Figura 6. Densidad de distribución logística Logi(0,1)

Su anotación tiene el siguiente formato: X ~ Logi(α,β), donde:

  • X es una variable aleatoria;
  • α es el parámetro de localización (-∞ ≤ α ≤ +∞ );
  • β es el parámetro de escala (0<β).

Alcance válido de la variable aleatoria X:  -∞ ≤ X ≤ +∞.

La clase CLogisticdist y la implementación de la distribución descrita arriba:

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.7 Distribución Exponencial

Echemos también un vistazo a la distribución exponencial de una variable aleatoria.

Una variable aleatoria X tiene la distribución exponencial con parámetro λ > 0, si su densidad se consigue con:


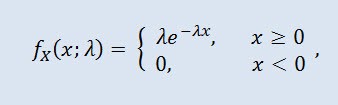
donde λ es el parámetro de escala (λ>0).


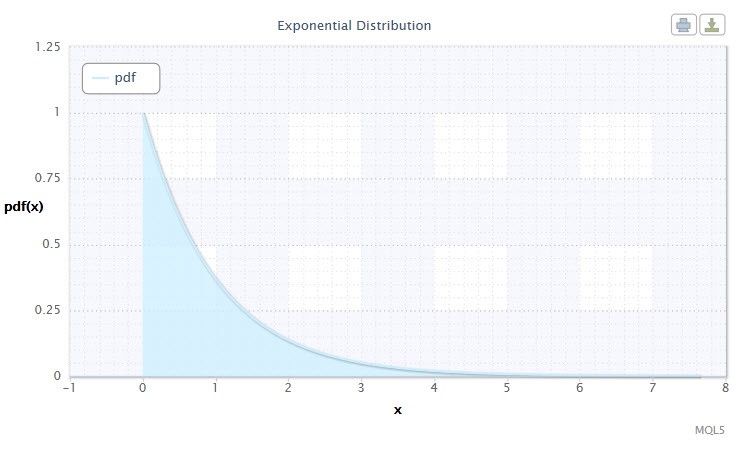
Figura 7. Densidad de distribución exponencial (1)

Su anotación tiene el siguiente formato: X ~ Exp(λ), donde:

  • X es una variable aleatoria;
  • λ es el parámetro de escala (λ>0).

Alcance válido de la variable aleatoria X:  0 ≤ X ≤ +∞.

Esta distribución destaca porque describe una secuencia de eventos que tienen lugar uno después del otro en determinados momentos. Por tanto, usando esta distribución, un trader puede analizar una serie de transferencias de pérdida y otros.

En código MQL5, la distribución se describe a través de la clase CExpondist:

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.8 Distribución Gamma

He elegido la distribución gamma como el siguiente tipo de distribución continua de variable aleatoria. 

En teoría de probabilidad, la distribución gamma es una familia de dos parámetros de distribuciones de probabilidad continua absolutas. Si el parámetro α es un número íntegro, esta distribución gamma también se llama distribución Erlang. La densidad toma la siguiente forma:

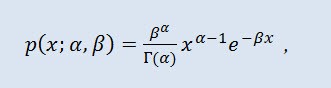
donde Г es la función Gamma de Euler, α es el parámetro de forma (0<α), y β es el parámetro de escala (0<β).


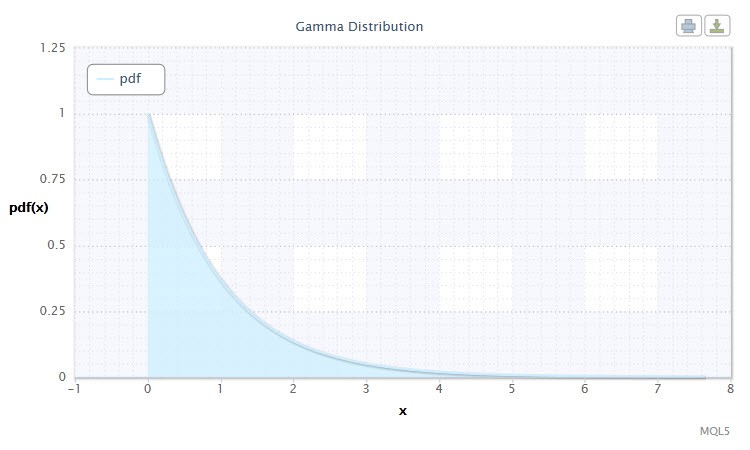
Figura 8. Densidad de la distribución Gamma Gam(1,1).

Su anotación tiene el siguiente formato: X ~ Gam(α,β), donde:

  • X es una variable aleatoria;
  • α es el parámetro de forma (0<α);
  • β es el parámetro de escala (0<β).

Alcance válido de la variable aleatoria X:  0 ≤ X ≤ +∞.

En la variante definida de clase CGammadist, tiene el siguiente aspecto:

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

La clase de distribución gamma deriva de la clase CGamma, que describe la función gamma incompleta.

La clase CGamma se define de la siguiente manera:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Tanto la clase CGamma como la clase CBeta tienen CGauleg18 como clase base.


2.1.9 Distribución Beta

Bien, revisemos ahora la distribución beta.

En teoría de probabilidad y estadística, la distribución beta es una familia de dos parámetros de distribuciones continuas absolutas. Se usa para describir las variables aleatorias cuyos valores se definen en un intervalo infinito. La densidad se define de la siguiente manera:

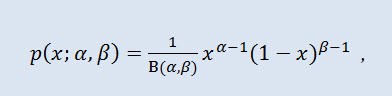
donde B es la función beta, α es el primer parámetro de forma (0<α), y β es el segundo parámetro de forma (0<β).


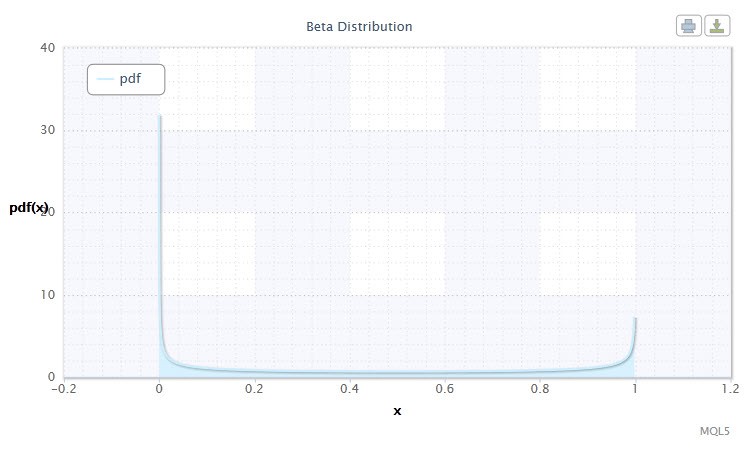
Figura 9. Densidad de la distribución beta Beta(0.5,0.5)

Su anotación tiene el siguiente formato: X ~ Beta(α,β), donde:

  • X es una variable aleatoria;
  • α es el primer parámetro de forma (0<α);
  • β es el segundo parámetro de forma (0<β).

Alcance válido de la variable aleatoria X:  0 ≤ X ≤ 1.

La clase CBetadist describe esta distribución de la siguiente forma:

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+


2.1.10 Distribución Laplace

Otra distribución continua destacable es la distribución Laplace (distribución exponencial doble). 

La distribución Laplace (distribución exponencial doble) en teoría de probabilidad es una distribución continua de una variable aleatoria en la que la densidad de probabilidad es:

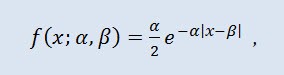
donde α es el parámetro de localización (-∞ ≤ α ≤ +∞ ), y β es el parámetro de escala (0<β).


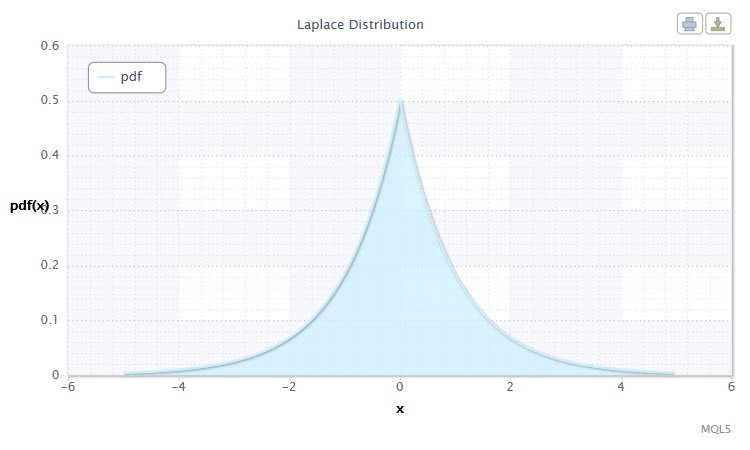
Figura 10. Densidad de la distribución Lap(0,1)

Su anotación tiene el siguiente formato: X ~ Lap(α,β), donde:

  • X es una variable aleatoria;
  • α es el parámetro de localización (-∞ ≤ α ≤ +∞ );
  • β es el parámetro de escala (0<β).

Alcance válido de la variable aleatoria X:  -∞ ≤ X ≤ +∞.

La clase CLaplacedist en términos de esta distribución se define de la siguiente manera:

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

De modo que utilizando el código MQL5 hemos creado 10 clases para las tres distribuciones continuas. Aparte de eso, se crearon algunas clases más que eran, digamos, complementarias, puesto que había una necesidad de funciones específicas y métodos (por ejemplo, CBeta y CGamma).

Ahora procedamos a las distribuciones discretas y creemos unas cuantas clases para esta categoría de distribución.


2.2.1 Distribución Binomial

Empecemos con la distribución binomial.

En teoría de probabilidad, la distribución binomial es una distribución del número de éxitos en una secuencia de experimentos aleatorios independientes donde la probabilidad de éxito en cada uno de ellos es igual. La densidad de probabilidad se consigue con la siguiente fórmula:

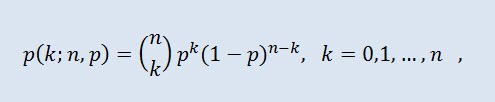
donde  (n k) es el coeficiente binomial, n es el número de pruebas (0 ≤ n), y p es la probabilidad de éxito (0 ≤ p ≤1).


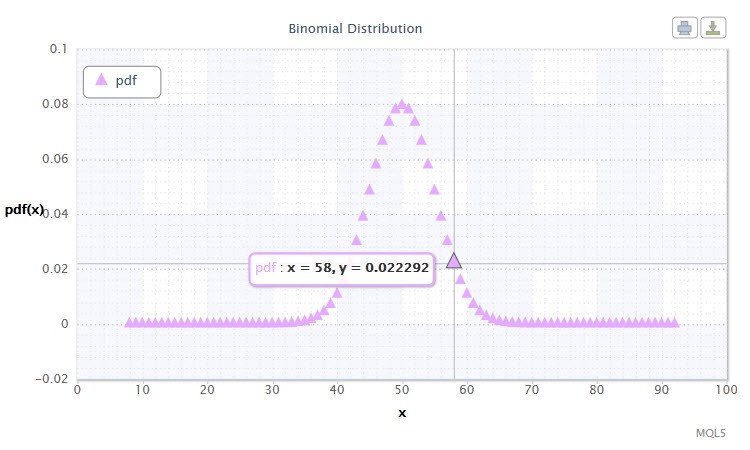
Figura 11. Densidad de distribución binomial Bin(100,0.5).

Su anotación tiene el siguiente formato: k ~ Bin(n,p), donde:

  • k es una variable aleatoria;
  • n es el número de pruebas (0 ≤ n);
  • p es la probabilidad de éxito (0 ≤ p ≤1).

Alcance válido de la variable aleatoria X:  0 or 1.

¿Le sugiere algo el alcance de posibles valores de la variable aleatoria X? Efectivamente, esta distribución nos puede ayudar a analizar el agregado de transferencias de ganancia (1) y pérdida (0) en el sistema de trading.

Creemos la clase СBinomialdist de la siguiente manera:

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+


2.2.2 Distribución Poisson

La siguiente distribución que estudiaremos será la distribución Poisson.

La distribución Poisson modela una variable aleatoria representada por un número de eventos que ocurren durante un período de tiempo fijo, suponiendo que estos eventos ocurran con una intensidad media fija e independientemente los unos de los otros. La densidad toma la siguiente forma:

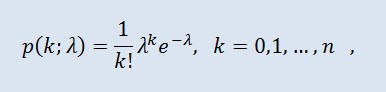
donde k! es el factorial, y λ parámetro de localización (0 < λ).


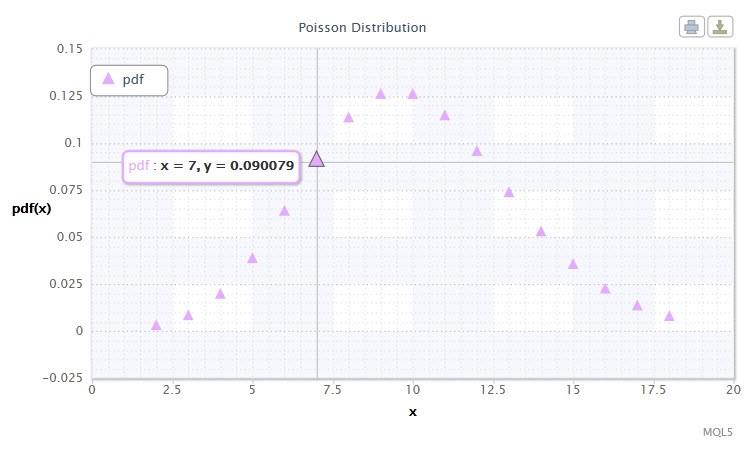
Figura 12. Densidad de la distribution Poisson Pois(10).

Su anotación tiene el siguiente formato: k ~ Pois(λ), donde:

  • k es una variable aleatoria;
  • λ es el parámetro de localización (0 < λ).

Alcance válido de la variable aleatoria X:  0 ≤ X ≤ +∞.

La distribución Poisson describe la "ley de eventos inusuales", que es importante a la hora de calcular el grado de riesgo.

La clase CPoissondist servirá los propósitos de esta distribución:

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

Obviamente, es imposible considerar todas las distribuciones estadísticas en un artículo, y probablemente ni siquiera es necesario. El usuario, si así lo desea, puede expandir la galería de distribuciones facilitada arriba. Las distribuciones creadas se pueden encontrar en el archivo Distribution_class.mqh.


3. Creación de Gráficos de Distribución

Ahora sugiero que veamos cómo se pueden usar las clases que creamos para las distribuciones en nuestro futuro trabajo.

En este punto, de nuevo utilizando OOP, he creado la clase CDistributionFigure, que procesa distribuciones de parámetro definidas por el usuario y las muestra en la pantalla por medios ya descritos en el artículo "Charts and Diagrams in HTML" ("Gráficos y Diagramas en HTML"). 

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

Omitir implementación Note que esta clase tiene miembros de datos como type y mode relativos a Dist_type y Dist_mode correspondientemente. Estos tipos son enumeraciones de las distribuciones que estamos estudiando y sus tipos.

De modo que tratemos de crear finalmente un gráfiico de una distribución.

Escribí el script continuousDistribution.mq5 para distribuciones continuas, y sus líneas clave son las siguientes:

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Para distribuciones discretas, se escribió el script discreteDistribution.mq5.

Ejecuté el script con parámetros estándar para la distribución Cauchy y obtuve el siguiente gráfico, tal y como se muestra en el siguiente vídeo:



Conclusión

En este artículo hemos presentado unas cuantas distribuciones teóricas de variable aleatoria, también codificadas para MQL5. Creo que el mercado de trading en sí mismo, y consecuentemente el trabajo de un sistema de trading debería basarse en las leyes fundamentales de probabilidad.

Y espero que este artículo sea de valor práctico para los lectores interesados. Yo, por mi parte, seguiré investigando el tema y dando ejemplos prácticos para demostrar cómo se pueden usar las distribuciones de probabilidad estadística en análisis de modelo de probabilidad.


Localización de archivos:

 #  
Archivo
 Ruta
 Descripción
 1
  Distribution_class.mqh
  %MetaTrader%\MQL5\Include  Galería de clases de distribución
 2  DistributionFigure_class.mqh            
 %MetaTrader%\MQL5\Include                           
 Clases de visualización gráfica de distribuciones            
 3  continuousDistribution.mq5   %MetaTrader%\MQL5\Scripts  Script para la creación de una distribución continua     
 4
  discreteDistribution.mq5
   %MetaTrader%\MQL5\Scripts  Script para la creación de una distribución discreta          
 5
  dataDist.txt
   %MetaTrader%\MQL5\Files  Datos de visualización de distribución
 6
  Distribution_function.htm
   %MetaTrader%\MQL5\Files  Gráfico HTML de distribución continua         
 7  Distribution_function_discr.htm          
  %MetaTrader%\MQL5\Files  Gráfico HTML de distribución discreta                
 8  exporting.js
   %MetaTrader%\MQL5\Files  Scritp Java para exportar un gráfico
 9  highcharts.js
   %MetaTrader%\MQL5\Files  Biblioteca JavaScript
 10  jquery.min.js   %MetaTrader%\MQL5\Files  Biblioteca JavaScript


Literatura:

  1. K. Krishnamoorthy. Handbook of Statistical Distributions with Applications (Manual de Distribuciones Estadísticas con Aplicaciones), Chapman and Hall/CRC 2006.
  2. W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing (Recetas Numéricas: el Arte de la Computación Científica), Tercera Edición, Cambridge University Press: 2007. - 1256 pp.
  3. S.V. Bulashev Statistics for Traders (Estadísticas para Traders). - M.: Kompania Sputnik +, 2003. - 245 pp.
  4. I. Gaidyshev Data Analysis and Processing: Special Reference Guide (Análisis y Procesamiento de Datos: Guía de Referencia Especial) - SPb: Piter, 2001. - 752 pp.: ill.
  5. A.I. Kibzun, E.R. Goryainova — Probability Theory and Mathematical Statistics (Teoría de Probabilidad y Estadísticas Matemáticas). Curso básico con ejemplos y problemas.
  6. N.Sh. Kremer Probability Theory and Mathematical Statistics (Teoría de Probabilidad y Estadísticas Matemáticas). M.: Unity-Dana, 2004. — 573 pp.

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/271

Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Rastreo, Depuración y Análisis Estructural de Código Fuente Rastreo, Depuración y Análisis Estructural de Código Fuente
Todos los problemas que supone la creación de una estructura de código ejecutado y su rastreo se pueden solucionar sin grandes dificultades. Esta posibilidad ha aparecido en MetaTrader 5 a causa de la nueva prestación del lenguaje MQL5: creación automática de variables de tipo complejo de datos (estructuras y clases) y su eliminación al salir del alcance local. Este artículo contiene la descripción de la metodología y la herramienta ya preparada.
Cómo instalar y utilizar OpenCL para efectuar cálculos Cómo instalar y utilizar OpenCL para efectuar cálculos
Ya ha pasado más de un año desde que surgiese en MQL5 la posibilidad de escribir programas para OpenCL. Sin embargo, ni mucho menos todos los usuarios han valorado como merecen las posibilidades que brinda el uso de cálculos paralelos en sus asesores, indicadores y scripts. Este artículo pretende ayudarle a configurar OpenCL en su computadora personal, de manera que usted pueda probar esta tecnología por sí mismo en el terminal comercial MetaTrader 5.
Cálculos Estadísticos Cálculos Estadísticos
El cálculo de parámetros estadísticos de una secuencia es muy importante, puesto que la mayoría de los modelos y métodos matemáticos se basan en suposiciones simples. Por ejemplo, la normalidad de la ley de distribución o valor de dispersión, u otros parámetros. Por tanto, al analizar y pronosticar series cronológicas necesitamos una herramienta simple y conveniente que nos permita calcular de forma rápida y clara los principales parámetros estadísticos. Este artículo describe brevemente los parámetros estadísticos más sencillos de secuencias aleatorias y varios métodos de su análisis visual. Ofrece además la implementación de estos métodos en MQL5 y los métodos de visualización del resultado de los cálculos usando la aplicación Gnuplot.
Principios de funcionamiento y ventajas de las señales comerciales MetaTrader 4 y MetaTrader 5 Principios de funcionamiento y ventajas de las señales comerciales MetaTrader 4 y MetaTrader 5
Las señales comerciales MetaTrader 4 / MetaTrader 5 - son un servicio que permite a los traders copiar las operaciones comerciales de un suministrador de señales. Nuestro objetivo ha sido crear un nuevo servicio masivo, que proteja a los suscriptores y les evite gastos innecesarios.