3 Méthodes d'Accélération des Indicateurs par l'Exemple de la Régression Linéaire

Vitesse de Calculs

Le calcul rapide des indicateurs est une tâche d'une importance capitale Les calculs peuvent être accélérés par différentes méthodes. Il y a plein d'articles sur ce sujet.

Et maintenant, nous allons examiner 3 autres méthodes pour accélérer les calculs et parfois même pour simplifier un code lui-même. Toutes les méthodes décrites sont algorithmiques, c'est-à-dire que nous ne réduirons pas la profondeur de l'historique ou n'activerons pas les noyaux supplémentaires de l'unité de traitement. Nous allons optimiser directement les algorithmes de calcul.

Indicateur de Base

L’indicateur qui est utilisé pour afficher les 3 méthodes estlinear regression indicator. Il crée une fonction de régression à chaque barre (selon le nombre défini des dernières barres) et indique quelle valeur devrait-elle avoir à cette barre. En conséquence, nous avons une ligne continue :

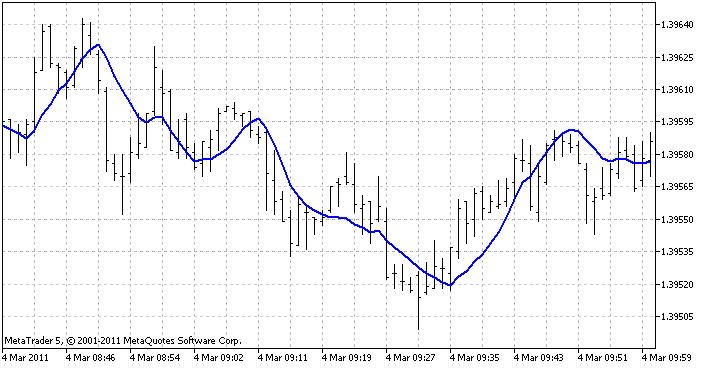
Voici à quoi ressemble l'indicateur dans le terminal

 

L'équation de régression linéaire se présente comme suit :

Dans notre cas, x est un nombre de barres et y sont des prix.

Les rapports de l'équation mentionnée sont calculés comme suit :

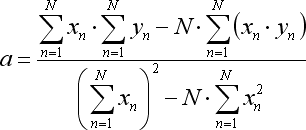
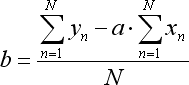
où N est le nombre de barres utilisées pour former la ligne de régression.

Voici à quoi ressemblent ces équations dans MQL5 (à l'intérieur du cycle de toutes les barres d'historique):

            // Finding intermediate values-sums
            Sx  = 0;
            Sy  = 0;
            Sxx = 0;
            Sxy = 0;
            for (int x = 1; x <= LRPeriod; x++)
              {
               double y = price[bar-LRPeriod+x];
               Sx  += x;
               Sy  += y;
               Sxx += x*x;
               Sxy += x*y;
              }

            // Regression ratios
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

Le code complet de l'indicateur est joint à l'article. Il comporte également toutes les méthodes décrites dans le présent article. Par conséquent, la méthode de calcul « Standard » doit être sélectionnée dans les paramètres de l'indicateur :

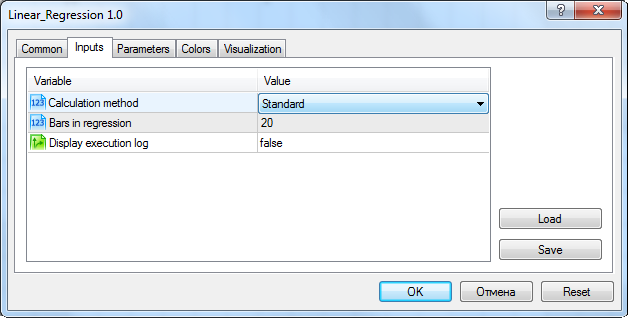
Fenêtre de réglage des paramètres d'entrée de l'indicateur lorsqu'il est défini sur le graphique 

Première Méthode d'Optimisation. Totaux Mobiles

Il existe une quantité énorme d'indicateurs dans lequel un chiffre total de certaines valeurs de séquence de barres est calculé pour chacun d'eux. Et cette séquence change constamment à chaque barre. L'exemple le plus connu est la moyenne mobile (MA). Il calcule la somme des N dernières barres puis cette valeur est divisée par leur nombre.

Je pense qu'un petit nombre de personnes sait qu'il existe un moyen élégant d'accélérer considérablement le calcul de ces totaux mobiles. J'utilisais cette méthode dans mes indicateurs depuis assez longtemps déjà, lorsque j'ai découvert que t est également utilisé dans les indicateurs MA réguliers de MetaTrader 4 et 5. (Ce n'est déjà pas le premier cas où je découvre que les indicateurs MetaTrader sont correctement optimisés par les développeurs. Il y a longtemps, je cherchais des indicateursfast ZigZag indicateur régulier s'est avéré plus efficace que la plupart des indicateurs externes. Par ailleurs, l’objet du forum mentionné comporte également des méthodes d'optimisation ZigZag, juste au cas où quelqu'un en aurait besoin).

Et maintenant, nous allons revenir aux totaux mobiles. Comparons les totaux calculés pour deux barres adjacentes. La figure ci-dessous indique que ces totaux ont une partie commune considérable (indiquée en vert). Le total calculé pour la barre 0 ne diffère du total pour la barre 1 que par le fait que le total ne comprend pas une barre obsolète (une barre rouge à gauche) mais comprend une nouvelle barre (une barre bleue à droite) :

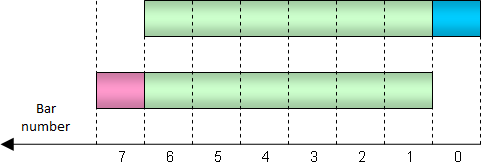
Valeurs exclues et incluses dans le total pendant un décalage d'une barre

 

Par conséquent, il n'est pas nécessaire de résumer à nouveau toutes les barres nécessaires tout en calculant un total pour la barre 0. Nous ne pouvons que prendre une somme de la barre 1, en déduire une valeur et en ajouter une nouvelle. Seules deux opérations arithmétiques sont nécessaires. En s’appuyant sur une telle méthode, nous pouvons considérablement accélérer le calcul des indicateurs.

En Moyenne Mobile, une telle méthode est utilisée de manière routinière, car l'indicateur conserve toutes les valeurs moyennes dans son unique tampon. Et ce n'est rien d'autre que les totaux divisés par N, c'est-à-dire le nombre de barres incluses dans le total. En multipliant une valeur du tampon par N, nous pouvons facilement obtenir un total pour n'importe quelle barre et appliquer la méthode décrite ci-dessus.

Maintenant, je vais vous montrer comment appliquer cette méthode dans l'indicateur plus compliqué - la régression linéaire. Vous avez déjà constaté que les équations pour le calcul des rapports des fonctions de régression comportent quatre totaux : x, y, x*x, x*y. Le calcul de ces totaux doit être tamponné. Les tampons pour chaque total de l'indicateur doivent être affectés pour y parvenir :

double ExtBufSx[], ExtBufSy[], ExtBufSxx[], ExtBufSxy[];

Le tampon peut ne pas être nécessairement visible sur un graphique. MetaTrader 5 dispose d’ un type detampon spécial – pour les calculs intermédiaires.. Nous l'utiliserons pour attribuer des numéros de tampon dans OnInit :

   SetIndexBuffer(1, ExtBufSx,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ExtBufSy,  INDICATOR_CALCULATIONS);
   SetIndexBuffer(3, ExtBufSxx, INDICATOR_CALCULATIONS);
   SetIndexBuffer(4, ExtBufSxy, INDICATOR_CALCULATIONS);

Le code de calcul de régression linéaire standard va maintenant changer pour les éléments suivants :

            // (The very first bar was calculated using the standard method)        
        
            // Previous bar
            int prevbar = bar-1;
            
            //--- Calculating new values of intermediate totals 
            //    from the previous bar values
            
            Sx  = ExtBufSx [prevbar]; 
            
            // An old price comes out, a new one comes in
            Sy  = ExtBufSy [prevbar] - price[bar-LRPeriod] + price[bar]; 
            
            Sxx = ExtBufSxx[prevbar];
            
            // All the old prices come out once, a new one comes in with an appropriate weight
            Sxy = ExtBufSxy[prevbar] - ExtBufSy[prevbar] + price[bar]*LRPeriod;
            
            //---

            // Regression ratios (calculated the same way as in the standard method)
            double a = (LRPeriod * Sxy - Sx * Sy) / (LRPeriod * Sxx - Sx * Sx);
            double b = (Sy - a * Sx) / LRPeriod;

            lrvalue = a*LRPeriod + b;

Le code complet de l'indicateur est joint à l'article. La méthode de calcul « Totaux Mobiles » doit être définie dans les paramètres de l'indicateur.

La Deuxième Méthode. Simplification

Cette méthode sera appréciée par les fans de Maths. Dans les équations compliquées, on trouve souvent des fragments qui semblent être les bonnes parties de certaines autres équations connues. Cela donne la possibilité de remplacer ces fragments par leurs parties gauches (qui consistent généralement en une seule variable). En d'autres termes, nous pouvons simplifier une équation compliquée. Et il peut sembler que certains éléments de cette équation simplifiée soient déjà réalisés en tant qu'indicateurs. Dans ce cas, le code de l'indicateur comprenant cette équation peut être considérablement simplifié à son tour.

En conséquence, nous avons au moins un code plus simple et plus efficace en termes d'espace. Et dans certains cas, cela peut aussi être plus rapide, au cas où les indicateurs implémentés dans le code sont bien optimisés pour la vitesse.

Il apparaît que l'équation de régression linéaire peut également être simplifiée et son calcul peut être remplacé par l'initialisation de plusieurs indicateurs standards MetaTrader 5. Nombre de ses éléments sont calculés dans l'indicateur Moyenne Mobile dans ses différents modes de calcul :

• la somme yest présente dans la Moyenne Mobile Simple :

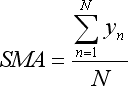
• la sommex*y est présente dans la Moyenne Mobile Pondérée Linéaire :

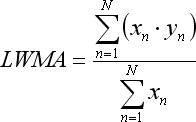
Notez que l'équation pour LWMA n'est vraie que dans le cas où nous énumérons les barres participant à la régression de 1 à N de manière ascendante du passé vers le futur :

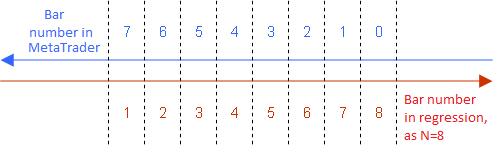
La façon d'énumérer de manière conventionnelle les barres de régression pour utiliser l'indicateur LWMA 

 

Par conséquent, la même énumération doit être utilisée dans toutes les autres équations.

Continuons avec la méthode :

• x total n'est rien d'autre que (1 + 2 + ... + N) total de séries de nombres qui peut être remplacé par l'équation suivante :

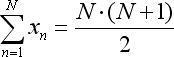
• x*xtotal est simplifié selon une autre équation :

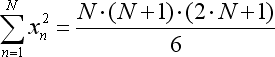
• pour construire un graphique indicateur, nous devons calculer le sens de la fonction de régression uniquement pour sa dernière barre dans laquelle x est égal à N.I.e, l'équation de la fonction de régression peut être remplacée par son cas particulier :

Par conséquent, les cinq dernières équations nous permettent d'obtenir des remplacements pour toutes les variables dans les équations de calcul des rapportsa et b et dans l'équation de régression elle-même. Après avoir terminé tous ces remplacements, nous obtiendrons une toute nouvelle équation pour le calcul de la valeur de régression. EIle se composera uniquement des valeurs des indicateurs de moyenne mobile et du chiffre N. Après toutes les réductions de ses éléments, nous obtiendrons une équation élégante :

Cette équation remplace tous les calculs exécutés dans l'indicateur de base de régression linéaire. Il est tout à fait évident que le code indicateur avec cette équation sera beaucoup plus efficace en termes d'espace. Dans le chapitre "Comparaison de vitesse", nous découvrirons également si le code fonctionne plus rapidement.

Partie indiquée de l'indicateur :

            double SMA [1];
            double LWMA[1];
            CopyBuffer(h_SMA,  0, rates_total-bar, 1, SMA);            
            CopyBuffer(h_LWMA, 0, rates_total-bar, 1, LWMA);

            lrvalue = 3*LWMA[0] - 2*SMA[0];

Les indicateurs LWMA et SMA sont préalablement créés dans OnInit :

      h_SMA  = iMA(NULL, 0, LRPeriod, 0, MODE_SMA,  PRICE_CLOSE);
      h_LWMA = iMA(NULL, 0, LRPeriod, 0, MODE_LWMA, PRICE_CLOSE);

Le code complet est joint à l'article. La méthode de calcul « Simplification » doit être définie dans les paramètres de l'indicateur.

Notez que dans cette méthode, nous avons utilisé les indicateurs intégrés au terminal, c'est-à-dire que la fonction iMA avec sélection des méthodes de lissage appropriées a été utilisée à la place deiCustom. C'est une chose importante car, en théorie, les indicateurs intégrés devraient fonctionner très rapidement. Certains autres indicateurs standard sont intégrés au terminal (ils sont créés par des fonctions ayant le préfixe "i" comme iMA). Lors de l'utilisation de la méthode de simplification, il est préférable de simplifier les équations à ces indicateurs.

La troisième méthode. Approximation

L'idée de cette méthode est que les indicateurs "lourds" utilisés par un expert peuvent être remplacés par des indicateurs beaucoup plus rapides qui à peu prés les valeurs nécessaires. En s’appuyant sur cette méthode, vous pouvez tester votre stratégie plus rapidement. Après tout, la précision de la prédiction n'est pas si importante au stade du débogage.

En outre, cette méthode peut être utilisée avec une stratégie de travail pour optimiser grossièrement les paramètres. Cela permet de trouver rapidement des zones de valeurs efficaces des paramètres. Et puis ils peuvent être traités par des indicateurs "lourds" pour un réglage fin.

Par ailleurs, il peut sembler qu'un calcul approximatif suffira pour permettre à une stratégie de fonctionner correctement. Dans ce cas, un indicateur « allégé » peut également être utilisé dans le trading réel.

Une équation rapide peut être créée pour la régression linéaire qui présente un impact similaire à la régression. Par exemple, nous pouvons répartir les barres de régression en deux groupes, calculer la valeur moyenne pour chacun d'eux, tracer une ligne à travers ces deux points moyens et définir la valeur de la ligne à la dernière barre :

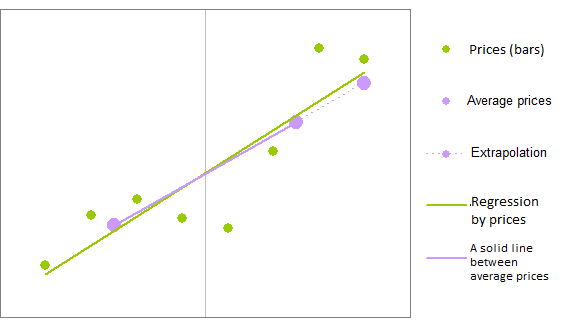
Les points ont été répartis en deux groupes - les gauche et droite - et les calculs ont été exécutés

 

Un tel calcul comporte moins d'opérations arithmétiques que dans le cas de la régression. C'est le moyen d'accélérer les calculs.

           // The interval midpoint
           int HalfPeriod = (int) MathRound(LRPeriod/2);
           
           // Average price of the first half
           double s1 = 0;
           for (int i = 0; i < HalfPeriod; i++)
              s1 += price[bar-i];
           s1 /= HalfPeriod;
              
           // Average price of the second half
           double s2 = 0;
           for (int i = HalfPeriod; i < LRPeriod; i++)
              s2 += price[bar-i];
           s2 /= (LRPeriod-HalfPeriod);
           
           // Price excess by one bar
           double k = (s1-s2)/(LRPeriod/2);
           
           // Extrapolated price at the last bar
           lrvalue = s1 + k * (HalfPeriod-1)/2;

Le code complet de l'indicateur est joint à l'article. La méthode de calcul "approximative" doit être définie dans les paramètres de l'indicateur.

Maintenant, analysons à quel point cela se rapproche de l'original. Pour y parvenir, nous devons définir des indicateurs avec des méthodes de calcul standard et approximatives sur un seul graphique. Il faut aussi ajouter tout autre indicateur sciemment et faiblement similaire à la régression. Néanmoins, il devrait également calculer une tendance en utilisant les barres passées. La Moyenne Mobile fera très bien l'affaire (j'ai utilisé LWMA, pas SMA - c'est beaucoup plus similaire au graphique de régression). A côté de cela, nous pouvons évaluer si nous avons une bonne approximation ou non. Je pense que c'est bon:

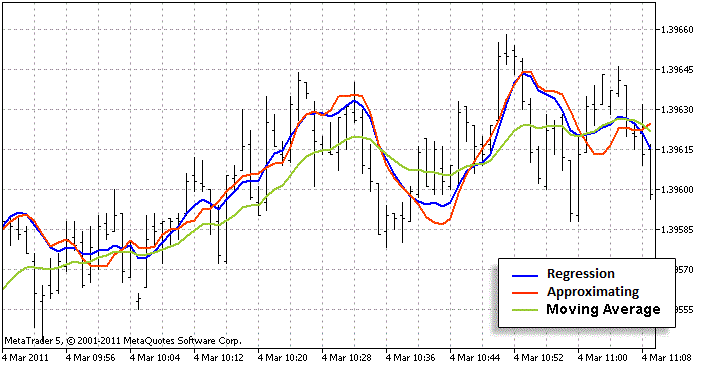
 La ligne rouge est plus proche de celle bleue que celle verte. Cela indique que l'algorithme d'approximation est bon

Comparaison de Vitesse

L'affichage du journal peut être activé dans les paramètres de l'indicateur :

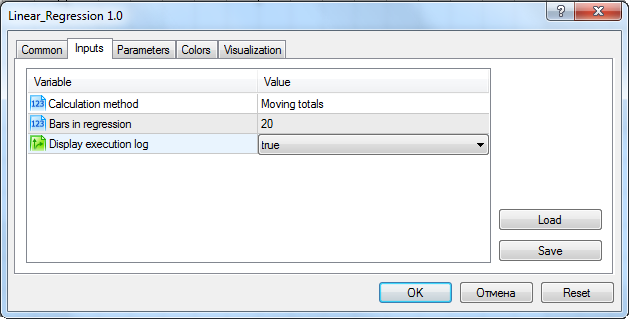
Définition de l'indicateur d'évaluation d'une vitesse d'exécution

 

Dans ce cas, l'indicateur affichera toutes les données nécessaires à l'évaluation de la vitesse dans le journal des messagesjournal des messages des experts: le temps de traitement du début et de fin de l’évènementOnInit() OnCalculate(). Je vais expliquer pourquoi la vitesse doit être évaluée par ces deux valeurs. L'agent OnInit() est exécuté quasiment instantanément dans le cas de n'importe quelle méthode et OnCalculate() démarre juste après OnInit() dans le cas de pratiquement n'importe quelle méthode. La seule exception est une méthode de simplification où les indicateurs SMA et LWMA sont créés dans OnInit(). Un retard est ressenti entre la fin de OnInit() et le début de OnCalculate() dans le cas (et seulement dans ce cas !) de la méthode mentionnée :

Journal d'exécution affiché par l'indicateur dans le journal des experts du terminal 

 

Cela indique que ce retard est causé par les nouveaux SMA et LWMA qui exécutaient certains calculs à ce moment-là. La durée de ces calculs doit également être prise en compte, par conséquent, nous évaluerons tout le temps "sans interruption" - depuis l'initialisation de l'indicateur de régression jusqu'à la fin de ses calculs.

Pour noter la différence entre les vitesses des différentes méthodes avec plus de précision, toutes les évaluations sont menées à l'aide d'un énorme tableau de données - période M1 avec une profondeur d'historique accessible au maximum. C'est plus de 4 millions de barres. Chaque méthode sera évaluée deux fois : avec 20 et 2000 barres en régression.

Les résultats sont les suivants:

 

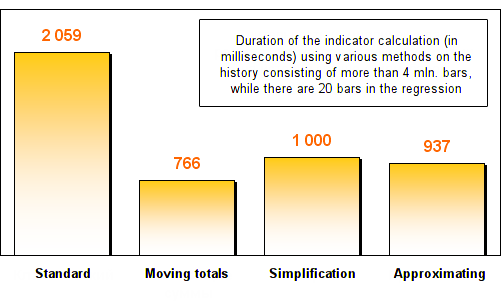
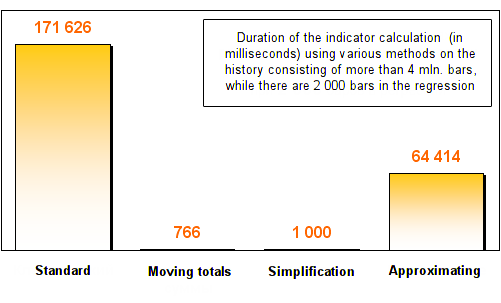
Comme vous pouvez le constater, les trois méthodes d'optimisation ont indiqué une augmentation de la vitesse d'au moins deux fois par rapport à la méthode de calcul de régression standard. Après l'augmentation du nombre de barres dans la régression, les totaux mobiles et les méthodes de simplification ont affiché une vitesse fantastique. Ils ont travaillé des centaines de fois plus vite qu'un standard !

Je dois noter que le temps nécessaire au calcul par ces deux méthodes est resté quasiment inchangé. Ce fait s'explique facilement : quel que soit le nombre de barres utilisées pour créer une régression, seules 2 actions sont exécutées dans la méthode des totaux mobiles - une ancienne barre s'éteint et une nouvelle arrive. Il n'y a pas de cycles qui dépendent de la longueur de la régression. Par conséquent, même si la régression contient 20000 ou 200000 barres, le temps d'exécution de la méthode augmentera de manière insignifiante par rapport à 20 barres.

La méthode de simplification utilise la moyenne mobile dans différents modes dans son équation. Comme je l'ai déjà noté, cet indicateur peut être facilement optimisé par la méthode des totaux mobiles et utilisé par les développeurs de terminaux. Il n'est pas étonnant que le temps d'exécution de la méthode de simplification ne change pas non plus si la longueur de régression est augmentée.

La méthode des totaux mobiles s'est avérée être la méthode de calcul la plus rapide dans notre expérience.

 

Conclusion

Certains traders restent immobiles et attendent la fin d'une autre procédure del'optimisation des paramètresde leurs systèmes de trading dans leurs testeurs. Mais il y a aussi des traders qui échangent et gagnent de l'argent déjà à ce moment-là. Les vitesses de calcul obtenues par les méthodes décrites expliquent clairement pourquoi il existe une telle différence entre ces groupes de traders. Et pourquoi il est si important de prêter attention à la qualité des algorithmes de trading.

Peu importe que vous écriviez vous-même les programmes pour le terminal ou que vous les commandiez à des programmeurs tiers (par exemple, à l'aide de la section "Emplois"). En tout état de cause, vous pouvez obtenir non seulement des indicateurs et des stratégies fonctionnels, mais également des indicateurs rapides, au cas où vous seriez prêt à faire des efforts ou à dépenser de l'argent.

Si vous utilisez une méthode d'accélération d'algorithme, vous obtenez un avantage de vitesse de dizaines à des centaines de fois par rapport aux algorithmes standard. Cela indique que vous pouvez,par exemple, optimiser les paramètres de vos stratégies de trading dans une testeur cent fois plus rapidement. Et faites-le plus soigneusement et fréquemment. Inutile de dire que cela entraîne une augmentation de vos revenus de trading..