Algorithmes d'optimisation de la population : Algorithme de Recherche Gravitationnelle (Gravitational Search Algorithm, GSA)

Sommaire

1. Introduction
2. Algorithme
3. Résultats des tests

1. Introduction

L'Algorithme de Recherche Gravitationnelle, ou Gravitational Search Algorithm (GSA) a été proposé par E. Rashedi pour résoudre les problèmes d'optimisation, en particulier les problèmes non linéaires, en suivant les principes de la loi de la gravitation de Newton. Dans l'algorithme proposé, les particules sont considérées comme des objets et leur performance est estimée en tenant compte de leur masse. La gravité est la tendance des masses à accélérer l'une vers l'autre. C'est l'une des 4 forces fondamentales de la nature (les autres sont la force électromagnétique, la force nucléaire faible et la force nucléaire forte).

Chaque particule de l'univers attire toutes les autres particules. La gravité existe partout. Bien qu'il s'agisse de la force la plus faible, c'est pourtant la plus visible. C'est grâce à la force gravitationnelle que les gens peuvent marcher sur la Terre et que les planètes peuvent tourner autour du Soleil. La force gravitationnelle d'un objet est proportionnelle à sa masse. Les objets ayant une masse plus importante ont donc une gravité plus élevée. Le caractère inéluctable de la gravité la distingue de toutes les autres forces de la nature. Le comportement de la force gravitationnelle de Newton est appelé action à distance. Il s'agit d'une loi physique générale déduite de l'observation empirique par ce que Isaac Newton appelait le raisonnement inductif. Elle fait partie de la mécanique classique formulée dans les Philosophiae Naturalis Principia Mathematica (Principia) de Newton, publiés pour la première fois le 5 juillet 1687.

Lorsqu'en avril 1686, Newton a présenté le premier livre non publié à la Royal Society, Robert Hooke a prétendu que Newton avait reçu de lui la loi de l'inverse du carré. Dans le langage d'aujourd'hui, la loi dit que toute masse ponctuelle attire toute autre masse ponctuelle par une force agissant le long d'une ligne qui coupe deux points.

2. Algorithme

L'article présente un algorithme d'optimisation basé sur la loi de la gravitation de Newton : "Chaque particule de l'univers attire toutes les autres particules avec une force qui est directement proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare". Dans l'algorithme proposé, les agents de recherche sont un ensemble de masses qui interagissent les unes avec les autres sur la base de la gravitation newtonienne et des lois du mouvement. Parallèlement, tous les agents peuvent échanger des informations entre eux, où qu'ils se trouvent dans l'espace de recherche, au moyen d'une force d'attraction qui dépend de la masse (calculée à partir des valeurs de la fonction objective) et de la distance qui les sépare.

Les agents sont traités comme des objets et leur aptitude est mesurée par leur masse. En termes généraux (avec les paramètres de l'algorithme proches des lois physiques réelles), tous ces objets sont attirés les uns vers les autres par la force de gravité. Cette force provoque également un mouvement global de tous les objets vers les objets ayant une masse plus importante. Par conséquent, les masses interagissent en utilisant une forme directe de connexion par le biais de la force gravitationnelle.

Dans le GSA classique, chaque particule a 3 types de masses :

a) la masse active
b) la masse passive
c) la masse inertielle

Dans la plupart des cas, il est pratique et opportun d'utiliser l'égalité de ces concepts pour simplifier les codes et les calculs et donc pour accroître l'efficacité des capacités de recherche de l'algorithme. Il n’y aura donc qu’une seule masse dans l'algorithme, et non trois. Les équations des lois physiques utilisées dans le GSA sont présentées dans la figure 1.

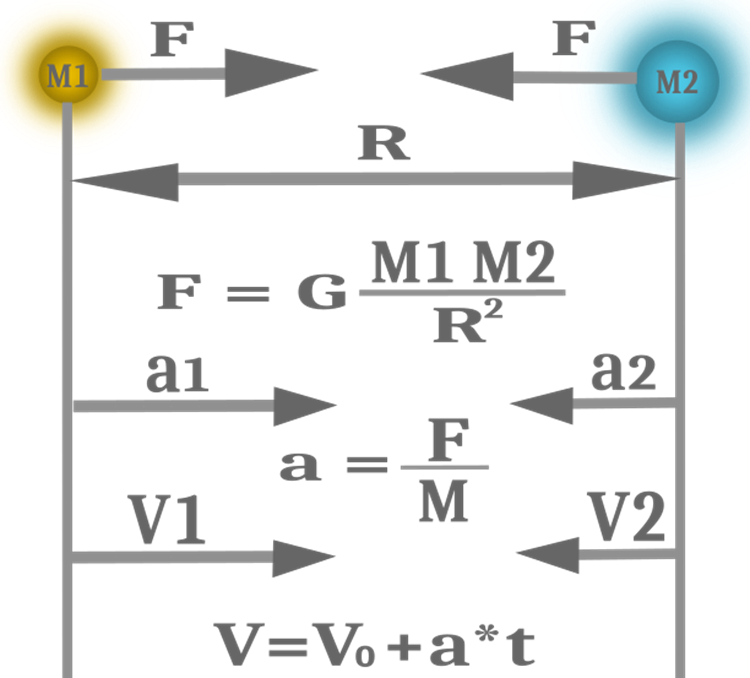
Figure 1. Force de gravité, accélération et vitesse

La position des particules fournit la solution au problème, et la fonction d'aptitude est utilisée pour calculer les masses. L'algorithme comporte 2 étapes : l'exploration et l'exploitation. Cet algorithme utilise des capacités d'intelligence au début pour éviter de rester bloqué dans l'optimum local, puis il exploite les régions d'extrema.

L'algorithme de recherche gravitationnelle doit transformer une particule se déplaçant dans l'espace en un objet d'une certaine masse. Ces objets sont attirés par l'interaction gravitationnelle entre eux. Chaque particule dans l'espace sera attirée par l'attraction mutuelle des particules créant des accélérations. Chaque particule est attirée par d'autres particules et se déplace dans la direction de la force. Les particules de faible masse se déplacent vers les particules de masse plus importante. Mais les objets massifs se déplacent également, mais à une vitesse inférieure inversement proportionnelle à la masse. La solution optimale est trouvée par les "grands" objets, qui affinent la solution en se déplaçant à faible vitesse par rapport aux "petits" objets qui se déplacent plus rapidement. Le GSA met en œuvre le transfert d'informations par le biais de l'interaction entre les objets.

Les étapes du GSA :

1. Initialisation de l'agent
2. Évolution de la condition physique
3. Calcul de la constante gravitationnelle
4. Calcul des masses des agents

1. Initialisation de l'agent
Tous les agents sont initialisés de manière aléatoire. Chaque agent est considéré comme une solution candidate. Pour que l'analyse de stabilité soit significative et fiable, il est extrêmement important de spécifier les conditions initiales d'équilibre. Car si le "disque" d’origine des objets n'est pas en équilibre, sa détente aux premiers instants de la simulation peut provoquer des instabilités qui sont de peu d'importance pour notre compréhension de la stabilité des "galaxies à disque". Malheureusement, aucune solution analytique n'est connue pour la densité, le champ de vitesse et la température d'un disque gazeux tridimensionnel en équilibre hydrostatique dans le potentiel externe du halo de matière noire et/ou du disque stellaire.

2. L'évolution de la condition physique (fitness)
La fiabilité et l'efficacité du GSA dépendent de l'équilibre entre les capacités de recherche et d'exploitation. Dans les premières itérations du processus de recherche de solutions, la préférence est donnée à l'exploration de l'espace de recherche. Elle peut être réalisée en permettant aux agents d'utiliser de grandes tailles de pas dans les premières itérations. Lors des itérations ultérieures, il est nécessaire d'affiner l'espace de recherche afin d'éviter que des optima globaux ne soient manquants. Les solutions candidates doivent donc avoir de petites tailles de pas afin d'être utilisées dans les itérations suivantes.

3. Calcul de la constante gravitationnelle
La constante gravitationnelle (également appelée constante universelle de gravitation, constante newtonienne de gravitation ou constante gravitationnelle de Cavendish), désignée par la lettre G, est une constante physique empirique qui intervient dans le calcul des effets gravitationnels dans la loi de la gravitation universelle d'Isaac Newton et dans la Théorie de la Relativité Générale d'Albert Einstein. Dans la loi de Newton, c'est la constante de proportionnalité reliant la force gravitationnelle entre deux corps au produit de leurs masses et à l'inverse du carré de leur distance. Dans les équations du champ d'Einstein, il quantifie la relation entre la géométrie de l'espace-temps et le tenseur énergie-momentum.

4. Calcul des masses des agents
La masse est la quantité de matière présente dans l'espace.

Pseudo-code de l'algorithme :

1. génération d’un système d'objets de manière aléatoire.
2. détermination de l'aptitude de chaque objet.
3. mise à jour des valeurs de la constante gravitationnelle, calcul des masses, du meilleur et du plus mauvais objet.
4. calcul des forces agissant sur chaque coordonnée.
5. calcul des accélérations et des vitesses des objets.
6. mise à jour de la position des objets.
7. détermination de l'aptitude de chaque objet.
8. répétition depuis le point 3 jusqu'à ce que le critère d'arrêt soit rempli.

Prenons le code du GSA. Pour décrire un objet dans le système d'interaction gravitationnelle, nous avons besoin de la structure S_Object, qui décrira toutes les propriétés physiques nécessaires de l'objet pour effectuer une recherche gravitationnelle : c[] - les coordonnées dans l'espace de recherche, v[] - le vecteur vitesse pour chacune des coordonnées (la dimension du tableau est le nombre de coordonnées), M - la masse de l'objet (dans le GSA, la masse est une valeur relative, c'est-à-dire une valeur calculée en fonction de la valeur de l'aptitude maximale et minimale sur l'ensemble du système d'objets), f - la valeur de l'aptitude, R[] - la distance euclidienne par rapport aux autres objets (la dimension du tableau est le nombre d'objets), F[] - le vecteur des forces pour chacune des coordonnées (la dimension du tableau est le nombre de coordonnées).

//——————————————————————————————————————————————————————————————————————————————
struct S_Object
{
  double c  [];   //coordinates
  double v  [];   //velocity
  double M;       //mass
  double f;       //fitness
  double R  [];   //euclidean distance to other objects
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Déclarons la classe de l'algorithme de recherche gravitationnelle C_AO_GSA. Parmi les propriétés physiques des objets participant à l'algorithme en tant qu'agents, une seule chose est nécessaire : les coordonnées qui représentent la meilleure solution - la valeur de fB. La classe déclare des plages valides de coordonnées de l'espace de recherche et un pas. Le système d'objets liés par la gravitation est représenté par un tableau de structures S_Object. Dans l'algorithme classique, il n'y a que 3 paramètres externes : G_constant, a_constant, e_constant, qui déterminent les propriétés de l'interaction gravitationnelle des objets. Le reste des constantes sont inclus dans les équations de calcul. Mais j'ai considéré qu'il était approprié de déplacer ces constantes dans les paramètres externes de l'algorithme, ce qui permet un ajustement plus flexible des propriétés de l'algorithme dans son ensemble. J'examinerai tous les paramètres plus en détail un peu plus tard, car ils influencent grandement le comportement de l'algorithme.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_GSA
{
  //----------------------------------------------------------------------------
  public: S_Object o       []; //object
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    objectsNumber;     //objects number
  private: double PowerOfdistance;   //power of distance
  private: double GraviPert_Min;     //gravitational perturbation Min
  private: double GraviPert_Max;     //gravitational perturbation Min
  private: double VelocPert_Min;     //velocity perturbation Min
  private: double VelocPert_Max;     //velocity perturbation Max
  private: double G_constant;        //G constant
  private: double a_constant;        //a constant
  private: double e_constant;        //e constant
  private: int    maxIterations;
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

La méthode publique Init() de l'algorithme est destinée à passer les paramètres externes de l'algorithme à des constantes internes pour initialiser les variables de service et assigner des tailles aux tableaux.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Init (const int    coordinatesNumberP, //coordinates number
                     const int    objectsNumberP,     //objects number
                     const double PowerOfdistanceP,   //power of distance
                     const double GraviPert_MinP,     //gravitational perturbation Min
                     const double GraviPert_MaxP,     //gravitational perturbation Min
                     const double VelocityPert_MinP,  //Velocity perturbation Min
                     const double VelocityPert_MaxP,  //Velocity perturbation Max
                     const double G_constantP,        //G constant
                     const double a_constantP,        //a constant
                     const double e_constantP,        //e constant
                     const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  objectsNumber     = objectsNumberP;
  PowerOfdistance   = PowerOfdistanceP;
  GraviPert_Min     = GraviPert_MinP;
  GraviPert_Max     = GraviPert_MaxP;
  VelocPert_Min     = VelocityPert_MinP;
  VelocPert_Max     = VelocityPert_MaxP;
  G_constant        = G_constantP;
  a_constant        = a_constantP;
  e_constant        = e_constantP;
  maxIterations     = maxIterationsP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);

  ArrayResize (o,  objectsNumber);

  for (int i = 0; i < objectsNumber; i++)
  {
    ArrayResize (o [i].c,  coordinatesNumber);
    ArrayResize (o [i].v,  coordinatesNumber);
    ArrayResize (o [i].R,  objectsNumber);
    ArrayResize (o [i].F,  coordinatesNumber);
    o [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

La première méthode publique appelée à chaque itération de l'itération est Moving(). Cette méthode contient toute la physique et la logique de l'algorithme GSA. Elle est assez volumineuse, nous allons donc l'examiner en la divisant en plusieurs parties. Notez que la méthode prend l'itération en cours comme paramètre, le paramètre est impliqué dans le calcul de la constante gravitationnelle, ajustant l'équilibre entre la recherche et l'exploitation.

Lors de la première itération, l'étape d'initialisation de l'objet a lieu. Pour toutes les coordonnées des objets, nous attribuons des valeurs aléatoires dans l’intervalle autorisé avec une distribution uniforme, et nous vérifions qu'il n'y a pas de dépassement de l’intervalle. Au début du processus d'optimisation, tous les objets ont une vitesse nulle, c'est-à-dire qu'ils sont immobiles dans l'espace de recherche en ce qui concerne les coordonnées. Notez que les objets n'ont pas de masse. Ils devraient donc se déplacer à la vitesse de la lumière. Mais nous enfreindrions les lois de la physique pour la première itération, car ce moment équivaut dans une certaine mesure au Big Bang. La condition physique des objets à cet instant est la plus petite des valeurs possibles du type "double". Lors du débogage de l'algorithme, il a été difficile de trouver des bugs liés à la masse zéro. Vous pouvez voir la solution ci-dessous.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < objectsNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      o [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      o [obj].v [c] = 0.0;
      o [obj].M     = 0.0;
      o [obj].f     = -DBL_MAX;
    }
  }

  revision = true;
}

Le reste du code de la méthode Moving() se réfère à la deuxième itération et aux itérations suivantes, au cours desquelles les objets acquièrent de la masse, de la vitesse et de l'accélération.

Tout d'abord, nous devons calculer la masse. Comme mentionné ci-dessus, la masse (une valeur scalaire positive par définition) des objets est calculée à partir des valeurs de la fonction d'aptitude. Il est donc nécessaire de déterminer les valeurs minimale et maximale de l'aptitude avant de calculer la masse sur la base des valeurs obtenues. À ce stade, la valeur de la fonction d'aptitude a déjà été obtenue à l'itération précédente.

//find the minimum and maximum fitness==========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  if (o [obj].f < Fmin) Fmin = o [obj].f;
  if (o [obj].f > Fmax) Fmax = o [obj].f;
}

À ce stade du code, la masse est calculée à l'aide de l'équation Mo = (Fo-Fmin) / (Fmax-Fmin), avec :

• Mo - la masse de l'objet
• Fo - l’aptitude à utiliser l’objet (fitness)
• Fmax - la valeur d'aptitude maximale parmi tous les objets (meilleure valeur)
• Fmin - la valeur d'aptitude minimale parmi tous les objets (valeur la plus faible)
  

Comme le montre l'équation, la masse ne peut prendre que des valeurs positives comprises entre 0 et 1 inclus. Comme nous avons vu précédemment que la masse ne doit pas être égale à zéro (sinon la vitesse serait égale à la vitesse de la lumière), nous limiterons la limite inférieure de la masse à 0,1. La valeur supérieure peut être égale à 1. N'oubliez pas non plus que si les valeurs minimales et maximales de la fonction d'aptitude sont égales, la masse de tous les objets sera la même pour tous et égale à 1. Cela correspond au cas où l'espace de recherche est homogène dans la zone où se trouvent les objets et où tous les objets sont égaux en termes de qualité de la fonction d'aptitude, et des mouvements dans n'importe quelle direction ont la même priorité. Il semblerait que dans ce cas, tous les objets devraient progressivement se déplacer et se concentrer vers un centre de masse commun, mais cela ne se produit pas en raison de l'action non linéaire de la force gravitationnelle.

//calculating the mass of objects===========================================
for (int obj = 0; obj < objectsNumber; obj++)
{
  Fo = o [obj].f;
  if (Fmax == Fmin) Mo = 1.0;
  else Mo = (Fo - Fmin) / (Fmax - Fmin);
  o [obj].M = Scale (Mo, 0.0, 1.0, 0.1, 1.0, false);
}

Nous avons calculé la masse des objets. Il faut maintenant calculer une autre composante de l'équation R : la distance euclidienne entre chaque objet et tous les autres objets. Le calcul consiste en 2 cycles d'énumération d'objets et 1 cycle de calcul pour chacune des coordonnées. Comme on s'en souvient, la distance euclidienne est la racine de la somme des carrés des différences de coordonnées.

//calculation of Euclidean distances between all objects====================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].R, 0.0);

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (o [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = o [obj].c [c] - o [obj2].c [c];
          o [obj].R [obj2] += diffDist * diffDist;
        }

        o [obj].R [obj2] = sqrt (o [obj].R [obj2]);
        o [obj2].R [obj] = o [obj].R [obj2];
      }
    }
  }
}

Nous pouvons maintenant calculer les vecteurs de force des objets. Pour cela, nous devons également parcourir tous les objets en 2 cycles et 1 cycle pour les coordonnées, puisque la vitesse est calculée séparément pour chaque coordonnée. Il faut ajouter une condition qui exclut la coïncidence des index des objets pour que l'objet exclue le calcul de lui-même dans le calcul de la force. Nous utilisons ici l'équation bien connue de Newton pour calculer la force gravitationnelle de deux objets (figure 1) en corrigeant la distance par le rapport e_constant. Calculons d'abord la constante gravitationnelle G, qui devrait évoluer à la baisse à chaque itération en supposant que l'algorithme s'intensifie à la fin de l'optimisation.

//calculate the force vector for each object================================
for (int obj = 0; obj < objectsNumber; obj++) ArrayInitialize (o [obj].F, 0.0);

double G = G_constant * exp (-a_constant * (iter / maxIterations));

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int obj2 = 0; obj2 < objectsNumber; obj2++)
  {
    if (obj != obj2)
    {
      for (int c = 0; c < coordinatesNumber; c++)
      {
        diffDist = o [obj2].c [c] - o [obj].c [c];

        if (o [obj].R [obj2] != 0.0)
        {
          o [obj] .F [c] += G * o [obj].M * o [obj2].M * diffDist / (pow (o [obj].R [obj2], PowerOfdistance) + e_constant);
        }
      }
    }
  }
}

Il ne reste plus qu'à calculer la vitesse pour que les objets commencent à se déplacer. L'équation de la figure 1 montre que le calcul de la vitesse implique l'accélération, et que l'accélération est égale à la force agissant sur le corps divisée par la masse. L'équation contient également le temps V = V0+a*t. Dans notre algorithme, l'itération joue le rôle du temps, le changement de vitesse n'est donc rien d'autre qu'une augmentation de la vitesse dans une itération. Le vecteur vitesse a déjà été calculé ci-dessus. Il reste à diviser par la masse. Les auteurs introduisent également la perturbation de la force et la perturbation de la vitesse. La perturbation est un nombre aléatoire uniformément distribué entre 0 et 1. Cela ajoute une composante aléatoire au mouvement des objets, sans laquelle le mouvement serait strictement déterminé et ne dépendrait que de la position initiale des corps. J'ai jugé raisonnable d'intégrer les indicateurs de perturbation dans les paramètres externes de l'algorithme, ce qui permettra de réguler le mouvement des objets d'une manière totalement déterministe à une manière totalement aléatoire.

//calculation of acceleration and velocity for all objects==================
double a = 0.0; //acceleration

for (int obj = 0; obj < objectsNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    a = o [obj].F [c] * r / o [obj].M;
    r = RNDfromCI (GraviPert_Min, GraviPert_Max);
    o [obj].v [c] = o [obj].v [c] * r + a;
    o [obj].c [c] = o [obj].c [c] + o [obj].v [c];

    if (o [obj].c [c] > rangeMax [c]) o [obj].c [c] = rangeMin [c];
    if (o [obj].c [c] < rangeMin [c]) o [obj].c [c] = rangeMax [c];

    o [obj].c [c] = SeInDiSp (o [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

La deuxième méthode Revision(), dont l'exécution est obligatoire à chaque itération. La méthode est conçue pour déterminer la meilleure valeur d'aptitude (fitness) pour l'itération en cours. Dans la boucle, il faut passer en revue tous les objets et remplacer la meilleure solution globale.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_GSA::Revision ()
{
  for (int s = 0; s < objectsNumber; s++)
  {
    if (o [s].f > fB)
    {
      fB = o [s].f;
      ArrayCopy (cB, o [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Résultats des tests

Passons maintenant aux résultats des tests. Voici les résultats du banc d'essai avec les meilleurs paramètres GSA que j'ai pu trouver :

2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD, M1) C_AO_GSA:10;2.0;0.2;0.6;0.0;1.0;2.0;20.0;0.01
2023.02.03 14:12:43.440    Test_AO_GSA (EURUSD, M1) =============================
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD, M1) 5 Rastrigin's ; Func runs 10000 result : 73.64619475145881
2023.02.03 14:12:52.198    Test_AO_GSA (EURUSD, M1) Score : 0.91252
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD, M1) 25 Rastrigin's ; Func runs 10000 result : 59.4327218024363
2023.02.03 14:13:06.105    Test_AO_GSA (EURUSD, M1) Score : 0.73640
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD, M1) 500 Rastrigin's ; Func runs 10000 result : 37.550565227034724
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD, M1) Score : 0.46527
2023.02.03 14:14:16.529    Test_AO_GSA (EURUSD, M1) =============================
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD, M1) 5 Forest's ; Func runs 10000 result : 0.741456333008312
2023.02.03 14:14:30.577    Test_AO_GSA (EURUSD, M1) Score : 0.41941
2023.02.03 14:14:50.281    Test_AO_GSA (EURUSD, M1) 25 Forest's ; Func runs 10000 result : 0.46894018717768426
2023.02.03 14:14:50.282    Test_AO_GSA (EURUSD, M1) Score : 0.26526
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD, M1) 500 Forest's ; Func runs 10000 result : 0.11382493516764165
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD, M1) Score : 0.06439
2023.02.03 14:16:01.856    Test_AO_GSA (EURUSD, M1) =============================
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD, M1) 5 Megacity's ; Func runs 10000 result : 5.279999999999999
2023.02.03 14:16:18.195    Test_AO_GSA (EURUSD, M1) Score : 0,44000
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD, M1) 25 Megacity's ; Func runs 10000 result : 2.296
2023.02.03 14:16:34.536    Test_AO_GSA (EURUSD, M1) Score : 0.19133
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD, M1) 500 Megacity's ; Func runs 10000 result : 0.23399999999999999
2023.02.03 14:17:46.887    Test_AO_GSA (EURUSD, M1) Score : 0.01950

Paramètres de l'algorithme :

input double PowerOfdistance_P = 2.0; // Puissance de la distance
input double GraviPert_Min_P = 0.2; // Perturbation gravitationnelle Min
input double GraviPert_Max_P = 0.6; // Perturbation gravitationnelle Max
input double VelocityPert_Min_P = 0.0; // Perturbation de la vitesse Min
input double VelocityPert_Max_P = 1.0; // Perturbation de la vitesse Max
input double G_constant_P = 2.0; // Constante G
input double a_constant_P = 20.0; // Constante a
input double e_constant_P = 0.01; // Constante e

PowerOfdistance_P - le degré auquel nous augmentons la distance entre les objets affecte la formation d'objets liés par la gravitation. Plus le degré de l'équation est élevé, moins les objets ont d'impact sur d'autres objets.

• GraviPert_Min_P - la limite inférieure de la plage de perturbation gravitationnelle.
• GraviPert_Max_P - la limite supérieure de la plage de perturbation gravitationnelle.
• Dans le cas de GraviPert_Min_P = 1.0 et GraviPert_Max_P = 1.0, il n'y a pas de perturbation gravitationnelle.
• VelocityPert_Min_P - la limite inférieure de la plage de perturbation de la vitesse.
• VelocityPert_Max_P - la limite supérieure de la plage de perturbation de la vitesse.

Dans le cas de VelocityPert_Min_P = 1.0 et VelocityPert_Max_P = 1.0, il n'y a pas de perturbation de la vitesse.

• G_constant_P - la constante gravitationnelle agit comme un facteur d'échelle : plus la valeur est élevée, plus les forces gravitationnelles agissent et plus la vitesse des objets change.
• a_constant_P - le facteur de correction pour la constante gravitationnelle destiné à réduire le champ de recherche pendant toute la durée de l'optimisation afin d'affiner les extrema trouvés.
• e_constant_P - le facteur de correction pour la distance entre les objets.

Examinons les résultats du test de visualisation. Le comportement de l'algorithme sur les fonctions de test est très particulier et intéressant. En fait, l'expérience montre le travail des forces gravitationnelles. Le mouvement des objets et les résultats d'optimisation obtenus sont fortement influencés par les paramètres externes de l'algorithme. Au départ, les objets dont la vitesse est nulle sont répartis de manière aléatoire dans l'espace de recherche et commencent à se déplacer à la prochaine itération. Les paramètres utilisés lors des tests (les meilleurs que j'ai trouvés) font en sorte que les objets se déplacent vers un centre de masse commun.

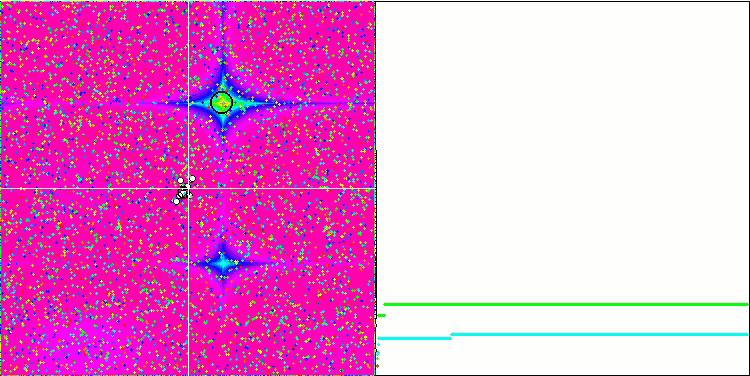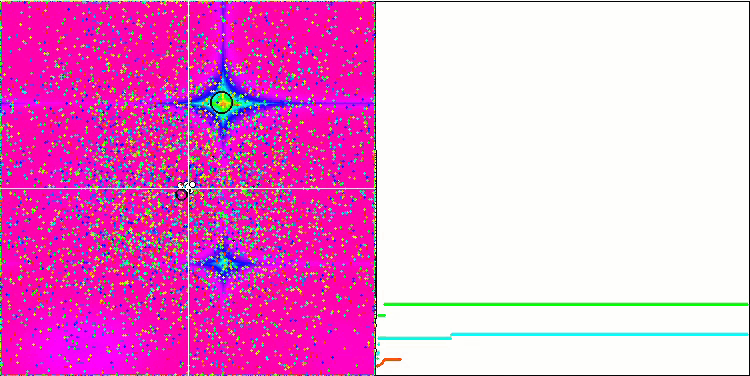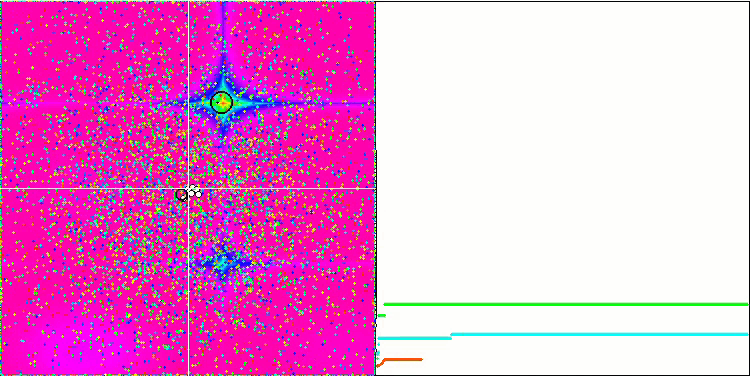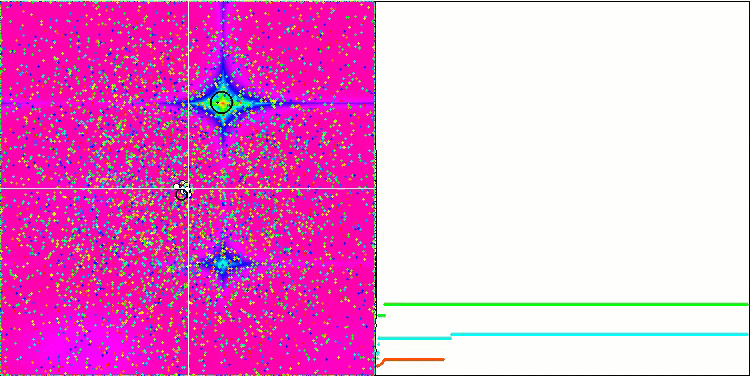
N'oubliez pas que la gravité de chaque objet affecte d'autres objets, dont les lois du mouvement sont décrites avec une précision suffisante dans l'algorithme. En se rapprochant du centre de masse commun, les objets continuent de se déplacer à grande vitesse. Cela ressemble au mouvement pulsé d'une masse de particules vers le centre de masse commun et vice-versa. Après un certain nombre d'itérations, le mouvement des objets modifie sa trajectoire sous l'influence du relief spatial de la fonction d'aptitude, qui agit comme une inhomogénéité gravitationnelle affectant la masse des objets. Comme nous l'avons vu précédemment, la masse des objets est calculée à partir de la valeur de la fonction d'aptitude. Cependant, la fonction de Rastrigin, symétrique selon les axes, a un effet assez uniforme sur le mouvement des objets et la répartition en groupes n'est pas particulièrement visible.

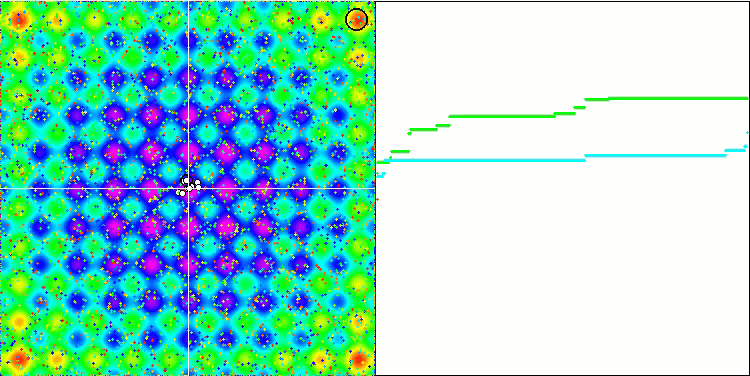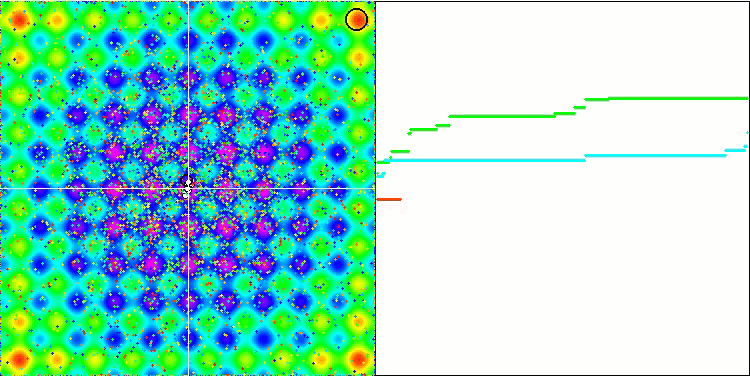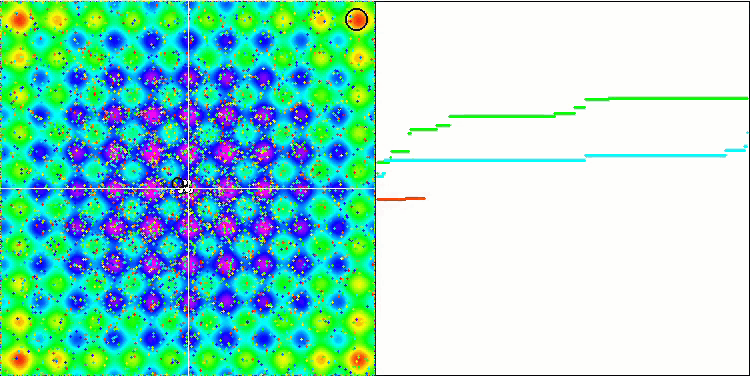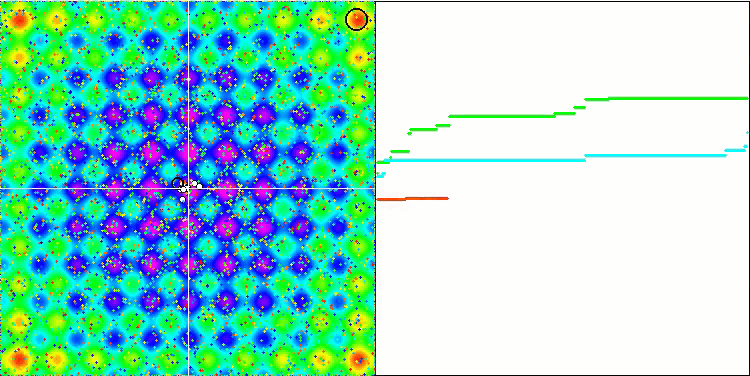
  GSA sur la fonction de test de Rastrigin.

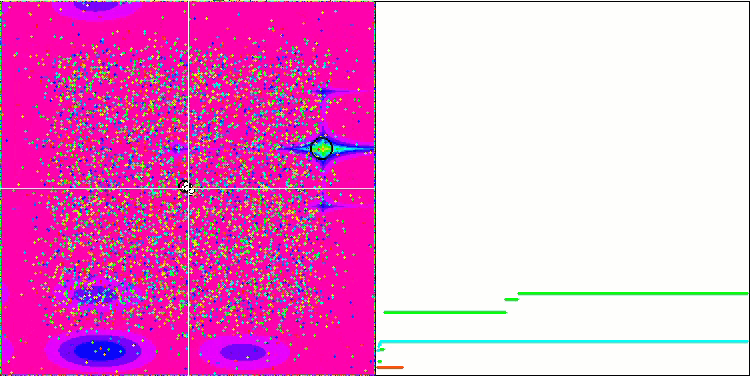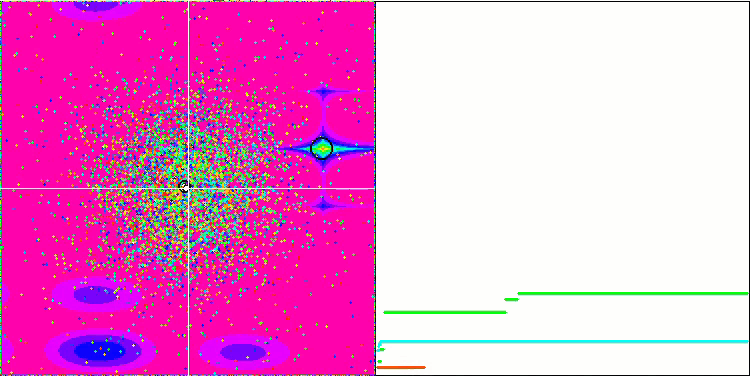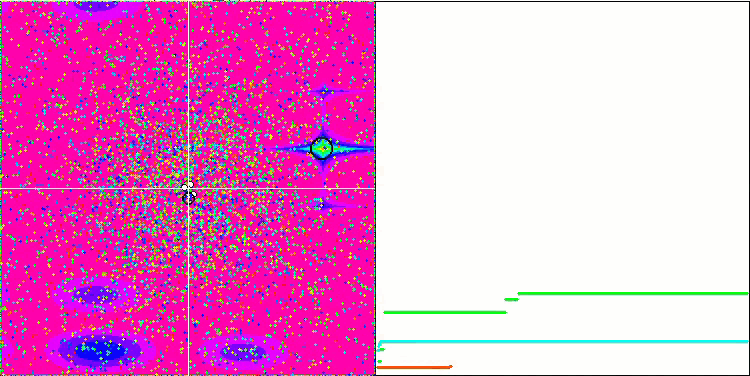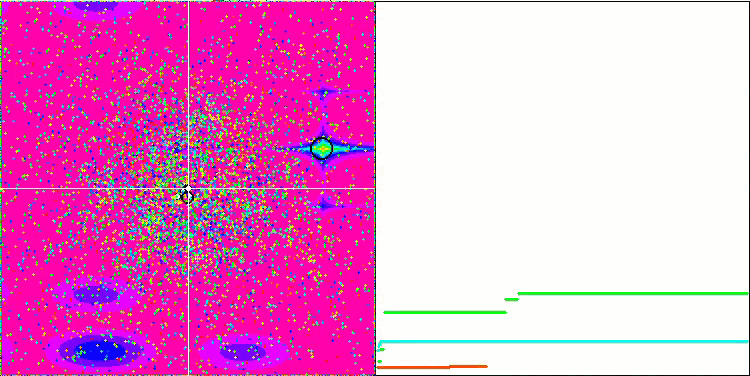
Les objets des fonctions Forest et Megacity présentent un comportement encore plus intéressant. Ces fonctions ne sont pas symétriques et ont donc un effet non uniforme sur l'ensemble du groupe d'objets.

  GSA sur la fonction de test Forest

GSA sur la fonction de test Megacity

Après de nombreuses expériences avec GSA, j'ai eu l'idée de créer un simulateur de mouvement d'objets spatiaux. Il n'a aucune valeur pratique, mais il donne une idée des lois physiques qui agissent sur les systèmes planétaires et stellaires. Le simulateur est une version du GSA dont le caractère aléatoire est désactivé. Trois objets imitant trois étoiles (une géante bleue, une étoile jaune et une naine blanche) sont également introduits. Les paramètres de masse sont affichés séparément dans les paramètres correspondants.

Une nouvelle fonction d'aptitude Universe a été créée avec un espace uniforme spécialement pour le simulateur. Le simulateur montre clairement comment le degré (paramètre) de la distance entre les objets affecte leur mouvement mutuel. Dans la visualisation ci-dessous, une puissance de 3 est appliquée au lieu de la valeur standard de 2 de la loi de Newton. La façon dont le degré affecte la formation de systèmes gravitationnellement liés, tels que les systèmes d'étoiles paires et triples, apparaît clairement.

Si, dans notre univers, le degré de distance avait été plus élevé, les galaxies se seraient formées beaucoup plus tôt que dans la réalité. L'animation montre clairement que des objets appariés circulant autour d'un centre de masse commun sont apparus dès les premières itérations. Comme on pouvait s'y attendre, la géante bleue a collecté le plus grand nombre d'objets autour d'elle.

Visualisation du simulateur de mouvement d'objets spatiaux basé sur l'algorithme GSA

Passons maintenant à l'analyse des résultats des tests du GSA. Les caractéristiques originales utilisées dans l'algorithme ne lui ont pas permis d'obtenir de bons résultats lors de nos tests. Les nombreuses variations des paramètres que j'ai essayées n'ont pas amélioré la convergence de l'algorithme. L'algorithme a montré des résultats positifs par rapport aux autres participants au test sur la fonction de Rastrigin lisse avec 10 variables et sur Megacity. Dans d'autres tests, le GSA obtient des résultats inférieurs à la moyenne dans le tableau, en se classant 8e sur 12.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)
IWO	Optimisation des mauvaises herbes envahissantes	1,00000	1,00000	0,35295	2,35295	0,79937	0,46349	0,41071	1,67357	0,75912	0,44903	0,94416	2,15231	100,000
ACOm	optimisation par colonies de fourmis M	0,36118	0,26810	0,20182	0,83110	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	0,15901	2,15901	96,805
COAm	algorithme d'optimisation coucou M	0,96423	0,69756	0,30792	1,96971	0,64504	0,34034	0,21362	1,19900	0,67153	0,34273	0,48451	1,49877	74,417
FAm	algorithme firefly M	0,62430	0,50653	0,20290	1,33373	0,55408	0,42299	0,64360	1,62067	0,21167	0,28416	1,00000	1,49583	70,740
BA	algorithme des chauves-souris	0,42290	0,95047	1,00000	2,37337	0,17768	0,17477	0,33595	0,68840	0,15329	0,07158	0,49268	0,71755	59,383
ABC	colonie d'abeilles artificielles	0,81573	0,48767	0,24656	1,54996	0,58850	0,21455	0,17249	0,97554	0,47444	0,26681	0,39496	1,13621	57,393
BFO	optimisation du butinage bactérien	0,70129	0,46155	0,13988	1,30272	0,41251	0,26623	0,26695	0,94569	0,42336	0,34491	0,53694	1,30521	55,563
GSA	algorithme de recherche gravitationnelle	0,73222	0,67404	0,00000	1,40626	0,31238	0,36416	0,42921	1,10575	0,51095	0,36658	0,00000	0,87753	52,786
FSS	recherche d'un banc de poissons	0,48850	0,37769	0,13383	1,00002	0,78060	0,05013	0,08423	0,91496	0,00000	0,01084	0,23493	0,24577	20,094
PSO	optimisation par essaims de particules	0,21339	0,12224	0,08478	0,42041	0,15345	0,10486	0,28099	0,53930	0,08028	0,02385	0,05550	0,15963	14,358
RND	aléatoire	0,17559	0,14524	0,09495	0,41578	0,08623	0,04810	0,06094	0,19527	0,00000	0,00000	0,13960	0,13960	8,117
GWO	optimiseur du loup gris	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,04119	0,07252	0,30348	1,000

En général, l'algorithme GSA est sensiblement sensible à la présence d'un gradient dans la fonction à optimiser. Sa faible évolutivité ne lui permet pas d'être utilisé pour des tâches sérieuses contenant de nombreuses variables. Je ne recommanderais donc pas l'utilisation de cet algorithme avec des réseaux neuronaux et pour l'optimisation de systèmes de trading. Je n'ai pas encore étudié toutes les possibilités de l'algorithme de recherche gravitationnelle. Des recherches supplémentaires pourraient permettre de découvrir de nouvelles caractéristiques positives inconnues de cet algorithme très intéressant et inhabituel. Les principaux avantages de l'algorithme sont l'indépendance par rapport à la meilleure solution globale trouvée et la capacité de tous les agents à interagir les uns avec les autres. 

La figure 2 montre les résultats du test de l'algorithme.

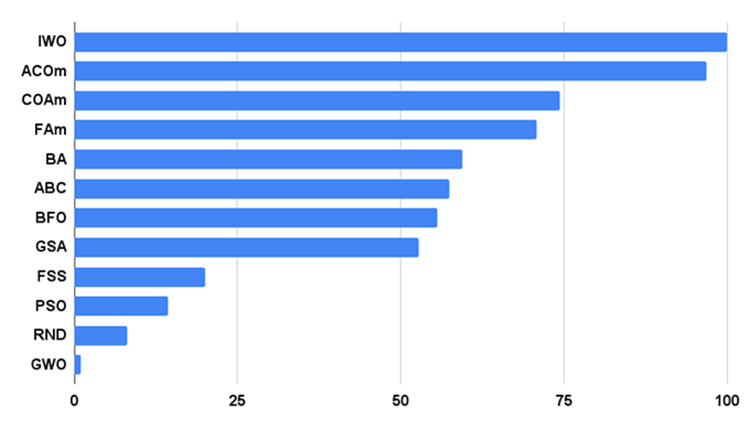
Figure 2. Histogramme des résultats des tests des algorithmes

Conclusions sur les propriétés de l'Algorithme de Recherche Gravitationnelle (GSA) :

Avantages :
1. Mise en œuvre facile.
2. Bonne performance sur des fonctions lisses avec peu de variables.

Inconvénients :
1. Complexité de calcul élevée.
2. Mauvais résultats sur les fonctions discrètes.
3. Mauvaise évolutivité.