Distribuzioni statistiche di probabilità in MQL5

MetaTrader 5 — Esempi | 17 dicembre 2021, 15:33

239

Denis Kirichenko

L'intera teoria della probabilità si basa sulla filosofia dell'indesiderabilità.
(Leonid Sukhorukov)

Introduzione

Per natura dell'attività, un trader molto spesso ha a che fare con categorie come probabilità e casualità. L'antipodo della casualità è una nozione di "regolarità". È notevole che in virtù delle leggi filosofiche generali la casualità di norma diventi regolarità. Non parleremo del contrario a questo punto. Fondamentalmente, la correlazione casualità-regolarità è una relazione chiave poiché, se presa nel contesto di mercato, influenza direttamente l'importo del profitto ricevuto da un trader.

In questo articolo esporrò gli strumenti teorici sottostanti che in futuro ci aiuteranno a trovare alcune regolarità di mercato.

1.Distribuzioni, Essenze, Tipi

Quindi, per descrivere alcune variabili casuali avremo bisogno di una distribuzione statistica unidimensionale di probabilità. Descriverà un campione di variabili casuali mediante una certa legge, ovvero l'applicazione di qualsiasi legge di distribuzione, richiederà un insieme di variabili casuali.

Perché analizzare le distribuzioni [teoriche]? Semplificano l'identificazione dei modelli di variazione della frequenza in base ai valori degli attributi variabili. Inoltre, si possono ottenere alcuni parametri statistici della distribuzione richiesta.

Per quanto riguarda i tipi di distribuzioni di probabilità, è consuetudine nella letteratura professionale dividere la famiglia di distribuzione in continua e discreta a seconda del tipo di insieme di variabili casuali. Esistono tuttavia altre classificazioni, ad esempio, secondo criteri come la simmetria della curva di distribuzione f(x) rispetto alla linea x=x0, parametro di posizione, numero di modi, intervallo di variabili casuali e altri.

Ci sono alcuni modi per definire la legge di distribuzione. Dobbiamo sottolineare i più popolari tra loro:

2. Distribuzioni di probabilità teoriche

Ora, proviamo a creare classi che descrivono le distribuzioni statistiche nel contesto di MQL5. Inoltre, vorrei aggiungere che la letteratura professionale fornisce molti esempi di codice scritto in C++ che può essere applicato con successo alla codifica MQL5. Quindi non ho reinventato la ruota e in alcuni casi ho usato le migliori pratiche del codice C++.

La sfida più grande che ho dovuto affrontare è stata la mancanza di supporto per l'ereditarietà multipla in MQL5. Ecco perché non sono riuscito a utilizzare gerarchie di classi complesse. Il libro intitolato Numerical Recipes: The Art of Scientific Computing [2] è diventata per me la fonte ottimale di codice C++ da cui ho preso in prestito la maggior parte delle funzioni. Il più delle volte hanno dovuto essere perfezionati in base alle esigenze di MQL5.

2.1.1 Distribuzione normale

Tradizionalmente, iniziamo con la distribuzione normale.

La distribuzione normale, detta anche distribuzione gaussiana, è una distribuzione di probabilità data dalla funzione di densità di probabilità:

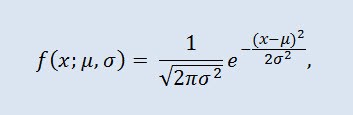
dove il parametro μ — è la media (aspettativa) di una variabile casuale e indica la coordinata massima della curva di densità di distribuzione, e σ² è la varianza.

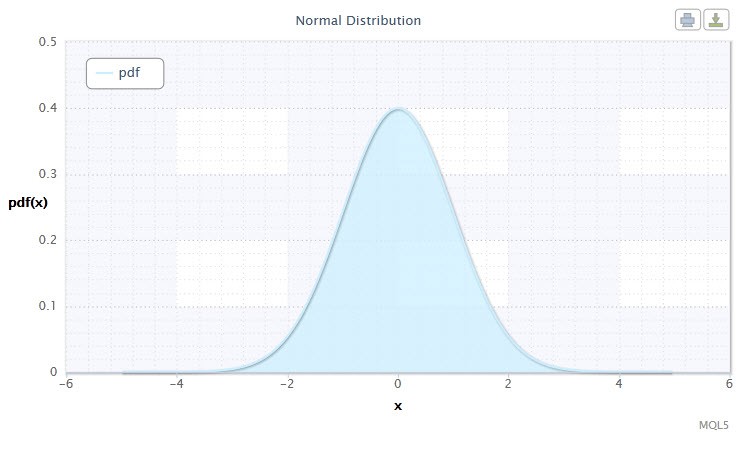
Figura 1. Densità di distribuzione normale Nor(0,1)

La sua notazione ha il seguente formato: X ~ Nor(μ, σ²), dove:

X è una variabile casuale selezionata dalla distribuzione normale Nor;
μ è il parametro medio (-∞ ≤ μ ≤ +∞);
σ è il parametro di varianza (0<σ).

Intervallo valido della variabile casuale X: -∞ ≤ X ≤ +∞.

Le formule utilizzate in questo articolo possono variare da quelle fornite in altre fonti. Tale differenza a volte non è matematicamente cruciale. In alcuni casi è subordinato a differenze di parametrizzazione.

La distribuzione normale gioca un ruolo importante nelle statistiche in quanto riflette la regolarità derivante dall'interazione tra un gran numero di cause casuali, nessuna delle quali ha un potere prevalente. E sebbene la distribuzione normale sia un caso raro nei mercati finanziari, è comunque importante confrontarla con le distribuzioni empiriche per determinare l'entità e la natura della loro anormalità.

Definiamo la classe CNormaldist per la distribuzione normale come segue:

//+------------------------------------------------------------------+
//|                Normal Distribution class definition              |
//+------------------------------------------------------------------+
class CNormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //mean parameter (μ)
   sig;                 //variance parameter (σ)
   //+------------------------------------------------------------------+
   //| CNormaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CNormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Normal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return(0.398942280401432678/sig)*exp(-0.5*pow((x-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5*erfc(-0.707106781186547524*(x-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)                |
   //| quantile function                                                |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Normal Distribution!");
      return -1.41421356237309505*sig*inverfc(2.*p)+mu;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };

//+------------------------------------------------------------------+

Come puoi notare, la classe CNormaldist deriva dalla classe base С Erf che a sua volta definisce la https://en.wikipedia.org/wiki/Error_function dell’errore. Sarà richiesto al momento del calcolo di alcuni metodi di classe CNormaldist. С La classe Erf e la funzione ausiliaria erfcc hanno più o meno questo aspetto:

//+------------------------------------------------------------------+
//|                Error Function class definition                   |
//+------------------------------------------------------------------+
class CErf
  {
public:
   int               ncof;    // coefficient array size
   double            cof[28]; // Chebyshev coefficient array
   //+------------------------------------------------------------------+
   //| CErf class constructor                                           |
   //+------------------------------------------------------------------+
   void CErf()
     {
      int Ncof=28;
      double Cof[28]=//Chebyshev coefficients
        {
         -1.3026537197817094,6.4196979235649026e-1,
         1.9476473204185836e-2,-9.561514786808631e-3,-9.46595344482036e-4,
         3.66839497852761e-4,4.2523324806907e-5,-2.0278578112534e-5,
         -1.624290004647e-6,1.303655835580e-6,1.5626441722e-8,-8.5238095915e-8,
         6.529054439e-9,5.059343495e-9,-9.91364156e-10,-2.27365122e-10,
         9.6467911e-11, 2.394038e-12,-6.886027e-12,8.94487e-13, 3.13092e-13,
         -1.12708e-13,3.81e-16,7.106e-15,-1.523e-15,-9.4e-17,1.21e-16,-2.8e-17
        };
      setCErf(Ncof,Cof);
     };
   //+------------------------------------------------------------------+
   //| Set-method for ncof                                              |
   //+------------------------------------------------------------------+
   void setCErf(int Ncof,double &Cof[])
     {
      ncof=Ncof;
      ArrayCopy(cof,Cof);
     };
   //+------------------------------------------------------------------+
   //| CErf class destructor                                            |
   //+------------------------------------------------------------------+
   void ~CErf(){};
   //+------------------------------------------------------------------+
   //| Error function                                                   |
   //+------------------------------------------------------------------+
   double erf(double x)
     {
      if(x>=0.0) return 1.0-erfccheb(x);
      else return erfccheb(-x)-1.0;
     }
   //+------------------------------------------------------------------+
   //| Complementary error function                                     |
   //+------------------------------------------------------------------+
   double erfc(double x)
     {
      if(x>=0.0) return erfccheb(x);
      else return 2.0-erfccheb(-x);
     }
   //+------------------------------------------------------------------+
   //| Chebyshev approximations for the error function                  |
   //+------------------------------------------------------------------+
   double erfccheb(double z)
     {
      int j;
      double t,ty,tmp,d=0.0,dd=0.0;
      if(z<0.) Alert("erfccheb requires nonnegative argument!");
      t=2.0/(2.0+z);
      ty=4.0*t-2.0;
      for(j=ncof-1;j>0;j--)
        {
         tmp=d;
         d=ty*d-dd+cof[j];
         dd=tmp;
        }
      return t*exp(-z*z+0.5*(cof[0]+ty*d)-dd);
     }
   //+------------------------------------------------------------------+
   //| Inverse complementary error function                             |
   //+------------------------------------------------------------------+
   double inverfc(double p)
     {
      double x,err,t,pp;
      if(p >= 2.0) return -100.0;
      if(p <= 0.0) return 100.0;
      pp=(p<1.0)? p : 2.0-p;
      t = sqrt(-2.*log(pp/2.0));
      x = -0.70711*((2.30753+t*0.27061)/(1.0+t*(0.99229+t*0.04481)) - t);
      for(int j=0;j<2;j++)
        {
         err=erfc(x)-pp;
         x+=err/(M_2_SQRTPI*exp(-pow(x,2))-x*err);
        }
      return(p<1.0? x : -x);
     }
   //+------------------------------------------------------------------+
   //| Inverse error function                                           |
   //+------------------------------------------------------------------+
   double inverf(double p)
     {return inverfc(1.0-p);}
  };
//+------------------------------------------------------------------+
double erfcc(const double x)
/* 
 complementary error function erfc(x) with
 a relative error of 1.2 * 10^(-7)               
*/
  {
   double t,z=fabs(x),ans;
   t=2./(2.0+z);
   ans=t*exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
             t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
             t*(-0.82215223+t*0.17087277)))))))));
   return(x>=0.0 ? ans : 2.0-ans);
  }
//+------------------------------------------------------------------+

2.1.2 Distribuzione log-normale

Ora diamo un'occhiata alla distribuzione log-normale.

La distribuzione lognormale nella teoria della probabilità è una famiglia a due parametri di distribuzioni assolutamente continue. Se una variabile casuale è distribuita lognormalmente, il suo logaritmo ha distribuzione normale.

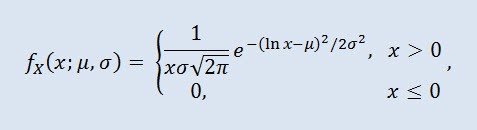
dove μ è il parametro di posizione (0<μ ), e σ è il parametro di scala (0<σ).

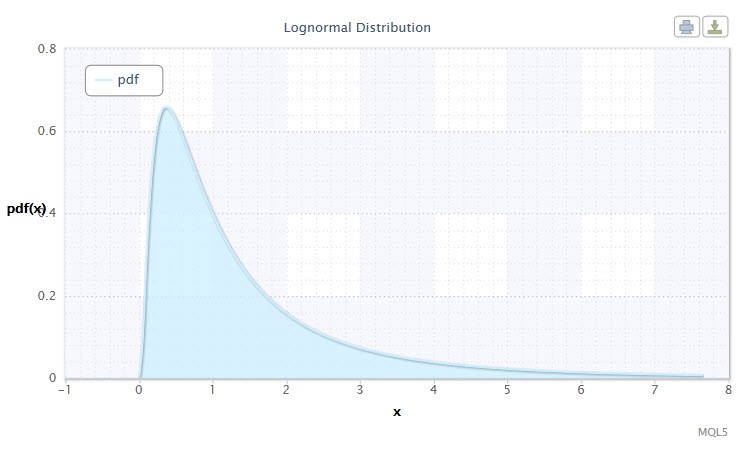
Figura 2. Densità di distribuzione log-normale Logn(0,1)

La sua notazione ha il seguente formato: X ~ Logn(μ, σ²), dove:

X è una variabile casuale selezionata dalla distribuzione log-normale Logn;
μ è il parametro di posizione (0<μ );
σ è il parametro di scala (0<σ).

Intervallo valido della variabile casuale X: 0 ≤ X ≤ +∞.

Creiamo la classe CLognormaldist descrivendo la distribuzione log-normale. Apparirà come segue:

//+------------------------------------------------------------------+
//|                Lognormal Distribution class definition           |
//+------------------------------------------------------------------+
class CLognormaldist : CErf // Erf class inheritance
  {
public:
   double            mu, //location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CLognormaldist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CLognormaldist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Lognormal Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return(0.398942280401432678/(sig*x))*exp(-0.5*pow((log(x)-mu)/sig,2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Lognormal Distribution!");
      if(x==0.) return 0.;
      return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf)(quantile)      |
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Lognormal Distribution!");
      return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Come si può vedere, la distribuzione log-normale non è molto diversa dalla distribuzione normale. La differenza è che il parametro x viene sostituito dal parametro log(x).

2.1.3 Distribuzione Cauchy

La distribuzione di Cauchy nella teoria della probabilità (in fisica chiamata anche distribuzione di Lorentz o distribuzione di Breit-Wigner) è una classe di distribuzioni assolutamente continue. Una variabile casuale distribuita di Cauchy è un esempio comune di una variabile che non ha aspettative né varianza. La densità assume la forma seguente:

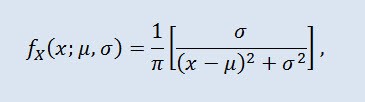
dove μ è il parametro di posizione (-∞ ≤ μ ≤ +∞ ) e σ è il parametro di scala (0<σ).

La notazione della distribuzione Cauchy ha il seguente formato: X ~ Cau(μ, σ), dove:

X è una variabile casuale selezionata dalla distribuzione di Cauchy Cau;
μ è il parametro di posizione (-∞ ≤ μ ≤ +∞ );
σ è il parametro di scala (0<σ).

Intervallo valido della variabile casuale X: -∞ ≤ X ≤ +∞.

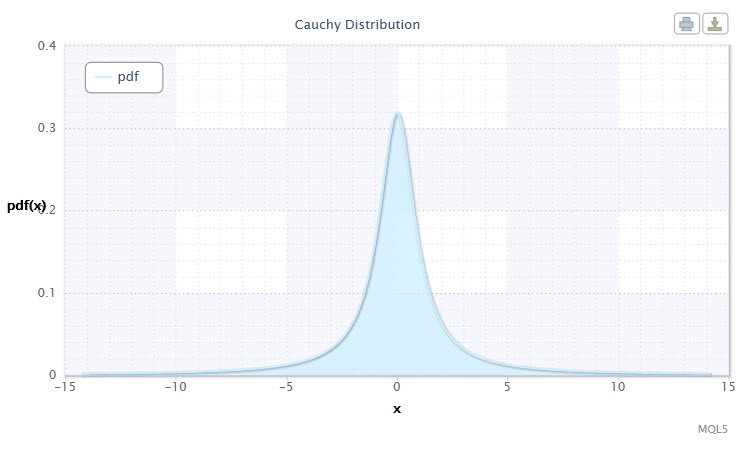
Figura 3. Densità di distribuzione Cauchy Cau(0,1)

Creato con l'aiuto della classe CCauchydist, in formato MQL5, si presenta come segue:

//+------------------------------------------------------------------+
//|                Cauchy Distribution class definition              |
//+------------------------------------------------------------------+
class CCauchydist //
  {
public:
   double            mu,//location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CCauchydist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CCauchydist() 
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Cauchy Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return 0.318309886183790671/(sig*(1.+pow((x-mu)/sig,2)));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 0.5+0.318309886183790671*atan2(x-mu,sig); //todo      
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Cauchy Distribution!");
      return mu+sig*tan(M_PI*(p-0.5));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Da notare qui che viene utilizzata la funzione atan2(), che restituisce il valore principale dell'arco tangente in radianti:

double atan2(double y,double x)
/*
 Returns the principal value of the arc tangent of y/x,
 expressed in radians. To compute the value, the function 
 uses the sign of both arguments to determine the quadrant.
 y - double value representing an y-coordinate.
 x - double value representing an x-coordinate. 
*/
  {
   double a;
   if(fabs(x)>fabs(y))
      a=atan(y/x);
   else
     {
      a=atan(x/y); // pi/4 <= a <= pi/4
      if(a<0.)
         a=-1.*M_PI_2-a; //a is negative, so we're adding
      else
         a=M_PI_2-a;
     }
   if(x<0.)
     {
      if(y<0.)
         a=a-M_PI;
      else
         a=a+M_PI;
     }
   return a;
  }

2.1.4 Distribuzione iperbolica delle secanti

La distribuzione iperbolica secante sarà di interesse per coloro che si occupano di analisi di rango finanziario.

Nella teoria della probabilità e nella statistica, la distribuzione secante iperbolica è una distribuzione di probabilità continua la cui funzione di densità di probabilità e funzione caratteristica sono proporzionali alla funzione secante iperbolica. La densità è data dalla formula:

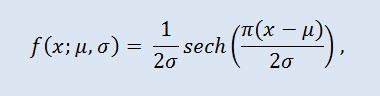
dove μ è il parametro di posizione (-∞ ≤ μ ≤ +∞ ) e σ è il parametro di scala (0<σ).

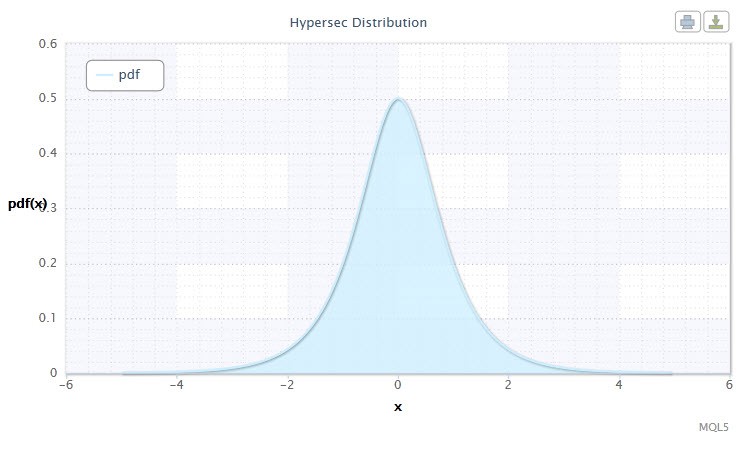
Figura 4. Densità di distribuzione secante iperbolica HS(0,1)

La sua notazione ha il seguente formato: X ~ HS(μ, σ), dove:

X è una variabile casuale;
μ è il parametro di posizione (-∞ ≤ μ ≤ +∞ );
σ è il parametro di scala (0<σ).

Intervallo valido della variabile casuale X: -∞ ≤ X ≤ +∞.

Descriviamolo utilizzando la classe CHypersecdist come segue:

//+------------------------------------------------------------------+
//|        Hyperbolic Secant Distribution class definition           |
//+------------------------------------------------------------------+
class CHypersecdist //
  {
public:
   double            mu,// location parameter (μ)
   sig;                 //scale parameter (σ)
   //+------------------------------------------------------------------+
   //| CHypersecdist class constructor                                 |
   //+------------------------------------------------------------------+
   void  CHypersecdist()
     {
      mu=0.0;sig=1.0; //default parameters μ and σ
      if(sig<=0.) Alert("bad sig in Hyperbolic Secant Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return sech((M_PI*(x-mu))/(2*sig))/2*sig;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      return 2/M_PI*atan(exp((M_PI*(x-mu)/(2*sig))));
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(!(p>0. && p<1.))
         Alert("bad p in Hyperbolic Secant Distribution!");
      return(mu+(2.0*sig/M_PI*log(tan(M_PI/2.0*p))));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Non è difficile vedere che questa distribuzione ha preso il nome dalla funzione secante iperbolica la cui funzione di densità di probabilità è proporzionale alla funzione secante iperbolica.

La funzione secante iperbolica sech è la seguente:

//+------------------------------------------------------------------+
//|              Hyperbolic Secant Function                          |
//+------------------------------------------------------------------+
double sech(double x)
// Hyperbolic Secant Function
  {
   return 2/(pow(M_E,x)+pow(M_E,-x));
  }

2.1.5 Distribuzione t di Student

La distribuzione t di Student è una distribuzione importante nelle statistiche.

Nella teoria della probabilità, la distribuzione t di Student è molto spesso una famiglia a un parametro di distribuzioni assolutamente continue. Tuttavia può essere considerata anche una distribuzione a tre parametri che è data dalla funzione di densità di distribuzione:

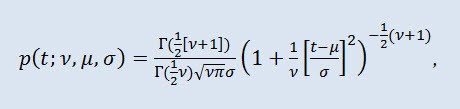
dove Г è la funzione Gamma di Eulero, ν è il parametro di forma (ν>0), μ è il parametro di posizione (-∞ ≤ μ ≤ +∞ ), σ è il parametro di scala (0<σ).

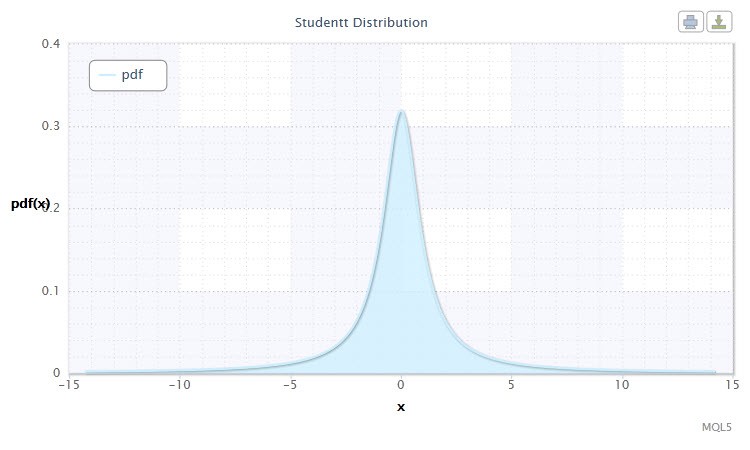
Figura 5. Densità di distribuzione t di Student Stt(1,0,1)

La sua notazione ha il seguente formato: t ~ Stt(ν,μ,σ), dove:

t è una variabile casuale selezionata dalla distribuzione t di Student Stt;
ν è il parametro di forma (ν>0)
μ è il parametro di posizione (-∞ ≤ μ ≤ +∞ );
σ è il parametro di scala (0<σ).

Intervallo valido della variabile casuale X: -∞ ≤ X ≤ +∞.

Spesso, specialmente nella verifica delle ipotesi, viene utilizzata una distribuzione t standard con μ=0 e σ=1. Quindi, si trasforma in una distribuzione a un parametro con parametro .

Questa distribuzione viene spesso utilizzata nella stima dell'aspettativa, dei valori proiettati e di altre caratteristiche mediante intervalli di confidenza, quando si testano ipotesi di valore di aspettativa, coefficienti di relazione di regressione, ipotesi di omogeneità, ecc.

Descriviamo la distribuzione tramite la classe CStudenttdist:

//+------------------------------------------------------------------+
//|                Student's t-distribution class definition         |
//+------------------------------------------------------------------+
class CStudenttdist : CBeta // CBeta class inheritance
  {
public:
   int               nu;     // shape parameter (ν)
   double            mu,     // location parameter (μ)
   sig,                     // scale parameter (σ)
   np,                      // 1/2*(ν+1)
   fac;                     // Г(1/2*(ν+1))-Г(1/2*ν)
   //+------------------------------------------------------------------+
   //| CStudenttdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CStudenttdist()
     {
      int Nu=1;double Mu=0.0,Sig=1.0; //default parameters ν, μ and σ
      setCStudenttdist(Nu,Mu,Sig);
     }
   void setCStudenttdist(int Nu,double Mu,double Sig)
     {
      nu=Nu;
      mu=Mu;
      sig=Sig;
      if(sig<=0. || nu<=0.) Alert("bad sig,nu in Student-t Distribution!");
      np=0.5*(nu+1.);
      fac=gammln(np)-gammln(0.5*nu);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-np*log(1.+pow((x-mu)/sig,2.)/nu)+fac)/(sqrt(M_PI*nu)*sig);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double t)
     {
      double p=0.5*betai(0.5*nu,0.5,nu/(nu+pow((t-mu)/sig,2)));
      if(t>=mu) return 1.-p;
      else return p;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Student-t Distribution!");
      double x=invbetai(2.*fmin(p,1.-p),0.5*nu,0.5);
      x=sig*sqrt(nu*(1.-x)/x);
      return(p>=0.5? mu+x : mu-x);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
   //+------------------------------------------------------------------+
   //| Two-tailed cumulative distribution function (aa) A(t|ν)          |
   //+------------------------------------------------------------------+
   double aa(double t)
     {
      if(t < 0.) Alert("bad t in Student-t Distribution!");
      return 1.-betai(0.5*nu,0.5,nu/(nu+pow(t,2.)));
     }
   //+------------------------------------------------------------------+
   //| Inverse two-tailed cumulative distribution function (invaa)      |
   //| p=A(t|ν)                                                         |
   //+------------------------------------------------------------------+
   double invaa(double p)
     {
      if(!(p>=0. && p<1.)) Alert("bad p in Student-t Distribution!");
      double x=invbetai(1.-p,0.5*nu,0.5);
      return sqrt(nu*(1.-x)/x);
     }
  };
//+------------------------------------------------------------------+

L'elenco delle classi CStudenttdist mostra che CBeta è una classe base che descrive la funzione https://en.wikipedia.org/wiki/Beta_function.

La classe CBeta appare come segue:

//+------------------------------------------------------------------+
//|            Incomplete Beta Function class definition             |
//+------------------------------------------------------------------+
class CBeta : public CGauleg18
  {
private:
   int               Switch;                     //when to use the quadrature method
   double            Eps,Fpmin;
public:
   //+------------------------------------------------------------------+
   //| CBeta class constructor                                          |
   //+------------------------------------------------------------------+
   void CBeta()
     {
      int swi=3000;
      setCBeta(swi,EPS,FPMIN);
     };
   //+------------------------------------------------------------------+
   //| CBeta class set-method                                           |
   //+------------------------------------------------------------------+
   void setCBeta(int swi,double eps,double fpmin)
     {
      Switch=swi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            betai(const double a,const double b,const double x); //incomplete beta function Ix(a,b)
   double            betacf(const double a,const double b,const double x);//continued fraction for incomplete beta function
   double            betaiapprox(double a,double b,double x); //Incomplete beta by quadrature
   double            invbetai(double p,double a,double b);    //Inverse of incomplete beta function
  };

Questa classe ha anche una classe base CGauleg18 che fornisce coefficienti per tale metodo di integrazione numerica come le quadrature Gauss-Legendre.

2.1.6 Distribuzione logistica

Propongo di considerare la logistica nel nostro prossimo studio.

Nella teoria della probabilità e nella statistica, la distribuzione logistica è una distribuzione di probabilità continua. La sua funzione di distribuzione cumulativa è la funzione logistica. Assomiglia alla distribuzione normale in forma ma ha code più pesanti. Densità di distribuzione:

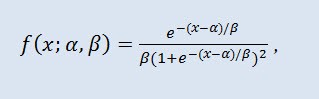
dove α è il parametro di posizione (-∞ ≤ α ≤ +∞ ), β è il parametro di scala (0<β).

Figura 6. Densità di distribuzione logistica Logi(0,1)

La sua notazione ha il seguente formato: X ~ Logi(α,β), dove:

X è una variabile casuale;
α è il parametro di posizione (-∞ ≤ α ≤ +∞ );
β è il parametro di scala (0<β).

Intervallo valido della variabile casuale X: -∞ ≤ X ≤ +∞.

La classe CLogisticdist è l'implementazione della distribuzione sopra descritta:

//+------------------------------------------------------------------+
//|                Logistic Distribution class definition            |
//+------------------------------------------------------------------+
class CLogisticdist
  {
public:
   double            alph,//location parameter (α)
   bet;                   //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLogisticdist class constructor                                  |
   //+------------------------------------------------------------------+
   void  CLogisticdist() 
     {
      alph=0.0;bet=1.0; //default parameters μ and σ
      if(bet<=0.) Alert("bad bet in Logistic Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-(x-alph)/bet)/(bet*pow(1.+exp(-(x-alph)/bet),2));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double et=exp(-1.*fabs(1.81379936423421785*(x-alph)/bet));
      if(x>=alph) return 1./(1.+et);
      else return et/(1.+et);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<=0. || p>=1.) Alert("bad p in Logistic Distribution!");
      return alph+0.551328895421792049*bet*log(p/(1.-p));
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.7 Distribuzione esponenziale

Diamo anche un'occhiata alla distribuzione esponenziale di una variabile casuale.

Una variabile casuale X ha distribuzione esponenziale con parametro λ > 0, se la sua densità è data da:

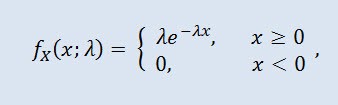
dove λ è il parametro di scala (λ>0).

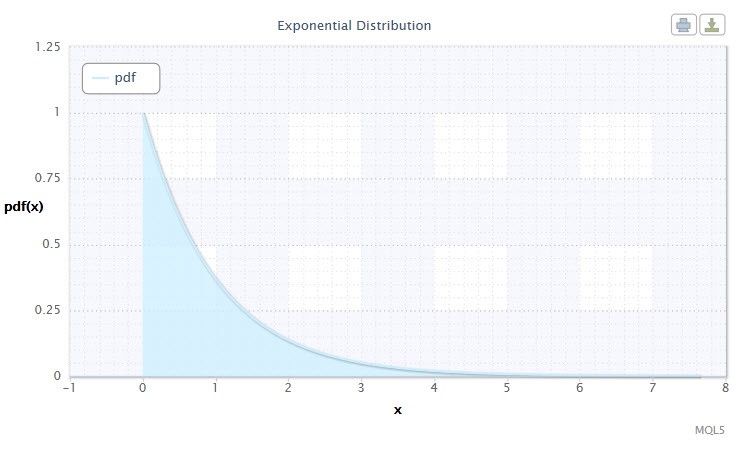
Figura 7. Densità di distribuzione esponenziale Exp(1)

La sua notazione ha il seguente formato: X ~ Esp(λ), dove:

X è una variabile casuale;
λ è il parametro di scala (λ>0).

Intervallo valido della variabile casuale X: 0 ≤ X ≤ +∞.

Questa distribuzione è notevole per il fatto che descrive una sequenza di eventi che si verificano uno per uno in determinati momenti. Pertanto, utilizzando questa distribuzione un trader può analizzare una serie di operazioni in perdita e altre.

Nel codice MQL5, la distribuzione è descritta tramite la classe CExpondist:

//+------------------------------------------------------------------+
//|                Exponential Distribution class definition         |
//+------------------------------------------------------------------+
class CExpondist
  {
public:
   double            lambda;   //scale parameter (λ)
   //+------------------------------------------------------------------+
   //| CExpondist class constructor                                     |
   //+------------------------------------------------------------------+
   void  CExpondist()
     {
      lambda=1.0;              //default parameter λ
      if(lambda<=0.) Alert("bad lambda in Exponential Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<0.) Alert("bad x in Exponential Distribution!");
      return lambda*exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x < 0.) Alert("bad x in Exponential Distribution!");
      return 1.-exp(-lambda*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Exponential Distribution!");
      return -log(1.-p)/lambda;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.8 DistribuzioneGamma

Ho scelto la distribuzione gamma come tipo successivo della distribuzione continua variabile casuale.

Nella teoria della probabilità, la distribuzione gamma è una famiglia a due parametri di distribuzioni di probabilità assolutamente continue. Se il parametro α è un numero intero, tale distribuzione gamma è anche chiamata distribuzione Erlang. La densità assume la forma seguente:

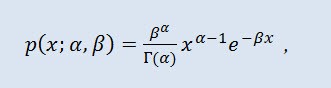
dove Г è la funzione Gamma di Eulero, α è il parametro di forma (0<α), β è il parametro di scala (0<β).

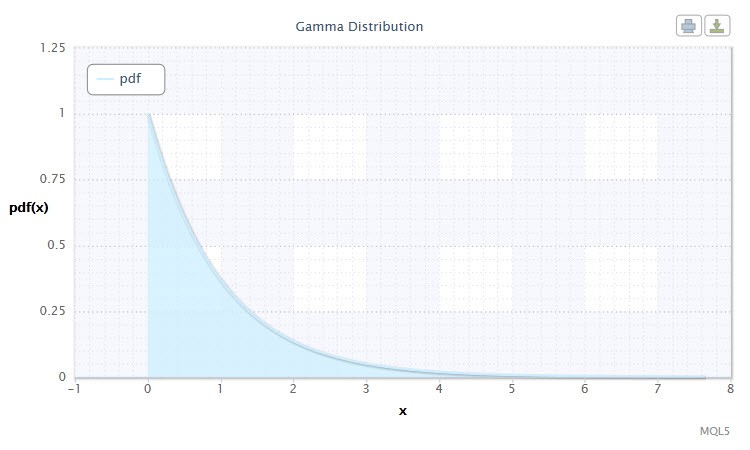
Figura 8. Densità gammadi distribuzione Gam(1,1).

La sua notazione ha il seguente formato: X ~ Gam(α,β), dove:

X è una variabile casuale;
α è il parametro di forma (0<α);
β è il parametro di scala (0<β).

Intervallo valido della variabile casuale X: 0 ≤ X ≤ +∞.

Nella variante definita dalla classe CGammadist appare come segue:

//+------------------------------------------------------------------+
//|                Gamma Distribution class definition               |
//+------------------------------------------------------------------+
class CGammadist : CGamma // CGamma class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous scale parameter  (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CGammaldist class constructor                                    |
   //+------------------------------------------------------------------+
   void  CGammadist()
     {
      setCGammadist();
     }
   void setCGammadist(double Alph=1.0,double Bet=1.0)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Gamma Distribution!");
      fac=alph*log(bet)-gammln(alph);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0.) Alert("bad x in Gamma Distribution!");
      return exp(-bet*x+(alph-1.)*log(x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0.) Alert("bad x in Gamma Distribution!");
      return gammp(alph,bet*x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>=1.) Alert("bad p in Gamma Distribution!");
      return invgammp(p,alph)/bet;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

La classe di distribuzione gamma deriva dalla classe CGamma, la quale descrive la funzione incompleta gamma.

La classe CGamma è definita come segue:

//+------------------------------------------------------------------+
//|            Incomplete Gamma Function class definition            |
//+------------------------------------------------------------------+
class CGamma : public CGauleg18
  {
private:
   int               ASWITCH;
   double            Eps,
   Fpmin,
   gln;
public:
   //+------------------------------------------------------------------+
   //| CGamma class constructor                                         |
   //+------------------------------------------------------------------+
   void CGamma()
     {
      int aswi=100;
      setCGamma(aswi,EPS,FPMIN);
     };
   void setCGamma(int aswi,double eps,double fpmin) //CGamma set-method
     {
      ASWITCH=aswi;
      Eps=eps;
      Fpmin=fpmin;
     };
   double            gammp(const double a,const double x); //incomplete gamma function
   double            gammq(const double a,const double x); //incomplete gamma function Q(a,x)
   void              gser(double &gamser,double a,double x,double &gln); //incomplete gamma function P(a,x)
   double            gcf(const double a,const double x); //incomplete gamma function Q(a,x)
   double            gammpapprox(double a,double x,int psig); //incomplete gamma by quadrature
   double            invgammp(double p,double a); //inverse of incomplete gamma function
  };
//+------------------------------------------------------------------+

Sia la classe CGamma che la classe CBeta hanno CGauleg18 come classe base.

2.1.9 Distribuzione Beta

Bene, esaminiamo ora la distribuzione beta.

Nella teoria della probabilità e nella statistica, la distribuzione beta è una famiglia a due parametri di distribuzioni assolutamente continue. Viene utilizzato per descrivere le variabili casuali i cui valori sono definiti su un intervallo finito. La densità è definita come segue:

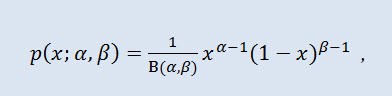
dove B è la funzione beta, α è il 1° parametro di forma (0<α), β è il 2° parametro di forma (0<β).

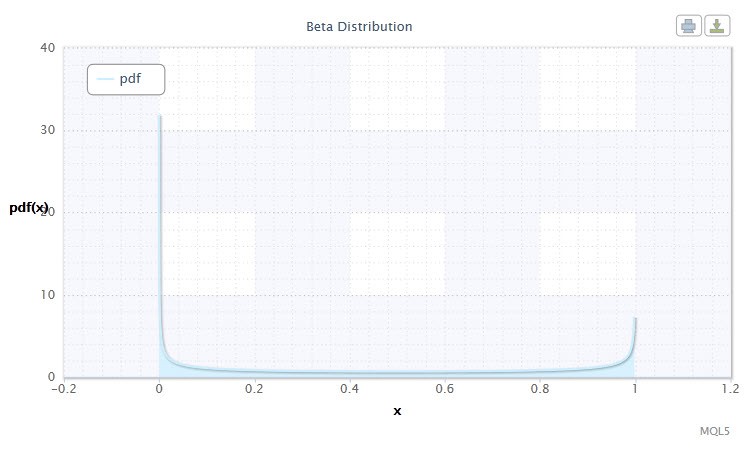
Figura 9. Densità beta di distribuzione Beta(0,5,0,5)

La sua notazione ha il seguente formato: X ~ Beta(α,β), dove:

X è una variabile casuale;
α è il 1° parametro di forma (0<α);
β è il 2° parametro di forma (0<β).

Intervallo valido della variabile casuale X: 0 ≤ X ≤ 1.

La classe CBetadist descrive questa distribuzione nel modo seguente:

//+------------------------------------------------------------------+
//|                Beta Distribution class definition                |
//+------------------------------------------------------------------+
class CBetadist : CBeta // CBeta class inheritance
  {
public:
   double            alph,//continuous shape parameter (α>0)
   bet,                   //continuous shape parameter (β>0)
   fac;                   //factor
   //+------------------------------------------------------------------+
   //| CBetadist class constructor                                      |
   //+------------------------------------------------------------------+
   void  CBetadist()
     {
      setCBetadist();
     }
   void setCBetadist(double Alph=0.5,double Bet=0.5)//default parameters α and β
     {
      alph=Alph; bet=Bet;
      if(alph<=0. || bet<=0.) Alert("bad alph,bet in Beta Distribution!");
      fac=gammln(alph+bet)-gammln(alph)-gammln(bet);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      if(x<=0. || x>=1.) Alert("bad x in Beta Distribution!");
      return exp((alph-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      if(x<0. || x>1.) Alert("bad x in Beta Distribution");
      return betai(alph,bet,x);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      if(p<0. || p>1.) Alert("bad p in Beta Distribution!");
      return invbetai(p,alph,bet);
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

2.1.10 Distribuzione di Laplace

Un'altra distribuzione continua notevole è la distribuzione Laplace (doppia distribuzione esponenziale).

La distribuzione di Laplace (distribuzione esponenziale doppia) nella teoria della probabilità è una distribuzione continua di una variabile casuale per cui la densità di probabilità è:

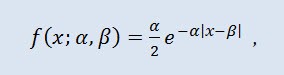
dove α è il parametro di posizione (-∞ ≤ α ≤ +∞ ), β è il parametro di scala (0<β).

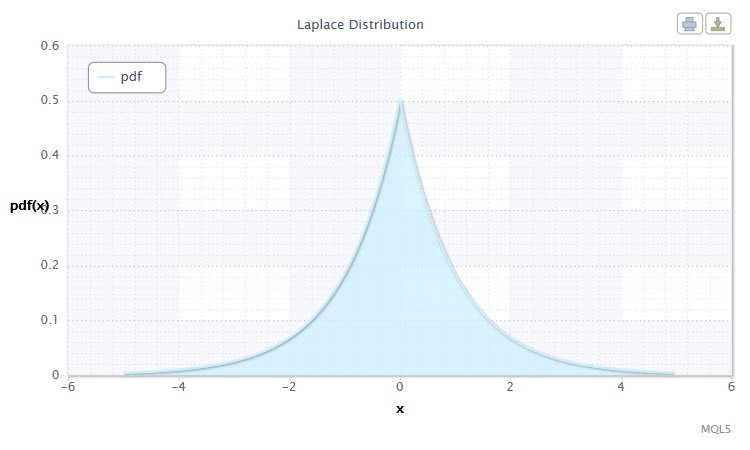
Figura 10. Densità Laplace di distribuzione di Lap(0,1)

La sua notazione ha il seguente formato: X ~ Lap(α,β), dove:

X è una variabile casuale;
α è il parametro di posizione (-∞ ≤ α ≤ +∞ );
β è il parametro di scala (0<β).

Intervallo valido della variabile casuale X: -∞ ≤ X ≤ +∞.

La classe CLaplacedist ai fini di questa distribuzione è definita come segue:

//+------------------------------------------------------------------+
//|                 Laplace Distribution class definition            |
//+------------------------------------------------------------------+
class CLaplacedist
  {
public:
   double            alph;   //location parameter (α)
   double            bet;    //scale parameter (β)
   //+------------------------------------------------------------------+
   //| CLaplacedist class constructor                                   |
   //+------------------------------------------------------------------+
   void  CLaplacedist()
     {
      alph=.0;               //default parameter α
      bet=1.;                //default parameter β
      if(bet<=0.) Alert("bad bet in Laplace Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(double x)
     {
      return exp(-fabs((x-alph)/bet))/2*bet;
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(double x)
     {
      double temp;
      if(x<0)
         temp=0.5*exp(-fabs((x-alph)/bet));
      else
         temp=1.-0.5*exp(-fabs((x-alph)/bet));
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   double invcdf(double p)
     {
      double temp;
      if(p<0. || p>=1.) Alert("bad p in Laplace Distribution!");
      if(p<0.5)
         temp=bet*log(2*p)+alph;
      else
         temp=-1.*(bet*log(2*(1.-p))+alph);
      return temp;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(double x)
     {
      return 1-cdf(x);
     }
  };
//+------------------------------------------------------------------+

Quindi, utilizzando il codice MQL5 abbiamo creato 10 classi per le dieci distribuzioni continue. Oltre a queste, sono state create altre classi che erano, per così dire, complementari poiché c'era bisogno di funzioni e metodi specifici (es. CBeta e CGamma).

Passiamo ora alle distribuzioni discrete e creiamo alcune classi per questa categoria di distribuzione.

2.2.1 Distribuzione binomiale

Iniziamo con la distribuzione binomiale.

Nella teoria della probabilità, la distribuzione binomiale è una distribuzione del numero di successi in una sequenza di esperimenti casuali indipendenti in cui la probabilità di successo in ognuno di essi è uguale. La densità di probabilità è data dalla seguente formula:

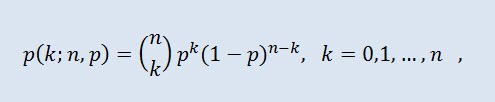
dove (nk) è il coefficiente binomiale, n è il numero di prove (0 ≤ n), p è la probabilità di successo (0 ≤ p ≤1).

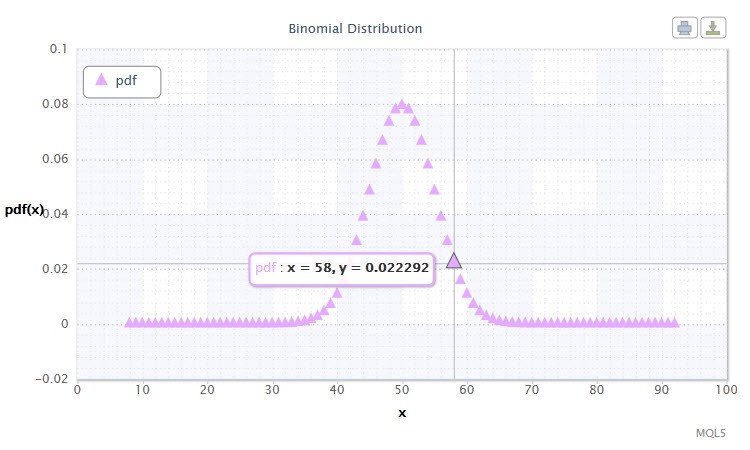
Figura 11. Densità binomiale di distribuzione Bin(100,0.5).

La sua notazione ha il seguente formato: k ~ Bin(n,p), dove:

k è una variabile casuale;
n è il numero di prove (0 ≤ n);
p è la probabilità di successo (0 ≤ p ≤1).

Intervallo valido della variabile casuale X: 0 o 1.

L'intervallo di possibili valori della variabile casuale X ti suggerisce qualcosa? In effetti, questa distribuzione può aiutarci ad analizzare l'aggregato di operazioni di vincita (1) e perdita (0) nel sistema di trading.

Creiamo la classe СBinomialdist come segue:

//+------------------------------------------------------------------+
//|               Binomial Distribution class definition             |
//+------------------------------------------------------------------+
class CBinomialdist : CBeta // CBeta class inheritance
  {
public:
   int               n;      //number of trials
   double            pe,     //success probability
   fac;                      //factor
   //+------------------------------------------------------------------+
   //| CBinomialdist class constructor                                  |
   //+------------------------------------------------------------------+
   void              CBinomialdist()
     {
      setCBinomialdist();
     }
   void setCBinomialdist(int N=100,double Pe=0.5)//default parameters n and pe
     {
      n=N; pe=Pe;
      if(n<=0 || pe<=0. || pe>=1.) Alert("bad args in Binomial Distribution!");
      fac=gammln(n+1.);
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k>n) return 0.;
      return exp(k*log(pe)+(n-k)*log(1.-pe)+fac-gammln(k+1.)-gammln(n-k+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int k)
     {
      if(k<0) Alert("bad k in Binomial Distribution!");
      if(k==0) return 0.;
      if(k>n) return 1.;
      return 1.-betai((double)k,n-k+1.,pe);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int k,kl,ku,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Binomial Distribution!");
      k=fmax(0,fmin(n,(int)(n*pe)));
      if(p<cdf(k))
        {
         do
           {
            k=fmax(k-inc,0);
            inc*=2;
           }
         while(p<cdf(k));
         kl=k; ku=k+inc/2;
           } else {
         do
           {
            k=fmin(k+inc,n+1);
            inc*=2;
           }
         while(p>cdf(k));
         ku=k; kl=k-inc/2;
        }
      while(ku-kl>1)
        {
         k=(kl+ku)/2;
         if(p<cdf(k)) ku=k;
         else kl=k;
        }
      return kl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int k)
     {
      return 1.-cdf(k);
     }
  };
//+------------------------------------------------------------------+

2.2.2 Distribuzione di Poisson

La prossima distribuzione in esame è la distribuzione di Poisson.

La distribuzione di Poisson modella una variabile casuale rappresentata da un numero di eventi che si verificano in un determinato periodo di tempo, a condizione che tali eventi si verifichino con un'intensità media fissa e indipendentemente l'uno dall'altro. La densità assume la forma seguente:

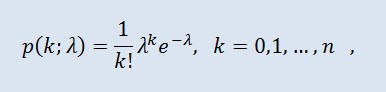
dove k! è fattoriale, λ è il parametro di posizione (0 < λ).

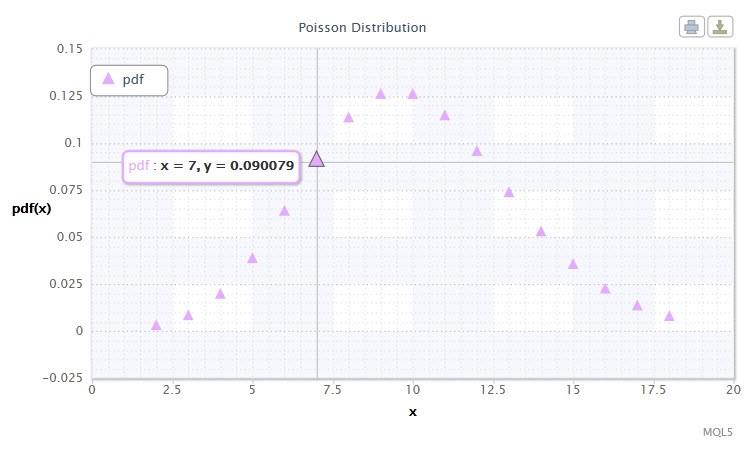
Figura 12. Densità Poisson di distribuzione di Pois(10).

La sua notazione ha il seguente formato: k ~ Pois(λ), dove:

k è una variabile casuale;
è il parametro di posizione (0 < λ).

Intervallo valido della variabile casuale X: 0 ≤ X ≤ +∞.

La distribuzione di Poisson descrive la "legge degli eventi rari" che è importante quando si stima il grado di rischio.

La classe CPoissondist servirà agli scopi di questa distribuzione:

//+------------------------------------------------------------------+
//|               Poisson Distribution class definition              |
//+------------------------------------------------------------------+
class CPoissondist : CGamma // CGamma class inheritance
  {
public:
   double            lambda;   //location parameter (λ)
   //+------------------------------------------------------------------+
   //| CPoissondist class constructor                                   |
   //+------------------------------------------------------------------+
   void CPoissondist()
     {
      lambda=15.;
      if(lambda<=0.) Alert("bad lambda in Poisson Distribution!");
     }
   //+------------------------------------------------------------------+
   //| Probability density function (pdf)                               |
   //+------------------------------------------------------------------+
   double pdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      return exp(-lambda+n*log(lambda)-gammln(n+1.));
     }
   //+------------------------------------------------------------------+
   //| Cumulative distribution function (cdf)                           |
   //+------------------------------------------------------------------+
   double cdf(int n)
     {
      if(n<0) Alert("bad n in Poisson Distribution!");
      if(n==0) return 0.;
      return gammq((double)n,lambda);
     }
   //+------------------------------------------------------------------+
   //| Inverse cumulative distribution function (invcdf) (quantile func)|
   //+------------------------------------------------------------------+
   int invcdf(double p)
     {
      int n,nl,nu,inc=1;
      if(p<=0. || p>=1.) Alert("bad p in Poisson Distribution!");
      if(p<exp(-lambda)) return 0;
      n=(int)fmax(sqrt(lambda),5.);
      if(p<cdf(n))
        {
         do
           {
            n=fmax(n-inc,0);
            inc*=2;
           }
         while(p<cdf(n));
         nl=n; nu=n+inc/2;
           } else {
         do
           {
            n+=inc;
            inc*=2;
           }
         while(p>cdf(n));
         nu=n; nl=n-inc/2;
        }
      while(nu-nl>1)
        {
         n=(nl+nu)/2;
         if(p<cdf(n)) nu=n;
         else nl=n;
        }
      return nl;
     }
   //+------------------------------------------------------------------+
   //| Reliability (survival) function (sf)                             |
   //+------------------------------------------------------------------+
   double sf(int n)
     {
      return 1.-cdf(n);
     }
  };
//+=====================================================================+

È ovviamente impossibile considerare tutte le distribuzioni statistiche all'interno di un articolo e probabilmente non è nemmeno necessario. L'utente, se lo desidera, può espandere la galleria di distribuzione di cui sopra. Le distribuzioni create possono essere trovate nel file Distribution_class.mqh.

3. Creazione di grafici di distribuzione

Ora suggerisco di vedere come le classi che abbiamo creato per le distribuzioni possono essere utilizzate nel nostro lavoro futuro.

A questo punto, sempre utilizzando OOP, ho creato la classe CDistributionFigure che elabora le distribuzioni di parametri definite dall'utente e le visualizza sullo schermo con i mezzi descritti nell'articolo "Grafici e diagrammi in HTML".

//+------------------------------------------------------------------+
//|           Distribution Figure class definition                   |
//+------------------------------------------------------------------+
class CDistributionFigure
  {
private:
   Dist_type         type;  //distribution type
   Dist_mode         mode;  //distribution mode
   double            x;     //step start
   double            x11;   //left side limit
   double            x12;   //right side limit
   int               d;     //number of points
   double            st;    //step

public:
   double            xAr[]; //array of random variables
   double            p1[];  //array of probabilities
   void              CDistributionFigure();  //constructor 
   void              setDistribution(Dist_type Type,Dist_mode Mode,double X11,double X12,double St); //set-method
   void              calculateDistribution(double nn,double mm,double ss); //distribution parameter calculation
   void              filesave(); //saving distribution parameters
  };
//+------------------------------------------------------------------+

Omettendo l'implementazione. Si noti che questa classe ha membri di dati come type e mode relativi a Dist_type e Dist_mode corrispondentemente. Questi tipi sono enumerazioni delle distribuzioni in esame e dei loro tipi.

Quindi, proviamo finalmente a creare un grafico di una certa distribuzione.

Ho scritto lo script continueDistribution.mq5 per le distribuzioni continue, le cui linee chiave sono le seguenti:

//+------------------------------------------------------------------+
//|                     Input variables                              |
//+------------------------------------------------------------------+

input Dist_type dist;  //Distribution Type
input Dist_mode distM; //Distribution Mode
input int nn=1;        //Nu
input double mm=0.,    //Mu
            ss=1.;    //Sigma
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//(Normal #0,Lognormal #1,Cauchy #2,Hypersec #3,Studentt #4,Logistic #5,Exponential #6,Gamma #7,Beta #8 , Laplace #9)
   double Xx1,      //left side limit
          Xx2,     //right side limit          
          st=0.05; //step
   if(dist==0) //Normal
     {
      Xx1=mm-5.0*ss/1.25;
      Xx2=mm+5.0*ss/1.25;
     }
   if(dist==2 || dist==4 || dist==5) //Cauchy,Studentt,Logistic
     {
      Xx1=mm-5.0*ss/0.35;
      Xx2=mm+5.0*ss/0.35;
     }
   else if(dist==1 || dist==6 || dist==7) //Lognormal,Exponential,Gamma
     {
      Xx1=0.001;
      Xx2=7.75;
     }
   else if(dist==8) //Beta
     {
      Xx1=0.0001;
      Xx2=0.9999;
      st=0.001;
     }
   else 
     {
      Xx1=mm-5.0*ss;
      Xx2=mm+5.0*ss;
     }
//---
   CDistributionFigure F;        //creation of the CDistributionFigure class instance 
   F.setDistribution(dist,distM,Xx1,Xx2,st);
   F.calculateDistribution(nn,mm,ss);
   F.filesave();
   string path=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\Distribution_function.htm";
   ShellExecuteW(NULL,"open",path,NULL,NULL,1);
  }
//+------------------------------------------------------------------+

Per le distribuzioni discrete, è stato scritto lo script discreteDistribution.mq5.

Ho eseguito lo script con i parametri standard per la distribuzione Cauchy e ho ottenuto il seguente grafico come mostrato nel video qui sotto.

Conclusione

Questo articolo ha introdotto alcune distribuzioni teoriche di una variabile casuale, anch'essa codificata in MQL5. Ritengo che il mercato di per sé e di conseguenza il lavoro di un sistema di negoziazione debba basarsi sulle leggi fondamentali della probabilità.

E spero che questo articolo rappresenterà un valore pratico per i lettori interessati. Io, da parte mia, espanderò questo argomento e fornirò esempi pratici per dimostrare come le distribuzioni statistiche di probabilità possono essere utilizzate nell'analisi del modello di probabilità.

Posizione del file:

#	File	Path	Descrizione
1	Distribution_class.mqh	%MetaTrader%\MQL5\Include	Gallery di distribuzione delle classi
2	DistributionFigure_class.mqh	%MetaTrader%\MQL5\Include	Classi di visualizzazione grafica delle distribuzioni
3	continuousDistribution.mq5	%MetaTrader%\MQL5\Scripts	Script per la creazione di una distribuzione continua
4	discreteDistribution.mq5	%MetaTrader%\MQL5\Scripts	Script per la creazione di una distribuzione discreta
5	dataDist.txt	%MetaTrader%\MQL5\Files	Dati di visualizzazione della distribuzione
6	Distribution_function.htm	%MetaTrader%\MQL5\Files	Grafico HTML a distribuzione continua
7	Distribution_function_discr.htm	%MetaTrader%\MQL5\Files	Grafico HTML a distribuzione discreta
8	exporting.js	%MetaTrader%\MQL5\Files	Script Java per esportare un grafico
9	highcharts.js	%MetaTrader%\MQL5\Files	Libreria JavaScript
10	jquery.min.js	%MetaTrader%\MQL5\Files	Libreria JavaScript

Letteratura:

K. Krishnamoorthy. Handbook of Statistical Distributions with Applications, Chapman and Hall/CRC 2006.
W.H. Press, et al. Numerical Recipes: The Art of Scientific Computing, Third Edition, Cambridge University Press: 2007. - 1256 pp.
S.V. Bulashev Statistics for Traders. - M.: Kompania Sputnik +, 2003. - 245 pp.
I. Gaidyshev Data Analysis and Processing: Special Reference Guide - SPb: Piter, 2001. - 752 pp.: ill.
A.I. Kibzun, E.R. Goryainova — Probability Theory and Mathematical Statistics. Basic Course with Examples and Problems
N.Sh. Kremer Probability Theory and Mathematical Statistics. M.: Unity-Dana, 2004. — 573 pp.

Tradotto dal russo da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/ru/articles/271

File allegati |

Scarica ZIP

distribution_class.mqh (108.26 KB)

continuousdistribution.mq5 (2.45 KB)

discretedistribution.mq5 (2.01 KB)

distribution_function.zip (59.99 KB)

distributionfigure_class.mqh (19.68 KB)

Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

Altri articoli di questo autore

Vai alla discussione

Tracciamento, debug e analisi strutturale del codice sorgente

L'intero complesso di problemi relativi alla creazione di una struttura di un codice eseguito e al suo tracciamento può essere risolto senza serie difficoltà. Questa possibilità è apparsa su MetaTrader 5 grazie alla nuova funzionalità del linguaggio MQL5: creazione automatica di variabili di tipo complesso di dati (strutture e classi) e loro eliminazione quando si esce dall'ambito locale. L'articolo contiene la descrizione della metodologia e dello strumento già pronto.

3 Metodi di accelerazione degli indicatori mediante l'esempio della regressione lineare

L'articolo tratta i metodi di ottimizzazione degli algoritmi di calcolo degli indicatori. Ciascuno troverà il metodo più adatto alle proprie esigenze. Qui sono descritti tre metodi. Uno di questi è abbastanza semplice, il successivo richiede una solida conoscenza della matematica e l'ultimo richiede un po' di arguzia. Gli indicatori o le funzionalità di progettazione del terminale MetaTrader5 vengono utilizzati per realizzare la maggior parte dei metodi descritti. I metodi sono abbastanza universali e possono essere utilizzati non solo per l'accelerazione del calcolo della regressione lineare, ma anche per molti altri indicatori.

Stime statistiche

La stima dei parametri statistici di una sequenza è molto importante poiché la maggior parte dei modelli e metodi matematici si basa su ipotesi diverse. Ad esempio, normalità della legge di distribuzione o valore di dispersione o altri parametri. Pertanto, durante l'analisi e la previsione delle serie temporali abbiamo bisogno di uno strumento semplice e conveniente che consenta di stimare in modo rapido e chiaro i principali parametri statistici. L'articolo descrive brevemente i parametri statistici più semplici di una sequenza casuale e diversi metodi della sua analisi visiva. Offre l'implementazione di questi metodi in MQL5 e i metodi di visualizzazione del risultato dei calcoli utilizzando l'applicazione Gnuplot.

Filtraggio dei segnali basati su dati statistici di correlazione dei prezzi

Esiste una correlazione tra il comportamento dei prezzi passati e le sue tendenze future? Perché il prezzo ripete oggi il carattere del suo movimento del giorno precedente? Le statistiche possono essere utilizzate per prevedere le dinamiche dei prezzi? C'è una risposta ed è positiva. Se hai qualche dubbio, allora questo articolo fa al caso tuo. Ti spiegherò come creare un filtro funzionante per un sistema di trading con MQL5, rivelando un modello interessante nelle variazioni di prezzo.