Pronosticación de series temporales (Parte 2): el método de los mínimos cuadrados de los vectores de soporte (LS-SVM)

Palabras clave: LS-SVM, SOM-LS-SVM, SOM

Introducción

En el presente artículo, continuaremos hablando de los algoritmos de pronosticación de series temporales. En la primera parte, hablamos del método de descomposición modal empírica (EMD) y el indicador TSA para el análisis estadístico de series temporales. En la segunda parte, nuestro objeto de investigación será el algoritmo de los vectores de soporte (support-vector machine, SVM) en su modificación de los mínimos cuadrados (Least-squares support-vector machine, LS-SVM). Esta tecnología todavía no ha sido implementada en MQL. Vamos a comenzar familiarizándonos con el aparato matemático.

El aparato matemático LS-SVM

El método de vectores de soporte (Support Vector Machine, SVM) es el nombre general usado para un grupo de algoritmos de análisis de datos utilizados para la clasificación y la regresión. En nuestro caso, nos interesa precisamente la regresión (artículo en la Wikipedia en inglés), porque detecta la dependencia entre variables dependientes e independientes (predictores). La tarea de la pronosticación se puede formular con la regresión como el hallazgo de una cierta función que depende de cálculos anteriores de la serie temporal (esos mismos predictores), y de tal naturalueza, que sus valores describan con el máximo de verosimilitud los futuros cálculos de la serie.

El algoritmo de SVM se basa el traslado de los datos fuente a un espacio de mayor dimensionalidad, donde cada vector de entrada se forma como una secuencia de puntos de origen con retrasos temporales. A continuación, estos vectores se usan como muestras de soporte, cuyas combinaciones sirven para calcular de una forma especial un hiperplano que describa la distribución de los datos con la precisión establecida. Los cálculos suponen la suma de todas las muestras de los llamados núcleos (kernels): las funciones uniformes de los parámetros de entrada. Estas funciones pueden ser lineales o no lineales (normalmente, en forma de campana), y se controlan mediante los parámetros que influyen en la precisión de la regresión. Entre los núcleos más extendidos, se encuentran:

• lineal ;
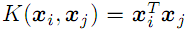• grado de polinomio d ;
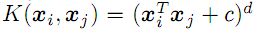• función de base radial con dispersión "sigma" (Gaussian, ver más abajo);
• sigmoide (tangente hiperbólica) ;

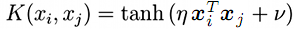Existe una modificación de SVM, Least-Squares SVM (LS-SVM) o en su traducción literal: "método de los mínimos cuadrados de los vectores de soporte". Est permite, junto con la tarea lineal original, resolver una equivalente en forma de sistema de ecuaciones lineales.

Supongamos que tenemos una serie temporal y, y que suponemos que podemos conocer su valor en el momento t como la función p de los puntos anteriores y ciertas variables externas q, con un error e. De forma general, la escribiríamos como:

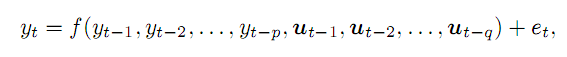 (1)

Como ejemplos de variables externas (para la rama aplicada del trading), podemos poner el número para la semana, el número de la hora en días, o el volumen de la barra correspondiente. En el presente artículo, nos limitaremos a los anteriores puntos de una serie temporal de precios. La complejidad del material no nos permite analizar todos los aspectos al mismo tiempo.

Los puntos anteriores tomados de la serie p forman un vector en un espacio p-dimensional. Desplazándonos por la serie original de izquierda a derecha, obtendremos un conjunto de vectores-predictores que marcaremos con una x; para un momento temporal t, su correspondencia con el pronóstico y se expresará en los siguientes términos:

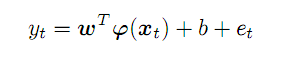 (2)

El vector desconocido de los coeficientes w y las funciones de transformación f funcionan en un espacio abstracto de símbolos, cuya dimensionalidad no está potencialmente limitada por nada, y puede ser incluso superior a p, mientras que el aspecto f, al igual que los valores de los coeficientes w precisamente lo deberemos encontrar durante la optimización:

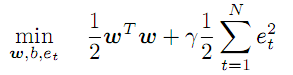 (3)

Esta condición dicta que debemos minimizar la magnitud de los coeficientes w e introducir un coeficiente "gamma" regulador para la magnitud de los errores. Cuanto mayor sea "gamma", con mayor precisión aproximará la regresión los datos originales. Si "gamma" disminuye, la posibilidad de que aprezcan desviaciones aumenta, incrementándose con ello la suavidad del modelo.

El sistema de ecuaciones (2) actúa como limitación para todas los t de 1 a N (número de vectores).

Para simplificar la tarea, se utilizan "trucos" matemáticos (uno de ellos es el así llamado "kernel trick"): en lugar de la tarea de optimización original, se resuelve la llamada tarea dual, que es en esencia equivalente, en la que logramos librarnos de los coeficientes w y las transformaciones f en el cambio por funciones nucleares (ver a continuación). Como resultado, la solución se reduce a un sistema lineal:

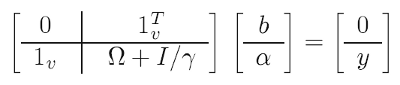 (4)

Datos conocidos en ella:

• y - vector que consta de todos los valores objetivo (de aprendizaje) del pronóstico;
• 1 - vectores unitarios (línea y columna);
• I - matriz unitaria;
• gamma - parámetro regulador descrito más arriba (debemos seleccionarlo guiándonos por la calidad del pronóstico en la muestra de prueba);
• omega - matriz calculada según la fórmula:

 (5)

Aquí, encontramos finalmente las funciones K anunciadas anteriormente, que se calculan en combinaciones pares entre todos los vectores de entrada x. Para la función de base radial en forma de Gaussiana simétrica (vamos a utilizar precisamente esta), la fórmula K tiene el aspecto que sigue:

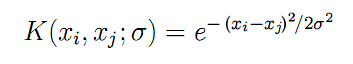 (6)

El parámetro "sigma" describe la anchura de la campana: se trata de otro parámetro más que deberemos seleccionar de forma iterativa en la práctica. Cuanto mayor sea "sigma", mayor será el número de vectores "circundantes" que participará en la regresión. Cuando "sigma" es pequeña, la función pasa de forma bastante precisa por los puntos del conjunto de datos de aprendizaje y deja de reaccionar a las muestras desconocidas (deja de generalizar).

Con la ayuda de los datos originales (x, y), según las fórmulas (4), (5) y (6), averiguamos todas las incógnitas con la ayuda de los mínimos cuadrados:

• b - miembro libre que figura en (2) y (7);
• a - vector de los coeficientes "alfa" incluidos en la fórmula final del modelo de regresión:

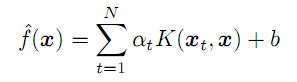 (7)

Para cualquier vector x aleatorio (que no pertenezca al grupo de aprendizaje), permite calcular el pronóstico como la suma de los productos de los coeficientes "alfa" y los núcleos de todos los vectores N originales, con una corrección del miembro libre b.

En la parte teórica, quedan por aclarar 2 cuestiones. En primer lugar, de qué forma averiguamos los parámtros libres "gamma" y "sigma". En segundo lugar, qué profundidad de retrasos temporales p debemos seleccionar para formar los vectores de entrada x de una serie de cotizaciones.

Los parámetros se definirán con el método de "prueba y error": en un ciclo por una red bidimensional de valores muy amplia, hacemos el cálculo del modelo para cada combinación, determinando luego su calidad. Entendemos por calidad la minimización del error de pronosticación en un conjunto de prueba de datos distinto al conjunto de aprendizaje. El proceso recurda y puede implicar la optimización en el simulador MetaTrader; sin embargo, para investigar intervalos amplios, necesitaremos cambiar de hecho los valores, pero no con un salto constante, sino en progresión geométrica, con la ayuda de la multiplicación. Por eso, necesitaremos tener en cuenta esta peculiaridad en el estadio de implementación.

En lo que respecta al tamaño del espacio de entrada p, recomendamos definirlo partiendo de las características de la serie pronosticada, en concreto, con la ayuda de función de autocorrelación parcial (PACF). En el artículo anterior, preparamos el instrumental para calcular la PACF, y vimos el aspecto que tiene en un EURUSD D1 diferenciado para un segmento concreto de la historia. Cada columna del histograma describe la influencia de las barras con el lag temporal correspondiente en la barra actual (es decir, en total en toda la muestra, por pares entre las barras con los índices que se diferencian en la magnitud del lag). Las 2 líneas curvas punteadas por encima y por debajo indican los límites del intervalo de fiabilidad del 95%. La mayor parte de las lecturas de la PACF se encuentra dentro del intervalo, pero algunas se salen de sus límites. Si hablamos con rigor, al formar los vectores de entrada, tiene sentido en primer lugar tomar las lecturas con valores grandes, dado que estas indican una relación entre la nueva barra y las barras pasadas correspondientes. En otras palabras, en el vector y podríamos sumar no todas las pasadas lecturas seguidas, sino, por ejemplo, la 6, la 8 y la 50, como en la imagen del artículo anterior. Sin embargo, esta situación es característica solo para una muestra concreta. Si tomamos, no 500 barras D1, sino 1000 o 250, obtendremos una nueva PACF con otras "crestas". De esta forma, necesitaremos "despejar" las lecturas de la serie original al darse cualquier cambio en los datos, y esto, a su vez, requerirá la optimización de los ajustes de LS-SVM (en concreto, de los parámetros "gamma" y "sigma"). Por eso, para aumentar la universalidad del algoritmo, aunque sea perdiendo efectividad, hemos decidido formar los vectores de entrada de todas las barras consecutivas en la profundidad p establecida, para que en este segmento inicial de la PACF los "valores atípicos" principales sean cubiertos por el intervalo fiable. En la práctica, esto significa p en el intervalo de 20 a 50 barras para EURUSD D1.

Finalmente, debemos destacar que la complejidad computacional de LS-SVM tiene una dependencia cuadrática de la longitud de la muestra N, ya que el tamaño de la matriz es igual a (N+1)*(N+1). Para las muestras de varios centenares o miles de barras, esto podría influir negativamente en el rendimiento. Existen muchas variantes de LS-SVM que tratan de luchar con esta "maldición del tamaño". Una de ella, por ejemplo, propone clusterizar primero todos los vectores con la red neuronal de Kohonen (SOM), y después realizar el entrenamiento de M modelos individuales para cada clúster (M es el número de clústeres).

Nosotros proponemos otro enfoque. Después de clusterizar el conjunto original de vectores con una der SOM, los clústeres encontrados se usarán como núcleos en lugar de los vectores originales. Por ejemplo, una muestra de 1000 vectores puede ser representada en una capa de Kohonen con un tamaño de 7*7, es decir, 49 vectores de apoyo, lo que de media nos da 20 muestras de origen para cada celda de la red.

La red de Kohonen ya fue analizada en los artículos Uso práctico de las redes neuronales de Kohonen en el trading algorítmico (Parte I, Parte II), por eso, resulta relativamente sencillo construirla en el motor LS-SVM creado.

Vamos a implementar el algoritmo en MQL.

LS-SVM en MQL

Reuniremos todos los cálculos en una sola clase LSSVM, que usará los "solucionadores" lineales de la biblioteca ALGLIB. Por eso, vamos a incluirla en el código fuente, y ya de paso, también la biblioteca CSOM.

  #include <Math/Alglib/dataanalysis.mqh>
  #include <CSOM/CSOM.mqh>

En la clase, posibilitamos el guardado de todos los vectores de entrada y las matrices LS-SVM:

  class LSSVM
  {
    protected:
      double X[];
      double Y[];
      double Alpha[];
      double Omega[];
      double Beta;
      
      double Sigma;
      double Sigma22; // 2 * Sigma * Sigma;
      double Gamma;
      
      int VectorNumber;
      int VectorSize;
      int Offset;
      int DifferencingOrder;
      ...

La clase rellenará por sí misma X e Y con los datos de las cotizaciones, guiándose por el número de vectores VectorNumber solicitados, su tamaño VectorSize, y el desplazamiento en la historia Offset (por defecto, 0 — los últimos precios): todo ello se transmite al constructor a través de los parámetros.

La clase da soporte al procesamiento no solo de la serie original (DifferencingOrder igual a 0), sino también de sus diferencias de órdenes de 1 a 3. Más tarde, profundizaremos en los matices del presente enfoque.

De forma opcional, la clusterización con la ayuda de la red de Kohonen proporciona el objeto KohonenMap, mientras que los clústeres encontrados por este entran en la matriz Kernels.

      double Kernels[];  // SOM clusters
      int KernelNumber;
      CSOM KohonenMap;
      ...

el tamaño de la red (se presupone una capa cuadrada, es decir, el número de KernelNumber deberá ser cuadrado de uno entero) es establecido por el usuario, y este número también se puede optimizar. Si KernelNumber es igual a 0 (por defecto) o al número total de vectores, SOM se desactivará, poniéndose en marcha el procesamiento con la ayuda de LS-SVM. El funcionamiento de la red se sale del marco temático del artículo, así que los lectores interesados podrán familiarizarse con sus métodos de preparación, entrenamiento e integración en los códigos adjuntos. Tenga en cuenta que, inicialmente, la red se aleatoriza, y por eso, para obtener los resultados reproducidos, deberemos llamar a srand con un valor concreto.

Los datos por defecto se leen a partir de la serie temporal de precios de apertura en el método buildXYVectors. En este artículo, trabajaremos solo con ellos. Para introducir los datos derivados, se ha pensado el método feedXYVectors, pero no lo hemos puesto a prueba.

    bool buildXYVectors()
    {
      ArrayResize(X, VectorNumber * VectorSize);
      ArrayResize(Y, VectorNumber);
      double open[];
      int k = 0;
      const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y
      CopyOpen(_Symbol, _Period, Offset, size, open);
      
      double diff[];
      ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction
      
      for(int i = 0; i < VectorNumber; i++)     // loop through anchor bars
      {
        for(int j = 0; j < VectorSize; j++)     // loop through successive bars
        {
          differentiate(open, i + j, diff);
          
          X[k++] = diff[0];
        }
        
        differentiate(open, i + VectorSize, diff);
        Y[i] = diff[0];
      }
      
      return true;
    }

El método differentiate auxiliar que hemos llamado aquí, permite calcular una diferencia de orden aleatorio para la matriz transmitida. El resultado se retorna a través de la matriz diff, cuya logitud es superior en 1 a DifferencingOrder.

    void differentiate(const double &open[], const int ij, double &diff[])
    {
      for(int q = 0; q <= DifferencingOrder; q++)
      {
        diff[q] = open[ij + q];
      }
      
      int d = DifferencingOrder;
      while(d > 0)
      {
        for(int q = 0; q < d; q++)
        {
          diff[q] = diff[q + 1] - diff[q];
        }
        d--;
      }
    }

La clase da soporte a la normalización de vectores con la ayuda de la resta de la media y la división por la desviación estándar en el método normalizeXYVectors (no se reproduce aquí).

La clase también dispone de un par de métodos de cálculo de núcleos, tanto para los vectores de X[] según sus índices, como para los vectores externos, por ejemplo:

    double kernel(const double &x1[], const double &x2[]) const
    {
      double sum = 0;
      for(int i = 0; i < VectorSize; i++)
      {
        sum += (x1[i] - x2[i]) * (x1[i] - x2[i]);
      }
      return exp(-1 * sum / Sigma22);
    }

El cálculo de la matriz "omega" es ejecutado por el método buildOmega (este utiliza el método kernel, recurriendo a los vectores X[] según los índices):

    void buildOmega()
    {
      KernelNumber = VectorNumber;
      
      ArrayResize(Omega, VectorNumber * VectorNumber);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        for(int j = i; j < VectorNumber; j++)
        {
          const double k = kernel(i, j);
          Omega[i * VectorNumber + j] = k;
          Omega[j * VectorNumber + i] = k;
          
          if(i == j)
          {
            Omega[i * VectorNumber + j] += 1 / Gamma;
            Omega[j * VectorNumber + i] += 1 / Gamma;
          }
        }
      }
    }

Propiamente, la resolución del sistema de ecuaciones y la obtención de los coeficientes "alfa" y "beta" buscados tiene lugar en el método solveSoLE.

    bool solveSoLE()
    {
      // |  0              |1|             |   |  Beta   |   |  0  |
      // |                                 | * |         | = |     |
      // | |1|  |Omega| + |Identity|/Gamma |   | |Alpha| |   | |Y| |
      
      CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1);
      
      for(int i = 1; i <= KernelNumber; i++)
      {
        for(int j = 1; j <= KernelNumber; j++)
        {
          MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]);
        }
      }
      
      MATRIX[0].Set(0, 0);
      for(int i = 1; i <= KernelNumber; i++)
      {
        MATRIX[i].Set(0, 1);
        MATRIX[0].Set(i, 1);
      }
      
      double B[];
      ArrayResize(B, KernelNumber + 1);
      B[0] = 0;
      for(int j = 1; j <= KernelNumber; j++)
      {
        B[j] = Y[j - 1];
      }
      
      int info;
      CDenseSolverLSReport rep;
      double x[];
      
      CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x);
      
      Beta = x[0];
      ArrayResize(Alpha, KernelNumber);
      ArrayCopy(Alpha, x, 0, 1);
      
      return true;
    }

El método principal de la clase de ejecución de la regresión es process. Desde el mismo, se inicia la formación de los datos de entrada/salida, la normalización, el cálculo de la matriz "omega", la resolución del sistema de ecuaciones y la obtención del error según la muestra.

    bool process()
    {
      if(!buildXYVectors()) return false;
      normalizeXYVectors();
      
      // least squares linear regression for demo purpose only
      if(KernelNumber == -1 || KernelNumber > VectorNumber)
      {
        return regress();
      }
      
      if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
      {
        buildOmega();
      }
      else                                                  // proposed SOM-LS-SVM
      {
        if(!buildKernels()) return false;
      }
      if(!solveSoLE()) return false;
      
      LSSVM_Error result;
      checkAll(result);
      ErrorPrint(result);
      return true;
    }

Para valorar la calidad de la optimización en la clase, se usan indicadores un tanto diferentes, que se calculan para un conjunto de datos al completo: el error medio cuadrático, el coeficiente de correlación, el coeficiente de determinación (R-squared) y el % de coincidencia según el símbolo (tiene sentido solo en los modos con diferenciación). Todos los indicadores se reúnen en la estructura LSSVM_Error:

    struct LSSVM_Error
    { // indices: 0 - training set, 1 - test set
      double RMSE[2]; // RMSE
      double CC[2];   // Correlation Coefficient
      double R2[2];   // R-squared
      double PCT[2];  // %
    };

El índice cero en las matrices se corresponde con la muestra de entrenamiento, el primero, con la muestra de prueba. Sería deseable usar una valoración más rigurosa de la significación estadística del pronóstico, por ejemplo, los criterios de Fisher, dado que los valores de correlación bonitos o R2 pueden resultar engañosos; no obstante, no parece posible abarcar todo de golpe.

El método de cálculo del error por toda la muestra es checkAll.

    void checkAll(LSSVM_Error &result)
    {
      result.RMSE[0] = result.RMSE[1] = 0;
      result.CC[0] = result.CC[1] = 0;
      result.R2[0] = result.R2[1] = 0;
      result.PCT[0] = result.PCT[1] = 0;
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      double out[];
      getResult(out);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        double given = Y[i];
        double trained = out[i];
        result.RMSE[0] += (given - trained) * (given - trained);
        // mean is 0 after normalization
        xy += (given) * (trained);
        x2 += (given) * (given);
        y2 += (trained) * (trained);
        
        if(given * trained > 0) correct++;
      }
      
      result.R2[0] = 1 - result.RMSE[0] / x2;
      result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber);
      result.CC[0] = xy / sqrt(x2 * y2);
      result.PCT[0] = correct * 100.0 / VectorNumber;
      
      crossvalidate(result); // fill metrics for test set (if attached)
    }

Antes del ciclo, se llama el método getResult, que ejecuta una aproximación para todos los vectores de entrada y rellena con estos valores la matriz out.

    void getResult(double &out[], const bool reverse = false) const
    {
      double data[];
      ArrayResize(out, VectorNumber);
      for(int i = 0; i < VectorNumber; i++)
      {
        vector(i, data);
        out[i] = approximate(data);
      }
      if(reverse) ArrayReverse(out);
    }

Aquí, se usa la función estándar de pronosticación para un modelo ya construido, la función approximate:

    double approximate(const double &x[]) const
    {
      double sum = 0;
      double data[];
      
      if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference)
      {
        for(int i = 0; i < ArraySize(x); i++)
        {
          sum += Solution[i] * x[i];
        }
        sum += Solution[ArraySize(x)];
      }
      else
      {
        if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
        {
          for(int i = 0; i < VectorNumber; i++)
          {
            vector(i, data);
            sum += Alpha[i] * kernel(x, data);
          }
        }
        else                                                  // proposed SOM-LS-SVM
        {
          for(int i = 0; i < KernelNumber; i++)
          {
            ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize);
            sum += Alpha[i] * kernel(x, data);
          }
        }
      }
      return sum + Beta;
    }

En ella, los coeficientes Alpha[] y Beta encontrados se aplican a la suma de funciones nucleares (los casos LS-SVM y SOM-LS-SVM).

La muestra de prueba se forma de forma análoga a la de entrenamiento, con la ayuda de otro objeto LSSVM; en este caso, además, se establece en el objeto principal una vinculación con el "primario".

  protected:
    LSSVM *crossvalidator;
  
  public:
    bool bindCrossValidator(LSSVM *tester)
    {
      if(tester.getVectorSize() == VectorSize)
      {
        crossvalidator = tester;
        return true;
      }
      return false;
    }
    
    void crossvalidate(LSSVM_Error &result)
    {
      const int vectorNumber = crossvalidator.getVectorNumber();
      
      double out[];
      double _Y[];
      crossvalidator.getY(_Y); // assumed normalized by validator
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      for(int i = 0; i < vectorNumber; i++)
      {
        crossvalidator.vector(i, out);
        
        double z = approximate(out);
        
        result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z);
        xy += (_Y[i]) * (z);
        x2 += (_Y[i]) * (_Y[i]);
        y2 += (z) * (z);
        
        if(_Y[i] * z > 0) correct++;
      }
      
      result.R2[1] = 1 - result.RMSE[1] / x2;
      result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber);
      result.CC[1] = xy / sqrt(x2 * y2);
      result.PCT[1] = correct * 100.0 / vectorNumber;
    }

En caso necesario, la clase premite ejecutar, en lugar de la optimización lineal según el algoritmo de LS-SVM/SOM-LS-SVM, la regresión lineal con el método de los mínimos cuadrados en el sistema, con el VeсtorSize de la variables y el VectorNumber de las ecuaciones. Para ello, se ha implementado el método regress.

    bool regress(void)
    {
      CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column
      
      for(int i = 0; i < VectorNumber; i++)
      {
        MATRIX[i].Set(VectorSize, Y[i]);
      }
      
      for(int i = 0; i < VectorSize; i++)
      {
        for(int j = 0; j < VectorNumber; j++)
        {
          MATRIX[j].Set(i, X[j * VectorSize + i]);
        }
      }
      
      CLinearModel LM;
      CLRReport AR;
      int info;
      
      CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR);
      if(info != 1)
      {
        Alert("Error in regression model!");
        return false;
      }
      
      int _size;
      CLinReg::LRUnpack(LM, Solution, _size);
      
      Print("RMSE=" + (string)AR.m_rmserror);
      ArrayPrint(Solution);
      
      return true;
    }

Este método pierde respecto a LS-SVM en cuanto a su precisión, y ha sido añadido para demostrar esto. Por otra parte, podría tener cierta demanda a la hora de realizar la regresión de datos más simples por su naturaleza, que las cotizaciones. La activación de este modo se ejecuta estableciendo KernelNumber = -1. En este caso, la solución se registra en la matriz Solution (Alpha[] y Beta, en este supuesto, no participan.

Vamos a crear un indicador de pronosticación basado en la clase LSSVM.

Indicador de pronosticación LS-SVM

La tarea del indicador SOMLSSVM.mq5 consistirá en crear 2 objetos LSSVM (uno para la muestra de entrenamiento, y otro para la muestra de prueba), ejecutar la regresión y representar los valores originales y los pronosticados con una valoración de la calidad del pronóstico en ambas muestras. Los parámetros "gamma" y "sigma" se considerarán ya seleccionados, y serán indicados por el usuario. Resulta más cómodo optimizar estos en el experto, con la ayuda del simulador estándar (a ello dedicaremos el apartado siguiente). En principio, el simulador también podría dar soporte a la posibilidad de optimizar indicadores, dado que esta limitación tiene un carácter artificial. Entonces, podríamos optimizar el modelo directamente en el indicador.

En el indicador tendremos 4 búferes en una ventana aparte. 2 búferes representarán los valores originales y pronosticados para la muestra de entrenamiento, mientras que los 2 otros representarán lo mismo para la muestra de prueba.

Parámetros de entrada:

  input int _VectorNumber = 250; // VectorNumber (training)
  input int _VectorNumber2 = 50; // VectorNumber (validating)
  input int _VectorSize = 20; // VectorSize
  input double _Gamma = 0; // Gamma (0 - auto)
  input double _Sigma = 0; // Sigma (0 - auto)
  input int _KernelNumber = 0; // KernelNumber (0 - auto)
  input int _TrainingOffset = 50; // Offset of training bars
  input int _ValidationOffset = 0; // Offset of validation bars
  input int DifferencingOrder = 1;

Los dos primeros establecen el tamaño de la muestra de entrenamiento y la muestra de prueba. El tamaño del vector se indica en VectorSize. Los parámetros Gamma y Sigma se pueden dejar iguales a 0, para que sus valores adopten automáticamente los valores basados en los datos de entrada, pero la calidad de este modo tan trivial no es la óptima, ni mucho menos: el modo solo se necesita para que el indicador trabaje con los valores por defecto. KernelNumber es mejor dejarlo igual a 0 para realizar la regresión con el método LS-SVM. El conjunto de prueba por defecto se ubica al final de la historia de cotizaciones, y el conjunto de entrenamiento, a la izquierda de este (antes, en orden cronológico).

Usando como base los parámetros de entrada, se inicializan los objetos.

  LSSVM *lssvm = NULL;
  LSSVM *test = NULL;
  
  int OnInit()
  {
    static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"};
    
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetString(i, PLOT_LABEL, titles[i]);
    }
    
    lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset);
    test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset);
    lssvm.setDifferencingOrder(DifferencingOrder);
    test.setDifferencingOrder(DifferencingOrder);
    
    return INIT_SUCCEEDED;
  }

El cálculo del indicador solo se realiza una vez, dado que ha sido creado con fines ilustrativos. Si fuera necesario, podríamos adaptarlo de forma que las lecturas se actualizaran en cada barra, pero la resolución del sistema, potencialmente superpuesta, se deberá ejecutar entonces solo una vez, y repetirse después de un periodo de tiempo bastante considerable.

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {
    ArraySetAsSeries(Open, true);
    ArraySetAsSeries(Time, true);
    
    static bool calculated = false;
    if(calculated) return rates_total;
    calculated = true;
    
    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }
    
    lssvm.bindCrossValidator(test);
    bool processed = lssvm.process(true);

En el manejador OnCalculate, incluimos el conjunto de prueba en el de entrenamiento e iniciamos la regresión. Si se ejecuta con éxito, representaremos todos los datos, tanto los pronósticos originales, como los obtenidos:

  if(processed)
  {
    const double m1 = lssvm.getMean();
    const double s1 = lssvm.getStdDev();
    const double m2 = test.getMean();
    const double s2 = test.getStdDev();
    
    // training
    
    double out[];
    lssvm.getY(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[0].set(_TrainingOffset, out);
    
    lssvm.getResult(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[1].set(_TrainingOffset, out);
    
    // validation
    
    test.getY(out, true);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      out[i] = out[i] * s2 + m2;
    }
    
    buffers[2].set(_ValidationOffset, out);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      test.vector(i, out);
      
      double z = lssvm.approximate(out);
      z = z * s2 + m2;
      buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z;
      ...
    }
  }

Dado que tenemos la opción de analizar una serie diferenciada, el indicador se mostrará en una ventana aparte. No obstante, en esencia, seguimos trabajando con precios, y resulta deseable representar el pronóstico en el gráfico principal. Para ello, podemos utilizar objetos. Sus coordenadas en el eje de los precios se deben restablecer a partir de la serie de diferencia. En el siguiente esquema se ilustra la indexación de los elementos en la serie original y en las series de diferencia derivadas de la misma, de distinto orden (la indexación se da cronológicamente):

    d0:  0   1   2   3   4   5  :y
    d1:    0   1   2   3   4
    d2:      0   1   2   3
    d3:        0   1   2

Por ejemplo, si la diferencia es de primer orden (d1), resultará obvio que:

y[i+1] = y[i] + d1[i]

Para las diferencias de segundo (d2) y tercer (d3) orden, las ecuaciones serán así:

y[i+2] = 2 * y[i+1] - y[i] + d2[i]

y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]

Podemos ver que, cuanto más sean los órdenes de diferenciación, mayor será el número de lecturas y anteriores que partcipa en los cálculos.

Aplicando los datos de la fórmula, podemos representar el pronóstico con objetos en el gráfico de precio.

      if(ShowPredictionOnChart)
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2]
                 + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z;
        }
        else
        {
          // unsupported yet
        }
        
        string name = prefix + (string)i;
        ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target);
        ObjectSetString(0, name, OBJPROP_TEXT, "l");
        ObjectSetString(0, name, OBJPROP_FONT, "Wingdings");
        ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER);
        ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed);
      }

Los órdenes indicados más arriba no han sido analizados, ya que tienen no solo un efecto positivo, sino también otro negativo. Recordemos que el factor positivo consiste en el aumento de la calidad del pronóstico conforme aumenta el orden, gracias a las estacionariedad creciente. Sin embargo, esto se refiere precisamente al pronóstico de un orden derivado existente, y no a la serie original. El efecto negativo de la diferenciación de órdenes altos es que en ellos, incluso un error pequeño aumenta significativamente con el posterior "despliegue" de los incrementos en la serie integrada. De esta forma, para el parámetro DifferencingOrder, también deberemos encontrar el "justo medio" mediante la optimización y la selección.

Ambos efectos se pueden observar en las dos siguientes capturas de pantalla (las líneas verde clara y verde son los datos reales de la muestra de entrenamiento y la de prueba; las líneas celeste y azul son el pronóstico de la muestra de entrenamiento y la de prueba):

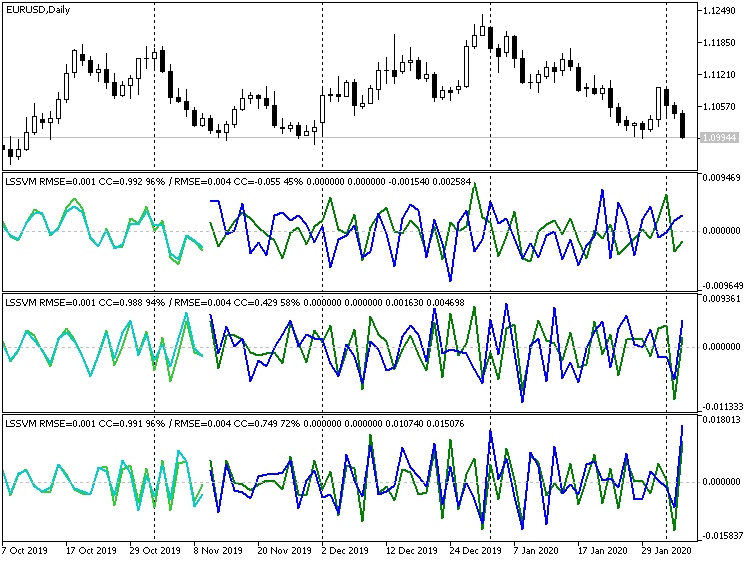
Indicadores LSSVM con distinto orden de diferenciación de la serie EURUSD D1

Aquí podemos ver 3 ejemplares del indicador con sus ajustes generales y distintos órdenes de diferenciación. Ajustes generales:

• _VectorNumber = 250; // VectorNumber (training)
• _VectorNumber2 = 60; // VectorNumber (validating)
• _VectorSize = 20; // VectorSize
• _Gamma = 2048; // Gamma (0 - auto)
• _Sigma = 8; // Sigma (0 - auto)
• _KernelNumber = 0; // KernelNumber (0 - auto)
• _TrainingOffset = 60; // Offset of training bars
• _ValidationOffset = 0; // Offset of validation bars

El orden de diferenciación es igual, respectivamente, a 1, 2 y 3. En el encabezado de cada ventana, después de la línea inclinada, se destacan los indicadores del pronósitico para la muestra de prueba (en este caso, de validación): estos aumentan de forma positiva (coeficiente de correlación: -0.055, 0.429, 0.749; porcentaje de signos de incremento coincidentes: 45%, 58%, 72%). En principio, la mejora en la coincidencia de las líneas se ve incluso a simple vista. No obstante, si restablecemos el pronóstico del tercer orden en el gráfico de precios, obtendremos la imagen siguiente:

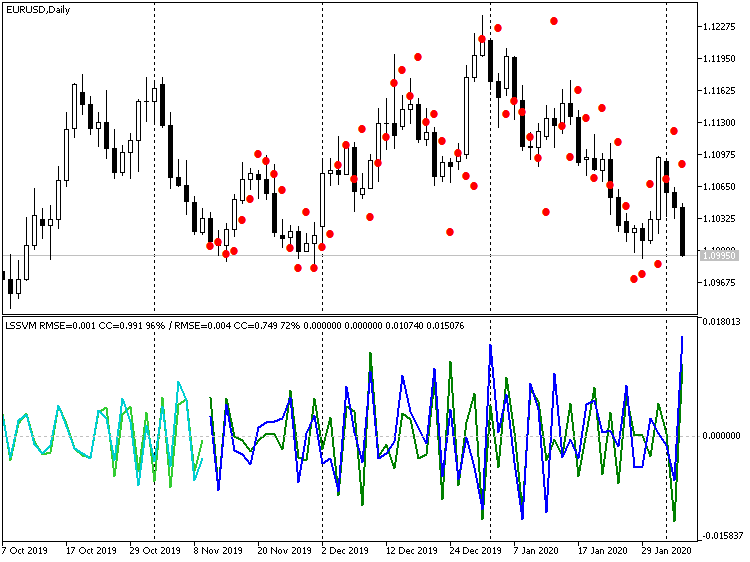
Indicador LSSVM de tercer orden de diferenciación con valores restablecidos para el pronóstico de precios EURUSD D1

Obviamente, muchos de los puntos se podrían definir como valores atípicos. Por otra parte, si desactivamos por completo la diferenciación, obtendremos:

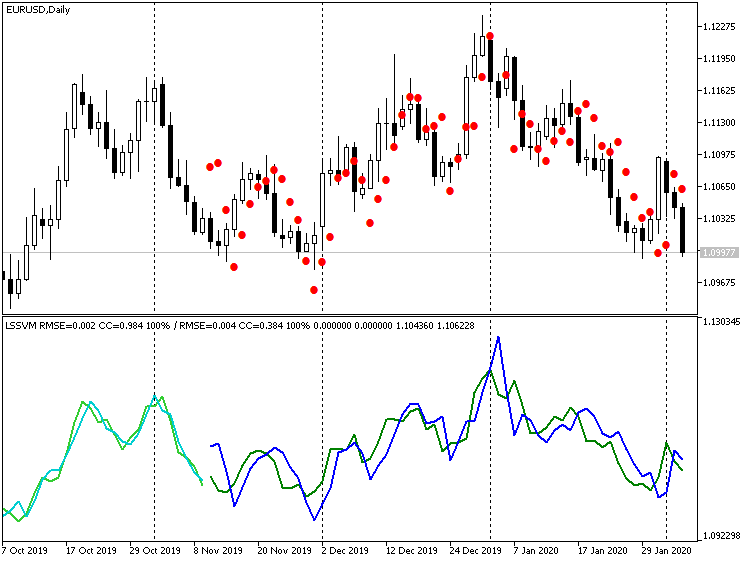
Indicador LSSVM sin diferenciación con valores restablecidos para el pronóstico de precios EURUSD D1

Aquí, los valores de precio están bastante más próximos a los reales, pero se percibe un retraso de fase del pronóstico, de aproximadamente 1 barra. La explicación de este efecto reside en que nuestro algoritmo es prácticamente equivalente al filtro digital, una especie de media móvil basada en N vectores de muestra. Teniendo en cuenta la cercanía de los niveles de precio, tiene sentido nivelar este retraso de 1-2 barra(s) pronosticando de golpe varios pasos por adelantado, es decir, después de obtener el pronóstico para la barra -1, podemos suministrarlo como lectura de entrada para el pronóstico de la barra -2, y así sucesivamente. Tendremos en cuenta este modo al crear el experto en el siguiente apartado.

Experto LS-SVM

El experto LSSVMbot.mq5 sirve para realizar dos tareas:

• la optimización de los parámetros "gamma" y "sigma" de LS-SVM en el modo virtual (sin comercio);
• el comercio en el simulador y, de forma opcional, la optimización de otros parámetros en el modo de comercio;

En el modo virtual, al igual que en el indicador, se usan 2 ejemplares de LSSVM: uno con la muestra de entrenamiento, y otro con la de prueba. Precisamente las lecturas de la muestra de prueba se toman para el cálculo. La optimización se realiza según el criterio personalizado. Todos ellos se reúnen en la enumeración:

  enum CUSTOM_ESTIMATOR
  {
    RMSE,   // RMSE
    CC,     // correlation
    R2,     // R-squared
    PCT,    // %
    TRADING // trading
  };

La variante TRADING se aplica para pasar el experto al modo de comercio. En él, el experto se puede optimizar de la forma acostumbrada según uno de los criterios incorporados (beneficio, reducción, etcétera).

El grupo principal de parámetros de entrada establece las mismas magnitudes que en el indicador.

  input int _VectorNumber = 250;  // VectorNumber (training)
  input int _VectorNumber2 = 25;  // VectorNumber (validating)
  input int _VectorSize = 20;     // VectorSize
  input double _Gamma = 0;        // Gamma (0 - auto)
  input double _Sigma = 0;        // Sigma (0 - auto)
  input int _KernelNumber = 0;    // KernelNumber (sqrt, 0 - auto)
  input int DifferencingOrder = 1;
  input int StepsAhead = 0;

Sin embargo, el desplazamiento de TrainingOffset y ValidationOffset las ha convertido en variables internas, y se establecen de forma automática. ValidationOffset es siempre igual a 0. TrainingOffset es igual al tamaño de la muestra de prueba VectorNumber2 en el modo virtual, o 0 en el modo comercial (dado que aquí se supone que todos los parámetros ya han sido encontrados, no hay muestra de prueba, y es mejor realizar la regresión con datos recientes).

Para utilizar SOM, en el parámetro KernelNumber debemos indicar el tamaño de uno de los lados; el tamaño completo del mapa se calculará como el cuadrado de este valor.

Para optimizar "gamma" y "sigma", se ha pensado un segundo grupo de parámetros de entrada:

  input int _GammaIndex = 0;     // Gamma Power Iterator
  input int _SigmaIndex = 0;     // Sigma Power Iterator
  input double _GammaStep = 0;   // Gamma Power Multiplier (0 - off)
  input double _SigmaStep = 0;   // Sigma Power Multiplier (0 - off)
  input CUSTOM_ESTIMATOR Estimator = R2;

Puesto que el intervalo de búsqueda es muy amplio, y el simulador estándar da soporte solo a la iteración mediante la adición del salto indicado, en el experto se aplica el siguiente enfoque. La optimización deberá estar activada según los parámetros GammaIndex y SigmaIndex. Cada uno de ellos determina cuántas veces hay que multiplicar los valores inicialies de Gamma y Sigma por los multiplicadores GammaStep y SigmaStep, respectivamente, para obtener los valores "gamma" y "sigma" de trabajo. Por ejemplo, si Gamma es igual a 1, GammaStep es igual a 2, y la optimización se realiza para GammaIndex en un intervalo de 0 a 5, el algoritmo evaluará los valores de "gamma" como 1, 2, 4, 8, 16, 32. Si GammaStep y SigmaStep no son iguales a 0, siempre se usarán para calcular los valores "gamma" y "sigma" de trabajo, incluso en una única pasada del simulador.

El experto trabaja por barras. Este no iniciará los cálculos antes de que esté disponible en la historia el número de barras (vectores) solicitado. Si en el simulador no hay barras suficientes, la pasada podría no arrojar resultados, eche un vistazo a los logs. Por desgracia, el número de barras cargadas por el simulador al iniciarse depende de muchos factores (el marco temporal, el número del día dentro del año, etcétera) y puede variar sustancialmente. En caso necesario, podrá mover la hora inicial de la simulación al pasado.

En el modo virtual, el entrenamiento tiene lugar solo una vez, y una de las características (seleccionada en el parámetro Estimator) es retornada desde la función OnTester como indicador de calidad (en caso de seleccionar RMSE, el error se retornará con signo inverso).

  bool optimize()
  {
    if(Estimator != TRADING) lssvm.bindCrossValidator(test);
    iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep);
    bool success = lssvm.process();
    if(success)
    {
      LSSVM::LSSVM_Error result;
      lssvm.checkAll(result);
      
      Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma());
      Print("  training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]);
      Print("  test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]);
      
      customResult = Estimator == CC ? result.CC[1]
                  : (Estimator == RMSE ? -result.RMSE[1] // the lesser |absolute error value| the better
                  : (Estimator == PCT ? result.PCT[1] : result.R2[1]));
    }
    return success;
  }
  
  void OnTick()
  {
    ...
    if(Estimator != TRADING)
    {
      if(!processed)
      {
        processed = optimize();
      }
    }
    ...
  }
  
  double OnTester()
  {
    return processed ? customResult : -1;
  }

En el modo de comercio, el entrenamiento del modelo también se realiza por defecto solo una vez, pero podemos indicar la reconstrucción de cada año, trimestre o mes. Para ello, deberemos escribir en el parámetro OPTIMIZATION (en el código se llama _2) "y", "q" o "m", respectivamente (las mayúsculas no tienen soporte). Recordemos que este proceso se refiere solo a la resolución del sistema de ecuaciones según los datos nuevos (recientes), sin embargo, los parámetros "gamma" y "sigma" permanecen iguales. En principio, podemos complicar el proceso, y seleccionar en cada reentrenamiento los parámetros sobre la marcha (lo que asignamos antes al simulador estándar); no obstante, en este caso, esta acción se deberá organizar dentro del experto, y por eso se ejecutará en un solo flujo.

Ahora, se presupone que los parámetros "gamma" y "sigma" seleccionados para los datos en un periodo temporal bastante amplio (un año y más) no deberían perder su actualidad durante los periodos temporales de menor longitud.

Una vez el modelo ha sido construido, el ejemplar de prueba de LSSVM se usa para leer los últimos precios conocidos, formar el vector de entrada a partir de ellos y normalizar los mismos. A continuación, el vector se transmite al método lssvm.approximate:

    static bool solved = false;
    if(!solved)
    {
      const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0);
      solved = opt ? optimize() : lssvm.process();
    }
    
    if(solved)
    {
      // test is used to read latest _VectorNumber2 prices
      if(!test.buildXYVectors())
      {
        Print("No vectors");
        return;
      }
      test.normalizeXYVectors();
      
      double out[];
      
      // read latest vector
      if(!test.buildVector(out))
      {
        Print("No last price");
        return;
      }
      test.normalizeVector(out);
      
      double z = lssvm.approximate(out);

Dependiendo del parámetro de entrada StepsAhead, el experto, o bien pondrá de inmediato a trabajar el valor z obtenido, transformándolo en una predicción del precio mediante la denormalización, o bien repetirá el número establecido de veces el pronóstico y solo después lo transformará en precio.

      for(int i = 0; i < StepsAhead; i++)
      {
        ArrayCopy(out, out, 0, 1);
        out[ArraySize(out) - 1] = z;
        z = lssvm.approximate(out);
      }
      
      z = test.denormalize(z);

Dado que la serie temporal podría ser diferenciada, tomaremos varios de los valores finales del precio, para restablecer según estos y el incremento pronosticado el siguiente valor de precio.

      double open[];
      if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = open[2] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * open[2] - open[1] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * open[2] - 3 * open[1] + open[0] + z;
        }
        else
        {
          // unsupported yet
        }

Dependiendo de la posición del precio pronosticado respecto al nivel actual, el experto abre una transacción. Si ya hay una transacción abierta en la dirección correcta, esta se conservará. Si la posición se encuentra en la dirección opuesta, se realizará un viraje.

        int mode = target >= open[2] ? +1 : -1;
        int dir = CurrentOrderDirection();
        if(dir * mode <= 0)
        {
          if(dir != 0) // there is an order
          {
            OrdersCloseAll();
          }
          
          if(mode != 0)
          {
            const int type = mode > 0 ? OP_BUY : OP_SELL;
            const double p = type == OP_BUY ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID);
            OrderSend(_Symbol, type, Lot, p, 100, 0, 0);
          }
        }
      }
    }

Vamos a comprobar cómo funciona el experto en ambos modos. Como instrumento de trabajo, tomaremos XAUUSD, por estar menos influido por las noticias nacionales (en comparación con las divisas). Marco temporal — D1.

Se adjunta el archivo con los ajustes (LSSVMbot.set). El tamaño del conjunto de entrenamiento VectorNumber lo hemos elegido voluntariamente como 200. Es un poco menos de un año. Los valores mayores, alrededor de 1000, pueden ralentizar sustancialmente la resolución del sistema de ecuaciones. El conjunto de prueba es VectorNumber2=50. El tamaño del vector es VectorSize=20 (mes). SOM no se utiliza (KernelNumber=0). La diferenciación está desactivada (DifferencingOrder=0), pero, para el estadio de comprobación en el modo comercial, tenemos una pronosticación de 2 saltos hacia adelante (StepsAhead=2), dado que, con la ayuda del indicador, hemos detectado un retraso poco significativo del pronóstico respecto a los precios. En el modo virtual, no se usa el parámetro de entrada StepsAhead al calcular el modelo.

Los valores Gamma y Sigma son iguales 1, pero sus multiplicadores Power Multiplier (GammaStep, SigmaStep) son iguales a 2, mientras que el número de multiplicaciones que se realizarán durante la optimización ha sido establecido en los iteradores GammaIndex y SigmaIndex, respectivamente, como intervalos de 5 a 35 y de 5 a 20, con un salto de 5. De esta forma, cuando GammaIndex sea igual a 15, Gamma obtendrá un valor igual a 1 * (2 a la 15 potencia), es decir 32768.

La selección de los intervalos correctos para la búsqueda de "gamma" y "sigma" es una tarea bastante rutinaria, dado que para esta, por desgracia, no existe otra solución que calcular en primer lugar según la red gruesa, y luego según la fina. Vamos a limitarnos a usar una red, ya que, al preparar el artículo, hemos hecho muchas pruebas que podríamos considerar como búsqueda en un intervalo más amplio.

Bien, en total, vamos a optimizar 2 parámetros: GammaIndex y SigmaIndex. Estos cambian indirectamente Gamma y Sigma en un intervalo amplio, con un salto variable en progresión geométrica.

Vamos a iniciar la optimización en el año 2018, según los precios de apertura. Realizaremos la optimización según un criterio de usuario, Estimator = R2.

Recordemos que, en este modo, el experto no comercia, sino que rellena con cotizaciones el sistema de ecuaciones y lo resuelve según el algoritmo de LS-SVM. En los cálculos participa un número de barras suficiente para formar el VectorNumber de los vectores de un tamaño VectorSize, con una corrección para la diferenciación posiblemente incluida (cada orden adicional de toma de diferencias necesita una barra adicional en los datos de entrada). Además, al experto se le requiere adicionalmente el VectorNumber2 de los vectores de prueba, que se ubican cronológicamente después de los vectores de entrenamiento, es decir, en las últimas barras. Precisamente en las barras de prueba (concretamente, en los vectores formados a partir de ellas) se valoran las peculiaridades de pronóstico del modelo obtenido para el retorno desde OnTester.

Todo es esto es importante, dado que el simulador no siempre tiene un número de barras suficiente en la historia al comenzar, y el experto podrá rellenar el sistema solo unos meses después de la fecha inicial. Por otra parte, no debemos olvidar que las barras de entrenamiento siempre comienzan antes de la fecha de la simulación (optimización), dado que al experto se le ofrece de inmediato una historia de una longitud determinada.

Después de finalizar la optimización, clasificamos los resultados según el criterio R2 (en orden descendente, es decir, los mejores se encuentran arriba). Supongamos que al comienzo se encuentran los ajustes GammaIndex=15 y SigmaIndex=5 (hemos dicho "supongamos" porque el orden de las pasadas con los mismos resultados, probablemente, puede cambiar).

Clicamos dos veces con el ratón sobre la primera entrada, para iniciar un test único (por ahora, en el modo virtual). En el log podremos ver algo más o menos así:

  2018.01.01 00:00:00   Bars required: 270
  2018.01.02 00:00:00   247 2017.01.03 00:00:00
  2018.02.02 00:00:00   Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270
  2018.02.02 00:00:00   G[15]=32768.0 S[5]=32.0
  2018.02.02 00:00:00   RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985
  2018.02.02 00:00:00   Parameters: 32768.0 32.0
  2018.02.02 00:00:00     training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0
  2018.02.02 00:00:00     test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0
  final balance 10000.00 USD
  OnTester result 0.9598497541714557

Esto se pruede tratar de la forma que sigue: para ejecutar el procedimiento complemto se requerían 270 barras, pero en el momento del inicio, 2018.01.02, solo había 247 barras. Solo ha aprecido un número suficiente el 2018.02.02 (es decir, un mes después), en este caso, además, los datos de entrenamiento (historia disponible) han comenzado el 2017.01.03. A continuación, se indican los parámetros de trabajo Gamma y Sigma (G[15]=32768.0 S[5]=32.0, entre corchetes, encontramos los parámetros-iteradores de optimización). Finalmente, en la línea con el indicador de calidad del entrenamiento, vemos la magnitud R2 (0.95985), que precisamente ha sido retornada por OnTester.

Ahora, desactivamos la automatización, ampliamos el intervalo de fechas desde 2017 hasta febrero de 2020, y establecemos en los parámetros del experto Estimator = TRADING (esto significa que el experto realizará operaciones comerciales). En el parámetro OPTIMIZATION (en el código — _2), introducimos el símbolo "q", que encarga al experto recalcular una vez al mes el modelo regresivo usando los nuevos datos (los últimos vectores VectorNumber en el momento actual). Pero "gamma" y "sigma" permanecerán iguales.

Vamos a iniciar el test único.

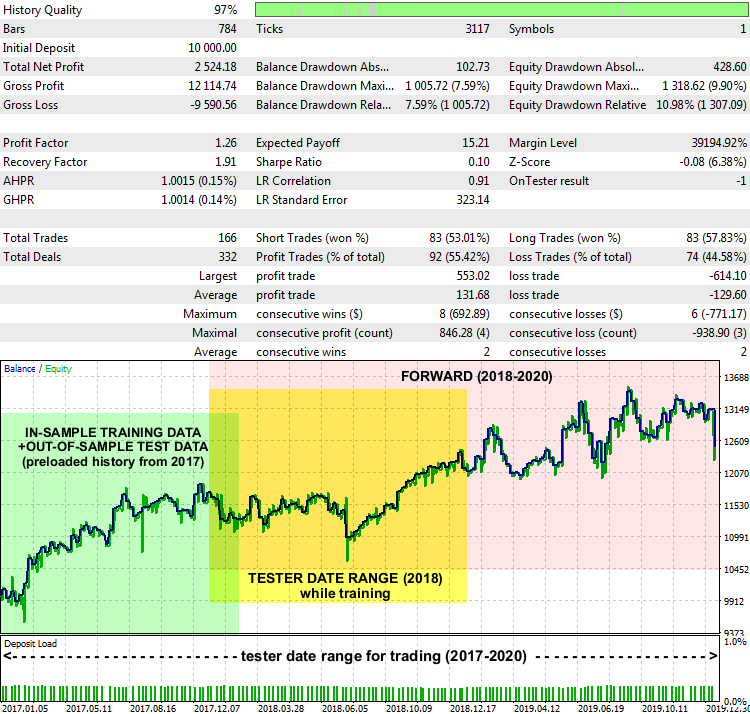
Informe del experto LSSVMbot con XAUUSD D1, 2017-2020

Las lecturas no son excepcionales, pero, en general, el sistema funciona. Hemos destacado en el gráfico los intervalos de fechas de donde se han tomado los datos de entrenamiento para encontrar las "gamma" y "sigma" óptimas (en verde), el intervalo que se ha indicado en el simulador en el modo de entrenamiento (en amarillo), y el intervalo en el que el experto ha comerciado con datos desconocidos (en rosa).

El método de interpretación del pronóstico y la construcción de la estrategia comercial en torno al mismo pueden ser diferentes. Concretamente, en nuestro experto de prueba existe el parámetro de entrada PreviousTargetCheck (por defecto, false). Si lo activamos, el comercio según el pronóstico se realizará con la ayuda de otra estrategia: la dirección de la transacción se determinará mediante la posición del pronóstico reciente con respecto al anterior. Asimismo, queda especio para realizar exprimentos con otros ajustes, por ejemplo, con la clusterización de SOM, el cambio de lote dependiendo de la fuerza del movimiento pronosticado, el incremento del volumen, etcétera.

Conclusión

En el presente artículo, nos hemos familiarizado con un algoritmo de pronosticación de series temporales basado en LS-SVM, que requiere del uso activo de matemáticas y un ajuste preciso. En la práctica, el uso exitoso de estos métodos (el EMD de la primera parte, y el LS-SVM de la presente, el segundo) puede depender fuertemente de las peculiaridades de las series temporales, mientras que, en su aplicación al trading, depende del instrumento financiero y el marco temporal. Por eso, la elección de un mercado que se corresponda con las posibilidades de un algoritmo concreto es tan importante como la implementación de cálculos complejos o laboriosos. Concretamente, las divisas de fórex resultan menos previsibles, y están más sometidas a influencias externas, lo cual reduce la eficacia de un pronóstico basado exclusivamente en datos de cotización históricos. Los dos métodos analizados resultan más adecuados para los metales, los índices y las cestas o portafolios equilibrados. Además, por extraordinario que nos parezca un pronóstico, no debemos olvidarnos de la gestión de riesgos, las órdenes stop protectoras y el monitoreo de noticias.

Los códigos fuente presentados le permitirán incorporar los nuevos métodos en sus propios proyectos MQL.