Pronosticación de series temporales (Parte 1): el método de descomposición modal empírica (EMD)

Introducción

El éxito de cada tráder depende, en primer lugar, de su capacidad de "echar un vistazo al futuro", es decir, de determinar qué precio habrá dentro de un determinado periodo de tiempo. Para resolver esta tarea, es importante disponer de un amplio conjunto de recursos, empezando por información operativa sobre las características fundamentales del mercado y terminando por los algoritmos de análisis técnico. Todos pueden ser, en uno u otro grado, potenciados con la ayuda de métodos matemáticos para la pronosticación de las series temporales, además, en calidad de series pueden actuar no solo los propios precios, sino también los indicadores técnicos, la volatilidad, los índices macroeconómicos, el balance del portafolio comercial u otros factores.

El tema de la pronosticación es muy amplio y se ha tratado en el sitio mql5.com en muchas ocasiones. Uno de los primeros artículos en introducir el tema, y además, de los más serios, fue Series temporales de previsión financiera, publicada en 2008. Entre la multitud de artículos y publicaciones presentes en CodeBase, existen herramientas preparadas para el uso en MetaTrader, que ofrecen, por ejemplo:

• Predicción de series de tiempo usando el ajuste exponencial (ES);
• Búsqueda de patrones semejantes con ayuda de la transformación dinámica de la escala temporal (WmiFor+DTW);
• Red neuronal con propagación inversa del error (BPNN);
• Red neuronal de Kohonen (SOM);

La lista completa se puede conseguir buscando los apartados correspondientes en el sitio web (artículos, CodeBase).

En el contexto de este material, vamos a completar la lista de instrumentos de pronosticación disponibles con dos nuevos. El primero de ellos se basa en el método de descomposición modal empírica (Empirical Mode Decomposition, EMD), que ya analizamos en el artículo Introducción al método de descomposición de modo empírico, pero sin aplicación en la pronosticación. El EMD será analizado en la primera parte de este material.

El segundo instrumento usa el método de vectores de apoyo(support-vector machine, SVM) en su modidificación de los cuadrados menores (Least-squares support-vector machine, LS-SVM). Volveremos a él en la segunda parte.

Algoritmo de pronosticación basado en EMD

Podrá encontrar una introducción completa a la tecnología del EMD en el artículo Introducción al método de descomposición de modo empírico. La esencia consiste en descomponer una serie temporal en componentes simples, las llamadas funciones de modo intrínsecas (Intrinsic Mode Functions, IMF). Cada forma supone una interpolación de splines de los máximos y mínimos de la serie temporal. En este caso, además, los extremos se buscan en primer lugar para la serie original, restándosele luego a la misma la IMF recién encontrada. Después de ello, la interpolación de splines se realiza ya para los extremos de la serie modificada. Este proceso de construcción de varias IMF continúa hasta que el resto no sea inferior al nivel de ruido establecido. El resultado de este trabajo recuerda visualmente a una descomposición en la serie de Fourier, pero, a diferencia de esta última, las formas características del EMD no son oscilaciones armónicas con determinadas frecuencias. El número de funciones obtenidas de la descomposición de las IMF depende de la serie original y los ajustes del algoritmo.

En el artículo mencionado, se presentan las clases ya preparadas para el cálculo del EMD, pero se propone obtener el resultado mediante la descomposición en forma de gráfico en un archivo HTML externo. Vamos a tomar las clases como base e introducir las adiciones necesarias para que el algoritmo sea un algoritmo de pronosticación.

Hemos adjuntado al artículo 2 archivos: CEMDecomp.mqh y CEMD_2.mqh. El segundo es una versión ligeramente mejorada del primero, del que precisamente vamos a partir. Lo copiamos con el nuevo nombre EMD.mqh y lo incluimos por ahora sin cambios en el indicador EMD.mq5.

  #include <EMD.mqh>

Asimismo, vamos a usar las clases especiales para la declaración simplificada de la matriz de búferes de indicador IndArray.mqh (el lector encontrará su descricpión en inglés en el blog, además, su versión actual se adjunta al artículo). Vamos a necesitar muchos búferes, que serán procesados de forma uniforme.

  #define BUF_NUM 18 // 16 IMF maximum (including input at 0-th index) + residue + reconstruction
  
  #property indicator_separate_window
  #property indicator_buffers BUF_NUM
  #property indicator_plots   BUF_NUM
  
  #include <IndArray.mqh>
  IndicatorArray buffers(BUF_NUM);
  IndicatorArrayGetter getter(buffers);

Como podemos ver, el indicador se muestra en una ventana aparte, y en él se reservan 18 indicadores para la representación de:

• la serie original;
• 16 componentes de su descomposición (no se usarán todos necesariamente);
• el resto ("la tendencia");
• la reconstrucción;

El último punto es el más interesante. La cuestión es que, después de obtener las funciones IMF, podemos unir varias de ellas (aunque no todas) y conseguir una versión suavizada de la serie original. Precisamente la reconstrucción suavizada actuará como fuente del pronóstico, dado que constituye la suma de splines conocidos que se pueden calcular en el futuro para las barras todavía ausentes (extrapolación de splines). Sin embargo, la profundidad del pronóstico se debe limitar a varias barras, puesto que las IMF halladas pierden su actualidad a medida que se alejan respecto al último punto conocido para el que fueron obtenidas.

Regresemos al archivo EMD.mqh. En este se define la clase CEMD, que realiza todo el trabajo. El proceso se inicia llamando el método decomp, al que se transmite la matriz con los cálculos de la serie temporal "y". Precisamente el tamaño de esta matriz determina la longitud de los N fragmentos de las funciones propias, IMFResult. El método arrayprepare se encarga de preparar las matrices auxiliares para su cálculo:

  class CEMD
  {
    private:
      int N;              // Input and output data size
      double IMFResult[]; // Result
      double X[];         // X-coordinate for the TimeSeries. X[]=0,1,2,...,N-1.
      ...
    
    public:
      int N;              // Input and output data size
      double Mean;        // Mean of input data
      ...
      
      int decomp(double &y[])
      {
        ...
        N = ArraySize(y);
        arrayprepare();
        for(i = 0; i < N; i++)
          X[i] = i;
        Mean = 0;
        for(i = 0; i < N; i++)
          Mean += (y[i] - Mean) / (i + 1.0); // Mean (average) of input data
        for(i = 0; i < N; i++)
        {
          a = y[i] - Mean;
          Imf[i] = a;
          IMFResult[i] = a;
        }
        // The loop of decomposition
          ...
          extrema(...);
          ...
        ...
      }
      
      
    private:
      int arrayprepare(void)
      {
        if(ArrayResize(IMFResult, N) != N) return (-1);
        ...
      }
  };

Para aumentar el número de puntos de cálculo, vamos a añadir al método extrapolate el nuevo parámetro extrapolate, que establece la profundidad del pronóstico. Aumentamos N en el número de cálculos solicitados en extrapolate, guardando preliminarmente la longitud real de la serie original en la variable local Nf (los cambios se han destacado en el código con comentarios marcados con "+" y "*", estos muestran qué se ha "añadido" y "modificado", respectivamente).

      int decomp(const double &y[], const int extrapolate = 0) // *
      {
        ...
        N = ArraySize(y);
        int Nf = N;                            // + preserve actual number of input data points
        N += extrapolate;                      // + 
        arrayprepare();
        for(i = 0; i < N; i++)
          X[i] = i;
        Mean = 0;
        for(i = 0; i < Nf; i++)                // * was N
          Mean += (y[i] - Mean) / (i + 1.0);
        for(i = 0; i < N; i++)
        {
          a = y[MathMin(i, Nf - 1)] - Mean;    // * was y[i]
          Imf[i] = a;
          IMFResult[i] = a;
        }
        // The loop of decomposition
          ...
          extrema(...);
          ...
        for(i = 0; i < N; i++)
        {
          IMFResult[i + N * nIMF] = IMFResult[i];
          IMFResult[i] = y[MathMin(i, Nf - 1)] - Mean; // * was y[i]
        }
        
      }

La construcción de IMF en las barras intermedias comienza desde el último valor conocido de la serie temporal.

Estos son casi todos los cambios necesarios para realizar el pronóstico. El código completo obtenido se muestra en el archivo adjunto EMDloose.mqh. Pero, ¿por qué EMDloose.mqh, y no EMD.mqh?

La cuestión es que este método de pronóstico no es correcto del todo. Dado que hemos aumentado el tamaño N de todas las matrices del objeto, esto incluye las barras pronosticadas en la búsqueda de extremos realizada en el método extrema. Hablando con rigor, en el futuro no existe ningún extremo. Todos los extremos formados durante los cálculos son extremos derivados de la suma de la extrepolación de splines (sin la serie original, que no existe en el futuro). Como resultado, las funciones de splines comienzan a construirse una respecto a la otra, tratando de suavizar su superposición. En cierto sentido, esto resulta cómodo, porque el pronóstico logra el equilibrio automático: el proceso de oscilación permanece cerca de los valores de la serie temporal y no se precipita al infinito. Sin embargo, el valor de este pronóstico es mínimo, pues ya no caracteriza la serie temporal original. Al mismo tiempo, este método, sin lugar a dudas, tiene derecho a existir, y todo aquel que lo desee podrán utilizarlo, incluyendo en el proyecto precisamente EMDloose.mqh.

Para corregir el problema, introduciremos varias modificaciones más y obtendremos la variante de trabajo definitiva EMD.mqh. Para comparar los efectos que dan los dos modos de pronosticación, vamos a comprobar más abajo el funcionamiento del indicador tanto con EMD.mqh, como con EMDloose.mqh.

Bien, tendremos que conseguir que la funciones de IMF se construyan en el futuro sobre los splines del último punto real de la serie temporal. En este caso, la profundidad del pronóstico tendrá una limitación física (aplicada), dado que los splines cúbicos, sin reajustes, tienden al infinito. Esto no tiene una importancia crítica, ya que la profundidad del pronóstico se debe limitar a varias barras.

La esencia de los cambios reside en guardar la longitud de la serie temporal original en la variable del objeto, y no de forma local en el método decomp.

  class CEMD
  {
    private:
      int N;       // Input and output data size
      int Nf;      // +
      
    public:
        int decomp(const double &y[], const int extrapolate = 0)
        {
          ...
          N = ArraySize(y);
          Nf = N;                            // + preserve actual number of input data points in the object
          N += extrapolate;                  // +
          ...
        }
  };

Entonces, podremos usar la variable Nf dentro del método extrema, sustituyéndola en los lugares correspondientes por N aumentado. De esta manera, se tomarán para el cálculo solo los extremos reales procedentes de la serie temporal. La forma más sencilla de ver todas las correcciones es usando la comparación contextual de los archivos EMD.mqh y EMDloose.mqh.

Con esto, podemos dar el algoritmo de pronosticación prácticamente por finalizado. Solo queda pulir un pequeño detalle relacionado con la obtención de los resultados de la descomposición. De ello se encarga el método getIMF de la clase CEMD. Inicialmente, a este se transmitían 2 parámetros: la matriz receptora x, y el número de "armonía" IMF solicitada, nn.

  void CEMD::getIMF(double &x[], const int nn, const bool reverse = false) const
  {
    ...
    if(reverse) ArrayReverse(x); // +
  }

Aquí, hemos añadido el parámetro opcional reverse, con ayuda del cual podemos clasificar la matriz en orden inverso. Esto es necesario para trabajar con los búferes de indicador, para los cuales resulta cómoda una indexación como en la "serie temporal" (el elemento 0 es el último cronológicamente).

Con esto, damos por finalizada la ampliación de la clase CEMD en cuanto a la pronosticación, y podemos proceder directamente a la implementación del indicador basado en EMD.

Indicador EMD.mq5

Para responder a fines demostrativos, el indicador funcionará directamente con las cotizaciones, sin embargo, este enfoque no se puede considerar adecuado para el comercio real. La pronosticación de series de precio mediante la extrapolación presupone la presencia, como mínimo, de un filtro de noticias, para así excluir la influencia en el horizonte de pronosticación. Para los marcos temporales menores, probablemente sea preferible el flat nocturno. Además, podemos recomendar usar marcos temporales mayores, ya que sufren menos el ruido, o cestas equilibradas sintéticas formadas por varios instrumentos.

Vamos a definir los parámetros de entrada del indicador:

  input int Length = 300;  // Length (bars, > 5)
  input int Offset = 0;    // Offset (0..P bars)
  input int Forecast = 0;  // Forecast (0..N bars)
  input int Reconstruction = 0; // Reconstruction (0..M IMFs)

Los parámetros Offset y Length establecen el desplazamiento y el número de barras para la serie analizada. Para simplificar el análisis de los pronósticos en la historia, el parámetro Offset se ha reforzado en la interfaz con una línea vertical punteada que se puede arrastrar con el ratón por el gráfico, recalculando con ello el pronóstico de forma interactiva (tenga en cuenta que el cálculo puede requerir una cantidad de tiempo considerable, dependiendo de la longitud, la forma y la potencia del procesador).

El parámetro Forecast representa el número de barras pronosticadas. Para el algoritmo estricto EMD.mqh, se recomienda no tomar un valor superior a 5-10. Para el algoritmo simplificado EMDloose.mqh, se permiten valores superiores.

El parámetro Reconstruction determina el número de funciones IMF que debemos descartar durante la reconstrucción de la serie temporal, de manera que el resto forme un pronóstico. Si aquí indicamos 0, la reconstrucción coincidirá con la serie original, y el pronóstico no resultará posible (hablando con rigor, será igual a la constante, es decir al último valor de precio, y por eso no tendrá sentido). Si indicamos 1, la reconstrucción se suavizará gracias al descarte de las oscilaciones más pequeñas, y si indicamos 2, se descartarán las "armonías" superiores, etcétera. Si introducimos una cifra igual al número de funciones IMF encontradas, la reconstrucción coincidirá con el resto ("la tendencia"). En todos estos casos, la serie suavizada tiene un pronóstico (uno concreto para cada combinación con la cantidad de IMF). Si se establece una cantidad superior al número de IMF, la reconstrucción y el pronóstico no serán determinados. El valor recomendado para el valor es igual a 2.

Cuanto menor sea la magnitud Reconstruction, más móvil será la reconstrucción, y más cercana se mostrará esta respecto a la serie original (semejante a una МА de periodo menor); no obstante, el pronóstico será muy volátil. Cuanto mayor sea esta magnitud, más suave y estable serán la reconstrucción y el pronóstico (semejante a una МА de periodo mayor).

En el manejador OnInit, estableceremos el desplazamiento de los búferes de acuerdo con la profundidad del mercado.

  int OnInit()
  {
    IndicatorSetString(INDICATOR_SHORTNAME, "EMD (" + (string)Length + ")");
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetInteger(i, PLOT_SHIFT, Forecast);
    }
    return INIT_SUCCEEDED;
  }

El indicador se calcula según los precios de apertura en el modo por barras. Veamos los principales puntos a considerar del manejador OnCalculate.

Describimos las variables locales y establecemos la indiexación de Open y Time establecidos como "serie temporal".

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {

    int i, ret;
    
    ArraySetAsSeries(Time, true);
    ArraySetAsSeries(Open, true);

CReamos el modo por barras.

    static datetime lastBar = 0;
    static int barCount = 0;
    
    if(Time[0] == lastBar && barCount == rates_total && prev_calculated != 0) return rates_total;
    lastBar = Time[0];
    barCount = rates_total;

Esperamos a disponer de datos suficientes.

    if(rates_total < Length || ArraySize(Time) < Length) return prev_calculated;
    if(rates_total - 1 < Offset || ArraySize(Time) - 1 < Offset) return prev_calculated;

Inicializamos los búferes de indicador.

    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }

Distribuimos la matriz local "yy" para transmitir la serie original al objeto y después obtener los resultados.

    double yy[];
    int n = Length;
    ArrayResize(yy, n, n + Forecast);

Rellenamos la matriz con la serie temporal para el análisis.

    for(i = 0; i < n; i++)
    {
      yy[i] = Open[n - i + Offset - 1]; // we need to reverse for extrapolation
    }

Iniciamos el algoritmo EMD con la ayuda del objeto correspondiente.

    CEMD emd;
    ret = emd.decomp(yy, Forecast);
    
    if(ret < 0) return prev_calculated;

En caso de éxito, leemos los datos obtenidos, ante todo, el número de funciones IMF y la media.

    const int N = emd.getN();
    const double mean = emd.getMean();

Ampliamos la matriz "yy" en el número de barras futuras. En ella anotaremos los puntos de cada función.

    n += Forecast;
    ArrayResize(yy, n);

Configuramos la visualización: la serie original, la reconstrucción y el pronóstico se representan con líneas gruesas, mientras que las IMF aparte se representan con líneas finas. Dado que el número de IMF cambia dinámicamente (depende de la forma de la serie original), este ajuste no puede realizarse una sola vez en OnInit.

    for(i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_SHOW_DATA, i <= N + 1);
      PlotIndexSetInteger(i, PLOT_LINE_WIDTH, i == N + 1 ? 2 : 1);
      PlotIndexSetInteger(i, PLOT_LINE_STYLE, STYLE_SOLID);
    }

Representamos la serie temporal original en el último búfer (solo para controlar los datos transmitidos, dado que en la práctica, por ejemplo, en el código de los expertos, no la necesitamos).

    emd.getIMF(yy, 0, true);
    if(Forecast > 0)
    {
      for(i = 0; i < Forecast; i++) yy[i] = EMPTY_VALUE;
    }
    buffers[N + 1].set(Offset, yy);

Distribuimos la matriz sum para la reconstrucción (suma de IMF). Iteramos en un ciclo por todas las IMF que participan en la reconstrucción, y sumamos los cálculos en esta matriz. Mostramos al mismo tiempo cada IMF en su búfer.

    double sum[];
    ArrayResize(sum, n);
    ArrayInitialize(sum, 0);
  
    for(i = 1; i < N; i++)
    {
      emd.getIMF(yy, i, true);
      buffers[i].set(Offset, yy);
      if(i > Reconstruction)
      {
        for(int j = 0; j < n; j++)
        {
          sum[j] += yy[j];
        }
      }
    }

El penúltimo búfer adopta el resto y lo representa con una línea punteada.

    PlotIndexSetInteger(N, PLOT_LINE_STYLE, STYLE_DOT);
    emd.getIMF(yy, N, true);
    buffers[N].set(Offset, yy);

En la práctica, los búferes del primero al último contienen todas las "armonías" de la descomposición en orden ascendente (primero las pequeñas, después las grandes, incluyendo la "tendencia").

Finalmente, sumamos los componentes según los cálculos en la matriz sum, obteniendo la reconstrucción definitiva.

    for(int j = 0; j < n; j++)
    {
      sum[j] += yy[j];
      if(j < Forecast && (Reconstruction == 0 || Reconstruction > N - 1)) // completely fitted curve can not be forecasted (gives a constant)
      {
        sum[j] = EMPTY_VALUE;
      }
    }
    buffers[0].set(Offset, sum);
    
    return rates_total;
  }

Representamos la suma junto con el pronóstico en el búfer cero. El índice cero se ha seleccionado precisamente para simplificar la lectura desde los expertos. Normalmente, el número de IMF y búferes implicados cambia con la llegada de una nueva barra, y por eso, los otros índices de los búferes no son constantes.

En el artículo, hemos omitido algunos matices referentes a la formalización de las etiquetas y el trabajo interactivo con la línea de desplazamiento de la historia. El código fuente al completo se adjunta al final del artículo.

Solo hay un detalle que merezca la pena destacar: al cambiar el desplazamiento del parámetro Offset con la ayuda de la línea vertical, el indicador solicita actualizar el gráfico llamando a ChartSetSymbolPeriod. Esta función se ha implementado en MetaTrader 5 de tal forma que resetea la caché de todos los marcos temporales del símbolo actual y los reconfigura de nuevo. Dependiendo del ajuste seleccionado para el número de barras en los gráficos y la potencia de la computadora, este proceso puede ocupar un tiempo considerable (en algunos casos, decenas de segundos, si, por ejemplo, hay gráficos M1 con millones de barras). Por desgracia, MQL API no ofrece un método más económico para construir un indicador aparte. Debido a ello, al surgir el problema mencionado, se recomienda cambiar el desplazamiento a través de la ventana de diálogo de las propiedades del indicador o reducir el número de barras mostradas en los gráficos (deberemos reiniciar el terminal). La línea-cursor vertical ha sido añadida para el posicionamiento interactivo, cómodo y sencillo al supuesto inicio de la muestra de datos.

Vamos a comprobar cómo funciona el indicador en los modos estricto y simplificado con diferentes ajustes (recordemos que el modo simplificado se obtiene recompilando con el archivo EMDloose.mqh, dado que no se trata del principal modo de trabajo). Para el gráfico EURUSD D1, usaremos los siguientes ajustes:

• Length = 250;
• Offset = 0;
• Forecast = 10;
• Reconstruction = 2;

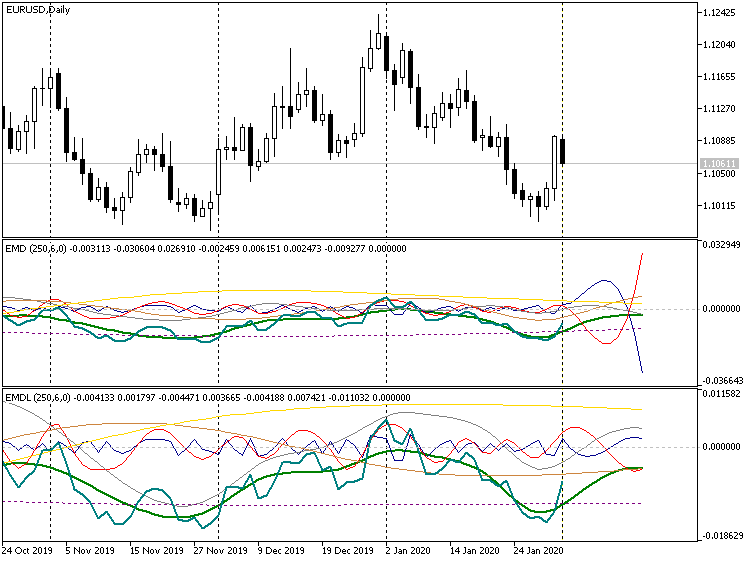
Pronóstico corto, indicadores EMD, EURUSD D1

En la captura de pantalla se muestran las dos versiones del indicador: la estricta, arriba, la simplificada, abajo. Notemos que en la versión estricta, algunas "armonías" tienden a "huir" en diferentes direcciones, hacia arriba y hacia abajo. Debido a ello, incluso la escala del primer indicador se ha hecho más pequeña que la del segundo (el cambio de escala constituye una advertencia visual de que la profundidad del pronóstico no es adecuada). En el modo simplificado, todos los componentes de la descomposición continúan oscilando junto al cero. Gracias a ello, podemos obtener un pronóstico más a largo plazo, poniendo en el parámetro Forecast, por ejemplo, el valor 100. Esto tiene buen aspecto, pero, normalmente, se encuentra bastante lejos de la realidad. El único uso de semejante predicción consistiría en la valoración del futuro intervalo de movimientos del precio, en el que podríamos intentar comerciar con el rebote en el interior y con la ruptura en el exterior.

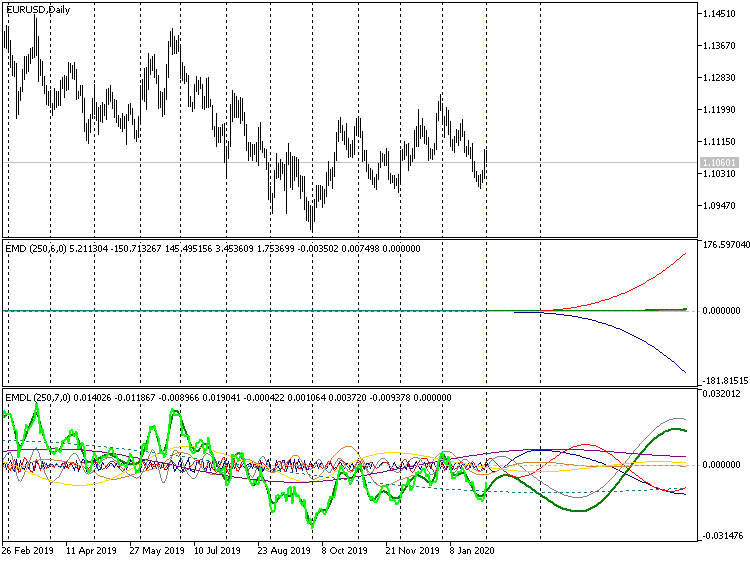
Pronóstico largo, indicadores EMD, EURUSD D1

En la variante estricta, esto provoca que veamos solo los extremos de los polinomios divergentes hacia el infinito, mientras que la parte sustancial del gráfico "colapsa" en la zona del cero.

En el encabezado de los indicadores, cuando el horizonte de pronóstico es ampliado, también se pueden ver las diferencias: si antes se encontraron en ambos casos 6 funciones propias (la segunda catidad se da entre paréntesis, tras el número de barras analizadas), ahora la variante simple usa 7, ya que, en su caso, las 100 barras de pronóstico solicitadas participan en los cálculos de los extremos. El pronóstico de 10 barras no ejerce esa influencia (para esta serie temporal). Podemos suponer que Forecast = 10 es la longitud máxima de pronóstico permitida, aunque no sea la recomendada. La longitud recomendada abarca 2-4 barras.

Para representar de forma visual la serie temporal original reconstruida y el pronóstico, resulta sencillo crear un indicador similar que represente el precio directamente en los gráficos: EMDPrice. Su construcción interna replica por completo el indicador EMD analizado, pero solo tiene un búfer (las IMF aparte participan en los cálculos, pero no se muestran, para no saturar el gráfico).

En EMDPrice se usa la forma breve del manejador OnCalculate, lo que permite seleccionar el tipo de precio para el cálculo, por el ejemplo, el típico. No obstante, al darse cualquier tipo de precio, salvo el de apertura, deberemos tener en cuenta que el indicador se calcula conforme a la apertura de las barras, y por eso, la última barra formada (con todos los tipos de precio) será la barra 1. En otras palabras, Offset puede ser igual a 0 solo para los precios de apertura, en el resto de los casos, será 1 o más.

En la captura de pantalla, mostramos el funcionamiento del indicador EMDPrice con un desplazamiento hacia el pasado de 15 barras.

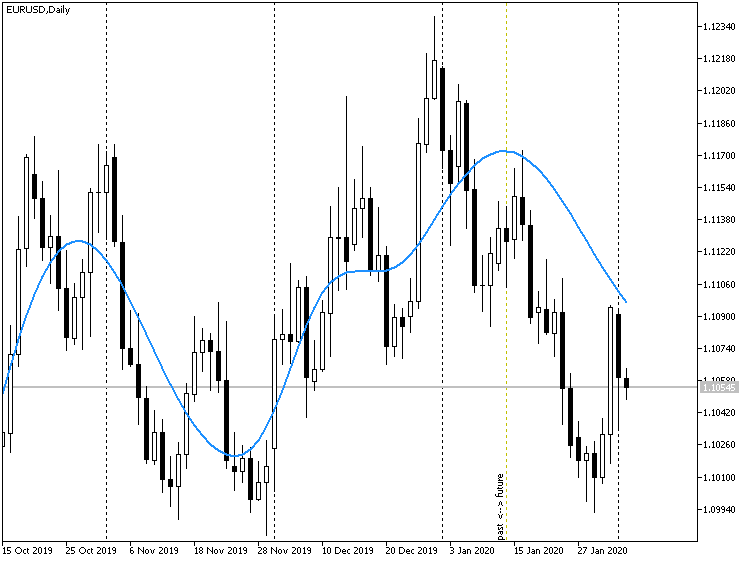
Pronóstico del indicador EMDPrice en el gráfico de precio EURUSD D1, con desplazamiento en la historia

Para comprobar las capacidades de pronosticación del indicador EMD, vamos a desarrollar un experto especial.

Experto de prueba basado en EMD

Vamos a crear el experto sencillo TestEMD, que creará un ejemplar del indicador EMD y, usando como base su pronóstico, realizará operaciones comerciales. El trabajo se realizará según la apertura de la barra, dado que el indicador usa para el pronóstico los precios de apertura.

Parámetros básicos del experto:

• Length — longitud de la serie temporal, se transmite al indicador;
• Forecast — número de barras del pronóstico, se transmite al indicador;
• Reconstruction - número de "armonías" menores descartadas al reconstruir el pronóstico, se transmite al indicador;
• SignalBar - número de la barra para la que se solicita el valor de pronóstico del precio desde el búfer de indicador;

Como señal comercial, tomaremos la diferencia entre la lectura del indicador en la barra SignalBar (para echar un vistazo en el futuro predicho, este parámetro se presupone negativo) y la brarra cero actual. Una diferencia positiva será la señal de compra, una diferencia negativa, la de venta.

Dado que el indicador EMD construye el pronóstico sobre el futuro, los números de las barras en SignalBar son normalmente negativos e iguales en cuanto al módulo al valor Forecast (en principio, también podemos tomar la señal de una barra menos alejada, no hay por qué calcular el pronóstico en un gran número de barras). Esto se refiere al método estándar de trabajo con la ejecución de operaciones comerciales. En este modo, al llamar el indicador EMD, su parámetro Offset siempre será igual a cero, dado que nosotros no investigamos los pronósticos basados en la historia.

No obstante, el experto también da soporte a otro modo especial no comercial, que permite optimizar rápidamente gracias al cálculo teórico de la rentabilidad de las transacciones virtuales en las últimas barras Forecast. El cálculo se ejecuta de forma consecutiva en cada nueva barra del intervalo de fechas elegido, y la estadística general en forma de factor de beneficio de la ejecución del pronóstico sobre el movimiento real del precio se retorna desde OnTester. En el simulador, deberemos elegir el criterio de usuario como objetivo de la optimización. Para activar este modo, deberemos introducir 0 en el parámetro SignalBar. En este caso, además, el propio experto pondrá automáticamente Offset como igual a Forecast. Precisamente esto permitirá al experto comprobar el pronóstico y el cambio del precio en las últimas barras Forecast.

Claro está que el experto también puede optimizarse en el modo estándar, junto con la ejecución de las operaciones comerciales y la selección de cualquier indicador de optimización incorporado. Esto es esepcialmente actual, debido a que el modo económico no comercial es aproximado (en concreto, no tiene en cuenta los spreads). Pero los máximos y los mínimos de ambas funciones de adecuación deberán coincidir de manera aproximada.

Debido a que el pronóstico puede realizarse en varias barras por adelantado, y que en este tiempo se abrirá una posición en la dirección existente, es posible la existencia simultánea de varias posiciones en direcciones opuestas. Por ejemplo, si Forecast es igual a 3, cada posición se mantiene en el mercado 3 barras, y en cada momento hay abiertas 3 posiciones, que además pueden ser de distintos tipos. Debido a ello, es necesario que la cuenta tenga cobertura.

El código completo del experto se adjunta al artículo, por lo que no lo describiremos con detalle aquí. La parte comercial se basa en la biblioteca MT4Orders, que simplifica la llamada de funciones comerciales. En el experto no existe el control de órdenes según el principio "propia-ajena" con la ayuda de números mágicos, así como el procesamiento estricto de errores, y los ajustes de los deslizamientos, stop loss y take profits. El lote fijo se indica en el parámetro de entrada Lot, el comercio se realiza con órdenes de mercado. Si el lector desea aplicar el EMD en expertos en funcionamiento, podrá completar este experto de prueba con las capacidades correspondientes según su criterio, o bien configurar el trabajo con el indicador EMD por analogía con sus propios expertos existentes.

Adjuntamos al artículo un ejemplo de ajustes para la optimización en forma de archivo TestEMD.set. La optimización de EURUSD D1 en 2018 en el modo acelerado da el siguiente "set" óptimo:

• Length=110
• Forecast=4
• Reconstruction=2

Por consiguiente, SignalBar debe ser igual a Forecast con el signo menos, es decir, -4.

Un test único con estos ajustes en el periodo desde inicios de 2018 hasta febrero de 2020, es decir, en tiempo real para el 2019 e inicios de 2020, da los resultados siguientes:

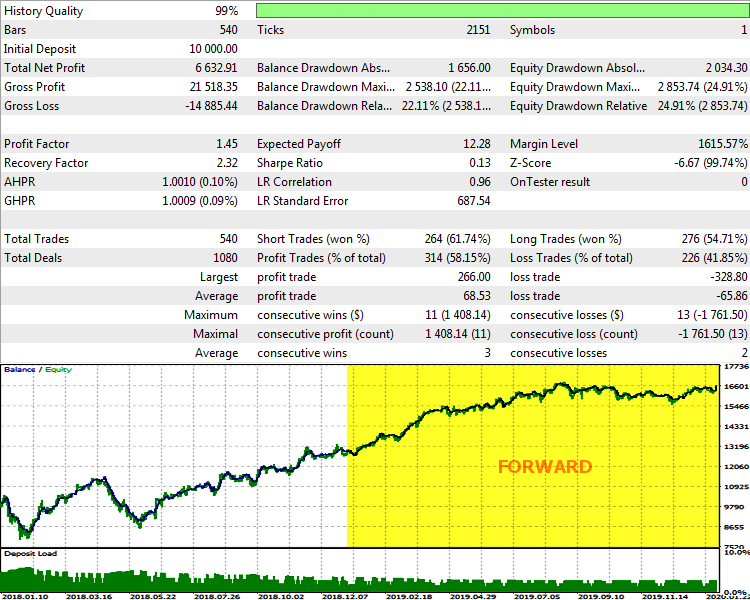
Informe del experto TestEMD para EURUSD D1, 2018-2020

Como podemos ver, el sistema permanece en positivo, aunque los indicadores dejan margen para buscar mejoras. En concreto, resulta lógico presuponer que una reoptimización más frecuente en el modo paso a paso y una selección del tamaño del salto sean capaces de mejorar el funcionamiento del robot.

En general, podemos constatar que el algoritmo de EMD permite detectar en los marcos temporales mayores las oscilaciones primarias (generadoras de inercia, en cierto sentido), y también crear sobre su base un sistema comercial rentable.

El EMD no es la única tecnología que vamos a analizar en el marco del presente artículo. Pero, antes de pasar a la segunda parte, necesitaremos "refrescar" cierto aparato matemático para la investigación de las series temporales.

Analizando las principales características de las series temporales en MQL : el indicador TSA

En el sitio web mql5.com ya se ha publicado un artículo con un nombre semejante: Análisis de las Características Principales de las Series Cronológicas. En dicho artículo se analiza el cálculo de magnitudes tales como la media, la mediana, la dispersión, los coeficientes de asimetría, la curtosis, el histograma de distribución, las funciones de autocorrelación, la autocorrelación parcial y mucho más. Todo ello se combina en la clase TSAnalysis, en el archivo TSAnalysis.mqh, que luego se usa con fines demostrativos en el script TSAexample.mq5. Por desgracia, para visualizar el funcionamiento de la clase, se ha usado un enfoque en el que se genera un archivo HTML externo, que se debe analizar en el navegador. Además, MetaTrader 5 ofrece diferentes recursos gráficos para representar las matrices de datos: en primer lugar, los búferes de indicador. Hemos modificado la clase ligeramente, haciéndola más "amistosa" para respecto a los indicadores. Después, hemos implementado un indicador que permite analizar las cotizaciones directamente en el termninal.

Llamaremos al nuevo archivo con la clase TSAnalysisMod.mqh. El principio básico de trabajo sigue siendo el mismo: con la ayuda del método Calc, transmitimos al objeto la serie temporal para la que hemos calculado el conjunto completo de lecturas durante el procesamiento. Todas ellas se dividen en 2 tipos: escalares y matrices. El código que realiza la llamada puede leer después cualquiera de las características.

Las características escalares se pueden reunir en la estructura única TSStatMeasures:

  struct TSStatMeasures
  {
    double MinTS;      // Minimum time series value
    double MaxTS;      // Maximum time series value
    double Median;     // Median
    double Mean;       // Mean (average)
    double Var;        // Variance
    double uVar;       // Unbiased variance
    double StDev;      // Standard deviation
    double uStDev;     // Unbiaced standard deviation
    double Skew;       // Skewness
    double Kurt;       // Kurtosis
    double ExKurt;     // Excess Kurtosis
    double JBTest;     // Jarque-Bera test
    double JBpVal;     // JB test p-value
    double AJBTest;    // Adjusted Jarque-Bera test
    double AJBpVal;    // AJB test p-values
    double maxOut;     // Sequence Plot. Border of outliers
    double minOut;     // Sequence Plot. Border of outliers
    double UPLim;      // ACF. Upper limit (5% significance level)
    double LOLim;      // ACF. Lower limit (5% significance level)
    int NLags;         // Number of lags for ACF and PACF Plot
    int IP;            // Autoregressive model order
  };

Marcaremos las matrices con puntos de la enumeración TSA_TYPE:

  enum TSA_TYPE
  {
    tsa_TimeSeries,
    tsa_TimeSeriesSorted,
    tsa_TimeSeriesCentered,
    tsa_HistogramX,
    tsa_HistogramY,
    tsa_NormalProbabilityX,
    tsa_ACF,
    tsa_ACFConfidenceBandUpper,
    tsa_ACFConfidenceBandLower,
    tsa_ACFSpectrumY,
    tsa_PACF,
    tsa_ARSpectrumY,
    tsa_Size //  
  };        //  ^ non-breaking space (to hide aux element tsa_Size name)

Para obtener la estructura TSStatMeasures rellena con los resultados del funcionamiento, se ha pensado el método getStatMeasures. Para obtener cualquiera de las matrices con la ayuda de una macro se han generado métodos uniformes del tipo getARRAYNAME, donde ARRAYNAME se corresponde con el sufijo de uno de los elementos de la enumeración TSA_TYPE. Por ejemplo, para leer una serie temporal clasificada, deberemos llamar al método getTimeSeriesSorted. Todos estos métodos tienen la signatura:

  int getARRAYNAME(double &result[]) const;

rellenan la matriz transmitida y retornan el número de elementos.

Además, dispone de un método universal para leer cualquier matriz:

  int getResult(const TSA_TYPE type, double &result[]) const

El método virtual show de la clase original ha sido completamente eliminado, ya que resultaba innecesario. Todas las tareas de la interfaz se han asignado al código que realiza la llamada.

El procesamiento con la ayuda de la clase TSAnalysis se realiza cómodamente desde el indicador especial TSA.mq5. Su objetivo principal es visualizar las características que suponen matrices. Si el lector lo desea, podrá complementarla con la capacidad de mostrar magnitudes escalares (en estos momentos, se imprimen en el log).

Dado que algunas matrices están lógicamente relacionadas entre sí como trío (por ejemplo, la función de autocorrelación tiene unos límites inferior y superior del intervalo de confianza del 95%), en el indicador se han reservado 3 búferes. Los estilos de representación de los búferes se ajustan dependiendo del sentido de los datos solicitados.

Parámetros de entrada del indicador:

• Type — tipo de matriz solicitada, elemento de la enumeración TSA_TYPE;
• Length — longitud en barras de la serie temporal analizada;
• Offset — desplazamiento inicial de la serie temporal, 0 - comienzo;
• Differencing — modo de diferenciación, determina si es necesario leer las cotizaciones como son o tomar la diferencia de primer orden;
• Smoothing — periodo de promediación;
• Method — método de promediación;
• Price — tipo de precio, por defecto, el precio de apertura;

El indicador se calcula según las barras.

Aquí vemos, por ejemplo, el aspecto que tiene la función de autocorrelación para EURUSD D1 en 500 barras, con diferenciación:

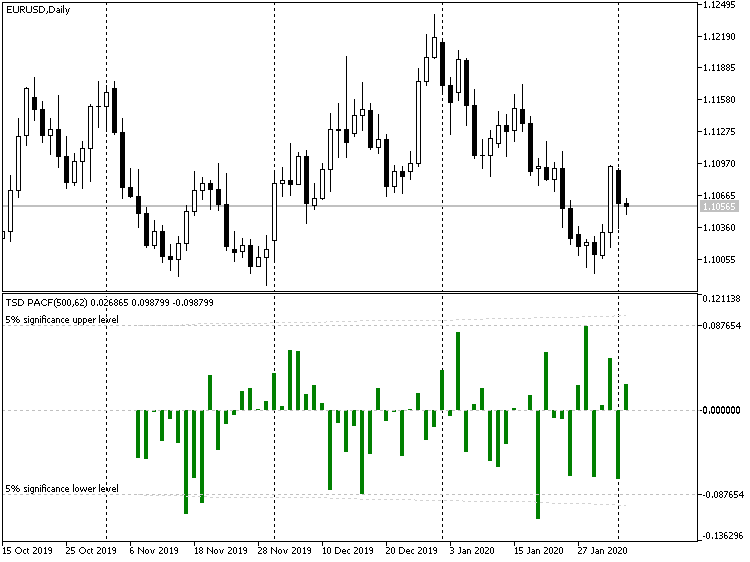
Indicador TSD, EURUSD D1

La toma de diferencias de primer orden permite aumentar la estacionariedad (y la predictibilidad) de la serie. En principio, la diferencia de segundo orden será todavía más estacionaria, y la de tercero, aún más, y así sucesivamente. Sin embargo, esto tiene sus desventajas, de las cuales hablaremos más tarde (en el segundo artículo).

La función de autocorrelación parcial no se ha elegido aquí por casualidad. La necesitaremos en la siguiente etapa, cuando pasemos al otro método de pronosticación. No obstante, dado que tenemos que estudiar un material considerable, hemos sacado este capítulo preparatorio a este artículo. Además, el análisis estadístico de las series temporales tiene un valor universal, y puede resultar útil en otros desarrollos personalizados de MQL.

Conclusión

En el presente artículo, hemos analizado las peculiaridades del algoritmo de descomposición modal empírica, que ofrece la posibilidad de ampliar su aplicabilidad a la esfera de la pronosticación a corto plazo de series temporales. Las clases implementadas en MQL, el indicador y el experto permiten usar la pronosticación EMD como factor adicional en la toma de decisiones comerciales, así como dentro de los sistemas comerciales automáticos. Además, hemos actualizado el instrumental de análisis estadístico de las series temporales, del cual nos valdremos en el siguiente artículo a la hora de analizar la pronosticación con el método LS-SVM.