El criterio de homogeneidad de Smirnov como indicador de la no estacionariedad de las series temporales

Introducción

Al empezar a analizar series temporales financieras, el investigador siempre se enfrenta al problema de la no estacionariedad de los datos, pues las series temporales de precios de divisas, acciones y futuros no son estacionarias. Para llevar estas series a una forma estacionaria, solemos usar las primeras diferencias de los logaritmos de los precios Ln(Xn/Xn-1) y seguimos trabajando con los datos modificados sobre esta base.

Pero surge la pregunta: podemos considerar como estacionaria una serie temporal modificada de este tipo? En este artículo intentaremos responder a esa pregunta, pero antes, vamos a recordar qué es la estacionariedad. Sin definiciones formales, la estacionariedad puede describirse como la constancia de las propiedades estadísticas de una serie temporal a lo largo del tiempo, tales como la esperanza matemática y la varianza. Si, además de estas propiedades, se supone que la función de distribución es constante en el tiempo, el proceso se denominará estacionario en sentido estricto.

En este artículo, comprobaremos la estacionariedad de las series temporales financieras precisamente en sentido estricto, utilizando funciones de distribución empíricas. La teoría de la probabilidad y la estadística matemática, como sección específica de la misma, se basan en supuestos de estacionariedad. Existen diversos métodos para analizar los procesos estacionarios, como el análisis de regresión, el análisis de autocorrelación, las técnicas de análisis espectral y el uso de redes neuronales. No obstante, la aplicación de estos métodos a datos no estacionarios puede dar lugar a errores significativos en las predicciones.

Para los tráders, la cuestión de la estacionariedad está estrechamente relacionada con la elección de la cantidad de datos para calcular diversos indicadores. En el caso de los procesos estacionarios, cuantos más datos estén disponibles, con mayor precisión podrán calcularse todas las características estadísticas. Sin embargo, resulta difícil determinar la cantidad óptima de datos cuando se analizan procesos no estacionarios. Un volumen demasiado grande puede contener información obsoleta que ya no influya en la situación actual; si se toman pocos datos, no podremos evaluar adecuadamente las propiedades estadísticas del proceso debido a que la representatividad será insuficiente.

La caracterización más completa de un proceso aleatorio será su ley de distribución (función de probabilidad). Por consiguiente, la construcción de un indicador que permita monitorear el cambio de la función de distribución de una serie temporal a lo largo del tiempo será una tarea importante. Este indicador, a su vez, servirá de señal que indicará la necesidad de revisar el volumen de datos para calcular los indicadores estándar del análisis técnico. En estadística matemática, la tarea de comprobar "si la función de distribución de alguna variable aleatoria ha cambiado con el tiempo" se denomina "prueba de la hipótesis de homogeneidad".

Hipótesis de homogeneidad

La homogeneidad de los datos de la muestra se comprueba usando criterios de homogeneidad. En la actualidad, se ha desarrollado un gran número de criterios de este tipo, entre los que podemos distinguir:

• El criterio de homogeneidad de Smirnov,

• El criterio de homogeneidad de Anderson,

• La prueba de homogeneidad chi-cuadrado de Pearson.

La hipótesis de homogeneidad no es más que la suposición de que las dos muestras de datos (x1,x2,x3,...xn) y (y1,y2,y3,...ym) obtenidas sobre las variables aleatorias X e Y obedecen a la misma ley de distribución o, lo que es lo mismo, las dos muestras proceden de la misma población general. Formalmente, esta hipótesis puede escribirse como H0 : F(x) = G(y). La hipótesis alternativa es que las dos muestras pertenecen a poblaciones generales distintas, pero no se especifica cuál, H1 : F(x) ≠ G(y).

• Fn(x) y Gm(y) - función de distribución empírica (muestral) de las variables aleatorias X e Y, respectivamente

• n, m – cantidad de datos para el cálculo

Criterio de homogeneidad de Smirnov

El criterio de homogeneidad de Smirnov, también conocido como criterio de Kolmogórov-Smirnov para dos muestras, es una prueba estadística que se utiliza para comprobar la hipótesis de que dos muestras proceden de la misma distribución continua. Este criterio se basa en la comparación de las funciones de distribución empíricas de dos muestras independientes.

El criterio de homogeneidad de Smirnov se usa ampliamente en el análisis estadístico para probar hipótesis sobre la igualdad de las distribuciones, lo cual puede ser útil en diversos campos como la bioestadística, la econometría y otros estudios en los que es necesario comparar dos muestras diferentes en función de sus propiedades estadísticas. Esto resulta especialmente cierto cuando los datos disponibles resultan insuficientes para utilizar métodos paramétricos más sofisticados.

Entonces se plantea la cuestión de qué tomar como medida de la divergencia entre dos funciones de distribución empíricas. Smirnov ofreció las siguientes estadísticas:

Dn,m = sup | Fn(x) - Gm(y) |

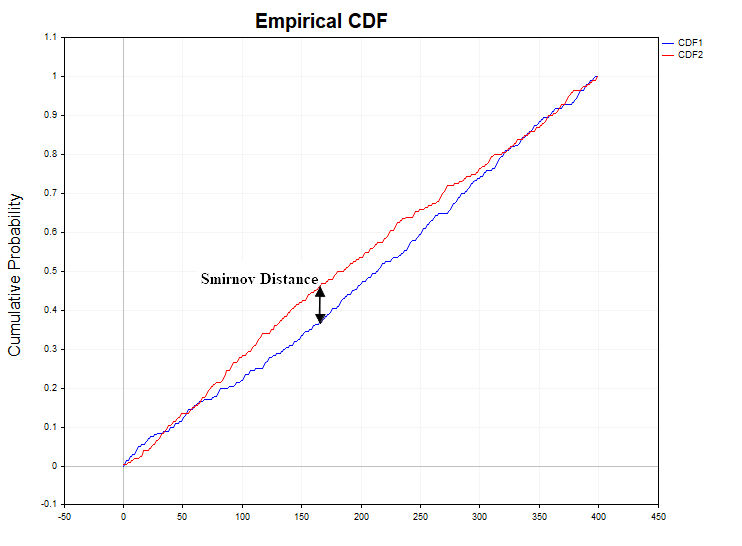
Este estadístico representa el límite superior exacto (máximo) del valor absoluto de la diferencia entre las funciones de distribución. Si la ley de distribución de una variable aleatoria no cambia de una muestra a otra, será natural esperar valores bajos de la estadísticaDn,m. A su vez, unos valores demasiado grandes de esta estadística constituirían una prueba en contra de la hipótesis nula de homogeneidad de los datos. En la práctica, para comprobar las hipótesis estadísticas, se calcula una estadística ligeramente modificada en lugar de la estadística D

lambda = D * ( sqrt(k) + 0,12 + 0,11/sqrt(k) ),

donde k = (m*n/(m+n)). La distribución de la estadística lambda en k → ∞ converge a su vez a la función de distribución de Kolmogórov:                                                  

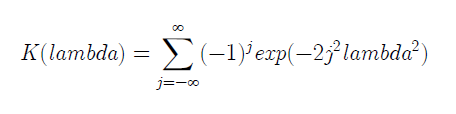
A veces se usa una fórmula más simplificada para calcular lambda: cuando n es igual a m:

lambda = D *sqrt(n/2)

A continuación, obteniendo determinados valores estadísticos, se comprueba la hipótesis de homogeneidad usando los datos de la muestra.

La hipótesis estadística se comprueba según el siguiente esquema:

• se formulan la hipótesis nula H0 (las muestras son homogéneas) y la hipótesis alternativa H1 (las muestras son heterogéneas),

• se toma el nivel de significación alpha (suelen usarse valores estándar de 0,1, 0,05, 0,01),

• el valor crítico de u(alpha) se calcula utilizando la distribución de Kolmogórov (por ejemplo, cuando el nivel de significación de alpha es 0,05, u(alpha) es 1,3581),

• se calcula el valor muestral de la estadística lambda,

• si lambda < u(alpha), se aceptará la hipótesis nula,

• si lambda > u(alpha), se rechazará la hipótesis nula al nivel de significación alpha por contradecir los datos observados.

También es posible otro final lógico para este esquema. En lugar del valor crítico u(alpha), se calcula la probabilidad PValue = 1 - K(lambda), que a su vez se compara con un nivel de significación alpha establecido. Si el nivel de significación alpha ≥ PValue entonces se rechazará la hipótesis nula, ya que se considerará que se ha producido un suceso improbable incompatible con el concepto de aleatoriedad y, por tanto, las muestras deberán reconocerse como diferentes.

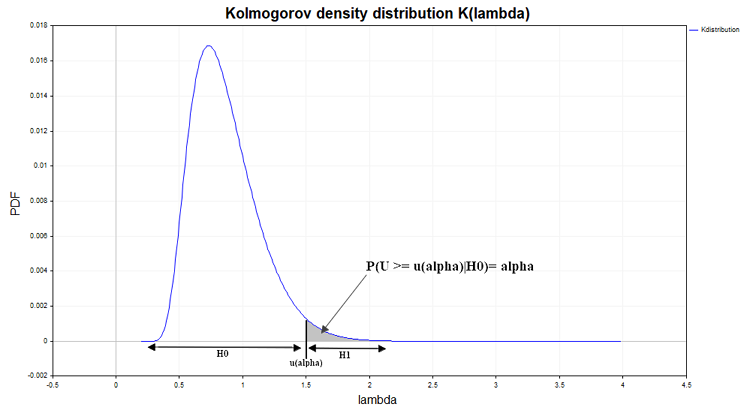
Aquí, la figura muestra la derivada de la función de distribución de Kolmogórov, es decir, la función de densidad de la probabilidad calculada bajo el supuesto de que la hipótesis nula es cierta. Si la función de densidad de probabilidad de la distancia de Smirnov calculada para los datos de la muestra se distingue de la función de Kolmogórov, esto podría indicar la heterogeneidad en los datos.

El criterio de homogeneidad de Smirnov no debe confundirse con el criterio de concordancia de Kolmogórov. En el criterio de homogeneidad de Smirnov (en inglés Two-sample Kolmogorov-Smirnov test) se comparan dos funciones de distribución empíricas, mientras que en el criterio de concordancia de Kolmogórov (One-sample Kolmogórov-Smirnov test) se comparan las funciones de distribución empíricas e hipotéticas.

Un punto muy importante es que las funciones de distribución empíricas deben calcularse necesariamente partiendo de datos de observación no agrupados, ya que la función de distribución de Kolmogórov se calcula bajo este supuesto.  También es importante destacar que el criterio de Smirnov no depende de un tipo concreto de función de distribución, y como al analizar series temporales financieras resulta difícil concluir si los datos observados pertenecen a uno u otro tipo de distribución hipotética, el valor de este criterio para el analista aumentará considerablemente. Sin realizar ninguna suposición sobre el tipo de distribución hipotética a la que pueden pertenecer los datos observados, podemos probar la hipótesis de homogeneidad basándonos únicamente en las funciones de distribución empíricas.  Para el análisis de series temporales, el criterio de Smirnov puede considerarse un indicador de la estacionariedad del proceso. Al fin y al cabo, según la definición de estacionariedad, un proceso se considera estacionario cuando su función de distribución de probabilidad no cambia en el tiempo.

Explicación sencilla de la metodología de cálculo

Vamos a imaginar que tenemos dos bolsas grandes de canicas de mármol. En una bolsa las canicas se fabrican en un país y en la otra en otro. Nuestra tarea consiste en averiguar si las canicas de ambas bolsas son iguales o diferentes.

1. Clasificación de canicas. Primero verteremos las canicas de ambas bolsas y las alinearemos por tamaños para cada una, de menor a mayor.

2. Comparación de canicas. Entonces empezaremos a mirar cada canica de la primera bolsa y buscamos una canica del mismo tamaño en la segunda bolsa. Luego mediremos la distancia entre canicas similares en dos filas. En este contexto, entenderemos por "distancia" la distancia entre las canicas de las filas cuando se observan sus posiciones.
   
   Supongamos que tenemos una canica de la primera bolsa que ocupa la quinta posición de la fila. Si una canica de tamaño similar de la segunda bolsa está en la vigésima posición de su fila, la distancia entre las dos canicas será de 15 posiciones (20 - 5 = 15). Este número muestra la distancia entre canicas similares en dos bolsas distintas (o en dos muestras de datos).
   
   En la prueba estadística de Kolmogórov-Smirnov, comparamos esas "distancias" para todas las canicas y buscamos el máximo de ellas. Si esta distancia máxima es superior a un valor determinado (que dependerá del número de canicas de las bolsas), esto puede indicar que las canicas de las bolsas difieren en algunas propiedades.
   

3. Buscando la mayor diferencia. Buscamos el lugar donde las diferencias ("distancias") entre las canicas de las dos filas son mayores. Por ejemplo, si las canicas tienen un tamaño muy semejante en un lugar y muy diferente en otro, marcaremos ese lugar.

4. Evaluando las diferencias. Si la mayor distancia entre las canicas es muy grande, esto puede significar que las canicas de las bolsas son realmente diferentes. Si todas las canicas están bastante juntas a lo largo de la fila, es posible que procedan del mismo lugar.

Así, si las diferencias entre dos filas de canicas son grandes, diremos que las bolsas de canicas son diferentes. Si las diferencias son pequeñas, es probable que las canicas sean las mismas. Esto nos ayudará a comprender si las canicas de dos lugares diferentes pueden considerarse iguales o no.

Análisis de datos usando el criterio de homogeneidad de Smirnov

Antes de proceder al análisis de las distancias D de Smirnov calculadas sobre cotizaciones reales, en primer lugar estudiaremos cómo se comporta esta estadística sobre modelos de procesos estacionarios con incrementos tanto dependientes como independientes. Para ello, generaremos 1 000 muestras (Samples) de series temporales con una función de distribución dada de 1 440 datos en cada fila. A continuación, calcularemos la distancia D de Smirnov entre estas muestras, comprobaremos el porcentaje de casos en los que se rechaza la hipótesis nula (H1/muestras) y construiremos una función de densidad de probabilidad empírica de estas distancias para compararlas con la función de densidad de Kolmogórov. La siguiente imagen muestra la serie de distancias de Smirnov sobre una muestra de N = 1440 datos obtenidos a partir de las distribuciones normal y uniforme.       

                               
                               

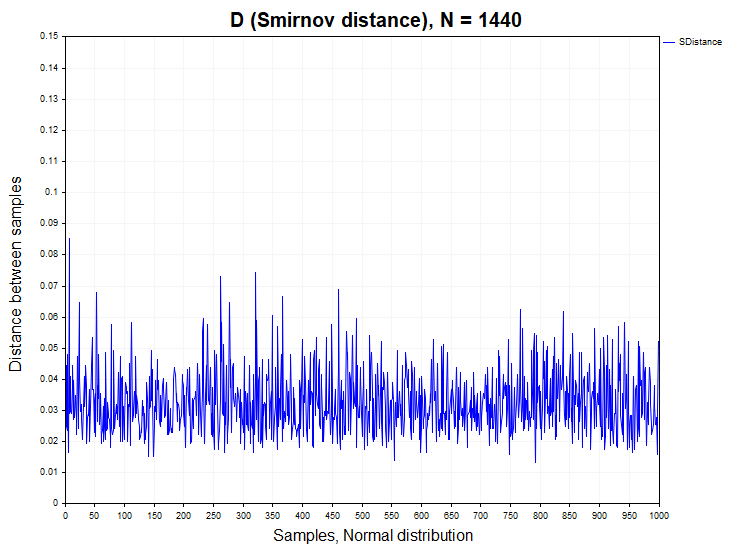
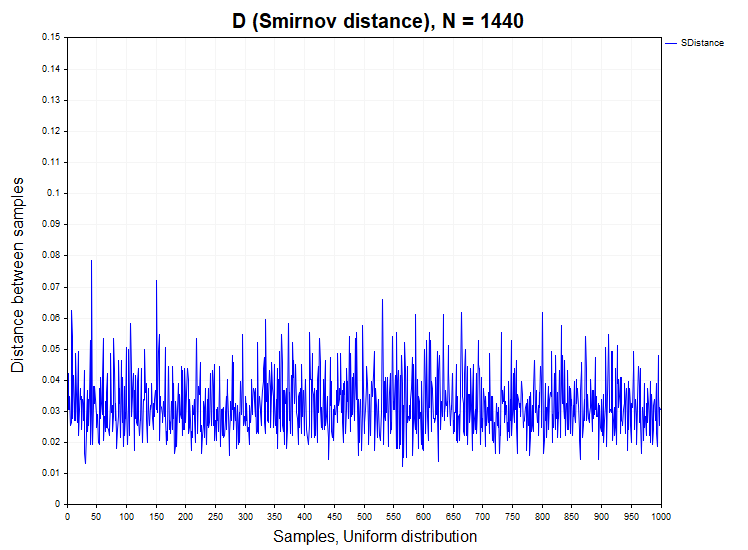
Para las muestras de distribución normal y uniforme, el falso rechazo de la hipótesis de homogeneidad se produce dentro del error aceptable del primer tipo (alpha= 0,05), es decir, en no más de 50 casos de cada 1 000 muestras. H1/ Samples = 50/1000 = 0.05. Más abajo mostramos los gráficos de densidad de probabilidad de muestra de las distancias de Smirnov para las distribuciones normal y uniforme.

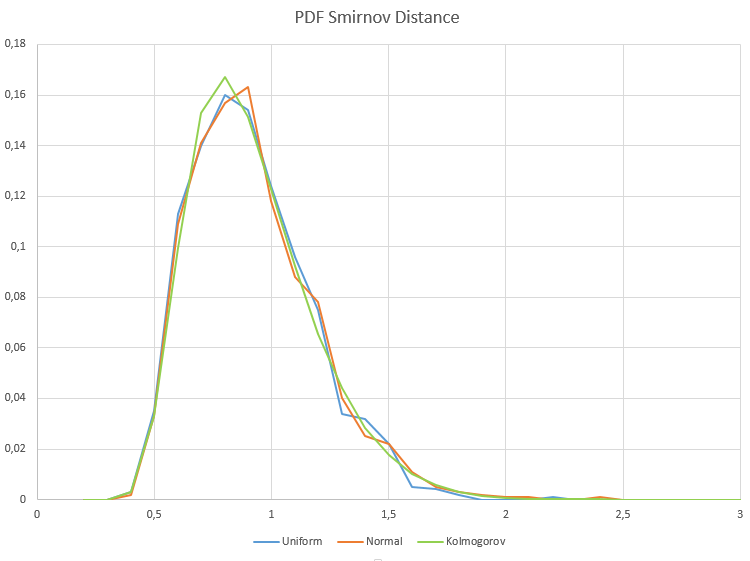
El eje X muestra el valor lambda

Como vemos, existe una coincidencia total de las distribuciones muestrales de la distancia de Smirnov para muestras de datos uniformes y normales y la distribución de Kolmogórov, a la que deberían converger si la hipótesis nula de homogeneidad es cierta.

Las distribuciones normal y uniforme que acabamos de ver son ejemplos de procesos estacionarios independientes. Como proceso estacionario pero dependiente, tomaremos una ecuación no lineal discreta que a menudo sirve de ejemplo en el campo del caos determinista: el mapa logístico:

Xn= R*Xn-1 *(1 – Xn-1), X0 = (0;1), R = 4

Es un sistema dinámico no lineal unidimensional que, cuando el parámetro R=4, muestra un comportamiento caótico casi indistinguible del ruido blanco. La función de autocorrelación de la serie temporal generada por esta ecuación oscilará en torno a cero. Sin embargo, este proceso contiene una dependencia no lineal y sería interesante comprobar cómo se refleja en la distribución de las distancias de Smirnov. La pregunta no es banal, ya que muchos creen que existen relaciones no lineales en los datos financieros, por lo que hemos incluido esta ecuación en el análisis.

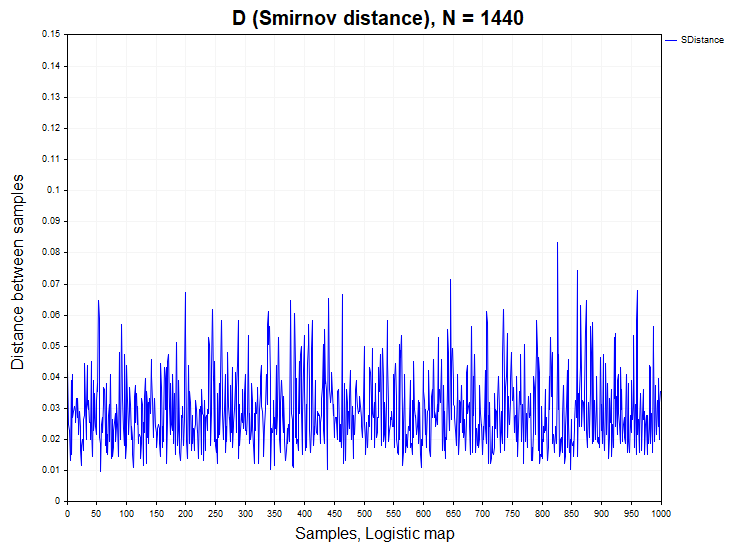
Ni que decir tiene que el análisis requiere un modelo con relaciones lineales, que también pueden estar presentes en los datos reales. Por consiguiente, un modelo autorregresivo lineal de primer orden actuará como segundo modelo del proceso dependiente estacionario:

ARt = 0.5 * ARt-1 + et

• et – variable aleatoria con media cero y varianza unitaria, ruido blanco gaussiano

El proceso autorregresivo en este caso también será un proceso gaussiano, pero ya dependiente.

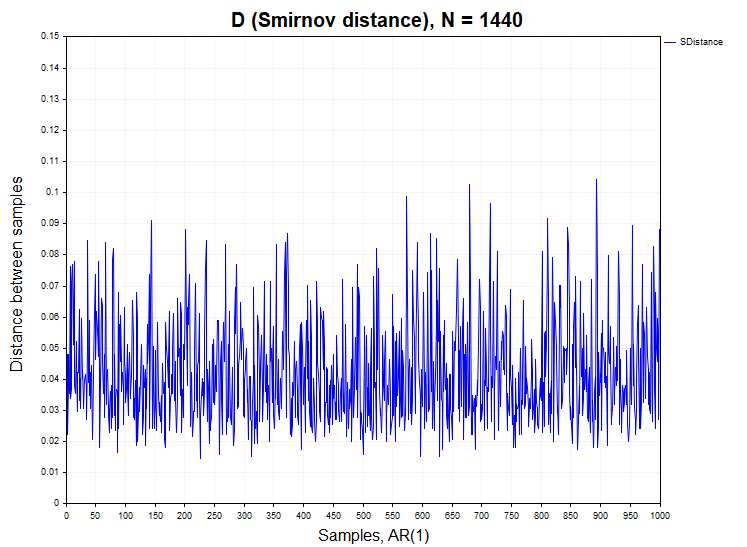
En los procesos con incrementos dependientes, la situación con el rechazo de la hipótesis de homogeneidad será un poco diferente. Para el mapa logístico aquí observamos un exceso insignificante del valor aceptable del error de primer orden de 0,058 (H1/ Samples= 58/1000), mientras que para la autorregresión de primer orden este error es ya de aproximadamente 0,25 (H1/ Samples= 250/1000), es decir, cinco veces el nivel aceptable bajo el supuesto de la hipótesis nula.

Hemos obtenido un resultado muy interesante. Resulta que, según el criterio de Smirnov, debemos reconocer tanto el mapa logístico como el AR(1) como procesos no homogéneos (es decir, no estacionarios), aunque ciertamente no sea el caso. ¿Cuál es el problema? Resulta que la función de densidad de probabilidad de las distancias de Smirnov para distribuciones estacionarias no depende del tipo de distribución del proceso estudiado solo si los datos observados son estadísticamente independientes. Y puesto que tanto el mapa logístico como la autorregresión son procesos con incrementos dependientes, en este caso la función de densidad de probabilidad de la distancia de Smirnov será distinta de la distribución de Kolmogórov. Esto a su vez significa que el criterio de Smirnov puede ser no solo un indicador de heterogeneidad (no estacionariedad del proceso) sino también un indicador de la presencia de dependencia en los datos (lineal o no lineal).

Vamos a analizar los datos reales. Como ejemplo, tomaremos las barras de minutos del par de divisas EURUSD y oro XAUUSD.

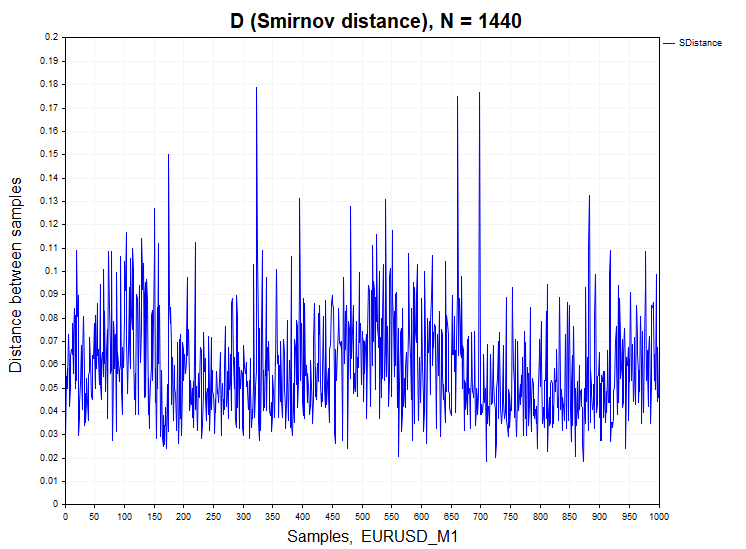
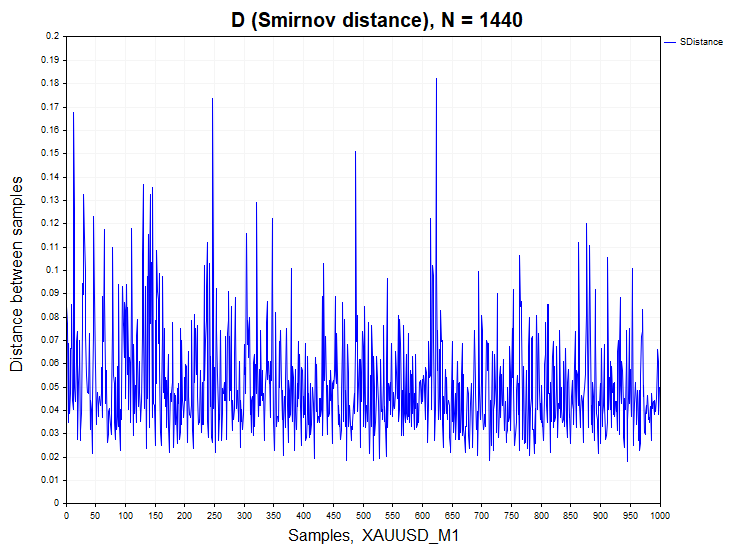
Para las cotizaciones por minutos, el porcentaje de rechazo de la hipótesis nula diferirá significativamente de los procesos estacionarios H1/ Samples = 466/1000 = 0.46 para XAUUSD y H1/ Samples= 640/1000 = 0.64 para el par de divisas EURUSD. Para mayor claridad, a continuación le mostramos un gráfico de la función de densidad de probabilidad de la distancia de Smirnov muestreada para los datos reales y los procesos dependientes de autorregresión y mapa logístico.

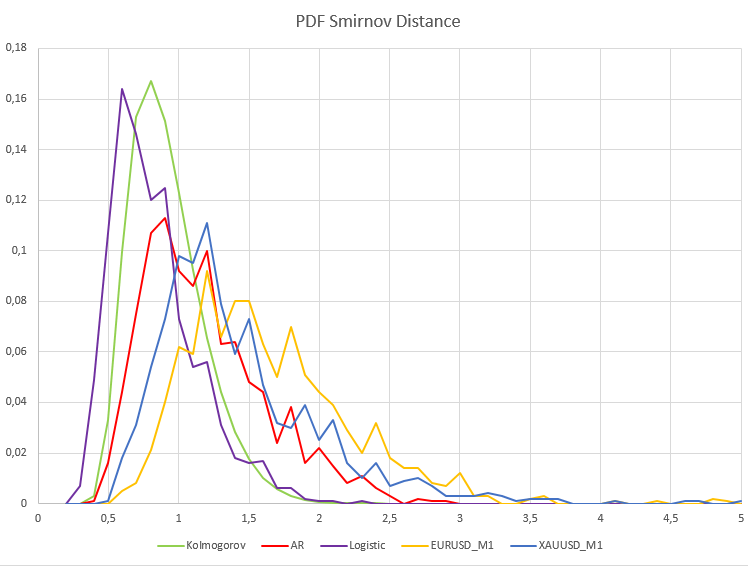
Como podemos ver, aquí se observa una imagen cualitativamente distinta, tanto para los procesos dependientes estacionarios como para las cotizaciones reales de EURUSD_M1 y XAUUSD_M1. Las densidades de probabilidad muestreadas de las distancias de Smirnov para estos procesos se distinguen notablemente de la distribución de Kolmogórov. En este caso, los procesos de mapa logístico y autorregresión de primer orden no convergen a la distribución de Kolmogórov solo por la presencia de dependencia estadística en estos datos.

En cuanto a los precios de los instrumentos financieros, incluso después de intentar hacerlos estacionarios usando las primeras diferencias, no son estacionarios. Es probable que cierta influencia en una cifra tan grande de rechazo de hipótesis nulas la ejerzan algunas dependencias que pueden estar presentes en las cotizaciones reales, como ya hemos visto en el análisis de los procesos dependientes estacionarios. En mi opinión, no es posible evaluar qué parte de la influencia se debe a dependencias en los datos y qué parte se debe simplemente al componente no estacionario presente en las series temporales de los instrumentos financieros. Sin embargo, el principal impacto se debe a la heterogeneidad de los datos, al cambio constante de la función de distribución de probabilidad de los incrementos de precios.

Para tener una idea clara del tipo de forma que puede tener la función de densidad de probabilidad de la distancia de Smirnov para dos muestras heterogéneas, realizaremos otro experimento en el que compararemos datos de muestras de dos distribuciones normales, pero pertenecientes a poblaciones generales diferentes. Estas distribuciones diferirán en los parámetros de esperanza matemática y varianza - N(0,1) frente a N(0,1,1,2). Obviamente, el criterio de Smirnov debería rechazar básicamente la hipótesis nula de homogeneidad. El error en este caso sería aceptar la hipótesis nula, mientras que la hipótesis alternativa resulta verdadera. 

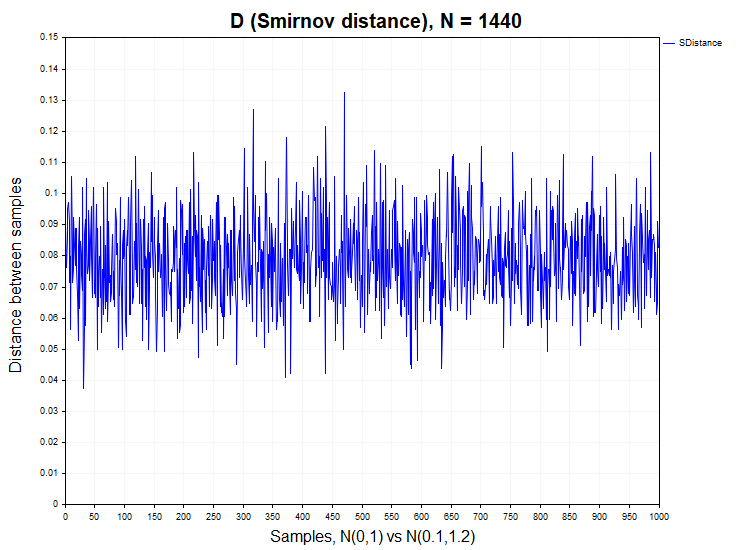
En este caso, tenemos un porcentaje de rechazo de la hipótesis nula igual a 0,98 (H1/ Samples = 980/1000). El siguiente gráfico muestra las funciones de densidad de probabilidad de la distribución de distancias de Smirnov para cotizaciones reales, el modelo de dos distribuciones normales heterogéneas y la distribución de Kolmogórov.

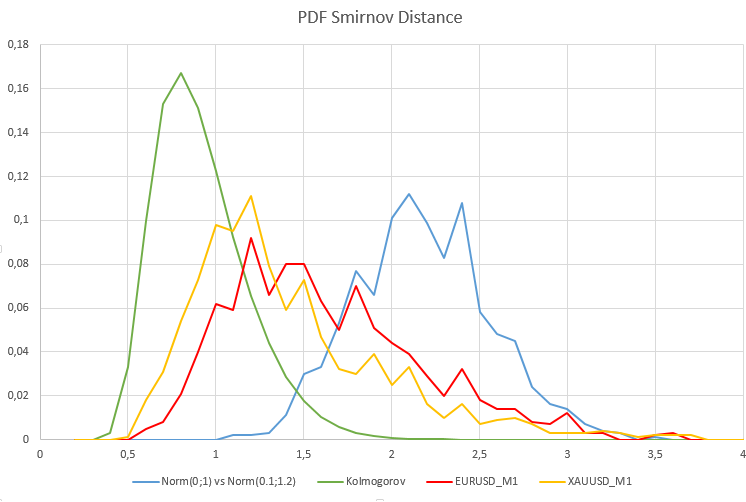
Como cabría esperar, en el caso modelo de heterogeneidad entre dos muestras normales, la función de densidad de probabilidad de la distancia de Smirnov se distingue significativamente de la distribución de Kolmogórov a la que deberían converger los datos homogéneos. Obsérvese lo sensible que resulta el criterio de Smirnov incluso a cambios relativamente pequeños en los parámetros de la distribución. 

Indicador iSmirnovDistance

El indicador iSmirnovDistance, a diferencia del análisis anterior, realiza los cálculos basándose únicamente en la cantidad de datos contenidos en cada uno de los dos días comerciales colindantes, sin permitir que los datos se solapen con los de otras sesiones comerciales. El propio indicador debe estar conectado en el marco temporal diario, todos los cálculos se realizan en los datos de 5 minutos del mismo instrumento. En el caso de las cotizaciones de divisas, esto supone 287 datos al día. Si no hay suficientes cotizaciones para los cálculos en alguno de los días (hemos tomado 270 datos como límite), los valores del indicador se igualarán a cero.

Así, al principio de cada día comercial obtendremos el valor de la estadística de Smirnov calculado a partir de los valores de los dos días comerciales anteriores. En realidad, este indicador solo puede tener un parámetro optimizable: el nivel de significación alpha. En esta versión hemos tomado un valor estándar de 0,05. La línea discontinua azul de la ventana del indicador muestra la distancia de Smirnov u(alpha) para el nivel de significación alpha = 0,05, es decir, para la hipótesis nula. Se calcula usando la fórmula anterior lambda = D*sqrt(n/2). Conociendo el valor crítico de lambda para la distribución de Kolmogórov igual a 1,3581 (existen tablas de la función de distribución de Kolmogórov) y la cantidad de datos para el marco temporal de 5 minutos igual a 287, encontramos la distancia correspondiente D = lambda / sqrt(n/2) = 1,3581/sqrt(287/2) = 0,1133. La superación de este valor por parte de los valores reales calculados indicará un cambio cualitativo en la estructura de la distribución de los datos. Los valores de los indicadores que se encuentren por debajo de la línea de puntos azul podrán considerarse homogéneos.

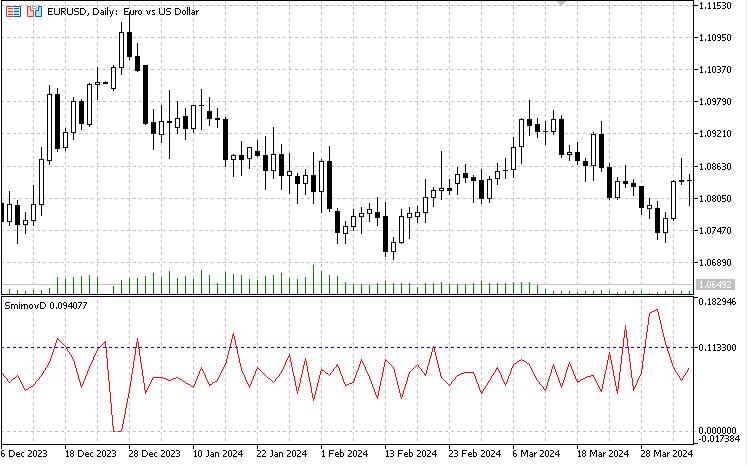
Vale la pena decir que existe una diferencia en el marco temporal en el que se calcula la distancia de Smirnov. Para los datos de minutos, como hemos visto, hay una no estacionariedad significativa en la serie, mientras que para el marco temporal de 5 minutos la serie es más estacionaria y la hipótesis de homogeneidad se rechaza con mucha menos frecuencia. En parte, esto se debe a la cantidad de datos: 1 440 para la franja de un minuto frente a 287 para la de 5 minutos. Con el aumento progresivo de los datos de 287 a 1 440, el índice de rechazo de la hipótesis nula aumenta, sin embargo la hipótesis de homogeneidad se rechaza con mayor frecuencia solo para el gráfico de minutos. 

Conclusión

Este artículo pretende responder a una serie de preguntas importantes sobre el análisis de series temporales bursátiles:

• La primera pregunta: "¿puede considerarse estacionaria la serie temporal de incrementos logarítmicos de precios?", en mi opinión, ha recibido una respuesta convincente y confirmada por cálculos numéricos: no puede considerarse, al menos para el marco temporal de los minutos. En cuanto al marco temporal de cinco minutos, aquí la serie parece más estacionaria en comparación con el marco temporal de un minuto, pero sigue mostrando un comportamiento no estacionario.

• La segunda pregunta a la que intenta responder este artículo es una continuación lógica de la primera: "¿cuántos datos deben tomarse para calcular un indicador concreto?". El indicador iSmirnovDistance, en mi opinión, ofrece la siguiente interpretación: para los cálculos resulta necesario tomar la cantidad de datos que entra en el periodo de tiempo entre dos rechazos de la hipótesis nula de homogeneidad. Mientras no se rechace la hipótesis nula, se aumentará gradualmente la cantidad de datos que hay que analizar. Una vez rechazada la hipótesis nula, los datos anteriores se descartarán por obsoletos y se iniciará de nuevo el cálculo de la cantidad de datos. Por tanto, la cantidad de datos que hay que analizar no es una magnitud fija. Es una magnitud que cambia constantemente en el tiempo, como debe ser, basándose en la naturaleza de un proceso aleatorio no estacionario.