Procesos no estacionarios y regresión espuria

Contenido:

• Introducción
• Investigación del problema de la no estacionariedad en el análisis de regresión
• Comprobación de hipótesis estadísticas sobre los parámetros del modelo de regresión
• Especificación incorrecta del modelo de regresión
• Conclusión

Introducción

El análisis de regresión, como una de las secciones de la estadística matemática aplicada, supone uno de los métodos más comunes de procesamiento de datos empíricos en el estudio de las relaciones entre variables aleatorias. Mientras que el análisis de correlación permite averiguar si dos variables aleatorias están relacionadas entre sí, el análisis de regresión ofrece una idea de la forma que puede adoptar la relación. En el análisis de regresión, se distingue entre regresión por pares y regresión múltiple. En este estudio, para simplificar la presentación, usaremos el conocido modelo de regresión lineal por pares:

                                                Yt = b0 + b1Xt + et                                 (1)

• Yt - variable dependiente (respuesta);
• Xt - variable independiente (o variable explicativa);
• b0, b1 parámetros del modelo; t - tiempo (0,1,2,...n) n - número de observaciones;
• et - componente aleatorio, normalmente ruido blanco gaussiano.

El índice t se da aquí para enfatizar que estamos tratando con una serie temporal, que la secuencia en la que se disponen las variables aleatorias resulta importante para nosotros.

El objetivo del análisis de regresión será:

• Estimar los parámetros del modelo de regresión seleccionado (en el caso lineal mediante el método de mínimos cuadrados ordinarios)
• Comprobar hipótesis estadísticas sobre los parámetros del modelo
• Construir intervalos de confianza para las estimaciones de los parámetros obtenidos

Si el modelo resulta estadísticamente significativo en el análisis, consideraremos que puede utilizarse para predecir la variable dependiente. Pero cuando aplicamos el análisis de regresión, especialmente al análisis de series temporales, siempre deberemos tener presente la limitación asociada al requisito de estacionariedad impuesto a las secuencias aleatorias estudiadas. El requisito de estacionariedad implica la invariancia de la función de distribución de una variable aleatoria a lo largo del tiempo y, por tanto, la invariancia de la esperanza matemática y la varianza de esta variable aleatoria. Los intentos de aplicar el análisis de regresión a procesos no estacionarios pueden llevar a falsas conclusiones sobre la presencia de una relación significativa entre las magnitudes estudiadas. En este caso, las pruebas estadísticas estándar, como las estadísticas F o t, dejan de funcionar y el riesgo de confundir una dependencia falsa con una verdadera se multiplica.

Investigación del problema de la no estacionariedad en el análisis de regresión

En este artículo queremos mostrar con la ayuda de simulaciones de Montecarlo cómo se produce una regresión espuria si se infringe el supuesto de estacionariedad, así como en los casos en los que el modelo de regresión está mal especificado en el caso estacionario. Para ello, utilizaremos la biblioteca estándar MQL5, concretamente la "Biblioteca Estadística" para generar números aleatorios y calcular los valores críticos de la distribución normal y la distribución de Student, así como la biblioteca gráfica Gráficos científicos para dibujar los resultados obtenidos. Para calcular los parámetros del modelo de regresión resultará muy cómodo utilizar los métodos del álgebra matricial, con su ayuda todos los cálculos se simplifican enormemente. Por ejemplo, la fórmula para encontrar los parámetros de un modelo de regresión por mínimos cuadrados en forma matricial se escribirá como:

(2) 

• X es la matriz de valores de las variables independientes;
• Y es el vector de columna de la variable dependiente;
• b es el vector de columna de parámetros desconocidos que deben estimarse a partir de la muestra.

En MQL5, el vector b (en nuestro caso de regresión lineal por pares, constará de dos elementos: b0 y b1) se puede encontrar calculando la matriz pseudo-inversa PInv() a partir de la matriz X y multiplicándola por el vector Y:

pinv = x.PInv(); 

Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS

Esta es una versión abreviada del cálculo. Puede calcularse paso a paso como se indica en la fórmula:

xt = x.Transpose();

xtm = xt.MatMul(x);
inv = xtm.Inv();      
invt = inv.MatMul(xt);
Coeff_B = invt.MatMul(Y); // vector of regression parameters using OLS

El resultado será el mismo.

Para el modelado, necesitaremos un modelo de paseo aleatorio como ejemplo de proceso no estacionario. Construiremos este modelo tanto para la variable dependiente Y como para la variable independiente X. A continuación, construiremos una regresión de Y sobre X y estimaremos el R-cuadrado (coeficiente de determinación), calcularemos las estadísticas t y analizaremos los residuos del modelo de regresión para detectar la dependencia de la correlación.                                            

 Yt = Yt-1 + zt                           (3)

  Xt = Xt-1 + vt                           (4)

zt y vt serán dos procesos generados independientemente de "ruido blanco" gaussiano con esperanza matemática cero y varianza unitaria N(0,1);

En la figura se muestran dos posibles trayectorias de este proceso. (1)

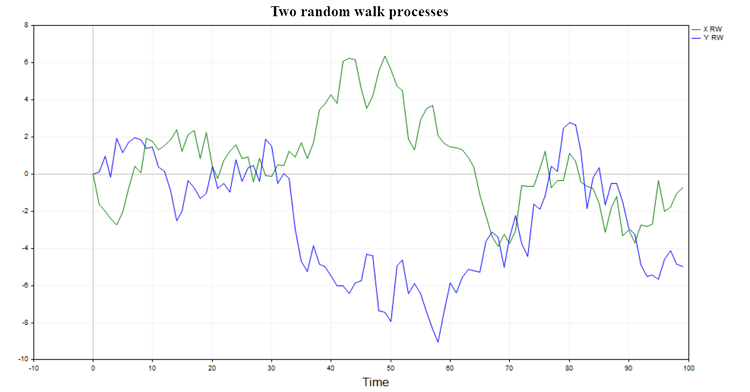
Figura 1.  Dos procesos de paseo aleatorio

Tales procesos no tienen memoria y no están relacionados entre sí, por lo que será natural esperar que la regresión de un paseo aleatorio sobre otro no ofrezca resultados significativos y la hipótesis de una relación entre dos paseos aleatorios se rechace normalmente (salvo en un pequeño porcentaje de casos debido al nivel de significación elegido).

En la fig.(2) se muestra un ejemplo de una posible regresión:

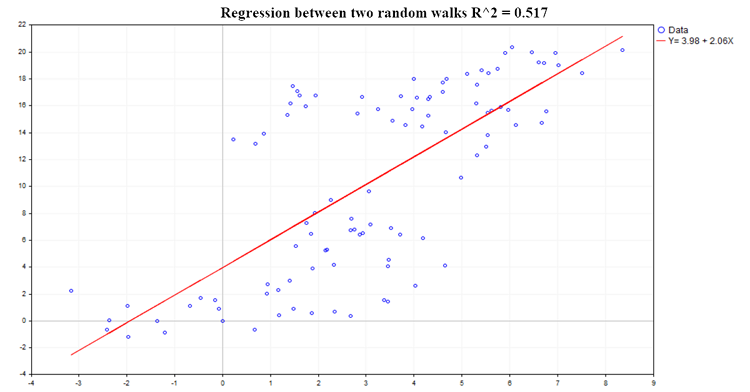
Figura 2. Regresión entre dos paseos aleatorios, R2=0,517

Tal característica de la dependencia de regresión estudiada como el coeficiente de determinación (R^2) se calculará mediante la fórmula: 

R^2 = 1 - SSE/TSS (5)

• SSE - suma de las estimaciones al cuadrado de los residuos (Sum of squared estimate of errors);
• RSS - suma de cuadrados explicados (Sum of squares due to regression);
• TSS - suma total de cuadrados (Total Sum of Squares = RSS+SSE);

Código para calcular todas las características principales de la regresión:

      pinv = x.PInv();
      Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS
      yRegression = x.MatMul(Coeff);  // y regression
      res = Y-yRegression;   //  regression residuals, y - y regression
      yMean = Y.Mean();
      reg_yMean = yRegression-yMean;  // y regression - mean y
      reg_yMeanT = reg_yMean.Transpose();
      RSS = reg_yMeanT.MatMul(reg_yMean);  // Sum( y regression - y mean )^2 , sum of squares due to regression
      resT = res.Transpose();
      SSE = resT.MatMul(res);  // Sum(y - regression y)^2
      TSS = RSS[0,0]+SSE[0,0];  // Total sum of squares
      RSquare = 1-SSE[0,0]/TSS;  // R-square determination ratio
      R2_data[s] = RSquare;

      Vres = SSE[0,0]/(T-2);           // residuals variance estimate
      SEb1 = MathSqrt(Vres/SX);        // estimate of the standard deviation of the b1 ratio deviation of the regression Y = b0 + b1*X;
      t_stat[s] = (Coeff[1,0]-0)/SEb1; // find the t-statistic for the b1 ratio under the hypothesis that b1 = 0;

Los valores de R^2 se situarán entre 0 y 1. En el caso de la regresión lineal por pares, R^2 será igual al cuadrado del coeficiente de correlación ordinaria entre X e Y. Cuando X no afecta a Y, entonces R^2 se aproximará a cero, y cuando la variable dependiente Y se explica por la variable dependiente X, entonces R^2 tenderá a uno. En nuestro caso de regresión de dos paseos aleatorios independientes, sería lógico esperar que se distribuyera cerca de cero.  Para comprobarlo, construiremos la distribución R^2 mediante la modelación de Montecarlo de 1 000 pares de paseos aleatorios de 100 observaciones cada uno, seguida del cálculo del coeficiente R^2 para cada par. Como resultado, obtendremos la siguiente distribución de la fig.(3):

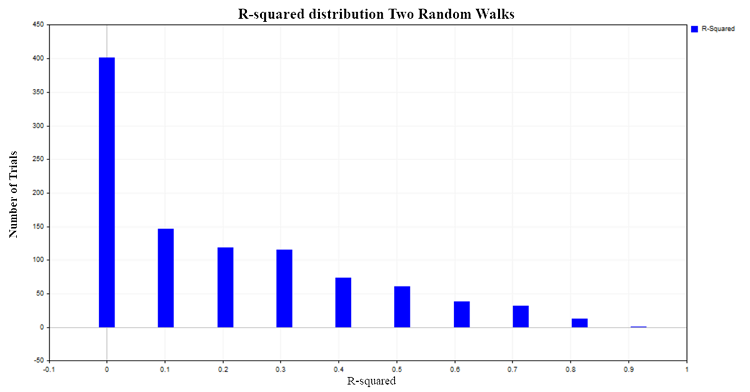
Fig. 3.  Distribución R2 para dos paseos aleatorios

En aproximadamente el 50% de los casos, el coeficiente de determinación mostrará valores superiores a 0,2, lo cual indica la presencia de una relación entre valores que en realidad no están relacionados entre sí. Para comparar, obtendremos la distribución R^2 para dos procesos independientes pero ya estacionarios. Un modelo de ruido blanco gaussiano resultará adecuado como proceso de este tipo.

                    Yt =  et                                   (6) 

 et - ruido blanco gaussiano N(0,1)

Generaremos 1 000 pares de procesos aleatorios estacionarios con 100 observaciones cada uno. Terminaremos con la distribución bastante esperada de R^2 cerca de cero de la fig.(4):

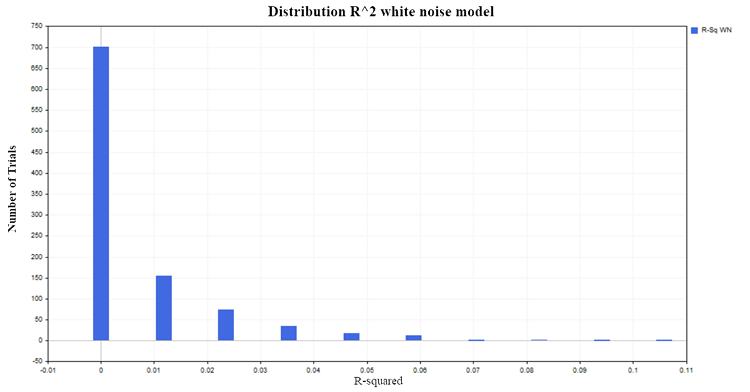
Figura 4. Distribución R2, modelo de ruido blanco

Regresemos al caso de los dos paseos aleatorios y veamos ahora cómo se comporta la estadística t, que se calculará para evaluar la significación de los parámetros de nuestro modelo de regresión lineal.

Comprobación de hipótesis estadísticas sobre los parámetros del modelo de regresión

Los coeficientes de regresión calculados a partir de la muestra son en sí mismos variables aleatorias, por lo que deberemos comprobar la significación de estas características de la muestra. Al comprobar la significación del parámetro de regresión b1, se planteará la hipótesis nula (H0) de que la variable explicativa X no afecta a la variable dependiente Y. Es decir, H0(i) : b1 = 0 y el parámetro b1 no será significativamente diferente de cero. La hipótesis alternativa (H1) afirma que el parámetro b1 será significativamente distinto de cero. Es decir, H1(i) :b1 ≠ 0 y, por tanto, el predictor X tendrá un efecto sobre la variable dependiente Y.

Para comprobar esta hipótesis se utilizaremos la estadística t:

                                               t = bi /SEi                                      (7)

SEi - desviación típica del parámetro bi estimado 

Esta estadística tendrá una distribución de Student ta/2 (n-p) con (n-p) grados de libertad.

• n - número de datos usados para el cálculo en el modelo de regresión (en nuestro caso 100);
• p - número de parámetros estimados (en nuestro caso de regresión por pares serán 2);
• a - nivel de significación (1,5,10%).

Para nuestro experimento, hemos elegido un nivel de significación del 5%. Entonces, si los valores de la estadística t del módulo superan el valor crítico de la distribución de Student {|t| > t0,025 (98) =1,9844}, podemos concluir que el parámetro de regresión b1 será distinto de cero y, en consecuencia, que existe una relación entre la variable explicativa X y la variable dependiente Y. Como hemos elegido un nivel de significación del 5%, solo deberíamos esperar aproximadamente un 5% de falsos rechazos de la hipótesis nula respecto al número total de pruebas realizadas. Pero según los resultados de la modelación, la estadística t rechaza la hipótesis nula con demasiada frecuencia (falsamente, porque no hay dependencia), aproximadamente el 75% de las veces, fig (5):

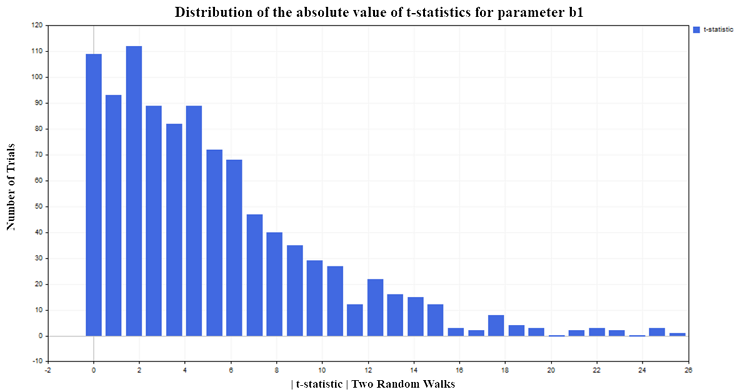
Figura 5. Distribución del valor absoluto de la estadística t para el parámetro b1

También nos gustaría señalar la siguiente tendencia. Cuantas más observaciones haya en la muestra, mayor será el porcentaje de rechazo de la hipótesis nula. Se da la situación aparentemente paradójica de que cuanto mayor sea la muestra, más afectará el predictor X a la variable independiente Y, y más fuerte será la relación entre las variables. Obviamente, en realidad no hay paradoja aquí, sino simplemente una aplicación del análisis de regresión a procesos a los que no es aplicable. Podemos observar que la estadística t estándar falla cuando la regresión se aplica al análisis de series temporales no estacionarias. Esta situación se denomina regresión espuria.

Especificación incorrecta del modelo de regresión

Pero la no estacionariedad es solo una de las razones por las que los criterios estadísticos estándar dejan de funcionar. Pueden inducir a error incluso si las dos series son estacionarias pero se incumple la especificación del modelo de regresión. Es decir, si elegimos una forma incorrecta de dependencia funcional entre variables (lineal en lugar de no lineal). O si el modelo omite una variable independiente X de la que depende realmente la variable Y, y en su lugar se utiliza por error una variable completamente irrelevante. Para explicarlo, construiremos dos procesos estacionarios independientes X e Y. Como ejemplo, utilizaremos el modelo autorregresivo de primer orden AR(1):

Yt = A*Yt-1 + zt                           (8)

 Xt = B*Xt-1 + vt                          (9)

• zt y vt son dos procesos gaussianos de "ruido blanco" generados independientemente, con esperanza matemática nula y varianza unitaria N(0,1);
• A y B son parámetros del modelo AR(1), que deben ser estrictamente inferiores a 1 por el modulo para cumplir la condición de estacionariedad.

Vamos a construir nuevamente una regresión de Y sobre X (por ejemplo, con parámetros AR(1) A=0,5, B=0,5) en las mismas condiciones que en el modelo de los dos paseos aleatorios (100 datos en cada ensayo, número de ensayos 1 000). Como resultado, obtendremos la siguiente distribución de estadística t para el parámetro de regresión b1 fig(6):

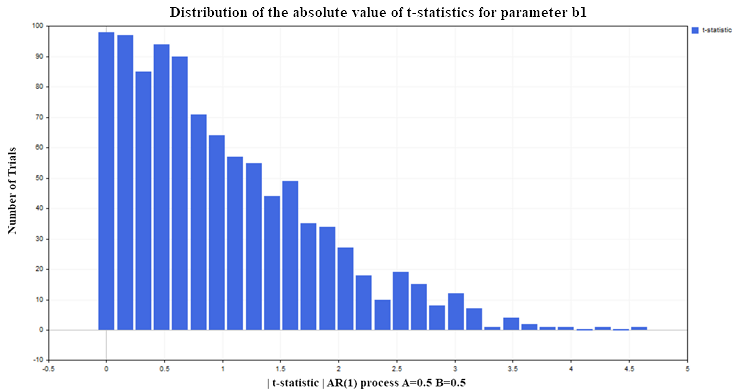
Fig. 6. Distribución del valor absoluto de la estadística t para el parámetro b1

Como podemos ver, aquí la situación con el rechazo de la hipótesis nula será mucho mejor que en el caso no estacionario. En total, alrededor del 12-13% de falsos rechazos con un nivel aceptable del 5% (recuérdese que el valor crítico de la distribución de Student para 98 grados de libertad = 1,9844). Para los procesos estacionarios, este porcentaje no aumentará al aumentar el tamaño de la muestra, sino que se mantendrá al mismo nivel. Esta vez la estadística t falla no porque las variables sean no estacionarias, no hay nada malo en ello, sino por una mala especificación del modelo de regresión.  Aunque la forma de la dependencia se ha elegido correctamente (lineal), asumiremos que la variable Y no depende de los valores de retardo de la misma variable, sino de los valores de la variable X, que no tiene nada que ver con la variable Y. Si dejamos la variable X en el modelo de regresión y le añadimos los valores de retardo Y, las propiedades estadísticas de los parámetros de regresión mejorarán y la estadística t dejará de dar conclusiones falsas con más frecuencia que el nivel de significación establecido (un 5%, en nuestro caso). En la práctica, para darnos cuenta de que el modelo de regresión es falso o está mal especificado, deberemos recurrir al análisis de residuos 

                                         Residuals =  Yt - Yreg_t                       (10)

• Yt - valores reales de la variable dependiente Y;
• Yreg_t - valores de regresión estimados

Si existe una autocorrelación significativa en los residuos del modelo, esto supondrá una señal para considerar que este modelo de regresión está mal especificado o es falso. 

Código para calcular la función de autocorrelación (ACF) y los intervalos de confianza del 99%

////////////////////////// ACF calculation /////////////////////////////////////////

   avgres = res.Mean();  // mean of residuals
   ArrayResize(acov,K);
   ArrayResize(acf,K);
   ArrayResize(se,K);
   ArrayResize(se2,K);

   for(i=0; i<K; i++)
     {
      ArrayResize(c,T-i);
      for(j=0; j<T-i; j++)
        {
         c[j] = (res[j,0]-avgres)*(res[j+i,0]-avgres);
        }
      acov[i] = double(MathSum(c)/T);  // Auto covariance
      acf [i] = acov [i]/acov [0];  // Auto correlation
      se[i] =   MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);    // 99% confidence intervals for ACF //
      se2[i] = -MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);
     }

La fig. (7) muestra el gráfico de la función de autocorrelación (ACF) de los residuos de regresión para el modelo de dos paseos aleatorios.  También se indican los límites de la región de confianza del 99% para la ACF calculada mediante la fórmula SE = MathQuantileNormal(0,995,0,1,err)/MathSqrt(T); T será el número de observaciones en el modelo de regresión.

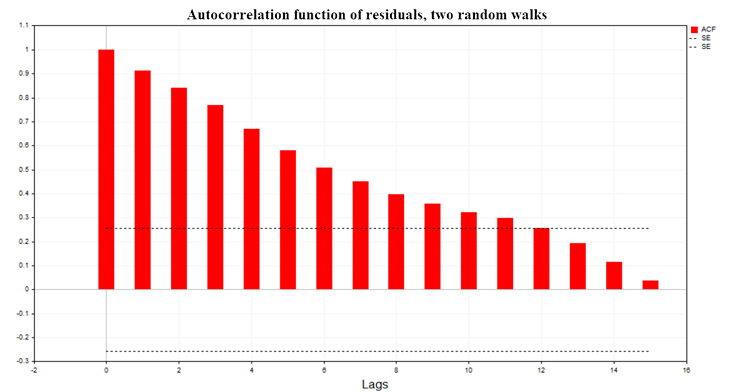
Fig. 7. Función de autocorrelación de los residuos, dos paseos aleatorios

La fig. (8) muestra el gráfico ACF de los residuos de regresión para el modelo de dos procesos AR(1) con parámetros (A=0.5, B=0.5)

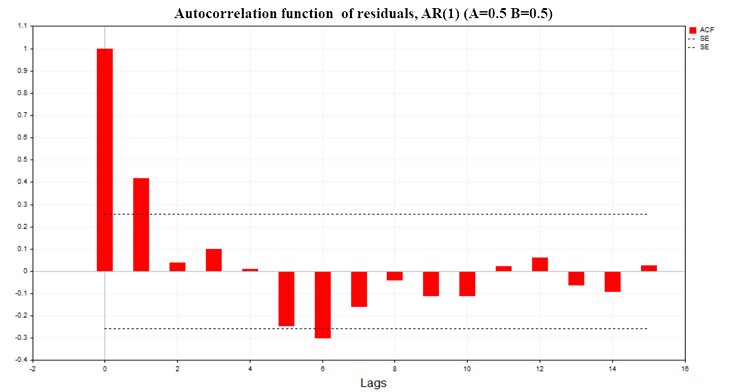
Fig. 8. Función de autocorrelación de residuos, AR(1) A=0,5 B=0,5

Como podemos ver en los gráficos, existe una autocorrelación significativa en los residuos de los modelos de regresión, por lo que nos encontramos ante un modelo de regresión mal especificado o una regresión espuria en general. También se ha construido el criterio de Durbin-Watson (criterio DW) a partir de la función de autocorrelación de los residuos. Se utilizará para comprobar la autocorrelación de los residuos de un modelo de regresión con un desfase igual a 1. 

                                            DW = 2*(1-ACF(1))                         (11)

En el caso de una regresión espuria, esta estadística se aproximará a cero.

Conclusión

El principal problema que quería abordar en este artículo era el límite de aplicabilidad de los métodos estadísticos, en particular los métodos de análisis de regresión. También quería demostrar las consecuencias derivadas del incumplimiento de esos límites. Resulta muy sencillo realizar los cálculos de manera formal, ver las estadísticas "significativas" y sacar la conclusión errónea de que existe una relación entre dos procesos aleatorios.

La conclusión que podemos extraer de todo lo anterior es: 

• Antes de construir un modelo de regresión, deberemos comprobar la estacionariedad de todas las variables del modelo.
• Si alguna variable es no estacionaria, deberemos reducirla a una forma estacionaria (normalmente tomando las primeras diferencias) y luego intentar construir un modelo con esta variable modificada.
• Tras construir el modelo, deberemos asegurarnos de examinar los residuos para ver si dependen de la autocorrelación.
• Si los valores de la función de autocorrelación de los residuos no superan la región de confianza del 99%, podremos proceder a evaluar la significación de los parámetros del modelo de regresión utilizando la estadística t.
• Si resulta ser significativa, entonces ya podremos empezar a predecir la variable dependiente Y utilizando el modelo construido.

Para reproducir todos los resultados anteriores, al principio del script, elegiremos los valores para la variable M = 1, 0 o 0,5, en función de los resultados del modelo que deseemos. Luego, en la parte inferior del script, deberemos descomentar el bloque de código responsable de mostrar ciertas estadísticas para cada modelo específico. También en el archivo Math.mqh necesitaremos comentar dos líneas de código para la función que calcula la función de densidad de probabilidad empírica (MathProbabilityDensityEmpirical) para mostrar las frecuencias en el gráfico.

 5432  //  for(int i=0; i<count; i++)
 5433 //    pdf[i]*=coef;