Kolmogorov-Smirnov-Test bei zwei Stichproben als Indikator für die Nicht-Stationarität von Zeitreihen

Einführung

Wenn Forscher mit der Analyse von Finanzzeitreihen beginnen, stehen sie immer vor dem Problem der Nicht-Stationarität der Daten. Zeitreihen von Währungskursen, Aktien und Futures sind nicht stationär. Um diese Reihen in eine stationäre Form zu bringen, werden üblicherweise die ersten Differenzen der Preislogarithmen Ln(Xn/Xn-1) verwendet, um mit den modifizierten Daten weiterzuarbeiten.

Aber kann eine solche modifizierte Zeitreihe als stationär angesehen werden? Im Folgenden werde ich versuchen, diese Frage zu beantworten, aber erinnern wir uns zunächst daran, was Stationarität ist. Ohne formale Definitionen kann Stationarität als die Konstanz der statistischen Eigenschaften einer Zeitreihe über die Zeit beschrieben werden, wie z. B. der mathematische Erwartungswert und die Varianz. Wenn zusätzlich zu diesen Eigenschaften die Konstanz der Verteilungsfunktion über die Zeit angenommen wird, dann wird der Prozess als stationär im engeren Sinne bezeichnet.

In dieser Studie werde ich Finanzzeitreihen mit Hilfe empirischer Verteilungsfunktionen auf Stationarität im engeren Sinne testen. Die Wahrscheinlichkeitstheorie und die mathematische Statistik, als ein spezieller Teilbereich der ersteren, beruhen auf der Annahme der Stationarität. Es gibt zahlreiche Methoden zur Analyse stationärer Prozesse, darunter die Regressionsanalyse, die Autokorrelationsanalyse, Methoden der Spektralanalyse und die Verwendung neuronaler Netze. Die Anwendung dieser Methoden auf nicht-stationäre Daten kann jedoch zu erheblichen Prognosefehlern führen.

Für Händler ist die Frage der Stationarität eng mit der Wahl der Datenmenge für die Berechnung der verschiedenen Indikatoren verbunden. Bei stationären Prozessen lassen sich alle statistischen Merkmale umso genauer berechnen, je mehr Daten zur Verfügung stehen. Bei der Analyse von nicht-stationären Prozessen ist es jedoch schwierig, die optimale Datenmenge zu bestimmen. Ein zu großer Umfang kann veraltete Informationen enthalten, die die aktuelle Situation nicht mehr betreffen. Wenn zu wenig Daten erhoben werden, können wir die statistischen Eigenschaften des Prozesses aufgrund der unzureichenden Repräsentativität nicht angemessen bewerten.

Das vollständigste Merkmal eines Zufallsprozesses ist sein Verteilungsgesetz (Wahrscheinlichkeitsfunktion). Daher ist es eine wichtige Aufgabe, einen Indikator zu konstruieren, der es ermöglicht, Veränderungen in der Verteilungsfunktion einer Zeitreihe im Laufe der Zeit zu verfolgen. Dieser Indikator wird wiederum als Signal für die Notwendigkeit dienen, das Datenvolumen für die Berechnung der Standardindikatoren der technischen Analyse zu überarbeiten. In der mathematischen Statistik wird das Problem der Prüfung, ob sich die Verteilungsfunktion einer Zufallsvariablen im Laufe der Zeit verändert hat, als „Prüfung der Homogenitätshypothese“ bezeichnet.

Homogenitätshypothese

Die Homogenität der Stichprobendaten wird mit Homogenitätstests geprüft. Gegenwärtig wurde eine große Anzahl solcher Kriterien entwickelt, von denen die folgenden unterschieden werden können:

• Kolmogorov-Smirnov-Test mit zwei Stichproben,

• Anderson-Homogenitätstest,

• Chi-Quadrat-Homogenitätstest nach Pearson.

Die Homogenitätshypothese ist nichts anderes als die Annahme, dass zwei Datenstichproben (x1,x2,x3,...xn) und (y1,y2,y3,...ym), die über zufällige X- und Y-Variablen gewonnen wurden, demselben Verteilungsgesetz folgen, oder, anders ausgedrückt, dass die beiden Stichproben aus derselben Grundgesamtheit stammen. Formal kann diese Hypothese als H0 formuliert werden: F(x) = G(y). Die Alternativhypothese lautet, dass die beiden Stichproben zu unterschiedlichen Populationen gehören, aber es wird nicht angegeben, zu welchen, H1: F(x) ≠ G(y).

• Fn(x) und Gm(y) ist eine empirische kumulative Verteilungsfunktion der Zufallsvariablen X bzw. Y.

• n, m – Menge der zu berechnenden Daten

Kolmogorov-Smirnov-Test bei zwei Stichproben

Der Kolmogorov-Smirnov-Test für zwei Stichproben ist ein statistischer Test, mit dem die Hypothese überprüft werden kann, dass zwei Stichproben aus derselben kontinuierlichen Verteilung gezogen wurden. Dieses Kriterium basiert auf einem Vergleich der empirischen Verteilungsfunktionen zweier unabhängiger Stichproben.

Der Kolmogorov-Smirnov-Test mit zwei Stichproben wird in der statistischen Analyse häufig verwendet, um Hypothesen über die Gleichheit von Verteilungen zu testen, was in verschiedenen Bereichen wie Biostatistik, Ökonometrie und anderen Studien nützlich sein kann, in denen es notwendig ist, zwei verschiedene Stichproben anhand ihrer statistischen Eigenschaften zu vergleichen. Dies ist besonders wichtig, wenn die verfügbaren Daten nicht ausreichen, um anspruchsvollere parametrische Methoden anzuwenden.

Es stellt sich die Frage, was als Maß für die Diskrepanz zwischen zwei empirischen Verteilungsfunktionen genommen werden sollte. Smirnow hat die folgenden Statistiken vorgelegt:

Dn,m = sup | Fn(x) - Gm(y) |

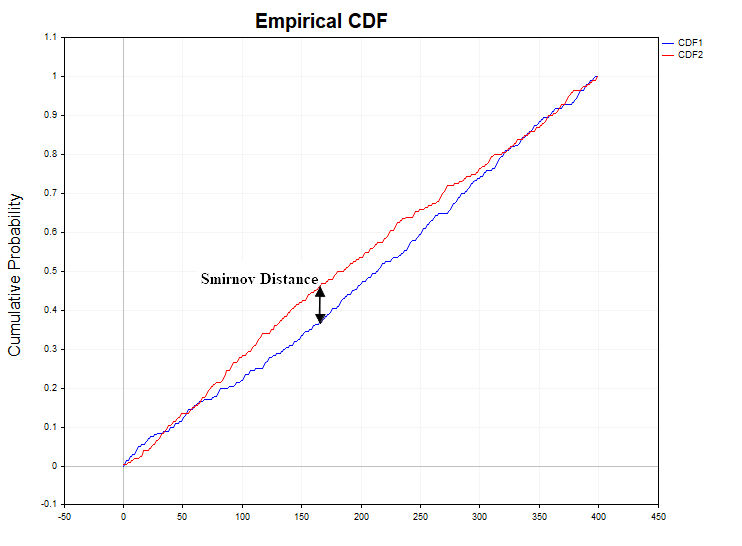
Diese Statistik stellt die genaue Obergrenze (Maximum) des absoluten Wertes der Differenz zwischen den Verteilungsfunktionen dar. Wenn sich das Verteilungsgesetz einer Zufallsvariablen von Stichprobe zu Stichprobe nicht ändert, sind natürlich niedrige Werte für die Statistik Dn,m zu erwarten. Übermäßig große Werte dieser Statistik sprechen wiederum gegen die Nullhypothese der Homogenität der Daten. Um statistische Hypothesen zu testen, wird anstelle der D-Statistik eine leicht modifizierte Statistik berechnet

lambda = D * ( sqrt(k) + 0,12 + 0,11/sqrt(k) ),

wobei k = (m*n/(m+n)). Die Verteilung der Lambda-Statistik mit k → ∞ konvergiert wiederum gegen die Kolmogorov-Verteilungsfunktion:                                                  

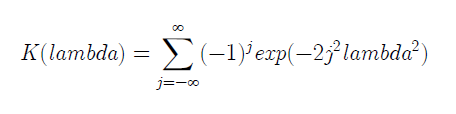
Manchmal wird eine vereinfachte Gleichung zur Berechnung von Lambda verwendet, wenn n gleich m ist:

lambda = D *sqrt(n/2)

Nachdem bestimmte statistische Werte ermittelt wurden, wird die Homogenitätshypothese anhand von Stichprobendaten getestet.

Die statistische Hypothese wird wie folgt getestet:

• Es werden die Nullhypothese H0 (die Stichproben sind homogen) und die Alternativhypothese H1 (die Stichproben sind heterogen) formuliert.

• Es wird das Alpha-Signifikanzniveau angenommen (üblicherweise werden die Standardwerte 0,1, 0,05 und 0,01 verwendet).

• Der kritische Wert u(alpha) wird nach der Kolmogorow-Verteilung berechnet (wenn z. B. alpha 0,05 ist, ist u(alpha) 1,3581).

• Es wird der Stichprobenwert der Lambda-Statistik berechnet.

• Es wird die Nullhypothese angenommen, wenn lambda < u(alpha).

• Es wird die Nullhypothese bezogen auf das Signifikanzniveau alpha abgelehnt, wenn lambda > u(alpha) ist, da sie im Widerspruch zu den beobachteten Daten steht.

Ein anderes logisches Ende dieser Struktur ist ebenfalls möglich. Anstelle des kritischen Werts u(alpha) wird die Wahrscheinlichkeit PValue = 1 - K(lambda) berechnet und mit dem angegebenen Signifikanzniveau alpha verglichen. Wenn alpha ≥ PValue ist, wird die Nullhypothese abgelehnt, da davon ausgegangen wird, dass ein unwahrscheinliches Ereignis eingetreten ist, das mit dem Konzept der Zufälligkeit unvereinbar ist, und die Stichproben daher als unterschiedlich zu beurteilen ist.

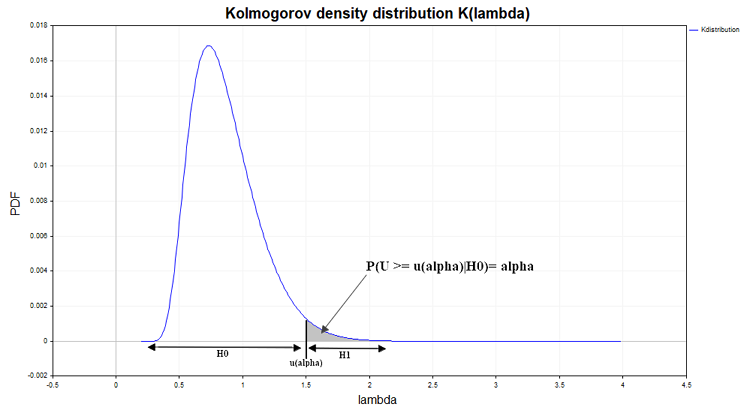
Die Abbildung zeigt die Ableitung der Kolmogorov-Verteilungsfunktion, d. h. die Wahrscheinlichkeitsdichtefunktion, die unter der Bedingung berechnet wird, dass die Nullhypothese wahr ist. Weicht die für die Stichprobendaten berechnete Smirnov-Distanz-Wahrscheinlichkeitsdichtefunktion von der Kolmogorov-Funktion ab, kann dies auf eine Heterogenität der Daten hinweisen.

Der Kolmogorov-Smirnov-Test mit zwei Stichproben sollte nicht mit dem Test mit einer Stichprobe verwechselt werden. Wir vergleichen wir zwei empirische Verteilungsfunktionen, während er eine empirische mit einer hypothetische Verteilungsfunktion vergleicht.

Ein sehr wichtiger Punkt ist, dass die empirischen Verteilungsfunktionen mit ungruppierten Beobachtungsdaten berechnet werden müssen, da die Kolmogorov-Verteilungsfunktion unter dieser Annahme berechnet wird. Es ist auch wichtig zu betonen, dass der Kolmogorov-Smirnov-Test für zwei Stichproben nicht von der spezifischen Art der Verteilungsfunktion abhängt. Da es bei der Analyse von Finanzzeitreihen schwierig sein kann, eine Aussage darüber zu treffen, ob die beobachteten Daten zu dem einen oder anderen hypothetischen Verteilungstyp gehören, steigt der Wert dieses Kriteriums für den Analysten erheblich. Ohne Annahmen über die Art der hypothetischen Verteilung zu treffen, zu der die beobachteten Daten gehören könnten, können wir die Homogenitätshypothese allein auf der Grundlage der empirischen Verteilungsfunktionen testen. Für die Zeitreihenanalyse kann das Smirnov-Kriterium als Indikator für die Stationarität des Prozesses angesehen werden. Denn nach der Definition der Stationarität gilt ein Prozess als stationär, wenn sich seine Wahrscheinlichkeitsverteilungsfunktion im Laufe der Zeit nicht ändert.

Erklärung der einfachen Berechnungsmethode

Nehmen wir an, wir haben zwei große Säcke mit Murmeln. In der einen Tüte sind Murmeln aus einem Land, in der anderen Murmeln aus einem anderen Land. Unsere Aufgabe ist es, herauszufinden, ob die Murmeln in den beiden Säcken gleich oder verschieden sind.

1. Murmeln sortieren. Zuerst schütten wir die Kugeln aus den beiden Beuteln und ordnen sie der Größe nach an - von der kleinsten zur größten.

2. Murmeln vergleichen. Dann schauen wir uns jede Murmel im ersten Beutel an und suchen nach einer Murmel der gleichen Größe im zweiten Beutel. Wir messen, wie weit ähnliche Murmeln in zwei Reihen voneinander entfernt sind. In diesem Zusammenhang bedeutet „Abstand“, wie weit die Murmeln in den Reihen voneinander entfernt sind, wenn man ihre Positionen betrachtet.
   
   Nehmen wir an, wir haben eine Murmel aus dem ersten Beutel, die die fünfte Position in der Reihe einnimmt. Befindet sich eine ähnlich große Kugel aus dem zweiten Beutel an der zwanzigsten Position in der Reihe, so beträgt der Abstand zwischen diesen beiden Kugeln 15 Positionen (20 - 5 = 15). Diese Zahl gibt an, wie weit ähnliche Murmeln in zwei verschiedenen Beuteln (oder zwei Datenproben) voneinander entfernt sind.
   
   Beim statistischen Kolmogorov-Smirnov-Test vergleichen wir solche „Abstände“ für alle Murmeln und suchen nach dem Maximum davon. Ist dieser maximale Abstand größer als ein bestimmter Wert (der von der Anzahl der Murmeln in den Beuteln abhängt), kann dies ein Hinweis darauf sein, dass sich die Murmeln in den Beuteln in einigen Eigenschaften unterscheiden.
   

3. Den größten Unterschied finden. Gesucht wird die Stelle, an der die Unterschiede („Abstände“) zwischen den Murmeln in den beiden Reihen am größten sind. Wenn zum Beispiel an einer Stelle die Murmeln sehr nah beieinander liegen und an einer anderen Stelle sehr große Unterschiede auftreten, markieren wir diese Stelle.

4. Bewertung der Unterschiede. Wenn der größte Abstand zwischen den Murmeln sehr groß ist, kann dies bedeuten, dass die Murmeln in den Beuteln tatsächlich unterschiedlich sind. Wenn alle Murmeln über die gesamte Länge der Reihe ziemlich nahe beieinander liegen, könnten sie tatsächlich vom selben Ort stammen.

Wenn also die Unterschiede zwischen zwei Reihen von Murmeln groß sind, sagt man, dass die Murmeln in den Säcken unterschiedlich sind. Wenn die Unterschiede gering sind, sind höchstwahrscheinlich die Murmeln gleich. Dies hilft uns zu verstehen, ob Murmeln aus zwei verschiedenen Orten als gleich angesehen werden können oder nicht.

Datenanalyse mittels Kolmogorov-Smirnov-Test bei zwei Stichproben

Bevor wir uns der Analyse der Smirnov-Distanzen widmen, die für reale Zitate berechnet werden, werden wir zunächst untersuchen, wie sich diese Statistik bei Modellen stationärer Prozesse verhält, sowohl bei abhängigen als auch bei unabhängigen Inkrementen. Zu diesem Zweck werde ich 1000 Stichproben (Samples) von Zeitreihen mit einer bestimmten Verteilungsfunktion mit einem Volumen von 1440 Daten in jeder Reihe erzeugen. Danach berechne ich den D-Smirnov-Abstand zwischen diesen Stichproben, prüfe, in wie viel Prozent der Fälle die Nullhypothese abgelehnt wird (H1/Stichproben) und konstruiere eine empirische Wahrscheinlichkeitsdichtefunktion dieser Abstände, um sie mit der Kolmogorov-Dichtefunktion zu vergleichen. Die folgende Abbildung zeigt die Smirnov-Abstandsreihe für eine Datenstichprobe von N = 1440, die aus einer Normal- und Gleichverteilung gewonnen wurde.       

                               
                               

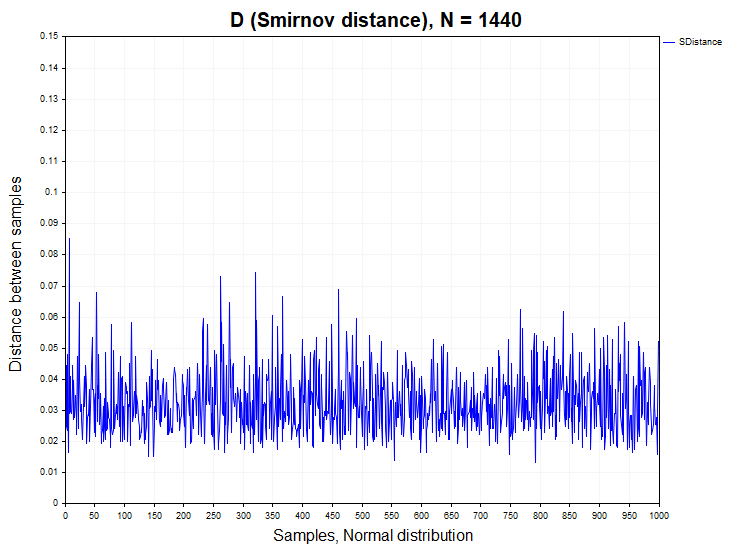
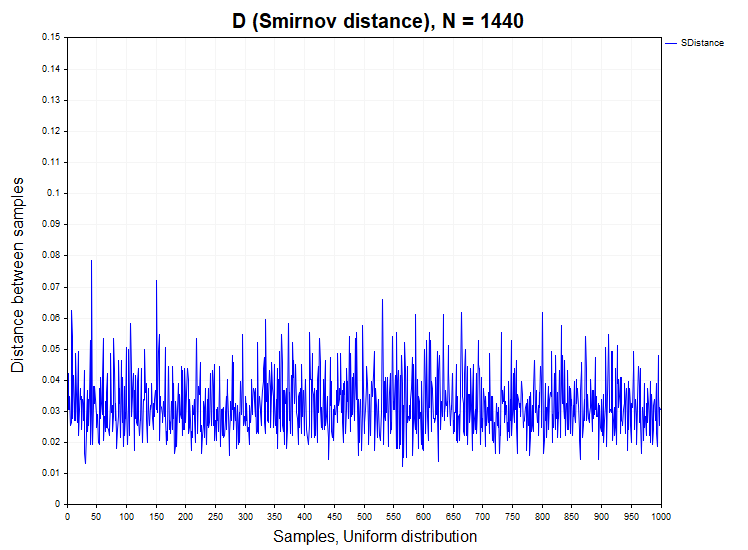
Bei Stichproben aus einer Normal- und Gleichverteilung tritt eine falsche Ablehnung der Homogenitätshypothese innerhalb des zulässigen Fehlers des ersten Typs (alpha = 0,05) auf, d. h. in höchstens 50 Fällen von 1000 Stichproben. H1/Proben = 50/1000 = 0,05. Nachfolgend finden Sie Diagramme der Stichprobenwahrscheinlichkeitsdichte von Smirnov-Distanzen für Normal- und Gleichverteilungen.

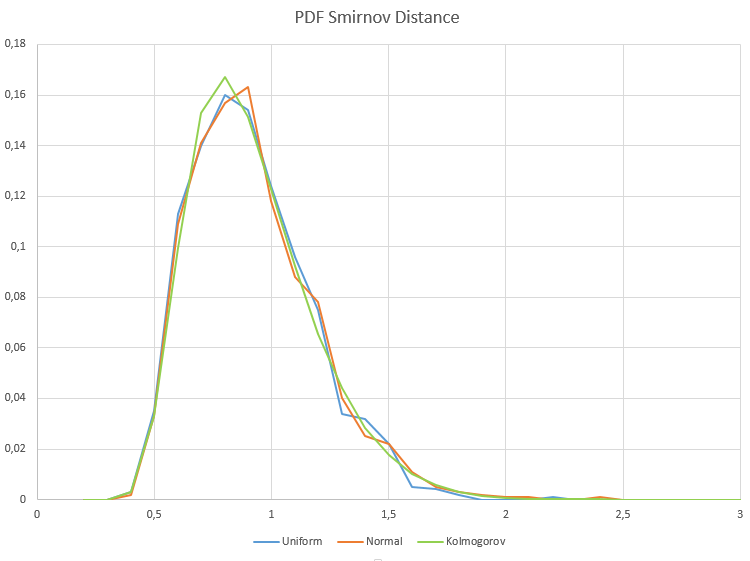
Die X-Achse zeigt den Lambda-Wert an.

Wie man sieht, stimmen die Stichprobenverteilungen des Smirnov-Abstands für gleichförmige und normale Datenstichproben und die Kolmogorov-Verteilung, zu der sie konvergieren sollten, vollständig überein, sofern die Nullhypothese der Homogenität wahr ist.

Die eben behandelten Normal- und Gleichverteilungen sind Beispiele für stationäre unabhängige Prozesse. Als stationären, aber abhängigen Prozess werde ich eine diskrete nichtlineare Gleichung nehmen, die oft als Beispiel auf dem Gebiet des deterministischen Chaos verwendet wird - die logistische Darstellung:

Xn= R*Xn-1 *(1 – Xn-1), X0 = (0;1), R = 4

Es handelt sich um ein eindimensionales nichtlineares dynamisches System, das bei einem Parameter von R=4 ein chaotisches Verhalten zeigt, das kaum von weißem Rauschen zu unterscheiden ist. Die Autokorrelationsfunktion der durch diese Gleichung erzeugten Zeitreihe schwankt um Null. Es gibt jedoch eine nichtlineare Abhängigkeit in diesem Prozess, und es wäre interessant zu prüfen, wie sich dies auf die Verteilung der Smirnov-Abstände auswirkt. Diese Frage ist nicht unberechtigt, da viele glauben, dass es nichtlineare Abhängigkeiten in Finanzdaten gibt, weshalb ich diese Gleichung in die Analyse einbezogen habe.

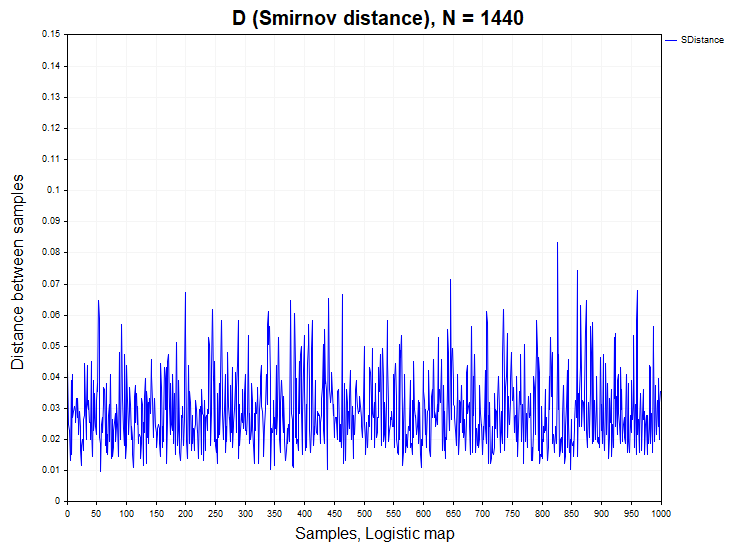
Natürlich erfordert die Analyse ein Modell mit linearen Abhängigkeiten, die auch in realen Daten vorhanden sein können. Daher wird das zweite Modell des stationären abhängigen Prozesses ein lineares autoregressives Modell erster Ordnung sein:

ARt = 0.5 * ARt-1 + et

• et – eine Zufallsvariable mit Mittelwert Null und Einheitsvarianz, weißes Gauß‘sches Rauschen

Der autoregressive Prozess ist auch in diesem Fall ein Gauß-Prozess, wenn auch ein bereits abhängiger.

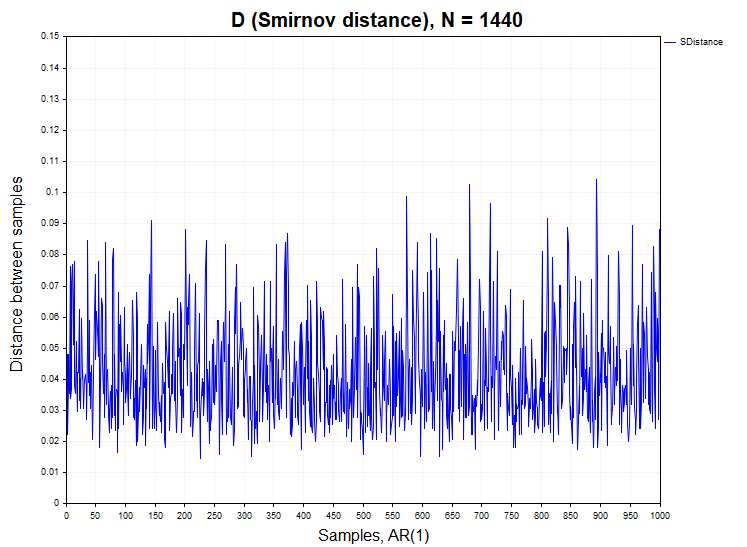
Bei Prozessen mit abhängigen Inkrementen stellt sich die Situation bei der Ablehnung der Homogenitätshypothese etwas anders dar. Für das logistische Mapping ergibt sich eine leichte Überschreitung des zulässigen Wertes des ersten Typfehlers von 0,058 (H1/Stichproben= 58/1000), während dieser Fehler bei der Autoregression erster Ordnung bereits bei ca. 0,25 (H1/Stichproben= 250/1000) liegt, d.h. fünfmal höher als der zulässige Wert unter der Nullhypothese.

Wir haben ein sehr interessantes Ergebnis erhalten. Es stellt sich heraus, dass nach dem Kolmogorov-Smirnov-Test mit zwei Stichproben sowohl die logistische Abbildung als auch AR(1) als inhomogene (nicht-stationäre) Prozesse erkannt werden sollten. Das ist aber natürlich nicht der Fall. Warum ist das so? Es stellt sich heraus, dass die Wahrscheinlichkeitsdichtefunktion der Smirnov-Distanzen für stationäre Verteilungen nur dann nicht von der Art der Verteilung des untersuchten Prozesses abhängt, wenn die beobachteten Daten statistisch unabhängig sind. Da es sich sowohl bei der logistischen Abbildung als auch bei der Autoregression um Prozesse mit abhängigen Inkrementen handelt, unterscheidet sich in diesem Fall die Wahrscheinlichkeitsdichte des Smirnow-Abstands von der Kolmogorow-Verteilung. Dies wiederum bedeutet, dass der Kolmogorov-Smirnov-Test mit zwei Stichproben nicht nur ein Indikator für Heterogenität (Nicht-Stationarität des Prozesses) sein kann, sondern auch ein Indikator für das Vorhandensein von Datenabhängigkeit (linear oder nicht-linear).

Kommen wir nun zur Analyse der realen Daten. Als Beispiel habe ich Minutenbalken für das Währungspaar EURUSD und XAUUSD (Gold) genommen.

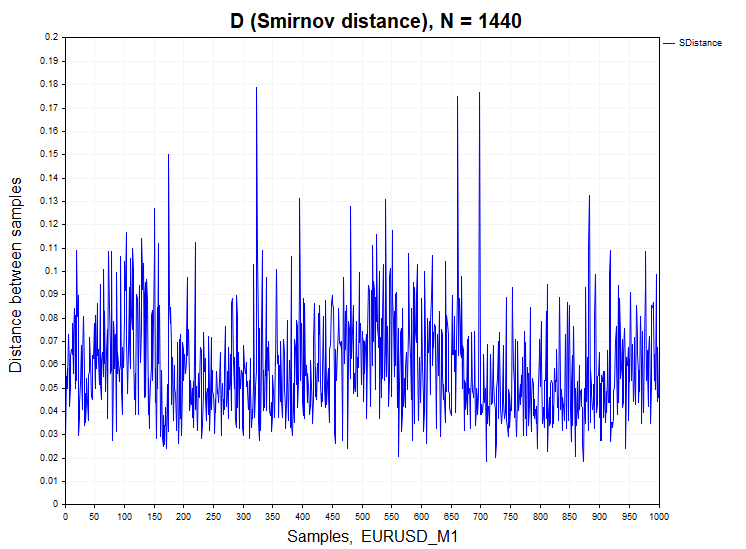
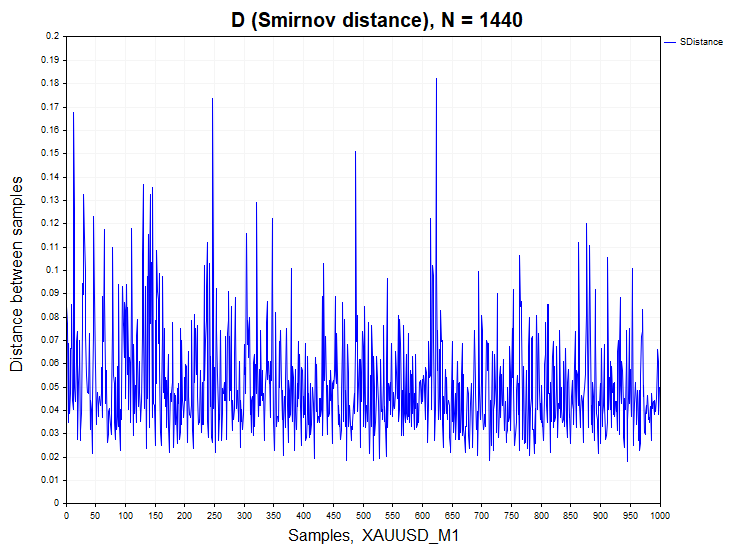
Bei den Minutenkursen weicht der Prozentsatz der Abweichung von der Nullhypothese signifikant von den stationären Prozessen ab: H1/Stichproben = 466/1000 = 0,46 für XAUUSD und H1/Stichproben = 640/1000 = 0,64 für EURUSD. Zur Verdeutlichung ist unten ein Diagramm der Stichproben-Wahrscheinlichkeitsdichtefunktion von Smirnov-Distanzen für reale Daten und abhängige Prozesse der Autoregression und der logistischen Darstellung dargestellt.

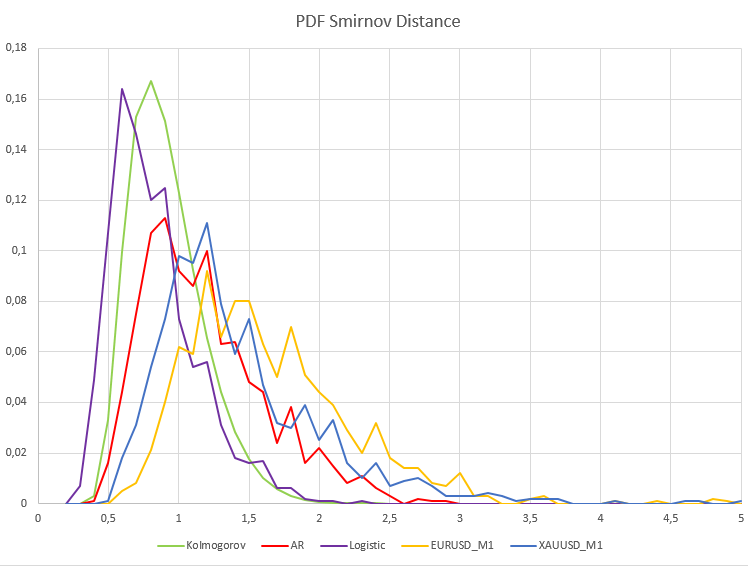
Wie wir sehen können, ergibt sich hier ein qualitativ unterschiedliches Bild sowohl für stationäre abhängige Prozesse als auch für reale EURUSD_M1- und XAUUSD_M1-Kurse. Die Stichprobenwahrscheinlichkeitsdichten der Smirnov-Distanzen für diese Prozesse unterscheiden sich deutlich von der Kolmogorov-Verteilung. In diesem Fall konvergieren die Prozesse der logistischen Darstellung und der Autoregression erster Ordnung nicht zur Kolmogorov-Verteilung, nur weil diese Daten statistische Abhängigkeiten aufweisen.

Was die Preise von Finanzinstrumenten betrifft, so sind sie selbst nach einem Versuch, sie mit Hilfe erster Differenzen auf eine stationäre Form zu reduzieren, nicht stationär. Ein gewisser Einfluss auf eine so große Zahl von Abweichungen von der Nullhypothese wird höchstwahrscheinlich durch einige Abhängigkeiten ausgeübt, die in realen Zitaten vorhanden sein können, wie wir bei der Analyse stationärer abhängiger Prozesse gesehen haben. Meiner Meinung nach ist es nicht möglich zu beurteilen, welcher Anteil des Einflusses auf Abhängigkeiten in den Daten zurückzuführen ist und welcher Anteil lediglich auf die nicht-stationäre Komponente in den Zeitreihen der Finanzinstrumente zurückzuführen ist. Der Haupteinfluss liegt jedoch nach wie vor in der Heterogenität der Daten sowie in der ständigen Veränderung der Wahrscheinlichkeitsverteilungsfunktion der Preiszuwächse.

Um eine klare Vorstellung davon zu bekommen, welche Form die Wahrscheinlichkeitsdichte der Smirnov-Distanzen für zwei heterogene Stichproben haben kann, führen wir ein weiteres Experiment durch, bei dem wir Daten von Stichproben aus zwei Normalverteilungen vergleichen, die zu verschiedenen allgemeinen Populationen gehören. Diese Verteilungen unterscheiden sich in der mathematischen Erwartung und Streuung - N(0,1) vs. N(0.1,1.2). Es ist offensichtlich, dass der Kolmogorov-Smirnov-Test mit zwei Stichproben die Nullhypothese der Homogenität im Allgemeinen zurückweisen sollte. Der Fehler wäre hier, die Nullhypothese zu akzeptieren, wenn die Alternativhypothese wahr ist. 

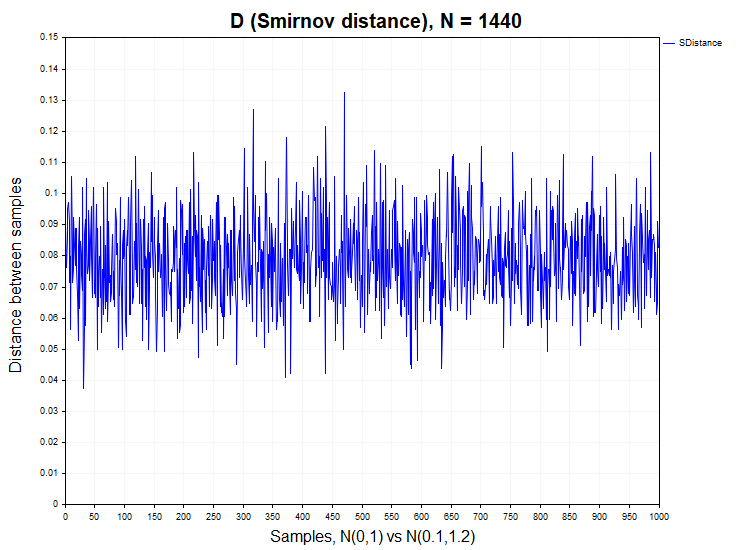
In diesem Fall liegt der Prozentsatz für eine Ablehnung der Nullhypothese bei 0,98 (H1/Stichproben = 980/1000). Das folgende Diagramm zeigt die Wahrscheinlichkeitsdichtefunktionen der Smirnow-Abstandsverteilung für reale Kurse, das Modell zweier ungleichmäßiger Normalverteilungen und die Kolmogorow-Verteilung.

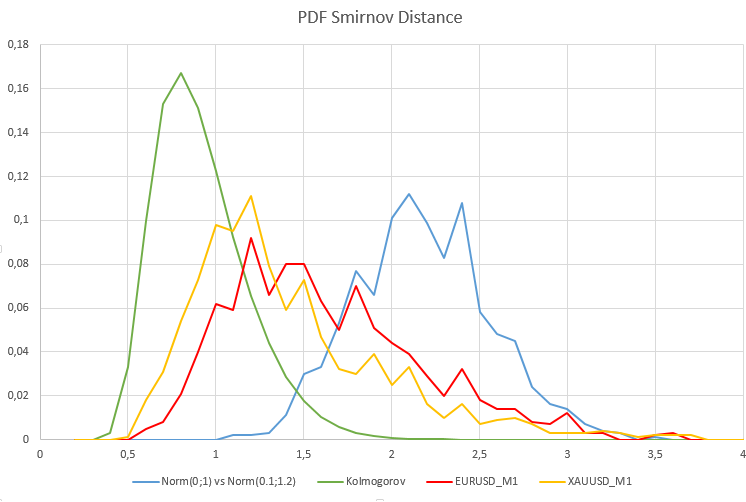
Wie erwartet, unterscheidet sich im Modellfall der Heterogenität zweier normaler Stichproben die Wahrscheinlichkeitsdichtefunktion der Smirnov-Distanzen erheblich von der Kolmogorov-Verteilung, zu der homogene Daten konvergieren sollten. Beachten Sie, wie empfindlich der Kolmogorov-Smirnov-Test mit zwei Stichproben selbst auf relativ kleine Änderungen der Verteilungsparameter reagiert. 

Der Idikator iSmirnovDistance

Im Gegensatz zur obigen Analyse führt der Indikator iSmirnovDistance eine Berechnung durch, die ausschließlich auf der Datenmenge zweier benachbarter Handelstage basiert, ohne dass sich die Daten mit anderen Handelssitzungen überschneiden dürfen. Der Indikator selbst sollte auf einem täglichen Zeitrahmen ausgeführt werden, alle Berechnungen werden auf 5-Minuten-Daten desselben Instruments durchgeführt. Bei Devisenkursen sind dies 287 Datenpunkte pro Tag. Wenn an einem der Tage nicht genügend Notierungen für die Berechnungen vorliegen (ich habe 270 Daten als Grenze genommen), werden die Indikatorwerte auf Null gesetzt.

So erhalten wir zu Beginn eines jeden Handelstages den Wert der Smirnow-Statistik, der auf der Grundlage der Werte der beiden vorangegangenen Handelstage berechnet wird. Dieser Indikator kann eigentlich nur einen Parameter haben, der optimiert werden kann - das Alpha-Signifikanzniveau. In dieser Version habe ich den Standardwert gleich 0,05 gesetzt. Die blau gestrichelte Linie im Indikatorfenster zeigt den Smirnov-Abstand u(alpha) für das Signifikanzniveau alpha = 0,05, d. h. für die Nullhypothese. Er wird nach der obigen Gleichung berechnet: lambda = D*sqrt(n/2). Da der kritische Wert von Lambda für die Kolmogorov-Verteilung gleich 1,3581 ist (es gibt Tabellen mit der Kolmogorov-Verteilungsfunktion) und die Datenmenge für den 5-Minuten-Zeitraum gleich 287 ist, ergibt sich der entsprechende Abstand D = Lambda / sqrt(n/2) = 1,3581/sqrt(287/2) = 0,1133. Eine Überschreitung dieses Wertes durch tatsächlich berechnete Werte deutet auf eine qualitative Veränderung in der Struktur der Datenverteilung hin. Die Indikatorwerte unterhalb der blau gestrichelten Linie können als homogen angesehen werden.

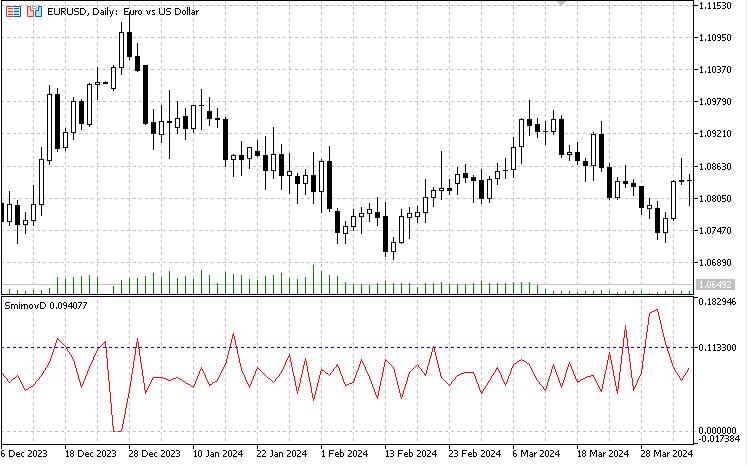
Wichtig ist auch der Zeitrahmen, für den der Smirnow-Abstand berechnet wird. Wie wir gesehen haben, gibt es bei den Minutendaten eine signifikante Nicht-Stationarität der Reihe, während die Reihe im 5-Minuten-Zeitrahmen stationärer ist und die Homogenitätshypothese viel seltener abgelehnt wird. Dies ist teilweise auf das Datenvolumen zurückzuführen – 1440 für M1 gegenüber 287 für M5. Mit einer allmählichen Zunahme der Daten von 287 auf 1440 steigt die Ablehnungsquote der Nullhypothese. Die Homogenitätshypothese wird jedoch häufiger für das Chart M1 abgelehnt. 

Schlussfolgerung

Dieser Artikel soll eine Reihe von wichtigen Fragen zur Analyse von Börsenzeitreihen beantworten:

• Die erste Frage lautet, ob eine Zeitreihe mit logarithmischen Preissteigerungen als stationär angesehen werden kann. Meiner Meinung nach haben wir eine überzeugende Antwort erhalten, die durch numerische Berechnungen bestätigt wurde: Nein, es ist nicht möglich, zumindest nicht für den Zeitrahmen M1. Was den Fünf-Minuten-Zeitrahmen betrifft, so sieht die Reihe im Vergleich zum Minuten-Zeitrahmen stationärer aus, zeigt aber immer noch ein nicht-stationäres Verhalten.

• Die zweite Frage, die diese Studie zu beantworten versucht, ist eine logische Fortsetzung der ersten: Welche Datenmenge ist für die Berechnung eines bestimmten Indikators erforderlich? Meiner Meinung nach liefert der Indikator iSmirnovDistance folgende Interpretation: Für die Berechnungen muss die Datenmenge genommen werden, die in den Zeitraum zwischen zwei Abweichungen von der Homogenitäts-Nullhypothese fällt. Bis zur Ablehnung der Nullhypothese nimmt die Menge der zu analysierenden Daten schrittweise zu. Nach Ablehnung der Nullhypothese werden die vorherigen Daten als veraltet verworfen und die Berechnung der Datenmenge beginnt von neuem. Die Menge der zu analysierenden Daten ist also kein fester Wert. Dies ist ein Wert, der sich im Laufe der Zeit ständig ändert, was aufgrund der Natur eines nicht-stationären Zufallsprozesses auch so sein sollte.