Nicht-stationäre Prozesse und unechte Regression

Inhalt

• Einführung
• Nicht-Stationarität in der Regressionsanalyse
• Prüfung statistischer Hypothesen über die Parameter des Regressionsmodells
• Ungültige Spezifikation des Regressionsmodells
• Schlussfolgerung

Einführung

Die Regressionsanalyse gehört zu den angewandten mathematischen Statistiken und ist eine der gängigsten Methoden zur Behandlung empirischer Daten bei der Untersuchung von Abhängigkeiten zwischen Zufallsvariablen. Während die Korrelationsanalyse Aufschluss darüber gibt, ob zwei Zufallsvariablen miteinander in Beziehung stehen, vermittelt die Regressionsanalyse eine Vorstellung davon, wie diese Beziehung aussehen könnte. Bei der Regressionsanalyse wird zwischen gepaarter und multipler Regression unterschieden. In dieser Studie werde ich der Einfachheit halber das bekannte gepaarte lineare Regressionsmodell verwenden:

                                                Yt = b0 + b1Xt + et                                 (1)

• Yt - abhängige Variable (Antwort);
• Xt - unabhängige Variable (oder erklärende Variable);
• b0, b1 Modellparameter; t - Zeit (0,1,2,...n) n - Anzahl der beobachteten Daten;
• et - Zufallskomponente, in der Regel weißes Gauß‘sches Rauschen.

Hier wird der Index t angegeben, um zu verdeutlichen, dass wir es mit einer Zeitreihe zu tun haben und dass die Reihenfolge, in der die Zufallsvariablen liegen, für uns wichtig ist.

Das ist die Aufgabe der Regressionsanalyse:

• Schätzung der Parameter des gewählten Regressionsmodells (im linearen Fall unter Verwendung der Methode der kleinsten Quadrate)
• Prüfung statistischer Hypothesen über die Modellparameter
• Erstellung von Konfidenzintervallen für die erhaltenen Parameterschätzungen

Wenn die Analyse ergibt, dass das Modell statistisch signifikant ist, wird es als geeignet für die Vorhersage der abhängigen Variable angesehen. Bei der Anwendung der Regressionsanalyse, insbesondere auf Zeitreihen, ist jedoch stets die Einschränkung zu beachten, die sich aus dem Erfordernis der Stationarität der untersuchten Zufallsfolgen ergibt. Das Erfordernis der Stationarität setzt die Invarianz der Verteilungsfunktion einer Zufallsvariablen über die Zeit und folglich die Invarianz der mathematischen Erwartung und Varianz dieser Zufallsvariablen voraus. Versuche, die Regressionsanalyse auf nicht-stationäre Prozesse anzuwenden, können zu falschen Schlussfolgerungen über das Vorhandensein einer signifikanten Beziehung zwischen den untersuchten Variablen führen. In diesem Fall funktionieren statistische Standardtests wie F-Statistiken und t-Statistiken nicht mehr, und das Risiko, eine falsche Abhängigkeit als wahr anzunehmen, steigt um ein Vielfaches.

Nicht-Stationarität in der Regressionsanalyse

In diesem Artikel werde ich anhand von Monte-Carlo-Simulationen zeigen, wie es zu Fehlregressionen kommt, wenn die Annahme der Stationarität verletzt wird, und auch, wenn das Regressionsmodell im stationären Fall falsch spezifiziert ist. Dazu werde ich die statistische Standardbibliothek MQL5 verwenden, um Zufallszahlen zu erzeugen und kritische Werte der Normalverteilung und der Student'schen Verteilung zu berechnen, sowie die Grafikbibliothek, um die erhaltenen Ergebnisse darzustellen. Die Berechnung des Regressionsmodells wird durch die Verwendung von Methoden der Matrixalgebra stark vereinfacht. Die Gleichung für die Ermittlung der Parameter des Regressionsmodells nach der Methode der kleinsten Quadrate in Matrixform lautet zum Beispiel

(2) 

• X - Matrix der Werte der unabhängigen Variablen;
• Y - Spaltenvektor der abhängigen Variable;
• b - Spaltenvektor der unbekannten Parameter, die anhand der Stichprobe zu schätzen sind.

In MQL5 kann der b-Vektor (in unserem Fall der gepaarten, linearen Regression besteht er aus zwei Elementen - b0 und b1) gefunden werden, indem die pseudoinverse Matrix PInv() der X-Matrix berechnet und mit dem Y-Vektor multipliziert wird:

pinv = x.PInv(); 

Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS

Dies ist eine verkürzte Version der Berechnung. Wir können Schritt für Schritt berechnen, wie in der Gleichung angegeben:

xt = x.Transpose();

xtm = xt.MatMul(x);
inv = xtm.Inv();      
invt = inv.MatMul(xt);
Coeff_B = invt.MatMul(Y); // vector of regression parameters using OLS

Das Ergebnis wird dasselbe sein.

Für die Modellierung benötigen wir ein Random-Walk-Modell als Beispiel für einen nicht-stationären Prozess. Wir werden dieses Modell sowohl für die abhängige Variable Y als auch für die unabhängige Variable X erstellen. Anschließend konstruieren wir eine Regression von Y auf X und bewerten einen Indikator wie das R-Quadrat (Bestimmtheitsmaß), berechnen die t-Statistik und analysieren die Residuen des Regressionsmodells auf Korrelationsabhängigkeit.                                            

 Yt = Yt-1 + zt                           (3)

  Xt = Xt-1 + vt                           (4)

zt und vt - zwei unabhängig voneinander erzeugte Gauß'sche Prozesse des „weißen Rauschens“ mit mathematischem Erwartungswert Null und der Einheitsvarianz N(0,1);

Zwei mögliche Verläufe eines solchen Prozesses sind in Abb. 1 dargestellt

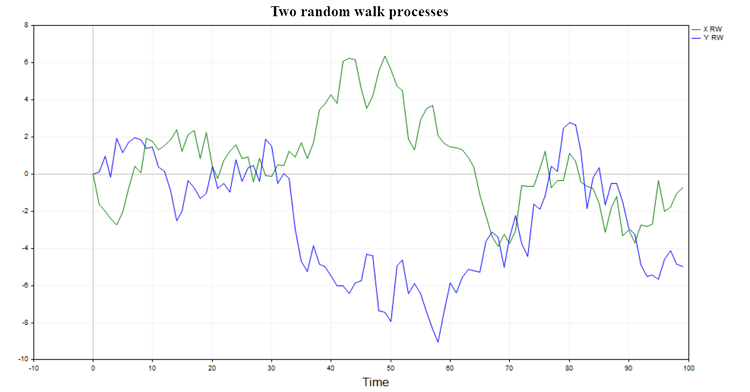
Abb. 1. Zwei Random Walks

Solche Prozesse haben kein Gedächtnis und stehen in keinerlei Beziehung zueinander, sodass man natürlich erwarten kann, dass die Regression eines Random Walks auf einen anderen keine signifikanten Ergebnisse liefert und die Hypothese eines Zusammenhangs zwischen zwei Random Walks in der Regel verworfen wird (mit Ausnahme eines kleinen Prozentsatzes von Fällen, die durch das gewählte Signifikanzniveau bestimmt werden).

Ein Beispiel für eine der möglichen Regressionen ist in Abb. 2 dargestellt:

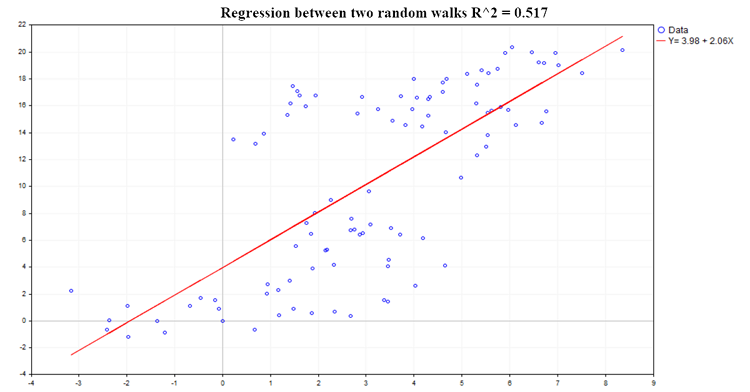
Abb. 2. Regression zwischen zwei Random Walks, R2=0,517

Der Bestimmungskoeffizient (R^2) wird anhand der folgenden Gleichung berechnet: 

R^2 = 1 - SSE/TSS                              (5)

• SSE - Summe der quadrierten Schätzung der Fehler;
• RSS - Summe der Quadrate aufgrund der Regression;
• TSS - Gesamtsumme der Quadrate = RSS+SSE;

Der Code zur Berechnung aller wichtigen Regressionsmerkmale:

      pinv = x.PInv();
      Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS
      yRegression = x.MatMul(Coeff);  // y regression
      res = Y-yRegression;   //  regression residuals, y - y regression
      yMean = Y.Mean();
      reg_yMean = yRegression-yMean;  // y regression - mean y
      reg_yMeanT = reg_yMean.Transpose();
      RSS = reg_yMeanT.MatMul(reg_yMean);  // Sum( y regression - y mean )^2 , sum of squares due to regression
      resT = res.Transpose();
      SSE = resT.MatMul(res);  // Sum(y - regression y)^2
      TSS = RSS[0,0]+SSE[0,0];  // Total sum of squares
      RSquare = 1-SSE[0,0]/TSS;  // R-square determination ratio
      R2_data[s] = RSquare;

      Vres = SSE[0,0]/(T-2);           // residuals variance estimate
      SEb1 = MathSqrt(Vres/SX);        // estimate of the standard deviation of the b1 ratio deviation of the regression Y = b0 + b1*X;
      t_stat[s] = (Coeff[1,0]-0)/SEb1; // find the t-statistic for the b1 ratio under the hypothesis that b1 = 0;

Die R^2-Werte reichen von 0 bis 1. Im Falle der gepaarten linearen Regression ist R^2 gleich dem Quadrat des gemeinsamen Korrelationsverhältnisses zwischen X und Y. Wenn X keinen Einfluss auf Y hat, ist R^2 nahe Null, und wenn die abhängige Variable Y durch die abhängige Variable X erklärt wird, tendiert R^2 gegen Eins. In unserem Fall der Regression zweier unabhängiger Random Walks wäre es logisch zu erwarten, dass sie um Null herum verteilt ist. Um dies zu überprüfen, werden wir die Verteilung von R^2 konstruieren, indem wir 1000 Paare von Random Walks mit jeweils 100 Beobachtungen nach der Monte-Carlo-Methode simulieren und anschließend das R^2-Verhältnis für jedes Paar berechnen. Als Ergebnis erhalten wir die folgende Verteilung (Abb. 3):

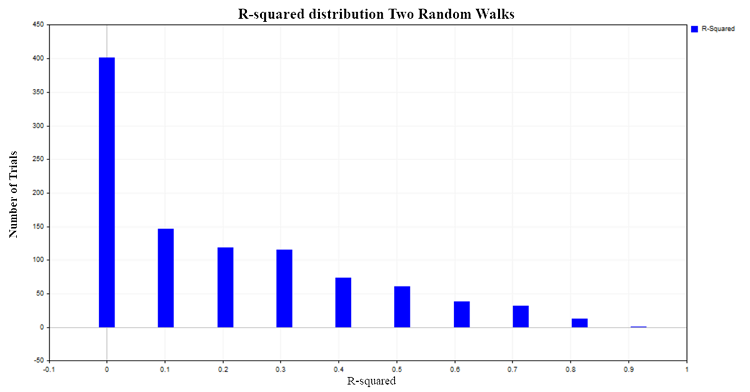
Abb. 3. R2-Verteilung für zwei Random Walks

In etwa 50 % der Fälle weist das Bestimmungsverhältnis Werte über 0,2 auf, was auf das Vorhandensein einer Beziehung zwischen Größen hinweist, die nicht miteinander verbunden sind. Zum Vergleich betrachten wir die R^2-Verteilung für zwei unabhängige, aber bereits stationäre Prozesse. Ein geeignetes Modell für einen solchen Prozess ist das Modell des weißen Gaußschen Rauschens.

                    Yt =  et                                   (6) 

 et  -  Gauß‘sches Weißes Rauschen N(0,1)

Erzeugen wir 1000 Paare von stationären Zufallsprozessen mit jeweils 100 Beobachtungen. Als Ergebnis erhält man die erwartete Verteilung von R^2 um Null, Abb. 4:

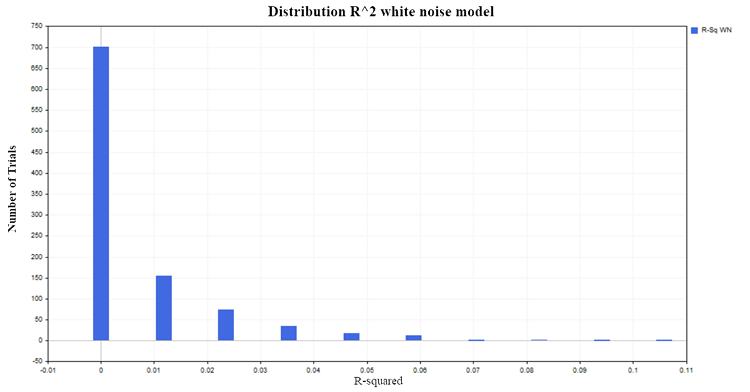
Abb. 4. R2-Verteilung, Modell des weißen Rauschens

Kehren wir zu den beiden Random Walks zurück und sehen wir uns das Verhalten der t-Statistik an, die berechnet wurde, um die Signifikanz der Parameter in unserem linearen Regressionsmodell zu bewerten.

Prüfung statistischer Hypothesen über die Parameter des Regressionsmodells

Die aus der Stichprobe berechneten Regressionskennzahlen sind selbst Zufallsvariablen, sodass die Signifikanz dieser Stichprobenmerkmale überprüft werden muss. Bei der Prüfung der Signifikanz des Regressionsparameters b1 wird die Nullhypothese (H0) aufgestellt, dass die erklärende Variable X keinen Einfluss auf die abhängige Variable Y hat. Mit anderen Worten: H0(i) : b1 = 0 und der Parameter b1 ist nicht signifikant von Null verschieden. Die Alternativhypothese (H1) besagt, dass der Parameter b1 signifikant von Null verschieden ist. Das heißt, H1(i):b1 ≠ 0 und somit beeinflusst der Prädiktor X die abhängige Variable Y.

Um diese Hypothese zu testen, wird die t-Statistik verwendet:

                                               t = bi /SEi                                      (7)

SEi - Standardabweichung des bi geschätzten Parameters 

Diese Statistik hat die Student'sche Verteilung ta/2 (n-p) mit (n-p) Freiheitsgraden.

• n - Menge der Daten, die für die Berechnung im Regressionsmodell verwendet werden (in unserem Fall 100);
• p - Anzahl der geschätzten Parameter (in unserem Fall der gepaarten Regression sind es 2);
• a - Signifikanzniveau (1,5,10%).

Für unser Experiment habe ich ein Signifikanzniveau von 5 % gewählt. Wenn die t-Statistiken in absoluten Werten den kritischen Wert der Student'schen Verteilung {|t| > t0.025 (98) =1.9844} überschreiten, können wir daraus schließen, dass der Regressionsparameter b von Null1 abweicht und folglich eine Beziehung zwischen der erklärenden Variable X und der abhängigen Variable Y besteht. Da ich das Signifikanzniveau von 5 % gewählt habe, sollten wir von der Gesamtzahl der durchgeführten Tests nur etwa 5 % falsche Ablehnungen der Nullhypothese erwarten. Den Simulationsergebnissen zufolge lehnt die t-Statistik die Nullhypothese jedoch zu häufig ab (fälschlicherweise, da keine Abhängigkeit besteht), nämlich in etwa 75 % der Fälle (Abb. 5):

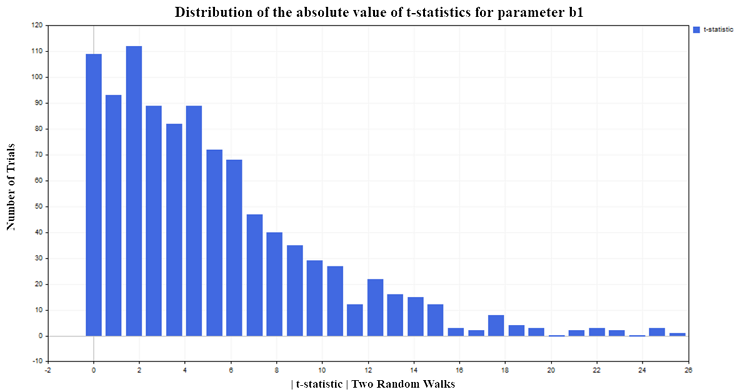
Abb. 5. Verteilung des absoluten Werts der t-Statistik für den Parameter b1

Außerdem möchte ich auf folgende Entwicklung hinweisen. Je mehr Beobachtungen in der Stichprobe enthalten sind, desto größer ist der Prozentsatz der Ablehnung der Nullhypothese. Es ergibt sich eine scheinbar paradoxe Situation: Je größer die Stichprobe, desto stärker wirkt sich der Prädiktor X auf die unabhängige Variable Y aus und desto stärker ist die Beziehung zwischen den Variablen. Es handelt sich hier natürlich nicht um ein Paradoxon, sondern einfach um die Anwendung der Regressionsanalyse auf Prozesse, auf die sie nicht anwendbar ist. Wir sehen, dass die Standard-t-Statistik versagt, wenn die Regression auf die Analyse von nicht-stationären Zeitreihen angewendet wird. Diese Situation wird als unechte Regression bezeichnet.

Ungültige Spezifikation des Regressionsmodells

Aber Nicht-Stationarität ist nur ein Grund, warum statistische Standardtests versagen. Sie können auch dann irreführend sein, wenn die beiden Reihen stationär sind, aber die Spezifikation des Regressionsmodells verletzt wird. Dies ist der Fall, wenn die falsche Form der funktionalen Abhängigkeit zwischen den Variablen gewählt wird (linear statt nicht-linear). Oder wenn das Modell die unabhängige Variable X, von der die Variable Y tatsächlich abhängt, auslässt und stattdessen fälschlicherweise eine völlig unbedeutende Variable verwendet wird. Um dies zu verdeutlichen, lassen Sie uns zwei unabhängige stationäre Prozesse X und Y konstruieren. Als Beispiel werde ich das autoregressive Modell erster Ordnung AR(1) verwenden:

Yt = A*Yt-1 + zt                           (8)

 Xt = B*Xt-1 + vt                          (9)

• zt und vt - zwei unabhängig voneinander erzeugte Gauß'sche Prozesse mit „weißem Rauschen“, mathematischer Erwartung Null und N(0,1) Einheitsvarianz;
• A und B sind Parameter des AR(1)-Modells, die im absoluten Wert strikt kleiner als 1 sein sollten, um die Stationaritätsbedingung zu erfüllen.

Konstruieren wir erneut eine Regression von Y auf X (z. B. mit den AR(1)-Parametern A=0,5, B=0,5) unter den gleichen Bedingungen wie für das Modell der beiden Random Walks (100 Daten in jedem Prozess, Anzahl der Tests 1000). Daraus ergibt sich die folgende t-Verteilung für den b-Regressionsparameter b1 (Abb. 6):

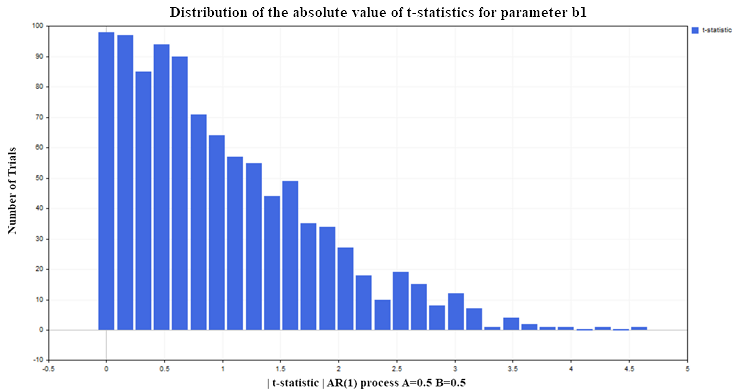
Abb. 6. Verteilung des absoluten Werts der t-Statistik für den Parameter b1

Wie wir sehen können, ist die Situation bei der Ablehnung der Nullhypothese hier viel besser als im nicht-stationären Fall. Nur etwa 12-13 % der falschen Ablehnungen bei einem akzeptablen Niveau von 5 % (der kritische Wert der Student'schen Verteilung für 98 Freiheitsgrade = 1,9844). Bei stationären Prozessen nimmt dieser Prozentsatz nicht zu, wenn sich der Stichprobenumfang erhöht, sondern bleibt auf demselben Niveau. Diesmal versagt die t-Statistik nicht, weil die Variablen nicht stationär sind, was in Ordnung ist, sondern weil das Regressionsmodell falsch spezifiziert ist. Obwohl die Form der Abhängigkeit richtig gewählt wurde (linear), haben wir angenommen, dass die Variable Y nicht von den verzögerten Werten derselben Variable abhängt, sondern von den Werten der Variable X, die in keinem Zusammenhang mit der Variable Y steht. Wenn wir die Variable X im Regressionsmodell belassen und verzögerte Werte von Y hinzufügen, verbessern sich die statistischen Eigenschaften der Regressionsparameter, und die t-Statistiken führen nicht mehr häufiger zu falschen Schlussfolgerungen als das festgelegte Signifikanzniveau (in unserem Fall 5 %). In der Praxis sollte man die Residuenanalyse nutzen, um festzustellen, ob ein Regressionsmodell fehlerhaft oder falsch spezifiziert ist. 

                                         Residuals =  Yt - Yreg_t                       (10)

• Yt - tatsächliche Werte der abhängigen Variable Y;
• Yreg_t - berechnete Regressionswerte

Wenn die Residuen des Modells eine signifikante Autokorrelation aufweisen, ist dies ein Zeichen dafür, dass das Regressionsmodell falsch spezifiziert oder verfälscht ist. 

Der Code zur Berechnung der Autokorrelationsfunktion (ACF) und der 99%-Konfidenzintervalle

////////////////////////// ACF calculation /////////////////////////////////////////

   avgres = res.Mean();  // mean of residuals
   ArrayResize(acov,K);
   ArrayResize(acf,K);
   ArrayResize(se,K);
   ArrayResize(se2,K);

   for(i=0; i<K; i++)
     {
      ArrayResize(c,T-i);
      for(j=0; j<T-i; j++)
        {
         c[j] = (res[j,0]-avgres)*(res[j+i,0]-avgres);
        }
      acov[i] = double(MathSum(c)/T);  // Auto covariance
      acf [i] = acov [i]/acov [0];  // Auto correlation
      se[i] =   MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);    // 99% confidence intervals for ACF //
      se2[i] = -MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);
     }

Abb. 7 zeigt das Diagramm der Autokorrelationsfunktion (ACF) der Regressionsresiduen für die beiden Random-Walk-Modelle. Ebenfalls dargestellt sind die Grenzen des 99%igen Konfidenzbereichs für die ACF, berechnet nach der Gleichung SE = MathQuantileNormal(0,995,0,1,err)/MathSqrt(T); T - Anzahl der Beobachtungen im Regressionsmodell.

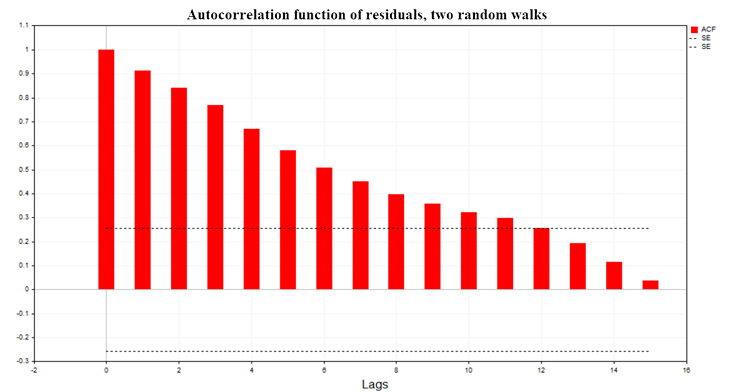
Abb. 7. Autokorrelationsfunktion der Residuen, zwei Random Walks

Abb. 8 zeigt das ACF-Diagramm der Regressionsresiduen für ein Modell aus zwei AR(1)-Prozessen mit den Parametern A=0,5, В=0,5

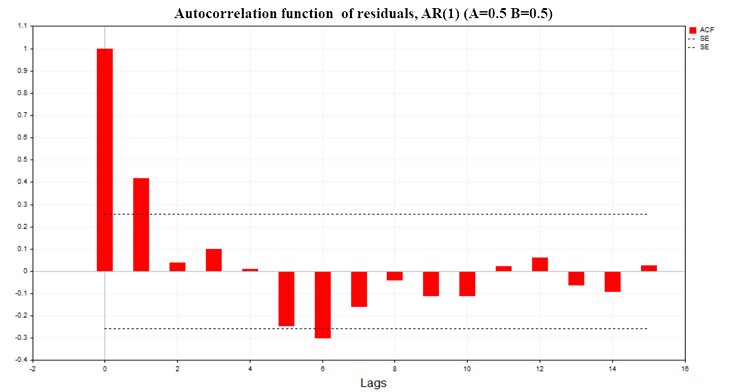
Abb. 8. Autokorrelationsfunktion der Residuen, AR(1) A=0,5 B=0,5

Wie aus den Diagrammen ersichtlich ist, besteht eine signifikante Autokorrelation in den Residuen der Regressionsmodelle. Es handelt sich also um ein falsch definiertes Regressionsmodell oder sogar um eine unechte Regression. Das Durbin-Watson-Kriterium (DW) wird ebenfalls auf der Grundlage der Autokorrelationsfunktion der Residuen erstellt. Sie wird verwendet, um die Autokorrelation der Residuen eines Regressionsmodells mit einer Verzögerung von 1 zu testen. 

                                            DW = 2*(1-ACF(1))                         (11)

Bei einer unechten Regression ist diese Statistik nahe Null.

Schlussfolgerung

In diesem Artikel ging es mir vor allem darum, die Grenzen der Anwendbarkeit statistischer Methoden, insbesondere der Regressionsanalyse, zu verstehen und die Folgen einer Verletzung dieser Grenzen aufzuzeigen. Es ist sehr einfach, formale Berechnungen durchzuführen, „signifikante“ Statistiken zu sehen und die falsche Schlussfolgerung über das Vorhandensein einer Verbindung zwischen zwei Zufallsprozessen zu ziehen.

Die Schlussfolgerung, die aus all dem gezogen werden kann: 

• Vor der Erstellung eines Regressionsmodells müssen zunächst alle Variablen des Modells auf Stationarität geprüft werden.
• Wenn eine Variable nicht stationär ist, sollte sie in eine stationäre Form gebracht werden (in der Regel durch Bildung erster Differenzen) und dann versucht werden, ein Modell mit dieser modifizierten Variable zu erstellen.
• Nach der Erstellung des Modells müssen die Residuen auf Autokorrelationsabhängigkeit untersucht werden.
• Wenn die Werte der Autokorrelationsfunktion der Residuen nicht über den Konfidenzbereich von 99 % hinausgehen, kann die Signifikanz der Parameter des Regressionsmodells mit Hilfe der t-Statistik bewertet werden.
• Wenn sie sich als signifikant erweist, können wir damit beginnen, die abhängige Variable Y anhand des konstruierten Modells vorherzusagen.

Um alle oben genannten Ergebnisse zu reproduzieren, wählen Sie zu Beginn des Skripts die Werte der Variablen M = 1, 0 oder 0,5, je nachdem, für welches Modell Sie die Ergebnisse erhalten möchten. Danach müssen Sie ganz unten im Skript den Codeblock deaktivieren, der für die Anzeige bestimmter Statistiken für jedes einzelne Modell zuständig ist. Kommentieren Sie außerdem in der Datei Math.mqh zwei Code-Strings für die Funktion aus, die die empirische Wahrscheinlichkeitsdichtefunktion (MathProbabilityDensityEmpirical) berechnet, um die Häufigkeiten im Diagramm anzuzeigen

 5432  //  for(int i=0; i<count; i++)
 5433 //    pdf[i]*=coef;