Red neuronal en la práctica: Pseudo inversa (II)

Introducción

Hola a todos, y bienvenidos a otro artículo sobre redes neuronales. 

En el artículo anterior "Red neuronal en la práctica: Pseudo inversa (I)", mostré cómo podríamos usar una función disponible en la biblioteca de MQL5 para calcular la pseudo inversa. Sin embargo, el método presente en la biblioteca de MQL5, al igual que en muchos otros lenguajes de programación, está diseñado para calcular la pseudo inversa cuando usamos matrices, o al menos algún tipo de estructura que pueda asemejarse a una matriz.

Pues bien, aunque en ese artículo se mostró cómo se haría la multiplicación de dos matrices, e incluso la factorización para obtener el determinante de cualquier matriz, lo cual es importante para saber si una matriz puede o no ser invertida, aún faltaba implementar otra factorización. Esto es para que tú, mi querido lector, puedas comprender cómo se realiza la factorización para obtener los valores de la pseudo inversa. Esa factorización consiste en generar la inversa de una matriz.

Quizás te estés preguntando: ¿Y qué pasa con la transpuesta? Bueno, en el artículo anterior mostré cómo podrías realizar la factorización para simular la multiplicación de una matriz por su transpuesta, lo que no supone un problema.

No obstante, el cálculo que nos falta implementar, que es precisamente obtener la matriz inversa, no es algo que realmente desee mostrar. No porque sea complicado de implementar, sino porque no veo la necesidad de mostrarlo. Esto se debe a que estos artículos tienen un enfoque didáctico y no están destinados a explicar cómo implementar cada funcionalidad. Con esto en mente, pensé en hacer algo un poco diferente en este artículo. En lugar de mostrar cómo implementar la factorización para obtener la inversa de una matriz, nos centraremos en cómo factorizar la pseudo inversa, usando los datos que hemos manejado desde el principio. Es decir, no tiene sentido montar y mostrar cómo factorizamos algo de manera genérica si podemos hacer lo mismo de forma especializada. Y lo mejor es que tú, querido lector, entenderás mucho mejor por qué las cosas funcionan así que si hubiéramos seguido una lógica genérica para crear la factorización, como se mostró en el artículo anterior, donde esas funciones eran genéricas. Pero podemos hacer el cálculo mucho más rápido si lo hacemos de manera específica. Para comprender mejor este concepto, pasemos a un nuevo tema.

¿Por qué generalizar, si podemos especializar los procedimientos?

El título que estamos utilizando en este tema es, como mínimo, controvertido o, en muchos casos, algo que muchos no entienden. Generalmente, muchos programadores prefieren crear las cosas de forma bastante genérica. O, al menos, creen que al hacer algo genérico, tendrán en sus manos una solución más útil y rápida en la mayoría de los casos. Sin embargo, a menudo buscan desarrollar algo que funcione en cualquier tipo de escenario. Pues bien, la cuestión de la generalización, en algunos casos, nos genera un costo que no necesitamos asumir. Esto se debe a que, si el objetivo puede alcanzarse mediante un procedimiento especializado, ¿por qué generalizar? En estos casos, la generalización no nos aporta ningún beneficio que justifique su existencia.

Si piensas que estoy diciendo tonterías, reflexionemos un poco y entenderás lo que quiero explicar. Para entender mejor, quiero que pienses y respondas a la siguiente pregunta:

¿Qué es un ordenador? ¿Por qué tiene tantos componentes y funciones? ¿Por qué de vez en cuando aparece un nuevo hardware en sustitución de un software?

Bueno, si tienes menos de 40 años o naciste después de los años 90 y no has investigado sobre tecnologías antiguas, lo que te voy a decir quizá te parezca absurdo. Pero entre los años 70 y mediados de los 80, los ordenadores no eran como los conocemos hoy. Para que te hagas una idea, los juegos electrónicos se programaban completamente en hardware, utilizando transistores, resistencias, condensadores y otros componentes. No existían juegos que usaran software. Todo se hacía mediante hardware. Ahora piensa en la dificultad de crear un juego, incluso algo tan simple como el PONG, usando solo componentes electrónicos. La gente de verdad era muy hábil en lo que hacía. No era una tarea sencilla.

Sin embargo, debido a que todo se hacía con componentes discretos, como se conocen en electrónica los transistores, resistencias y condensadores, las cosas eran mucho más lentas y debían ser simples. Pero cuando aparecieron los primeros kits de montaje, ya fuera un Z80 o un 6502, las cosas empezaron a cambiar. Estos procesadores, que aún se pueden encontrar hoy en día, ayudaron mucho a que el software tomara protagonismo. Era mucho más sencillo y rápido programar un cálculo mediante software que realizar el mismo cálculo usando hardware. Así comenzó la era del software. Pero, ¿qué tiene esto que ver con redes neuronales y con lo que estamos implementando? Paciencia, querido lector, ya llegaremos a ello.

El simple hecho de poder programar algo relativamente complejo mediante instrucciones simples hizo que el ordenador se convirtiera en una herramienta fascinante. Muchas cosas primero se desarrollan en software de forma bastante genérica. El hecho de que esto ocurra permite que el desarrollo de nuevas soluciones sea tan rápido que muchas veces es difícil de seguir el ritmo. Tanto es así que gran parte de lo que vemos hoy en las GPUs (tarjetas gráficas) primero nace en software. Estas soluciones se refinan al máximo hasta que son lo suficientemente simples como para ser implementadas en hardware. Y aquí radica la clave de este tema. Podemos generalizar las cosas, pero esto las hace lentas, no en su implementación, sino en su ejecución. Al generalizar, debemos realizar pruebas constantes para asegurarnos de que no se generen errores extraños durante la ejecución de las factorizaciones. Sin embargo, si lo hacemos de manera especializada, podemos reducir la frecuencia de las pruebas, permitiendo que las ejecuciones sean mucho más rápidas.

Bien, pero ¿por qué preocuparnos por esto si estamos manejando solo cuatro valores en la base de datos? Esta es la cuestión, querido lector. Primero creamos un sistema que pueda trabajar con pocos datos, y luego escalamos a una cantidad cada vez mayor. Llega un momento en que el tiempo de ejecución deja de ser eficiente. Es en ese momento cuando surge la necesidad de un hardware especializado para realizar el mismo tipo de cálculo que antes se hacía vía software. Así nacen las nuevas tecnologías en términos de hardware.

Si has seguido el desarrollo del hardware, habrás notado que tiende a dirigirse hacia ciertas tecnologías. ¿Pero por qué? El motivo es precisamente este. La solución vía software se vuelve más costosa que la misma solución vía hardware. Entonces, antes de que decidas comprar una nueva GPU solo porque se promociona con alguna funcionalidad que acelera los cálculos para redes neuronales, tú, querido lector y entusiasta, debes saber cómo aprovechar de la mejor manera posible el hardware que ya tienes. Y para hacerlo, necesitamos un cálculo que no sea genérico, sino especializado en realizar una tarea específica. En nuestro caso actual, queremos optimizar el cálculo de la pseudo inversa. Por eso, en lugar de crear un artículo con un cálculo genérico para mostrar cómo factorizar la pseudo inversa, hemos decidido implementar un cálculo un poco más especializado. Aunque cabe mencionar que no estará optimizado en términos de poder de computación ya que el objetivo es ser didáctico, no eficiente en ese aspecto. Y cuando digo esto, me refiero a cómo se implementarán las cosas. Es decir, no pretendo llegar a un punto de maximización del poder computacional en el que se vuelva necesaria la implementación de la factorización en un modelo de hardware especializado. Esto es, precisamente, lo que sucede cuando surge una nueva tecnología de hardware.

Mucho se ha hablado de las tarjetas gráficas o incluso de los procesadores con capacidades de cálculo para redes neuronales. Pero tú, querido lector, ¿sabes si este tipo de enfoque es realmente lo que necesitas? Para responder a esta pregunta, primero debes entender qué está sucediendo en términos de software. Entonces, pasemos al siguiente tema, donde veremos qué se implementará en términos de software.

Pseudo inversa, una propuesta para su abordaje

Muy bien, creo que tú, mi querido lector, has logrado entender el tema anterior. Así que pensemos en lo siguiente: En nuestra base de datos, cada información puede visualizarse en un gráfico de dos coordenadas, siendo X y Y, que usamos para intentar crear algún tipo de relación matemática entre los datos. Bien, esto ha sido explorado desde el inicio de esta pequeña secuencia. El hecho de poder utilizar una regresión lineal nos ayuda mucho en lo que necesitamos implementar en términos de código. Ya mostré en artículos anteriores cómo hacer el cálculo escalar para poder encontrar el coeficiente angular y el punto de intersección, lo que nos permite crear la ecuación que se muestra a continuación.

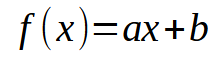
En esta, los puntos buscados son los valores de < a > y < b >. Sin embargo, existe otra forma además de la ya mostrada. Esta involucra factorizaciones de matrices. Básicamente, lo que necesitamos implementar es una pseudo inversa. El cálculo para hacer esto se muestra justo abajo.

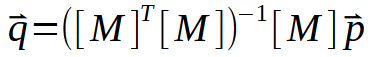
Aquí, los valores para las constantes < a > y < b > están en el vector < q >. Así, la matriz M deberá pasar por una pequeña secuencia de factorizaciones hasta que se logre generar el vector < q >. Pero lo interesante no se ve en la imagen de arriba, sino en la imagen de abajo.

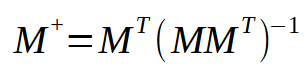
Esta imagen es justamente lo que necesitamos implementar, ya que es la representación de lo que ocurre en la pseudo inversa. Observa que el resultado es una matriz que recibe un nombre especial: pseudo inversa. Como puedes ver en la imagen anterior, esta se multiplica por un vector < p >, dando origen al vector < q >. Y este vector < q > es el resultado que queremos obtener.

En el artículo anterior y al inicio de este, mencioné que la función pseudo inversa se implementa en bibliotecas, de manera que utiliza matrices para ello. Pero aquí no estamos usando matrices. Estamos usando algo similar a ellas: los arrays. Bien, en este punto tenemos un problema cuya solución es: convertir el array en una matriz, o implementar la pseudo inversa para usar arrays. Debido a que quiero mostrar cómo se implementa el cálculo, optaremos por el segundo enfoque, es decir, implementar la pseudo inversa. El cálculo para esto se muestra en el fragmento justo abajo.

01. //+------------------------------------------------------------------+
02. matrix __PInv(const double &A[])
03. {
04.     double M[], T[4], Det;
05. 
06.     ArrayResize(M, A.Size() * 2);
07.     M[0] = M[1] = 0;
08.     M[3] = (double)A.Size();
09.     for (uint c = 0; c < M[3]; c++)
10.     {
11.         M[0] += (A[c] * A[c]);
12.         M[2] = (M[1] += A[c]);
13.     }
14.     Det = (M[0] * M[3]) - (M[1] * M[2]);
15.     T[0] = M[3] / Det;
16.     T[1] = T[2] = -(M[1] / Det);
17.     T[3] = M[0] / Det;
18.     ZeroMemory(M);
19.     for (uint c = 0; c < A.Size(); c++)
20.     {
21.         M[(c * 2) + 0] = (A[c] * T[0]) + T[1];
22.         M[(c * 2) + 1] = (A[c] * T[2]) + T[3];
23.     }
24. 
25.     matrix Ret;
26.     Ret.Init(A.Size(), 2);
27.     for (uint c = 0; c < A.Size(); c++)
28.     {
29.         Ret[c][0] = M[(c * 2) + 0];
30.         Ret[c][1] = M[(c * 2) + 1];
31.     }
32. 
33.     return Ret;
34. }
35. //+------------------------------------------------------------------+

Este fragmento, mostrado arriba, hace todo el trabajo por nosotros. Parece algo increíblemente complicado, pero no lo es. En realidad, es bastante simple y directo. Aquí recibimos un vector en formato de array con varios valores del tipo double. Podríamos usar otro tipo, pero es bueno que tú, mi querido lector, comiences a acostumbrarte a usar valores double de ahora en adelante. El motivo será comprendido pronto. Después de que todas las factorizaciones se hayan ejecutado, obtendremos como resultado una matriz de valores del tipo double.

Ahora presta atención: El array que estamos aplicando es del tipo sencillo. Pero aun así será tratado como si fuera una matriz con dos columnas. ¿Pero cómo es esto posible? Bien, entendamos esto antes de ver cómo utilizar este código.

En la línea seis, creamos una matriz que tendrá tantas filas como elementos haya en el array. Pero esta matriz tendrá dos columnas, a diferencia del array que internamente solo tiene una columna. Ahora, en las líneas siete y ocho, inicializamos la matriz M de una forma bastante específica. Para entenderlo, observa la imagen de abajo.

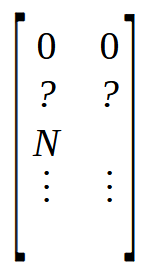
Notamos que las dos primeras posiciones están en cero, seguidas de otras dos con un signo de interrogación, ya que no conocemos el valor real que hay allí. Pero inmediatamente después tenemos una posición con el valor N. Este valor es el tamaño del array. ¿Por qué estoy colocando el tamaño del array en la matriz? El motivo es simple. Es más rápido buscar el valor en una posición conocida que hacerlo en una función. Y como necesitamos cuatro posiciones libres al inicio de la matriz, coloco el tamaño del array en la posición indicada como N. Esto es lo que se está haciendo en las líneas siete y ocho.

Muy bien, observando la imagen antes del fragmento, vemos que lo primero que se debe hacer es multiplicar una matriz por su transpuesta. Pero aquí aún no tenemos ninguna matriz. Todo lo que tenemos es un vector, o mejor dicho, un array. Entonces, ¿cómo realizaremos dicha multiplicación? Es simple, para esto usaremos el bucle presente en la línea nueve. Pero, ¿qué es esto? ¿Te has vuelto loco? Esto no tiene ningún sentido. ¿Qué estás tratando de hacer? Bien, vamos a entenderlo mirando la imagen de abajo.

Un array no es más que una colección de valores, que aquí están representados de a0 an. Si visualizas el concepto no como un array, sino como una matriz, podrás ver una matriz de una columna o de una fila, dependiendo, claro está, de cómo estén organizados los datos. Bien, si realizas una operación entre una matriz de una columna y otra de una fila, obtendrás un valor escalar, no una matriz. Recuerda que la fórmula de la pseudo inversa primero realiza la multiplicación entre una matriz y su transpuesta. Pero podemos interpretar este array mostrado anteriormente como algo similar a lo que se ve en la imagen de abajo.

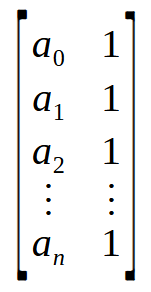
¡Wow! Ahora sí, tenemos la matriz que necesitamos. Así, al multiplicar una matriz de n x por su transpuesta, obtenemos como resultado una matriz de 2 x 2. Es decir, logramos transformar un vector, o mejor dicho, un array, en una matriz 2 x 2. Y esto es lo que el bucle for de la línea nueve está haciendo: multiplicando una matriz por su transpuesta y colocando el resultado en la parte superior de la matriz que declaramos en la línea seis.

Ahora necesitamos encontrar la matriz inversa de la que acabamos de construir. En una matriz 2 x 2, la forma más rápida y sencilla de encontrar la inversa es usando el determinante. Nota lo siguiente: no necesitamos un método genérico para encontrar la matriz inversa ni el determinante. Tampoco necesitamos un método genérico para multiplicar la matriz por su transpuesta. Podemos hacer todo de manera directa, ya que lo hemos reducido a una matriz 2 x 2, lo que simplifica mucho el trabajo y lo hace más rápido. De esta manera, para encontrar el determinante, usamos la línea 14. Listo, ahora podemos buscar la matriz inversa. Este cálculo, que de forma genérica sería muy lento, se hace de manera extremadamente rápida simplemente porque hemos tomado algunas decisiones. Entonces, en las líneas 15 a 17, generamos la inversa de la matriz que obtuvimos a partir del array. Ahora, casi todo está listo. Lo siguiente que debemos hacer es limpiar la matriz M, lo cual se realiza en la línea 18. Ahora presta atención: La matriz T contiene la matriz inversa y el array A contiene los valores sobre los que queremos factorizar la pseudo inversa. Lo único que falta por hacer es multiplicar una por el otro y colocar el resultado en la matriz M. El detalle es que la matriz T es de tipo 2 x 2, y el array puede verse como una matriz n x 2. Así obtendremos como resultado una matriz n x 2 que contendrá precisamente los valores de la pseudo inversa.

Esta factorización se realiza en el bucle de la línea 19. Luego, en las líneas 21 y 22, colocamos los valores dentro de la matriz M. Y ahí está el resultado de la pseudo inversa. Este cálculo que te estoy mostrando puede trasladarse a un bloque en OpenCL, aprovechando así las capacidades de la GPU para calcular la regresión lineal de una base de datos muy grande. En algunos casos, usar la CPU haría que los cálculos tomaran varios minutos, pero al delegar todo el trabajo a la GPU, se completaría mucho más rápido. Esta es la optimización a la que me referí al inicio de este artículo.

Todo lo que nos queda por hacer es transferir el resultado del array M a una matriz. Esto se realiza entre las líneas 25 y 31. Sin embargo, lo que ya se encuentra en M es el resultado que buscamos. En el anexo, dejaré un código para que veas cómo funcionan las cosas. Así podrás compararlo con lo mostrado en el código del artículo anterior. Aunque, como todo, no es perfecto. Observa que no estoy realizando ninguna prueba dentro de esta función. Esto se debe a que, aunque es didáctica, la idea aquí es que se asemeje a algo que podría implementarse en hardware. Y en ese caso, las pruebas se harían de otra manera, ahorrándonos así tiempo de procesamiento.

Muy bien, pero esto no responde una pregunta: ¿Cómo puede esta pseudo inversa (PInv) generar tan rápidamente la regresión lineal? Bueno, para responder esto, vamos a ver un nuevo tema.

Velocidad máxima

En el tema anterior, vimos cómo, a partir de un array, podíamos realizar el cálculo de la pseudo inversa. Sin embargo, podemos acelerar aún más las cosas, de manera que el valor que obtengamos no sea el de la pseudo inversa, sino el de la regresión lineal. Y para hacer esto, necesitaremos modificar un poco el código visto en el tema anterior. Pero esta pequeña modificación será suficiente para que podamos usar toda la potencia de la GPU, o incluso de una CPU dedicada, para encontrar los factores de la ecuación lineal. Recordemos que los factores que buscamos son el coeficiente angular y el punto de intersección. El nuevo fragmento de código puede verse justo abajo.

01. //+------------------------------------------------------------------+
02. void Straight_Function(const double &Infos[], double &Ret[])
03. {
04.     double M[], T[4], Det;
05.     uint n = (uint)(Infos.Size() / 2);
06. 
07.     if (!ArrayIsDynamic(Ret))
08.     {
09.         Print("Response array must be of the dynamic type...");
10.         Det = (1 / MathAbs(0));
11.     }
12.     ArrayResize(M, Infos.Size());
13.     M[0] = M[1] = 0;
14.     M[3] = (double)(n);
15.     for (uint c = 0; c < n; c++)
16.     {
17.         M[0] += (Infos[c * 2] * Infos[c * 2]);
18.         M[2] = (M[1] += Infos[c * 2]);
19.     }
20.     Det = (M[0] * M[3]) - (M[1] * M[2]);
21.     T[0] = M[3] / Det;
22.     T[1] = T[2] = -(M[1] / Det);
23.     T[3] = M[0] / Det;
24.     ZeroMemory(M);
25.     for (uint c = 0; c < n; c++)
26.     {
27.         M[(c * 2) + 0] = (Infos[c * 2] * T[0]) + T[1];
28.         M[(c * 2) + 1] = (Infos[c * 2] * T[2]) + T[3];
29.     }
30.     ArrayResize(Ret, 2);
31.     ZeroMemory(Ret);
32.     for (uint c = 0; c < n; c++)
33.     {
34.         Ret[0] += (Infos[(c * 2) + 1] * M[(c * 2) + 0]);
35.         Ret[1] += (Infos[(c * 2) + 1] * M[(c * 2) + 1]);
36.     }
37. }
38. //+------------------------------------------------------------------+

Observa que en este fragmento de código anterior ya se está realizando una prueba. Esta prueba busca verificar si el array de retorno es de tipo dinámico. En caso contrario, la aplicación deberá cerrarse. Este cierre se realiza en la línea 10. En el artículo anterior, expliqué el significado de esta línea, así que, si tienes dudas, te sugiero revisarlo para más detalles. Fuera de eso, casi todo el código sigue funcionando de la misma manera que se vio en el tema anterior. Hasta que llegamos a la línea 30, donde las cosas toman otra dirección. Pero retrocedamos un poco para entender mejor. Al observar este código, podrías estar sorprendido por lo que está ocurriendo, ya que la multiplicación de la transpuesta con la matriz, o mejor dicho, con el array, parece algo diferente. Lo mismo ocurre con la multiplicación de la matriz inversa con la matriz original para calcular la pseudo inversa.

¿Qué significa esto que estamos viendo en este fragmento? Pues bien, lo que parece ser algo extremadamente complicado no es más que una "matriz de puntos". Para entenderlo mejor, observa la imagen a continuación.

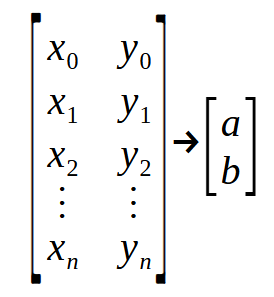
Fíjate que tenemos una "matriz" de entrada y una "matriz" de salida. En la declaración de la línea dos, el parámetro Infos es la primera matriz que se ve en la imagen anterior, y Ret es la segunda matriz de la imagen. Los valores < a > y < b > son los que estamos buscando para crear la ecuación de la recta. Ahora presta mucha atención. Cada una de las filas de la matriz de la izquierda representa un punto en el gráfico. Los valores en posiciones pares son los utilizados en la función vista en el tema anterior. Mientras que los valores en las posiciones impares representan los vectores en la fórmula mencionada al inicio de este artículo. Es decir, el vector < p >.

Como esta función, vista al inicio de este tema, recibe todos los puntos del gráfico y retorna la ecuación de la regresión lineal. Necesitamos de alguna manera separar los elementos. Y la forma de hacerlo es vincular todo entre los valores pares e impares. Por eso este código parece tan diferente al del tema anterior. Aunque en realidad no lo es, al menos hasta que llegamos a la línea 30. En ese punto, se hace algo que no se realizó en el código anterior. Tomamos el resultado de la pseudo inversa que se encuentra en la matriz M y lo multiplicamos por los vectores que están en la parte impar del parámetro Infos. Esto resulta en el vector Ret, que no es más que las constantes necesarias para crear la ecuación de la recta o la regresión lineal, como prefieras llamarlo.

Si realizas la misma operación utilizando los valores devueltos por la función PInv que vimos en el artículo anterior, obtendrás el mismo resultado que en este fragmento. Con una única diferencia: el código mostrado en este fragmento podría ser el utilizado para construir hardware dedicado a cálculos en redes neuronales. Esto daría lugar a una nueva tecnología que se integraría en procesadores. Donde la industria podría afirmar que un procesador o circuito dado contiene mecanismos de inteligencia artificial o de redes neuronales. Pero no es nada realmente revolucionario. Simplemente convertirían algo genérico, que antes se hacía en software, en algo especializado en hardware. De este modo, convirtiendo lo genérico en algo especializado.

Consideraciones finales

Muy bien, mis queridos lectores y entusiastas. Con todo lo que hemos visto hasta ahora, considero que hemos finalizado el tema sobre lo esencial que necesitas saber acerca de redes neuronales e inteligencia artificial. Aunque hasta este momento, lo que hemos tratado no se refiere a una red neuronal en sí, sino al uso y construcción de una sola neurona. Ya que solo hemos realizado un único cálculo. En el caso de una red neuronal, tenemos un conjunto de estos mismos cálculos simples, pero ejecutados en una escala mayor. Aunque en este momento puede que no te quede claro, una red neuronal no es más que la implementación de una arquitectura de grafo, donde cada nodo representa una neurona o una función de regresión lineal. Dependiendo de los resultados calculados, se sigue una dirección u otra.

Sé que puede parecer desalentador, o incluso algo trivial pensar en una red neuronal de esta forma, pero esa es la verdad. No hay nada mágico o fantástico detrás del tema, aunque los medios o personas que no entienden o no estudian este campo quieran hacértelo creer. Cualquier cosa que haga una máquina no es más que simples cálculos matemáticos. Si entiendes estos cálculos, podrás comprender una red neuronal. Y te digo más, serás capaz de entender cómo simular comportamientos de seres vivos. No es que los seres vivos sean máquinas orgánicas, aunque en algunos casos podamos pensarlo así. Pero esa es otra conversación para quienes estén más cerca de mí.

Lo que deseo para ti, mi querido y estimado lector, es que logres entender lo que realmente es una red neuronal en su forma más simple, es decir, utilizando solo una única neurona, que es justamente lo que hemos hecho hasta ahora.

En los próximos artículos, que aún no sé cómo serán, organizaremos esta neurona única en una pequeña red, para que pueda aprender algo. Como no quiero mostrar nada relacionado con mercados financieros usando estos conceptos, no esperes ver eso en el futuro, al menos no de mi parte. Mi objetivo es que entiendas, aprendas y seas capaz de explicar, basado en tu propia experiencia, qué es y cómo una red neuronal puede aprender. Y para lograr esto, será necesario que experimentes con un sistema lo suficientemente sencillo.

Así que, mantente atento a una nueva secuencia sobre este tema. Estoy pensando en algo interesante para mostrarte, algo que realmente valga la pena. En los anexos tienes los códigos para comenzar a estudiar cómo funciona una sola neurona.