非定常過程と偽回帰

内容

• はじめに
• 回帰分析における非定常性
• 回帰モデルのパラメータに関する統計的仮説の検定
• 回帰モデルの無効な仕様
• 結論

はじめに

応用数理統計学のセクションの1つである回帰分析は、確率変数間の依存関係の研究において経験的データを扱う最も一般的な方法の1つです。相関分析では、2つの確率変数が互いに関連しているかどうかを調べることができますが、回帰分析では、この関係がどのような形をとるかを知ることができます。回帰分析では、対回帰と重回帰が区別されます。この研究では、単純化のために、よく知られた対線形回帰モデルを使用します。

                                                Yt = b0 + b1Xt + et                                 (1)

• Yt：従属変数（レスポンス）
• Xt：独立変数（または説明変数）
• b0、b1：モデルパラメータ、t - 時間 (0,1,2,...n)、n - 観測データ数
• et：ランダム成分（通常はガウスホワイトノイズ）

ここでは、時系列を扱っていること、そして確率変数が位置するシーケンスが重要であることを強調するために、インデックスtを示しています。

回帰分析の課題は

• 選択された回帰モデルのパラメータを推定する（線形の場合は、通常の最小2乗法を使用する）
• モデルパラメータに関する統計的仮説を検証する
• 得られたパラメータ推定値の信頼区間を構築する

分析によってモデルが統計的に有意であることがわかれば、そのモデルは従属変数の予測に使用するのに適していると考えられます。しかし、回帰分析を適用するとき、特に時系列に適用するときは、調査対象のランダム系列に課される定常性の要件に伴う限界を常に覚えておく必要があります。定常性の要件は、確率変数の分布関数が時間にわたって不変であり、その結果、この確率変数の数学的期待値と分散が不変であることを仮定しています。非定常過程に回帰分析を適用しようとすると、調査対象の変数間に有意な関係が存在するという誤った結論を導く可能性があります。この場合、F統計やt統計のような標準的な統計的検定は機能しなくなり、誤った依存性を真実として受け入れてしまうリスクが何倍にも高まります。

回帰分析における非定常性

この記事では、モンテカルロシミュレーションを使用して、定常性の仮定が破られたときに、また定常性の場合に回帰モデルが誤って指定されたときに、どのようにスプリアス回帰が起こるかを示します。このために、私は標準的なMQL5統計ライブラリを使用して乱数を生成し、正規分布とt分布の臨界値を計算し、得られた結果をプロットするためにグラフィックライブラリを使用します。回帰モデルの計算は、行列代数の手法を使用することで大幅に簡略化されます。たとえば、最小2乗法を用いて回帰モデルのパラメータを行列形式で求める式は、次のように書かれます。

(2) 

• X：独立変数の値の行列
• Y：従属変数列ベクトル
• b：サンプルから推定される未知のパラメータの列ベクトル

MQL5では、X行列の擬似逆行列PInv()を計算し、それにYベクトルを乗算することによって、bベクトル（ここでの対線形回帰のケースでは、b0とb1の2つの要素で構成）を見つけることができます。

pinv = x.PInv(); 

Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS

これは計算の短縮版です。式で示されるように、段階的に計算することができます。

xt = x.Transpose();

xtm = xt.MatMul(x);
inv = xtm.Inv();      
invt = inv.MatMul(xt);
Coeff_B = invt.MatMul(Y); // vector of regression parameters using OLS

結果は同じでしょう。

モデル化のためには、非定常過程の例としてランダムウォークモデルが必要です。このモデルを従属変数Yと独立変数Xの両方について構築します。その後、YのXに対する回帰を構築し、R2乗（決定比）などの指標を評価し、t統計量を計算し、相関依存性について回帰モデルの残差を分析します。                                            

 Yt = Yt-1 + zt                           (3)

  Xt = Xt-1 + vt                           (4)

ztとvtは、数学的期待値がゼロで単位分散がN(0,1)の独立に生成された2つのガウス「ホワイトノイズ」過程です。

このようなプロセスの2つの可能な軌跡を図1に示します。

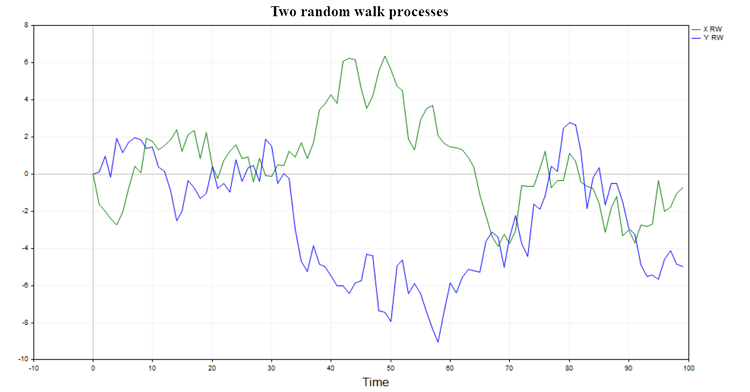
図1： 2つのランダムウォーク

このような過程は、記憶を持たず、お互いに何の関係もないので、あるランダムウォークを別のランダムウォークに回帰しても有意な結果は得られず、2つのランダムウォークの間の関連性の仮説は通常棄却されると予想するのが自然です（選択された有意水準によって決定されるごく一部のケースを除いて）。

可能な回帰の一例を図2に示します。

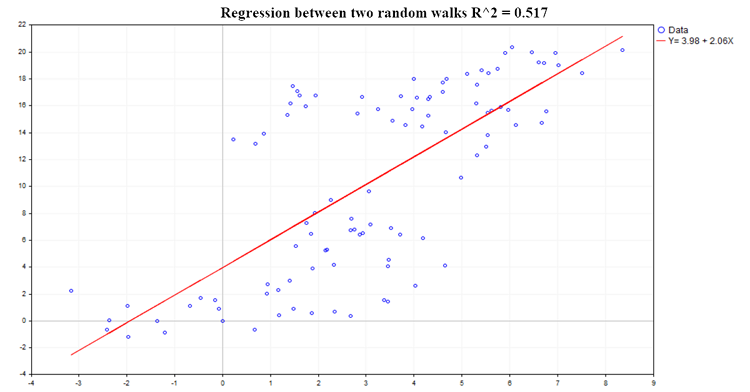
図2：2つのランダムウォーク間の回帰、R2=0.517

決定係数(R^2)は式を使用して計算されます。 

R^2 = 1 - SSE/TSS                              (5)

• SSE：二乗推定誤差の合計
• RSS：回帰による平方和
• TSS：二乗の総和 = RSS+SSE

以下は、すべての主要回帰特性を計算するコードです。

      pinv = x.PInv();
      Coeff = pinv.MatMul(Y);  // vector of linear regression parameters using OLS
      yRegression = x.MatMul(Coeff);  // y regression
      res = Y-yRegression;   //  regression residuals, y - y regression
      yMean = Y.Mean();
      reg_yMean = yRegression-yMean;  // y regression - mean y
      reg_yMeanT = reg_yMean.Transpose();
      RSS = reg_yMeanT.MatMul(reg_yMean);  // Sum( y regression - y mean )^2 , sum of squares due to regression
      resT = res.Transpose();
      SSE = resT.MatMul(res);  // Sum(y - regression y)^2
      TSS = RSS[0,0]+SSE[0,0];  // Total sum of squares
      RSquare = 1-SSE[0,0]/TSS;  // R-square determination ratio
      R2_data[s] = RSquare;

      Vres = SSE[0,0]/(T-2);           // residuals variance estimate
      SEb1 = MathSqrt(Vres/SX);        // estimate of the standard deviation of the b1 ratio deviation of the regression Y = b0 + b1*X;
      t_stat[s] = (Coeff[1,0]-0)/SEb1; // find the t-statistic for the b1 ratio under the hypothesis that b1 = 0;

R^2の値は0から1の範囲です。対になった線形回帰の場合、R^2はXとYの共通相関比の2乗に等しくなります。XがYに影響を与えない場合、R^2はゼロに近くなり、従属変数Yが従属変数Xによって説明される場合、R^2は1に近づきます。2つの独立したランダムウォークの回帰の場合、ゼロ付近に分布すると予想するのが論理的でしょう。これを確認するために、モンテカルロ法を用いて、それぞれ100個の観測を持つ1000組のランダムウォークをシミュレートしてR^2の分布を構築し、その後各組のR^2比を計算します。その結果、以下のような分布が得られました（図3）。

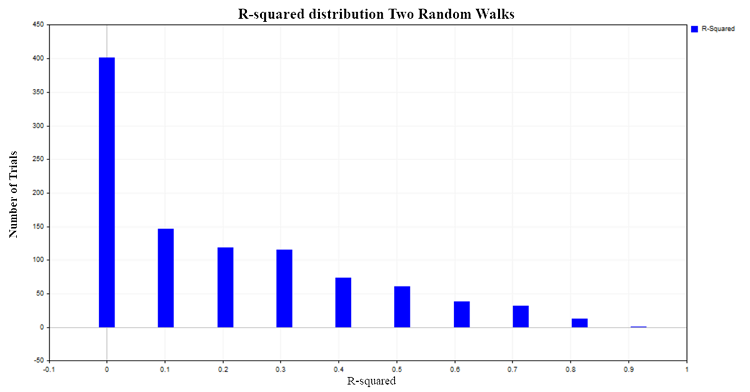
図3： 2つのランダムウォークのR2分布

約50%の場合、決定比は0.2より大きい値を示し、互いに関係のない量の間に関係があることを示しています。比較のために、2つの独立した、しかしすでに定常化している過程のR^2分布を求めましょう。このようなプロセスに適したモデルは、ガウスホワイトノイズモデルです。

                    Yt =  et                                   (6) 

 et：ガウスホワイトノイズ N(0,1)

それぞれ100個の観測を持つ1000組の定常確率過程を生成しましょう。その結果、図4に示すように、R^2のゼロ付近の予想分布が得られます。

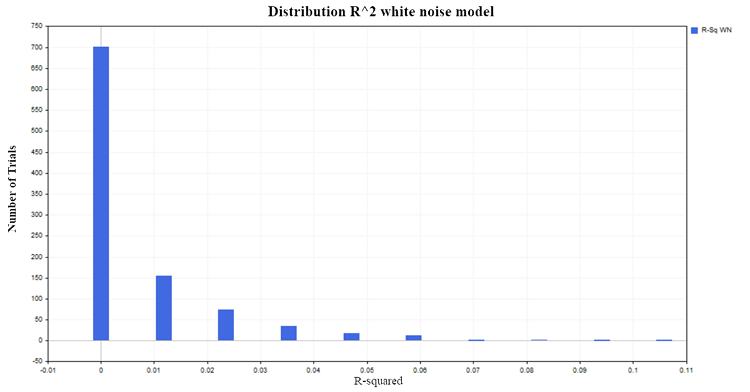
図4：R2分布、ホワイトノイズモデル

2つのランダムウォークに戻り、線形回帰モデルのパラメータの有意性を評価するために計算されたt統計量の振る舞いを見てみましょう。

回帰モデルのパラメータに関する統計的仮説の検定

サンプルから計算された回帰比は、それ自体がランダム変数であるため、これらのサンプル特性の有意性をチェックする必要があります。b1回帰パラメータの有意性を検定する場合、説明変数Xは従属変数Yに影響を与えないという帰無仮説(H0)が立てられます。言い換えると、H0(i) : b1 = 0であり、b1パラメータはゼロと有意に異ならないということです。対立仮説(H1)は、パラメータb1がゼロから有意に異なるとします。すなわち，H1(i):b1≠0であり，したがって予測変数Xは従属変数Yに影響します。

この仮説を検証するために、t統計量を用います。

                                               t = bi /SEi                                      (7)

SEi：2つの推定パラメータの標準偏差 

この統計量は、自由度(n-p)を持つtの分布ta/2 (n-p)を持ちます。

• n：回帰モデルで計算に使用されるデータ量（ここでは100）
• p：推定されたパラメータの数（対回帰の場合，2個）
• a：有意水準（1、5、10%）

今回の実験では、有意水準5%を選んです。そして、絶対値でのt統計量がt分布の臨界値{|t| > t0.025 (98) =1.9844}を超えると、回帰パラメータbがゼロ1から異なり、結果として説明変数Xと従属変数Yの間に関係があると結論づけることができます。5%の有意水準を選択したので、実行されたテストの総数のうち、帰無仮説の誤った棄却は約5%のみになると予想されます。しかし、シミュレーション結果によると、t統計量は帰無仮説を棄却する頻度が高すぎ（依存性がないため、誤って）、およそ75%のケースで帰無仮説を棄却しています（図5）。

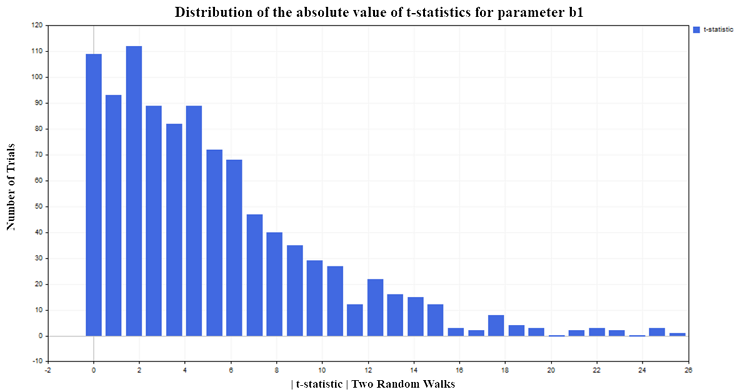
図5：b1パラメータのt統計量の絶対値の分布

また、次のような傾向にも注目したいです。標本中の観測が多ければ多いほど、帰無仮説が棄却されるパーセンテージが高くなります。標本が大きければ大きいほど，X予測変数がY独立変数に影響し，変数間の関係が強くなるという一見逆説的な状況が生じます。もちろん、ここにはパラドックスはなく、回帰分析が適用できないプロセスに回帰分析を適用しているだけです。非定常時系列の分析に回帰を適用した場合、標準的なt統計量は失敗することがわかります。このような状況はスプリアス回帰と呼ばれます。

回帰モデルの無効な仕様

しかし、非定常性は標準的な統計検定が失敗する理由の一つに過ぎません。2つの系列が定常であっても、回帰モデルの仕様に違反している場合は、誤解を招く可能性があります。つまり、変数間の関数従属性の形式を誤った場合（非線形ではなく線形）です。あるいは、Y変数が実際に依存しているX独立変数がモデルから省かれ、その代わりにまったく重要でない変数が誤って使用されている場合です。これを明確にするために、2つの独立したXとYの定常過程を作りましょう。例として、一次自己回帰モデルAR(1)を使用します。

Yt = A*Yt-1 + zt                           (8)

 Xt = B*Xt-1 + vt                          (9)

• ztとvtは、数学的期待値がゼロで単位分散がN(0,1)の独立に生成された2つのガウス「ホワイトノイズ」過程です。
• AとBはAR(1)モデルのパラメータで、定常性条件を満たすためには絶対値が厳密に1より小さくなければなりません。

2つのランダムウォークモデルの場合と同じ条件（各プロセス100データ，検定数1000）で，Xに対するYの回帰（たとえば，AR(1) パラメータ A=0.5, B=0.5）を再び構築しましょう。その結果、b回帰パラメータb1のt統計量分布は以下のようになります（図6）。

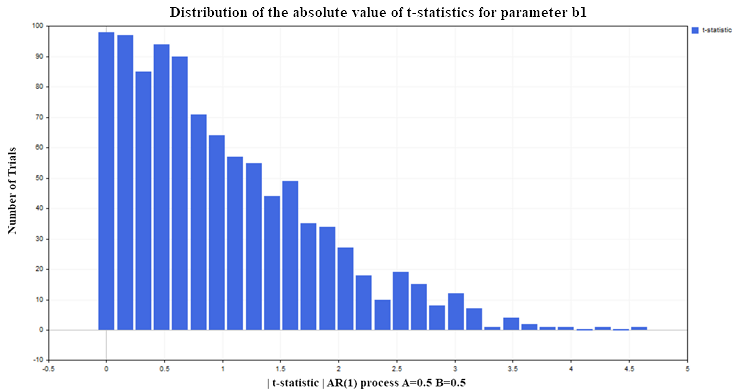
図6：b1パラメータのt統計量の絶対値の分布

見てわかるように、帰無仮説の棄却の状況は、非定常の場合よりもはるかに良好です。許容レベル5%（自由度98のt分布の臨界値＝1.9844）の誤棄却は約12～13%のみ。定常過程では、この割合はサンプル数が増えても増加せず、同じレベルにとどまります。今回t統計量が失敗したのは、変数が非定常であるからではなく (これは問題ありません)、回帰モデルが誤って指定されているためです。従属性の形は正しく選択（線形）されたにもかかわらず、Y変数は同じ変数のラグ値に依存するのではなく、Y変数と関係のないX変数の値に依存すると仮定したのです。もし変数Xを回帰モデルに残し、それにYのラグ値を追加すれば、回帰パラメータの統計的特性は改善され、t統計量は確立された有意水準（このケースでは5%）よりも頻繁に誤った結論を出さなくなります。実際には、回帰モデルがスプリアス（偽）であったり、正しく規定されていないことを理解するためには、残差分析をおこなうべきです。 

                                         Residuals =  Yt - Yreg_t                       (10)

• Yt：Y従属変数の実際の値
• Yreg_t：回帰計算値

モデルの残差に有意な自己相関がある場合，これは回帰モデルが誤って仕様化されているかスプリアスであるとみなすシグナルです。 

以下は、自己相関関数(ACF)と99%信頼区間を計算するコードです。

////////////////////////// ACF calculation /////////////////////////////////////////

   avgres = res.Mean();  // mean of residuals
   ArrayResize(acov,K);
   ArrayResize(acf,K);
   ArrayResize(se,K);
   ArrayResize(se2,K);

   for(i=0; i<K; i++)
     {
      ArrayResize(c,T-i);
      for(j=0; j<T-i; j++)
        {
         c[j] = (res[j,0]-avgres)*(res[j+i,0]-avgres);
        }
      acov[i] = double(MathSum(c)/T);  // Auto covariance
      acf [i] = acov [i]/acov [0];  // Auto correlation
      se[i] =   MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);    // 99% confidence intervals for ACF //
      se2[i] = -MathQuantileNormal(0.995,0,1,err)/MathSqrt(T);
     }

図7は、2つのランダムウォークモデルの回帰残差の自己相関関数(ACF)のグラフです。 また、式「SE = MathQuantileNormal(0.995,0,1,err)/MathSqrt(T)」を使用して計算されたACFの99%信頼区間の境界も表示されます。ここで、Tは回帰モデル内の観測値の数です。

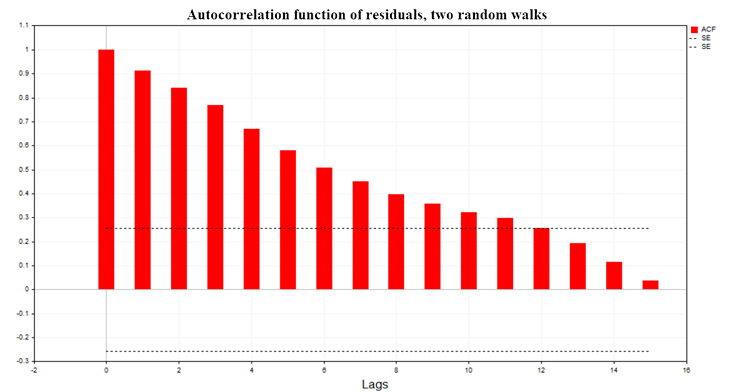
図7：残差の自己相関関数、2つのランダムウォーク

図8は、パラメータA=0.5、В=0.5の2つのAR(1)過程モデルの回帰残差のACFチャートです。

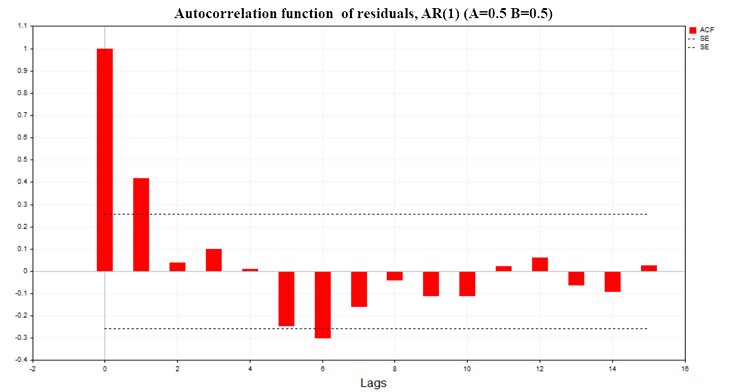
図8：残差の自己相関関数、AR(1) A=0.5 B=0.5

グラフからわかるように、回帰モデルの残差には有意な自己相関があります。したがって、私たちは間違った回帰モデル、あるいは偽の回帰を扱っていることになります。ダービン・ワトソン統計量(DW)基準も残差の自己相関関数に基づいて構築されます。これは、ラグが1の回帰モデルの残差の自己相関を検定するために使用されます。 

                                            DW = 2*(1-ACF(1))                         (11)

擬似相関では、この統計量はゼロに近くなります。

結論

私がこの記事で扱いたかった主な問題は、統計的手法、特に回帰分析手法の適用限界を理解することと、その限界に違反した場合の結果を示すことです。形式的に計算をおこない、「有意な」統計を見て、2つのランダム過程間の関連性について間違った結論を導き出すことは非常に簡単です。

以上のことから導き出される結論は、次の通りです。 

• 回帰モデルを構築する前に、まずモデル内のすべての変数の定常性をテストする必要があります。
• ある変数が非定常である場合、その変数を（通常は第一差分をとることによって）定常型に戻し、それからこの修正された変数でモデルを構築してみます。
• モデルを構築した後、残差の自己相関依存性を調べる必要があります。
• 残差の自己相関関数の値が99%信頼領域を超えない場合、t統計量を用いて回帰モデルのパラメータの有意性の評価に進むことができます。
• それが有意であることがわかったら、構築したモデルを用いてY従属変数の予測を始めることができます。

上記の結果をすべて再現するには、スクリプトの冒頭で、結果を得たいモデルに応じて、変数M = 1.0または0.5の値を選択します。その後、スクリプトの一番下にある、特定のモデルごとに特定の統計情報を表示するコードのブロックをコメントアウトします。また、付属のMath.mqhファイルでは、経験的確率密度関数(MathProbabilityDensityEmpirical)を計算する関数のコードの2つの文字列をコメントアウトして、グラフ上に度数を表示します。

 5432  //  for(int i=0; i<count; i++)
 5433 //    pdf[i]*=coef;