
Algoritmos de optimización de la población: Modificamos la forma y desplazamos las distribuciones de probabilidad y realizamos pruebas con el cefalópodo inteligente (Smart Cephalopod, SC)
Contenido:
1. Introducción2. Banco de pruebas para comprobar distribuciones
3. Construcción de números aleatorios con la ley de distribución requerida
4. Plantilla del algoritmo de optimización - Algoritmo del cefalópodo inteligente (SC)
5. Conclusiones
1. Introducción
La teoría de la probabilidad es una teoría matemática que estudia los fenómenos aleatorios y determina la probabilidad de que ocurran; así, permite describir y analizar procesos aleatorios. Los conceptos básicos de la teoría de la probabilidad son: probabilidad, variable aleatoria, distribución de probabilidad, esperanza matemática, dispersión.
La probabilidad es una característica numérica que determina la probabilidad de que ocurra un determinado acontecimiento.
Una variable aleatoria es una función que asigna algún número a cada resultado de un experimento aleatorio.
Una distribución de probabilidad es una función que define la probabilidad de aparición de cada uno de los valores posibles de una variable aleatoria.
La esperanza matemática es el valor medio de una variable aleatoria que puede obtenerse repitiendo el experimento muchas veces.
La dispersión es una medida de la variación de los valores de una variable aleatoria con respecto a su esperanza matemática.
El momento es una característica numérica de una variable aleatoria que describe su distribución. Los momentos se usan para determinar el centro de la distribución (expectativa) y su dispersión (varianza y desviación típica), así como para analizar la forma de la distribución (asimetría y curtosis). El primer momento (n=1) es la esperanza matemática, que determina el centro de distribución de la variable aleatoria. El segundo momento (n=2) es la varianza, que describe la dispersión de una variable aleatoria con respecto a su esperanza matemática. El tercer momento (n=3) es una medida de la asimetría de la distribución y el cuarto momento (n=4) es una medida de la curtosis (convexidad) de la distribución.
Las distribuciones de probabilidad desempeñan un papel importante en la modelación de fenómenos aleatorios y el análisis de datos, así como en la estadística para la valoración de parámetros y la comprobación de hipótesis. Permiten describir las propiedades probabilísticas de variables y sucesos aleatorios y determinar la probabilidad de distintos resultados.
La teoría de la probabilidad y la optimización son dos importantes disciplinas científicas con amplias aplicaciones en diversos campos de la ciencia y la tecnología, como la economía, las finanzas, la ingeniería, la biología, la medicina y muchos otros. El desarrollo de estos campos y la aplicación de sus métodos de investigación y optimización nos permiten resolver problemas complejos y crear nuevas tecnologías, aumentando la eficacia y la calidad del trabajo en diversos campos de actividad. Un ejemplo sería el desarrollo de la tecnología moderna para crear ordenadores cuánticos, comunicaciones seguras superrápidas, redes neuronales generativas e inteligencia artificial.
Los cálculos probabilísticos basados en la teoría de la probabilidad desempeñan un papel fundamental en el modelado de fenómenos aleatorios y el análisis de datos. La optimización, por su parte, tiene como objetivo encontrar soluciones óptimas a diversos problemas y permite hallar las mejores soluciones entre muchas opciones posibles. Sin embargo, en los problemas del mundo real existe incertidumbre y aleatoriedad, y aquí es donde entran en juego las distribuciones de probabilidad. Estas permiten la aleatoriedad y la incertidumbre en los problemas de optimización.
Las distribuciones de probabilidad también se usan mucho en los algoritmos evolutivos y poblacionales. En estos algoritmos, la generación aleatoria de nuevos estados en el espacio de búsqueda se modela usando las distribuciones de probabilidad correspondientes. Esto nos permite explorar el espacio de parámetros y encontrar soluciones óptimas considerando la aleatoriedad y la diversidad de la población.
Los métodos de optimización más sofisticados usan distribuciones de probabilidad para modelar la incertidumbre y aproximar funciones complejas. Nos permiten explorar eficazmente el espacio de parámetros y encontrar soluciones óptimas considerando la aleatoriedad y el ruido de los datos.
En este artículo estudiaremos distintos tipos de distribuciones de probabilidad, así como sus propiedades y su aplicación práctica como las correspondientes funciones en código. Al generar números aleatorios con diferentes tipos de distribuciones en la práctica, uno puede enfrentarse a muchos problemas como la infinidad de la longitud de las colas o el desplazamiento de las probabilidades al establecer los límites de varianza. Asimismo, también al diseñar y crear algoritmos de optimización muy a menudo es necesario desplazar las probabilidades con respecto a la esperanza matemática. El objetivo de este artículo es abordar estos problemas y crear funciones que permitan trabajar con probabilidades para su posterior aplicación en algoritmos de optimización.
2. Banco de pruebas para comprobar distribuciones
Para probar y visualizar las distribuciones de variables aleatorias, se necesita un banco de pruebas que permita visualizar la forma de las distribuciones. Esto es importante a la hora de diseñar algoritmos de optimización, puesto que una representación visual y la comprensión de hacia dónde debe desplazarse la probabilidad de una variable aleatoria ayudan a obtener los mejores resultados.
Para construir una distribución de probabilidad deberemos crear algo parecido a una serie de casillas en las que caerán números aleatorios. Las casillas son esencialmente contadores. Por ejemplo, tenemos una situación de este tipo con una recta numérica delimitada a la izquierda por "min" y a la derecha por "max", entre dichos límites se sitúa "in"; podemos visualizar todo de la siguiente manera:
min|-----|-----|-----|-----|-----|-----|in|--|--|--|--|--|--|max
Vemos que el valor de "in" se desplaza en la línea numérica más cerca de "max". Si generamos números aleatorios en el rango [min;max], la cantidad de números aleatorios que caen en el rango [min;in] será mayor que en el rango [in;max], por lo que la probabilidad de que los números caigan se desplazará hacia la izquierda, creando un desequilibrio; pero nosotros necesitamos que la cantidad de números que caen a la izquierda y a la derecha sea la misma de media, así que necesitaremos cambiar la forma de la distribución sin desplazar las probabilidades. Para ello, el número de casillas a izquierda y derecha deberá ser el mismo (en el ejemplo esquemático anterior, son 6 casillas cada una a izquierda y derecha).
Así pues, el banco de pruebas para construir distribuciones debe ser bastante sencillo, y la esencia de su funcionamiento podría ser la siguiente:
- creamos un objeto CCanvas para trabajar con el lienzo
- generamos un número aleatorio con la distribución seleccionada en los ajustes
- comprobamos en qué zona de la casilla correspondiente ha caído el número aleatorio y añadimos 1 a la casilla
- calculamos el número mínimo y máximo de aciertos entre todas las casillas
- dibujamos círculos en el lienzo para cada casilla, lo cual se corresponde con la cantidad de números aleatorios en las casillas
- pintamos los círculos de colores que van del azul (raramente) al rojo (a menudo)
El objetivo general del código es visualizar la distribución de probabilidad en el lienzo usando un gráfico en el que cada círculo es la cantidad de números aleatorios que caen en las casillas, normalizado por el número mínimo/máximo de todas las casillas.
#property script_show_inputs #include <Canvas\Canvas.mqh> enum E_Distribution { uniform = 0, gauss = 1, power = 2, levi = 3 }; //--- input parameters input double MinP = -100.0; input double InpP = 0; input double MaxP = 100.0; input int CNT = 1000000; input int Size = 1000; input double SigmaP = 3; //Sigma for "Gauss" distribution input double PowerP = 2; //Power for "Power law" distribution input double LeviPowerP = 2; //Power for "Levy flights" distribution input E_Distribution Distr_P = gauss; //Distribution type //—————————————————————————————————————————————————————————————————————————————— void OnStart () { CCanvas Canvas; int W = 750; int H = 400; int O = 10; int CountL []; int CountR []; ArrayResize (CountL, Size); ArrayInitialize (CountL, 0); ArrayResize (CountR, Size); ArrayInitialize (CountR, 0); string canvasName = "Test_Probability_Distribution_Canvas"; if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError ()); return; } ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); Canvas.Erase (COLOR2RGB (clrWhite)); Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB (clrBlack)); int ind = 0; double X = 0.0; for (int i = 0; i < CNT; i++) { switch (Distr_P) { case uniform: X = UniformDistribution (InpP, MinP, MaxP); break; case gauss: X = GaussDistribution (InpP, MinP, MaxP, SigmaP); break; case power: X = PowerDistribution (InpP, MinP, MaxP, PowerP); break; case levi: X = LeviDistribution (InpP, MinP, MaxP, LeviPowerP); break; } if (X < InpP) { ind = (int)Scale (X, MinP, InpP, 0, Size, false); if (ind >= Size) ind = Size - 1; if (ind < 0) ind = 0; CountL [ind] += 1; } else { ind = (int)Scale (X, InpP, MaxP, 0, Size, false); if (ind >= Size) ind = Size - 1; if (ind < 0) ind = 0; CountR [ind] += 1; } } int minCNT = CNT; int maxCNT = 0; for (int i = 0; i < Size; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; if (CountR [i] > maxCNT) maxCNT = CountR [i]; if (CountL [i] < minCNT) minCNT = CountL [i]; if (CountR [i] < minCNT) minCNT = CountR [i]; } int x = 0.0; int y = 0.0; color clrF; int centre = 0; int stepL = 0; int stH_L = 0; int stepR = 0; int stH_R = 0; centre = (int)Scale (InpP, MinP, MaxP, 10, W - 11, false); stepL = (centre - O) / Size; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; stepR = (W - O - centre) / Size; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; for (int i = 0; i < Size; i++) { x = (int)Scale (i, 0, Size - 1, O, centre - stH_L, false); y = (int)Scale (CountL [i], 0, maxCNT, O, H - O, true); clrF = DoubleToColor (CountL [i], minCNT, maxCNT, 0, 255); Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); x = (int)Scale (i, 0, Size - 1, centre + stH_R, W - O, false); y = (int)Scale (CountR [i], 0, maxCNT, O, H - O, true); clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); } Canvas.Update (); } //——————————————————————————————————————————————————————————————————————————————
3. Construcción de números aleatorios con la ley de distribución requerida
Distribución uniforme (Uniform distribution)
Una distribución uniforme es una distribución de probabilidad en la que todos los valores de una variable aleatoria en un intervalo dado tienen la misma probabilidad. La distribución uniforme se usa ampliamente para modelar variables aleatorias que tienen la misma probabilidad de tomar valores en un intervalo determinado.

Figura 1. Distribución uniforme de los números sin desplazamiento.
Entre las distribuciones, la más fácil de aplicar es la distribución uniforme. El único punto a considerar aquí es que no podemos simplemente generar números en el rango [min;max], así que generaremos un número aleatorio a la izquierda de In o a la derecha de In dependiendo del número aleatorio generado previamente en el rango [0.0;1.0]. Por lo tanto, la cantidad de números generados a la izquierda y a la derecha son igualmente probables en cualquier posición de In con respecto a [min;max]. Aquí no hay problemas de salida del rango ni artefactos en la distribución.
Podemos usar la distribución uniforme siempre que necesitemos generar un número en un rango determinado con la misma probabilidad de acierto en todo el rango.
//—————————————————————————————————————————————————————————————————————————————— double UniformDistribution (const double In, const double outMin, const double outMax) { double rnd = RNDfromCI (0.0, 1.0); if (rnd >= 0.5) return RNDfromCI (In, outMax); else return RNDfromCI (outMin, In); } //——————————————————————————————————————————————————————————————————————————————
Distribución normal (distribución gaussiana)
La distribución normal es una distribución de probabilidad que describe muchos fenómenos aleatorios en la naturaleza, la economía y otros campos. Se caracteriza por su forma de campana y su simetría con respecto al valor medio. La media y la varianza de una distribución normal definen esta completamente.
Una de las propiedades clave de la distribución normal es su simetría respecto a la media. Esto significa que la probabilidad de que una variable aleatoria tome un valor igual a la media es mayor, mientras que la probabilidad de que tome un valor distinto de la media disminuye a medida que se aleja de la media. Esta propiedad hace que la distribución normal resulte especialmente útil para el modelado y el análisis de datos, ya que nos permite describir y predecir fenómenos aleatorios que posee una media y desviaciones respecto a ella.
La distribución normal también tiene muchas propiedades matemáticas que la hacen cómoda para su uso en métodos y modelos estadísticos. Por ejemplo, si las variables aleatorias son independientes y tienen una distribución normal, su suma también tendrá una distribución normal. Esta propiedad permite usar la distribución normal para modelar y analizar sistemas complejos formados por muchas variables aleatorias. La distribución normal tiene muchas aplicaciones en estadística, física, economía, finanzas y otros campos. Es la base de muchos métodos y modelos estadísticos, tales como la regresión lineal y el análisis de series temporales.
Para los algoritmos de optimización, la distribución normal resulta útil cuando queremos destacar un lugar concreto de una recta numérica. En este caso, es posible que solo necesitemos la parte de la curva que forma la distribución. Por ejemplo, queremos utilizar la dispersión dentro de solo tres desviaciones estándar, para todo lo que se salga de estos límites no podremos simplemente establecer los valores de nuevo hacia los bordes de los límites. Si lo hacemos así, obtendremos una frecuencia de caída en los límites superior a la frecuencia en la media. Este problema se demuestra en la fig. 2, que resolveremos en la descripción que sigue.
El método de Box-Muller puede usarse para generar una variable aleatoria con una ley de distribución normal.
- En primer lugar, necesitaremos generar dos números aleatorios uniformemente distribuidos u1 (0, 1] y u2 [0, 1]
- A continuación, deberemos calcular la variable aleatoria z0 mediante la fórmula:
z0 = sqrt(-2 * ln(u1)) * cos(2 * pi * u2)
- La variable aleatoria resultante z0 tendrá una distribución normal estándar
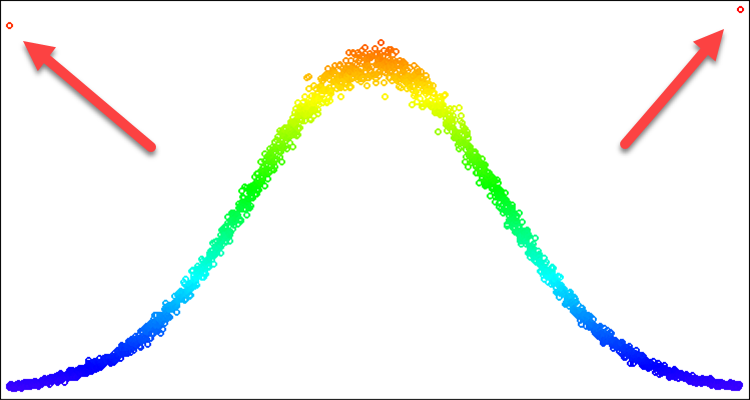
Figura 2. Distribución normal con sigma=3 y artefactos al intentar recortar todo lo que se encuentra más allá de 3 sigmas.
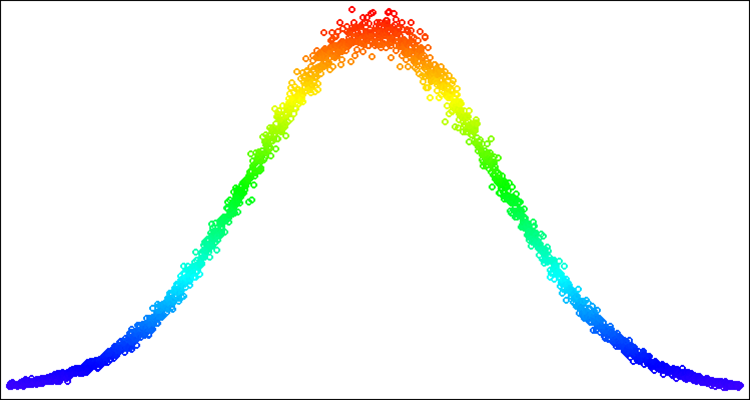
Figura 3. Distribución normal con sigma=3 con el problema resuelto de los artefactos (salida de los límites de la distribución).
Luego escribiremos una implementación de la función GaussDistribution que genere valores aleatorios con distribución normal respecto al valor medio "in":
- Y estableceremos los parámetros de la función: el valor de entrada (in), los valores mínimo y máximo del rango de salida (outMin y outMax), la desviación estándar (sigma).
- Después calcularemos el logaritmo natural de u1, que se generará aleatoriamente entre 0 y 1.
- Si u1 es menor o igual que 0, asignaremos a logN el valor 0,000000000000001; en caso contrario, logN será igual a u1.
- El valor z0 se calculará utilizando la fórmula de la distribución normal.
- A continuación, comprobaremos que el valor de entrada "sigma" no supere el rango del valor máximo posible de desviación estándar de 8,583864105157389.
- Si z0 es mayor o igual que sigmaN, entonces a z0 se le asignará un valor aleatorio entre 0 y sigmaN, en caso contrario, si z0 es menor o igual que -sigmaN, entonces a z0 se le asignará un valor aleatorio entre -sigmaN y 0,0.
- Si z0 es mayor o igual que 0, se retornará el valor calculado mediante la función Scale para el rango de 0 a sigmaN y el rango de salida de "in" a "outMax"; en caso contrario se retornará el valor calculado mediante la función Scale para el rango de -sigmaN a 0 y el rango de salida de "outMin" a in.
Hemos resaltado en amarillo la solución al problema de la frecuencia de valores atípicos en los bordes de una desviación típica dada. De este modo, simplemente "repartiremos" la probabilidad que caiga fuera de los límites hacia el interior de la parte correspondiente de la curva de distribución. De esta manera, no se alterará la forma de la distribución.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SC::GaussDistribution (const double In, const double outMin, const double outMax, const double sigma) { double logN = 0.0; double u1 = RNDfromCI (0.0, 1.0); double u2 = RNDfromCI (0.0, 1.0); logN = u1 <= 0.0 ? 0.000000000000001 : u1; double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2); double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma; if (z0 >= sigmaN) z0 = RNDfromCI (0.0, sigmaN); if (z0 <= -sigmaN) z0 = RNDfromCI (-sigmaN, 0.0); if (z0 >= 0.0) z0 = Scale (z0, 0.0, sigmaN, 0.0, outMax - In, false); else z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false); return In + z0; } //——————————————————————————————————————————————————————————————————————————————
A continuación le mostramos un ejemplo de números aleatorios con distribución normal en la fig. 4. En este ejemplo y en los siguientes, las distribuciones en torno al valor buscado "50" irán de "-100" a "100" [-100;50;100].
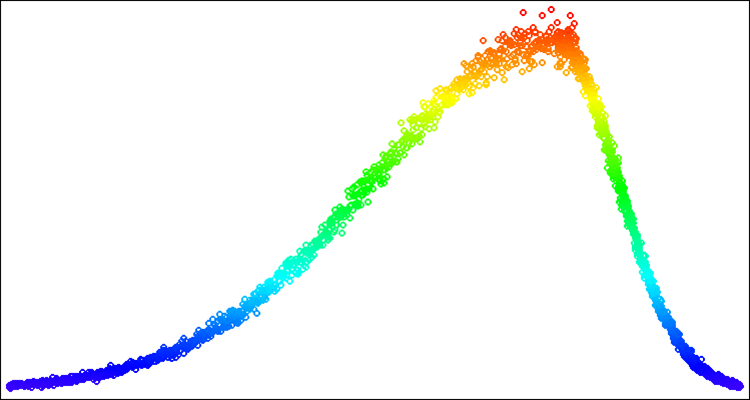
Figura 4. Distribución normal con sigma=3, [-100;50;100].
Una distribución de ley de potencia es una distribución de probabilidad que describe variables aleatorias cuya probabilidad de tomar valores muy elevados disminuye según la ley de potencia. Esta distribución también se denomina ley de Pareto o ley de Zipf. La distribución de ley de potencia encuentra aplicaciones en diversos campos de la ciencia y la ingeniería, por ejemplo, se utiliza en física para modelar distribuciones de masa y energía en sistemas multipartículas como cúmulos estelares y galaxias. También se usa en economía y sociología para analizar la distribución de la renta y la riqueza.
La distribución de ley de potencia tiene varias propiedades interesantes. En primer lugar, la distribución es de cola pesada, lo cual significa que la probabilidad de que una variable aleatoria tome valores muy elevados no es cero. En segundo lugar, no tiene una esperanza matemática finita, lo cual significa que la media de una variable aleatoria puede ser infinita.
La distribución de ley de potencia tiene una forma muy útil, en algunos casos, para su uso en algoritmos de optimización. Nos permite concentrar la densidad de números aleatorios en sitios del espacio de búsqueda que requieren especial atención, refinamiento. Sin embargo, en su forma pura no resulta adecuada para demarcar claramente los límites de los números aleatorios, porque tiene colas de longitud infinita que no se pueden "envolver hacia dentro" tan fácilmente como en el caso de la distribución normal.
Para una implementación clásica de la distribución de ley de potencia necesitaremos utilizar la función inversa, sin embargo, para deshacernos del infinito en las colas de la distribución que nos dificulta la generación de valores dentro de límites conocidos, podremos utilizar un valor uniformemente distribuido elevado a una potencia. Aunque esta no es la forma correcta de especificar la ley de potencia de la distribución, nos permitirá deshacernos del infinito en las colas de la distribución, manteniendo al mismo tiempo una forma de distribución razonablemente cercana a la distribución teórica. Para los algoritmos de optimización estocástica, esto será más que suficiente.
La función PowerDistribution toma como entrada cuatro valores de tipo double: "in", "outMin", "outMax" y "power". Genera un número aleatorio "rnd" en el intervalo comprendido entre [-1,0;1,0], calcula el valor de "r" que es el resultado de elevar a la potencia "power" y, a continuación, escala este valor del intervalo [0,0;1,0] a un intervalo de valores dado utilizando la función Scale. Si "rnd" es un número negativo, el escalado se realizará al rango [outMin;in], en caso contrario, al rango [in;outMax]. El resultado de la ejecución de la función se retornará como un valor de tipo double.
- Si "power" es inferior a 1, la mayoría de los valores de la distribución resultante se concentrarán cerca de cero, y la cola de la distribución estará muy truncada. Esta distribución se parecerá a una parábola.
- Si "power" es 1, la distribución resultante será uniforme.
- Si la "power" es mayor que 1, la mayoría de los valores de la distribución resultante se distribuirán lejos de cero, y la cola de la distribución será larga. Dicha distribución tendrá una cola gruesa y se parecerá a la distribución de Pareto o a la ley de potencia de la distribución.
- Si "power" tiende a infinito, la distribución resultante se parecerá a una función delta centrada en cero.
Así, se nos abre un campo de posibilidades adicionales con el uso de diferentes valores del grado "power", y con ello, más posibilidades de estudio para elegir la distribución óptima y obtener el mejor resultado en el algoritmo de optimización en el contexto de la resolución de un problema de optimización particular.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SC::PowerDistribution (const double In, const double outMin, const double outMax, const double power) { double rnd = RNDfromCI (-1.0, 1.0); double r = pow (fabs (rnd), power); if (rnd >= 0.0) return In + Scale (r, 0.0, 1.0, 0.0, outMax - In, false); else return In - Scale (r, 0.0, 1.0, 0.0, In - outMin, false); } //——————————————————————————————————————————————————————————————————————————————
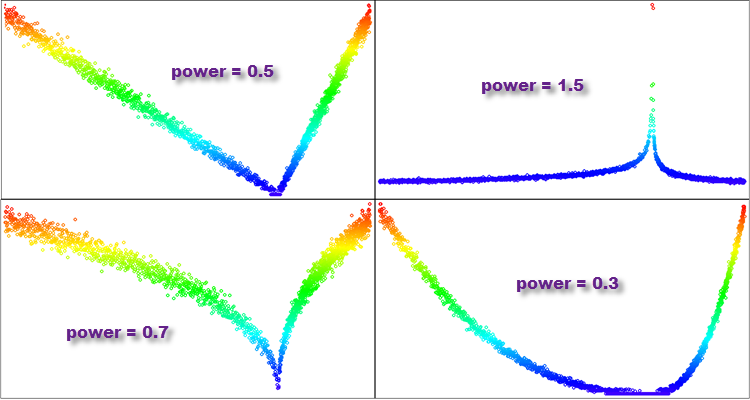
Figura 5. Ejemplos de distribuciones de la función "PowerDistribution" con diferentes grados de "power".
Distribución de Levy (Levy distribution)
Los vuelos de Levy son paseos aleatorios en los que la longitud de cada paso viene determinada por una distribución de Levy.
La distribución de Levy es un ejemplo de distribución con momentos no limitados. Describe variables aleatorias con colas pesadas, lo cual significa que la probabilidad de valores muy elevados es alta. En la distribución de Levy, los momentos pueden ser infinitos o inexistentes, lo cual la hace especial y diferente de las distribuciones con momentos acotados, como la distribución normal.
Las colas gruesas de la distribución de Levy y sus momentos no acotados la hacen útil para modelar fenómenos que pueden tener valores extremos o una gran variabilidad. Los vuelos de Levy tienen muchas aplicaciones en diversos campos, como la física, las matemáticas financieras, el análisis de riesgos, la ecología, la economía y la ingeniería. Por ejemplo, pueden utilizarse para modelar procesos aleatorios en física, como la difusión, la turbulencia y el transporte en plasmas. También pueden utilizarse para modelar estrategias de búsqueda de animales y poblaciones, y para optimizar parámetros en ingeniería y finanzas.
La distribución de Levy fue introducida por el matemático francés Paul Levy en 1925 y ha hallado numerosas aplicaciones en diversos campos de la ciencia y la ingeniería.
Si hablamos del incremento a partir de un valor de parámetro concreto en la optimización, en los vuelos de Levy cada incremento se selecciona a partir de la distribución de Levy y la dirección se elige aleatoriamente. Esto provoca que en los vuelos de Levy algunos pasos puedan ser muy largos, lo cual permite realizar una exploración del espacio de parámetros más rápida que en los paseos aleatorios con una longitud de paso (incremento) fija.
La forma de la distribución del Vuelo de Levy es similar a la de la distribución de ley de potencia, pero en algunos casos puede ser más eficaz utilizar una u otra distribución. Como en el caso de la ley de distribución de ley de potencia, tendremos que deshacernos de las colas pesadas, pero en este caso lo haremos de una forma diferente, más adecuada para esta distribución. Experimentalmente, se comprobó que resulta óptimo utilizar el intervalo [1,0;20,0] para los números aleatorios uniformemente distribuidos que intervienen en la generación. Deberemos calcular el valor mínimo al final de la distribución para números aleatorios en el grado "power" que nos servirá como límite para escalar el número generado en el rango [0,0;1,0].
La función LeviDistribution tomará como entrada cuatro valores de tipo doble: "in", "outMin", "outMax" y "power" y realizará los siguientes pasos:
- Lo primero que hará la función es determinar el valor mínimo "min" en función del parámetro "power", este será el valor mínimo posible de la función para el escalado posterior.
- A continuación, se generarán dos números aleatorios "r1" y "r2" a partir de una distribución uniforme en los intervalos [0,0;1,0] y [1,0;20,0], respectivamente.
- El valor de "y" se calculará llevando "r2" al grado negativo de "power" y escalándolo del intervalo [min, 1,0] a [0,0;1,0] mediante la función Scale.
- Por último, la función retornará el valor generado escalado por el intervalo [outMin, outMax], en función del valor de "r1". Si r1 >= 0.5, el valor se escalará por el intervalo [in, outMax], de lo contrario se escalará por el intervalo [outMin, in].
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SC::LeviDistribution (const double In, const double outMin, const double outMax, const double power) { double min = pow (20.0, -power); double r1 = RNDfromCI (0.0, 1.0); double r2 = RNDfromCI (1.0, 20.0); double y = pow (r2, -power); y = Scale (y, min, 1.0, 0.0, 1.0, false); if (r1 >= 0.5) return In + Scale (y, 0.0, 1.0, 0.0, outMax - In, false); else return In - Scale (y, 0.0, 1.0, 0.0, In - outMin, false); } //——————————————————————————————————————————————————————————————————————————————
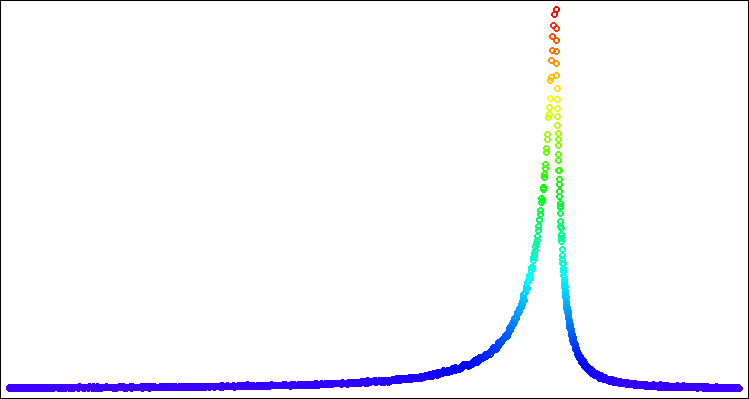
Figura 6. Distribución de Levy con power = 1,0.
4. Plantilla del algoritmo de optimización - Algoritmo del cefalópodo inteligente (SC)
Vamos a pasar ahora a la parte más interesante de nuestra investigación. Comprobaremos todas las distribuciones utilizando un algoritmo de optimización especialmente creado para este fin llamado..... ¿Cómo vamos a llamarlo?
Probaremos la idea de un algoritmo de este tipo: vamos a imaginar un cefalópodo inteligente que busca el lugar más sabroso para comer, así que supondremos que su cabeza está en el epicentro de la comida y que está comiendo algo. Al mismo tiempo, sus tentáculos se extienden constantemente en busca de nuevos depósitos de alimento. En cuanto uno de los tentáculos palpa un lugar «apetitoso», la cabeza se mueve. No sería mala idea un algoritmo inspirado en criaturas marinas. Entonces ya sabemos cómo llamarlo: ¡será el cefalópodo inteligente!
Estoy seguro de que será un experimento apasionante que nos permitirá entender mejor cómo funcionan las distintas distribuciones y cómo pueden ayudarnos a resolver problemas de optimización complejos. Así que vamos a comenzar, a ver qué podemos averiguar en este interesante estudio.
Lo lógico será ajustar las propiedades de las patas del cefalópodo a las leyes de distribución correspondientes. Entonces el código para tantear nuevos lugares con las patas del cefalópodo sería así:
//---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double X = 0.0; double in = cB [c]; double min = rangeMin [c]; double max = rangeMax [c]; switch (distr) { case uniformDistr: X = UniformDistribution (in, min, max); break; case gaussDistr: X = GaussDistribution (in, min, max, powers); break; case powerDistr: X = PowerDistribution (in, min, max, powers); break; case leviDistr: X = LeviDistribution (in, min, max, powers); break; } a [i].c [c] = SeInDiSp (X, rangeMin [c], rangeMax [c], rangeStep [c]); } }
Este código supone dos ciclos anidados que recorren cada agente del array "a" de tamaño popSize, generando un nuevo valor para cada elemento de las coordenadas. El nuevo valor se generará seleccionando uno de los cuatro tipos de distribuciones y aplicando la función de distribución correspondiente (UniformDistribution, GaussDistribution, PowerDistribution o LeviDistribution) al valor "in" actual, que se tomará del array "cB" que representa la mejor solución del momento (donde se encuentra la cabeza en ese momento). El nuevo valor "X" resultante se normalizará mediante la función SeInDiSp utilizando los valores rangeMin y rangeMax y el paso rangeStep para ese elemento. El valor resultante se almacenará en el array "a" para el agente y la coordenada dados.
Trabajando en este artículo y en los métodos de clase específicos para generar números aleatorios con las distribuciones adecuadas para ser utilizados en la construcción de algoritmos de optimización, me dí cuenta de que la función Rastrigin tiene algunos inconvenientes graves que no eran evidentes en el momento en que elegí esta función de prueba y decidí abandonarla. La vieja Rastrigin será sustituida por la función Peaks (en el próximo artículo encontrará una explicación más completa).
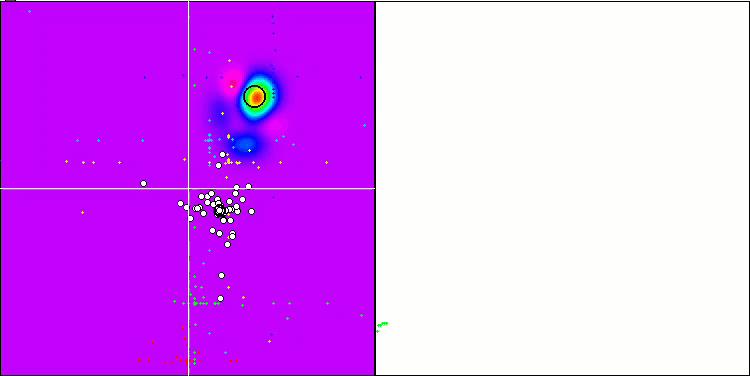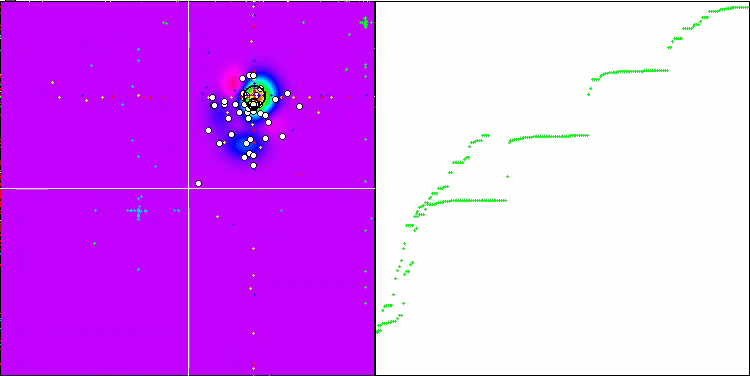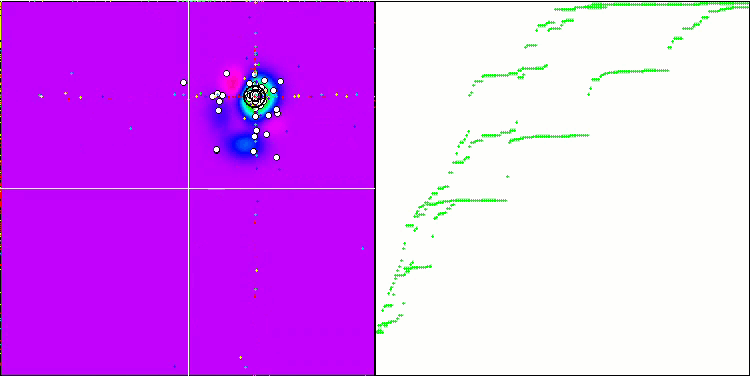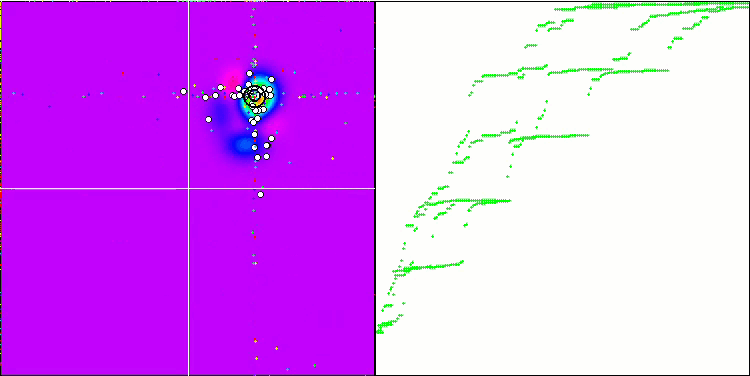
El "cefalópodo inteligente" en acción.
5. Conclusiones
En resumen, nuestro experimento con el cefalópodo inteligente ha ofrecido algunos resultados interesantes. La animación demuestra cómo un algoritmo aleatorio que aplica una distribución determinada realiza con éxito la tarea. No voy a revelar exactamente qué distribución y ajustes se han utilizado, pero le doy la oportunidad de hacer sus propios experimentos con el conjunto completo de herramientas de este artículo. Me encantaría que compartiera sus éxitos en los comentarios.
El cefalópodo inteligente no se considerará en la tabla de clasificación, ya que supone solo un experimento para ayudarnos a ser más conscientes de la optimización.
Mis conclusiones generales son que la aplicación de la distribución de probabilidades y la elección de la estrategia de búsqueda desempeñan un papel importante en el problema de la optimización porque nos permite considerar los factores estocásticos y explorar el espacio de soluciones de forma más eficaz y descubrir zonas con altas probabilidades de encontrar la mejor de las soluciones.
Sin embargo, la simple aplicación de la distribución de probabilidades no será suficiente. También es importante considerar la elección y las particularidades de la estrategia de búsqueda. Las distintas estrategias de búsqueda pueden tener ventajas e inconvenientes según el problema de optimización.
Por consiguiente, para conseguir mejores resultados en el diseño de algoritmos de optimización, tanto en un problema concreto como en general, será necesario el uso conjunto de la distribución de probabilidades y la selección de estrategias de búsqueda. Estos elementos deberán funcionar de forma conjunta para ofrecer el rendimiento requerido del algoritmo de optimización (OA) desarrollado. En general, los resultados de este experimento ponen de relieve la importancia de un planteamiento consciente de la optimización. Por ejemplo, la aplicación de distribuciones de probabilidad y la selección de una estrategia de búsqueda adecuada pueden resultar útiles en el campo del aprendizaje automático, donde es necesario optimizar y encontrar soluciones óptimas.
Una de las características importantes del conjunto de herramientas presentado en este artículo es la capacidad de desplazar distribuciones dentro de un rango determinado de valores. No encontrará capacidades de desplazamiento de distribución en bibliotecas especializadas centradas en tareas de propósito general. Esto permitirá a los investigadores controlar y ajustar las distribuciones de probabilidad en función de las características deseadas del algoritmo de optimización. Ajustar y controlar el desplazamiento de la probabilidad junto con los elementos de estrategia de búsqueda puede hacer verdaderas maravillas.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13893
 Características del Wizard MQL5 que debe conocer (Parte 09): Combinación de clusterización de K-medias con ondas fractales
Características del Wizard MQL5 que debe conocer (Parte 09): Combinación de clusterización de K-medias con ondas fractales
 Redes neuronales: así de sencillo (Parte 68): Optimización de políticas offline basada en preferencias
Redes neuronales: así de sencillo (Parte 68): Optimización de políticas offline basada en preferencias
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso