Algorithmen zur Optimierung mit Populationen: Umformen, Verschieben von Wahrscheinlichkeitsverteilungen und der Test auf Smart Cephalopod (SC)
135
0
Inhalt
1. Einführung2. Testumgebung zur Kontrolle von Verteilungen
3. Konstruktion von Zufallszahlen mit dem erforderlichen Verteilungsgesetz
4. Vorlage für einen Optimierungsalgorithmus - der Algorithmus „Smart Cephalopod“
5. Schlussfolgerungen
1. Einführung
Die Wahrscheinlichkeitstheorie ist eine mathematische Theorie, die Zufallsphänomene untersucht und die Wahrscheinlichkeit ihres Auftretens bestimmt. Sie ermöglicht die Beschreibung und Analyse von Zufallsprozessen. Die Grundbegriffe der Wahrscheinlichkeitstheorie sind Wahrscheinlichkeit, Zufallsvariable, Wahrscheinlichkeitsverteilung, mathematische Erwartung und Streuung.
Die Wahrscheinlichkeit ist ein numerisches Merkmal, das die Eintrittswahrscheinlichkeit eines bestimmten Ereignisses bestimmt.
Eine Zufallsvariable ist eine Funktion, die jedes Ergebnis eines Zufallsexperiments mit einer bestimmten Zahl verknüpft.
Die Wahrscheinlichkeitsverteilung ist eine Funktion, die die Wahrscheinlichkeit für jeden der möglichen Werte einer Zufallsvariablen bestimmt.
Der mathematische Erwartungswert ist ein Durchschnittswert einer Zufallsvariablen, der durch mehrfache Wiederholung des Experiments ermittelt werden kann.
Die Streuung ist ein Maß für die Verteilung der Werte einer Zufallsvariablen im Verhältnis zu ihrer mathematischen Erwartung.
Das Moment ist ein numerisches Merkmal einer Zufallsvariablen, das ihre Verteilung beschreibt. Momente werden zur Bestimmung des Zentrums einer Verteilung (Erwartungswert) und ihrer Streuung (Streuung und Standardabweichung) sowie zur Analyse der Form der Verteilung (Schiefe und Kurtosis) verwendet. Das erste Moment (n=1) ist der mathematische Erwartungswert, der das Zentrum der Zufallsvariablenverteilung bestimmt. Der zweite Punkt (n=2) ist die Streuung, die die Streuung einer Zufallsvariablen relativ zu ihrer mathematischen Erwartung beschreibt. Das dritte Moment (n=3) ist ein Maß für die Schiefe der Verteilung, und das vierte Moment (n=4) ist ein Maß für die Kurtosis (Konvexität) der Verteilung.
Wahrscheinlichkeitsverteilungen spielen eine wichtige Rolle bei der Modellierung von Zufallsphänomenen und der Datenanalyse sowie in der Statistik bei der Schätzung von Parametern und der Prüfung von Hypothesen. Sie ermöglichen es, die probabilistischen Eigenschaften von Zufallsvariablen und Ereignissen zu beschreiben und die Wahrscheinlichkeit verschiedener Ergebnisse zu bestimmen.
Wahrscheinlichkeitstheorie und Optimierung sind zwei wichtige wissenschaftliche Disziplinen, die in verschiedenen Bereichen von Wissenschaft und Technik, wie Wirtschaft, Finanzen, Ingenieurwesen, Biologie, Medizin und vielen anderen, weit verbreitet sind. Die Entwicklung dieser Bereiche und die Anwendung ihrer Untersuchungs- und Optimierungsmethoden ermöglichen es, komplexe Probleme zu lösen und neue Technologien zu schaffen, die die Effizienz und Qualität der Arbeit in verschiedenen Bereichen steigern, darunter die Entwicklung moderner Technologien für die Schaffung von Quantencomputern, sicherer superschneller Kommunikation, generativer neuronaler Netze und künstlicher Intelligenz.
Wahrscheinlichkeitsberechnungen auf der Grundlage der Wahrscheinlichkeitstheorie spielen eine Schlüsselrolle bei der Modellierung von Zufallsphänomenen und der Analyse von Daten. Die Optimierung wiederum zielt darauf ab, optimale Lösungen für verschiedene Probleme zu finden und ermöglicht es, die besten Lösungen unter vielen möglichen Optionen zu finden. Probleme in der realen Welt sind jedoch durch Ungewissheit und Zufälligkeit gekennzeichnet, und hier kommen die Wahrscheinlichkeitsverteilungen ins Spiel. Sie ermöglichen die Berücksichtigung von Zufälligkeiten und Unsicherheiten bei Optimierungsproblemen.
Wahrscheinlichkeitsverteilungen werden auch aktiv in Evolutions- und Populationsalgorithmen eingesetzt. Bei diesen Algorithmen wird die zufällige Erzeugung neuer Zustände im Suchraum durch geeignete Wahrscheinlichkeitsverteilungen modelliert. Auf diese Weise können wir den Parameterraum erforschen und optimale Lösungen unter Berücksichtigung der Zufälligkeit und Vielfalt in der Population finden.
Anspruchsvollere Optimierungsmethoden verwenden Wahrscheinlichkeitsverteilungen, um Unsicherheiten zu modellieren und komplexe Funktionen zu approximieren. Sie ermöglichen es uns, den Parameterraum effizient zu erforschen und optimale Lösungen zu finden, wobei die Zufälligkeit und das Rauschen in den Daten berücksichtigt werden.
In diesem Artikel werden wir uns mit verschiedenen Arten von Wahrscheinlichkeitsverteilungen, ihren Eigenschaften und ihrer praktischen Umsetzung in Form von entsprechenden Funktionen im Code beschäftigen. Bei der Generierung von Zufallszahlen mit verschiedenen Verteilungsarten können zahlreiche Probleme auftreten, wie z. B. Enden, die unendlich sind, oder die Verschiebung von Wahrscheinlichkeiten bei der Festlegung von Streuungsgrenzen. Bei der Entwicklung und Erstellung von Optimierungsalgorithmen besteht häufig die Notwendigkeit, Wahrscheinlichkeiten relativ zur mathematischen Erwartung zu verschieben. Das Ziel dieses Artikels ist es, diese Probleme zu lösen und Arbeitsfunktionen für den Umgang mit Wahrscheinlichkeiten zu erstellen, die dann in Optimierungsalgorithmen verwendet werden können.
2. Testumgebung zur Kontrolle von Verteilungen
Um Verteilungen von Zufallsvariablen zu testen und zu visualisieren, benötigen wir eine Testumgebung, der es uns ermöglicht, die Form der Verteilungen klar darzustellen. Dies ist wichtig für die Entwicklung von Optimierungsalgorithmen, da die visuelle Darstellung und das Verständnis dafür, in welche Richtung die Wahrscheinlichkeit einer Zufallsvariablen zu verschieben ist, dazu beitragen, die besten Ergebnisse zu erzielen.
Um eine Wahrscheinlichkeitsverteilung zu erstellen, müssen wir so etwas wie eine Reihe von Einteilungen (boxes) erstellen, in die die Zufallszahlen fallen. Diese Einteilungen sind im Wesentlichen Zähler. Eine Zahlengerade, die links durch „min“ und rechts durch „max“ begrenzt ist und „in“ dazwischen, kann man sich zum Beispiel so vorstellen:
min|-----|-----|-----|-----|-----|-----|in|--|--|--|--|--|--|max
Wir sehen, dass der Wert „in“ auf der Zahlenreihe näher an „max“ herangerückt ist. Wenn wir Zufallszahlen im Bereich [min;max] generieren, dann wird die Anzahl der Zufallszahlen im Bereich [min;in] größer sein als im Bereich [in;max], wodurch die Wahrscheinlichkeit, dass Zahlen herausfallen, nach links verschoben wird, was zu einem Ungleichgewicht führt, aber wir brauchen die Anzahl der Abfälle auf der linken und rechten Seite im Durchschnitt gleich, wir müssen die Form der Verteilung ändern, ohne die Wahrscheinlichkeiten zu verschieben. Dazu muss die Anzahl der Einteilungen links und rechts gleich sein (im obigen schematischen Beispiel sind dies 6 Kästchen links und rechts).
Die Testumgebung für das Erstellen von Verteilungen ist also recht einfach. Der Kern ihrer Arbeit ist der folgende:
- erstelle ein CCanvas-Objekt, um mit der Leinwand zu arbeiten,
- erzeuge eine Zufallszahl mit der in den Einstellungen gewählten Verteilung,
- prüfe, in welchen Bereich des entsprechenden Kästchens die Zufallszahl gefallen ist, und addieren 1 zu der Einteilung,
- zähle die kleinste und größte Anzahl von Tropfen in allen Einteilungen
- zeichne Kreise auf dem Hintergrund für jede Einteilung, die der Anzahl der Zufallszahlen in der Einteilung entsprechen,
- färbe die Kreise in Farben von blau (selten) bis rot (häufig)
Das übergeordnete Ziel des Codes ist es, die Wahrscheinlichkeitsverteilung auf dem Hintergrund mit Hilfe eines Graphen zu visualisieren, wobei jeder Kreis die Anzahl der in den Einteilungen gezogenen Zufallszahlen angibt, normalisiert durch die Min/Max-Zahl in allen Einteilungen.
#property script_show_inputs #include <Canvas\Canvas.mqh> enum E_Distribution { uniform = 0, gauss = 1, power = 2, levi = 3 }; //--- input parameters input double MinP = -100.0; input double InpP = 0; input double MaxP = 100.0; input int CNT = 1000000; input int Size = 1000; input double SigmaP = 3; //Sigma for "Gauss" distribution input double PowerP = 2; //Power for "Power law" distribution input double LeviPowerP = 2; //Power for "Levy flights" distribution input E_Distribution Distr_P = gauss; //Distribution type //—————————————————————————————————————————————————————————————————————————————— void OnStart () { CCanvas Canvas; int W = 750; int H = 400; int O = 10; int CountL []; int CountR []; ArrayResize (CountL, Size); ArrayInitialize (CountL, 0); ArrayResize (CountR, Size); ArrayInitialize (CountR, 0); string canvasName = "Test_Probability_Distribution_Canvas"; if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError ()); return; } ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); Canvas.Erase (COLOR2RGB (clrWhite)); Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB (clrBlack)); int ind = 0; double X = 0.0; for (int i = 0; i < CNT; i++) { switch (Distr_P) { case uniform: X = UniformDistribution (InpP, MinP, MaxP); break; case gauss: X = GaussDistribution (InpP, MinP, MaxP, SigmaP); break; case power: X = PowerDistribution (InpP, MinP, MaxP, PowerP); break; case levi: X = LeviDistribution (InpP, MinP, MaxP, LeviPowerP); break; } if (X < InpP) { ind = (int)Scale (X, MinP, InpP, 0, Size, false); if (ind >= Size) ind = Size - 1; if (ind < 0) ind = 0; CountL [ind] += 1; } else { ind = (int)Scale (X, InpP, MaxP, 0, Size, false); if (ind >= Size) ind = Size - 1; if (ind < 0) ind = 0; CountR [ind] += 1; } } int minCNT = CNT; int maxCNT = 0; for (int i = 0; i < Size; i++) { if (CountL [i] > maxCNT) maxCNT = CountL [i]; if (CountR [i] > maxCNT) maxCNT = CountR [i]; if (CountL [i] < minCNT) minCNT = CountL [i]; if (CountR [i] < minCNT) minCNT = CountR [i]; } int x = 0.0; int y = 0.0; color clrF; int centre = 0; int stepL = 0; int stH_L = 0; int stepR = 0; int stH_R = 0; centre = (int)Scale (InpP, MinP, MaxP, 10, W - 11, false); stepL = (centre - O) / Size; stH_L = stepL / 2; if (stH_L == 0) stH_L = 1; stepR = (W - O - centre) / Size; stH_R = stepR / 2; if (stH_R == 0) stH_R = 1; for (int i = 0; i < Size; i++) { x = (int)Scale (i, 0, Size - 1, O, centre - stH_L, false); y = (int)Scale (CountL [i], 0, maxCNT, O, H - O, true); clrF = DoubleToColor (CountL [i], minCNT, maxCNT, 0, 255); Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); x = (int)Scale (i, 0, Size - 1, centre + stH_R, W - O, false); y = (int)Scale (CountR [i], 0, maxCNT, O, H - O, true); clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255); Canvas.Circle (x, y, 2, COLOR2RGB (clrF)); Canvas.Circle (x, y, 3, COLOR2RGB (clrF)); } Canvas.Update (); } //——————————————————————————————————————————————————————————————————————————————
3. Konstruktion von Zufallszahlen mit dem erforderlichen Verteilungsgesetz
Gleichverteilung
Die Gleichverteilung ist eine Wahrscheinlichkeitsverteilung, bei der alle Werte einer Zufallsvariablen in einem bestimmten Intervall die gleiche Wahrscheinlichkeit haben. Die Gleichverteilung wird häufig verwendet, um Zufallsvariablen zu modellieren, die mit gleicher Wahrscheinlichkeit Werte innerhalb eines bestimmten Intervalls annehmen.
Bild 1. Eine Gleichverteilung von Zahlen ohne Verschiebung
Die Gleichverteilung ist am einfachsten zu implementieren. Der einzige Punkt, der hier zu beachten ist, ist, dass wir nicht einfach Zahlen im Bereich [min;max] generieren können, also werden wir eine Zufallszahl links von In oder rechts von In generieren, abhängig von der zuvor generierten Zufallszahl im Bereich [0.0;1.0]. Daher ist die Anzahl der erzeugten Zahlen auf der linken und rechten Seite für jede Position von In relativ zu [min;max] gleich wahrscheinlich. Es gibt keine Probleme mit Bereichsüberschreitungen oder Artefakten in der Verteilung.
Die Gleichverteilung kann in allen Fällen verwendet werden, in denen es notwendig ist, eine Zahl in einem bestimmten Bereich mit der gleichen Wahrscheinlichkeit zu erzeugen, dass sie im gesamten Bereich auftritt.
//—————————————————————————————————————————————————————————————————————————————— double UniformDistribution (const double In, const double outMin, const double outMax) { double rnd = RNDfromCI (0.0, 1.0); if (rnd >= 0.5) return RNDfromCI (In, outMax); else return RNDfromCI (outMin, In); } //——————————————————————————————————————————————————————————————————————————————
Normalverteilung (Gauß)
Die Normalverteilung ist eine Wahrscheinlichkeitsverteilung, die viele Zufallsphänomene in der Natur, der Wirtschaft und anderen Bereichen beschreibt. Sie ist durch eine Glockenform und Symmetrie um den Mittelwert gekennzeichnet. Der Mittelwert und die Varianz einer Normalverteilung bestimmen sie vollständig.
Eine der wichtigsten Eigenschaften der Normalverteilung ist ihre Symmetrie um den Mittelwert. Das bedeutet, dass die Wahrscheinlichkeit, dass eine Zufallsvariable einen Wert annimmt, der dem Mittelwert entspricht, am größten ist, und die Wahrscheinlichkeit, dass sie einen vom Mittelwert abweichenden Wert annimmt, abnimmt, je weiter sie sich vom Mittelwert entfernt. Diese Eigenschaft macht die Normalverteilung besonders nützlich für die Modellierung und Datenanalyse, da sie uns erlaubt, Zufallsphänomene zu beschreiben und vorherzusagen, die einen Mittelwert und Abweichungen davon haben.
Die Normalverteilung hat auch viele mathematische Eigenschaften, die sie für den Einsatz in statistischen Methoden und Modellen geeignet machen. Wenn beispielsweise die Zufallsvariablen unabhängig sind und eine Normalverteilung aufweisen, dann ist auch ihre Summe normalverteilt. Aufgrund dieser Eigenschaft kann die Normalverteilung zur Modellierung und Analyse komplexer Systeme verwendet werden, die aus vielen Zufallsvariablen bestehen. Die Normalverteilung hat viele Anwendungen in der Statistik, der Physik, der Wirtschaft, dem Finanzwesen und anderen Bereichen. Sie ist die Grundlage für viele statistische Methoden und Modelle, wie z. B. die lineare Regression und die Zeitreihenanalyse.
Für Optimierungsalgorithmen ist die Normalverteilung nützlich, wenn wir die Aufmerksamkeit auf eine bestimmte Stelle auf der Zahlenreihe lenken wollen. In diesem Fall brauchen wir vielleicht nur einen Teil der Kurve, die die Verteilungsform bildet. Wir wollen zum Beispiel eine Verteilung mit nur drei Standardabweichungen verwenden. Bei allem, was außerhalb dieser Grenzen liegt, können wir die Werte nicht einfach an den Rand der Grenze zurückschieben. Wenn wir dies tun, erhalten wir eine Häufigkeit von Aussetzern an den Rändern, die die Häufigkeit am Durchschnittswert übersteigt. Dieses Problem ist in Abb. 2 dargestellt. Wir werden sie in der folgenden Beschreibung lösen.
Um eine Zufallsvariable mit einem Normalverteilungsgesetz zu erzeugen, kann man die Box-Muller-Methode anwenden.
- Zunächst müssen wir zwei gleichmäßig verteilte Zufallszahlen u1 (0, 1] und u2 [0, 1] erzeugen
- Dann müssen wir die Zufallsvariable z0 anhand der Gleichung berechnen:
z0 = sqrt(-2 * ln(u1)) * cos(2 * pi * u2)
- Die resultierende Zufallsvariable z0 hat eine Standardnormalverteilung
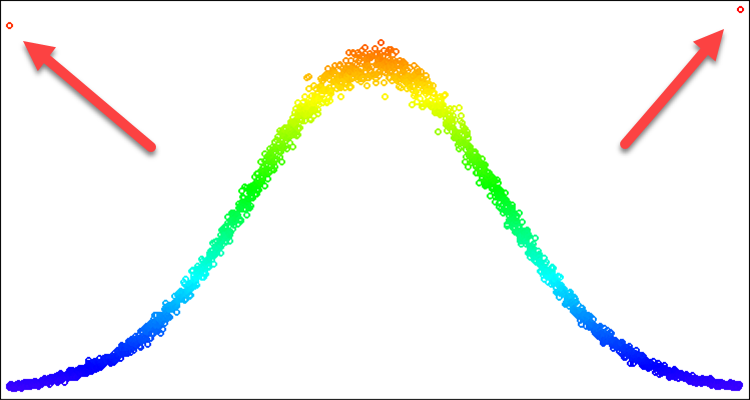
Bild 2. Normalverteilung mit Sigma=3 und Artefakte beim Versuch, alles jenseits von 3 Sigmas abzuschneiden
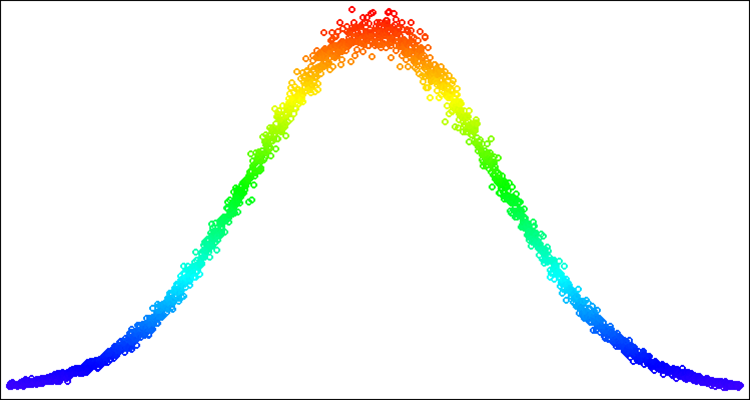
Abb. 3. Normalverteilung mit Sigma=3 mit einem gelösten Problem der Artefakte (Überschreitung der Verteilungsgrenzen)
Schreiben wir eine Implementierung der Funktion GaussDistribution, die Zufallswerte mit einer Normalverteilung in Bezug auf den Durchschnittswert „in“ erzeugt:
- Die folgenden Funktionsparameter werden eingestellt: Eingangswert (in), Minimal- und Maximalwert des Ausgangsbereichs (outMin und outMax) und Standardabweichung (sigma).
- Es wird der natürliche Logarithmus von u1 berechnet, der zufällig im Bereich von 0 bis 1 erzeugt wird.
- Wenn u1 kleiner oder gleich 0 ist, wird logN der Wert 0.000000000000001 zugewiesen. Andernfalls ist logN gleich u1.
- Der z0-Wert wird anhand der Gleichung der Normalverteilung berechnet.
- Die Eingabe „sigma“ wird daraufhin überprüft, ob sie außerhalb des Bereichs der maximal möglichen Standardabweichung von 8,583864105157389 liegt.
- Wenn z0 größer oder gleich sigmaN ist, wird z0 ein Zufallswert im Bereich von 0 bis sigmaN zugewiesen. Andernfalls, wenn z0 kleiner oder gleich -sigmaN ist, wird z0 ein Zufallswert im Bereich von -sigmaN bis 0,0 zugewiesen.
- Wenn z0 größer oder gleich 0 ist, wird der mit der Funktion „Scale“ berechnete Wert für den Bereich von 0 bis sigmaN und der Ausgabebereich von „in“ bis „outMax“ zurückgegeben, andernfalls wird der mit der Funktion „Scale“ berechnete Wert für den Bereich von -sigmaN bis 0 und den Ausgabebereich von „outMin“ bis „in“ zurückgegeben.
Der gelb markierte Punkt ist eine Lösung für das Problem der Häufigkeit von Ausfällen an den Rändern einer bestimmten Standardabweichung. Wir „verteilen“ also einfach die Wahrscheinlichkeit, die außerhalb der Grenzen liegt, in den entsprechenden Teil der Verteilungskurve. In diesem Fall wird die Verteilungsform nicht verletzt.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SC::GaussDistribution (const double In, const double outMin, const double outMax, const double sigma) { double logN = 0.0; double u1 = RNDfromCI (0.0, 1.0); double u2 = RNDfromCI (0.0, 1.0); logN = u1 <= 0.0 ? 0.000000000000001 : u1; double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2); double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma; if (z0 >= sigmaN) z0 = RNDfromCI (0.0, sigmaN); if (z0 <= -sigmaN) z0 = RNDfromCI (-sigmaN, 0.0); if (z0 >= 0.0) z0 = Scale (z0, 0.0, sigmaN, 0.0, outMax - In, false); else z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false); return In + z0; } //——————————————————————————————————————————————————————————————————————————————
Nachfolgend ein Beispiel für Zufallszahlen mit Normalverteilung (Abb. 4). In diesem Beispiel und dem unten - Verteilungen um den gewünschten Wert „50“ im Bereich von „-100“ bis „100“ [-100;50;100].
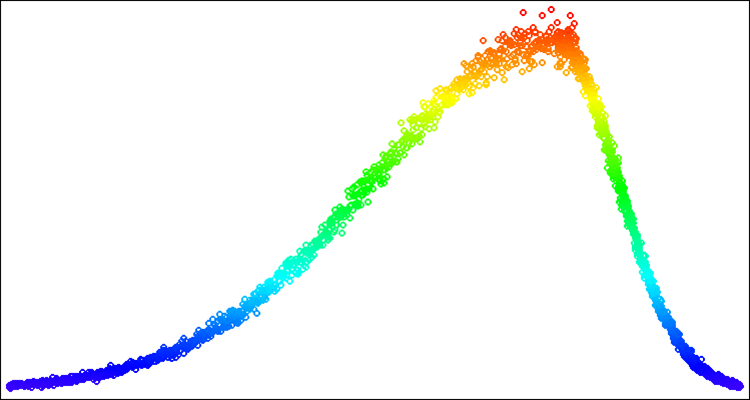
Abb. 4. Normalverteilung mit sigma=3, [-100;50;100]
Die Potenzgesetzverteilung ist eine Wahrscheinlichkeitsverteilung, die Zufallsvariablen beschreibt, deren Wahrscheinlichkeit, sehr große Werte anzunehmen, nach einem Potenzgesetz abnimmt. Diese Verteilung wird auch als Pareto-Prinzip oder Zipfsches Gesetz bezeichnet. Die Energieverteilung wird in verschiedenen Bereichen von Wissenschaft und Technik eingesetzt. In der Physik wird sie zum Beispiel verwendet, um die Verteilung von Masse und Energie in Systemen mit vielen Teilchen, wie Sternhaufen und Galaxien, zu modellieren. Sie wird auch in der Wirtschaft und Soziologie verwendet, um die Verteilung von Einkommen und Vermögen zu analysieren.
Die Potenzgesetz-Verteilung hat mehrere interessante Eigenschaften. Erstens ist sie „heavy-tailed“, was bedeutet, dass die Wahrscheinlichkeit, dass die Zufallsvariable sehr große Werte annimmt, nicht Null ist. Zweitens hat sie keinen endlichen mathematischen Erwartungswert, was bedeutet, dass der Durchschnittswert einer Zufallsvariablen unendlich sein kann.
Die Potenzgesetz-Verteilung hat eine sehr nützliche Form für die Verwendung in Optimierungsalgorithmen. Sie ermöglicht es, die Dichte der Zufallszahlen an Stellen im Suchraum zu konzentrieren, die besondere Aufmerksamkeit und Klärung erfordern. In ihrer reinen Form ist sie jedoch ungeeignet, wenn es darum geht, die Grenzen der Zufallszahlen klar zu begrenzen, da sie unendlich lange Schwänze hat, die nicht so einfach „nach innen gewickelt“ werden können wie bei der Normalverteilung.
Für die klassische Umsetzung der Potenzgesetzverteilung muss die Umkehrfunktion verwendet werden. Um jedoch die Unendlichkeit in den Schwänzen der Verteilung zu beseitigen, die die Erzeugung von Werten innerhalb bekannter Grenzen stört, können wir einen gleichmäßig verteilten Wert verwenden, der auf eine Potenz erhöht wird. Obwohl dies nicht die korrekte Art und Weise ist, eine Potenzgesetz-Verteilung zu spezifizieren, ermöglicht es uns, die Unendlichkeit in den Enden (tails) der Verteilung loszuwerden und gleichzeitig eine Verteilungsform beizubehalten, die der theoretischen ziemlich nahe kommt. Für stochastische Optimierungsalgorithmen ist dies mehr als ausreichend.
Die Funktion PowerDistribution benötigt vier Werte des Typs double als Eingaben: „in“, „outMin“, „outMax“ und „power“. Sie erzeugt eine Zufallszahl „rnd“ im Bereich [-1,0;1,0], berechnet den Wert „r“, der das Ergebnis der Potenzierung von „power“ ist, und skaliert dann diesen Wert aus dem Bereich [0,0;1,0] mit Hilfe der Funktion Scale auf den angegebenen Wertebereich. Ist „rnd“ eine negative Zahl, erfolgt die Skalierung im Bereich [outMin;in], andernfalls - im Bereich [in;outMax]. Das Ergebnis der Funktion wird als Double-Wert zurückgegeben.
- Wenn die „Potenz“ kleiner als 1 ist, sind die meisten Werte in der resultierenden Verteilung in der Nähe von Null konzentriert, und das Ende der Verteilung wird stark abgeschnitten. Diese Verteilung wird einer Parabel ähneln.
- Ist „power“, der Exponent, gleich 1, so ist die resultierende Verteilung gleichmäßig.
- Wenn „power“ größer als 1 ist, sind die meisten Werte in der resultierenden Verteilung weit von Null entfernt, und das Ende der Verteilung ist lang. Eine solche Verteilung hat ein langes Ende und ähnelt der Pareto-Verteilung oder der Potenzgesetz-Verteilung.
- Wenn „power“ gegen unendlich tendiert, ähnelt die resultierende Verteilung einer bei Null konzentrierten Deltafunktion.
So eröffnet sich uns ein Feld zusätzlicher Möglichkeiten, wenn wir verschiedene Werte des „power“-Grads verwenden, und wir haben somit mehr Möglichkeiten bei der Untersuchung der Auswahl der optimalen Verteilung, um das beste Ergebnis im Optimierungsalgorithmus im Rahmen der Lösung eines spezifischen Optimierungsproblems zu erhalten.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SC::PowerDistribution (const double In, const double outMin, const double outMax, const double power) { double rnd = RNDfromCI (-1.0, 1.0); double r = pow (fabs (rnd), power); if (rnd >= 0.0) return In + Scale (r, 0.0, 1.0, 0.0, outMax - In, false); else return In - Scale (r, 0.0, 1.0, 0.0, In - outMin, false); } //——————————————————————————————————————————————————————————————————————————————
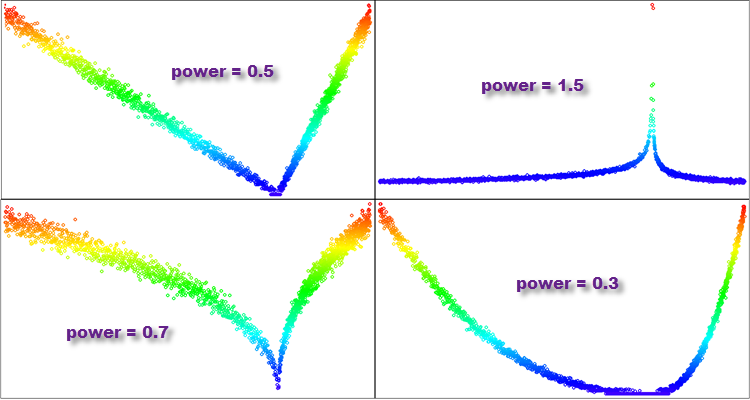
Abbildung 5. Beispiele für Verteilungen der Funktion PowerDistribution mit unterschiedlichen Exponenten.
Die Lévy-Verteilung
Lévys Flüge sind zufällige Spaziergänge, bei denen die Länge der einzelnen Schritte durch die Lévy-Verteilung bestimmt wird.
Die Lévy-Verteilung ist ein Beispiel für eine Verteilung mit unbeschränkten Momenten. Sie beschreibt Zufallsvariablen mit starkem Enden (tails), was bedeutet, dass die Wahrscheinlichkeit sehr großer Werte hoch ist. Bei der Lévy-Verteilung können die Momente unendlich oder nicht vorhanden sein, wodurch sie sich von Verteilungen mit begrenzten Momenten, wie der Normalverteilung, unterscheidet.
Die starken Enden der Lévy-Verteilung und ihre unbegrenzten Momente machen sie nützlich für die Modellierung von Phänomenen, die extreme Werte oder eine hohe Variabilität aufweisen können. Die Lévy-Flüge finden in vielen Bereichen Anwendung, darunter Physik, Finanzmathematik, Risikoanalyse, Ökologie, Wirtschaft und Technik. Sie können zum Beispiel zur Modellierung von Zufallsprozessen in der Physik, wie Diffusion, Turbulenz und Transport in Plasmen, verwendet werden. Sie können auch zur Modellierung der Suchstrategien von Tieren und Populationen sowie zur Optimierung von Parametern im Ingenieur- und Finanzwesen verwendet werden.
Die Lévy-Verteilung wurde 1925 von dem französischen Mathematiker Paul Lévy eingeführt und hat zahlreiche Anwendungen in verschiedenen Bereichen der Wissenschaft und Technik gefunden.
Wenn es sich um ein Inkrement ausgehend von einem bestimmten Parameterwert in der Optimierung handelt, dann wird bei Lévy-Flügen jedes Inkrement aus der Lévy-Verteilung ausgewählt, und die Richtung wird zufällig gewählt. Dies führt dazu, dass bei Lévy-Flügen einige Schritte sehr lang sein können, was eine schnellere Erkundung des Parameterraums ermöglicht als bei Random Walks mit einer festen Schrittlänge (Inkrement).
Die Form der Verteilung von Lévy-Flügen ähnelt der Form der Potenzgesetzverteilung, aber in manchen Fällen ist es effektiver, die eine andere Verteilung zu verwenden. Wie bei der Potenzgesetz-Verteilung müssen wir die starken Enden entfernen. In diesem Fall werden wir es jedoch auf eine andere Art und Weise tun, die für diese Verteilung besser geeignet ist. Es wurde experimentell herausgefunden, dass es optimal ist, den Bereich [1.0;20.0] für gleichmäßig verteilte Zufallszahlen zu verwenden, die an der Erzeugung beteiligt sind. Wir müssen den Mindestwert am Ende der Verteilung für Zufallszahlen hoch dem Exponenten „power“ berechnen, der uns als Grenze für die Skalierung der erzeugten Zahl in den Bereich [0,0;1,0] dienen wird.
Die Funktion LeviDistribution nimmt vier Doppelwerte als Eingaben entgegen: „in“, „outMin“, „outMax“ und „power“ und führt die folgenden Schritte durch:
- Zunächst bestimmt die Funktion den Mindestwert „min“ auf der Grundlage des Parameters „power“. Dies ist der kleinstmögliche Funktionswert für die anschließende Skalierung.
- Dann werden zwei Zufallszahlen „r1“ und „r2“ aus einer Gleichverteilung auf den Intervallen [0,0;1,0] bzw. [1,0;20,0] erzeugt.
- Der Wert von „y“ wird berechnet, indem „r2“ auf die negative Potenz von „power“ angehoben und mit der Funktion „Scale“ vom Intervall [min, 1.0] auf [0.0;1.0] skaliert wird.
- Schließlich gibt die Funktion den erzeugten Wert zurück, skaliert mit dem Intervall [outMin, outMax] in Abhängigkeit vom Wert von „r1“. Wenn r1 >= 0,5 ist, wird der Wert um das Intervall [in, outMax] skaliert, andernfalls - um das Intervall [outMin, in].
//—————————————————————————————————————————————————————————————————————————————— double C_AO_SC::LeviDistribution (const double In, const double outMin, const double outMax, const double power) { double min = pow (20.0, -power); double r1 = RNDfromCI (0.0, 1.0); double r2 = RNDfromCI (1.0, 20.0); double y = pow (r2, -power); y = Scale (y, min, 1.0, 0.0, 1.0, false); if (r1 >= 0.5) return In + Scale (y, 0.0, 1.0, 0.0, outMax - In, false); else return In - Scale (y, 0.0, 1.0, 0.0, In - outMin, false); } //——————————————————————————————————————————————————————————————————————————————
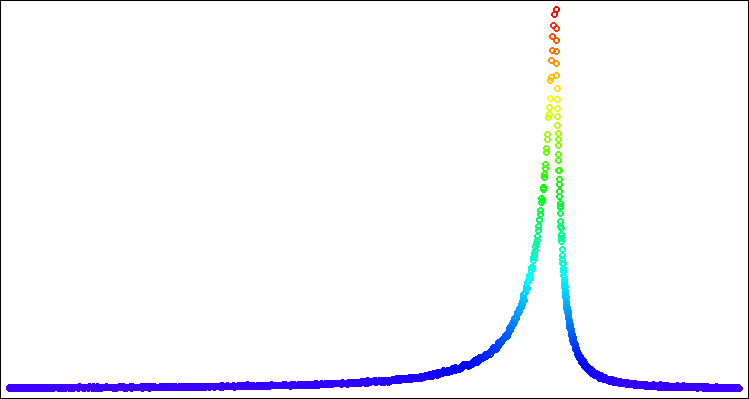
Abbildung 6. Lévy-Verteilung mit power = 1,0
4. Vorlage für einen Optimierungsalgorithmus - der Algorithmus „Smart Cephalopod“
Kommen wir nun zum interessantesten Teil unserer Untersuchung! Überprüfen wir alle Verteilungen mit einem speziell für diese Zwecke entwickelten Optimierungsalgorithmus namens.... Hmm, wie sollen wir es nennen?
Testen wir die Idee eines solchen Algorithmus: Stellen wir uns einen intelligenten Kopffüßer vor, der nach dem leckersten Ort sucht, nehmen wir also an, dass sich sein Kopf im Zentrum der Nahrung befindet und etwas isst. Gleichzeitig spreizen sich seine Tentakel auf der Suche nach neuen Nahrungsvorkommen ständig nach den Seiten aus. Sobald einer der Tentakel eine schmackhafte Stelle findet, bewegt sich der Kopf. Vielleicht ist dies eine gute Idee für einen Algorithmus, der von Meeresbewohnern inspiriert ist. Dann wissen wir, wie wir ihn nennen sollen - er wird Smart Cephalopod heißen!
Ich bin sicher, dass dies ein spannendes Experiment sein wird, das es uns ermöglichen wird, besser zu verstehen, wie verschiedene Verteilungen funktionieren und wie sie uns helfen können, komplexe Optimierungsprobleme zu lösen. Fangen wir also an und sehen wir, was wir in dieser interessanten Studie herausfinden können!
Es ist logisch, die Eigenschaften der Beine des Kopffüßers an die entsprechenden Verteilungsgesetze anzupassen. Dann sieht der Code für das Ertasten neuer Orte mit den Füßen des Kopffüßlers so aus:
//---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double X = 0.0; double in = cB [c]; double min = rangeMin [c]; double max = rangeMax [c]; switch (distr) { case uniformDistr: X = UniformDistribution (in, min, max); break; case gaussDistr: X = GaussDistribution (in, min, max, powers); break; case powerDistr: X = PowerDistribution (in, min, max, powers); break; case leviDistr: X = LeviDistribution (in, min, max, powers); break; } a [i].c [c] = SeInDiSp (X, rangeMin [c], rangeMax [c], rangeStep [c]); } }
Dieser Code besteht aus zwei verschachtelten Schleifen, die jeden Agenten im Array „a“ von popSize durchlaufen und einen neuen Wert für jedes Koordinatenelement erzeugen. Die Generierung eines neuen Wertes erfolgt durch die Auswahl einer von vier Verteilungsarten und die Anwendung der entsprechenden Verteilungsfunktion (UniformDistribution, GaussDistribution, PowerDistribution oder LeviDistribution) auf den aktuellen Wert von „in“, der aus dem Array „cB“ entnommen wird, das die beste Lösung im Moment darstellt (wo sich der Kopf gerade befindet). Der sich daraus ergebende neue X-Wert wird dann von der Funktion SeInDiSp unter Verwendung der Werte rangeMin und rangeMax und des rangeStep für dieses Element normalisiert. Der resultierende Wert wird im Array „a“ für den angegebenen Agenten und die Koordinate gespeichert.
Die Arbeit an diesem Artikel und an speziellen Klassenmethoden zur Erzeugung von Zufallszahlen mit den erforderlichen Verteilungen, die für die Entwicklung von Optimierungsalgorithmen geeignet sind, führte zu der Erkenntnis, dass die Rastrigin-Funktion mehrere schwerwiegende Mängel aufweist, die zum Zeitpunkt der Auswahl dieser Testfunktion nicht offensichtlich waren, sodass ich beschlossen habe, sie nicht zu verwenden. Der gute alte Rastrigin wird durch die Funktion Peaks ersetzt (eine ausführlichere Begründung wird im nächsten Artikel gegeben).
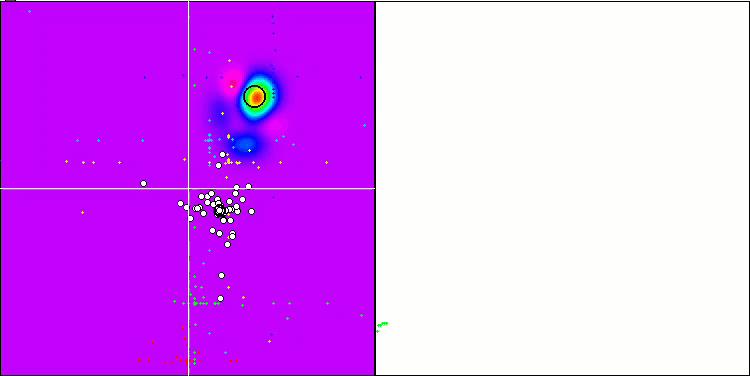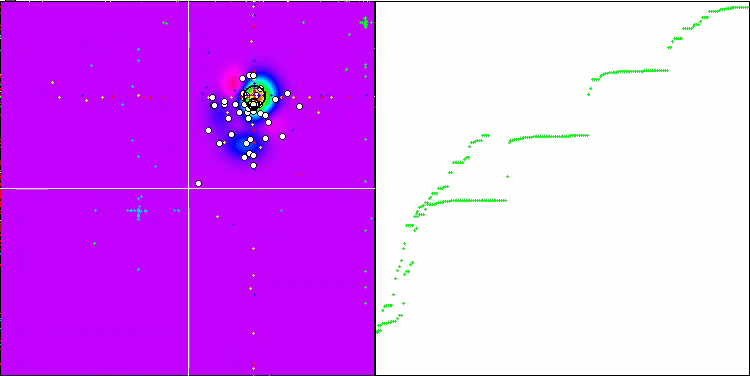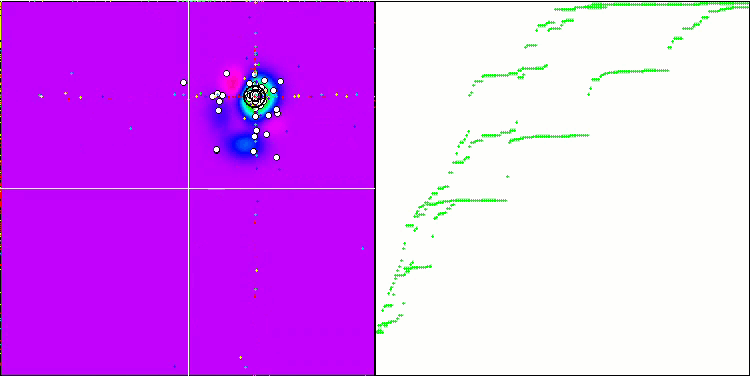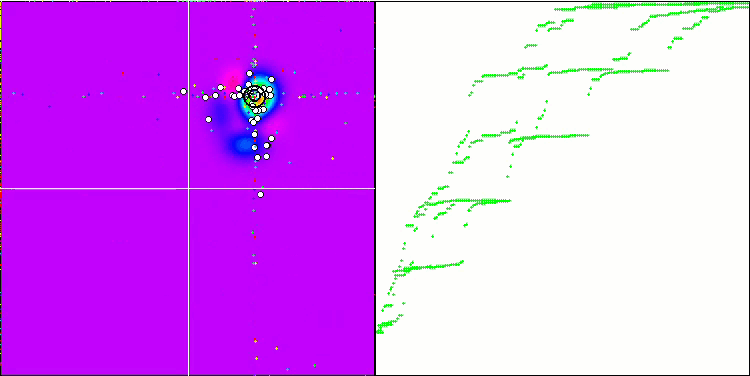
“Intelligenter Kopffüßer“ in Aktion
5. Zusammenfassung
Zusammenfassend lässt sich sagen, dass unser Experiment mit dem „Smart Cephalopod“ interessante Ergebnisse brachte. Die Animation zeigt, wie ein Zufallsalgorithmus, der eine bestimmte Verteilung anwendet, eine Aufgabe erfolgreich erledigt. Ich werde nicht verraten, welche Verteilung oder Einstellungen genau verwendet wurden, sondern überlasse es Ihnen, Ihre eigenen Experimente mit dem vollständigen Satz von Werkzeugen in diesem Artikel durchzuführen. Ich würde mich freuen, wenn Sie Ihren Erfolg in den Kommentaren mitteilen würden.
„Smart Cephalopod“ wird in der Bewertungstabelle nicht berücksichtigt, da es sich nur um ein Experiment handelt, das uns helfen soll, bewusster auf die Optimierung zu achten.
Meine allgemeinen Schlussfolgerungen lauten, dass die Anwendung einer Wahrscheinlichkeitsverteilung und die Wahl der Suchstrategie eine wichtige Rolle bei einem Optimierungsproblem spielen, da sie es ermöglichen, stochastische Faktoren zu berücksichtigen und den Lösungsraum effizienter zu erkunden und Bereiche mit einer hohen Wahrscheinlichkeit für die besten Lösungen zu entdecken.
Es reicht jedoch nicht aus, nur die Wahrscheinlichkeitsverteilung zu verwenden. Es ist auch wichtig, die Wahl und die Merkmale der Suchstrategie zu berücksichtigen. Verschiedene Suchstrategien können je nach Optimierungsproblem Vor- und Nachteile haben.
Um noch bessere Ergebnisse bei der Entwicklung von Optimierungsalgorithmen sowohl für ein bestimmtes Problem als auch im Allgemeinen zu erzielen, ist es daher notwendig, die Wahrscheinlichkeitsverteilung und die Auswahl der Suchstrategie gemeinsam zu nutzen. Diese Elemente sollten zusammenwirken, um die erforderliche Leistung des entwickelten Optimierungsalgorithmus zu gewährleisten. Insgesamt machen die Ergebnisse dieses Experiments deutlich, wie wichtig ein bewusster Ansatz bei der Optimierung ist. Die Anwendung von Wahrscheinlichkeitsverteilungen und die Wahl einer geeigneten Suchstrategie können beispielsweise im Bereich des maschinellen Lernens nützlich sein, wo es um Optimierung und das Finden optimaler Lösungen geht.
Eines der wichtigsten Merkmale der in diesem Artikel vorgestellten Werkzeuge ist die Möglichkeit, Verteilungen in einem bestimmten Wertebereich zu verschieben. In spezialisierten Bibliotheken, die sich auf allgemeine Probleme konzentrieren, werden Sie keine Funktionen zur Verteilungsumstellung finden. Dies ermöglicht es den Forschern, Wahrscheinlichkeitsverteilungen entsprechend den erforderlichen Eigenschaften des Optimierungsalgorithmus zu manipulieren und abzustimmen. Die Anpassung und Kontrolle der Wahrscheinlichkeitsverzerrung zusammen mit Elementen der Suchstrategie kann wahre Wunder bewirken!
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/13893
Algorithmen zur Optimierung mit Populationen: Der Algorithmus Simulated Isotropic Annealing (SIA). Teil II
Algorithmen zur Optimierung mit Populationen: der Algorithmus Simulated Annealing (SA). Teil I
Implementierung des Augmented Dickey Fuller-Tests in MQL5
Quantitative Analyse in MQL5: Implementierung eines vielversprechenden Algorithmus
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.