Neuronales Netz in der Praxis: Pseudoinverse (II)

Einführung

Ich freue mich, Sie zu einem neuen Artikel über neuronale Netze begrüßen zu dürfen. 

Im vorherigen Artikel „Neuronales Netz in der Praxis: Pseudoinverse (I)“ habe ich gezeigt, wie man eine in der MQL5-Bibliothek verfügbare Funktion zur Berechnung der Pseudoinverse verwenden kann. Die Methode in der MQL5-Bibliothek ist jedoch, wie in vielen anderen Programmiersprachen auch, dazu gedacht, die Pseudoinverse zu berechnen, wenn man Matrizen oder zumindest eine Struktur verwendet, die einer Matrix ähneln könnte.

Obwohl dieser Artikel zeigt, wie man zwei Matrizen multipliziert und sogar faktorisiert, um die Determinante einer beliebigen Matrix zu erhalten (die wichtig ist, um zu wissen, ob eine Matrix invertiert werden kann oder nicht), müssen wir noch eine weitere Faktorisierung durchführen. Dies ist notwendig, damit Sie verstehen, wie die Faktorisierung durchgeführt wird, um pseudoinverse Werte zu erhalten. Diese Faktorisierung besteht in der Erzeugung der inversen Matrix.

Aber was ist mit der Umsetzung? Nun, im vorigen Artikel habe ich gezeigt, wie man eine Faktorisierung durchführt, die die Multiplikation einer Matrix mit ihrer Transponierten simuliert. Die Durchführung eines solchen Vorgangs ist also kein Problem.

Die Berechnung, die wir noch durchführen müssen, d. h. die Ermittlung der Inversen einer Matrix, möchte ich jedoch nicht im Detail behandeln. Das liegt nicht an der Komplexität, sondern daran, dass diese Artikel eher als Lehrmaterial denn als Anleitung für die Implementierung bestimmter Funktionen gedacht sind. Deshalb habe ich beschlossen, in diesem Artikel einen anderen Ansatz zu wählen. Anstatt uns auf die allgemeine Faktorisierung zu konzentrieren, die zur Berechnung der Inversen einer Matrix erforderlich ist, werden wir uns mit der Faktorisierung der Pseudo-Inversen beschäftigen und dabei die Daten verwenden, mit denen wir von Anfang an gearbeitet haben. Mit anderen Worten, anstatt eine allgemeine Methode vorzustellen, werden wir einen speziellen Ansatz wählen. Das Beste daran ist, dass Sie viel besser verstehen werden, warum alles so funktioniert, wie es funktioniert, als wenn wir der allgemeinen Logik bei der Erstellung der Faktorisierung folgen würden, wie im vorherigen Artikel gezeigt, wo diese Funktionen allgemein waren. Sie werden sehen, dass Berechnungen viel schneller durchgeführt werden können, wenn wir sie auf eine spezielle Weise durchführen. Um dieses Konzept besser zu verstehen, wollen wir uns nun einem neuen Thema zuwenden.

Warum verallgemeinern, wenn wir uns spezialisieren können?

Der Titel dieses Abschnitts mag umstritten oder zumindest für manche schwer verständlich sein. Viele Programmierer ziehen es vor, sehr generische Lösungen zu entwickeln. Sie glauben, dass sie durch die Entwicklung generischer Implementierungen über Werkzeuge verfügen werden, die allgemein anwendbar und häufig effizient sind. Sie bemühen sich, Lösungen zu entwickeln, die in jedem Szenario funktionieren. Dieses Streben nach Verallgemeinerung kann jedoch zu einem Aufwand führen, der nicht immer notwendig sind. Warum verallgemeinern, wenn ein spezialisierter Ansatz das gleiche Ziel effektiver erreicht? In solchen Fällen bietet die Verallgemeinerung keine sinnvollen Vorteile.

Wenn Sie denken, dass ich seltsame Dinge sage, lassen Sie uns ein wenig darüber diskutieren, dann werden Sie verstehen, was ich erklären will. Zur Veranschaulichung möchte ich Ihnen ein Beispiel geben. Überlegen Sie sich die folgenden Fragen:

Was ist ein Computer, und warum besteht er aus so vielen Komponenten? Warum ersetzen neue Hardware-Innovationen häufig Software-Lösungen?

Wenn Sie unter 40 Jahre alt oder nach 1990 geboren sind und sich nicht mit älteren Technologien befasst haben, mag das, was ich jetzt sage, überraschend erscheinen. In den 1970er und frühen 1980er Jahren waren Computer noch nicht so weit wie heute. Um Ihnen eine Vorstellung davon zu geben: Videospiele wurden vollständig in Hardware programmiert, wobei Transistoren, Widerstände, Kondensatoren und andere diskrete Komponenten verwendet wurden. Softwarebasierte Spiele gab es nicht. Alles wurde in Hardware implementiert. Stellen Sie sich vor, wie schwierig es ist, selbst ein einfaches Spiel wie PONG nur mit elektronischen Bauteilen zu entwickeln. Die Ingenieure der damaligen Zeit waren unglaublich geschickt.

Die Verwendung von diskreten Bauteilen wie Transistoren, Widerständen und Kondensatoren bedeutete jedoch, dass die Systeme langsam waren und einfach bleiben mussten. Als die ersten Assembler-Kits wie der Z80 oder der 6502-Prozessor auf den Markt kamen, begann sich alles zu ändern. Mit diesen (auch heute noch erhältlichen) Prozessoren war es viel einfacher und schneller, Berechnungen in Software zu programmieren als sie in Hardware zu implementieren. Dies war der Beginn der Software-Ära. Was hat das mit neuronalen Netzen und unserer derzeitigen Implementierung zu tun? Geduld, liebe Leserin, lieber Leser, wir werden es schaffen.

Die Fähigkeit, relativ komplexe Aufgaben mit einfachen Anweisungen zu programmieren, machte Computer extrem vielseitig. Viele Innovationen beginnen als Software, weil Software schneller zu entwickeln und zu verfeinern ist. Nach der Verfeinerung können bestimmte Funktionen dann in Hardware-Implementierungen überführt werden, um die Effizienz zu steigern. Diese Entwicklung zeigt sich bei den Grafikprozessoren, wo viele Funktionen, die ursprünglich in Software entwickelt wurden, im Laufe der Zeit optimiert werden, bevor sie in die Hardware integriert werden. Damit sind wir wieder beim eigentlichen Thema dieser Diskussion angelangt. Eine Verallgemeinerung ist zwar möglich, führt aber oft zu Ineffizienzen - nicht bei der Entwicklung, sondern bei der Ausführung. Generische Implementierungen erfordern häufig zusätzliche Tests, um sicherzustellen, dass während der Ausführung keine unerwarteten Fehler auftreten. Andererseits sind spezialisierte Ansätze weniger fehleranfällig und können für eine schnellere Ausführung optimiert werden.

Sie fragen sich vielleicht, warum das wichtig ist, wenn Sie mit nur vier Werten in einer Datenbank arbeiten. Hier ist der Grund, lieber Leser. Oft beginnen wir mit der Entwicklung eines Systems, das mit einem kleinen Datensatz arbeiten kann, und skalieren es schrittweise, um größere Datenmengen zu verarbeiten. Mit der Zeit werden die Ausführungszeiten ineffizient. Das ist der Zeitpunkt, an dem die Spezialisierung der Hardware notwendig wird, um die gleichen Berechnungen durchzuführen, die zuvor mit Software durchgeführt wurden. Genau so entstehen neue Hardwaretechnologien.

Wenn Sie die Entwicklung von Hardware verfolgt haben, ist Ihnen wahrscheinlich ein Trend zu spezialisierten Technologien aufgefallen. Aber warum ist das so? Dieser Trend ist darauf zurückzuführen, dass softwarebasierte Lösungen mit der Zeit weniger kosteneffektiv werden als hardwarebasierte Alternativen. Bevor Sie einen neuen Grafikprozessor kaufen, der als Beschleuniger für neuronale Netzwerkberechnungen angepriesen wird, sollten Sie zunächst wissen, wie Sie Ihre vorhandene Hardware optimieren können. Dies erfordert spezielle Berechnungen anstelle allgemeiner Berechnungen. Aus diesem Grund werden wir uns auf die Optimierung der Berechnungen für die Pseudoinverse konzentrieren. Anstatt also einen Artikel mit allgemeinen Berechnungen zu erstellen, der zeigt, wie man eine Pseudoinverse faktorisiert, habe ich beschlossen, eine speziellere Berechnung zu implementieren. Bitte beachten Sie jedoch, dass es in Bezug auf die Rechenleistung nicht optimiert sein wird, da es sich um eine Ausbildung handelt, die in dieser Hinsicht nicht effizient ist. Mit Optimierung meine ich den Weg, wie alles umgesetzt wird. Wir werden nicht die Maximierung der Rechenleistung erreichen, bei der es notwendig wird, die Faktorisierung auf spezialisierter Hardware zu implementieren. Das ist genau das, was passiert, wenn eine neue Gerätetechnik auftaucht.

Es wurde viel über GPUs und CPUs mit der Fähigkeit zur Berechnung neuronaler Netze gesprochen. Aber ist dieser Ansatz wirklich das, was Sie brauchen? Um diese Frage zu beantworten, müssen wir zunächst verstehen, was aus Sicht der Software vor sich geht. Kommen wir nun zum nächsten Thema, wo wir sehen werden, was in Bezug auf die Software umgesetzt wird.

Pseudoinverse: Ein vorgeschlagener Ansatz

Ich hoffe, Sie haben inzwischen die wichtigsten Punkte verstanden. Betrachten wir nun das Folgende: In unserer Datenbank kann jede Information als zweidimensionales Diagramm mit X- und Y-Koordinaten dargestellt werden. Diese Visualisierung ermöglicht es uns, mathematische Beziehungen zwischen Datenpunkten herzustellen. Zu Beginn dieser Reihe haben wir uns mit der linearen Regression als Mittel zur Erreichung dieses Ziels befasst. In früheren Artikeln habe ich erklärt, wie man eine Skalarberechnung durchführt, um die Steigung und den Achsenabschnitt zu ermitteln, was uns die Ableitung der unten stehenden Gleichung ermöglicht.

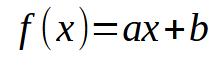
In diesem Fall sind die gewünschten Punkte die Werte < a > und < b >. Es gibt jedoch noch einen anderen Ansatz, der die Matrixfaktorisierung beinhaltet. Konkret müssen wir eine Pseudoinverse implementieren. Die Berechnungen dazu sind unten aufgeführt.

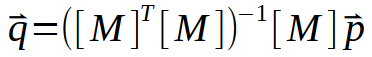
Hier stehen die Werte der Konstanten < a > und < b > in dem Vektor < q >. Um < q > zu berechnen, muss die Matrix M eine Reihe von Faktorisierungen durchlaufen. Der interessanteste Teil liegt jedoch in dem in der folgenden Abbildung dargestellten Prozess:

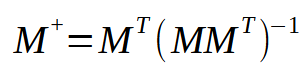
Dieses Bild ist genau das, was wir umsetzen müssen. Sie stellt dar, was im Pseudoinversum geschieht. Man beachte, dass die resultierende Matrix einen besonderen Namen hat: Pseudoinverse. Wie in der obigen Abbildung zu sehen ist, wird er mit dem Vektor < p > multipliziert, wodurch der Vektor < q > entsteht. Dieser Vektor < q > ist das Ergebnis, das wir erhalten wollen.

Im vorigen Artikel und zu Beginn dieses Artikels haben wir erwähnt, dass die Pseudoinversionsfunktion in Bibliotheken implementiert ist, sodass dafür Matrizen verwendet werden. Aber hier verwenden wir keine Matrizen, sondern etwas, das ihnen ähnlich ist: Arrays. An diesem Punkt haben wir also ein Problem, dessen Lösung darin besteht, entweder die Matrix in eine Matrix umzuwandeln oder eine Pseudoinverse für die Arrays zu implementieren. Da ich zeigen möchte, wie die Berechnung durchgeführt wird, wählen wir den zweiten Ansatz, d. h. die Pseudoinversionsimplementierung. Die entsprechenden Berechnungen sind nachstehend aufgeführt.

01. //+------------------------------------------------------------------+
02. matrix __PInv(const double &A[])
03. {
04.     double M[], T[4], Det;
05. 
06.     ArrayResize(M, A.Size() * 2);
07.     M[0] = M[1] = 0;
08.     M[3] = (double)A.Size();
09.     for (uint c = 0; c < M[3]; c++)
10.     {
11.         M[0] += (A[c] * A[c]);
12.         M[2] = (M[1] += A[c]);
13.     }
14.     Det = (M[0] * M[3]) - (M[1] * M[2]);
15.     T[0] = M[3] / Det;
16.     T[1] = T[2] = -(M[1] / Det);
17.     T[3] = M[0] / Det;
18.     ZeroMemory(M);
19.     for (uint c = 0; c < A.Size(); c++)
20.     {
21.         M[(c * 2) + 0] = (A[c] * T[0]) + T[1];
22.         M[(c * 2) + 1] = (A[c] * T[2]) + T[3];
23.     }
24. 
25.     matrix Ret;
26.     Ret.Init(A.Size(), 2);
27.     for (uint c = 0; c < A.Size(); c++)
28.     {
29.         Ret[c][0] = M[(c * 2) + 0];
30.         Ret[c][1] = M[(c * 2) + 1];
31.     }
32. 
33.     return Ret;
34. }
35. //+------------------------------------------------------------------+

Dieses Fragment, das oben vorgestellt wurde, nimmt uns die ganze Arbeit ab. Auf den ersten Blick mag es etwas kompliziert erscheinen, aber in Wirklichkeit ist es recht einfach und effizient. Im Wesentlichen haben wir es mit einem Array zu tun, das verschiedene „Double“-Werte enthält. Wir könnten zwar auch andere Typen verwenden, aber es ist wichtig, dass Sie, liebe Leserin, lieber Leser, sich von nun an mit der Verwendung von „double“-Werten vertraut machen. Der Grund dafür wird bald klar werden. Wenn alle Schritte der Faktorisierung abgeschlossen sind, erhalten wir als Ergebnis eine Matrix aus Doppelwerten.

Also, aufgepasst: Das Array, mit dem wir arbeiten, ist ein einfaches Array. Wir werden sie jedoch so behandeln, als wäre sie eine Matrix mit zwei Spalten. Aber wie ist das möglich? Bevor wir erörtern, wie wir diesen Code verwenden können, wollen wir ihn näher erläutern.

In Zeile 6 erstellen wir eine Matrix, die so viele Zeilen hat, wie Elemente im Array vorhanden sind. Aber es wird zwei Spalten haben. Dies unterscheidet sich vom Array, das intern nur eine einzige Spalte hat. In den Zeilen 7 und 8 initialisieren wir die Matrix M auf eine ganz bestimmte Weise. Um dies zu verstehen, werfen Sie einen Blick auf das folgende Bild.

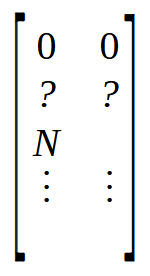
Beachten Sie, dass die ersten beiden Positionen auf Null gesetzt sind, gefolgt von zwei weiteren Positionen, die mit Fragezeichen versehen sind, da wir ihre genauen Werte noch nicht kennen. Kurz darauf folgt eine mit N gekennzeichnete Position. Dieser Wert N steht für die Größe des Arrays. Aber warum setzen wir die Größe des Arrays in die Matrix? Der Grund dafür ist einfach: Es ist schneller, auf einen Wert an einer bekannten Stelle zuzugreifen, als denselben Wert über eine Funktion zu suchen. Da wir vier freie Positionen am Anfang der Matrix benötigen, setzen wir die Größe des Arrays an die mit N bezeichnete Position. Dies geschieht in den Zeilen 7 und 8.

Wie in der vorigen Abbildung gezeigt, ist der erste Schritt, den wir durchführen müssen, die Multiplikation einer Matrix mit ihrer Transponierten. Aber hier haben wir keine Matrix. Alles, was wir haben, ist ein Array, oder genauer gesagt, ein Vektor. Wie führen wir also die Multiplikation durch? Es ist ganz einfach. Wir verwenden dazu die Schleife in Zeile 9. Aber was macht diese Schleife? Das mag auf den ersten Blick rätselhaft erscheinen, aber sehen wir uns das folgende Bild an.

Ein Array ist im Wesentlichen eine Sammlung von Werten, hier dargestellt von a0 bis an. Anstatt sie als Array zu betrachten, kann man sie als Matrix mit einer einzigen Spalte oder einer einzigen Zeile betrachten, je nachdem, wie die Daten organisiert sind. Wenn Sie nun eine Operation zwischen einer Matrix mit einer Spalte und einer anderen Matrix mit einer Zeile durchführen, erhalten Sie einen Einzelwert anstelle einer Matrix. Denken Sie daran, dass die Formel für die Pseudoinverse zunächst die Multiplikation einer Matrix mit ihrer Transponierten erfordert. Wir können das oben gezeigte Array jedoch implizit als eine Matrix betrachten. Siehe das Bild unten.

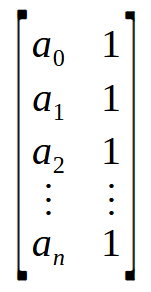
Wow! Jetzt haben wir die Matrix, die wir brauchen. Multipliziert man eine n x 2-Matrix mit ihrer Transponierung, so erhält man eine 2 x 2-Matrix. Mit anderen Worten: Wir haben ein Array, genauer gesagt einen Vektor, erfolgreich in eine 2 x 2 Matrix umgewandelt. Dies ist genau das, was die for-Schleife in Zeile 9 tut - sie multipliziert eine Matrix mit ihrer Transponierung und platziert das Ergebnis am Anfang der in Zeile 6 deklarierten Matrix.

Als Nächstes müssen wir die Inverse der soeben konstruierten Matrix finden. Bei einer 2 x 2-Matrix lässt sich die Inverse am schnellsten und einfachsten über die Determinante berechnen. Das Wichtigste dabei ist, dass wir keine allgemeine Methode brauchen, um die inverse Matrix oder die Determinante zu finden. Wir brauchen auch keine generische Methode, um die Matrix mit ihrer Transponierung zu multiplizieren. Wir können all dies direkt handhaben, da wir alles auf eine einfache 2 x 2 Matrix reduziert haben, was die Aufgabe viel einfacher und schneller macht. Um die Determinante zu berechnen, verwenden wir also Zeile 14. Nun können wir fortfahren und die Inverse der Matrix berechnen. Diese umgekehrte Berechnung, die bei einer generischen Implementierung langsam wäre, wird aufgrund der von uns getroffenen Entscheidungen extrem schnell durchgeführt. In den Zeilen 15 bis 17 wird die Inverse der über das Array erhaltenen Matrix erzeugt. Zu diesem Zeitpunkt ist fast alles fertig. Der nächste Schritt besteht darin, die Matrix M zu löschen, was in Zeile 18 geschieht. Also, aufgepasst. Die Matrix T enthält die inverse Matrix, und das Feld A enthält die Werte, die wir in die Pseudoinverse faktorisieren wollen. Alles, was bleibt, ist, das eine mit dem anderen zu multiplizieren und das Ergebnis in die Matrix M einzutragen. Das wichtigste Detail dabei ist, dass die Matrix T 2 x 2 ist, während die Anordnung A als n x 2-Matrix betrachtet werden kann. Diese Multiplikation führt zu einer n x 2 Matrix, die die Werte der Pseudoinverse enthält.

Diese Faktorisierung wird in der Schleife in Zeile 19 durchgeführt. In den Zeilen 21 und 22 setzen wir die Werte in die Matrix M. Und voilà, wir haben das Ergebnis der Pseudoinverse. Der Prozess, den ich hier beschreibe, könnte in einen OpenCL-Block portiert werden, der die GPU-Fähigkeiten zur Berechnung der linearen Regression für eine sehr große Datenbank nutzt. In manchen Fällen würden Berechnungen mit der CPU mehrere Minuten dauern, aber wenn man die Aufgabe an die GPU überträgt, geht es viel schneller. Dies ist die Optimierung, die ich bereits in diesem Artikel erwähnt habe.

Jetzt müssen wir nur noch das Ergebnis von Array M in eine Matrix einfügen. Dies geschieht in den Zeilen 25 bis 31. Was Sie in M finden, stellt bereits das gewünschte Ergebnis dar. Im Anhang stelle ich den Code zur Verfügung, damit Sie sehen können, wie alles funktioniert, und damit Sie es mit dem vergleichen können, was im vorherigen Artikel gezeigt wurde. Aber nicht alles ist perfekt. Beachten Sie, dass ich innerhalb dieser Funktion keine Tests durchführe. Das liegt daran, dass die Funktion zwar lehrreich ist, das Ziel aber darin besteht, sie so zu gestalten, dass sie in Hardware umgesetzt werden kann. In diesem Fall würden die Tests anders durchgeführt werden, was uns Bearbeitungszeit spart.

Damit ist eine entscheidende Frage noch nicht beantwortet: Wie kann diese Funktion PInv (Pseudoinverse) so schnell lineare Regressionsergebnisse erzeugen? Um diese Frage zu beantworten, sollten wir zum nächsten Thema übergehen.

Maximale Geschwindigkeit

Im vorigen Abschnitt haben wir gesehen, wie wir auf der Grundlage eines Arrays die Pseudoinverse berechnen können. Wir können diesen Prozess jedoch noch weiter beschleunigen. Anstatt nur die Pseudoinverse zurückzugeben, können wir auch die linearen Regressionswerte zurückgeben. Dazu müssen wir den Code aus dem vorherigen Abschnitt geringfügig anpassen. Diese Änderungen reichen aus, um die volle Geschwindigkeit des Grafikprozessors oder einer dedizierten CPU zu nutzen, um die Faktoren der linearen Gleichung zu finden. Die gesuchten Koeffizienten sind die Steigung und der Schnittpunkt. Das aktualisierte Fragment ist unten zu sehen.

01. //+------------------------------------------------------------------+
02. void Straight_Function(const double &Infos[], double &Ret[])
03. {
04.     double M[], T[4], Det;
05.     uint n = (uint)(Infos.Size() / 2);
06. 
07.     if (!ArrayIsDynamic(Ret))
08.     {
09.         Print("Response array must be of the dynamic type...");
10.         Det = (1 / MathAbs(0));
11.     }
12.     ArrayResize(M, Infos.Size());
13.     M[0] = M[1] = 0;
14.     M[3] = (double)(n);
15.     for (uint c = 0; c < n; c++)
16.     {
17.         M[0] += (Infos[c * 2] * Infos[c * 2]);
18.         M[2] = (M[1] += Infos[c * 2]);
19.     }
20.     Det = (M[0] * M[3]) - (M[1] * M[2]);
21.     T[0] = M[3] / Det;
22.     T[1] = T[2] = -(M[1] / Det);
23.     T[3] = M[0] / Det;
24.     ZeroMemory(M);
25.     for (uint c = 0; c < n; c++)
26.     {
27.         M[(c * 2) + 0] = (Infos[c * 2] * T[0]) + T[1];
28.         M[(c * 2) + 1] = (Infos[c * 2] * T[2]) + T[3];
29.     }
30.     ArrayResize(Ret, 2);
31.     ZeroMemory(Ret);
32.     for (uint c = 0; c < n; c++)
33.     {
34.         Ret[0] += (Infos[(c * 2) + 1] * M[(c * 2) + 0]);
35.         Ret[1] += (Infos[(c * 2) + 1] * M[(c * 2) + 1]);
36.     }
37. }
38. //+------------------------------------------------------------------+

Beachten Sie, dass im obigen Code die Prüfung bereits läuft. Mit dieser Prüfung wird überprüft, ob das zurückgegebene Array vom dynamischen Typ ist. Andernfalls muss die Anwendung geschlossen werden. Der Abschluss erfolgt in Zeile 10. Im vorangegangenen Artikel habe ich die Bedeutung dieser Zeile erläutert (für weitere Einzelheiten siehe dort, falls erforderlich). Ansonsten funktioniert der größte Teil des Codes ähnlich wie im vorherigen Abschnitt beschrieben, bis zu Zeile 30, wo die Dinge eine andere Richtung einschlagen. Aber lassen Sie uns für einen Moment zurücktreten. Wenn Sie sich diesen Code ansehen, werden Sie ihn vielleicht ungewöhnlich finden, insbesondere die Art und Weise, wie die Transponierung mit der Matrix bzw. dem Array multipliziert wird, und wie die inverse Matrix dann mit der ursprünglichen Matrix multipliziert wird, um die Pseudoinverse zu berechnen.

Welche Bedeutung hat das, was wir in diesem Fragment sehen? Was wie etwas sehr Komplexes aussieht, ist nichts weiter als eine „Punktmatrix“. Zum besseren Verständnis sehen Sie sich bitte die folgende Abbildung an.

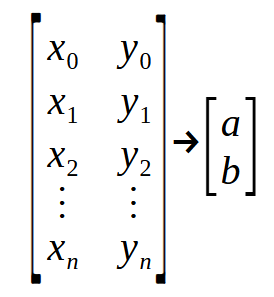
Beachten Sie, dass eine „Matrix“ eintritt und eine andere „Matrix“ austritt. In der Deklaration in Zeile 2 steht der Parameter Infos für die erste im Bild gezeigte Matrix, während Ret für die zweite Matrix steht. Die Werte < a > und < b > sind die Koeffizienten, die wir zu bestimmen versuchen, um die Gleichung der Geraden aufzustellen. Passen Sie jetzt gut auf: Jede Zeile der Matrix auf der linken Seite stellt einen Punkt auf dem Diagramm dar. Die geradzahligen Werte entsprechen denen, die in der zuvor besprochenen Funktion verwendet werden. In der Zwischenzeit stellen die ungeraden Werte die Vektoren in der eingangs erwähnten Formel dar, d. h. den Vektor < p >.

Diese Funktion, die zu Beginn dieses Themas besprochen wurde, nimmt alle Punkte des Diagramms und gibt die lineare Regressionsgleichung zurück. Um dies zu erreichen, müssen wir die Daten auf irgendeine Weise trennen, indem wir die geraden und ungeraden Werte organisieren. Das ist der Grund, warum der Code so anders aussieht als der im vorherigen Abschnitt. Sie funktionieren jedoch auf dieselbe Weise, zumindest bis Zeile 30. An diesem Punkt führen wir etwas aus, das im früheren Code nicht zu sehen war. Hier wird das Ergebnis der in der Matrix M gespeicherten Pseudoinverse genommen und mit den Vektoren multipliziert, die sich in den ungeraden Positionen des Parameters Infos befinden. Daraus ergibt sich der Ret-Vektor, der aus den Konstanten besteht, die für die Definition der Geradengleichung oder der linearen Regression erforderlich sind, wie Sie es wünschen.

Wenn Sie dieselbe Operation mit den Werten durchführen, die von der Funktion PInv aus dem vorherigen Artikel zurückgegeben werden, erhalten Sie dasselbe Ergebnis wie in diesem Fragment gezeigt. Der einzige Unterschied besteht darin, dass diese spezielle Implementierung so konzipiert ist, dass sie sich für eine hardwarebasierte Ausführung eignet, z. B. in einer speziellen Recheneinheit für neuronale Netze. Dies kann dazu führen, dass neue Technologien in Prozessoren integriert werden, sodass die Hersteller behaupten können, ein bestimmter Prozessor oder eine bestimmte Schaltung verfüge über eingebaute künstliche Intelligenz oder neuronale Netzwerkfunktionen. Dies ist jedoch weder revolutionär noch bahnbrechend. Es geht einfach darum, etwas in Hardware zu implementieren, was vorher in Software ausgeführt wurde, und so ein allgemeines System in ein spezialisiertes zu verwandeln.

Abschließende Überlegungen

Liebe Leserinnen und Leser, liebe Interessierte. Ich glaube, dass wir mit dem bisher Besprochenen alles abgedeckt haben, was Sie zu diesem Zeitpunkt über neuronale Netze und künstliche Intelligenz wissen müssen. Bisher haben wir jedoch nicht das neuronale Netz als solches besprochen, sondern die Verwendung und Konstruktion eines einzelnen Neurons, da wir nur eine Berechnung durchgeführt haben. In einem neuronalen Netz werden dieselben Berechnungen mehrfach durchgeführt, allerdings in einem größeren Maßstab. Auch wenn Ihnen das nicht sofort einleuchtet, ist ein neuronales Netz einfach die Umsetzung einer Graphenarchitektur, bei der jeder Knoten ein Neuron oder eine lineare Regressionsfunktion darstellt. Je nach den berechneten Ergebnissen werden bestimmte Wege eingeschlagen.

Ich verstehe, dass diese Perspektive uninspirierend oder sogar trivial erscheinen mag. Aber das ist die Realität. Neuronale Netze haben nichts Magisches oder Fantastisches an sich, ganz gleich, wie sie in den Medien oder von unkundigen Personen dargestellt werden. Alles, was eine Maschine tut, ist nichts anderes als eine einfache mathematische Berechnung. Wenn Sie diese Berechnungen verstehen, werden Sie auch neuronale Netze verstehen. Außerdem erhalten Sie Einblicke in die Simulation des Verhaltens von lebenden Organismen. Das liegt nicht daran, dass lebende Organismen organische Maschinen sind, auch wenn man in einigen Fällen behaupten könnte, dass sie das sind. Aber das ist ein Thema für ein anderes Mal.

Ich hoffe, dass Sie, verehrter Leser, das Wesen eines neuronalen Netzes auf der einfachsten Ebene begreifen, indem Sie das Konzept eines einzelnen Neurons verstehen, was genau das ist, was wir bis jetzt erforscht haben.

In den nächsten Artikeln werde ich Ihnen zeigen, wie Sie ein einzelnes Neuron in ein kleines Netzwerk einbinden, damit es etwas lernen kann. Ich vermeide es absichtlich, diese Konzepte auf die Finanzmärkte anzuwenden, also erwarten Sie das in Zukunft nicht von mir. Mein Ziel ist es, Ihnen dabei zu helfen, zu verstehen, zu lernen und durch eigene Erfahrung erklären zu können, was ein neuronales Netz ist und wie es lernt. Zu diesem Zweck müssen Sie mit einem System experimentieren, das einfach genug ist, um es zu verstehen.

Bleiben Sie also dran, wenn dieses Thema weiter behandelt wird. Ich werde mir etwas Spannendes einfallen lassen, das ich mit Ihnen teilen kann, etwas, das es wirklich wert ist, erforscht zu werden. In der Zwischenzeit enthalten die beigefügten Materialien den notwendigen Code, um die Funktionsweise eines einzelnen Neurons zu studieren.