Нейронная сеть на практике: Псевдообратная (II)

Введение

Рад приветствовать всех в новой статье о нейронных сетях. 

В предыдущей статье "Нейронная сеть на практике: Псевдообратная (I)", я показал, как можно использовать функцию, доступную в библиотеке MQL5, для вычисления псевдообратной. Однако метод, присутствующий в библиотеке MQL5, как и во многих других языках программирования, предназначен для вычисления псевдообратной при использовании матриц или хотя бы какой-то структуры, которая может напоминать матрицу.

Хотя в данной статье показано, как выполняется умножение двух матриц, и даже факторизация для получения определителя любой матрицы (который важен для того, чтобы знать, можно ли матрицу инвертировать или нет), нам всё равно пришлось реализовать еще одну факторизацию. Это нужно для того, чтобы вы могли понять, как выполняется факторизация для получения значений псевдообратной. Данная факторизация заключается в генерации обратной матрицы.

Вы можете задать вопрос: а как же транспонирование? В предыдущей статье я показал, как можно выполнить факторизацию для симуляции умножения матрицы на ее транспонирование, что не является проблемой.

Но вычисления, которые нам еще предстоит выполнить, а именно получение обратной матрицы, - это на самом деле не то, что я хотел показать. И это связано не с тем, что это сложно реализовать, просто я не вижу в этом необходимости. Дело в том, что данные статьи имеют образовательную цель и не предназначены для объяснения того, как реализовать тот или иной функционал. Учитывая это, я решил, что в данной статье будет осуществлено что-то немного другое. Вместо того, чтобы показывать, как применять факторизацию для получения обратной матрицы, мы сосредоточимся на том, как получить псевдообратную, используя данные, с которыми мы работали с самого начала. То есть, нет смысла показывать, как мы что-то определяем общим способом, если мы можем сделать то же самое особым способом. И самое приятное, что вы гораздо лучше поймете, почему всё работает именно так, чем если бы мы следовали общей логике при создании факторизации, как это было показано в предыдущей статье, где эти функции были общими. Однако мы можем выполнить вычисления гораздо быстрее, если сделаем это определенным образом. Чтобы лучше понять эту концепцию, давайте перейдем к новой теме.

Зачем обобщать, если можно специализировать процедуры?

Название, которое мы используем в этой статье, мягко говоря, спорное и, во многих случаях, непонятное. Как правило, многие программисты предпочитают создавать разные элементы в достаточно общем виде. Или, по крайней мере, они считают, что они получат более полезное и быстрое решение, когда создадут что-то общее. Однако они часто стремятся разработать что-то, что будет работать при любом сценарии. Итак, вопрос обобщения в некоторых случаях влечет за собой расходы, которые нам не нужно нести. Потому что если цель может быть достигнута с помощью конкретной процедуры, зачем обобщать? В этих случаях обобщение не приносит нам никакой пользы.

Если вы думаете, что я говорю странные вещи, давайте немного поразмышляем, и тогда вам станет понятным то, что я хочу объяснить. Для лучшего понимания, я попрошу вас найти ответ на следующий вопрос:

Что такое компьютер, почему у него так много компонентов и функций и почему время от времени появляется новое оборудование (hardware), заменяющее программное обеспечение?

Если вам меньше 40 или вы родились после 1990-х годов и не изучали старые технологии, то информация, о которой я вам сейчас расскажу, может показаться абсурдной. Но в период с 1970-х до середины 1980-х годов компьютеры не были такими, какими мы знаем их сегодня. Чтобы вы понимали, компьютерные игры программировались полностью за счет оборудования, с использованием транзисторов, резисторов, конденсаторов и других компонентов. Не было ни одной игры с использованием программного обеспечения. Всё было сделано посредством оборудования. А теперь подумайте, насколько сложно создать игру, даже такую примитивную, как PONG, используя только электронные компоненты. Настоящие люди были очень ловки в своем деле, ведь задача была не из легких.

Однако, поскольку всё делалось с помощью дискретных компонентов (так в электронике называются транзисторы, резисторы и конденсаторы), всё происходило гораздо медленнее и должно было быть простым. Но когда появились первые наборы для сборки, например Z80 или 6502, ситуация начала меняться. Эти процессоры, которые можно встретить и сегодня, в значительной степени помогли программному обеспечению занять центральное место. Запрограммировать вычисления с помощью программного обеспечения было гораздо проще и быстрее, чем сделать вычисления с помощью оборудования. Так началась эра программного обеспечения. Но какое отношение это имеет к нейронным сетям и тому, что мы реализуем? Терпение, дойдем и до этого.

Сам факт наличия возможности запрограммировать что-то относительно сложное, используя простые инструкции, сделал компьютер увлекательным инструментом. Многие вещи сначала разрабатываются в программном обеспечении в довольно общем виде. Благодаря этому разработка новых решений происходит стремительно быстро. Настолько, что многое из того, что мы видим сегодня в графических процессорах (видеокартах), сначала появилось в программном обеспечении. Данные решения дорабатываются по мере возможности, пока они не станут достаточно простыми для реализации в оборудовании, и в этом кроется ключ к решению проблемы. Мы можем обобщать вещи, но это делает их медленными, не при их реализации, а при их исполнении. При обобщении необходимо постоянно проверять, чтобы при выполнении факторизации не возникало странных ошибок. Однако если сделать это конкретным образом, то можно уменьшить частоту тестирования, что позволит выполнять задачи гораздо быстрее.

Хорошо, но зачем столько забот, если мы работаем только с четырьмя значениями в базе данных? В этом и вопрос, дорогие читатели. Сначала мы создаем систему, которая может работать с небольшим объемом данных, а затем масштабируем ее до всё больших и больших объемов, и так наступит момент, когда время выполнения перестанет быть эффективным. Именно в этот момент возникает необходимость в специализированном оборудовании для выполнения тех же вычислений, которые ранее выполнялись с помощью программного обеспечения. Так рождаются новые технологии в области оборудования.

Если вы следите за развитием оборудования, то наверняка заметили, что оно тяготеет к определенным технологиям. Но почему так? Причина этого кроется в следующем: Решение путем программного обеспечения становится дороже аналогичного решения оборудования. Итак, прежде чем вы решитесь на покупку нового графического процессора только потому что он «ускоряет» работу нейронных сетей, вам следует узнать, как наилучшим образом использовать уже имеющееся у вас оборудование. А для этого нам нужен не общий расчет, а специализирующийся на выполнении конкретной задачи. В нашем случае мы хотим оптимизировать вычисление псевдообратной. Поэтому вместо того, чтобы создавать статью с общим расчетом, показывающим, как провести факторизацию псевдообратной, мы решили реализовать несколько более специализированный расчет. Хотя стоит отметить, что он не будет оптимизирован с точки зрения вычислительной мощности, так как его цель - обучающая, которая не эффективна в этом отношении. И когда я говорю об этом, я имею в виду то, как всё будет реализовано. То есть мы не собираемся достигать точки максимизации вычислительной мощности, когда станет необходимо реализовать факторизацию на специализированном оборудовании. Именно так происходит при появлении новой технологии оборудования.

Много говорилось о видеокартах и даже процессорах с возможностями вычисления нейронных сетей. Но действительно ли такой подход - это то, что вам нужно? Чтобы ответить на данный вопрос, нужно сначала понять, что происходит с точки зрения программного обеспечения. Давайте теперь перейдем к следующей теме, в которой мы увидим то, что будет реализовано в плане программного обеспечения.

Псевдообратная: подход к ней

Хорошо, я думаю, что вы сумели разобраться в этой теме. Так что давайте подумаем о следующем: В нашей базе данных каждый фрагмент информации можно представить в виде графика с двумя координатами - X и Y, с помощью которого мы пытаемся создать некую математическую связь между данными. Это исследовалось с самого начала этой маленькой серии статей. Умение использовать линейную регрессию очень помогает нам в том, что понадобится реализовать в условиях кода. В предыдущих статьях мы уже рассмотрели, как выполнить скалярное вычисление, чтобы найти угловой коэффициент и точку пересечения, что позволяет нам составить уравнение, показанное ниже.

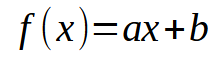
В данном случае искомыми точками являются значения < a > и < b >. Однако есть и другой способ. Для этого используются матричные факторизации. По сути, нам нужно реализовать псевдообратную. Расчеты для этого приведены ниже.

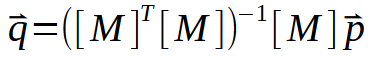
Здесь значения констант < a > и < b > находятся в векторе < q >. Таким образом, матрица M должна пройти через небольшую последовательность факторизаций, пока не будет получен вектор < q >. Но самое интересное находится не на картинке выше, а на картинке ниже.

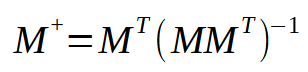
Это изображение - именно то, что нам нужно реализовать, поскольку оно представляет то, что происходит в псевдообратной. Обратите внимание, что в результате получается матрица со специальным названием: псевдообратная. Как видно на рисунке выше, он умножается на вектор < p >, в результате чего образуется вектор < q >. Данный вектор < q > и есть тот результат, который мы хотим получить.

В предыдущей статье и в начале данной статьи мы упоминали, что псевдообратная функция реализована в библиотеках, поэтому для нее используются матрицы. Но здесь мы не используем матрицы, мы используем нечто похожее на них: массивы. Итак, на этом этапе мы имеем проблему, решение которой таково: преобразовать массив в матрицу или реализовать псевдообратную для использования массивов. Поскольку я хочу показать, как реализуется вычисление, мы выберем второй подход, то есть реализацию псевдообратной. Расчеты для этого показаны в приведенном ниже фрагменте.

01. //+------------------------------------------------------------------+
02. matrix __PInv(const double &A[])
03. {
04.     double M[], T[4], Det;
05. 
06.     ArrayResize(M, A.Size() * 2);
07.     M[0] = M[1] = 0;
08.     M[3] = (double)A.Size();
09.     for (uint c = 0; c < M[3]; c++)
10.     {
11.         M[0] += (A[c] * A[c]);
12.         M[2] = (M[1] += A[c]);
13.     }
14.     Det = (M[0] * M[3]) - (M[1] * M[2]);
15.     T[0] = M[3] / Det;
16.     T[1] = T[2] = -(M[1] / Det);
17.     T[3] = M[0] / Det;
18.     ZeroMemory(M);
19.     for (uint c = 0; c < A.Size(); c++)
20.     {
21.         M[(c * 2) + 0] = (A[c] * T[0]) + T[1];
22.         M[(c * 2) + 1] = (A[c] * T[2]) + T[3];
23.     }
24. 
25.     matrix Ret;
26.     Ret.Init(A.Size(), 2);
27.     for (uint c = 0; c < A.Size(); c++)
28.     {
29.         Ret[c][0] = M[(c * 2) + 0];
30.         Ret[c][1] = M[(c * 2) + 1];
31.     }
32. 
33.     return Ret;
34. }
35. //+------------------------------------------------------------------+

Данный фрагмент делает всю работу за нас. Звучит невероятно сложно, но это не так, на самом деле всё очень просто и понятно. Здесь мы получаем вектор в формате массива с несколькими значениями типа double. Мы могли бы использовать и другой вид, но хорошо бы, чтобы вы с этого момента начали привыкать к использованию значений double. Причина скоро станет понятна. После выполнения всех факторизаций мы получим матрицу значений типа double.

Теперь обратите внимание: Массив, который мы применяем, относится к простому виду, но он всё равно будет рассматриваться как матрица с двумя столбцами. Но как это возможно? Давайте разберемся в этом, прежде чем рассматривать, как использовать данный код.

В шестой строке мы создаем матрицу, в которой будет столько строк, сколько элементов в массиве. Однако этот массив будет иметь два столбца, в отличие от массива, который внутри имеет только один столбец. Теперь, в строках 7 и 8, мы инициализируем матрицу M довольно специфическим образом. Чтобы понять это, нужно посмотреть на изображение ниже.

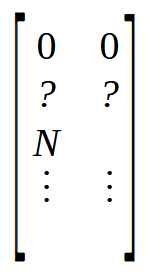
Отметим, что первые две позиции равны нулю, а две другие отмечены вопросительным знаком, поскольку мы не знаем, какое значение там находится. Но сразу после этого у нас есть позиция со значением N. Это значение - размер массива. Почему я помещаю размер массива в матрицу? Причина проста: Быстрее найти значение в известной позиции, чем искать его в функции. И поскольку нам нужны четыре свободные позиции в начале массива, я помещаю размер массива в позицию, обозначенную как N. Именно это и делается в строках семь и восемь.

Теперь, глядя на изображение перед фрагментом, мы видим, что первое, что нужно сделать, - это умножить матрицу на её транспонирование. Но здесь у нас по-прежнему нет матрицы. Всё, что у нас есть, - это вектор, или, скорее, массив. Итак, как же нам выполнить это умножение? Всё просто, для этого мы воспользуемся циклом, присутствующим в девятой строке. Что это? Разве такое возможно? Это бессмыслица. Что вы пытаетесь сделать? Давайте разберемся в этом, посмотрите на изображение ниже.

Массив - это не что иное, как набор значений, которые здесь представлены как a0 an. Если представить эту концепцию не как массив, а как матрицу, то мы увидим матрицу с одним столбцом или одной строкой, в зависимости от того, как организованы данные. Если мы выполняем операцию между матрицей с одним столбцом и матрицей с одной строкой, то мы получим скалярное значение, а не матрицу. Помните, что формула псевдообратной сначала выполняет умножение между матрицей и ее транспонированием, но мы можем интерпретировать этот массив, показанный выше, как нечто подобное тому, что вы видите на изображении ниже.

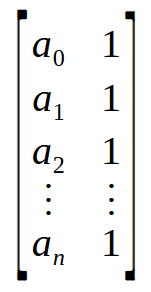
Ух ты! Теперь у нас есть необходимая матрица. Таким образом, умножив матрицу n x на ее транспонирование, мы получим матрицу 2 x 2. Другими словами, нам удается преобразовать вектор, а точнее, массив, в матрицу 2 x 2. Именно это и делает цикл for в девятой строке: умножает матрицу на его транспонирование и помещает результат в начало матрицы, который мы объявили в шестой строке.

Теперь нам нужно найти матрицу, обратную только что построенной. В матрице 2 x 2 самый быстрый и простой способ найти обратную величину - это использовать определитель. Обратите внимание: нам не нужен общий метод для нахождения обратной матрицы или определителя. Нам также не нужен общий метод умножения матрицы на ее транспонирование. Мы можем сделать это просто, поскольку всё сведено к матрице 2 x 2, что значительно упрощает и ускоряет работу. Таким образом, чтобы найти определитель, мы используем строку 14. Теперь мы можем искать обратную матрицу. Данный расчет, который в общем случае был бы очень медленным, выполняется очень быстро просто потому, что мы уже приняли некоторые решения. Затем, в строках 15-17, мы генерируем обратную матрицу, полученную из массива. Теперь почти всё готово. Следующее, что нужно сделать, - это очистить матрицу M, что делается в строке 18. Теперь обратите внимание: Матрица T содержит обратную матрицу, а массив A - значения, по которым мы хотим разложить псевдообратную матрицу. Осталось только умножить одно на другое и поместить результат в матрицу M. Дело в том, что матрица T имеет вид 2 x 2, а массив можно рассматривать как матрицу n x 2. В результате получится матрица n x 2, в которой содержится именно значения псевдообратной.

Данная факторизация выполняется в цикле строки 19. Затем, в строках 21 и 22, мы помещаем значения внутрь матрицы M. И вот мы получаем результат псевдообратной. Этот расчет можно преобразовать в блок в OpenCL, используя возможности GPU для расчета линейной регрессии очень большой базы данных. В некоторых случаях при использовании центрального процессора вычисления занимают несколько минут, но если передать всю работу процессору, они будут выполнены гораздо быстрее. Это та самая оптимизация, о которой мы говорили в начале статьи.

Осталось только перевести результат массива M в матрицу. Это делается в строках с 25 по 31. Однако то, что уже есть в М, и есть тот результат, к которому мы стремимся. В приложении оставим несколько кодов, чтобы вы могли увидеть, как всё работает. Затем вы можете сравнить его с кодом, показанным в предыдущей статье. Однако он не идеален, как и всё остальное. Обратите внимание, что я не выполняю никаких тестов в данной функции. Это связано с тем, что, несмотря на обучающую направленность проекта, он должен напоминать то, что можно реализовать в оборудовании. И в этом случае тесты будут проводиться по-другому, что позволит нам сэкономить время на обработку.

Очень хорошо, но это не отвечает на один вопрос: как эта псевдообратная (PInv) может так быстро генерировать линейную регрессию? Чтобы ответить на данный вопрос, давайте обратимся к новой теме.

Максимальная скорость

В предыдущей теме мы рассмотрели, как из массива можно вычислить псевдообратую. Однако мы можем еще больше ускорить процесс, и тогда полученное значение будет не псевдообратной, а значением линейной регрессии. Для этого нам придется немного изменить код, рассмотренный в предыдущей теме. Но этой небольшой модификации будет достаточно, чтобы мы могли использовать всю мощь GPU или даже выделенного CPU для нахождения коэффициентов линейного уравнения. Напомним, что искомыми коэффициентами являются угловой коэффициент и точка пересечения. Новый фрагмент кода можно рассмотреть ниже.

01. //+------------------------------------------------------------------+
02. void Straight_Function(const double &Infos[], double &Ret[])
03. {
04.     double M[], T[4], Det;
05.     uint n = (uint)(Infos.Size() / 2);
06. 
07.     if (!ArrayIsDynamic(Ret))
08.     {
09.         Print("Response array must be of the dynamic type...");
10.         Det = (1 / MathAbs(0));
11.     }
12.     ArrayResize(M, Infos.Size());
13.     M[0] = M[1] = 0;
14.     M[3] = (double)(n);
15.     for (uint c = 0; c < n; c++)
16.     {
17.         M[0] += (Infos[c * 2] * Infos[c * 2]);
18.         M[2] = (M[1] += Infos[c * 2]);
19.     }
20.     Det = (M[0] * M[3]) - (M[1] * M[2]);
21.     T[0] = M[3] / Det;
22.     T[1] = T[2] = -(M[1] / Det);
23.     T[3] = M[0] / Det;
24.     ZeroMemory(M);
25.     for (uint c = 0; c < n; c++)
26.     {
27.         M[(c * 2) + 0] = (Infos[c * 2] * T[0]) + T[1];
28.         M[(c * 2) + 1] = (Infos[c * 2] * T[2]) + T[3];
29.     }
30.     ArrayResize(Ret, 2);
31.     ZeroMemory(Ret);
32.     for (uint c = 0; c < n; c++)
33.     {
34.         Ret[0] += (Infos[(c * 2) + 1] * M[(c * 2) + 0]);
35.         Ret[1] += (Infos[(c * 2) + 1] * M[(c * 2) + 1]);
36.     }
37. }
38. //+------------------------------------------------------------------+

Обратите внимание, что в приведенном фрагменте кода тест уже выполняется. Данный тест проверяет, является ли возвращаемый массив динамическим типом. В противном случае приложение надо будет закрыть. Закрытие происходит на строке 10. В предыдущей статье я объяснил значение данной строки, так что если вы сомневаетесь, советую ознакомиться с ней подробнее. В остальном, большая часть кода работает так же, как и в предыдущей теме, пока мы не дойдем до строки 30, где ситуация меняется. Но давайте немного отступим назад, чтобы лучше понять ситуацию. Взглянув на этот код, можно удивиться происходящему, поскольку умножение транспонирования на матрицу, а точнее, на массив, выглядит несколько иначе. То же самое относится и к умножению обратной матрицы на исходную для вычисления псевдообратную.

В чем смысл того, что мы видим в этом фрагменте? То, что кажется чем-то очень сложным, - не более чем "матрица точек". Для лучшего понимания рассмотрите рисунок ниже.

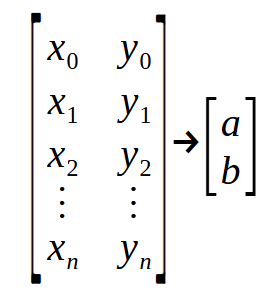
Обратите внимание, что у нас есть входная "матрица" и выходная "матрица". В объявлении во второй строке параметр Infos - это первая матрица, показанная на изображении выше, а Ret - это вторая матрица на изображении. Значения < a > и < b > мы ищем, чтобы составить уравнение прямой линии. Теперь надо обратить всё свое внимание. Каждая строка левой матрицы представляет собой точку на графике. Значения в четных позициях - это значения, которые используются в функции, рассмотренной в предыдущей теме, в то время как значения в нечетных позициях представляют собой векторы в формуле, упомянутой в начале статьи, то есть вектор < p >.

Данная функция, рассмотренная в начале этой темы, получает все точки графика и возвращает уравнение линейной регрессии. Нужно как-то разделить элементы, и способ сделать это - связать всё между четными и нечетными значениями. Вот почему этот код кажется таким непохожим на предыдущую тему, но на самом деле это не так, по крайней мере, пока мы не дойдем до 30-й строки. В этот момент выполняется то, что не было сделано в предыдущем коде. Мы берем результат псевдообратной матрицы M и умножаем его на векторы, находящиеся в нечетной части параметра Infos. В результате получается вектор Ret, который представляет собой константы, необходимые для создания уравнения линии или линейной регрессии, в зависимости от того, как вы предпочитаете это называть.

Если выполнить ту же операцию со значениями, возвращаемыми функцией PInv, которую мы рассматривали в предыдущей статье, мы получим тот же результат, что и в этом отрывке, с одной лишь разницей: код, показанный в данном фрагменте, можно использовать для создания аппаратного обеспечения, предназначенного для вычислений нейронных сетей. Это приведет к появлению новой технологии, которая будет интегрирована в процессоры, где отрасль может заявить, что тот или иной процессор или схема содержит искусственный интеллект или нейросетевые механизмы, но в этом нет ничего революционного. Они просто превращают нечто общее, ранее выполнявшееся в программном обеспечении, в нечто специализирующееся на оборудование, превращая таким образом общее в специализированное.

Заключительные идеи

Итак, мои дорогие читатели. Учитывая всё, что мы видели до сих пор, я считаю, что мы усвоили самое необходимое, что нужно знать о нейронных сетях и искусственном интеллекте. Однако до сих пор мы обсуждали не нейронную сеть как таковую, а использование и построение одного нейрона, так как мы произвели только один расчет. В случае с нейронной сетью мы имеем набор таких же простых вычислений, но выполненных в более широком масштабе. Хотя сейчас это может быть не совсем понятно, но нейронная сеть - это не что иное, как реализация архитектуры графа, где каждый узел представляет собой нейрон или функцию линейной регрессии, в зависимости от результатов расчетов выбирается то или иное направление.

Я знаю, что такое представление о нейронной сети может показаться обескураживающим или даже тривиальным, но это правда. За этой темой не сокрыто ничего магического или фантастического, хотя средства массовой информации или люди, не понимающие и не изучающие эту область, хотели бы, чтобы вы в это поверили. Всё, что делает машина, - не более чем простые математические расчеты. Если понять эти вычисления, то вы сможете понять, что такое нейронная сеть. Более того, вы тоже сможете понять, как моделировать поведение живых существ. Дело не в том, что живые существа - это органические машины, хотя в некоторых случаях мы можем думать именно так (но это уже другой разговор для тех, кто ближе ко мне):

я хочу, чтобы вы поняли, что такое нейронная сеть в ее простейшей форме, то есть с использованием только одного нейрона, что мы и делали до сих пор.

В следующих статьях (хотя я еще не знаю, как они будут выглядеть), мы организуем этот одиночный нейрон в небольшую сеть, чтобы он мог чему-то научиться. Поскольку я не хочу показывать ничего, связанного с финансовыми рынками с использованием данных концепций, не ждите этого в будущем, по крайней мере, от меня. Моя цель - чтобы вы поняли, изучили и смогли объяснить, основываясь на собственном опыте, что такое нейронная сеть и как она может обучаться. А чтобы добиться этого, нам придется поэкспериментировать с достаточно простой системой.

Так что следите за новыми статьями на эту тему. Я думаю о том, как показать вам что-то интересное и действительно стоящее. В приложениях вы найдете коды, с помощью которых можно начать изучение работы одного нейрона.