Aprendizaje automático y Data Science (Parte 10): Regresión de cresta

Introducción 

La regresión de cresta (ridge regression) es un método para valorar los coeficientes de los modelos de regresión múltiple cuando las variables independientes están altamente correlacionadas. El método ofrece una mayor eficiencia en los problemas de estimación de parámetros gracias al grado de desplazamiento permitido. Similar a la regresión de Lasso (reducción mínima absoluta y operador de selección), introduce un factor de penalización al imponer una restricción, pero a diferencia de ella, toma el cuadrado en lugar de la magnitud de los coeficientes. Este método de análisis de regresión se encarga tanto de seleccionar como de regularizar las variables para mejorar la precisión de la predicción y la interpretabilidad de las estadísticas resultantes. Aunque la estimación de la cresta está desplazada, tiene una varianza bastante baja. El uso del coeficiente nos permite elegir el mejor subconjunto, y el llamado umbral suave también está asociado con ellos. Además, al igual que sucede con la regresión lineal estándar, las estimaciones de los coeficientes no tienen que ser únicas si las covariables son colineales.

Ahora, para entender por qué necesitamos dichos modelos, primero deberemos comprender los términos de desplazamiento y varianza.

Desplazamiento 

Se trata de la incapacidad del aprendizaje automático para captar la verdadera relación entre la variable independiente y la variable de respuesta.

¿Y qué significa esto para el modelo?

• Un modelo de bajo desplazamiento hará menos suposiciones sobre la forma de la función objetivo.
• Con un desplazamiento alto, el modelo hará más suposiciones y podrá captar relaciones en el conjunto de datos de entrenamiento.

Dispersión

La varianza muestra cuánto se distingue la variable aleatoria respecto al valor esperado.
Métodos para reducir un desplazamiento alto:

• Aumentar los parámetros de entrada, ya que el modelo no está bien ajustado
• Reducir el periodo de regularización
• Usar modelos más complejos, como los que implican funciones polinómicas

Métodos para reducir una varianza alta:

• Disminuir los parámetros de entrada, ya que se produce un ajuste con una gran varianza
• Usar un modelo no demasiado complejo
• Aumentar la muestra de entrenamiento
• Ampliar del periodo de regularización

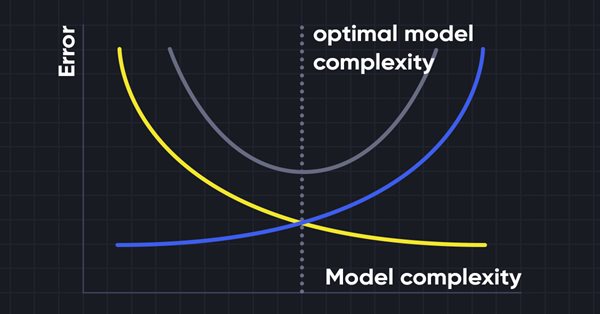
Un compromiso entre desplazamiento y dispersión

Al construir un modelo de aprendizaje automático, resulta esencial tener cuidado con el desplazamiento y la varianza para evitar el ajuste excesivo del modelo. Si el modelo es muy simple y tiene menos parámetros, tenderá a mostrar más desplazamiento pero poca varianza, mientras que los modelos complejos a menudo tienen un desplazamiento bajo pero una varianza alta. Por lo tanto, deberemos encontrar un equilibrio entre el desplazamiento y los errores de varianza. La búsqueda de tal equilibrio se denomina compensación entre desplazamiento y varianza.

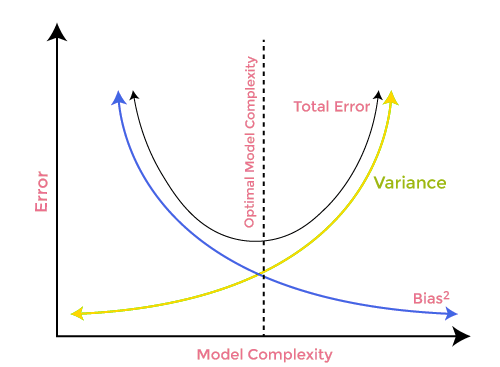
Al mismo tiempo, los algoritmos requieren un desplazamiento y una varianza más bajos para realizar predicciones precisas del modelo, pero esto resulta prácticamente imposible, ya que el desplazamiento y la varianza están relacionados negativamente entre sí.

Si aumentamos el desplazamiento, la varianza disminuirá y viceversa.

Regresión de cresta

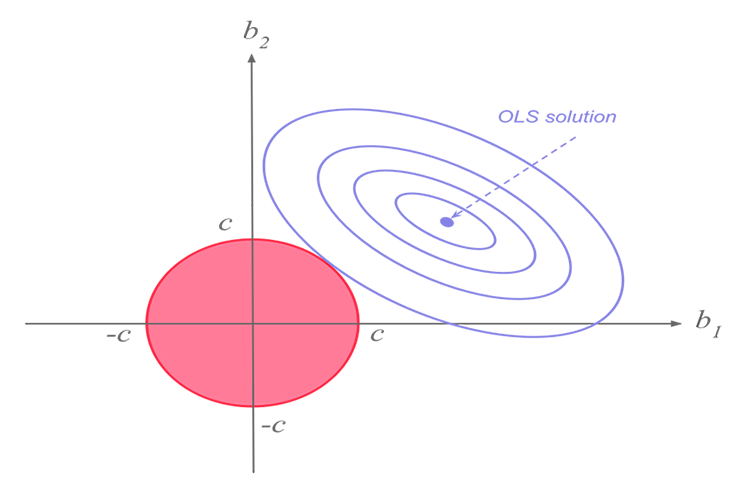
La regresión de cresta y la regresión de Lasso realizan una función similar, pero tienen una diferencia significativa que veremos más adelante cuando profundicemos en las matemáticas e intentemos descubrir cómo funciona cada algoritmo.

La idea de la regresión de cresta

Al trabajar con muchas medidas correlacionadas linealmente, podemos afirmar con seguridad que el método de los mínimos cuadrados mostrará perfectamente la relación entre la variable objetivo y la independiente.

Mire el siguiente ejemplo de la relación entre el tamaño y el peso del ratón.

Pero, ¿qué sucede si solo tenemos dos dimensiones en nuestro conjunto de datos y el resto se usa como conjunto de datos de prueba? Ajustar el modelo con el método de mínimos cuadrados dará como resultado un ajuste perfecto que ofrecerá una suma cero de los cuadrados de los restos.

Ahora probaremos este modelo con un nuevo conjunto de datos:

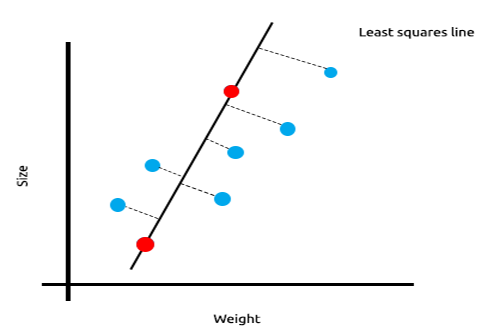
La suma del cuadrado de los errores en los datos de entrenamiento es cero, pero la suma del cuadrado de los restos en los datos de prueba es significativa, lo cual significa que nuestro modelo posee una varianza alta. En cuanto al aprendizaje automático, esto significa que el modelo se ha ajustado a los datos de entrenamiento.

La idea básica de la regresión de cresta y Lasso es encontrar un modelo que no se ajuste a los datos de entrenamiento.

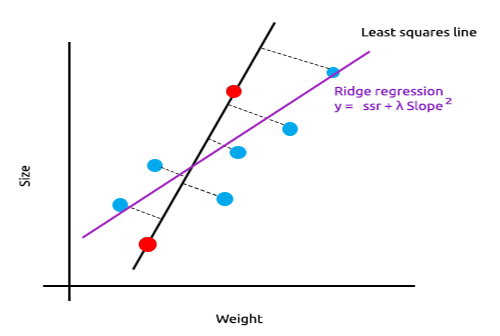
La regresión de cresta introduce un pequeño desplazamiento, lo cual redunda en una reducción significativa de la varianza. Como la regresión de cresta ha introducido un pequeño desplazamiento, el modelo ahora tiene un ajuste deficiente y los resultados en el conjunto de entrenamiento y en los datos de prueba nos permiten evaluar el modelo como fiable a largo plazo.

Cuándo utilizar estos modelos regularizados

Tal vez un modelo de regresión lineal/modelo de mínimos cuadrados también pueda funcionar bien, ¿por qué usar esos modelos L1Norm y L2Norm?

Para comprender esto, veamos cómo funciona la regresión lineal multivariable con un conjunto de datos de entrenamiento.

Para demostrar el enfoque, hemos preparado un conjunto de datos de los osciladores y un indicador de volumen para el instrumento EURUSD:

Incluso sin mirar la matriz de correlación, cualquiera que esté familiarizado con estos indicadores sabrá con certeza que no resultan adecuados para problemas de regresión. A continuación, le mostramos la matriz de correlación.

    ArrayPrint(matrix_utils.csv_header);
    Print(Matrix.CorrCoef(false));

Resultado:

CS      0       06:29:41.493    TestEA (EURUSD,H1)      "Stochastic" "Rsi"        "Volume"     "Bears"      "Bulls"      "EURUSD"    
CS      0       06:29:41.493    TestEA (EURUSD,H1)      [[1,0.680705511991766,0.02399740959375265,0.6910892641498844,0.7291018045506749,0.1490856367010467]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.680705511991766,1,0.07620207894739518,0.8184961346648213,0.8258569040865805,0.1567269000583347]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.02399740959375265,0.07620207894739518,1,0.3752014290536041,-0.1289026185114097,-0.1024017077869821]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.6910892641498844,0.8184961346648213,0.3752014290536041,1,0.7826404088603456,0.07283638913665436]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.7291018045506749,0.8258569040865805,-0.1289026185114097,0.7826404088603456,1,0.08392530400705019]
CS      0       06:29:41.493    TestEA (EURUSD,H1)       [0.1490856367010467,0.1567269000583347,-0.1024017077869821,0.07283638913665436,0.08392530400705019,1]]

Como podemos ver, la correlación es inferior al 20% para la columna EURUSD en comparación con todos los indicadores. El estocástico y el RSI están ligeramente mejor correlacionados que los demás, pero todavía con un valor de alrededor del 14% y el 15%, respectivamente. Vamos a crear un modelo de regresión lineal comenzando con el estocástico y luego continuaremos añadiendo variables explicativas/lecturas de otros indicadores.

Tabla de resultados:

Variables independientes	Puntuación R2 (precisión)
Estocástico	1.2 %
Estocástico y RSI	1.8 %
Estocástico, RSI y Volume	2.8 %
Estocástico, RSI, Volume, Bear Power y Bull Power (Todas las variables independientes)	4.9%

¿Qué conclusión podemos sacar de esta tabla? A medida que aumenta el número de variables independientes, la precisión del modelo lineal entrenado siempre aumentará sin importar cuáles sean las variables. La correlación de las variables independientes usadas en este ejemplo es muy baja, por lo que obtendremos una ligera mejora en la precisión cada vez que añadamos una nueva variable independiente. Pero la situación puede resultar distinta si las variables están correlacionadas en un 30%-40%aproximadamente. Si introducimos demasiadas variables independientes en el modelo, el modelo podría incluso alcanzar un 90 %de precisión durante la fase de entrenamiento.

El aumento de las variables independientes aumentará la varianza. Obviamente, este modelo funcionará peor en una muestra nueva, ya que este modelo estará sobreajustado. Las regresiones de cresta y Lasso se desarrollaron para hacer frente a tales situaciones. Como hemos dicho antes, añaden un pequeño cambio para lograr una reducción significativa en la varianza.

Teoría de la regresión de cresta

En sí misma, la regresión de cresta (ridge regression) es un método que sirve para estimar los coeficientes de un modelo de regresión lineal cuando las variables independientes están altamente correlacionadas.

La regresión de cresta se desarrolló como una posible solución a la imprecisión de las estimaciones de los mínimos cuadrados cuando los modelos de regresión lineal tienen cierta multicolinealidad (están altamente correlacionados), mediante la creación de una estimación de regresión de cresta (RR). Esto se logra gracias a la mayor precisión de los parámetros de la cresta, ya que su varianza y desplazamiento suelen ser inferiores a los de las estimaciones de los mínimos cuadrados.

Valoración de cresta

Por analogía con la estimación habitual de los mínimos cuadrados, una estimación de cresta simple viene dada por la expresión 

Donde y es la matriz de variables independientes, X es la matriz de diseño, I es la matriz identidad y λ es el parámetro de cresta igual o mayor que cero.

Vamos a escribirlo todo en el código:

CRidgeregression::CRidgeregression(matrix &_matrix)
 {
    
    n = _matrix.Rows();
    k = _matrix.Cols();
    
    pre_processing.Standardization(_matrix);
    m_dataset.Copy(_matrix);
    
    matrix_utils.XandYSplitMatrices(_matrix,XMatrix,yVector);
    
    YMatrix = matrix_utils.VectorToMatrix(yVector);
    
//---

    Id_matrix.Resize(k,k);
    
    Id_matrix.Identity();

 }

El constructor de funciones realiza tres cosas importantes. La primera es la estandarización de datos. Al igual que el descenso de gradiente multivariable y muchas otras técnicas de aprendizaje automático, la regresión de cresta funciona con un conjunto de datos estandarizados. En segundo lugar, los datos se dividen en matrices x e y; asimismo, se crea una matriz de identidad.

Dentro de la función L2Norm:

vector CRidgeregression::L2Norm(double lambda)
 {    
   matrix design = matrix_utils.DesignMatrix(XMatrix);
   
   matrix XT = design.Transpose();
   
   matrix XTX = XT.MatMul(design);
   
   matrix lamdaxI = lambda * Id_matrix;
   
   //Print("LambdaxI \n",lamdaxI);
   
   //Print("XTX\n",XTX);
   
   matrix sum_matrix = XTX + lamdaxI;
   
   matrix Inverse_sum = sum_matrix.Inv();
   
   matrix XTy = XT.MatMul(YMatrix);
   
   Betas = Inverse_sum.MatMul(XTy);
 
   #ifdef DEBUG_MODE
      Print("Betas\n",Betas);
   #endif 
   
  return(matrix_utils.MatrixToVector(Betas));
 } 

Esta función encuentra los coeficientes usando la regresión de cresta exactamente como se muestra en la fórmula anterior.

Para probar cómo funciona todo, usaremos otro conjunto de datos NASDAQ_DATA.csv con el que los lectores de esta serie de artículos ya estarán familiarizados.

int OnInit()
  {
//---
    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); 
   
    pre_processing.Standardization(Matrix);
    Linear_reg = new  CLinearRegression(Matrix);
    
    ridge_reg = new CRidgeregression(Matrix);
    
    ridge_reg.L2Norm(0.3);
 }    

Hemos establecido un valor de penalización aleatorio de 0,3 para la regresión de cresta para ver qué sucede. Ahora, ejecutamos la función y miramos qué coeficientes se obtienen de ella:

CS 0 10:27:41.338 TestEA (EURUSD,H1) [[5.015577002384403e-16]

CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6013523727380532]

CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3381524618200134]

CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.2119467984461254]]

También ejecutamos un modelo de regresión lineal en el mismo conjunto de datos y observamos los coeficientes resultantes. Como los mínimos cuadrados no estandarizan la muestra, también la estandarizaremos antes de transmitir los datos al modelo.

    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",","); 
   
    pre_processing.Standardization(Matrix);
    Linear_reg = new  CLinearRegression(Matrix);

Información mostrada:

CS 0 10:27:41.338 TestEA (EURUSD,H1) Betas

CS 0 10:27:41.338 TestEA (EURUSD,H1) [[-4.143037461930866e-14]

CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.6034777119810752]

CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.3363532376334173]

CS 0 10:27:41.338 TestEA (EURUSD,H1) [0.21126507562567]]

Los coeficientes se ven un poco diferentes, así que creo que nuestra función es operativa. Vamos a entrenar y probar cada uno de los modelos, y luego dibujaremos los gráficos correspondientes para ver aún más información.

Dado que la regresión de cresta no es un modelo en sí mismo, sino solo una estimación de los coeficientes que luego se debe usar con un modelo de regresión lineal, hemos realizado algunos cambios en la clase de regresión lineal que analizamos en la Parte 3. 

El modelo se entrena en el constructor de clases de regresión lineal. En esta parte, los coeficientes se almacenan para que otras funciones puedan utilizarlos. Hemos añadido un nuevo constructor que nos permite transmitir coeficientes al modelo. Gracias a ello, requeriremos un esfuerzo apenas mínimo la próxima vez que usemos diferentes estimaciones para obtener coeficientes que usar en nuestro modelo de regresión.

class CLinearRegression
  {
   public: 
                        CLinearRegression(matrix &Matrix_); //Least squares estimator
                        CLinearRegression(matrix<double> &Matrix_, double Lr, uint iters = 1000); //Lr by Gradient descent
                        CLinearRegression(matrix &Matrix_, vector &coeff_vector);
                        
                       ~CLinearRegression(void);

Regresión de cresta y lineal

    Print("----> Ridge regression");
    
    ridge_reg = new CRidgeregression(Matrix);
    vector coeff = ridge_reg.L2Norm(0.3);
    
    Linear_reg = new CLinearRegression(Matrix,coeff); //passing the coefficients made by ridge regression
                                                      // to the Linear regression model
    double acc =0;
    
    vector ridge_predictions = Linear_reg.LRModelPred(Matrix,acc); //making the predictions and storing them to a vector
    
    delete(Linear_reg); //deleting that instance
    
    Print("----> Linear Regression");
   
    pre_processing.Standardization(Matrix);
     
    Linear_reg = new CLinearRegression(Matrix); //new Linear reg instance that gets coefficients by least squares
    
    vector linear_pred = Linear_reg.LRModelPred(Matrix,acc); 

Resultado

CS 0 11:35:52.153 TestEA (EURUSD,H1) ----> Ridge regression

CS 0 11:35:52.153 TestEA (EURUSD,H1) Betas

CS 0 11:35:52.153 TestEA (EURUSD,H1) [[-4.142058558619502e-14]

CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.601352372738047]

CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.3381524618200102]

CS 0 11:35:52.153 TestEA (EURUSD,H1) [0.2119467984461223]]

CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982949 Adjusted R 0.982926

CS 0 11:35:52.154 TestEA (EURUSD,H1) ----> Linear Regression

CS 0 11:35:52.154 TestEA (EURUSD,H1) Betas

CS 0 11:35:52.154 TestEA (EURUSD,H1) [[5.014846059117108e-16]

CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.6034777119810601]

CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.3363532376334217]

CS 0 11:35:52.154 TestEA (EURUSD,H1) [0.2112650756256718]]

CS 0 11:35:52.154 TestEA (EURUSD,H1) R squared 0.982933 Adjusted R 0.982910

El rendimiento de los modelos resulta ligeramente distinto cuando se usan todos los datos para el entrenamiento.

Ahora guardaremos los resultados y los trazaremos en el gráfico a lo largo del mismo eje:

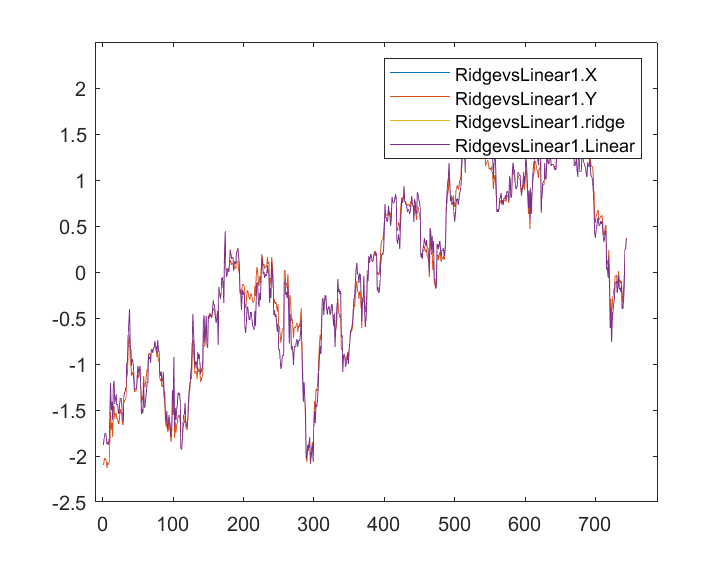
Apenas se perciben diferencias entre el modelo lineal y el predictor marcado en azul: solo podemos ver la diferencia entre los dos modelos, y la regresión de cresta no se ajusta muy bien al conjunto de datos, lo cual es una buena noticia. Vamos a entrenar y poner a prueba ambos modelos por separado.

    matrix_utils.TrainTestSplitMatrices(Matrix,TrainMatrix,TestMatrix);
    
    Print("----> Ridge regression | Train ");
    
    ridge_reg = new CRidgeregression(TrainMatrix);
    vector coeff = ridge_reg.L2Norm(0.3);
    
    Linear_reg = new CLinearRegression(TrainMatrix,coeff); //passing the coefficients made by ridge regression
                                                      // to the Linear regression model
    Linear_reg.LRModelPred(TrainMatrix,acc);
    
    printf("Accuracy %.5f ",acc);
    
    Print("----> Ridge regression | Test");
    
    vector ridge_predictions = Linear_reg.LRModelPred(TestMatrix,acc); //making the predictions and storing them to a vector
    
    printf("Accuracy %.5f ",acc);
    
    delete(Linear_reg); //deleting that instance
    
    Print("\n----> Linear Regression | Train ");
     
    Linear_reg = new CLinearRegression(TrainMatrix); //new Linear reg instance that gets coefficients by least squares
    
    Linear_reg.LRModelPred(TrainMatrix,acc);
    
    printf("Accuracy %.5f ",acc);
    
    Print("----> Linear Regression | Test ");
    
    vector linear_pred = Linear_reg.LRModelPred(TestMatrix,acc); 
    
    printf("Accuracy %.5f ",acc);
    

Información mostrada:

CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Ridge regression | Train 

CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580 

CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Ridge regression | Test

CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78620 

CS 0 13:27:40.744 TestEA (EURUSD,H1)

CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Linear Regression | Train 

CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.97580 

CS 0 13:27:40.744 TestEA (EURUSD,H1) ----> Linear Regression | Test 

CS 0 13:27:40.744 TestEA (EURUSD,H1) Accuracy 0.78540 

Parece que ambos modelos tenían aproximadamente la misma precisión de entrenamiento, pero han mostrado poca diferencia en el conjunto de datos de prueba, lo cual no está mal si tenemos en cuenta que la penalización de 0,3 utilizada por la regresión de cresta para penalizar las variables explicativas es bastante pequeña. Todavía debemos determinar cómo elegir la penalización correcta.

Al configurar el valor lambda en 10, la precisión del entrenamiento de la regresión de cresta se ha reducido de 0,97580 a 0,95760, mientras que la precisión de la prueba ha aumentado de 0,78540 a 0,80050, lo cual, por supuesto, supone una pequeña ganancia.

Elegir el valor de penalización correcto (lambda)

Para encontrar los valores lambda correctos, usaremos el método LEAVE ONE OUT CROSS VALIDATION (LOOCV). Se trata de un método que encuentra los parámetros óptimos de algunos modelos en aprendizaje automático. Para lograr esto, el método itera por todo el conjunto de datos, excluyendo algunas muestras del mismo. Luego entrena el modelo con el resto del conjunto de datos, que es n-1. A continuación, usa la única muestra que ha sido excluida para la prueba; luego ejecuta todo el conjunto de datos hasta la enésima muestra y mide la pérdida de todos los valores en cada iteración. Después, el método halla dónde se encontraba la función de pérdida mínima para ciertos valores de lambda, y el que ofrezca el menor error será el mejor parámetro.

Vamos a importar una clase de validación cruzada para encontrar el valor lambda óptimo.

#include <MALE5\cross_validation.mqh>
CCrossValidation *cross_validation;

A continuación, le mostramos el código de LOOCV para la regresión de cresta:

double CCrossValidation::LeaveOneOut(double init, double step, double finale)
 {
    matrix XMatrix;
    vector yVector;
    
    matrix_utils.XandYSplitMatrices(Matrix,XMatrix,yVector);
 
    matrix train = Matrix; vector test = {};
    
    int size = int(finale/step);
    vector validation_output(ulong(size));
    vector lambda_vector(ulong(size));
    
    vector forecast(n); 
    vector actual = yVector;
    
    double lambda = init;
    
     for (int i=0; i<size; i++)
       {
         lambda += step;
         
          for (ulong j=0; j<n; j++)
            {               
               train.Copy(Matrix);
               ZeroMemory(test);
               
               test = XMatrix.Row(j);
               
               matrix_utils.MatrixRemoveRow(train,j);
               
               vector coeff = {};
               double acc =0;
               
                switch(selected_model)
                  {
                   case  RIDGE_REGRESSION:

                        ridge_regression = new CRidgeregression(train);
                        coeff = ridge_regression.L2Norm(lambda); //ridge regression
                        
                        Linear_reg = new CLinearRegression(train,coeff);   

                        forecast[j] =  Linear_reg.LRModelPred(test);  
                        
                        //---
                        
                        delete (Linear_reg); 
                        delete (ridge_regression);
                        
                     break; 
                  }
            }
          
          validation_output[i] = forecast.Loss(actual,LOSS_MSE)/double(n); 
          
          lambda_vector[i] = lambda;
          
          #ifdef DEBUG_MODE
             printf("%.5f LOOCV mse %.5f",lambda_vector[i],validation_output[i]);
          #endif           
       }

//---

      #ifdef  DEBUG_MODE
         matrix store_matrix(size,2);
         
         store_matrix.Col(validation_output,0);
         store_matrix.Col(lambda_vector,1); 
         
         string name = EnumToString(selected_model)+"\\LOOCV.csv";
         
         string header[2] = {"Validation output","lambda"};
         matrix_utils.WriteCsv(name,store_matrix,header);
      #endif 
      
    return(lambda_vector[validation_output.ArgMin()]);
 }

Vamos a hacer que todo cobre vida:

int OnInit()
  {    
    matrix Matrix = matrix_utils.ReadCsv("NASDAQ_DATA.csv",",");  
    
    ridge_reg = new CRidgeregression(Matrix);
    
    cross_validation = new CCrossValidation(Matrix,RIDGE_REGRESSION);
    
    double best_lambda = cross_validation.LeaveOneOut(0,1,10);
    
    Print("Best lambda ",best_lambda);

Información mostrada:

CS      0       10:12:51.346    ridge_test (EURUSD,H1)  1.00000 LOOCV mse 0.00020
CS      0       10:12:51.465    ridge_test (EURUSD,H1)  2.00000 LOOCV mse 0.00020
CS      0       10:12:51.576    ridge_test (EURUSD,H1)  3.00000 LOOCV mse 0.00020
CS      0       10:12:51.684    ridge_test (EURUSD,H1)  4.00000 LOOCV mse 0.00020
CS      0       10:12:51.788    ridge_test (EURUSD,H1)  5.00000 LOOCV mse 0.00020
CS      0       10:12:51.888    ridge_test (EURUSD,H1)  6.00000 LOOCV mse 0.00020
CS      0       10:12:51.987    ridge_test (EURUSD,H1)  7.00000 LOOCV mse 0.00021
CS      0       10:12:52.090    ridge_test (EURUSD,H1)  8.00000 LOOCV mse 0.00021
CS      0       10:12:52.201    ridge_test (EURUSD,H1)  9.00000 LOOCV mse 0.00021
CS      0       10:12:52.317    ridge_test (EURUSD,H1)  10.00000 LOOCV mse 0.00021
CS      0       10:12:52.319    ridge_test (EURUSD,H1)  Best lambda 1.0

Si todo está correcto en el código, el mejor valor de lambda será igual a la unidad al buscar del 1 al 10. Resulta que el valor lambda para este modelo es algo inferior, así que hemos decidido ejecutar un ciclo de 0 a 10, estableciendo un tamaño de paso igual a 0,01 (1000 iteraciones en total). La operación ha ocupado alrededor de 5 minutos, pero hemos conseguido obtener un valor de 0.09 como el mejor valor de lambda. A continuación, mostramos el gráfico:

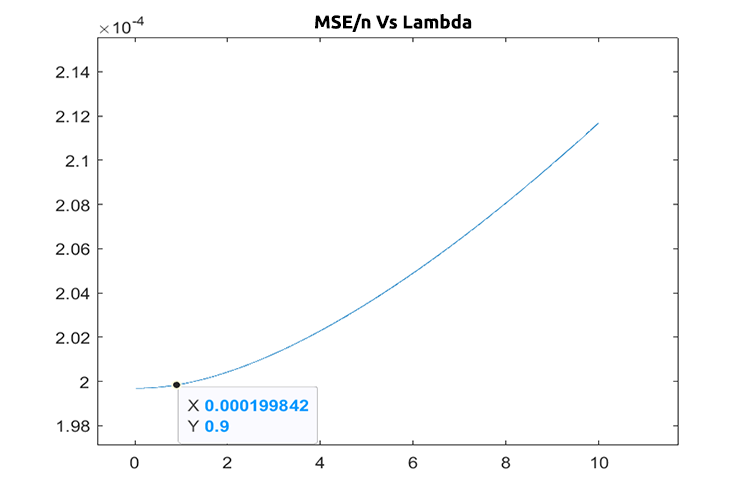
Genial, ahora todo funciona en la regresión de cresta.

Ventajas de la regresión de cresta

• Veamos cuáles son las ventajas de usar la estimación de la regresión de cresta
•  Protege el modelo contra el sobreajuste
•  Reduce la complejidad del modelo
•  Funciona bien como regresión lineal con un conjunto de datos con muchas variables
•  No utiliza estimaciones no desplazadas

Desventajas de la regresión de cresta

•  Incluye todos los predictores en el modelo final
•  No puede seleccionar opciones
•  Contrae los coeficientes hacia el cero
•  Cambia la varianza por el desplazamiento

Reflexiones finales

La regresión de cresta puede ayudar a evitar el sobreajuste de un modelo de regresión cuando se usan muchas variables, pero sigue siendo importante eliminar manualmente del modelo las variables no deseadas. Por ejemplo, de nuestro conjunto NASDAQ_DATA, podríamos eliminar la columna RSI porque todos sabemos que no se correlaciona con nuestra variable objetivo. Bueno, esto es todo lo que queríamos comentar en este artículo. En general, el tema es muy extenso y no podemos abarcarlo todo ahora.

Podrá seguir el desarrollo del tema de la regresión de cresta en mi repositorio de GitHub https://github.com/MegaJoctan/MALE5

Nombre del archivo	Descripción
cross_validation.mqh	Al igual que la validación cruzada sklearn, el archivo contiene técnicas de validación LOOCV
Linear regression.mqh	Este archivo contiene el método de mínimos cuadrados/modelo de regresión lineal
matrix_utils.mqh	Esta función de clase de servicio contiene funciones de operaciones matriciales adicionales
Preprocessing.mqh	Al igual que sklearn.preprocessing, la clase contiene funciones para controlar y escalar conjuntos de datos
Ridge Regression.mqh	Este archivo contiene el modelo de regresión de cresta y las funciones relacionadas.
ridge_test.mq5	Este script se usa para probar todo lo analizado en este artículo.
prepare_dataset.mq5	Este script crea un conjunto de datos para los indicadores de osciladores discutidos anteriormente. Los datos se guardan en el archivo Oscillators.csv
NASDAQ_DATA.csv	Este archivo CSV contiene el conjunto de datos que hemos usado en este artículo.