Statistical Distributions in MQL5 - taking the best of R and making it faster

Let us consider the functions for working with the basic statistical distributions implemented in the R language.

Those include the Cauchy, Weibull, normal, log-normal, logistic, exponential, uniform, gamma distributions, the central and noncentral beta, chi-squared, Fisher's F-distribution, Student's t-distribution, as well as the discrete binomial and negative binomial distributions, geometric, hypergeometric and Poisson distributions. In addition, there are functions for calculating theoretical moments of distributions, which allow to evaluate the degree of conformity of the real distribution to the modeled one.

The MQL5 standard library has been supplemented with numerous mathematical functions from R. Moreover, an increase in operation speed of 3 to 7 times has been achieved, compared to the initial versions in the R language. At the same time, errors in implementation of certain functions in R have been found.

Contents

1. Functions for calculating the statistical characteristics of array elements
   
   
   • 1.1. MathMean()
   • 1.2. MathVariance()
   • 1.3. MathSkewness()
   • 1.4. MathKurtosis()
   • 1.5. MathMoments()
   • 1.6. MathMedian()
   • 1.7. MathStandardDeviation()
   • 1.8. MathAverageDeviation()


2. Functions for working with statistical distributions
   
   2.1. Normal distribution
   
   • 2.1.1. MathProbabilityDensityNormal()
   • 2.1.2. MathCumulativeDistributionNormal()
   • 2.1.3. MathQuantileNormal()
   • 2.1.4. MathRandomNormal()
   • 2.1.5. MathMomentsNormal()
   
   2.2. Log-normal distribution
   
   • 2.2.1. MathProbabilityDensityLognormal()
   • 2.2.2. MathCumulativeDistributionLognormal()
   • 2.2.3. MathQuantileLognormal()
   • 2.2.4. MathRandomLognormal()
   • 2.2.5. MathMomentsLognormal()
   
   2.3. Beta distribution
   
   • 2.3.1. MathProbabilityDensityBeta()
   • 2.3.2. MathCumulativeDistributionBeta()
   • 2.3.3. MathQuantileBeta()
   • 2.3.4. MathRandomBeta()
   • 2.3.5. MathMomentsBeta()
   
   2.4. Noncentral beta distribution
   
   • 2.4.1. MathProbabilityDensityNoncentralBeta()
   • 2.4.2. MathCumulativeDistributionNoncentralBeta()
   • 2.4.3. MathQuantileNoncentralBeta()
   • 2.4.4. MathRandomNoncentralBeta()
   • 2.4.5. MathMomentsNoncentralBeta()
   
   2.5. Gamma distribution
   
   • 2.5.1. MathProbabilityDensityGamma()
   • 2.5.2. MathCumulativeDistributionGamma()
   • 2.5.3. MathQuantileGamma()
   • 2.5.4. MathRandomGamma()
   • 2.5.5. MathMomentsGamma()
   
   2.6. Chi-squared distribution
   
   • 2.6.1. MathProbabilityDensityChiSquare()
   • 2.6.2. MathCumulativeDistributionChiSquare()
   • 2.6.3. MathQuantileChiSquare()
   • 2.6.4. MathRandomChiSquare()
   • 2.6.5. MathMomentsChiSquare()
   
   2.7. Noncentral chi-squared distribution
   
   • 2.7.1. MathProbabilityDensityNoncentralChiSquare()
   • 2.7.2. MathCumulativeDistributionNoncentralChiSquare()
   • 2.7.3. MathQuantileNoncentralChiSquare()
   • 2.7.4. MathRandomNoncentralChiSquare()
   • 2.7.5. MathMomentsNoncentralChiSquare()
   
   2.8. Exponential distribution
   
   • 2.8.1. MathProbabilityDensityExponential()
   • 2.8.2. MathCumulativeDistributionExponential()
   • 2.8.3. MathQuantileExponential()
   • 2.8.4. MathRandomExponential()
   • 2.8.5. MathMomentsExponential()
   
   2.9. F-distribution
   
   • 2.9.1. MathProbabilityDensityF()
   • 2.9.2. MathCumulativeDistributionF()
   • 2.9.3. MathQuantileF()
   • 2.9.4. MathRandomF()
   • 2.9.5. MathMomentsF()
   
   2.10. Noncentral F-distribution
   
   • 2.10.1. MathProbabilityDensityNoncentralF()
   • 2.10.2. MathCumulativeDistributionNoncentralF()
   • 2.10.3. MathQuantileNoncentralF()
   • 2.10.4. MathRandomNoncentralF()
   • 2.10.5. MathMomentsNoncentralF()
   
   2.11. t-distribution
   
   • 2.11.1. MathProbabilityDensityT()
   • 2.11.2. MathCumulativeDistributionT()
   • 2.11.3. MathQuantileT()
   • 2.11.4. MathRandomT()
   • 2.11.5. MathMomentsT()
   
   2.12 Noncentral t-distribution
   
   • 2.12.1. MathProbabilityDensityNoncentralT()
   • 2.12.2. MathCumulativeDistributionNoncentralT()
   • 2.12.3. MathQuantileNoncentralT()
   • 2.12.4. MathRandomNoncentralT()
   • 2.12.5. MathMomentsNoncentralT()
   
   2.13. Logistic distribution
   
   • 2.13.1. MathProbabilityDensityLogistic()
   • 2.13.2. MathCumulativeDistributionLogistic()
   • 2.13.3. MathQuantileLogistic()
   • 2.13.4. MathRandomLogistic()
   • 2.13.5. MathMomentsLogistic()
   
   2.14. Cauchy distribution
   
   • 2.14.1. MathProbabilityDensityCauchy()
   • 2.14.2. MathCumulativeDistributionCauchy()
   • 2.14.3. MathQuantileCauchy()
   • 2.14.4. MathRandomCauchy()
   • 2.14.5. MathMomentsCauchy()
   
   2.15. Uniform distribution
   
   • 2.15.1. MathProbabilityDensityUniform()
   • 2.15.2. MathCumulativeDistributionUniform()
   • 2.15.3. MathQuantileUniform()
   • 2.15.4. MathRandomUniform()
   • 2.15.5. MathMomentsUniform()
   
   2.16. Weibull distribution
   
   • 2.16.1. MathProbabilityDensityWeibull()
   • 2.16.2. MathCumulativeDistributionWeibull()
   • 2.16.3. MathQuantileWeibull()
   • 2.16.4. MathRandomWeibull()
   • 2.16.5. MathMomentsWeibull()
   
   2.17. Binomial distribution
   
   • 2.17.1. MathProbabilityDensityBinomial()
   • 2.17.2. MathCumulativeDistributionBinomial()
   • 2.17.3. MathQuantileBinomial()
   • 2.17.4. MathRandomBinomial()
   • 2.17.5. MathMomentsBinomial()
   
   2.18. Negative binomial distribution
   
   • 2.18.1. MathProbabilityDensityNegativeBinomial()
   • 2.18.2. MathCumulativeDistributionNegativeBinomial()
   • 2.18.3. MathQuantileNegativeBinomial()
   • 2.18.4. MathRandomNegativeBinomial()
   • 2.18.5. MathMomentsNegativeBinomial()
   
   2.19. Geometric distribution
   
   • 2.19.1. MathProbabilityDensityGeometric()
   • 2.19.2. MathCumulativeDistributionGeometric()
   • 2.19.3. MathQuantileGeometric()
   • 2.19.4. MathRandomGeometric()
   • 2.19.5. MathMomentsGeometric()
   
   2.20. Hypergeometric distribution
   
   • 2.20.1. MathProbabilityDensityHypergeometric()
   • 2.20.2. MathCumulativeDistributionHypergeometric()
   • 2.20.3. MathQuantileHypergeometric()
   • 2.20.4. MathRandomHypergeometric()
   • 2.20.5. MathMomentsHypergeometric()
   
   2.21. Poisson distribution
   
   • 2.21.1. MathProbabilityDensityPoisson()
   • 2.21.2. MathCumulativeDistributionPoisson()
   • 2.21.3. MathQuantilePoisson()
   • 2.21.4. MathRandomPoisson()
   • 2.21.5. MathMomentsPoisson()
   
   
3. Table of correspondence to the statistical functions in R
   
   
4. An example of using the functions
   
   
5. Comparison of calculation speed
   
   
6. Detected calculation errors in R
   
   
7. References

Introduction

The R language is one of the best tools of statistical processing and analysis of data.

Thanks to availability and support of multiple statistical distributions, it had become widespread in the analysis and processing of various data. Using the apparatus of probability theory and mathematical statistics allows for a fresh look at the financial market data and provides new opportunities to create trading strategies. With the statistical library, all these features are now available in the MQL5.

The statistical library contains functions for calculating the statistical characteristics of data, as well as functions for working with statistical distributions.

This article considers the main functions of the library and an example of their practical use.

1. Functions for calculating the statistical characteristics of array elements

This group of functions calculates the standard characteristics (mean, variance, skewness, kurtosis, median, root-mean-square and standard deviations) of array elements.

1.1. MathMean

The function calculates the mean (first moment) of array elements. In case of error it returns NaN (not a number). Analog of the mean() in R.

double MathMean(
  const double   &array[]         // [in] Array with data
);

1.2. MathVariance

The function calculates the variance (second moment) of array elements. In case of error it returns NaN. Analog of the var() in R.

double MathVariance(
  const double   &array[]         // [in] Array with data
);

1.3. MathSkewness

The function calculates the skewness (third moment) of array elements. In case of error it returns NaN. Analog of the skewness() in R (e1071 library).

double MathSkewness(
  const double   &array[]         // [in] Array with data
);

1.4. MathKurtosis

The function calculates the kurtosis (fourth moment) of array elements. In case of error it returns NaN. Analog of the kurtosis() in R (e1071 library).

double MathKurtosis(
  const double   &array[]         // [in] Array with data
);

1.5. MathMoments

The function calculates the first 4 moments (mean, variance, skewness, kurtosis) of array elements. Returns true if the moments have been calculated successfully, otherwise false.

bool MathMoments(
  const double   &array[],         // [in]  Array with data
  double         &mean,            // [out] Variable for the mean (1st moment)
  double         &variance,        // [out] Variable for the variance (2nd moment)
  double         &skewness,        // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,        // [out] Variable for the kurtosis (4th moment)
  const int      start=0,          // [in]  Initial index for calculation
  const int      count=WHOLE_ARRAY // [in]  The number of elements for calculation
);

1.6. MathMedian

The function calculates the median value of array elements. In case of error it returns NaN. Analog of the median() in R.

double MathMedian(
  double         &array[]         // [in] Array with data
);

1.7. MathStandardDeviation

The function calculates the standard deviation of array elements. In case of error it returns NaN. Analog of the sd() in R.

double MathStandardDeviation(
  const double   &array[]         // [in] Array with data
  );

1.8. MathAverageDeviation

The function calculates the average absolute deviation of array elements. In case of error it returns NaN. Analog of the aad() in R.

double MathAverageDeviation(
  const double   &array[]         // [in] Array with data
);

All functions that calculate the kurtosis use the excess kurtosis around the normal distribution (excess kurtosis=kurtosis-3), i.e. the excess kurtosis of a normal distribution is zero.

It is positive if the peak of the distribution around the expected value is sharp, and negative if the peak is flat.

2. Statistical distributions

The statistical library of the MQL5 contains 5 functions for working with the statistical distributions:

1. Calculation of probability density (the MathProbabilityDensityX() functions);
   
2. Calculation of probabilities (the MathCumulativeDistributionX() functions);
   The probability distribution function is equal to the probability of a random variable falling within the range of (-inf; x]).
   
3. Calculation of distribution quantiles (the MathQuantileX() functions);
   The quantile x of a distribution corresponds to a random value falling within the range of (-inf, x] with the specified probability for the given distribution parameters.
   
4. Generating random numbers with the specified distribution (the MathRandomX() functions);
5. Calculation of the theoretical moments of the distributions (the MathMomentsX() functions);

2.1. Normal Distribution

2.1.1. MathProbabilityDensityNormal

The function calculates the value of the probability density function of normal distribution with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  mean (expected value) parameter of the distribution
  const double   sigma,       // [in]  sigma (root-mean-square) parameter of the distribution
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of normal distribution with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  mean (expected value) parameter of the distribution
  const double   sigma,       // [in]  sigma (root-mean-square) parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function calculates the values of the probability density function of normal distribution with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the dnorm() in R.

bool MathProbabilityDensityNormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  mean (expected value) parameter of the distribution
  const double   sigma,       // [in]  sigma (root-mean-square) parameter of the distribution
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the values of the probability density function of normal distribution with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityNormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  mean (expected value) parameter of the distribution
  const double   sigma,       // [in]  sigma (root-mean-square) parameter of the distribution
  double         &result[]    // [out] Array for values of the probability density function
);

2.1.2. MathCumulativeDistributionNormal

The function calculates the value of the normal distribution function with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the normal distribution function with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the normal distribution function with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the pnorm() in R.

bool MathCumulativeDistributionNormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the normal distribution function with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionNormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  double         &result[]    // [out] Array for values of the probability function
);

2.1.3. MathQuantileNormal

For the specified probability, the function calculates the value of inverse normal distribution function with the mu and sigma parameters. In case of error it returns NaN.

double MathQuantileNormal(
  const double   probability, // [in]  Probability value of random variable
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  const bool     tail,        // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,    // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code  // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse normal distribution function with the mu and sigma parameters. In case of error it returns NaN.

double MathQuantileNormal(
  const double   probability, // [in]  Probability value of random variable
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  int            &error_code  // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the values of inverse normal distribution function with the mu and sigma parameters. In case of error it returns false. Analog of the qnorm() in R.

bool MathQuantileNormal(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   mu,            // [in]  Expected value
  const double   sigma,         // [in]  Root-mean-square deviation
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the values of inverse normal distribution function with the mu and sigma parameters. In case of error it returns false.

bool MathQuantileNormal(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   mu,            // [in]  Expected value
  const double   sigma,         // [in]  Root-mean-square deviation
  double         &result[]      // [out] Array with values of quantiles
);

2.1.4. MathRandomNormal

The function generates a pseudorandom variable distributed according to the normal law with the mu and sigma parameters. In case of error it returns NaN.

double MathRandomNormal(
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the normal law with the mu and sigma parameters. In case of error it returns false. Analog of the rnorm() in R.

bool MathRandomNormal(
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.1.5. MathMomentsNormal

The function calculates the theoretical numerical values of the first 4 moments of the normal distribution. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsNormal(
  const double   mu,          // [in]  Expected value
  const double   sigma,       // [in]  Root-mean-square deviation
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.2. Log-normal distribution

2.2.1. MathProbabilityDensityLognormal

The function calculates the value of the probability density function of log-normal distribution with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityLognormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of log-normal distribution with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityLognormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of log-normal distribution with the mu and sigma parameters for an array of random variables x[]. In case of error it returns NaN. Analog of the dlnorm() in R.

bool MathProbabilityDensityLognormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of log-normal distribution with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityLognormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  double         &result[]    // [out] Array for values of the probability density function
);

2.2.2. MathCumulativeDistributionLognormal

The function calculates the value of the log-normal distribution function with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionLognormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the log-normal distribution function with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionLognormal(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the log-normal distribution function with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the plnorm() in R.

bool MathCumulativeDistributionLognormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the log-normal distribution function with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionLognormal(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  double         &result[]    // [out] Array for values of the probability function
);

2.2.3. MathQuantileLognormal

The function calculates the value of the inverse log-normal distribution function with the mu and sigma parameters for the specified probability. In case of error it returns NaN.

double MathQuantileLognormal(
  const double   probability, // [in]  Probability value of random variable occurrence
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const bool     tail,        // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,    // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the inverse log-normal distribution function with the mu and sigma parameters for the specified probability. In case of error it returns NaN.

double MathQuantileLognormal(
  const double   probability, // [in]  Probability value of random variable occurrence
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  int            &error_code  // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the values of inverse log-normal distribution function with the mu and sigma parameters. In case of error it returns false. Analog of the qlnorm() in R.

bool MathQuantileLognormal(
  const double   &probability[], // [in]  Array with probability values of random variable
  const double   mu,             // [in]  Logarithm of the expected value (log mean)
  const double   sigma,          // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const bool     tail,           // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,       // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]       // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the values of inverse log-normal distribution function with the mu and sigma parameters. In case of error it returns false.

bool MathQuantileLognormal(
  const double   &probability[], // [in]  Array with probability values of random variable
  const double   mu,             // [in]  Logarithm of the expected value (log mean)
  const double   sigma,          // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  double         &result[]       // [out] Array with values of quantiles
);

2.2.4. MathRandomLognormal

The function generates a pseudorandom variable distributed according to the log-normal law with the mu sigma parameters. In case of error it returns NaN.

double MathRandomLognormal(
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the log-normal law with the mu and sigma parameters. In case of error it returns false. Analog of the rlnorm() in R.

bool MathRandomLognormal(
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.2.5. MathMomentsLognormal

The function calculates the theoretical numerical values of the first 4 moments of the log-normal distribution. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsLognormal(
  const double   mu,          // [in]  Logarithm of the expected value (log mean)
  const double   sigma,       // [in]  Logarithm of the root-mean-square deviation (log standard deviation)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.3. Beta distribution

2.3.1. MathProbabilityDensityBeta

The function calculates the value of the probability density function of beta distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of beta distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of beta distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the dbeta() in R.

bool MathProbabilityDensityBeta(
  const double   &x[],        // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of beta distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityBeta(
  const double   &x[],        // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  double         &result[]    // [out] Array for values of the probability density function
);

2.3.2. MathCumulativeDistributionlBeta

The function calculates the value of the probability distribution function of beta distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of beta distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of beta distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the pbeta() in R.

bool MathCumulativeDistributionBeta(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of beta distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionBeta(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  double         &result[]    // [out] Array for values of the probability function
);

2.3.3. MathQuantileBeta

For the specified probability, the function calculates the value of inverse beta distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileBeta(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse beta distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileBeta(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the values of inverse beta distribution function with the a and b parameters. In case of error it returns false. Analog of the qbeta() in R.

bool MathQuantileBeta(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the values of inverse beta distribution function with the a and b parameters. In case of error it returns false.

bool MathQuantileBeta(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  double         &result[]      // [out] Array with values of quantiles
);

2.3.4. MathRandomBeta

The function generates a pseudorandom variable distributed according to the law of beta distribution with the a and b parameters. In case of error it returns NaN.

double MathRandomBeta(
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of beta distribution with the a and b parameters. In case of error it returns false. Analog of the rbeta() in R.

bool MathRandomBeta(
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.3.5. MathMomentsBeta

The function calculates the theoretical numerical values of the first 4 moments of the beta distribution. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsBeta(
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.4. Noncentral beta distribution

2.4.1. MathProbabilityDensityNoncentralBeta

The function calculates the value of the probability density function of noncentral beta distribution with the a, b and lambda parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral beta distribution with the a, b and lambda parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral beta distribution with the a, b and lambda parameters for an array of random variables x[]. In case of error it returns false. Analog of the dbeta() in R.

bool MathProbabilityDensityNoncentralBeta(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of noncentral beta distribution with the a, b and lambda parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityNoncentralBeta(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability density function
);

2.4.2. MathCumulativeDistributionNoncentralBeta

The function calculates the value of the probability distribution function of noncentral beta distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral beta distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralBeta(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral beta distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the pbeta() in R.

bool MathCumulativeDistributionNoncentralBeta(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of noncentral beta distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionNoncentralBeta(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability function
);

2.4.3. MathQuantileNoncentralBeta

The function calculates the value of the inverse probability distribution function of noncentral beta distribution with the a, b and lambda parameters for the occurrence of a random variable x. In case of error it returns NaN.

double MathQuantileNoncentralBeta(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,        // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

The function calculates the value of the inverse probability distribution function of noncentral beta distribution with the a, b and lambda parameters for the occurrence of a random variable x. In case of error it returns NaN.

double MathQuantileNoncentralBeta(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,        // [in]  Noncentrality parameter
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse probability distribution function of noncentral beta distribution with the a, b and lambda parameters. In case of error it returns false. Analog of the qbeta() in R.

bool MathQuantileNoncentralBeta(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,        // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse probability distribution function of noncentral beta distribution with the a, b and lambda parameters. In case of error it returns false.

bool MathQuantileNoncentralBeta(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  The first parameter of beta distribution (shape1)
  const double   b,             // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,        // [in]  Noncentrality parameter
  double         &result[]      // [out] Array with values of quantiles
);

2.4.4. MathRandomNoncentralBeta

The function generates a pseudorandom variable distributed according to the law of noncentral beta distribution the a, b and lambda parameters. In case of error it returns NaN.

double MathRandomNoncentralBeta(
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of noncentral beta distribution the a, b and lambda parameters. In case of error it returns false. Analog of the rbeta() in R.

bool MathRandomNoncentralBeta(
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.4.5. MathMomentsNoncentralBeta

The function calculates the theoretical numerical values of the first 4 moments of the noncentral beta distribution with the a, b and lambda parameters. Returns true if calculation of the moments has been successful, otherwise false.

double MathMomentsNoncentralBeta(
  const double   a,           // [in]  The first parameter of beta distribution (shape1)
  const double   b,           // [in]  The second parameter of beta distribution (shape2)
  const double   lambda,      // [in]  Noncentrality parameter
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.5. Gamma distribution

2.5.1. MathProbabilityDensityGamma

The function calculates the value of the probability density function of gamma distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityGamma(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of gamma distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityGamma(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of gamma distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the dgamma() in R.

bool MathProbabilityDensityGamma(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of gamma distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityGamma(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  double         &result[]    // [out] Array for values of the probability density function
);

2.5.2. MathCumulativeDistributionGamma

The function calculates the value of the gamma distribution function with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionGamma(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the gamma distribution function with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionGamma(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the gamma distribution function with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the pgamma() in R.

bool MathCumulativeDistributionGamma(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the gamma distribution function with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionGamma(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  double         &result[]    // [out] Array for values of the probability function
);

2.5.3. MathQuantileGamma

For the specified probability, the function calculates the value of inverse gamma distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileGamma(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  The first parameter of distribution (shape)
  const double   b,             // [in]  The second parameter of distribution (scale)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse gamma distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileGamma(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  The first parameter of distribution (shape)
  const double   b,             // [in]  The second parameter of distribution (scale)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse gamma distribution function with the a and b parameters. In case of error it returns false. Analog of the qgamma() in R.

bool MathQuantileGamma(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  The first parameter of distribution (shape)
  const double   b,             // [in]  The second parameter of distribution (scale)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse gamma distribution function with the a and b parameters. In case of error it returns false.

bool MathQuantileGamma(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  The first parameter of distribution (shape)
  const double   b,             // [in]  The second parameter of distribution (scale)
  double         &result[]      // [out] Array with values of quantiles
);

2.5.4. MathRandomGamma

The function generates a pseudorandom variable distributed according to the law of gamma distribution with the a and b parameters. In case of error it returns NaN.

double MathRandomGamma(
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of gamma distribution with the a and b parameters. In case of error it returns false. Analog of the rgamma() in R.

bool MathRandomGamma(
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.5.5. MathMomentsGamma

The function calculates the theoretical numerical values of the first 4 moments of the gamma distribution with the a and b parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsGamma(
  const double   a,           // [in]  The first parameter of distribution (shape)
  const double   b,           // [in]  The second parameter of distribution (scale)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.6. Chi-squared distribution

2.6.1. MathProbabilityDensityChiSquare

The function calculates the value of the probability density function of chi-squared distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of chi-squared distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of chi-squared distribution with the nu parameter for an array of random variables x[]. In case of error it returns false. Analog of the dchisq() in R.

bool MathProbabilityDensityChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of chi-squared distribution with the nu parameter for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  double         &result[]    // [out] Array for values of the probability density function
);

2.6.2. MathCumulativeDistributionChiSquare

The function calculates the value of the probability distribution function of chi-squared distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of chi-squared distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of chi-squared distribution with the nu parameter for an array of random variables x[]. In case of error it returns false. Analog of the pchisq() in R.

bool MathCumulativeDistributionChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of chi-squared distribution with the nu parameter for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  double         &result[]    // [out] Array for values of the probability function
);

2.6.3. MathQuantileChiSquare

For the specified probability, the function calculates the value of inverse chi-squared distribution function. In case of error it returns NaN.

double MathQuantileChiSquare(  
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse chi-squared distribution function. In case of error it returns NaN.

double MathQuantileChiSquare(  
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse chi-squared distribution function. In case of error it returns false. Analog of the qchisq() in R.

bool MathQuantileChiSquare(  
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse chi-squared distribution function. In case of error it returns false.

bool MathQuantileChiSquare(  
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  double         &result[]      // [out] Array with values of quantiles
);

2.6.4. MathRandomChiSquare

The function generates a pseudorandom variable distributed according to the law of chi-squared distribution with the nu parameter. In case of error it returns NaN.

double MathRandomChiSquare(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of chi-squared distribution with the nu parameter. In case of error it returns false. Analog of the rchisq() in R.

bool MathRandomChiSquare(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.6.5. MathMomentsChiSquare

The function calculates the theoretical numerical values of the first 4 moments of the chi-squared distribution with the nu parameter. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsChiSquare(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.7. Noncentral chi-squared distribution

2.7.1. MathProbabilityDensityNoncentralChiSquare

The function calculates the value of the probability density function of noncentral chi-squared distribution with the nu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral chi-squared distribution with the nu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral chi-squared distribution with the nu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the dchisq() in R.

bool MathProbabilityDensityNoncentralChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of noncentral chi-squared distribution with the nu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityNoncentralChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability density function
);

2.7.2. MathCumulativeDistributionNoncentralChiSquare

The function calculates the value of the probability distribution function of noncentral chi-squared distribution with the nu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral chi-squared distribution with the nu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralChiSquare(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral chi-squared distribution with the nu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the pchisq() in R.

bool MathCumulativeDistributionNoncentralChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of noncentral chi-squared distribution with the nu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionNoncentralChiSquare(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability function
);

2.7.3. MathQuantileNoncentralChiSquare

For the specified probability, the function calculates the value of inverse noncentral chi-squared distribution function with the nu and sigma parameters. In case of error it returns NaN.

double MathQuantileNoncentralChiSquare(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse noncentral chi-squared distribution function with the nu and sigma parameters. In case of error it returns NaN.

double MathQuantileNoncentralChiSquare(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse noncentral chi-squared distribution function with the nu and sigma parameters. In case of error it returns false. Analog of the qchisq() in R.

bool MathQuantileNoncentralChiSquare(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse noncentral chi-squared distribution function with the nu and sigma parameters. In case of error it returns false.

bool MathQuantileNoncentralChiSquare(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  double         &result[]      // [out] Array with values of quantiles
);

2.7.4. MathRandomNoncentralChiSquare

The function generates a pseudorandom variable distributed according to the law of noncentral chi-squared distribution with the nu and sigma parameters. In case of error it returns NaN.

double MathRandomNoncentralChiSquare(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of noncentral chi-squared distribution with the nu and sigma parameters. In case of error it returns false. Analog of the rchisq() in R.

bool MathRandomNoncentralChiSquare(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.7.5. MathMomentsNoncentralChiSquare

The function calculates the theoretical numerical values of the first 4 moments of the noncentral chi-squared distribution with the nu and sigma parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsNoncentralChiSquare(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.8. Exponential distribution

2.8.1. MathProbabilityDensityExponential

The function calculates the value of the probability density function of exponential distribution with the mu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityExponential(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of exponential distribution with the mu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityExponential(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of exponential distribution with the mu parameter for an array of random variables x[]. In case of error it returns false. Analog of the dexp() in R.

bool MathProbabilityDensityExponential(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of exponential distribution with the mu parameter for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityExponential(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  double         &result[]    // [out] Array for values of the probability density function
);

2.8.2. MathCumulativeDistributionExponential

The function calculates the value of the exponential distribution function of probabilities with the mu parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionExponential(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the exponential distribution function of probabilities with the mu parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionExponential(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the exponential distribution function of probabilities with the mu parameter for a random variable x. In case of error it returns false. Analog of the pexp() in R.

bool MathCumulativeDistributionExponential(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the exponential distribution function of probabilities with the mu parameter for a random variable x. In case of error it returns false.

bool MathCumulativeDistributionExponential(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  double         &result[]    // [out] Array for values of the probability function
);

2.8.3. MathQuantileExponential

For the specified probability, the function calculates the value of inverse exponential distribution function with the mu parameter. In case of error it returns NaN.

double MathQuantileExponential(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   mu,            // [in]  Parameter of the distribution (expected value)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse exponential distribution function with the mu parameter. In case of error it returns NaN.

double MathQuantileExponential(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   mu,            // [in]  Parameter of the distribution (expected value)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse exponential distribution function with the mu parameter. In case of error it returns false. Analog of the qexp() in R.

bool MathQuantileExponential(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   mu,            // [in]  Parameter of the distribution (expected value)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse exponential distribution function with the mu parameter. In case of error it returns false.

bool MathQuantileExponential(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   mu,            // [in]  Parameter of the distribution (expected value)
  double         &result[]      // [out] Array with values of quantiles
);

2.8.4. MathRandomExponential

The function generates a pseudorandom variable distributed according to the law of exponential distribution with the mu parameter. In case of error it returns NaN.

double MathRandomExponential(
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of exponential distribution with the mu parameter. In case of error it returns false. Analog of the rexp() in R.

bool MathRandomExponential(
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.8.5. MathMomentsExponential

The function calculates the theoretical numerical values of the first 4 moments of the exponential distribution with the mu parameter. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsExponential(
  const double   mu,          // [in]  Parameter of the distribution (expected value)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.9. F-distribution

2.9.1. MathProbabilityDensityF

The function calculates the value of the probability density function of Fisher's F-distribution with the nu1 and nu2 parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of Fisher's F-distribution with the nu1 and nu2 parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of Fisher's F-distribution with the nu1 and nu2 parameters for an array of random variables x[]. In case of error it returns false. Analog of the df() in R.

bool MathProbabilityDensityF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of Fisher's F-distribution with the nu1 and nu2 parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  double         &result[]    // [out] Array for values of the probability density function
);

2.9.2. MathCumulativeDistributionF

The function calculates the value of the probability distribution function of Fisher's F-distribution with the nu1 and nu2 parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of Fisher's F-distribution with the nu1 and nu2 parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of Fisher's F-distribution with the nu1 and nu2 parameters for an array of random variables x[]. In case of error it returns false. Analog of the pf() in R.

bool MathCumulativeDistributionF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of Fisher's F-distribution with the nu1 and nu2 parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  double         &result[]    // [out] Array for values of the probability function
);

2.9.3. MathQuantileF

For the specified probability, the function calculates the value of inverse Fisher's F-distribution function with the nu1 and nu2 parameters. In case of error it returns NaN.

double MathQuantileF(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse Fisher's F-distribution function with the nu1 and nu2 parameters. In case of error it returns NaN.

double MathQuantileF(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse Fisher's F-distribution function with the nu1 and nu2 parameters. In case of error it returns false. Analog of the qf() in R.

bool MathQuantileF(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified probability, the function calculates the value of inverse Fisher's F-distribution function with the nu1 and nu2 parameters. In case of error it returns false.

bool MathQuantileF(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  double         &result[]      // [out] Array with values of quantiles
);

2.9.4. MathRandomF

The function generates a pseudorandom variable distributed according to the law of Fisher's F-distribution with the nu1 and nu2 parameters. In case of error it returns NaN.

double MathRandomF(
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of Fisher's F-distribution with the nu1 and nu2 parameters. In case of error it returns false. Analog of the rf() in R.

bool MathRandomF(
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.9.5. MathMomentsF

The function calculates the theoretical numerical values of the first 4 moments of the Fisher's F-distribution with the nu1 and nu2 parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsF(
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.10. Noncentral F-distribution

2.10.1. MathProbabilityDensityNoncentralF

The function calculates the value of the probability density function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the df() in R.

double MathProbabilityDensityNoncentralF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for an array of random variables x[]. In case of error it returns false.

double MathProbabilityDensityNoncentralF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability density function
);

2.10.2. MathCumulativeDistributionlNoncentralF

The function calculates the value of the probability distribution function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralF(
  const double   x,           // [in]  Value of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for a random variable x. In case of error it returns false. Analog of the pf() in R.

bool MathCumulativeDistributionNoncentralF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters for a random variable x. In case of error it returns NaN.

bool MathCumulativeDistributionNoncentralF(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability function
);

2.10.3. MathQuantileNoncentralF

For the specified probability, the function calculates the value of inverse noncentral Fisher's F-distribution function with the nu1, nu2 and sigma parameters. In case of error it returns NaN.

double MathQuantileNoncentralF(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse noncentral Fisher's F-distribution function with the nu1, nu2 and sigma parameters. In case of error it returns NaN.

double MathQuantileNoncentralF(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse noncentral Fisher's F-distribution function with the nu1, nu2 and sigma parameters. In case of error it returns false. Analog of the qf() in R.

bool MathQuantileNoncentralF(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified probability, the function calculates the value of inverse noncentral Fisher's F-distribution function with the nu1, nu2 and sigma parameters. In case of error it returns false.

bool MathQuantileNoncentralF(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  double         &result[]      // [out] Array with values of quantiles
);

2.10.4. MathRandomNoncentralF

The function generates a pseudorandom variable distributed according to the law of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters. In case of error it returns NaN.

double MathRandomNoncentralF(
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  int            &error_code    // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters. In case of error it returns false. Analog of the rf() in R.

bool MathRandomNoncentralF(
  const double   nu1,           // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,           // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,         // [in]  Noncentrality parameter
  double         &result[]      // [out] Array with values of quantiles
);

2.10.5. MathMomentsNoncentralF

The function calculates the theoretical numerical values of the first 4 moments of the noncentral Fisher's F-distribution with the nu1, nu2 and sigma parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsNoncentralF(
  const double   nu1,         // [in]  The first parameter of distribution (number of degrees of freedom)
  const double   nu2,         // [in]  The second parameter of distribution (number of degrees of freedom)
  const double   sigma,       // [in]  Noncentrality parameter
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
e.)

2.11. t-distribution

2.11.1. MathProbabilityDensityT

The function calculates the value of the probability density function of Student's t-distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityT(
  const double   x,             // [in]  Value of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     log_mode,      // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code    // [out] Variable for the error code
);

The function calculates the value of the probability density function of Student's t-distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityT(
  const double   x,             // [in]  Value of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code    // [out] Variable for the error code
);

The function calculates the value of the probability density function of Student's t-distribution with the nu parameter for an array of random variables x[]. In case of error it returns false. Analog of the dt() in R.

bool MathProbabilityDensityT(
  const double   &x[],          // [in]  Array with the values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     log_mode,      // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]      // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of Student's t-distribution with the nu parameter for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityT(
  const double   &x[],          // [in]  Array with the values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  double         &result[]      // [out] Array for values of the probability density function
);

2.11.2. MathCumulativeDistributionT

The function calculates the value of the Student's t-distribution function with the nu parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionT(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the Student's t-distribution function with the nu parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionT(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the Student's t-distribution function with the nu parameter for an array of random variables x[]. In case of error it returns false. Analog of the pt() in R.

bool MathCumulativeDistributionT(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the Student's t-distribution function with the nu parameter for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionT(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  double         &result[]    // [out] Array for values of the probability function
);

2.11.3. MathQuantileT

For the specified probability, the function calculates the value of inverse Student's t-distribution function with the nu parameter. In case of error it returns NaN.

double MathQuantileT(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse Student's t-distribution function with the nu parameter. In case of error it returns NaN.

double MathQuantileT(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse Student's t-distribution function with the nu parameter. In case of error it returns false. Analog of the qt() in R.

bool MathQuantileT(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse Student's t-distribution function with the nu parameter. In case of error it returns false.

bool MathQuantileT(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  double         &result[]      // [out] Array with values of quantiles
);

2.11.4. MathRandomT

The function generates a pseudorandom variable distributed according to the law of Student's t-distribution with the nu parameter. In case of error it returns NaN.

double MathRandomT(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of Student's t-distribution with the nu parameter. In case of error it returns false. Analog of the rt() in R.

bool MathRandomT(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.11.5. MathMomentsT

The function calculates the theoretical numerical values of the first 4 moments of the Student's t-distribution with the nu parameter. Returns true if calculation of the moments has been successful, otherwise false.

double MathMomentsT(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.12. Noncentral t-distribution

2.12.1. MathProbabilityDensityNoncentralT

The function calculates the value of the probability density function of noncentral Student's t-distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralT(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral Student's t-distribution with the nu parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNoncentralT(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of noncentral Student's t-distribution with the nu parameter for an array of random variables x[]. In case of error it returns false. Analog of the dt() in R.

bool MathProbabilityDensityNoncentralT(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of noncentral Student's t-distribution with the nu parameter for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityNoncentralT(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability density function
);

2.12.2. MathCumulativeDistributionlNoncentralT

The function calculates the value of the probability distribution function of noncentral Student's t-distribution with the nu and delta parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralT(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral Student's t-distribution with the nu and delta parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNoncentralT(
  const double   x,           // [in]  Value of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of noncentral Student's t-distribution with the nu and delta parameters for an array of random variables x[]. In case of error it returns false. Analog of the pt() in R.

bool MathCumulativeDistributionNoncentralT(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function of noncentral Student's t-distribution with the nu and delta parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionNoncentralT(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  double         &result[]    // [out] Array for values of the probability function
);

2.12.3. MathQuantileNoncentralT

For the specified probability, the function calculates the value of inverse noncentral Student's t-distribution function with the nu and delta parameters. In case of error it returns NaN.

double MathQuantileNoncentralT(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,         // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse noncentral Student's t-distribution function with the nu and delta parameters. In case of error it returns NaN.

double MathQuantileNoncentralT(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,         // [in]  Noncentrality parameter
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse noncentral Student's t-distribution function with the nu and delta parameters. In case of error it returns false. Analog of the qt() in R.

bool MathQuantileNoncentralT(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,         // [in]  Noncentrality parameter
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse noncentral Student's t-distribution function with the nu and delta parameters. In case of error it returns false.

bool MathQuantileNoncentralT(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,         // [in]  Noncentrality parameter
  double         &result[]      // [out] Array with values of quantiles
);

2.12.4. MathRandomNoncentralT

The function generates a pseudorandom variable distributed according to the law of noncentral Student's t-distribution with the nu and delta parameters. In case of error it returns NaN.

double MathRandomNoncentralT(
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,         // [in]  Noncentrality parameter
  int            &error_code    // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of noncentral Student's t-distribution with the nu and delta parameters. In case of error it returns false. Analog of the rt() in R.

bool MathRandomNoncentralT(
  const double   nu,            // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,         // [in]  Noncentrality parameter
  const int      data_count,    // [in]  Amount of required data
  double         &result[]      // [out] Array with values of pseudorandom variables
);

2.12.5. MathMomentsNoncentralT

The function calculates the theoretical numerical values of the first 4 moments of the noncentral Student's t-distribution with the nu and delta parameters. Returns true if calculation of the moments has been successful, otherwise false.

double MathMomentsNoncentralT(
  const double   nu,          // [in]  Parameter of distribution (number of degrees of freedom)
  const double   delta,       // [in]  Noncentrality parameter
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.13. Logistic distribution

2.13.1. MathProbabilityDensityLogistic

The function calculates the value of the probability density function of logistic distribution with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityLogistic(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of logistic distribution with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityLogistic(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of logistic distribution with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the dlogis() in R.

bool MathProbabilityDensityLogistic(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of logistic distribution with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityLogistic(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  double         &result[]    // [out] Array for values of the probability density function
);

2.13.2. MathCumulativeDistributionlLogistic

The function calculates the value of the logistic distribution function with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionLogistic(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the logistic distribution function with the mu and sigma parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionLogistic(
  const double   x,           // [in]  Value of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the logistic distribution function with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the plogis() in R.

bool MathCumulativeDistributionLogistic(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the logistic distribution function with the mu and sigma parameters for an array of random variables x[]. In case of error it returns false. Analog of the plogis() in R.

bool MathCumulativeDistributionLogistic(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  double         &result[]    // [out] Array for values of the probability function
);

2.13.3. MathQuantileLogistic

For the specified probability, the function calculates the value of inverse logistic distribution function with the mu and sigma parameters. In case of error it returns NaN.

double MathQuantileLogistic(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   mu,            // [in]  mean parameter of the distribution
  const double   sigma,         // [in]  scale parameter of the distribution
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse logistic distribution function with the mu and sigma parameters. In case of error it returns NaN.

double MathQuantileLogistic(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   mu,            // [in]  mean parameter of the distribution
  const double   sigma,         // [in]  scale parameter of the distribution
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse logistic distribution function with the mu and sigma parameters. In case of error it returns false. Analog of the qlogis() in R.

bool MathQuantileLogistic(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   mu,            // [in]  mean parameter of the distribution
  const double   sigma,         // [in]  scale parameter of the distribution
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse logistic distribution function with the mu and sigma parameters. In case of error it returns false.

bool MathQuantileLogistic(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   mu,            // [in]  mean parameter of the distribution
  const double   sigma,         // [in]  scale parameter of the distribution
  double         &result[]      // [out] Array with values of quantiles
);

2.13.4. MathRandomLogistic

The function generates a pseudorandom variable distributed according to the law of logistic distribution with the mu and sigma parameters. In case of error it returns NaN.

double MathRandomLogistic(
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of logistic distribution with the mu and sigma parameters. In case of error it returns false. Analog of the rlogis() in R.

bool MathRandomLogistic(
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.13.5. MathMomentsLogistic

The function calculates the theoretical numerical values of the first 4 moments of the logistic distribution with the mu and sigma parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsLogistic(
  const double   mu,          // [in]  mean parameter of the distribution
  const double   sigma,       // [in]  scale parameter of the distribution
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.14. Cauchy distribution

2.14.1. MathProbabilityDensityCauchy

The function calculates the value of the probability density function of Cauchy distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityCauchy(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of Cauchy distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityCauchy(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of Cauchy distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the dcauchy() in R.

bool MathProbabilityDensityCauchy(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of Cauchy distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityCauchy(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  double         &result[]    // [out] Array for values of the probability density function
);

2.14.2. MathCumulativeDistributionCauchy

The function calculates the value of the probability distribution function of Cauchy distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionCauchy(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of Cauchy distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionCauchy(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function of Cauchy distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the pcauchy() in R.

bool MathCumulativeDistributionCauchy(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability distribution function of Cauchy distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionCauchy(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  double         &result[]    // [out] Array for values of the probability density function
);

2.14.3. MathQuantileCauchy

For the specified probability, the function calculates the value of inverse Cauchy distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileCauchy(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  mean parameter of the distribution
  const double   b,             // [in]  scale parameter of the distribution
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse Cauchy distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileCauchy(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  mean parameter of the distribution
  const double   b,             // [in]  scale parameter of the distribution
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse Cauchy distribution function with the a and b parameters. In case of error it returns false. Analog of the qcauchy() in R.

bool MathQuantileCauchy(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  mean parameter of the distribution
  const double   b,             // [in]  scale parameter of the distribution
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse Cauchy distribution function with the a and b parameters. In case of error it returns false.

bool MathQuantileCauchy(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  mean parameter of the distribution
  const double   b,             // [in]  scale parameter of the distribution
  double         &result[]      // [out] Array with values of quantiles
);

2.14.4. MathRandomCauchy

The function generates a pseudorandom variable distributed according to the law of Cauchy distribution with the a and b parameters. In case of error it returns NaN.

double MathRandomCauchy(
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of Cauchy distribution with the a and b parameters. In case of error it returns false. Analog of the rcauchy() in R.

double MathRandomCauchy(
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.14.5. MathMomentsCauchy

The function calculates the theoretical numerical values of the first 4 moments of the Cauchy distribution. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsCauchy(
  const double   a,           // [in]   mean parameter of the distribution
  const double   b,           // [in]  scale parameter of the distribution
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.15. Uniform distribution

2.15.1. MathProbabilityDensityUniform

The function calculates the value of the probability density function of uniform distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityUniform(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of uniform distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityUniform(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of uniform distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the dunif() in R.

bool MathProbabilityDensityUniform(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of uniform distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityUniform(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  double         &result[]    // [out] Array for values of the probability density function
);

2.15.2. MathCumulativeDistributionUniform

The function calculates the value of the uniform distribution function with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionUniform(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the uniform distribution function with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionUniform(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the uniform distribution function with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the punif() in R.

bool MathCumulativeDistributionUniform(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the uniform distribution function with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionUniform(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  double         &result[]    // [out] Array for values of the probability density function
);

2.15.3. MathQuantileUniform

For the specified probability, the function calculates the value of inverse uniform distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileUniform(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  Distribution parameter a (lower bound)
  const double   b,             // [in]  Distribution parameter b (upper bound)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse uniform distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileUniform(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  Distribution parameter a (lower bound)
  const double   b,             // [in]  Distribution parameter b (upper bound)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse uniform distribution function with the a and b parameters. In case of error it returns false. Analog of the qunif() in R.

bool MathQuantileUniform(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  Distribution parameter a (lower bound)
  const double   b,             // [in]  Distribution parameter b (upper bound)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse uniform distribution function with the a and b parameters. In case of error it returns false.

bool MathQuantileUniform(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  Distribution parameter a (lower bound)
  const double   b,             // [in]  Distribution parameter b (upper bound)
  double         &result[]      // [out] Array with values of quantiles
);

2.15.4. MathRandomUniform

The function generates a pseudorandom variable distributed according to the law of uniform distribution with the a and b parameters. In case of error it returns NaN.

double MathRandomUniform(
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of uniform distribution with the a and b parameters. In case of error it returns false. Analog of the runif() in R.

bool MathRandomUniform(
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.15.5. MathMomentsUniform

The function calculates the theoretical numerical values of the first 4 moments for the uniform distribution. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsUniform(
  const double   a,           // [in]  Distribution parameter a (lower bound)
  const double   b,           // [in]  Distribution parameter b (upper bound)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.16. Weibull distribution

2.16.1. MathProbabilityDensityWeibull

The function calculates the value of the probability density function of Weibull distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityWeibull(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of Weibull distribution with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityWeibull(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability density function of Weibull distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false. Analog of the dweibull() in R.

bool MathProbabilityDensityWeibull(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability density function of Weibull distribution with the a and b parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityWeibull(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  double         &result[]    // [out] Array for values of the probability density function
);

2.16.2. MathCumulativeDistributionWeibull

The function calculates the value of the Weibull distribution function with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionWeibull(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the Weibull distribution function with the a and b parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionWeibull(
  const double   x,           // [in]  Value of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the Weibull distribution function with the a and b parameters for a random variable x. In case of error it returns false. Analog of the pweibull() in R.

bool MathCumulativeDistributionWeibull(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the Weibull distribution function with the a and b parameters for a random variable x. In case of error it returns false.

bool MathCumulativeDistributionWeibull(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  double         &result[]    // [out] Array for values of the probability density function
);

2.16.3. MathQuantileWeibull

For the specified probability, the function calculates the value of inverse Weibull distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileWeibull(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  Parameter of the distribution (shape)
  const double   b,             // [in]  Parameter of the distribution (scale)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the value of inverse Weibull distribution function with the a and b parameters. In case of error it returns NaN.

double MathQuantileWeibull(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   a,             // [in]  Parameter of the distribution (shape)
  const double   b,             // [in]  Parameter of the distribution (scale)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse Weibull distribution function with the a and b parameters. In case of error it returns false. Analog of the qweibull() in R.

bool MathQuantileWeibull(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  Parameter of the distribution (shape)
  const double   b,             // [in]  Parameter of the distribution (scale)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the value of inverse Weibull distribution function with the a and b parameters. In case of error it returns false.

bool MathQuantileWeibull(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   a,             // [in]  Parameter of the distribution (shape)
  const double   b,             // [in]  Parameter of the distribution (scale)
  double         &result[]      // [out] Array with values of quantiles
);

2.16.4. MathRandomWeibull

The function generates a pseudorandom variable distributed according to the law of Weibull distribution with the a and b parameters. In case of error it returns NaN.

double MathRandomWeibull(
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of Weibull distribution with the a and b parameters. In case of error it returns false. Analog of the rweibull() in R.

bool MathRandomWeibull(
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.16.5. MathMomentsWeibull

The function calculates the theoretical numerical values of the first 4 moments of the Weibull distribution. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsWeibull(
  const double   a,           // [in]  Parameter of the distribution (shape)
  const double   b,           // [in]  Parameter of the distribution (scale)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.17. Binomial distribution

2.17.1. MathProbabilityDensityBinomial

The function calculates the value of the probability mass function of binomial distribution with the n and p parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of binomial distribution with the n and p parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of binomial distribution with the n and p parameters for an array of random variables x[]. In case of error it returns false. Analog of the dbinom() in R.

bool MathProbabilityDensityBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability mass function of binomial distribution with the n and p parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  double         &result[]    // [out] Array for values of the probability density function
);

2.17.2. MathCumulativeDistributionBinomial

The function calculates the value of the probability distribution function for binomial law with the n and p parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for binomial law with the n and p parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for binomial law with the n and p parameters for an array of random variables x[]. In case of error it returns false. Analog of the pbinom() in R.

bool MathCumulativeDistributionBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability distribution function for binomial law with the n and p parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  double         &result[]    // [out] Array for values of the probability density function
);

2.17.3. MathQuantileBinomial

For the specified probability, the function calculates the inverse value of function distribution for binomial law with the n and p parameters. In case of error it returns NaN.

double MathQuantileBinomial(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   n,             // [in]  Parameter of the distribution (number of tests)
  const double   p,             // [in]  Parameter of the distribution (probability of success for each test)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the inverse value of function distribution for binomial law with the n and p parameters. In case of error it returns NaN.

double MathQuantileBinomial(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   n,             // [in]  Parameter of the distribution (number of tests)
  const double   p,             // [in]  Parameter of the distribution (probability of success for each test)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for binomial law with the n and p parameters. In case of error it returns false. Analog of the qbinom() in R.

bool MathQuantileBinomial(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   n,             // [in]  Parameter of the distribution (number of tests)
  const double   p,             // [in]  Parameter of the distribution (probability of success for each test)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for binomial law with the n and p parameters. In case of error it returns false.

bool MathQuantileBinomial(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   n,             // [in]  Parameter of the distribution (number of tests)
  const double   p,             // [in]  Parameter of the distribution (probability of success for each test)
  double         &result[]      // [out] Array with values of quantiles
);

2.17.4. MathRandomBinomial

The function generates a pseudorandom variable distributed according to the law of binomial distribution with the n and p parameters. In case of error it returns NaN.

double MathRandomBinomial(
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of binomial distribution with the n and p parameters. In case of error it returns false. Analog of the rbinom() in R.

bool MathRandomBinomial(
  const double   n,           // [in]  Parameter of the distribution (number of tests)
  const double   p,           // [in]  Parameter of the distribution (probability of success for each test)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.17.5. MathMomentsBinomial

The function calculates the theoretical numerical values of the first 4 moments of the binomial distribution with the n and p parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsBinomial(
  const double   n,           // [in]  Number of tests
  const double   p,           // [in]  Probability of success in each test
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.18. Negative binomial distribution

2.18.1. MathProbabilityDensityNegativeBinomial

The function calculates the value of the probability mass function of negative binomial distribution with the r and p parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNegativeBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of negative binomial distribution with the r and p parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityNegativeBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of negative binomial distribution with the r and p parameters for an array of random variables x[]. In case of error it returns false. Analog of the dnbinom() in R.

bool MathProbabilityDensityNegativeBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability mass function of negative binomial distribution with the r and p parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityNegativeBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  double         &result[]    // [out] Array for values of the probability density function
);

2.18.2. MathCumulativeDistributionNegativeBinomial

The function calculates the value of the probability distribution function for negative binomial law with the r and p parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNegativeBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for negative binomial law with the r and p parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionNegativeBinomial(
  const double   x,           // [in]  Value of random variable (integer)
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for negative binomial law with the r and p parameters for an array of random variables x[]. In case of error it returns false. Analog of the pnbinom() in R.

bool MathCumulativeDistributionNegativeBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability distribution function for negative binomial law with the r and p parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionNegativeBinomial(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  double         &result[]    // [out] Array for values of the probability function
);

2.18.3. MathQuantileNegativeBinomial

For the specified probability, the function calculates the inverse value of function distribution for negative binomial law with the r and p parameters. In case of error it returns NaN.

double MathQuantileNegativeBinomial(
  const double   probability,   // [in]  Probability value of random variable occurrence 
  const double   r,             // [in]  Number of successful tests
  double         p,             // [in]  Probability of success
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the inverse value of function distribution for negative binomial law with the r and p parameters. In case of error it returns NaN.

double MathQuantileNegativeBinomial(
  const double   probability,   // [in]  Probability value of random variable occurrence 
  const double   r,             // [in]  Number of successful tests
  double         p,             // [in]  Probability of success
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for negative binomial law with the r and p parameters. In case of error it returns false. Analog of the qnbinom() in R.

bool MathQuantileNegativeBinomial(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   r,             // [in]  Number of successful tests
  double         p,             // [in]  Probability of success
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for negative binomial law with the r and p parameters. In case of error it returns false.

bool MathQuantileNegativeBinomial(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   r,             // [in]  Number of successful tests
  double         p,             // [in]  Probability of success
  double         &result[]      // [out] Array with values of quantiles
);

2.18.4. MathRandomNegativeBinomial

The function generates a pseudorandom variable distributed according to the law of negative binomial distribution with the r and p parameters. In case of error it returns NaN.

double MathRandomNegativeBinomial(
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of negative binomial distribution with the r and p parameters. In case of error it returns false. Analog of the rnbinom() in R.

bool MathRandomNegativeBinomial(
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.18.5. MathMomentsNegativeBinomial

The function calculates the theoretical numerical values of the first 4 moments of the negative binomial distribution with the r and p parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsNegativeBinomial(
  const double   r,           // [in]  Number of successful tests
  double         p,           // [in]  Probability of success
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.19. Geometric distribution

2.19.1. MathProbabilityDensityGeometric

The function calculates the value of the probability mass function of geometric distribution with the p parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityGeometric(
  const double   x,           // [in]  Value of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of geometric distribution with the p parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityGeometric(
  const double   x,           // [in]  Value of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of geometric distribution with the p parameter for an array of random variables x[]. In case of error it returns false. Analog of the dgeom() in R.

bool MathProbabilityDensityGeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability mass function of geometric distribution with the p parameter for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityGeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  double         &result[]    // [out] Array for values of the probability density function
);

2.19.2. MathCumulativeDistributionGeometric

The function calculates the value of the probability distribution function for geometric law with the p parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionGeometric(
  const double   x,           // [in]  Value of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const bool     tail,        // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,    // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for geometric law with the p parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionGeometric(
  const double   x,           // [in]  Value of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for geometric law with the p parameter for an array of random variables x[]. In case of error it returns false. Analog of the pgeom() in R.

bool MathCumulativeDistributionGeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const bool     tail,        // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,    // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability distribution function for geometric law with the p parameter for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionGeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  double         &result[]    // [out] Array for values of the probability density function
);

2.19.3. MathQuantileGeometric

For the specified probability, the function calculates the inverse value of function distribution for geometric law with the p parameter. In case of error it returns NaN.

double MathQuantileGeometric(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   p,             // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the inverse value of function distribution for geometric law with the p parameter. In case of error it returns NaN.

double MathQuantileGeometric(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   p,             // [in]  Parameter of the distribution (probability of event occurrence in one test)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for geometric law with the p parameter. In case of error it returns false. Analog of the qgeom() in R.

bool MathQuantileGeometric(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   p,             // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for geometric law with the p parameter. In case of error it returns false.

bool MathQuantileGeometric(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   p,             // [in]  Parameter of the distribution (probability of event occurrence in one test)
  double         &result[]      // [out] Array with values of quantiles
);

2.19.4. MathRandomGeometric

The function generates a pseudorandom variable distributed according to the law of geometric distribution with the p parameter. In case of error it returns NaN.

double MathRandomGeometric(
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of geometric distribution with the p parameter. In case of error it returns false. Analog of the rgeom() in R.

bool MathRandomGeometric(
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.19.5. MathMomentsGeometric

The function calculates the theoretical numerical values of the first 4 moments of the geometric distribution with the p parameter. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsGeometric(
  const double   p,           // [in]  Parameter of the distribution (probability of event occurrence in one test)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.20. Hypergeometric distribution

2.20.1. MathProbabilityDensityHypergeometric

The function calculates the value of the probability mass function of hypergeometric distribution with the m, k and n parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityHypergeometric(
  const double   x,           // [in]  Value of random variable (integer)
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of hypergeometric distribution with the m, k and n parameters for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityHypergeometric(
  const double   x,           // [in]  Value of random variable (integer)
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of hypergeometric distribution with the m, k and n parameters for an array of random variables x[]. In case of error it returns false. Analog of the dhyper() in R.

bool MathProbabilityDensityHypergeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the probability mass function of hypergeometric distribution with the m, k and n parameters for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityHypergeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  double         &result[]    // [out] Array for values of the probability function
);

2.20.2. MathCumulativeDistributionHypergeometric

The function calculates the value of the probability distribution function for hypergeometric law with the m, k and n parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionHypergeometric(
  const double   x,           // [in]  Value of random variable (integer)
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  const bool     tail,        // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,    // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for hypergeometric law with the m, k and n parameters for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionHypergeometric(
  const double   x,           // [in]  Value of random variable (integer)
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability distribution function for hypergeometric law with the m, k and n parameters for an array of random variables x[]. In case of error it returns false. Analog of the phyper() in R.

bool MathCumulativeDistributionHypergeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  const bool     tail,        // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,    // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]    // [out] Array for values of the distribution function
);

The function calculates the value of the probability distribution function for hypergeometric law with the m, k and n parameters for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionHypergeometric(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  double         &result[]    // [out] Array for values of the distribution function
);

2.20.3. MathQuantileHypergeometric

For the specified probability, the function calculates the inverse value of function distribution for hypergeometric law with the m, k and n parameters. In case of error it returns NaN.

double MathQuantileHypergeometric(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   m,             // [in]  Total number of objects (целочисленное)
  const double   k,             // [in]  Number of objects with the desired characteristic (integer)
  const double   n,             // [in]  Number of object draws (integer)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the inverse value of function distribution for hypergeometric law with the m, k and n parameters. In case of error it returns NaN.

double MathQuantileHypergeometric(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   m,             // [in]  Total number of objects (integer)
  const double   k,             // [in]  Number of objects with the desired characteristic (integer)
  const double   n,             // [in]  Number of object draws (integer)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for hypergeometric law with the m, k and n parameters. In case of error it returns false. Analog of the qhyper() in R.

bool MathQuantileHypergeometric(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   m,             // [in]  Total number of objects (integer)
  const double   k,             // [in]  Number of objects with the desired characteristic (integer)
  const double   n,             // [in]  Number of object draws (integer)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of function distribution for hypergeometric law with the m, k and n parameters. In case of error it returns false.

bool MathQuantileHypergeometric(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   m,             // [in]  Total number of objects (integer)
  const double   k,             // [in]  Number of objects with the desired characteristic (integer)
  const double   n,             // [in]  Number of object draws (integer)
  double         &result[]      // [out] Array with values of quantiles
);

2.20.4. MathRandomHypergeometric

The function generates a pseudorandom variable distributed according to the law of hypergeometric distribution with the m, n and k parameters. In case of error it returns NaN.

double MathRandomHypergeometric(
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of hypergeometric distribution with the m, n and k parameters. In case of error it returns false. Analog of the rhyper() in R.

bool MathRandomHypergeometric(
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  const int      data_count,  // [in]  Amount of required data
  double         &result[]    // [out] Array with values of pseudorandom variables
);

2.20.5. MathMomentsHypergeometric

The function calculates the theoretical numerical values of the first 4 moments of the hypergeometric distribution with the m, n and k parameters. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsHypergeometric(
  const double   m,           // [in]  Total number of objects (integer)
  const double   k,           // [in]  Number of objects with the desired characteristic (integer)
  const double   n,           // [in]  Number of object draws(integer)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

2.21. Poisson distribution

2.21.1. MathProbabilityDensityPoisson

The function calculates the value of the probability mass function of Poisson distribution with the lambda parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityPoisson(
  const double   x,           // [in]  Value of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of Poisson distribution with the lambda parameter for a random variable x. In case of error it returns NaN.

double MathProbabilityDensityPoisson(
  const double   x,           // [in]  Value of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the probability mass function of Poisson distribution with the lambda parameter for an array of random variables x[]. In case of error it returns false. Analog of the dpois() in R.

bool MathProbabilityDensityPoisson(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability density is returned
  double         &result[]    // [out] Array for values of the probability density function
);

The function calculates the value of the probability mass function of Poisson distribution with the lambda parameter for an array of random variables x[]. In case of error it returns false.

bool MathProbabilityDensityPoisson(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  double         &result[]    // [out] Array for values of the probability density function
);

2.21.2. MathCumulativeDistributionPoisson

The function calculates the value of the Poisson distribution function with the lambda parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionPoisson(
  const double   x,           // [in]  Value of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the Poisson distribution function with the lambda parameter for a random variable x. In case of error it returns NaN.

double MathCumulativeDistributionPoisson(
  const double   x,           // [in]  Value of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  int            &error_code  // [out] Variable for the error code
);

The function calculates the value of the Poisson distribution function with the lambda parameter for an array of random variables x[]. In case of error it returns false. Analog of the ppois() in R.

bool MathCumulativeDistributionPoisson(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  const bool     tail,        // [in]  Flag of calculation, if true, then the probability of random variable not exceeding x is calculated
  const bool     log_mode,    // [in]  Flag to calculate the logarithm of the value, if log_mode=true, then the natural logarithm of the probability is calculated
  double         &result[]    // [out] Array for values of the probability function
);

The function calculates the value of the Poisson distribution function with the lambda parameter for an array of random variables x[]. In case of error it returns false.

bool MathCumulativeDistributionPoisson(
  const double   &x[],        // [in]  Array with the values of random variable
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  double         &result[]    // [out] Array for values of the probability function
);

2.21.3. MathQuantilePoisson

For the specified probability, the function calculates the inverse value of Poisson distribution function with the lambda parameter. In case of error it returns NaN.

double MathQuantilePoisson(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   lambda,        // [in]  Parameter of the distribution (mean)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  int            &error_code    // [out] Variable for the error code
);

For the specified probability, the function calculates the inverse value of Poisson distribution function with the lambda parameter. In case of error it returns NaN.

double MathQuantilePoisson(
  const double   probability,   // [in]  Probability value of random variable occurrence
  const double   lambda,        // [in]  Parameter of the distribution (mean)
  int            &error_code    // [out] Variable for the error code
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of Poisson distribution function with the lambda parameter. In case of error it returns false. Analog of the qpois() in R.

double MathQuantilePoisson(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   lambda,        // [in]  Parameter of the distribution (mean)
  const bool     tail,          // [in]  Flag of calculation, if false, then calculation is performed for 1.0-probability
  const bool     log_mode,      // [in]  Flag of calculation, if log_mode=true, calculation is performed for Exp(probability)
  double         &result[]      // [out] Array with values of quantiles
);

For the specified 'probability[]' array of probability values, the function calculates the inverse value of Poisson distribution function with the lambda parameter. In case of error it returns false.

double MathQuantilePoisson(
  const double   &probability[],// [in]  Array with probability values of random variable
  const double   lambda,        // [in]  Parameter of the distribution (mean)
  double         &result[]      // [out] Array with values of quantiles
);

2.21.4. MathRandomPoisson

The function generates a pseudorandom variable distributed according to the law of Poisson distribution with the lambda parameter. In case of error it returns NaN.

double MathRandomPoisson(
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  int            &error_code  // [out] Variable for the error code
);

The function generates pseudorandom variables distributed according to the law of Poisson distribution with the lambda parameter. In case of error it returns false. Analog of the rpois() in R.

double MathRandomPoisson(
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  int            &error_code  // [out] Variable for the error code
);

2.21.5. MathMomentsPoisson

The function calculates the theoretical numerical values of the first 4 moments of the Poisson distribution with the lambda parameter. Returns true if calculation of the moments has been successful, otherwise false.

bool MathMomentsPoisson(
  const double   lambda,      // [in]  Parameter of the distribution (mean)
  double         &mean,       // [out] Variable for the mean (1st moment)
  double         &variance,   // [out] Variable for the variance (2nd moment)
  double         &skewness,   // [out] Variable for the skewness (3rd moment)
  double         &kurtosis,   // [out] Variable for the kurtosis (4th moment)
  int            &error_code  // [out] Variable for the error code
);

3. Table of correspondence to the statistical functions in R

For convenience, the tables 1-2 contain the functions of the statistical library and the corresponding functions of the R language.

No.	Calculated value	Functions in MQL5	Functions in R
1	Mean	MathMean	mean
2	Variance	MathVariance	var
3	Skewness	MathSkewness	skewness
60	Kurtosis	MathKurtosis	kurtosis
5	Median value	MathMedian	median
6	Standard Deviation	MathStandardDeviation	sd
7	Average deviation	MathAverageDeviation	aad

Table 1. Functions for calculating the statistical characteristics of array data

No.	Distribution	Density function	Functions in MQL5	Functions in R
1	Normal		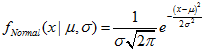MathProbabilityDensityNormal MathCumulativeDistributionNormal MathQuantileNormal MathRandomNormal	dnorm pnorm qnorm rnorm
2	Beta		MathProbabilityDensityBeta MathCumulativeDistributionBeta MathQuantileBeta MathRandomBeta	dbeta pbeta qbeta rbeta
3	Binomial		MathProbabilityDensityBinomial MathCumulativeDistributionBinomial MathQuantileBinomial MathRandomBinomial	dbinom pbinom qbinom rbinom
60	Cauchy		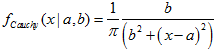MathProbabilityDensityCauchy MathCumulativeDistributionCauchy MathQuantileCauchy MathRandomCauchy	dcauchy pcauchy qcauchy rcauchy
5	Chi-squared		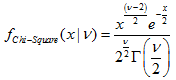MathProbabilityDensityChiSquare MathCumulativeDistributionChiSquare MathQuantileChiSquare MathRandomChiSquare	dchisq pchisq qchisq rchisq
6	Exponential		MathProbabilityDensityExponential MathCumulativeDistributionExponential MathQuantileExponential MathRandomExponential	dexp pexp qexp rexp
7	F-distribution		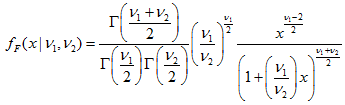MathProbabilityDensityF MathCumulativeDistributionF MathQuantileF MathRandomF	df pf qf rf
8	Gamma		MathProbabilityDensityGamma MathCumulativeDistributionGamma MathQuantileGamma MathRandomGamma	dgamma pgamma qgamma rgamma
9	Geometric		MathProbabilityDensityGeometric MathCumulativeDistributionGeometric MathQuantileGeometric MathRandomGeometric	dgeom pgeom qgeom rgeom
10	Hypergeometric		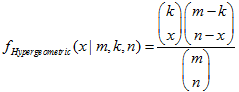MathProbabilityDensityHypergeometric MathCumulativeDistributionHypergeometric MathQuantileHypergeometric MathRandomHypergeometric	dhyper phyper qhyper rhyper
11	Logistic		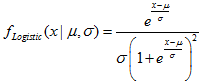MathProbabilityDensityLogistic MathCumulativeDistributionLogistic MathQuantileLogistic MathRandomLogistic	dlogis plogis qlogis rlogis
12	Log-normal		MathProbabilityDensityLognormal MathCumulativeDistributionLognormal MathQuantileLognormal MathRandomLognormal	dlnorm plnorm qlnorm rlnorm
13	Negative binomial		MathProbabilityDensityNegativeBinomial MathCumulativeDistributionNegativeBinomial MathQuantileNegativeBinomial MathRandomNegativeBinomial	dnbinom pnbinom qnbinom rnbinom
14	Noncentral beta		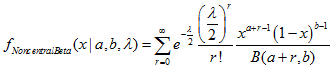MathProbabilityDensityNoncentralBeta MathCumulativeDistributionNoncentralBeta MathQuantileNoncentralBeta MathRandomNoncentralBeta	dbeta pbeta qbeta rbeta
15	Noncentral chi-squared		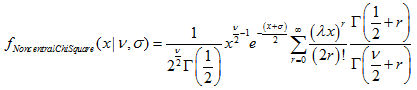MathProbabilityDensityNoncentralChiSquare MathCumulativeDistributionNoncentralChiSquare MathQuantileNoncentralChiSquare MathRandomNoncentralChiSquare	dchisq pchisq qchisq rchisq
16	Noncentral F-distribution		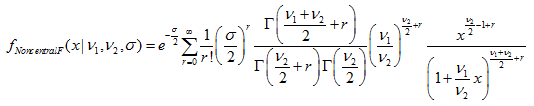MathProbabilityDensityNoncentralF() MathCumulativeDistributionNoncentralF() MathQuantileNoncentralF() MathRandomNoncentralF()	df pf qf rf
17	Noncentral t-distribution		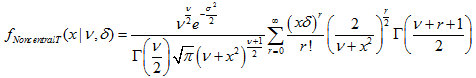MathProbabilityDensityNoncentralT MathCumulativeDistributionNoncentralT MathQuantileNoncentralT MathRandomNoncentralT	dt pt qt rt
18	Poisson		MathProbabilityDensityPoisson MathCumulativeDistributionPoisson MathQuantilePoisson MathRandomPoisson	dpois ppois qpois rpois
19	t-distribution		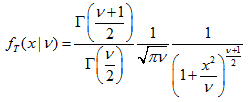MathProbabilityDensityT MathCumulativeDistributionT MathQuantileT MathRandomT	dt pt qt rt
20	Uniform		MathProbabilityDensityUniform MathCumulativeDistributionUniform MathQuantileUniform MathRandomUniform	dunif punif qunif runif
21	Weibull		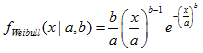MathProbabilityDensityWeibull MathCumulativeDistributionWeibull MathQuantileWeibull MathRandomWeibull	dweibull pweibull qweibull rweibull

Table 2. Functions for working with statistical distributions

The MQL5 statistical library also provides functions for calculating the mathematical functions on arrays, they are listed below in the Table 3.

Description	MQL5	R
Generates a sequence of values	bool MathSequence(const double from,const double to,const double step,double &result[]) bool MathSequenceByCount(const double from,const double to,const int count,double &result[]) bool MathSequence(const int from,const int to,const int step,int &result[]) bool MathSequenceByCount(const int from,const int to,const int count,int &result[])	seq()
Generates a repeating sequence	bool MathReplicate(const double &array[],const int count,double &result[]) bool MathReplicate(const int &array[],const int count,int &result[])	rep()
Generates an array with reverse order of elements	bool MathReverse(const double &array[],double &result[]) bool MathReverse(const int &array[],int &result[])	rev(x)
Compares arrays and returns true if all elements match	bool MathIdentical(const double &array1[],const double &array2[]) bool MathIdentical(const int &array1[],const int &array2[])	identical()
Generates an array with unique values only	bool MathUnique(const double &array[],double &result[]) bool MathUnique(const int &array[],int &result[])	unique()
Generates an integer array with permutation according to order of the array elements after sorting	bool MathOrder(const double &array[],int &result[]) bool MathOrder(const int &array[],int &result[])	order()
Generates a random sample from the array elements. The replace=true argument allows to perform random sampling of the elements with replacement back to the original sequence. The probabilities[] array defines the probabilities for sampling the elements.	bool MathSample(const double &array[],const int count,double &result[]) bool MathSample(const double &array[],const int count,const bool replace,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,const bool replace,double &result[]) bool MathSample(const int &array[],const int count,int &result[]) bool MathSample(const int &array[],const int count,const bool replace,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,const bool replace,int &result[])	sample()
Returns the sum of array elements	double MathSum(const double &array[])	sum()
Returns the product of array elements	double MathProduct(const double &array[])	prod()
Generates an array with the cumulative sums	bool MathCumulativeSum(const double &array[],double &result[]) bool MathCumulativeSum(double &array[])	cumsum()
Generates an array with the cumulative products	bool MathCumulativeProduct(const double &array[],double &result[]) bool MathCumulativeProduct(double &array[])	cumprod()
Generates an array with the cumulative minima	bool MathCumulativeMin(const double &array[],double &result[]) bool MathCumulativeMin(double &array[])	cummin()
Generates an array with the cumulative maxima	bool MathCumulativeMax(const double &array[],double &result[]) bool MathCumulativeMax(double &array[])	cummax()
Generates an array with element differences of y[i]=x[i+lag]-x[i]	bool MathDifference(const double &array[],const int lag,double &result[]) bool MathDifference(const double &array[],const int lag,const int differences,double &result[]) bool MathDifference(const int &array[],const int lag,int &result[]) bool MathDifference(const int &array[],const int lag,const int differences,int &result[])	diff()
Returns the minima of array elements	double MathMin(const double &array[])	min()
Returns the maxima of array elements	double MathMax(const double &array[])	max()
Calculates the minima and maxima of array elements	bool MathRange(const double &array[],double &min,double &max)	range()
Calculates the mean values of array elements	double MathMean(const double &array[])	mean()
Calculates the standard deviations of array elements	double MathStandardDeviation(const double &array[])	sd()
Calculates the median values of array elements	double MathMedian(double &array[])	median()
Calculates the ranks of array elements	bool MathRank(const int &array[],double &rank[]) bool MathRank(const double &array[],double &rank[])	rank()
Calculates the Pearson's, Spearman's and Kendall's correlation coefficients	bool MathCorrelationPearson(const double &array1[],const double &array2[],double &r) bool MathCorrelationPearson(const int &array1[],const int &array2[],double &r) bool MathCorrelationSpearman(const double &array1[],const double &array2[],double &r) bool MathCorrelationSpearman(const int &array1[],const int &array2[],double &r) bool MathCorrelationKendall(const double &array1[],const double &array2[],double &tau) bool MathCorrelationKendall(const int &array1[],const int &array2[],double &tau)	corr()
Calculates sample quantiles corresponding to the specified probabilities	bool MathQuantile(const double &array[],const double &probs[],double &quantile[])	qunatile()
Calculates the Tukey's five number summary (minimum, lower-hinge, median, upper-hinge, maximum) for array elements	bool MathTukeySummary(const double &array[],const bool removeNAN,double &minimum,double &lower_hinge,double &median,double &upper_hinge,double &maximum)	fivenum()
Calculates logarithms of array elements (natural and to a given base)	bool MathLog(const double &array[],double &result[]) bool MathLog(const double &array[],const double base,double &result[]) bool MathLog(double &array[]) bool MathLog(double &array[],const double base)	log()
Calculates logarithms of array elements to base 2	bool MathLog2(const double &array[],double &result[]) bool MathLog2(double &array[])	log2()
Calculates logarithms of array elements to base 10	bool MathLog10(const double &array[],double &result[]) bool MathLog10(double &array[])	log10()
Calculates the values of the log(1+x) function for array elements	bool MathLog1p(const double &array[], double &result[]) bool MathLog1p(double &array[])	log1p()
Calculates the values of the exp(x) function for array elements	bool MathExp(const double &array[], double &result[]) bool MathExp(double &array[])	exp()
Calculates the values of the exp(x)-1 function for array elements	bool MathExpm1(const double &array[], double &result[]) bool MathExpm1(double &array[])	expm1()
Calculates the values of the sin(x) function for array elements	bool MathSin(const double &array[], double &result[]) bool MathSin(double &array[])	sin()
Calculates the values of the cos(x) function for array elements	bool MathCos(const double &array[], double &result[]) bool MathCos(double &array[])	cos()
Calculates the values of the tan(x) function for array elements	bool MathTan(const double &array[], double &result[]) bool MathTan(double &array[])	tan()
Calculates the values of the arcsin(x) function for array elements	bool MathArcsin(const double &array[], double &result[]) bool MathArcsin(double &array[])	arcsin()
Calculates the values of the arccos(x) function for array elements	bool MathArccos(const double &array[], double &result[]) bool MathArccos(double &array[])	arccos()
Calculates the values of the arctan(x) function for array elements	bool MathArctan(const double &array[], double &result[]) bool MathArctan(double &array[])	arctan()
Calculates the values of the arctan(y/x) function for array elements	bool MathArctan2(const double &array1[], const double &array2[], double &result[])	arctan2()
Calculates the values of the sin(pi*x) function for array elements	bool MathSinPi(const double &array[], double &result[]) bool MathSinPi(double &array[])	sinpi()
Calculates the values of the cos(pi*x) function for array elements	bool MathCosPi(const double &array[], double &result[]) bool MathCosPi(const double &array[])	cospi()
Calculates the values of the tan(pi*x) function for array elements	bool MathTanPi(const double &array[], double &result[]) bool MathTanPi(double &array[])	tanpi()
Calculates the absolute values of array elements	bool MathAbs(const double &array[], double &result[]) bool MathAbs(double &array[])	abs()
Calculates the square roots of array elements	bool MathSqrt(const double &array[], double &result[]) bool MathSqrt(double &array[])	sqrt()
Returns the nearest larger integers for array elements	bool MathCeil(const double &array[], double &result[]) bool MathCeil(double &array[])	ceil()
Returns the nearest smaller integers for array elements	bool MathFloor(const double &array[], double &result[]) bool MathFloor(double &array[])	floor()
Calculates the integer parts of array elements	bool MathTrunc(const double &array[], const int digits, double &result[]) bool MathTrunc(double &array[])	trunc()
Calculates the rounded values of array elements	bool MathRound(const double &array[], const int digits, double &result[]) bool MathRound(double &array[],int digits)	round()
For array elements, calculates the value rounded to the specified number of digits in the mantissa	bool MathSignif(const double &array[], const int digits, double &result[]) bool MathSignif(double &array[], const int digits)	signinf()
Calculates the values of the sinh(x) function for array elements	bool MathSinh(const double &array[],double &result[]) bool MathSinh(double &array[])	sinh()
Calculates the values of the cosh(x) function for array elements	bool MathCosh(const double &array[],double &result[]) bool MathCosh(double &array[])	cosh()
Calculates the values of the tanh(x) function for array elements	bool MathTanh(const double &array[],double &result[]) bool MathTanh(double &array[])	tanh()
Calculates the values of the arcsinh(x) function for array elements	bool MathArcsinh(const double &array[],double &result[]) bool MathArcsinh(double &array[])	asinh()
Calculates the values of the arccosh(x) function for array elements	bool MathArccosh(const double &array[],double &result[]) bool MathArccosh(double &array[])	acosh()
Calculates the values of the arctanh(x) function for array elements	bool MathArctanh(const double &array[],double &result[]) bool MathArctanh(double &array[])	atanh()
Calculates the result of bitwise NOT operation for array elements	bool MathBitwiseNot(const int &array[],int &result[]) bool MathBitwiseNot(int &array[])	bitwNot()
Calculates the result of bitwise AND operation for specified arrays	bool MathBitwiseAnd(const int &array1[],const int &array2[],int &result[])	bitwAnd()
Calculates the result of bitwise OR operation for specified arrays	bool MathBitwiseOr(const int &array1[],const int &array2[],int &result[])	bitwOr()
Calculates the result of bitwise XOR operation for specified arrays	bool MathBitwiseXor(const int &array1[],const int &array2[],int &result[])	bitwXor()
Calculates the result of bitwise SHL operation for array elements	bool MathBitwiseShiftL(const int &array[],const int n,int &result[]) bool MathBitwiseShiftL(int &array[],const int n)	bitwShiftL()
Calculates the result of bitwise SHR operation for array elements	bool MathBitwiseShiftR(const int &array[],const int n,int &result[]) bool MathBitwiseShiftR(int &array[],const int n)	bitwShiftR()

Table 3. Mathematical functions for calculating values in arrays

4. An example of using the functions

Let us consider the practical application of statistical functions on the example of a normal distribution.

Suppose the following problems need to be solved:

1. Calculate the probability of a random variable, distributed according to the normal law with the mu and sigma parameters, falling within the range of [mu-sigma,mu+sigma].
2. Find the value range of random variable x, distributed according to the normal law with the mu and sigma parameters, which is symmetrical to mu and which corresponds to 95% of the confidence probability.
3. Generate 1000000 random numbers, distributed according to the normal law with the mu and sigma parameters, calculate the histogram of the obtained values, the first 4 moments and compare with the theoretical values.

Example of solution in the NormalExample script:

//+------------------------------------------------------------------+
//|                                                NormalExample.mq5 |
//|                        Copyright 2016, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
//--- include the functions for calculating the normal distribution
#include <Math\Stat\Normal.mqh>
//+------------------------------------------------------------------+
//| CalculateHistogram                                               |
//+------------------------------------------------------------------+
void CalculateHistogram(double &data[],const int ncells=200,const string filename="normal.csv")
  {
   if(ArraySize(data)<=0)
      return;

   int n=ArraySize(data);
//--- find the minimum and maximum data values in the 'data' array
   double minv,maxv,range;
   minv=data[0];
   maxv=data[0];
   for(int i=1; i<n; i++)
     {
      minv=MathMin(minv,data[i]);
      maxv=MathMax(maxv,data[i]);
     }
//--- calculate the range
   range=maxv-minv;
//   Print("Min=",minv," Max=",maxv," range=",range," size=",n);
   if(range==0)
      return;
//--- arrays for the histogram calculation
   double x[];
   double y[];
//--- set the histogram values
   ArrayResize(x,ncells);
   ArrayResize(y,ncells);
   for(int i=0; i<ncells; i++)
     {
      x[i]=minv+i*range/(ncells-1);
      y[i]=0;
     }
//--- calculate the histogram
   for(int i=0; i<n; i++)
     {
      double v=(maxv-data[i])/range;
      int ind=int((v*(ncells-1)));
      y[ind]++;
     }
//--- check the file name
   if(filename=="")
      return;
//--- open the file for writing
   ResetLastError();
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_TXT|FILE_ANSI);
//--- write data to the file
   if(filehandle!=INVALID_HANDLE)
     {
      for(int i=0; i<ncells; i++)
        {
         string str=StringFormat("%6.20f;%6.20f",x[i],y[i]);
         FileWrite(filehandle,str);
        }
      FileClose(filehandle);
      PrintFormat("Histogram saved to file %s",filename);
     }
   else
      PrintFormat("Error calling FileOpen, error code=%d",GetLastError());
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- 1. Calculate the probability of a random variable, 
//--- distributed according to the normal law with the mu and sigma parameters, falling within the range of [mu-sigma,mu+sigma]
//--- set the distribution parameters
   double mu=5.0;
   double sigma=1.0;
//--- set the interval
   double x1=mu-sigma;
   double x2=mu+sigma;
//--- variables for probability calculation
   double cdf1,cdf2,probability;
//--- variables for error codes
   int error_code1,error_code2;
//--- calculate the values of distribution functions
   cdf1=MathCumulativeDistributionNormal(x1,mu,sigma,error_code1);
   cdf2=MathCumulativeDistributionNormal(x2,mu,sigma,error_code2);
//--- check the error codes
   if(error_code1==ERR_OK && error_code2==ERR_OK)
     {
      //--- calculate the probability
      probability=cdf2-cdf1;
      //--- output the result
      PrintFormat("x1=%5.8f, x2=%5.8f, Probability=%5.8f",x1,x2,probability);
     }
//--- 2. Find the value range of random variable x, distributed according to the normal law with the mu and sigma parameters, 
//--- which is symmetrical to mu and which corresponds to 95% of the confidence probability.
//--- set the confidence probability
   probability=0.95;
//--- set the probabilities at the interval bounds
   double p1=(1.0-probability)*0.5;
   double p2=probability+(1.0-probability)*0.5;
//--- calculate the interval bounds
   x1=MathQuantileNormal(p1,mu,sigma,error_code1);
   x2=MathQuantileNormal(p2,mu,sigma,error_code2);
//--- check the error codes
   if(error_code1==ERR_OK && error_code2==ERR_OK)
     {
      //--- output the result  
      PrintFormat("x1=%5.8f, x2=%5.8f",x1,x2);
     }
//--- 3. Generate 1000000 random numbers, distributed according to the normal law with the mu and sigma parameters,
//--- calculate the histogram of the obtained values, the first 4 moments and compare with the theoretical values
//--- set the number of values and prepare an array
   int data_count=1000000;
   double data[];
   ArrayResize(data,data_count);
//--- generate random values and store them into the array
   for(int i=0; i<data_count; i++)
     {
      data[i]=MathRandomNormal(mu,sigma,error_code1);
     }
//--- set the index of the initial value and the amount of data for calculation
   int start=0;
   int count=data_count;
//--- calculate the first 4 moments of the generated values
   double mean=MathMean(data,start,count);
   double variance=MathVariance(data,start,count);
   double skewness=MathSkewness(data,start,count);
   double kurtosis=MathKurtosis(data,start,count);
//--- variables for the theoretical moments
   double normal_mean=0;
   double normal_variance=0;
   double normal_skewness=0;
   double normal_kurtosis=0;
//--- display the values of the calculated moments
   PrintFormat("              mean=%.10f,         variance=%.10f         skewness=%.10f         kurtosis=%.10f",mean,variance,skewness,kurtosis);
//--- calculate the theoretical values of the moments and compare them with the obtained values
   if(MathMomentsNormal(mu,sigma,normal_mean,normal_variance,normal_skewness,normal_kurtosis,error_code1))
     {
      PrintFormat("Normal mean=%.10f,  Normal variance=%.10f  Normal skewness=%.10f  Normal kurtosis=%.10f",normal_mean,normal_variance,normal_skewness,normal_kurtosis);
      PrintFormat("delta mean=%.4f, delta variance=%.4f  delta skewness=%.4f  delta kurtosis=%.4f",mean-normal_mean,variance-normal_variance,skewness-normal_skewness,kurtosis-normal_kurtosis);
     }
//--- calculate the distribution histogram and save it to the normal.csv file
   int ncells=50;
   CalculateHistogram(data,ncells,"normal.csv");
  }

Script execution results:

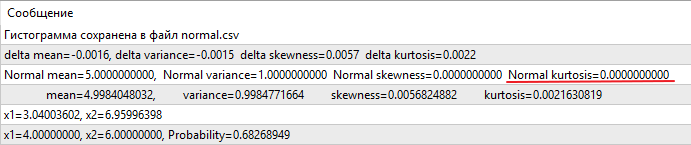
Fig. 1. TestNormal.mq5 script operation result

Note that all calculations of the 'kurtosis' parameter value use "excess kurtosis=kurtosis-3", i.e. for a normal distribution it equals zero.

The calculated histogram is saved to the normal.csv file (fig. 2)

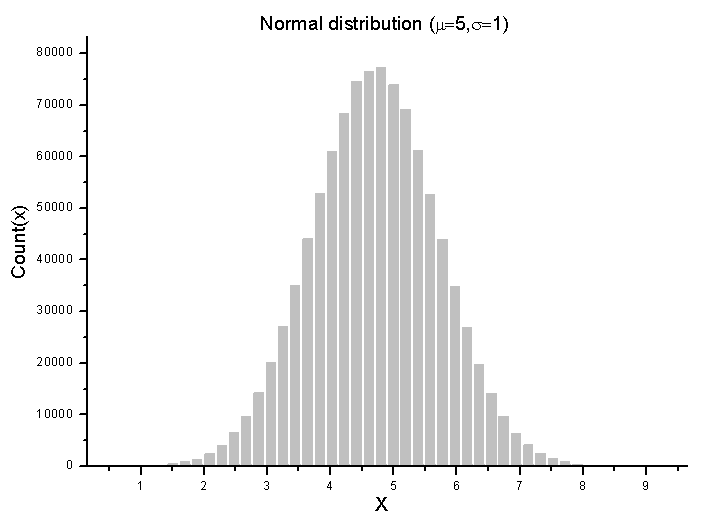
Fig. 2. Distribution histogram of random numbers, generated according to the normal distribution with the parameters mu=5 and sigma=1

5. Comparison of calculation speed

To compare the calculation speed of statistical functions, the scripts for measuring calculation times have been prepared for the probability density functions (pdf), cumulative distribution functions (cdf), quantile calculation functions and pseudorandom number generation functions.

The calculations have been performed on an array of 51 values. For continuous distributions, the calculation of function values has been performed in the range from 0 to 1; for discrete distributions - from 0 to 50. The calculation time of the statistical functions of the R language has been carried out using the microbenchmark library. The calculation time of the MQL5 functions has been measured with the GetMicrosecondCount() function. The TestStatBenchmark.mq5 calculation script can be found under the terminal_data_folder\MQL5\Scripts\UnitTests\Stat. The script for the R and results of calculation speed measurements are provided in the Appendix.

The calculations have been made on Intel Core i7-4790, CPU 3.6 Ghz, 16 GB RAM, Windows 10 x64.

The results of calculation time measurements (in microseconds, µs) are shown in Table 3.

No.	Distribution	MQL5 time for calculating the PDF (µs)	R time for calculating the PDF (µs)	PDF R/MQL5	MQL5 time for calculating the CDF (µs)	R time for calculating the CDF (µs)	CDF R/MQL5	MQL5 time for calculating the quantiles (µs)	R time for calculating the quantiles (µs)	Quantile R/MQL5	MQL5 time for generating random numbers (µs)	R time for generating random numbers (µs)	Random R/MQL5
1	Binomial	4.39	11.663	2.657	13.65	25.316	1.855	50.18	66.845	1.332	318.73	1816.463	5.699
2	Beta	1.74	17.352	9.972	4.76	15.076	3.167	48.72	129.992	2.668	688.81	1723.45	2.502
3	Gamma	1.31	8.251	6.347	8.09	14.792	1.828	50.83	64.286	1.265	142.84	1281.707	8.973
60	Cauchy	0.45	1.423	3.162	1.33	15.078	11.34	1.37	2.845	2.077	224.19	588.517	2.625
5	Exponential	0.85	3.13	3.682	0.77	2.845	3.695	0.53	2.276	4.294	143.18	389.406	2.72
6	Uniform	0.42	2.561	6.098	0.45	1.423	3.162	0.18	2.846	15.81	40.3	247.467	6.141
7	Geometric	2.3	5.121	2.227	2.12	4.552	2.147	0.81	5.407	6.675	278	1078.045	3.879
8	Hypergeometric	1.85	11.095	5.997	0.9	8.819	9.799	0.75	9.957	13.28	302.55	880.356	2.91
9	Logistic	1.27	4.267	3.36	1.11	4.267	3.844	0.71	3.13	4.408	178.65	626.632	3.508
10	Weibull	2.99	5.69	1.903	2.74	4.268	1.558	2.64	6.828	2.586	536.37	1558.472	2.906
11	Poisson	2.91	5.974	2.053	6.26	8.534	1.363	3.43	13.085	3.815	153.59	303.219	1.974
12	F	3.86	10.241	2.653	9.94	22.472	2.261	65.47	135.396	2.068	1249.22	1801.955	1.442
13	Chi Square	2.47	5.974	2.419	7.71	13.37	1.734	44.11	61.725	1.399	210.24	1235.059	5.875
14	Noncentral ChiSquare	8.05	14.223	1.767	45.61	209.068	4.584	220.66	10342.96	46.873	744.45	1997.653	2.683
15	Noncentral F	19.1	28.446	1.489	14.67	46.935	3.199	212.21	2561.991	12.073	1848.9	2912.141	1.575
16	Noncentral Beta	16.3	26.739	1.64	10.48	43.237	4.126	153.66	2290.915	14.909	2686.82	2839.893	1.057
17	Negative Binomial	6.13	11.094	1.81	12.21	19.627	1.607	14.05	60.019	4.272	1130.39	1936.498	1.713
18	Normal	1.15	4.267	3.71	0.81	3.983	4.917	0.7	2.277	3.253	293.7	696.321	2.371
19	Lognormal	1.99	5.406	2.717	3.19	8.819	2.765	3.18	6.259	1.968	479.75	1269.761	2.647
20	T	2.32	11.663	5.027	8.01	19.059	2.379	50.23	58.596	1.167	951.58	1425.92	1.498
21	Noncentral T	38.47	86.757	2.255	27.75	39.823	1.435	1339.51	1930.524	1.441	1550.27	1699.84	1.096
			<PDF R/MQL5>	3.474		<CDF R/MQL5>	3.465		<Quantile R/MQL5>	7.03		<Random R/MQL5>	3.13

Table 4. Calculation times of the statistical functions in R and MQL5 (in microseconds)

The minimum time values have been taken for R, and the mean values (pdf_mean, cdf_mean, quantile_mean, random_mean) have been taken for MQL5.

Table 3 shows that even under such conditions, calculations of the statistical library functions in MQL5 are performed several times faster than those in R. On average, MQL5 computes 3 to 7 times faster than R, even taking into account that the compared versions of the R functions are actually written in C++.

In practice, the MQL5 compiler turned out to be much faster than C++ implementations of the functions in R, which shows the high quality of our developments. Translation of programs from R to MQL5 can give a significant boost in speed, and there will be no need to use a third-party DLL.

6. Detected calculation errors in R

During the testing of R, an error in the calculation of quantiles of the noncentral t-distribution has been detected.

For example:

> n <- 10
> k <- seq(0,1,by=1/n)
> nt_pdf<-dt(k, 10,8, log = FALSE)
> nt_cdf<-pt(k, 10,8, log = FALSE)
> nt_quantile<-qt(nt_cdf, 10,8, log = FALSE)
> nt_pdf
 [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e-13
 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11
> nt_cdf
 [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13
 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12
> k
 [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
> nt_quantile
 [1]           -Inf -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154
 [7] -1.340781e+154   7.000000e-01   8.000000e-01   9.000000e-01   1.000000e+00

For calculating the Student's t-distribution the R language uses the AS 243 algorithm, proposed by Lenth [6]. The advantage of this method is a fast recursive computation of infinite series members with an incomplete beta function. But the article [7] had shown that, due to a mistake in accuracy estimation during summation of the series members, this algorithm leads to errors (table 2 in the article [7]), especially for large values of the delta parameter for noncentrality. Authors of the article [7] have proposed a corrected algorithm for recursive calculation of probability of the noncentral t-distribution.

The MQL5 statistical library uses the correct algorithm for calculating the probabilities suggested in article [7], which provides accurate results.

It should be noted that in the R language, the definition of probability densities for the Gamma, Chi-Square and Noncentral Chi-Square distributions at point x=0 leads to infinite expressions:

> dgamma(0,0.5,1)
[1] Inf
> dchisq(0,df=0.5,ncp=1)
[1] Inf
> dchisq(0,df=0.5,ncp=0)
[1] Inf

Thus, in the R language, limit values are used in the definition of probability density at point x=0. Despite the infinity at point x=0, in this case the divergencies do not occur during integration, and the integrals of the density are finite.

When calculating the probabilities (for example, for x=0.1), they match the values from Wolfram Alpha (Gamma, ChiSquare, NoncentralChiSquare).

> pgamma(0.1,0.5,1)
[1] 0.3452792
> pchisq(0.1,df=0.5,ncp=0)
[1] 0.5165553
> pchisq(0.1,df=0.5,ncp=1)
[1] 0.3194965

The Wolfram Alpha (Mathematica) and Matlab make use of a different definition of the density at point x=0:

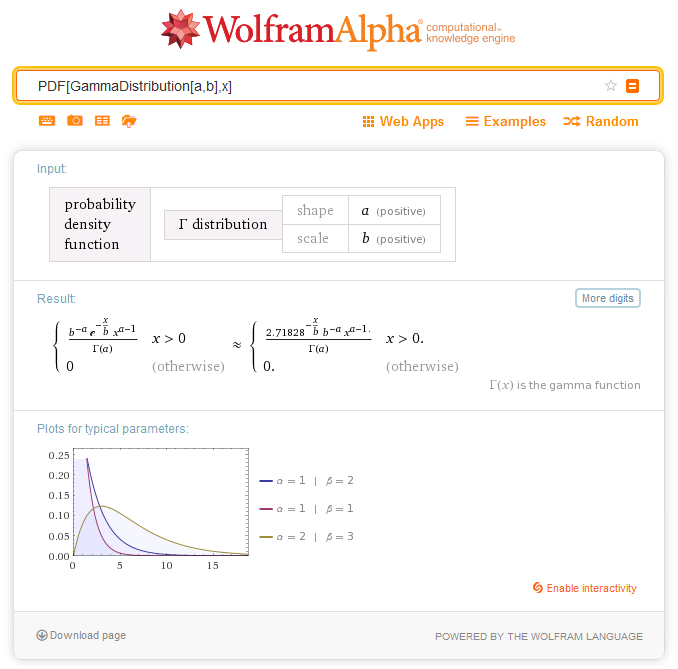
Fig. 3. Definition of the probability density of the Gamma distribution in Wolfram Alpha

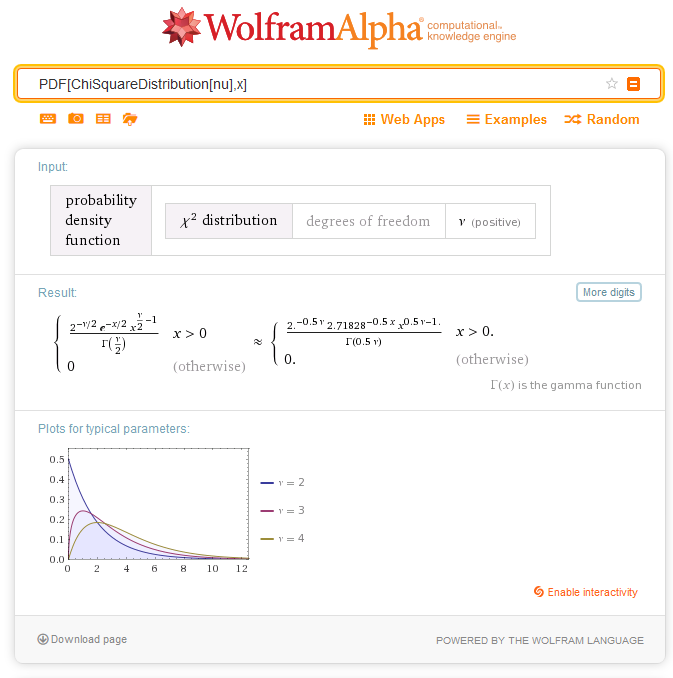
Fig. 4. Definition of the probability density of the Chi-Square distribution in Wolfram Alpha

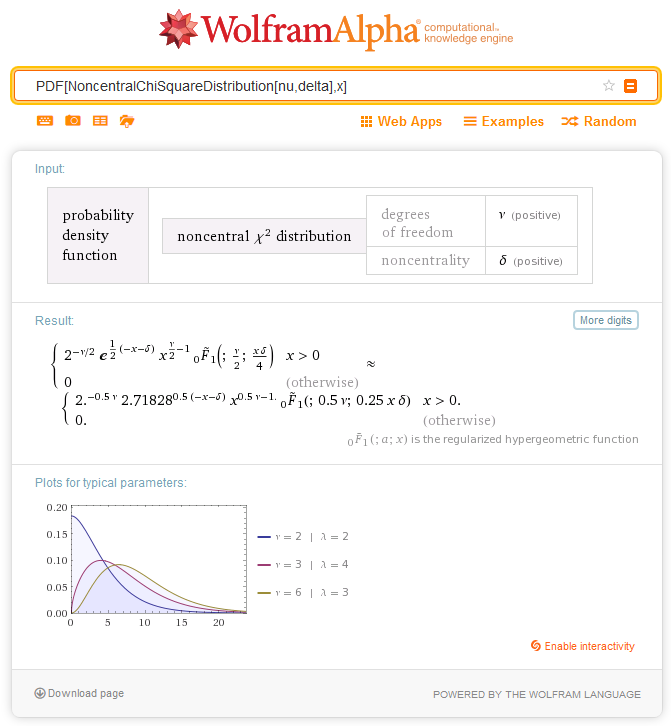
Fig. 5. Definition of the probability density of the Noncentral Chi-Square distribution in Wolfram Alpha

In the MQL5 statistical library, the densities of these distributions at point x=0 are considered to be equal to zero by definition.

In order to ensure the calculation accuracy and to allow third-party developers to test the quality of the library, multiple unit test scripts are included in the standard delivery. They can be found in the /Scripts/UnitTests/Stat folder.

Conclusion

The article considers the main functions of the MQL5 statistical library.

They allow to perform calculation of the statistical characteristics of data and to work with the basic statistical distributions implemented in the R language. In addition, the library also contains the functions for calculating theoretical moments of distributions, which allow to evaluate the degree of conformity of the real distribution to the modeled one.

Due to the high performance of the new 64-bit compiler of the MQL5, complex mathematical calculations are carried out several times faster than in R, which significantly facilitates the process of research.

References

1. The R Project for Statistical Computing.
2. N. Balakrishnan, N. L. Johnson, S. Kotz  "Continuous Univariate Distributions: Volume 1." Wiley-Interscience, 1994.
3. N. Balakrishnan, N. L. Johnson, S. Kotz  "Continuous Univariate Distributions: Volume 2." Wiley-Interscience, 2000.
4. N. L. Johnson, S. Kotz, A. W. Kemp  "Univariate Discrete Distributions", Wiley-Interscience, 2005.
5. Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions", 4th Edition, John Wiley and Sons, 2011.
6. Lenth, R.V., "Cumulative distribution function of the noncentral t distribution", Appled Statistics,  vol. 38 (1989), 185–189.
7. D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient",  Computational Statistics & Data Analysis, 43, (2003), 249-267

Appendix. Results of measuring the calculation time of the statistical functions

The script for evaluating the calculation time of the statistical functions in R and its operation results are provided in the Appendix, as well as the results of the TestStatBenchmark.mq5 script operation.

Script in R:

library(microbenchmark)
n <- 50
k <- seq(0,n,by=1)
binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
print(binomial_pdf)
print(binomial_cdf)
print(binomial_quantile)
print(binomial_random)

n <- 50
k <- seq(0,1,by=1/n)
beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
print(beta_pdf)
print(beta_cdf)
print(beta_quantile)
print(beta_random)

n <- 50
k <- seq(0,1,by=1/n)
gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
print(gamma_pdf)
print(gamma_cdf)
print(gamma_quantile)
print(gamma_random)

n <- 50
k <- seq(0,1,by=1/n)
cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
print(cauchy_pdf)
print(cauchy_cdf)
print(cauchy_quantile)
print(cauchy_random)

n <- 50
k <- seq(0,1,by=1/n)
exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
exponential_random <- microbenchmark(random<-rexp(10000, 2))
print(exponential_pdf)
print(exponential_cdf)
print(exponential_quantile)
print(exponential_random)


n <- 50
k <- seq(0,1,by=1/n)
uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
print(uniform_pdf)
print(uniform_cdf)
print(uniform_quantile)
print(uniform_random)


n <- 50
k <- seq(0,n,by=1)
geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
print(geometric_pdf)
print(geometric_cdf)
print(geometric_quantile)
print(geometric_random)

n <- 50
k <- seq(0,n,by=1)
hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
print(hypergeometric_pdf)
print(hypergeometric_cdf)
print(hypergeometric_quantile)
print(hypergeometric_random)

n <- 50
k <- seq(0,1,by=1/n)
logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
print(logistic_pdf)
print(logistic_cdf)
print(logistic_quantile)
print(logistic_random)

n <- 50
k <- seq(0,1,by=1/n)
weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
print(weibull_pdf)
print(weibull_cdf)
print(weibull_quantile)
print(weibull_random)

n <- 50
k <- seq(0,n,by=1)
poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
poisson_random <- microbenchmark(random<-rpois(10000, 1))
print(poisson_pdf)
print(poisson_cdf)
print(poisson_quantile)
print(poisson_random)

n <- 50
k <- seq(0,1,by=1/n)
f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
f_random <- microbenchmark(random<-rf(10000, 10,20))
print(f_pdf)
print(f_cdf)
print(f_quantile)
print(f_random)

n <- 50
k <- seq(0,1,by=1/n)
chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
print(chisquare_pdf)
print(chisquare_cdf)
print(chisquare_quantile)
print(chisquare_random)

n <- 50
k <- seq(0,1,by=1/n)
nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
print(nchisquare_pdf)
print(nchisquare_cdf)
print(nchisquare_quantile)
print(nchisquare_random)

n <- 50
k <- seq(0,1,by=1/n)
nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
print(nf_pdf)
print(nf_cdf)
print(nf_quantile)
print(nf_random)

n <- 50
k <- seq(0,1,by=1/n)
nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
print(nbeta_pdf)
print(nbeta_cdf)
print(nbeta_quantile)
print(nbeta_random)

n <- 50
k <- seq(0,n,by=1)
nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
print(nbinom_pdf)
print(nbinom_cdf)
print(nbinom_quantile)
print(nbinom_random)

n <- 50
k <- seq(0,1,by=1/n)
normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
print(normal_pdf)
print(normal_cdf)
print(normal_quantile)
print(normal_random)

n <- 50
k <- seq(0,1,by=1/n)
lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
print(lognormal_pdf)
print(lognormal_cdf)
print(lognormal_quantile)
print(lognormal_random)

n <- 50
k <- seq(0,1,by=1/n)
t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
t_random <- microbenchmark(random<-rt(10000, 8))
print(t_pdf)
print(t_cdf)
print(t_quantile)
print(t_random)

n <- 50
k <- seq(0,1,by=1/n)
nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
nt_random <- microbenchmark(random<-rt(10000, 10,1))
print(nt_pdf)
print(nt_cdf)
print(nt_quantile)
print(nt_random)

Result:

R version 3.2.5 (2016-04-14) -- "Very, Very Secure Dishes"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-w64-mingw32/x64 (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.

R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.

Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.

[Workspace loaded from ~/Test/111/.RData]

> library(microbenchmark)
> n <- 50
> k <- seq(0,n,by=1)
> binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
> binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
> binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
> binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
> print(binomial_pdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 pdf <- dbinom(k, 50, 0.6, log = FALSE) 11.663 11.948 13.37888 12.233 12.233 47.503   100
> print(binomial_cdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 cdf <- pbinom(k, 50, 0.6, log = FALSE) 25.316 25.602 29.63195 25.886 35.557 93.868   100
> print(binomial_quantile)
Unit: microseconds
                                          expr    min    lq     mean median     uq     max neval
 quantile <- qbinom(cdf, 50, 0.6, log = FALSE) 66.845 67.13 72.09098 67.699 73.672 130.276   100
> print(binomial_random)
Unit: milliseconds
                             expr      min      lq     mean   median       uq      max neval
 random <- rbinom(10000, 50, 0.6) 1.816463 1.89056 1.948185 1.929814 1.989262 2.308835   100
> 
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
> beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
> beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
> beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
> print(beta_pdf)
Unit: microseconds
                               expr    min     lq     mean median     uq     max neval
 pdf <- dbeta(k, 2, 4, log = FALSE) 17.352 17.637 19.99512 17.638 18.206 109.797   100
> print(beta_cdf)
Unit: microseconds
                               expr    min     lq     mean median      uq    max neval
 cdf <- pbeta(k, 2, 4, log = FALSE) 15.076 15.361 16.83489 15.646 15.9295 75.379   100
> print(beta_quantile)
Unit: microseconds
                                      expr     min      lq     mean   median     uq     max neval
 quantile <- qbeta(cdf, 2, 4, log = FALSE) 129.992 130.277 140.8325 131.4145 143.93 201.672   100
> print(beta_random)
Unit: milliseconds
                           expr     min       lq     mean   median       uq      max neval
 random <- rbeta(10000, 2, 4, ) 1.72345 1.794132 1.862292 1.836515 1.901226 2.823963   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
> gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
> gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
> gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
> print(gamma_pdf)
Unit: microseconds
                                expr   min     lq     mean median    uq     max neval
 pdf <- dgamma(k, 1, 1, log = FALSE) 8.251 8.8195 10.92684  9.104 9.389 122.312   100
> print(gamma_cdf)
Unit: microseconds
                                expr    min     lq     mean median     uq     max neval
 cdf <- pgamma(k, 1, 1, log = FALSE) 14.792 15.646 20.43306 20.055 21.334 106.099   100
> print(gamma_quantile)
Unit: microseconds
                                       expr    min     lq     mean median    uq     max neval
 quantile <- qgamma(cdf, 1, 1, log = FALSE) 64.286 64.854 70.09419 65.139 67.13 162.988   100
> print(gamma_random)
Unit: milliseconds
                          expr      min       lq     mean   median       uq      max neval
 random <- rgamma(10000, 1, 1) 1.281707 1.330347 1.410961 1.362631 1.421226 2.322204   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
> cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
> cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
> cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
> print(cauchy_pdf)
Unit: microseconds
                                 expr   min    lq   mean median    uq    max neval
 pdf <- dcauchy(k, 2, 1, log = FALSE) 1.423 1.708 2.8431  1.709 2.278 67.415   100
> print(cauchy_cdf)
Unit: microseconds
                                expr    min     lq     mean median     uq    max neval
 cdf <- pgamma(k, 2, 1, log = FALSE) 15.078 15.646 16.51914  15.93 16.215 33.281   100
> print(cauchy_quantile)
Unit: microseconds
                                        expr   min   lq   mean median    uq    max neval
 quantile <- qcauchy(cdf, 2, 1, log = FALSE) 2.845 3.13 3.8044  3.131 3.415 56.606   100
> print(cauchy_random)
Unit: microseconds
                           expr     min      lq     mean   median      uq      max neval
 random <- rcauchy(10000, 2, 1) 588.517 615.823 663.8658 637.7255 674.845 1520.356   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
> exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
> exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
> exponential_random <- microbenchmark(random<-rexp(10000, 2))
> print(exponential_pdf)
Unit: microseconds
                           expr  min    lq    mean median    uq    max neval
 pdf <- dexp(k, 2, log = FALSE) 3.13 3.414 4.08887  3.415 3.415 67.699   100
> print(exponential_cdf)
Unit: microseconds
                           expr   min   lq    mean median     uq    max neval
 cdf <- pexp(k, 2, log = FALSE) 2.845 3.13 4.38756  3.414 3.5565 58.597   100
> print(exponential_quantile)
Unit: microseconds
                                  expr   min    lq    mean median    uq    max neval
 quantile <- qexp(cdf, 2, log = FALSE) 2.276 2.561 3.80729 2.5615 2.846 44.659   100
> print(exponential_random)
Unit: microseconds
                     expr     min       lq     mean   median       uq      max neval
 random <- rexp(10000, 2) 389.406 408.8895 440.9583 418.4185 444.8715 1371.875   100
> 
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
> uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
> uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
> uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
> print(uniform_pdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 pdf <- dunif(k, 0, 10, log = FALSE) 2.561 2.846 3.78734   3.13 3.131 66.277   100
> print(uniform_cdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 cdf <- punif(k, 0, 10, log = FALSE) 1.423 1.708 2.41635  1.992 1.993 53.477   100
> print(uniform_quantile)
Unit: microseconds
                                       expr   min    lq    mean median     uq    max neval
 quantile <- qunif(cdf, 0, 10, log = FALSE) 2.846 3.131 5.13561  3.415 3.6995 82.774   100
> print(uniform_random)
Unit: microseconds
                          expr     min       lq     mean   median       uq      max neval
 random <- runif(10000, 0, 10) 247.467 258.7035 317.1567 279.6095 357.2635 1267.769   100
> 
> 
> n <- 50
> k <- seq(0,n,by=1)
> geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
> geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
> geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
> geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
> print(geometric_pdf)
Unit: microseconds
                              expr   min    lq    mean median    uq    max neval
 pdf <- dgeom(k, 0.3, log = FALSE) 5.121 5.122 6.14258  5.406 5.406 60.304   100
> print(geometric_cdf)
Unit: microseconds
                              expr   min    lq    mean median     uq    max neval
 cdf <- pgeom(k, 0.3, log = FALSE) 4.552 4.836 5.50548  4.837 5.1215 46.081   100
> print(geometric_quantile)
Unit: microseconds
                                     expr   min    lq    mean median    uq    max neval
 quantile <- qgeom(cdf, 0.3, log = FALSE) 5.407 5.974 7.12107  5.975 6.259 71.681   100
> print(geometric_random)
Unit: milliseconds
                        expr      min       lq     mean   median       uq      max neval
 random <- rgeom(10000, 0.3) 1.078045 1.127681 1.192608 1.156125 1.199361 1.604267   100
> 
> n <- 50
> k <- seq(0,n,by=1)
> hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
> hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
> hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
> hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
> print(hypergeometric_pdf)
Unit: microseconds
                                      expr    min     lq     mean median     uq     max neval
 pdf <- dhyper(k, 12, 38, 11, log = FALSE) 11.095 13.939 17.07667 14.224 14.935 101.548   100
> print(hypergeometric_cdf)
Unit: microseconds
                                      expr   min    lq     mean median     uq   max neval
 cdf <- phyper(k, 12, 38, 11, log = FALSE) 8.819 9.387 12.60515  9.672 12.517 62.01   100
> print(hypergeometric_quantile)
Unit: microseconds
                                             expr   min      lq     mean median     uq    max neval
 quantile <- qhyper(cdf, 12, 38, 11, log = FALSE) 9.957 10.3835 13.00618  10.81 11.948 64.286   100
> print(hypergeometric_random)
Unit: microseconds
                                expr     min       lq     mean   median       uq      max neval
 random <- rhyper(10000, 12, 38, 11) 880.356 938.9515 993.8324 963.9835 996.8365 1375.289   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
> logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
> logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
> logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
> print(logistic_pdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 pdf <- dlogis(k, 1, 2, log = FALSE) 4.267 4.552 5.94354  4.553 4.837 53.477   100
> print(logistic_cdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 cdf <- plogis(k, 1, 2, log = FALSE) 4.267 4.552 5.96056  4.837 4.837 96.428   100
> print(logistic_quantile)
Unit: microseconds
                                       expr  min    lq   mean median    uq    max neval
 quantile <- qlogis(cdf, 1, 2, log = FALSE) 3.13 3.415 4.1742  3.415 3.699 56.036   100
> print(logistic_random)
Unit: microseconds
                          expr     min      lq     mean   median      uq      max neval
 random <- rlogis(10000, 1, 2) 626.632 649.956 696.2128 675.2725 715.805 1589.191   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
> weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
> weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
> weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
> print(weibull_pdf)
Unit: microseconds
                                  expr  min    lq    mean median    uq    max neval
 pdf <- dweibull(k, 5, 1, log = FALSE) 5.69 5.974 7.21775  5.975 6.259 85.619   100
> print(weibull_cdf)
Unit: microseconds
                                  expr   min    lq    mean median    uq    max neval
 cdf <- pweibull(k, 5, 1, log = FALSE) 4.268 4.552 7.83782 4.8365 7.966 90.455   100
> print(weibull_quantile)
Unit: microseconds
                                         expr   min    lq    mean median    uq    max neval
 quantile <- qweibull(cdf, 5, 1, log = FALSE) 6.828 7.112 7.96587  7.113 7.397 48.641   100
> print(weibull_random)
Unit: milliseconds
                            expr      min      lq     mean   median       uq      max neval
 random <- rweibull(10000, 5, 1) 1.558472 1.59744 1.659753 1.632853 1.679502 2.616603   100
> 
> n <- 50
> k <- seq(0,n,by=1)
> poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
> poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
> poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
> poisson_random <- microbenchmark(random<-rpois(10000, 1))
> print(poisson_pdf)
Unit: microseconds
                            expr   min    lq    mean median    uq    max neval
 pdf <- dpois(k, 1, log = FALSE) 5.974 6.543 7.30316  6.544 6.828 54.046   100
> print(poisson_cdf)
Unit: microseconds
                            expr   min    lq     mean median    uq    max neval
 cdf <- ppois(k, 1, log = FALSE) 8.534 8.819 10.25846  9.104 9.388 64.286   100
> print(poisson_quantile)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 quantile <- qpois(cdf, 1, log = FALSE) 13.085 13.086 14.37438  13.37 13.654 61.157   100
> print(poisson_random)
Unit: microseconds
                      expr     min       lq     mean  median      uq     max neval
 random <- rpois(10000, 1) 303.219 314.8815 327.5787 324.552 341.335 373.477   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
> f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
> f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
> f_random <- microbenchmark(random<-rf(10000, 10,20))
> print(f_pdf)
Unit: microseconds
                              expr    min    lq     mean median     uq    max neval
 pdf <- df(k, 10, 20, log = FALSE) 10.241 10.81 12.43159 10.811 11.095 71.112   100
> print(f_cdf)
Unit: microseconds
                              expr    min     lq     mean median      uq    max neval
 cdf <- pf(k, 10, 20, log = FALSE) 22.472 22.757 25.66972 23.041 23.3265 86.189   100
> print(f_quantile)
Unit: microseconds
                                     expr     min     lq     mean   median      uq     max neval
 quantile <- qf(cdf, 10, 20, log = FALSE) 135.396 136.25 166.7057 157.7255 186.171 255.717   100
> print(f_random)
Unit: milliseconds
                        expr      min       lq     mean   median      uq      max neval
 random <- rf(10000, 10, 20) 1.801955 1.889706 1.947645 1.929528 1.98272 2.725546   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
> chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
> chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
> chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
> print(chisquare_pdf)
Unit: microseconds
                             expr   min    lq    mean median    uq    max neval
 pdf <- dchisq(k, 2, log = FALSE) 5.974 6.259 7.06416 6.4015 6.544 52.339   100
> print(chisquare_cdf)
Unit: microseconds
                             expr   min     lq     mean median    uq    max neval
 cdf <- pchisq(k, 2, log = FALSE) 13.37 13.655 15.46392 13.655 13.94 99.841   100
> print(chisquare_quantile)
Unit: microseconds
                                    expr    min      lq     mean  median    uq     max neval
 quantile <- qchisq(cdf, 2, log = FALSE) 61.725 62.2945 68.40176 62.7215 72.25 132.553   100
> print(chisquare_random)
Unit: milliseconds
                       expr      min      lq    mean   median       uq      max neval
 random <- rchisq(10000, 2) 1.235059 1.29408 1.38993 1.333903 1.401743 2.205582   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
> nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
> nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
> nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
> print(nchisquare_pdf)
Unit: microseconds
                                expr    min     lq    mean median      uq    max neval
 pdf <- dchisq(k, 2, 1, log = FALSE) 14.223 14.509 17.3866 14.793 15.6455 37.548   100
> print(nchisquare_cdf)
Unit: microseconds
                                expr     min     lq     mean   median      uq     max neval
 cdf <- pchisq(k, 2, 1, log = FALSE) 209.068 210.49 231.6357 223.1475 240.499 309.193   100
> print(nchisquare_quantile)
Unit: milliseconds
                                       expr      min       lq     mean   median       uq      max neval
 quantile <- qchisq(cdf, 2, 1, log = FALSE) 10.34296 10.65955 10.90239 10.83733 11.02563 12.31558   100
> print(nchisquare_random)
Unit: milliseconds
                          expr      min       lq     mean   median       uq      max neval
 random <- rchisq(10000, 2, 1) 1.997653 2.073457 2.187417 2.114845 2.183111 3.134576   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
> nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
> nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
> nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
> print(nf_pdf)
Unit: microseconds
                                 expr    min     lq     mean median     uq    max neval
 pdf <- df(k, 10, 20, 2, log = FALSE) 28.446 30.153 34.12338 30.438 31.291 68.836   100
> print(nf_cdf)
Unit: microseconds
                                 expr    min      lq     mean median     uq     max neval
 cdf <- pf(k, 10, 20, 2, log = FALSE) 46.935 61.8685 64.53899 63.433 65.708 106.953   100
> print(nf_quantile)
Unit: milliseconds
                                        expr      min       lq     mean  median       uq      max neval
 quantile <- qf(cdf, 10, 20, 2, log = FALSE) 2.561991 2.640355 2.719223 2.68999 2.744461 3.737598   100
> print(nf_random)
Unit: milliseconds
                           expr      min       lq     mean   median       uq      max neval
 random <- rf(10000, 10, 20, 2) 2.912141 2.989225 3.100073 3.035163 3.110825 4.062433   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
> nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
> nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
> nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
> print(nbeta_pdf)
Unit: microseconds
                                  expr    min     lq     mean median      uq    max neval
 pdf <- dbeta(k, 2, 4, 1, log = FALSE) 26.739 27.308 31.31301 27.592 30.5795 56.891   100
> print(nbeta_cdf)
Unit: microseconds
                                  expr    min     lq     mean median      uq     max neval
 cdf <- pbeta(k, 2, 4, 1, log = FALSE) 43.237 43.806 55.11814 56.321 57.7435 167.255   100
> print(nbeta_quantile)
Unit: milliseconds
                                         expr      min       lq     mean   median      uq      max neval
 quantile <- qbeta(cdf, 2, 4, 1, log = FALSE) 2.290915 2.375111 2.440959 2.431146 2.49927 2.644764   100
> print(nbeta_random)
Unit: milliseconds
                            expr      min       lq     mean   median       uq      max neval
 random <- rbeta(10000, 2, 4, 1) 2.839893 3.002737 3.143906 3.073848 3.150932 4.302789   100
> 
> n <- 50
> k <- seq(0,n,by=1)
> nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
> nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
> nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
> nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
> print(nbinom_pdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 pdf <- dnbinom(k, 2, 0.5, log = FALSE) 11.094 11.379 13.37031 11.664 11.948 78.508   100
> print(nbinom_cdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq     max neval
 cdf <- pnbinom(k, 2, 0.5, log = FALSE) 19.627 19.913 22.94469 20.197 20.482 130.277   100
> print(nbinom_quantile)
Unit: microseconds
                                          expr    min     lq     mean median     uq     max neval
 quantile <- qnbinom(cdf, 2, 0.5, log = FALSE) 60.019 60.588 69.73866 61.442 74.099 122.028   100
> print(nbinom_random)
Unit: milliseconds
                             expr      min       lq     mean   median       uq      max neval
 random <- rnbinom(10000, 2, 0.5) 1.936498 2.029226 2.086237 2.072035 2.125084 2.354061   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
> normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
> normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
> normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
> print(normal_pdf)
Unit: microseconds
                               expr   min    lq   mean median    uq    max neval
 pdf <- dnorm(k, 1, 1, log = FALSE) 4.267 4.552 5.7927  4.553 4.837 75.663   100
> print(normal_cdf)
Unit: microseconds
                               expr   min    lq    mean median    uq    max neval
 cdf <- pnorm(k, 1, 1, log = FALSE) 3.983 4.269 5.94911  4.553 4.979 50.632   100
> print(normal_quantile)
Unit: microseconds
                                      expr   min    lq    mean median    uq    max neval
 quantile <- qnorm(cdf, 1, 1, log = FALSE) 2.277 2.561 3.42042  2.845 2.846 45.227   100
> print(normal_random)
Unit: microseconds
                         expr     min      lq     mean   median       uq     max neval
 random <- rnorm(10000, 1, 1) 696.321 728.747 779.1994 749.7965 778.3835 1541.12   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
> lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
> lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
> lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
> print(lognormal_pdf)
Unit: microseconds
                                    expr   min   lq    mean median    uq    max neval
 pdf <- dlnorm(k, 0.5, 0.6, log = FALSE) 5.406 5.69 6.89638  5.975 6.259 50.917   100
> print(lognormal_cdf)
Unit: microseconds
                                    expr   min    lq    mean median      uq    max neval
 cdf <- plnorm(k, 0.5, 0.6, log = FALSE) 8.819 9.387 12.3463 9.3885 12.6595 71.681   100
> print(lognormal_quantile)
Unit: microseconds
                                           expr   min    lq    mean median    uq    max neval
 quantile <- qlnorm(cdf, 0.5, 0.6, log = FALSE) 6.259 6.544 7.38277  6.544 6.828 58.881   100
> print(lognormal_random)
Unit: milliseconds
                              expr      min       lq     mean   median       uq      max neval
 random <- rlnorm(10000, 0.5, 0.6) 1.269761 1.329209 1.380386 1.362632 1.401743 2.247395   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
> t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
> t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
> t_random <- microbenchmark(random<-rt(10000, 8))
> print(t_pdf)
Unit: microseconds
                         expr    min     lq     mean median      uq    max neval
 pdf <- dt(k, 8, log = FALSE) 11.663 12.233 15.71413 12.517 16.0725 76.517   100
> print(t_cdf)
Unit: microseconds
                         expr    min      lq     mean median     uq     max neval
 cdf <- pt(k, 8, log = FALSE) 19.059 20.6235 23.23485  21.05 21.619 127.717   100
> print(t_quantile)
Unit: microseconds
                                expr    min     lq     mean median    uq     max neval
 quantile <- qt(cdf, 8, log = FALSE) 58.596 58.882 64.84339 59.166 62.01 151.611   100
> print(t_random)
Unit: milliseconds
                   expr     min       lq     mean  median       uq     max neval
 random <- rt(10000, 8) 1.42592 1.480676 1.553132 1.51424 1.569565 2.44679   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
> nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
> nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
> nt_random <- microbenchmark(random<-rt(10000, 10,1))
> print(nt_pdf)
Unit: microseconds
                             expr    min     lq     mean median      uq     max neval
 pdf <- dt(k, 10, 1, log = FALSE) 86.757 88.037 92.88671 89.317 91.4505 130.276   100
> print(nt_cdf)
Unit: microseconds
                             expr    min      lq     mean  median     uq    max neval
 cdf <- pt(k, 10, 1, log = FALSE) 39.823 40.2505 44.51695 40.6765 49.352 70.829   100
> print(nt_quantile)
Unit: milliseconds
                                    expr      min       lq     mean median       uq      max neval
 quantile <- qt(cdf, 10, 1, log = FALSE) 1.930524 1.981866 2.038755 2.0224 2.079715 2.594987   100
> print(nt_random)
Unit: milliseconds
                       expr     min       lq     mean   median       uq      max neval
 random <- rt(10000, 10, 1) 1.69984 1.764693 1.867469 1.814044 1.893263 2.856959   100

Result of the TestStatBenchmark.mq5 operation script:

IG    0    13:06:15.252    TestStatBenchmark (EURUSD,H1)    Unit tests for Package Statistic Benchmark
PP    0    13:06:15.252    TestStatBenchmark (EURUSD,H1)   
KJ    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds):      pdf_mean=4.39,      pdf_median=4.00,      pdf_min=3.00,      pdf_max=40.00,       pdf_stddev=2.21,       pdf_avgdev=0.95
MS    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds):      cdf_mean=13.65,      cdf_median=12.00,      cdf_min=11.00,      cdf_max=54.00,       cdf_stddev=4.09,       cdf_avgdev=2.37
GF    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds): quantile_mean=50.18, quantile_median=45.00, quantile_min=43.00, quantile_max=108.00,  quantile_stddev=9.97,  quantile_avgdev=7.41
QO    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds):   random_mean=318.73,   random_median=312.00,   random_min=284.00,   random_max=478.00,    random_stddev=28.74,    random_avgdev=22.22
LP    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds):      pdf_mean=1.74,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=18.00,       pdf_stddev=1.07,       pdf_avgdev=0.53
EI    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds):      cdf_mean=4.76,      cdf_median=4.00,      cdf_min=3.00,      cdf_max=68.00,       cdf_stddev=3.07,       cdf_avgdev=1.19
LM    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds): quantile_mean=48.72, quantile_median=44.00, quantile_min=43.00, quantile_max=111.00,  quantile_stddev=10.21,  quantile_avgdev=6.96
QG    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds):   random_mean=688.81,   random_median=680.00,   random_min=625.00,   random_max=976.00,    random_stddev=43.92,    random_avgdev=31.81
HE    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds):      pdf_mean=1.31,      pdf_median=1.00,      pdf_min=1.00,      pdf_max=13.00,       pdf_stddev=0.82,       pdf_avgdev=0.47
GL    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds):      cdf_mean=8.09,      cdf_median=7.00,      cdf_min=7.00,      cdf_max=92.00,       cdf_stddev=3.67,       cdf_avgdev=1.40
CF    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds): quantile_mean=50.83, quantile_median=46.00, quantile_min=45.00, quantile_max=106.00,  quantile_stddev=9.27,  quantile_avgdev=6.72
GR    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds):   random_mean=142.84,   random_median=132.00,   random_min=128.00,   random_max=260.00,    random_stddev=19.73,    random_avgdev=15.32
QD    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds):      pdf_mean=0.45,      pdf_median=0.00,      pdf_min=0.00,      pdf_max=11.00,       pdf_stddev=0.85,       pdf_avgdev=0.54
QK    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds):      cdf_mean=1.33,      cdf_median=1.00,      cdf_min=1.00,      cdf_max=12.00,       cdf_stddev=0.81,       cdf_avgdev=0.48
MR    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds): quantile_mean=1.37, quantile_median=1.00, quantile_min=1.00, quantile_max=14.00,  quantile_stddev=0.89,  quantile_avgdev=0.51
IK    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds):   random_mean=224.19,   random_median=215.00,   random_min=200.00,   random_max=352.00,    random_stddev=26.86,    random_avgdev=20.34
PQ    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds):      pdf_mean=0.85,      pdf_median=1.00,      pdf_min=0.00,      pdf_max=18.00,       pdf_stddev=1.40,       pdf_avgdev=0.54
GK    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds):      cdf_mean=0.77,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=16.00,       cdf_stddev=0.94,       cdf_avgdev=0.47
HE    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds): quantile_mean=0.53, quantile_median=0.00, quantile_min=0.00, quantile_max=10.00,  quantile_stddev=0.78,  quantile_avgdev=0.54
HL    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds):   random_mean=143.18,   random_median=130.00,   random_min=128.00,   random_max=272.00,    random_stddev=21.58,    random_avgdev=16.98
LK    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds):      pdf_mean=0.42,      pdf_median=0.00,      pdf_min=0.00,      pdf_max=12.00,       pdf_stddev=0.82,       pdf_avgdev=0.52
CE    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds):      cdf_mean=0.45,      cdf_median=0.00,      cdf_min=0.00,      cdf_max=16.00,       cdf_stddev=0.96,       cdf_avgdev=0.55
LO    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds): quantile_mean=0.18, quantile_median=0.00, quantile_min=0.00, quantile_max=1.00,  quantile_stddev=0.38,  quantile_avgdev=0.29
GE    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds):   random_mean=40.30,   random_median=36.00,   random_min=35.00,   random_max=83.00,    random_stddev=7.61,    random_avgdev=5.41
OP    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds):      pdf_mean=2.30,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=14.00,       pdf_stddev=1.30,       pdf_avgdev=0.52
DK    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds):      cdf_mean=2.12,      cdf_median=2.00,      cdf_min=1.00,      cdf_max=18.00,       cdf_stddev=1.69,       cdf_avgdev=0.53
NE    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds): quantile_mean=0.81, quantile_median=1.00, quantile_min=0.00, quantile_max=10.00,  quantile_stddev=0.68,  quantile_avgdev=0.39
IL    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds):   random_mean=278.00,   random_median=271.00,   random_min=251.00,   random_max=429.00,    random_stddev=28.23,    random_avgdev=21.62
PG    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds):      pdf_mean=1.85,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=15.00,       pdf_stddev=1.07,       pdf_avgdev=0.48
CM    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds):      cdf_mean=0.90,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=17.00,       cdf_stddev=0.85,       cdf_avgdev=0.32
NP    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds): quantile_mean=0.75, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00,  quantile_stddev=0.96,  quantile_avgdev=0.48
FE    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds):   random_mean=302.55,   random_median=295.00,   random_min=272.00,   random_max=466.00,    random_stddev=30.20,    random_avgdev=22.99
ML    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds):      pdf_mean=1.27,      pdf_median=1.00,      pdf_min=0.00,      pdf_max=91.00,       pdf_stddev=3.04,       pdf_avgdev=0.56
DR    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds):      cdf_mean=1.11,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=17.00,       cdf_stddev=1.34,       cdf_avgdev=0.40
IH    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds): quantile_mean=0.71, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00,  quantile_stddev=0.79,  quantile_avgdev=0.47
GL    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds):   random_mean=178.65,   random_median=164.00,   random_min=162.00,   random_max=309.00,    random_stddev=24.09,    random_avgdev=17.94
MJ    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds):      pdf_mean=2.99,      pdf_median=3.00,      pdf_min=2.00,      pdf_max=17.00,       pdf_stddev=1.63,       pdf_avgdev=0.57
GD    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds):      cdf_mean=2.74,      cdf_median=3.00,      cdf_min=2.00,      cdf_max=19.00,       cdf_stddev=1.23,       cdf_avgdev=0.58
FO    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds): quantile_mean=2.64, quantile_median=2.00, quantile_min=2.00, quantile_max=19.00,  quantile_stddev=1.64,  quantile_avgdev=0.76
DJ    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds):   random_mean=536.37,   random_median=526.00,   random_min=483.00,   random_max=759.00,    random_stddev=46.99,    random_avgdev=34.40
HR    0    13:06:18.485    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds):      pdf_mean=2.91,      pdf_median=3.00,      pdf_min=2.00,      pdf_max=15.00,       pdf_stddev=1.40,       pdf_avgdev=0.58
IL    0    13:06:18.486    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds):      cdf_mean=6.26,      cdf_median=6.00,      cdf_min=5.00,      cdf_max=23.00,       cdf_stddev=2.38,       cdf_avgdev=1.07
HE    0    13:06:18.486    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds): quantile_mean=3.43, quantile_median=3.00, quantile_min=2.00, quantile_max=20.00,  quantile_stddev=1.48,  quantile_avgdev=0.68
DL    0    13:06:18.486    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds):   random_mean=153.59,   random_median=144.00,   random_min=138.00,   random_max=265.00,    random_stddev=18.57,    random_avgdev=13.99
IH    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds):      pdf_mean=3.86,      pdf_median=4.00,      pdf_min=3.00,      pdf_max=21.00,       pdf_stddev=1.78,       pdf_avgdev=0.76
GS    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds):      cdf_mean=9.94,      cdf_median=9.00,      cdf_min=7.00,      cdf_max=36.00,       cdf_stddev=3.82,       cdf_avgdev=2.15
OI    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds): quantile_mean=65.47, quantile_median=59.00, quantile_min=57.00, quantile_max=147.00,  quantile_stddev=12.99,  quantile_avgdev=9.64
DE    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds):   random_mean=1249.22,   random_median=1213.00,   random_min=1127.00,   random_max=1968.00,    random_stddev=117.69,    random_avgdev=72.17
EL    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds):      pdf_mean=2.47,      pdf_median=2.00,      pdf_min=2.00,      pdf_max=13.00,       pdf_stddev=1.32,       pdf_avgdev=0.65
JK    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds):      cdf_mean=7.71,      cdf_median=7.00,      cdf_min=7.00,      cdf_max=23.00,       cdf_stddev=1.91,       cdf_avgdev=0.88
KQ    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds): quantile_mean=44.11, quantile_median=41.00, quantile_min=40.00, quantile_max=120.00,  quantile_stddev=8.17,  quantile_avgdev=5.38
CL    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds):   random_mean=210.24,   random_median=196.00,   random_min=190.00,   random_max=437.00,    random_stddev=29.14,    random_avgdev=21.00
HD    0    13:06:21.098    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds):      pdf_mean=8.05,      pdf_median=8.00,      pdf_min=7.00,      pdf_max=24.00,       pdf_stddev=2.41,       pdf_avgdev=1.09
MR    0    13:06:21.098    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds):      cdf_mean=45.61,      cdf_median=42.00,      cdf_min=41.00,      cdf_max=97.00,       cdf_stddev=8.25,       cdf_avgdev=5.70
FN    0    13:06:21.098    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds): quantile_mean=220.66, quantile_median=211.50, quantile_min=196.00, quantile_max=362.00,  quantile_stddev=24.71,  quantile_avgdev=19.45
LI    0    13:06:21.099    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds):   random_mean=744.45,   random_median=728.00,   random_min=672.00,   random_max=1082.00,    random_stddev=62.42,    random_avgdev=43.24
RE    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds):      pdf_mean=19.10,      pdf_median=18.00,      pdf_min=16.00,      pdf_max=50.00,       pdf_stddev=4.67,       pdf_avgdev=2.64
FS    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds):      cdf_mean=14.67,      cdf_median=13.00,      cdf_min=12.00,      cdf_max=39.00,       cdf_stddev=3.94,       cdf_avgdev=2.44
EN    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds): quantile_mean=212.21, quantile_median=203.00, quantile_min=189.00, quantile_max=347.00,  quantile_stddev=24.37,  quantile_avgdev=19.30
EF    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds):   random_mean=1848.90,   random_median=1819.00,   random_min=1704.00,   random_max=2556.00,    random_stddev=118.75,    random_avgdev=78.66
EN    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds):      pdf_mean=16.30,      pdf_median=15.00,      pdf_min=14.00,      pdf_max=43.00,       pdf_stddev=4.32,       pdf_avgdev=2.43
EP    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds):      cdf_mean=10.48,      cdf_median=10.00,      cdf_min=8.00,      cdf_max=32.00,       cdf_stddev=3.02,       cdf_avgdev=1.72
ME    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds): quantile_mean=153.66, quantile_median=141.00, quantile_min=135.00, quantile_max=283.00,  quantile_stddev=20.83,  quantile_avgdev=16.16
QJ    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds):   random_mean=2686.82,   random_median=2649.00,   random_min=2457.00,   random_max=3753.00,    random_stddev=150.32,    random_avgdev=98.23
OO    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds):      pdf_mean=6.13,      pdf_median=6.00,      pdf_min=5.00,      pdf_max=24.00,       pdf_stddev=2.38,       pdf_avgdev=1.22
DG    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds):      cdf_mean=12.21,      cdf_median=11.00,      cdf_min=11.00,      cdf_max=33.00,       cdf_stddev=3.07,       cdf_avgdev=1.58
LJ    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds): quantile_mean=14.05, quantile_median=13.00, quantile_min=12.00, quantile_max=82.00,  quantile_stddev=4.81,  quantile_avgdev=2.28
EM    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds):   random_mean=1130.39,   random_median=1108.00,   random_min=1039.00,   random_max=1454.00,    random_stddev=69.41,    random_avgdev=51.70
GP    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds):      pdf_mean=1.15,      pdf_median=1.00,      pdf_min=0.00,      pdf_max=19.00,       pdf_stddev=1.34,       pdf_avgdev=0.45
OI    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds):      cdf_mean=0.81,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=17.00,       cdf_stddev=1.16,       cdf_avgdev=0.49
CN    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds): quantile_mean=0.70, quantile_median=1.00, quantile_min=0.00, quantile_max=13.00,  quantile_stddev=0.82,  quantile_avgdev=0.49
EG    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds):   random_mean=293.70,   random_median=281.00,   random_min=256.00,   random_max=537.00,    random_stddev=43.28,    random_avgdev=31.62
FD    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds):      pdf_mean=1.99,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=18.00,       pdf_stddev=1.48,       pdf_avgdev=0.48
PN    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds):      cdf_mean=3.19,      cdf_median=3.00,      cdf_min=2.00,      cdf_max=17.00,       cdf_stddev=1.61,       cdf_avgdev=0.64
DH    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds): quantile_mean=3.18, quantile_median=3.00, quantile_min=2.00, quantile_max=19.00,  quantile_stddev=1.77,  quantile_avgdev=0.64
NR    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds):   random_mean=479.75,   random_median=468.00,   random_min=428.00,   random_max=754.00,    random_stddev=48.26,    random_avgdev=34.30
FL    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds):      pdf_mean=2.32,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=15.00,       pdf_stddev=1.29,       pdf_avgdev=0.54
QE    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds):      cdf_mean=8.01,      cdf_median=7.00,      cdf_min=6.00,      cdf_max=39.00,       cdf_stddev=3.13,       cdf_avgdev=1.73
MM    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds): quantile_mean=50.23, quantile_median=45.00, quantile_min=44.00, quantile_max=113.00,  quantile_stddev=10.28,  quantile_avgdev=7.73
KG    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds):   random_mean=951.58,   random_median=931.00,   random_min=859.00,   random_max=1439.00,    random_stddev=78.14,    random_avgdev=49.72
CQ    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds):      pdf_mean=38.47,      pdf_median=35.00,      pdf_min=32.00,      pdf_max=164.00,       pdf_stddev=9.66,       pdf_avgdev=6.38
OO    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds):      cdf_mean=27.75,      cdf_median=25.00,      cdf_min=24.00,      cdf_max=80.00,       cdf_stddev=7.02,       cdf_avgdev=4.63
PF    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds): quantile_mean=1339.51, quantile_median=1306.00, quantile_min=1206.00, quantile_max=2262.00,  quantile_stddev=128.18,  quantile_avgdev=74.83
OR    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds):   random_mean=1550.27,   random_median=1520.00,   random_min=1418.00,   random_max=2317.00,    random_stddev=112.08,    random_avgdev=73.74
LQ    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)   
GH    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    21 of 21 passed