Regression models of the Scikit-learn Library and their export to ONNX

ONNX (Open Neural Network Exchange) is a format for describing and exchanging machine learning models, providing the capability to transfer models between different machine learning frameworks. In deep learning and neural networks, data types like float32 are frequently used. They are widely applied because they usually provide acceptable accuracy and efficiency for training deep learning models.

Some classical machine learning models are difficult to represent as ONNX operators. Therefore, additional ML operators (ai.onnx.ml) were introduced to implement them in ONNX. It's worth noting that according to the ONNX specification, the key operators in this set (LinearRegressor, SVMRegressor, TreeEnsembleRegressor) can accept various types of input data (tensor(float), tensor(double), tensor(int64), tensor(int32)), but they always return the type tensor(float) as output. The parameterization of these operators is also performed using floating-point numbers, which may limit the accuracy of calculations, especially if double precision numbers were used to define the parameters of the original model.

This can lead to a loss of accuracy when converting models or using different data types in the process of converting and processing data in ONNX. Much depends on the converter, as we will see later; some models manage to bypass these limitations and ensure full portability of ONNX models, allowing work with them in double precision without losing accuracy. It's important to consider these characteristics when working with models and their representation in ONNX, especially in cases where the accuracy of data representation matters.

Scikit-learn is one of the most popular and widely used libraries for machine learning in the Python community. It offers a wide range of algorithms, a user-friendly interface, and good documentation. The previous article, "Classification Models of the Scikit-learn Library and Their Export to ONNX", covered classification models.

In this article, we will explore the application of regression models in the Scikit-learn package, compute their parameters with double precision for the test dataset, attempt to convert them to the ONNX format for float and double precision, and use the obtained models in programs on MQL5. Additionally, we will compare the accuracy of the original models and their ONNX versions for float and double precision. Furthermore, we will examine the ONNX representation of regression models, which will provide a better understanding of their internal structure and operation.

Contents

• If it bothers you, welcome to contribute
  
  
• 1. Test Dataset
  The script for displaying the test dataset
  
  
• 2. Regression Models
  2.0. List of Scikit-learn Regression Models
  
  
• 2.1. Scikit-learn Regression Models that convert to ONNX models float and double
  
  
• 2.1.1. sklearn.linear_model.ARDRegression
  2.1.1.1. Code for creating the ARDRegression
  2.1.1.2. MQL5 code for executing ONNX Models
  2.1.1.3. ONNX representation of the ard_regression_float.onnx and ard_regression_double.onnx
  
  
• 2.1.2. sklearn.linear_model.BayesianRidge
  2.1.2.1. Code for creating the BayesianRidge model and exporting it to ONNX for float and double
  2.1.2.2. MQL5 code for executing ONNX Models
  2.1.2.3. ONNX representation of the bayesian_ridge_float.onnx and bayesian_ridge_double.onnx
  
  
• 2.1.3. sklearn.linear_model.ElasticNet
  2.1.3.1. Code for creating the ElasticNet model and exporting it to ONNX for float and double
  2.1.3.2. MQL5 code for executing ONNX Models
  2.1.3.3. ONNX representation of the elastic_net_float.onnx and elastic_net_double.onnx
  
  
• 2.1.4. sklearn.linear_model.ElasticNetCV
  2.1.4.1. Code for creating the ElasticNet model and exporting it to ONNX for float and double
  2.1.4.2. MQL5 code for executing ONNX Models
  2.1.4.3. ONNX representation of the elastic_net_cv_float.onnx and elastic_net_cv_double.onnx
  
  
• 2.1.5. sklearn.linear_model.HuberRegressor
  2.1.5.1. Code for creating the HuberRegressor model and exporting it to ONNX for float and double
  2.1.5.2. MQL5 code for executing ONNX Models
  2.1.5.3. ONNX representation of the huber_regressor_float.onnx and huber_regressor_double.onnx
  
  
• 2.1.6. sklearn.linear_model.Lars
  2.1.6.1. Code for creating the Lars model and exporting it to ONNX for float and double
  2.1.6.2. MQL5 code for executing ONNX Models
  2.1.6.3. ONNX representation of the lars_float.onnx and lars_double.onnx
  
  
• 2.1.7. sklearn.linear_model.LarsCV
  2.1.7.1. Code for creating the LarsCV model and exporting it to ONNX for float and double
  2.1.7.2. MQL5 code for executing ONNX Models
  2.1.7.3. ONNX representation of the lars_cv_float.onnx and lars_cv_double.onnx
  
  
• 2.1.8. sklearn.linear_model.Lasso
  2.1.8.1. Code for creating the Lasso model and exporting it to ONNX for float and double
  2.1.8.2. MQL5 code for executing ONNX Models
  2.1.8.3. ONNX representation of the lasso_float.onnx and lasso_double.onnx
  
  
• 2.1.9. sklearn.linear_model.LassoCV
  2.1.9.1. Code for creating the LassoCV model and exporting it to ONNX for float and double
  2.1.9.2. MQL5 code for executing ONNX Models
  2.1.9.3. ONNX representation of the lasso_cv_float.onnx and lasso_cv_double.onnx
  
  
• 2.1.10. sklearn.linear_model.LassoLars
  2.1.10.1. Code for creating the LassoLars model and exporting it to ONNX for float and double
  2.1.10.2. MQL5 code for executing ONNX Models
  2.1.10.3. ONNX representation of the lasso_lars_float.onnx and lasso_lars_double.onnx
  
  
• 2.1.11. sklearn.linear_model.LassoLarsCV
  2.1.11.1. Code for creating the LassoLarsCV model and exporting it to ONNX for float and double
  2.1.11.2. MQL5 code for executing ONNX Models
  2.1.11.3. ONNX representation of the lasso_lars_cv_float.onnx and lasso_lars_cv_double.onnx
  
  
• 2.1.12. sklearn.linear_model.LassoLarsIC
  2.1.12.1. Code for creating the LassoLarsIC model and exporting it to ONNX for float and double
  2.1.12.2. MQL5 code for executing ONNX Models
  2.1.12.3. ONNX representation of the lasso_lars_ic_float.onnx and lasso_lars_ic_double.onnx
  
  
• 2.1.13. sklearn.linear_model.LinearRegression
  2.1.13.1. Code for creating the LinearRegression model and exporting it to ONNX for float and double
  2.1.13.2. MQL5 code for executing ONNX Models
  2.1.13.3. ONNX representation of the linear_regression_float.onnx and linear_regression_double.onnx
  
  
• 2.1.14. sklearn.linear_model.Ridge
  2.1.14.1. Code for creating the Ridge model and exporting it to ONNX for float and double
  2.1.14.2. MQL5 code for executing ONNX Models
  2.1.14.3. ONNX representation of the ridge_float.onnx and ridge_double.onnx
  
  
• 2.1.15. sklearn.linear_model.RidgeCV
  2.1.15.1. Code for creating the RidgeCV model and exporting it to ONNX for float and double
  2.1.15.2. MQL5 code for executing ONNX Models
  2.1.15.3. ONNX representation of the ridge_cv_float.onnx and ridge_cv_double.onnx
  
  
• 2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit
  2.1.16.1. Code for creating the OrthogonalMatchingPursuit model and exporting it to ONNX for float and double
  2.1.16.2. MQL5 code for executing ONNX Models
  2.1.16.3. ONNX representation of the orthogonal_matching_pursuit_float.onnx and orthogonal_matching_pursuit_double.onnx
  
  
• 2.1.17. sklearn.linear_model.PassiveAggressiveRegressor
  2.1.17.1. Code for creating the PassiveAggressiveRegressor model and exporting it to ONNX for float and double
  2.1.17.2. MQL5 code for executing ONNX Models
  2.1.17.3. ONNX representation of the passive_aggressive_regressor_float.onnx and passive_aggressive_regressor_double.onnx
  
  
• 2.1.18. sklearn.linear_model.QuantileRegressor
  2.1.18.1. Code for creating the QuantileRegressor model and exporting it to ONNX for float and double
  2.1.18.2. MQL5 code for executing ONNX Models
  2.1.18.3. ONNX representation of the quantile_regressor_float.onnx and quantile_regressor_double.onnx
  
  
• 2.1.19. sklearn.linear_model.RANSACRegressor
  2.1.19.1. Code for creating the RANSACRegressor model and exporting it to ONNX for float and double
  2.1.19.2. MQL5 code for executing ONNX Models
  2.1.19.3. ONNX representation of the ransac_regressor_float.onnx and ransac_regressor_double.onnx
  
  
• 2.1.20. sklearn.linear_model.TheilSenRegressor
  2.1.20.1. Code for creating the TheilSenRegressor model and exportingg it to ONNX for float and double
  2.1.20.2. MQL5 code for executing ONNX Models
  2.1.20.3. ONNX representation of the theil_sen_regressor_float.onnx and theil_sen_regressor_double.onnx
  
  
• 2.1.21. sklearn.linear_model.LinearSVR
  2.1.21.1. Code for creating the LinearSVR model and exporting it to ONNX for float and double
  2.1.21.2. MQL5 code for executing ONNX Models
  2.1.21.3. ONNX representation of the linear_svr_float.onnx and linear_svr_double.onnx
  
  
• 2.1.22. sklearn.linear_model.MLPRegressor
  2.1.22.1. Code for creating the MLPRegressor model and exporting it to ONNX for float and double
  2.1.22.2. MQL5 code for executing ONNX Models
  2.1.22.3. ONNX representation of the mlp_regressor_float.onnx and mlp_regressor_double.onnx
  
  
• 2.1.23. sklearn.cross_decomposition.PLSRegression
  2.1.23.1. Code for creating the PLSRegression model and exporting it to ONNX for float and double
  2.1.23.2. MQL5 code for executing ONNX Models
  2.1.23.3. ONNX representation of the pls_regression_float.onnx and pls_regression_double.onnx
  
  
• 2.1.24. sklearn.linear_model.TweedieRegressor
  2.1.24.1. Code for creating the TweedieRegressor model and exporting it to ONNX for float and double
  2.1.24.2. MQL5 code for executing ONNX Models
  2.1.24.3. ONNX representation of the tweedie_regressor_float.onnx and tweedie_regressor_double.onnx
  
  
• 2.1.25. sklearn.linear_model.PoissonRegressor
  2.1.25.1. Code for creating the PoissonRegressor model and exporting it to ONNX for float and double
  2.1.25.2. MQL5 code for executing ONNX Models
  2.1.25.3. ONNX representation of the poisson_regressor_float.onnx and poisson_regressor_double.onnx
  
  
• 2.1.26. sklearn.neighbors.RadiusNeighborsRegressor
  2.1.26.1. Code for creating the RadiusNeighborsRegressor model and exporting it to ONNX for float and double
  2.1.26.2. MQL5 code for executing ONNX Models
  2.1.26.3. ONNX representation of the radius_neighbors_regressor_float.onnx and radius_neighbors_regressor_double.onnx
  
  
• 2.1.27. sklearn.neighbors.KNeighborsRegressor
  2.1.27.1. Code for creating the KNeighborsRegressor model and exporting it to ONNX for float and double
  2.1.27.2. MQL5 code for executing ONNX Models
  2.1.27.3. ONNX representation of the kneighbors_regressor_float.onnx and kneighbors_regressor_double.onnx
  
  
• 2.1.28. sklearn.gaussian_process.GaussianProcessRegressor
  2.1.28.1. Code for creating the GaussianProcessRegressor model and exporting it to ONNX for float and double
  2.1.28.2. MQL5 code for executing ONNX Models
  2.1.28.3. ONNX representation of the gaussian_process_regressor_float.onnx and gaussian_process_regressor_double.onnx
  
  
• 2.1.29. sklearn.linear_model.GammaRegressor
  2.1.29.1. Code for creating the GammaRegressor model and exporting it to ONNX for float and double
  2.1.29.2. MQL5 code for executing ONNX Models
  2.1.29.3. ONNX representation of the gamma_regressor_float.onnx and gamma_regressor_double.onnx
  
  
• 2.1.30. sklearn.linear_model.SGDRegressor
  2.1.30.1. Code for creating the SGDRegressor model and exporting it to ONNX for float and double
  2.1.30.2. MQL5 code for executing ONNX Models
  2.1.30.3. ONNX representation of the sgd_regressor_float.onnx and sgd_rgressor_double.onnx
  
  
  
• 2.2. Regression models from the Scikit-learn library that are converted only into float precision ONNX models
  
  
• 2.2.1. sklearn.linear_model.AdaBoostRegressor
  2.2.1.1. Code for creating the AdaBoostRegressor model and exporting it to ONNX for float and double
  2.2.1.2. MQL5 code for executing ONNX Models
  2.2.1.3. ONNX representation of the adaboost_regressor_float.onnx and adaboost_regressor_double.onnx
  
  
• 2.2.2. sklearn.linear_model.BaggingRegressor
  2.2.2.1. Code for creating the BaggingRegressor model and exporting it to ONNX for float and double
  2.2.2.2. MQL5 code for executing ONNX Models
  2.2.2.3. ONNX representation of the bagging_regressor_float.onnx and bagging_regressor_double.onnx
  
  
• 2.2.3. sklearn.linear_model.DecisionTreeRegressor 
  2.2.3.1. Code for creating the DecisionTreeRegressor model and exporting it to ONNX for float and double
  2.2.3.2. MQL5 code for executing ONNX Models
  2.2.3.3. ONNX representation of the decision_tree_regressor_float.onnx and decision_tree_regressor_double.onnx
  
  
• 2.2.4. sklearn.linear_model.ExtraTreeRegressor
  2.2.4.1. Code for creating the ExtraTreeRegressor model and exporting it to ONNX for float and double
  2.2.4.2. MQL5 code for executing ONNX Models
  2.2.4.3. ONNX representation of the extra_tree_regressor_float.onnx and extra_tree_regressor_double.onnx
  
  
• 2.2.5. sklearn.ensemble.ExtraTreesRegressor
  2.2.5.1. Code for creating the ExtraTreesRegressor model and exporting it to ONNX for float and double
  2.2.5.2. MQL5 code for executing ONNX Models
  2.2.5.3. ONNX representation of the extra_trees_regressor_float.onnx and extra_trees_regressor_double.onnx
  
  
• 2.2.6. sklearn.svm.NuSVR
  2.2.6.1. Code for creating the NuSVR model and exporting it to ONNX for float and double
  2.2.6.2. MQL5 code for executing ONNX Models
  2.2.6.3. ONNX representation of the nu_svr_float.onnx and nu_svr_double.onnx
  
  
• 2.2.7. sklearn.ensemble.RandomForestRegressor
  2.2.7.1. Code for creating the RandomForestRegressor model and exporting it to ONNX for float and double
  2.2.7.2. MQL5 code for executing ONNX Models
  2.2.7.3. ONNX representation of the random_forest_regressor_float.onnx and random_forest_regressor_double.onnx
  
  
• 2.2.8. sklearn.ensemble.GradientBoostingRegressor
  2.2.8.1. Code for creating the GradientBoostingRegressor model and exporting it to ONNX for float and double
  2.2.8.2. MQL5 code for executing ONNX Models
  2.2.8.3. ONNX representation of the gradient_boosting_regressor_float.onnx and gradient_boosting_regressor_double.onnx
  
  
• 2.2.9. sklearn.ensemble.HistGradientBoostingRegressor
  2.2.9.1. Code for creating the HistGradientBoostingRegressor model and exporting it to ONNX for float and double
  2.2.9.2. MQL5 code for executing ONNX Models
  2.2.9.3. ONNX representation of the hist_gradient_boosting_regressor_float.onnx and hist_gradient_boosting_regressor_double.onnx
  
  
• 2.2.10. sklearn.svm.SVR
  2.2.10.1. Code for creating the SVR model and exporting it to ONNX for float and double
  2.2.10.2. MQL5 code for executing ONNX Models
  2.2.10.3. ONNX representation of the svr_float.onnx and svr_double.onnx
  
  
  
• 2.3. Regression Models that encountered problems when converting to ONNX
  
  
• 2.3.1. sklearn.dummy.DummyRegressor
  Code for creating the DummyRegressor
  
  
• 2.3.2. sklearn.kernel_ridge.KernelRidge
  Code for creating the KernelRidge
  
  
• 2.3.3. sklearn.isotonic.IsotonicRegression
  Code for creating the IsotonicRegression
  
  
• 2.3.4. sklearn.cross_decomposition.PLSCanonical
  Code for creating the PLSCanonical
  
  
• 2.3.5. sklearn.cross_decomposition.CCA
  Code for creating the CCA
  
  
• Conclusion
  
  
• Summary
  

If it bothers you, welcome to contribute

On the ONNX Runtime developer forum, one of the users reported an error "[ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor:LinearRegressor(1)" when executing a model through ONNX Runtime.

Hi all, getting this error when trying to inferance a linear regression model. PLease help me resolve this.

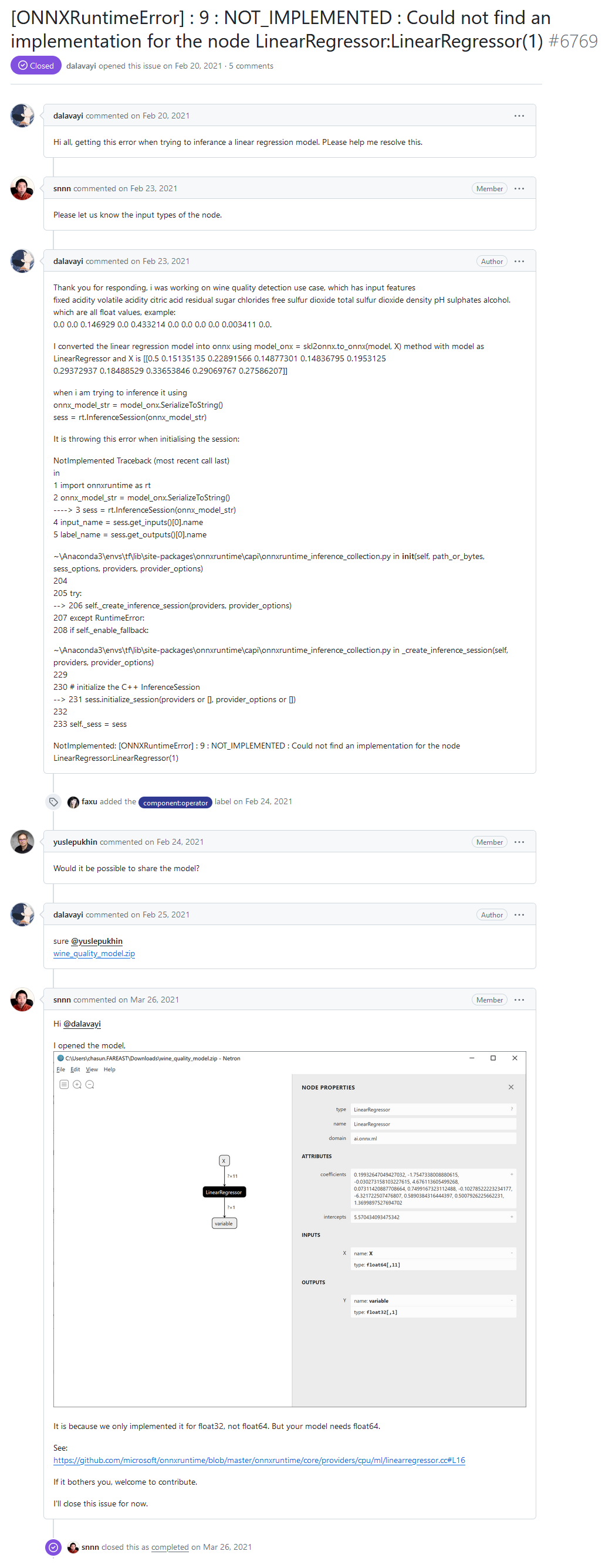
"NOT_IMPLEMENTED : Could not find an implementation for the node LinearRegressor:LinearRegressor(1)" error from ONNX Runtime developer forum

Developer's response:

It is because we only implemented it for float32, not float64. But your model needs float64.

See:
https://github.com/microsoft/onnxruntime/blob/master/onnxruntime/core/providers/cpu/ml/linearregressor.cc#L16

If it bothers you, welcome to contribute.

In the user's ONNX model, the ai.onnx.ml.LinearRegressor operator is called with double (float64) data type, and the error message arises because the ONNX Runtime lacks support for the LinearRegressor() operator with double precision.

According to the specification of the ai.onnx.ml.LinearRegressor operator, the double input data type is possible (T: tensor(float), tensor(double), tensor(int64), tensor(int32)); however, the developers intentionally chose not to implement it.

The reason for this is that the output always returns Y: tensor(float) value. Furthermore, the computational parameters are float numbers (coefficients: list of floats, intercepts: list of floats).

Consequently, when the calculations are performed in double precision, this operator reduces the precision to float, and its implementation in double precision calculations has questionable value.

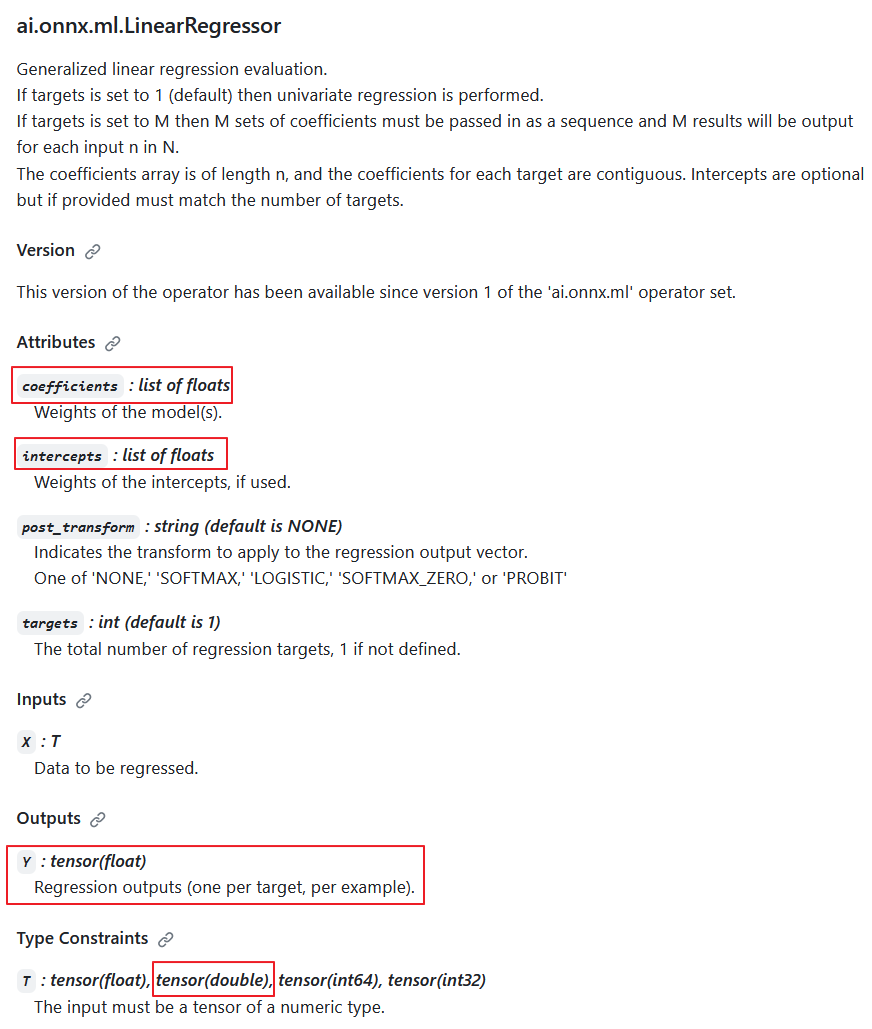
ai.onnx.ml.LinearRegressor operator description

Thus, the reduction of precision to float in the parameters and output value makes it impossible for the ai.onnx.ml.LinearRegressor to fully operate with double (float64) numbers. Presumably, for this reason, the ONNX Runtime developers decided to refrain from implementing it for the double type

The method of "adding double support" was demonstrated by the developers in code comments (highlighted in yellow).

In ONNX Runtime, its computation is performed using the LinearRegressor class (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.h).

The operator's parameters, coefficients_, and intercepts_, are stored as std::vector<float>:

#pragma once

#include "core/common/common.h"
#include "core/framework/op_kernel.h"
#include "core/util/math_cpuonly.h"
#include "ml_common.h"

namespace onnxruntime {
namespace ml {

class LinearRegressor final : public OpKernel {
 public:
  LinearRegressor(const OpKernelInfo& info);
  Status Compute(OpKernelContext* context) const override;

 private:
  int64_t num_targets_;
  std::vector<float> coefficients_;
  std::vector<float> intercepts_;
  bool use_intercepts_;
  POST_EVAL_TRANSFORM post_transform_;
};

}  // namespace ml
}  // namespace onnxruntime

The implementation of LinearRegressor operator (https://github.com/microsoft/onnxruntime/blob/main/onnxruntime/core/providers/cpu/ml/linearregressor.cc)

// Copyright (c) Microsoft Corporation. All rights reserved.
// Licensed under the MIT License.

#include "core/providers/cpu/ml/linearregressor.h"
#include "core/common/narrow.h"
#include "core/providers/cpu/math/gemm.h"

namespace onnxruntime {
namespace ml {

ONNX_CPU_OPERATOR_ML_KERNEL(
    LinearRegressor,
    1,
    // KernelDefBuilder().TypeConstraint("T", std::vector<MLDataType>{
    //                                            DataTypeImpl::GetTensorType<float>(),
    //                                            DataTypeImpl::GetTensorType<double>()}),
    KernelDefBuilder().TypeConstraint("T", DataTypeImpl::GetTensorType<float>()),
    LinearRegressor);

LinearRegressor::LinearRegressor(const OpKernelInfo& info)
    : OpKernel(info),
      intercepts_(info.GetAttrsOrDefault<float>("intercepts")),
      post_transform_(MakeTransform(info.GetAttrOrDefault<std::string>("post_transform", "NONE"))) {
  ORT_ENFORCE(info.GetAttr<int64_t>("targets", &num_targets_).IsOK());
  ORT_ENFORCE(info.GetAttrs<float>("coefficients", coefficients_).IsOK());

  // use the intercepts_ if they're valid
  use_intercepts_ = intercepts_.size() == static_cast<size_t>(num_targets_);
}

// Use GEMM for the calculations, with broadcasting of intercepts
// https://github.com/onnx/onnx/blob/main/docs/Operators.md#Gemm
//
// X: [num_batches, num_features]
// coefficients_: [num_targets, num_features]
// intercepts_: optional [num_targets].
// Output: X * coefficients_^T + intercepts_: [num_batches, num_targets]
template <typename T>
static Status ComputeImpl(const Tensor& input, ptrdiff_t num_batches, ptrdiff_t num_features, ptrdiff_t num_targets,
                          const std::vector<float>& coefficients,
                          const std::vector<float>* intercepts, Tensor& output,
                          POST_EVAL_TRANSFORM post_transform,
                          concurrency::ThreadPool* threadpool) {
  const T* input_data = input.Data<T>();
  T* output_data = output.MutableData<T>();

  if (intercepts != nullptr) {
    TensorShape intercepts_shape({num_targets});
    onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans,
                                      num_batches, num_targets, num_features,
                                      1.f, input_data, coefficients.data(), 1.f,
                                      intercepts->data(), &intercepts_shape,
                                      output_data,
                                      threadpool);
  } else {
    onnxruntime::Gemm<T>::ComputeGemm(CBLAS_TRANSPOSE::CblasNoTrans, CBLAS_TRANSPOSE::CblasTrans,
                                      num_batches, num_targets, num_features,
                                      1.f, input_data, coefficients.data(), 1.f,
                                      nullptr, nullptr,
                                      output_data,
                                      threadpool);
  }

  if (post_transform != POST_EVAL_TRANSFORM::NONE) {
    ml::batched_update_scores_inplace(gsl::make_span(output_data, SafeInt<size_t>(num_batches) * num_targets),
                                      num_batches, num_targets, post_transform, -1, false, threadpool);
  }
  return Status::OK();
}

Status LinearRegressor::Compute(OpKernelContext* ctx) const {
  Status status = Status::OK();

  const auto& X = *ctx->Input<Tensor>(0);
  const auto& input_shape = X.Shape();

  if (input_shape.NumDimensions() > 2) {
    return ORT_MAKE_STATUS(ONNXRUNTIME, INVALID_ARGUMENT, "Input shape had more than 2 dimension. Dims=",
                           input_shape.NumDimensions());
  }

  ptrdiff_t num_batches = input_shape.NumDimensions() <= 1 ? 1 : narrow<ptrdiff_t>(input_shape[0]);
  ptrdiff_t num_features = input_shape.NumDimensions() <= 1 ? narrow<ptrdiff_t>(input_shape.Size())
                                                            : narrow<ptrdiff_t>(input_shape[1]);
  Tensor& Y = *ctx->Output(0, {num_batches, num_targets_});
  concurrency::ThreadPool* tp = ctx->GetOperatorThreadPool();

  auto element_type = X.GetElementType();

  switch (element_type) {
    case ONNX_NAMESPACE::TensorProto_DataType_FLOAT: {
      status = ComputeImpl<float>(X, num_batches, num_features, narrow<ptrdiff_t>(num_targets_), coefficients_,
                                  use_intercepts_ ? &intercepts_ : nullptr,
                                  Y, post_transform_, tp);

      break;
    }
    case ONNX_NAMESPACE::TensorProto_DataType_DOUBLE: {
      // TODO: Add support for 'double' to the scoring functions in ml_common.h
      // once that is done we can just call ComputeImpl<double>...
      // Alternatively we could cast the input to float.
    }
    default:
      status = ORT_MAKE_STATUS(ONNXRUNTIME, FAIL, "Unsupported data type of ", element_type);
  }

  return status;
}

}  // namespace ml
}  // namespace onnxruntime

It turns out that there is an option to use double numbers as input values and perform the operator's computation with float parameters. Another possibility could be to reduce the precision of the input data to float. However, none of these options can be considered a proper solution.

The specification of the ai.onnx.ml.LinearRegressor operator restricts the capability for full operation with double numbers since the parameters and output value are limited to the float type.

A similar situation occurs with other ONNX ML operators, such as ai.onnx.ml.SVMRegressor and ai.onnx.ml.TreeEnsembleRegressor.

As a result, all developers utilizing ONNX model execution in double precision face this limitation of the specification. A solution might involve extending the ONNX specification (or adding similar operators like LinearRegressor64, SVMRegressor64, and TreeEnsembleRegressor64 with parameters and output values in double). However, at present, this issue remains unresolved.

Much depends on the ONNX converter. For models calculated in double, it might be preferable to avoid using these operators (though this may not always be possible). In this particular case, the converter to ONNX did not work optimally with the user's model.

As we will see later, the sklearn-onnx converter manages to bypass the limitation of LinearRegressor: for ONNX double models, it uses ONNX operators MatMul() and Add() instead. Thanks to this method, numerous regression models of the Scikit-learn library are successfully converted into ONNX models calculated in double, preserving the accuracy of the original double models.

1. Test Dataset

To run the examples, you will need to install Python (we used version 3.10.8), additional libraries (pip install -U scikit-learn numpy matplotlib onnx onnxruntime skl2onnx), and specify the path to Python in the MetaEditor (in the menu Tools->Options->Compilers->Python).

As a test dataset, we will use generated values of the function y = 4X + 10sin(X*0.5).

To display a graph of such a function, open MetaEditor, create a file named RegressionData.py, copy the script text, and run it by clicking the "Compile" button.

The script for displaying the test dataset

# RegressionData.py
# The code plots the synthetic data, used for all regression models
# Copyright 2023, MetaQuotes Ltd.
# https://mql5.com

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

# set the figure size
plt.figure(figsize=(8,5))

# plot the initial data for regression
plt.scatter(X, y, label='Regression Data', marker='o')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title('Regression data')
plt.show()

As a result, a graph of the function will be displayed, which we will use to test regression methods.

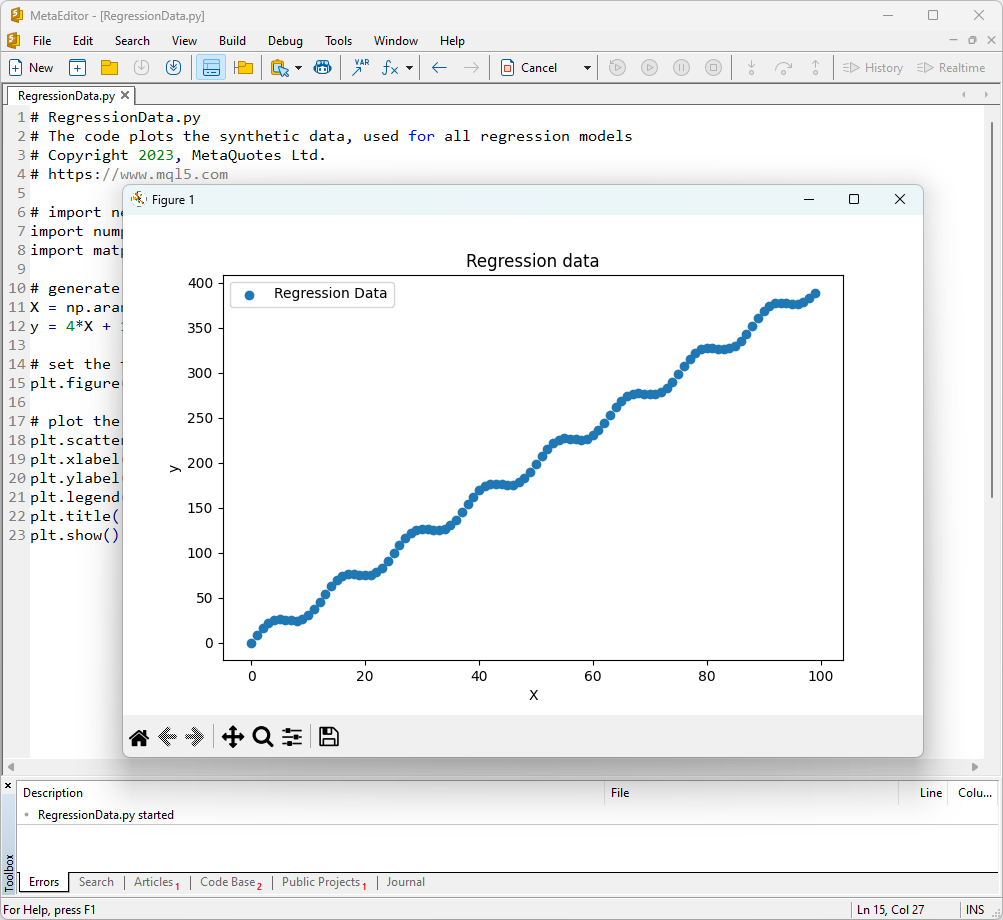
Fig.1. Function for testing regression models

2. Regression Models

The goal of a regression task is to find a mathematical function or model that best describes the relationship between features and the target variable to predict numerical values for new data. This allows making forecasts, optimizing solutions, and making informed decisions based on data.

Let's consider the main regression models in the scikit-learn package.

2.0. List of Scikit-learn Regression Models

To display a list of available scikit-learn regression models, you can use the script:

# ScikitLearnRegressors.py
# The script lists all the regression algorithms available inb scikit-learn
# Copyright 2023, MetaQuotes Ltd.
# https://mql5.com

# print Python version
from platform import python_version  
print("The Python version is ", python_version()) 

# print scikit-learn version
import sklearn
print('The scikit-learn version is {}.'.format(sklearn.__version__))

# print scikit-learn regression models
from sklearn.utils import all_estimators

regressors = all_estimators(type_filter='regressor')
for index, (name, RegressorClass) in enumerate(regressors, start=1):
    print(f"Regressor {index}: {name}")

Output:

The Python version is  3.10.8
The scikit-learn version is 1.3.2.
Regressor 1: ARDRegression
Regressor 2: AdaBoostRegressor
Regressor 3: BaggingRegressor
Regressor 4: BayesianRidge
Regressor 5: CCA
Regressor 6: DecisionTreeRegressor
Regressor 7: DummyRegressor
Regressor 8: ElasticNet
Regressor 9: ElasticNetCV
Regressor 10: ExtraTreeRegressor
Regressor 11: ExtraTreesRegressor
Regressor 12: GammaRegressor
Regressor 13: GaussianProcessRegressor
Regressor 14: GradientBoostingRegressor
Regressor 15: HistGradientBoostingRegressor
Regressor 16: HuberRegressor
Regressor 17: IsotonicRegression
Regressor 18: KNeighborsRegressor
Regressor 19: KernelRidge
Regressor 20: Lars
Regressor 21: LarsCV
Regressor 22: Lasso
Regressor 23: LassoCV
Regressor 24: LassoLars
Regressor 25: LassoLarsCV
Regressor 26: LassoLarsIC
Regressor 27: LinearRegression
Regressor 28: LinearSVR
Regressor 29: MLPRegressor
Regressor 30: MultiOutputRegressor
Regressor 31: MultiTaskElasticNet
Regressor 32: MultiTaskElasticNetCV
Regressor 33: MultiTaskLasso
Regressor 34: MultiTaskLassoCV
Regressor 35: NuSVR
Regressor 36: OrthogonalMatchingPursuit
Regressor 37: OrthogonalMatchingPursuitCV
Regressor 38: PLSCanonical
Regressor 39: PLSRegression
Regressor 40: PassiveAggressiveRegressor
Regressor 41: PoissonRegressor
Regressor 42: QuantileRegressor
Regressor 43: RANSACRegressor
Regressor 44: RadiusNeighborsRegressor
Regressor 45: RandomForestRegressor
Regressor 46: RegressorChain
Regressor 47: Ridge
Regressor 48: RidgeCV
Regressor 49: SGDRegressor
Regressor 50: SVR
Regressor 51: StackingRegressor
Regressor 52: TheilSenRegressor
Regressor 53: TransformedTargetRegressor
Regressor 54: TweedieRegressor
Regressor 55: VotingRegressor

For convenience in this list of regressors, they are highlighted in different colors. Models that require base regression model are highlighted in gray, while other models can be used independently. Note that models successfully exported to the ONNX format are marked in green, models that encounter errors during conversion in the current version of scikit-learn 1.2.2 are marked in red. Methods unsuitable for the considered test task are highlighted in blue.

Regression quality analysis uses regression metrics, which are functions of true and predicted values. In MQL5 language, several different metrics are available, detailed in the article "Evaluating ONNX models using regression metrics".

In this article, three metrics will be used to compare the quality of different models:

1. Coefficient of determination R-squared (R2);
2. Mean Absolute Error (MAE);
3. Mean Squared Error (MSE).

2.1. Scikit-learn Regression Models that convert to ONNX models float and double

This section presents regression models that are successfully converted into ONNX formats in both float and double precisions.

All the regression models discussed further are presented in the following format:

1. Model description, working principle, advantages, and limitations
2. Python script for creating the model, exporting it to ONNX files in float and double formats, and executing the obtained models using ONNX Runtime in Python. Metrics like R^2, MAE, MSE, calculated using sklearn.metrics, are used to evaluate the quality of the original and ONNX models.
   
3. MQL5 script for executing ONNX models (float and double) via ONNX Runtime, with metrics calculated using RegressionMetric().
   
4. ONNX model representation in Netron for float and double precision.

2.1.1. sklearn.linear_model.ARDRegression

ARDRegression (Automatic Relevance Determination Regression) is a regression method designed to address regression problems while automatically determining the importance (relevance) of features and establishing their weights during the model training process.

ARDRegression enables the detection and use of only the most important features to build a regression model, which can be beneficial when dealing with a large number of features.

Working Principle of ARDRegression:

1. Linear Regression: ARDRegression is based on linear regression, assuming a linear relationship between the independent variables (features) and the target variable.
2. Automatic Feature Importance Determination: The main distinction of ARDRegression is its automatic determination of which features are most important for predicting the target variable. This is achieved by introducing prior distributions (regularization) over the weights, allowing the model to automatically set zero weights for less significant features.
3. Estimation of Posterior Probabilities: ARDRegression computes posterior probabilities for each feature, enabling the determination of their importance. Features with high posterior probabilities are considered relevant and receive non-zero weights, while features with low posterior probabilities receive zero weights.
4. Dimensionality Reduction: Thus, ARDRegression can lead to data dimensionality reduction by removing insignificant features.

Advantages of ARDRegression:

• Automatic Determination of Important Features: The method automatically identifies and uses only the most important features, potentially enhancing model performance and reducing the risk of overfitting.
• Resilience to Multicollinearity: ARDRegression handles multicollinearity well, even when features are highly correlated.

Limitations of ARDRegression:

• Requires Selection of Prior Distributions: Choosing suitable prior distributions might require experimentation.
• Computational Complexity: Training ARDRegression can be computationally expensive, particularly for large datasets.

ARDRegression is a regression method that automatically determines feature importance and establishes their weights based on posterior probabilities. This method is useful when considering only significant features for building a regression model and reducing data dimensionality is necessary.

2.1.1.1. Code for creating the ARDRegression model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.ARDRegression model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# ARDRegression.py
# The code demonstrates the process of training ARDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ARDRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name="ARDRegression"
onnx_model_filename = data_path + "ard_regression"

# create an ARDRegression model
regression_model = ARDRegression()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)

print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)

print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

The script creates and trains the sklearn.linear_model.ARDRegression model (the original model is considered in double), then exports the model to ONNX for float and double (ard_regression_float.onnx and ard_regression_double.onnx) and compares the accuracy of its operation.

It also generates files ARDRegression_plot_float.png and ARDRegression_plot_double.png, allowing a visual assessment of the results of ONNX models for float and double (Fig. 2-3).

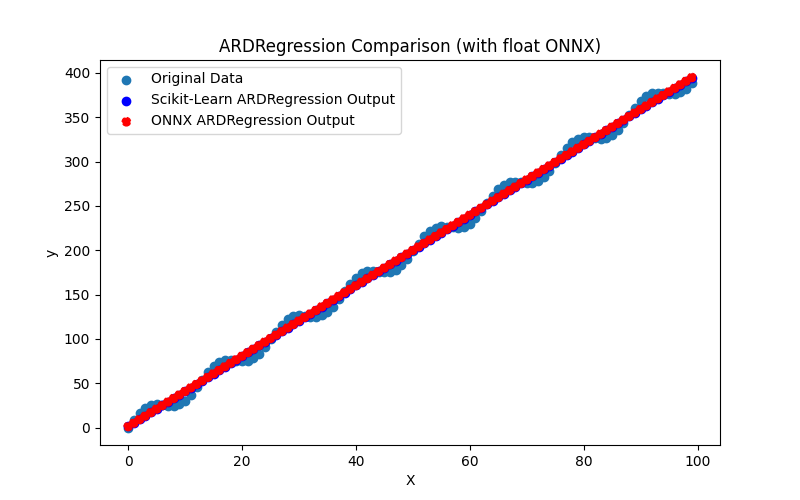
Fig.2. Results of the ARDRegression.py (float)

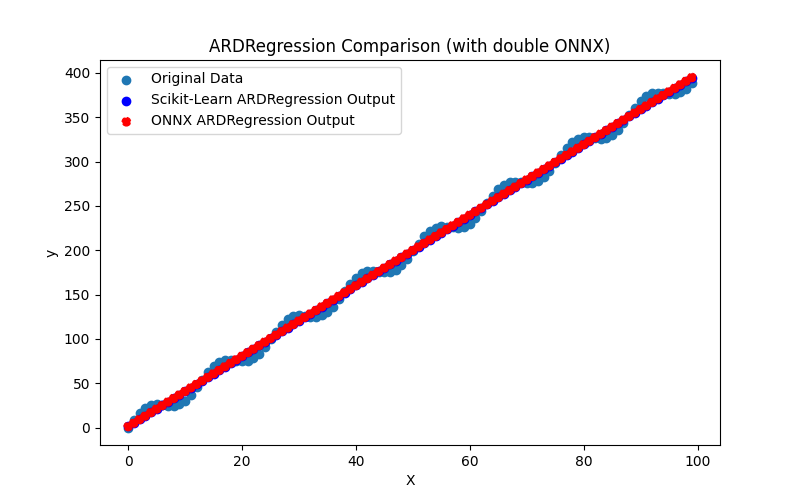
Fig.3. Results of the ARDRegression.py (double)

Visually, the ONNX models for float and double look the same (Fig. 2-3), detailed information can be found in the Journal tab:

Python  ARDRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891289
Python  
Python  ARDRegression ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382627587808
Python  Mean Absolute Error: 6.347568283744705
Python  Mean Squared Error: 49.778160054267204
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  ARDRegression ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ard_regression_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891289
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

In this example, the original model was considered in double, then it was exported into ONNX models ard_regression_float.onnx and ard_regression_double.onnx for float and double, respectively.

If the accuracy of the model is evaluated by Mean Absolute Error (MAE), the accuracy of the ONNX model for float is up to 6 decimal places, while the ONNX model using double showed accuracy retention up to 15 decimal places, in line with the precision of the original model.

Properties of the ONNX models can be viewed in MetaEditor (Fig. 4-5).

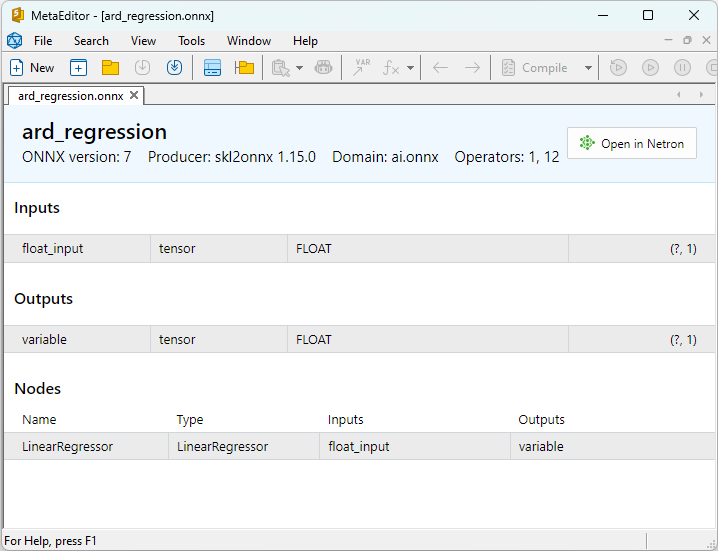
Fig.4. ard_regression_float.onnx ONNX-model in MetaEditor

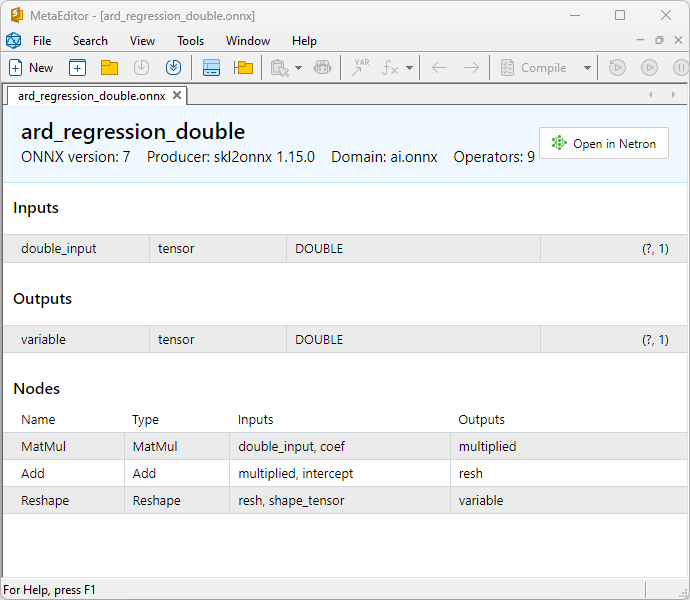
Fig.5. ard_regression_double.onnx ONNX model in MetaEditor

A comparison between float and double ONNX models shows that in this case, the computation of ONNX models for ARDRegression occurs differently: for float numbers, the LinearRegressor() operator from ONNX-ML is used, whereas for double numbers, ONNX operators MatMul(), Add(), and Reshape() are used.

The implementation of the model in ONNX depends on the converter; in the examples for exporting to ONNX, the skl2onnx.convert_sklearn() function from the skl2onnx library will be used.

2.1.1.2. MQL5 code for executing ONNX Models

This code executes the saved ard_regression_float.onnx and ard_regression_double.onnx ONNX models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                ARDRegression.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ARDRegression"
#define   ONNXFilenameFloat  "ard_regression_float.onnx"
#define   ONNXFilenameDouble "ard_regression_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

ARDRegression (EURUSD,H1)       Testing ONNX float: ARDRegression (ard_regression_float.onnx)
ARDRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382627587808
ARDRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475682837447049
ARDRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781600542671896
ARDRegression (EURUSD,H1)       
ARDRegression (EURUSD,H1)       Testing ONNX double: ARDRegression (ard_regression_double.onnx)
ARDRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382628120845
ARDRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475680128537597
ARDRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781593489128795

Comparison with the original double model in Python:

Testing ONNX float: ARDRegression (ard_regression_float.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475682837447049
       
Testing ONNX double: ARDRegression (ard_regression_double.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475680128537597

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.1.3. The ONNX representations of models ard_regression_float.onnx and ard_regression_double.onnx

Netron (web version) is a tool for visualizing models and analyzing computation graphs, which can be used for models in the ONNX (Open Neural Network Exchange) format.

Netron presents model graphs and their architecture in a clear and interactive form, allowing the exploration of the structure and parameters of deep learning models, including those created using ONNX.

Key features of Netron include:

• Graph Visualization: Netron displays the model's architecture as a graph, enabling you to see the layers, operations, and connections between them. You can easily comprehend the structure and data flow within the model.
• Interactive Exploration: You can select nodes in the graph to obtain additional information about each operator and its parameters.
• Support for Various Formats: Netron supports a variety of deep learning model formats, including ONNX, TensorFlow, PyTorch, CoreML, and others.
• Parameter Analysis Capability: You can view the model's parameters and weights, which is useful for understanding the values used in different parts of the model.

Netron is convenient for developers and researchers in the field of machine learning and deep learning, as it simplifies the visualization and analysis of models, aiding in the understanding and debugging of complex neural networks.

This tool allows for quick model inspection, exploring their structure and parameters, easing the work with deep neural networks.

For more details about Netron, refer to the articles: Visualizing your Neural Network with Netron and Visualize Keras Neural Networks with Netron.

Video about Netron::

The ard_regression_float.onnx model is shown at Fig.6:

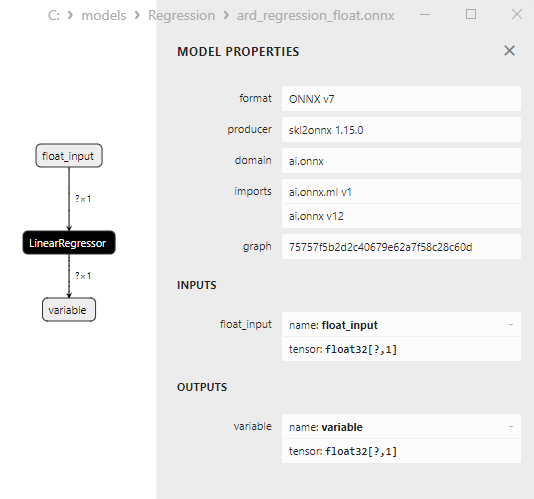
Fig.6. ONNX representation of the ard_regression_float.onnx model in Netron

The  ai.onnx.ml LinearRegressor() ONNX operator is part of the ONNX standard, describing a model for regression tasks. This operator is used for regression, which involves predicting numerical (continuous) values based on input features

It takes model parameters as input, such as weights and bias, along with the input features, and executes linear regression. Linear regression estimates parameters (weights) for each input feature and then performs a linear combination of these features with the weights to generate a prediction.

This operator performs the following steps:

1. Takes the model's weights and bias, along with input features.
2. For each example of input data, performs a linear combination of weights with the corresponding features.
3. Adds the bias to the resulting value.

The result is the prediction of the target variable in the regression task.

The LinearRegressor() parameters are shown in Fig.7.

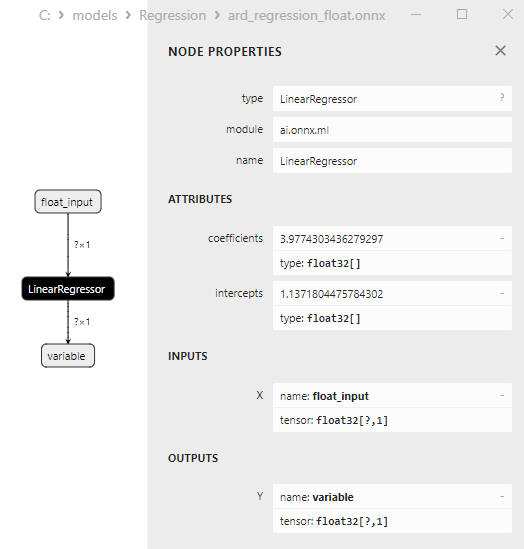
Fig.7. The LinearRegressor() operator properties of the ard_regression_float.onnx model in Netron

The ard_regression_double.onnx ONNX model is shown at Fig.8:

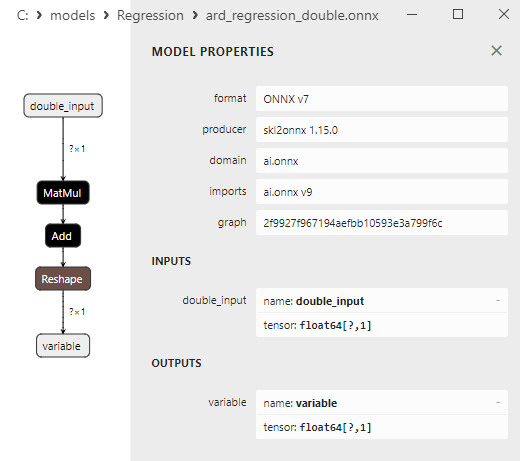
Fig.8. ONNX representation of the ard_regression_double.onnx model in Netron

The parameters of the MatMul(), Add() and Reshape() ONNX-operators is shown at Fig.9-11.

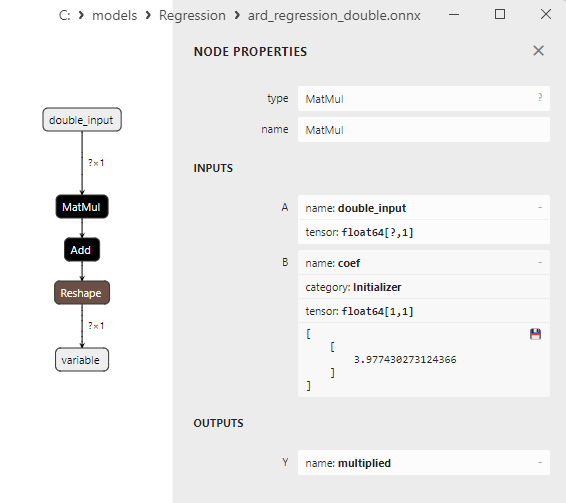
Fig.9. Properties of the MatMul operator in the ard_regression_double.onnx model in Netron

The MatMul (matrix multiplication) ONNX operator performs the multiplication of two matrices.

It takes two inputs: two matrices and returns their matrix product.

If you have two matrices, A and B, then the result of Matmul(A, B) is a matrix C, where each element C[i][j] is calculated as the sum of the products of the elements from row i of matrix A by the elements from column j of matrix B.

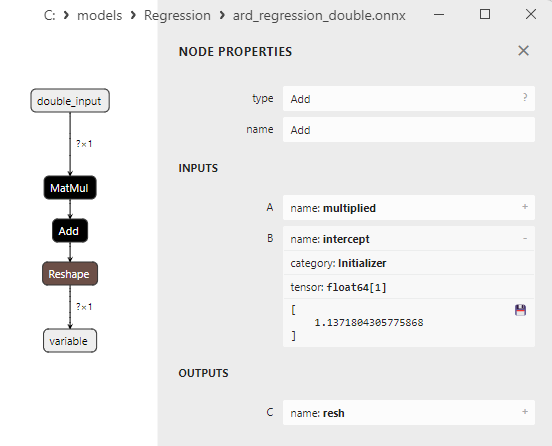
Fig.10. Properties of the Add operator in the ard_regression_double.onnx model in Netron

The Add() ONNX operator performs element-wise addition of two tensors or arrays of the same shape.

It takes two inputs and returns the result, where each element of the resulting tensor equals the sum of the corresponding elements of the input tensors.

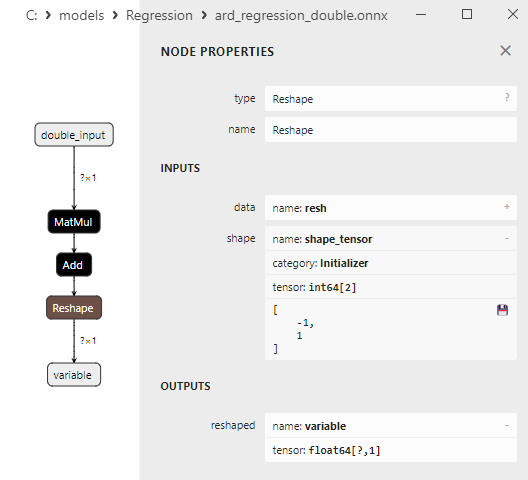
Fig.11. Properties of the Reshape operator in the ard_regression_double.onnx model in Netron

The Reshape(-1,1) ONNX operator is used to modify the shape (or dimension) of input data. In this operator, the value -1 for the dimension indicates that the size of that dimension should be automatically computed based on the other dimensions to ensure data consistency.

The value 1 in the second dimension specifies that after the shape transformation, each element will have a single sub-dimension.

2.1.2. sklearn.linear_model.BayesianRidge

BayesianRidge is a regression method that utilizes a Bayesian approach to estimate model parameters. This method enables modeling the prior distribution of parameters and updating it considering the data to obtain the posterior distribution of parameters.

BayesianRidge is a Bayesian regression method designed to predict the dependent variable based on one or several independent variables.

Working Principle of BayesianRidge:

1. Prior distribution of parameters: It begins with defining the prior distribution of model parameters. This distribution represents prior knowledge or assumptions about model parameters before considering the data. In the case of BayesianRidge, Gaussian-shaped prior distributions are used.
2. Updating the parameter distribution: Once the prior parameter distribution is set, it is updated based on the data. This is done using Bayesian theory, where the posterior distribution of parameters is computed considering the data. An essential aspect is the estimation of hyperparameters, which influence the form of the posterior distribution.
3. Prediction: After estimating the posterior distribution of parameters, predictions can be made for new observations. This results in a distribution of forecasts rather than a single point value, allowing for uncertainty in predictions to be considered.

Advantages of BayesianRidge:

• Uncertainty consideration: BayesianRidge accounts for uncertainty in model parameters and predictions. Instead of point predictions, confidence intervals are provided.
• Regularization: The Bayesian regression method can be useful for model regularization, aiding in preventing overfitting.
• Automatic feature selection: BayesianRidge can automatically determine feature importance by reducing the weights of insignificant features.

Limitations of BayesianRidge:

• Computational complexity: The method requires computational resources to estimate parameters and compute the posterior distribution.
• High abstraction level: A deeper understanding of Bayesian statistics may be required to comprehend and use BayesianRidge.
• Not always the best choice: BayesianRidge may not be the most suitable method in certain regression tasks, particularly when dealing with limited data.

BayesianRidge is useful in regression tasks where the uncertainty of parameters and predictions is important and in cases where model regularization is needed.

2.1.2.1. Code for creating the BayesianRidge model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.BayesianRidge model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# BayesianRidge.py
# The code demonstrates the process of training BayesianRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import BayesianRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "BayesianRidge"
onnx_model_filename = data_path + "bayesian_ridge"

# create a Bayesian Ridge regression model
regression_model = BayesianRidge()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ", compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')


# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  BayesianRidge Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891288
Python  
Python  BayesianRidge ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382627587808
Python  Mean Absolute Error: 6.347568283744705
Python  Mean Squared Error: 49.778160054267204
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  BayesianRidge ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bayesian_ridge_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382628120845
Python  Mean Absolute Error: 6.347568012853758
Python  Mean Squared Error: 49.77815934891288
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

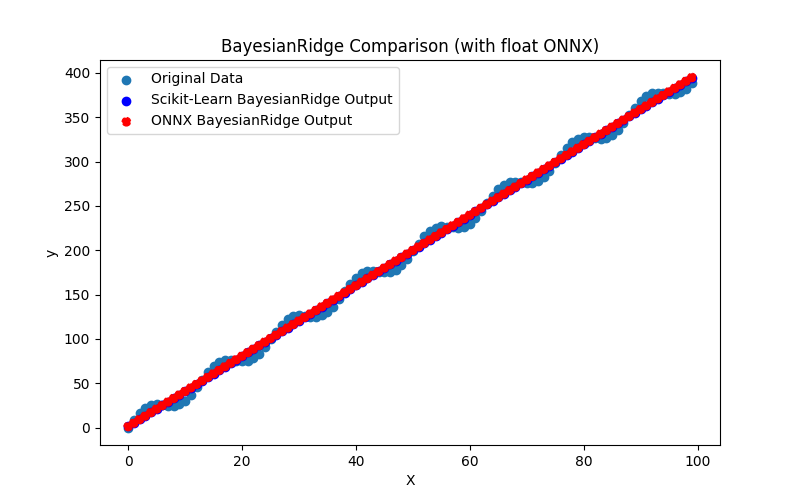
Fig.12. Results of the BayesianRidge.py (float ONNX)

2.1.2.2. MQL5 code for executing ONNX Models

This code executes the saved  bayesian_ridge_float.onnx and bayesian_ridge_double.onnx ONNX models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                BayesianRidge.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "BayesianRidge"
#define   ONNXFilenameFloat  "bayesian_ridge_float.onnx"
#define   ONNXFilenameDouble "bayesian_ridge_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

BayesianRidge (EURUSD,H1)       Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx)
BayesianRidge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382627587808
BayesianRidge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475682837447049
BayesianRidge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781600542671896
BayesianRidge (EURUSD,H1)       
BayesianRidge (EURUSD,H1)       Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx)
BayesianRidge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382628120845
BayesianRidge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3475680128537624
BayesianRidge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781593489128866

Comparison with the original double model in Python:

Testing ONNX float: BayesianRidge (bayesian_ridge_float.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475682837447049

Testing ONNX double: BayesianRidge (bayesian_ridge_double.onnx)
Python  Mean Absolute Error: 6.347568012853758
MQL5:   Mean Absolute Error: 6.3475680128537624

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.2.3. ONNX representation of bayesian_ridge_float.onnx and bayesian_ridge_double.onnx

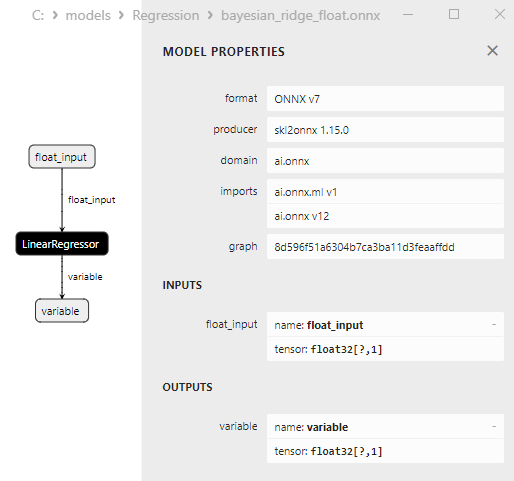
Fig.13. ONNX representation of the bayesian_ridge_float.onnx in Netron

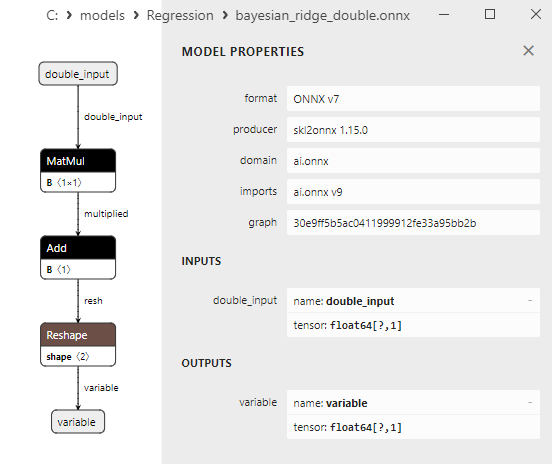
Fig.14. ONNX representation of the bayesian_ridge_double.onnx in Netron

Note on ElasticNet and ElasticNetCV Methods

ElasticNet and ElasticNetCV are two related machine learning methods used for regularizing regression models, especially linear regression. They share common functionality but differ in their manner of use and application.

    ElasticNet (Elastic Net Regression):

• Working Principle: ElasticNet is a regression method that combines Lasso (L1 regularization) and Ridge (L2 regularization). It adds two regularization components to the loss function: one penalizes the model for large absolute values of coefficients (like Lasso), and the other penalizes the model for large squares of coefficients (like Ridge).
• ElasticNet is commonly used when there is multicollinearity in the data (when features are highly correlated) and when dimensionality reduction is needed, as well as controlling coefficient values.

    ElasticNetCV (Elastic Net Cross-Validation):

• Working Principle: ElasticNetCV is an extension of ElasticNet that involves automatically selecting optimal hyperparameters alpha (the mixing coefficient between L1 and L2 regularization) and lambda (the regularization strength) using cross-validation. It iterates through various alpha and lambda values, choosing the combination that performs best in cross-validation.
• Advantages: ElasticNetCV automatically tunes model parameters based on cross-validation, allowing for the selection of optimal hyperparameter values without the need for manual tuning. This makes it more convenient to use and helps prevent model overfitting.

Thus, the main difference between ElasticNet and ElasticNetCV is that ElasticNet is the regression method applied to data, while ElasticNetCV is a tool that automatically finds optimal hyperparameter values for the ElasticNet model using cross-validation. ElasticNetCV is helpful when you need to find the best model parameters and make the tuning process more automated.

2.1.3. sklearn.linear_model.ElasticNet

ElasticNet is a regression method that represents a combination of L1 (Lasso) and L2 (Ridge) regularization.

This method is used for regression, which means predicting numerical values of a target variable based on a set of features. ElasticNet helps control overfitting and considers both L1 and L2 penalties on model coefficients.

Operation Principle of ElasticNet:

1. Input Data: It starts with the original dataset where we have features (independent variables) and corresponding values of the target variable.
2. Objective Function: ElasticNet minimizes the loss function that includes two components - mean squared error (MSE) and two regularizations: L1 (Lasso) and L2 (Ridge). This means the objective function looks like this:
   Objective Function = MSE + α * L1 + β * L2
   Where α and β are hyperparameters that control the weights of L1 and L2 regularization, respectively.
3. Finding Optimal α and β: The method of cross-validation is usually used to find the best values of α and β. This allows selecting values that strike a balance between reducing overfitting and preserving essential features.
4. Model Training: ElasticNet trains the model considering the optimal α and β by minimizing the objective function.
5. Prediction: After the model is trained, ElasticNet can be used to predict target variable values for new data.

Advantages of ElasticNet:

• Feature Selection Capability: ElasticNet can automatically select the most important features by setting weights to zero for insignificant features (similar to Lasso).
• Overfitting Control: ElasticNet allows controlling overfitting due to L1 and L2 regularization.
• Dealing with Multicollinearity: This method is useful when multicollinearity exists (high correlation between features) as L2 regularization can reduce the influence of multicollinear features.

Limitations of ElasticNet:

• Requires tuning of hyperparameters α and β, which can be a non-trivial task.
• Depending on parameter choices, ElasticNet may retain too few or too many features, affecting the model's quality.

ElasticNet is a powerful regression method that can be beneficial in tasks where feature selection and overfitting control are crucial.

2.1.3.1. Code for creating the ElasticNet model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.ElasticNet model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# ElasticNet.py
# The code demonstrates the process of training ElasticNet model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ElasticNet"
onnx_model_filename = data_path + "elastic_net"

# create an ElasticNet model
regression_model = ElasticNet()

# fit the model to the data
regression_model.fit(X,y)

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  ElasticNet Original model (double)
Python  R-squared (Coefficient of determination): 0.9962377031744798
Python  Mean Absolute Error: 6.344394662876524
Python  Mean Squared Error: 49.78556489812415
Python  
Python  ElasticNet ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962377032416807
Python  Mean Absolute Error: 6.344395027824294
Python  Mean Squared Error: 49.78556400887057
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  6
Python  float ONNX model precision:  5
Python  
Python  ElasticNet ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962377031744798
Python  Mean Absolute Error: 6.344394662876524
Python  Mean Squared Error: 49.78556489812415
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

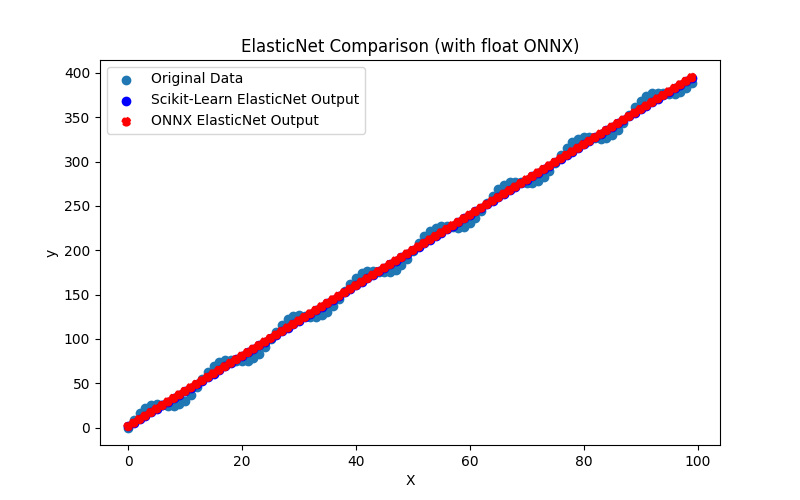
Fig.15. Results of the ElasticNet.py (float ONNX)

2.1.3.2. MQL5 code for executing ONNX Models

This code executes the saved elastic_net_double.onnx and elastic_net_float.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                   ElasticNet.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ElasticNet"
#define   ONNXFilenameFloat  "elastic_net_float.onnx"
#define   ONNXFilenameDouble "elastic_net_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

ElasticNet (EURUSD,H1)  Testing ONNX float: ElasticNet (elastic_net_float.onnx)
ElasticNet (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9962377032416807
ElasticNet (EURUSD,H1)  MQL5:   Mean Absolute Error: 6.3443950278242944
ElasticNet (EURUSD,H1)  MQL5:   Mean Squared Error: 49.7855640088705869
ElasticNet (EURUSD,H1)  
ElasticNet (EURUSD,H1)  Testing ONNX double: ElasticNet (elastic_net_double.onnx)
ElasticNet (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9962377031744798
ElasticNet (EURUSD,H1)  MQL5:   Mean Absolute Error: 6.3443946628765220
ElasticNet (EURUSD,H1)  MQL5:   Mean Squared Error: 49.7855648981241217

Comparison with the original double model in Python:

Testing ONNX float: ElasticNet (elastic_net_float.onnx)
Python  Mean Absolute Error: 6.344394662876524
MQL5:   Mean Absolute Error: 6.3443950278242944
  
Testing ONNX double: ElasticNet (elastic_net_double.onnx)
Python  Mean Absolute Error: 6.344394662876524
MQL5:   Mean Absolute Error: 6.3443946628765220

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.3.3. ONNX representation of elastic_net_float.onnx and elastic_net_double.onnx

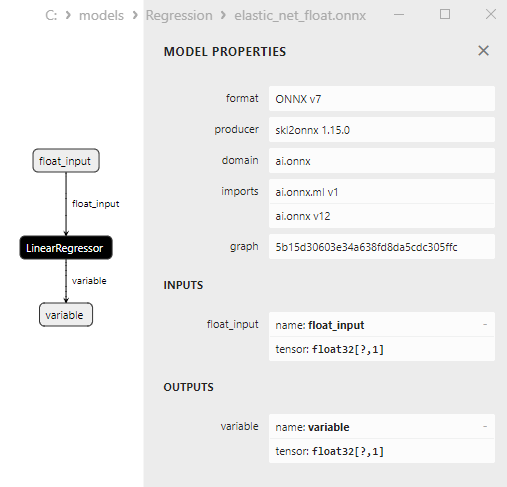
Fig.16. ONNX representation of the elastic_net_float.onnx in Netron

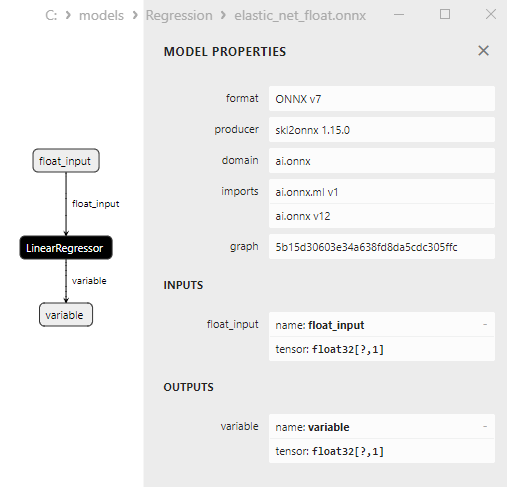
Fig.17. ONNX representation of the elastic_net_double.onnx in Netron

2.1.4. sklearn.linear_model.ElasticNetCV

ElasticNetCV is an extension of the ElasticNet method designed for automatically selecting optimal values of hyperparameters α and β (L1 and L2 regularization) using cross-validation

This allows finding the best combination of regularizations for the ElasticNet model without the need for manual parameter tuning.

Operation Principle of ElasticNetCV:

1. Input Data: It begins with the original dataset containing features (independent variables) and their corresponding target variable values.
2. Defining the α and β Range: The user specifies the range of values for α and β to be considered during optimization. These values are typically chosen on a logarithmic scale.
3. Data Splitting: The dataset is divided into multiple folds for cross-validation. Each fold is used as a test dataset while the others are used for training.
4. Cross-Validation: For each combination of α and β within the specified range, cross-validation is performed. The ElasticNet model is trained on the training data and then evaluated on the test data.
5. Performance Evaluation: The average error on test datasets in the cross-validation is computed for each α and β combination.
6. Selection of Optimal Parameters: Values of α and β corresponding to the minimum average error obtained during cross-validation are determined.
7. Model Training with Optimal Parameters: The ElasticNetCV model is trained using the found optimal values of α and β.
8. Prediction: After training, the model can be used to predict target variable values for new data.

Advantages of ElasticNetCV:

• Automatic Hyperparameter Selection: ElasticNetCV automatically finds optimal values of α and β, simplifying model tuning.
• Overfitting Prevention: Cross-validation aids in selecting a model with good generalization ability.
• Noise Robustness: This method is robust against data noise and can identify the best combination of regularizations while considering noise.

Limitations of ElasticNetCV:

• Computational Complexity: Performing cross-validation over a large parameter range can be time-consuming.
• Optimal Parameters Depend on the Range Choice: Results might depend on the choice of the α and β range, so it's important to carefully adjust this range.

ElasticNetCV is a powerful tool for automatically tuning regularization in the ElasticNet model and enhancing its performance.

2.1.4.1. Code for creating the ElasticNetCV model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.ElasticNetCV model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# ElasticNetCV.py
# The code demonstrates the process of training ElasticNetCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNetCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ElasticNetCV"
onnx_model_filename = data_path + "elastic_net_cv"

# create an ElasticNetCV model
regression_model = ElasticNetCV()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  ElasticNetCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962137763338385
Python  Mean Absolute Error: 6.334487104423225
Python  Mean Squared Error: 50.10218299945999
Python  
Python  ElasticNetCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962137770260989
Python  Mean Absolute Error: 6.334486542922601
Python  Mean Squared Error: 50.10217383894468
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  ElasticNetCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\elastic_net_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962137763338385
Python  Mean Absolute Error: 6.334487104423225
Python  Mean Squared Error: 50.10218299945999
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

<

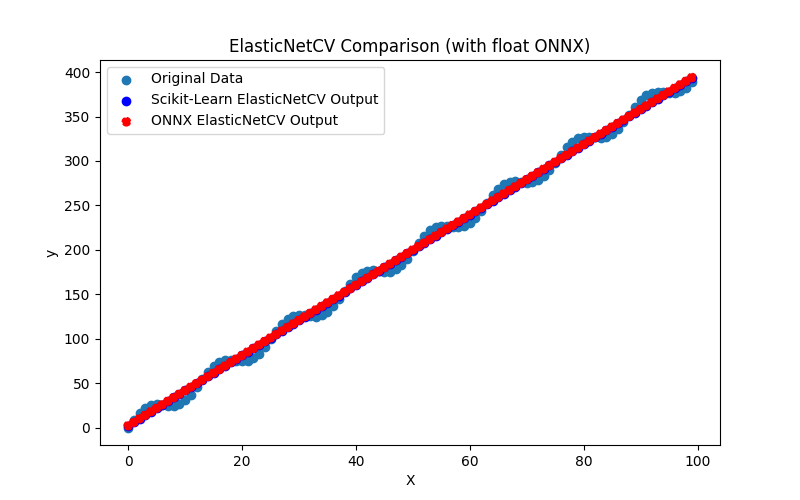
Fig.18. Results of the ElasticNetCV.py (float ONNX)

2.1.4.2. MQL5 code for executing ONNX Models

This code executes the saved elastic_net_cv_float.onnx and elastic_net_cv_double.onnx ONNX models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                 ElasticNetCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ElasticNetCV"
#define   ONNXFilenameFloat  "elastic_net_cv_float.onnx"
#define   ONNXFilenameDouble "elastic_net_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

ElasticNetCV (EURUSD,H1)        Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx)
ElasticNetCV (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962137770260989
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3344865429226038
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Squared Error: 50.1021738389446938
ElasticNetCV (EURUSD,H1)        
ElasticNetCV (EURUSD,H1)        Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx)
ElasticNetCV (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962137763338385
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3344871044232205
ElasticNetCV (EURUSD,H1)        MQL5:   Mean Squared Error: 50.1021829994599983

Comparison with the original double model in Python:

Testing ONNX float: ElasticNetCV (elastic_net_cv_float.onnx)
Python  Mean Absolute Error: 6.334487104423225
MQL5:   Mean Absolute Error: 6.3344865429226038

Testing ONNX double: ElasticNetCV (elastic_net_cv_double.onnx)
Python  Mean Absolute Error: 6.334487104423225
MQL5:   Mean Absolute Error: 6.3344871044232205

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.4.3. ONNX representation of the elastic_net_cv_float.onnx and elastic_net_cv_double.onnx

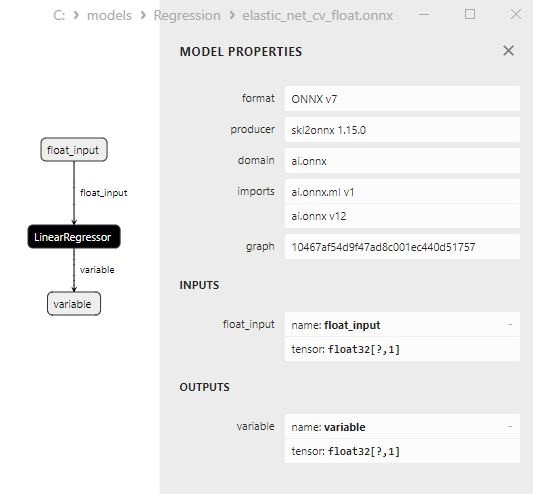
Fig.19. ONNX representation of the elastic_net_cv_float.onnx in Netron

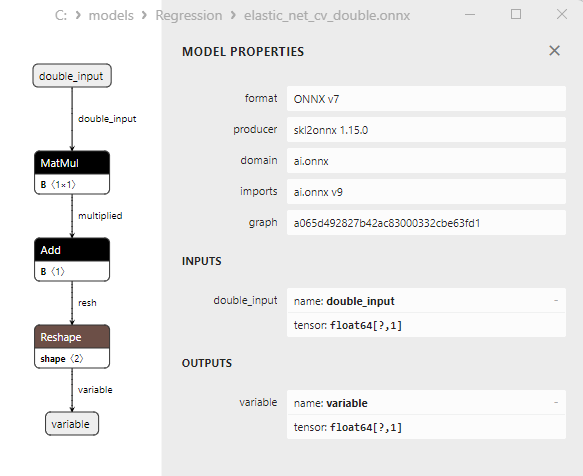
Fig.20. ONNX representation of the elastic_net_cv_double.onnx in Netron

2.1.5. sklearn.linear_model.HuberRegressor

HuberRegressor - is a machine learning method used for regression tasks, which is a modification of the Ordinary Least Squares (OLS) method and is designed to be robust to outliers in the data.

Unlike OLS, which minimizes the squares of errors, HuberRegressor minimizes a combination of squared errors and absolute errors. This allows the method to work more robustly in the presence of outliers in the data.

Working Principle of HuberRegressor:

1. Input Data: It starts with the original dataset, where there are features (independent variables) and their corresponding target variable values.
2. Huber Loss Function: HuberRegressor utilizes the Huber loss function, which combines a quadratic loss function for small errors and a linear loss function for large errors. This makes the method more resilient to outliers.
3. Model Training: The model is trained on data using the Huber loss function. During training, it adjusts the weights (coefficients) for each feature and the bias.
4. Prediction: After training, the model can be used to predict target variable values for new data.

Advantages of HuberRegressor:

• Robustness to Outliers: HuberRegressor is more robust to outliers in the data compared to OLS, making it useful in tasks where data might contain anomalous values.
• Error Estimation: The Huber loss function contributes to the estimation of prediction errors, which can be useful for analyzing model results.
• Regularization Level: HuberRegressor can also incorporate a level of regularization, which can reduce overfitting.

Limitations of HuberRegressor:

• Not as Accurate as OLS in the Absence of Outliers: In cases where there are no outliers in the data, OLS might provide more accurate results.
• Parameter Tuning: HuberRegressor has a parameter that defines the threshold for what is considered "large" to switch to the linear loss function. This parameter requires tuning.

HuberRegressor is valuable in regression tasks where data may contain outliers, and a model that is robust to such anomalies is required.

2.1.5.1. Code for creating the HuberRegressor model and exporting it to ONNX for float and double

This code creates the  sklearn.linear_model.HuberRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX..

# HuberRegressor.py
# The code demonstrates the process of training HuberRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import HuberRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "HuberRegressor"
onnx_model_filename = data_path + "huber_regressor"

# create a Huber Regressor model
huber_regressor_model = HuberRegressor()

# fit the model to the data
huber_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = huber_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(huber_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(huber_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  HuberRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9962363935647066
Python  Mean Absolute Error: 6.341633708569641
Python  Mean Squared Error: 49.80289464784336
Python  
Python  HuberRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962363944236795
Python  Mean Absolute Error: 6.341633300252807
Python  Mean Squared Error: 49.80288328126165
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  HuberRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\huber_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962363935647066
Python  Mean Absolute Error: 6.341633708569641
Python  Mean Squared Error: 49.80289464784336
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

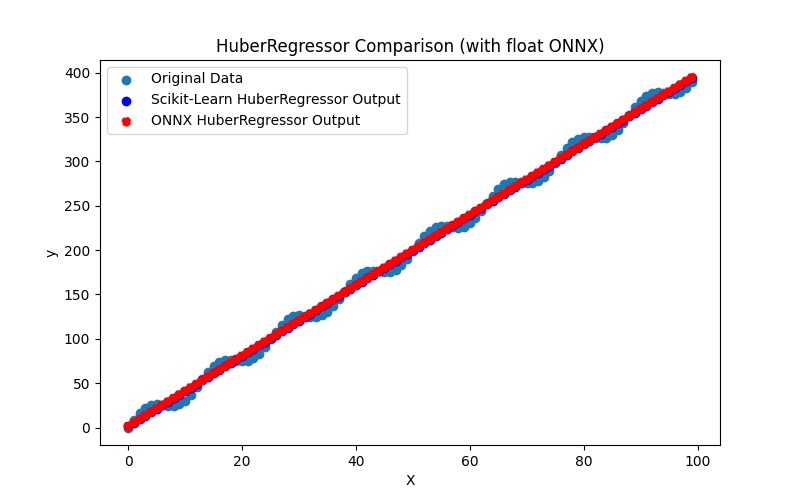
Fig.21. Results of the HuberRegressor.py (float ONNX)

2.1.5.2. MQL5 code for executing ONNX Models

This code executes the saved huber_regressor_float.onnx and huber_regressor_double.onnx ONNX models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                               HuberRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "HuberRegressor"
#define   ONNXFilenameFloat  "huber_regressor_float.onnx"
#define   ONNXFilenameDouble "huber_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

HuberRegressor (EURUSD,H1)      Testing ONNX float: HuberRegressor (huber_regressor_float.onnx)
HuberRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962363944236795
HuberRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3416333002528074
HuberRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 49.8028832812616571
HuberRegressor (EURUSD,H1)      
HuberRegressor (EURUSD,H1)      Testing ONNX double: HuberRegressor (huber_regressor_double.onnx)
HuberRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962363935647066
HuberRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3416337085696410
HuberRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 49.8028946478433525

Comparison with the original double model in Python:

Testing ONNX float: HuberRegressor (huber_regressor_float.onnx)
Python  Mean Absolute Error: 6.341633708569641
MQL5:   Mean Absolute Error: 6.3416333002528074
      
Testing ONNX double: HuberRegressor (huber_regressor_double.onnx)
Python  Mean Absolute Error: 6.341633708569641
MQL5:   Mean Absolute Error: 6.3416337085696410

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.5.3. ONNX representation of the huber_regressor_float.onnx and huber_regressor_double.onnx

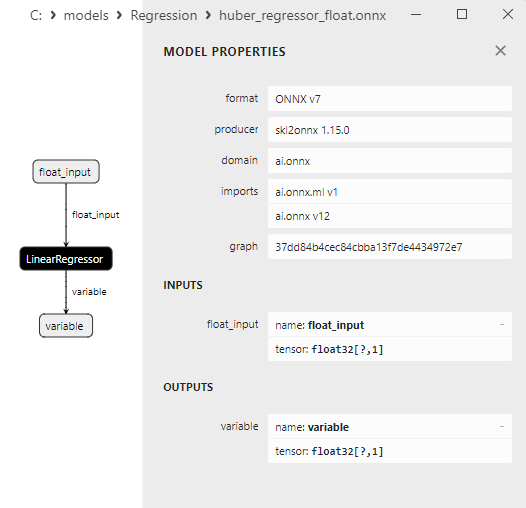
Fig.22. ONNX representation of the huber_regressor_float.onnx in Netron

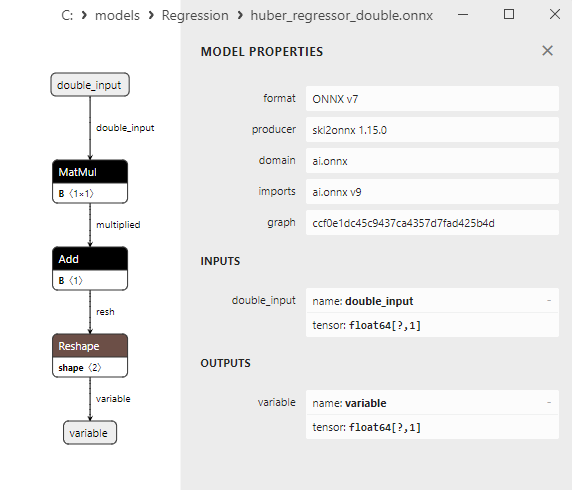
Fig.23. ONNX representation of the huber_regressor_double.onnx in Netron

2.1.6. sklearn.linear_model.Lars

LARS (Least Angle Regression) is a machine learning method used for regression tasks. It's an algorithm that constructs a linear regression model by selecting active features (variables) during the learning process

LARS attempts to find the fewest features that provide the best approximation to the target variable.

Working Principle of LARS:

1. Input Data: It starts with the original dataset, comprising features (independent variables) and their corresponding target variable values.
2. Initialization: It begins with a null model, meaning no active features. All coefficients are set to zero.
3. Feature Selection: At each step, LARS selects the feature most correlated with the model's residuals. This feature is then added to the model, and its corresponding coefficient is adjusted using the least squares method.
4. Regression Along Active Features: After adding the feature to the model, LARS updates the coefficients of all active features to accommodate changes in the new model.
5. Repetitive Steps: This process continues until all features are selected or a specified stopping criterion is met.
6. Prediction: After model training, it can be used to predict target variable values for new data.

Advantages of LARS:

• Efficiency: LARS can be an efficient method, especially when there are many features, but only a few significantly affect the target variable.
• Interpretability: Since LARS aims to select only the most informative features, the model remains relatively interpretable.

Limitations of LARS:

• Linear Model: LARS builds a linear model, which might be insufficient for modeling complex nonlinear relationships.
• Noise Sensitivity: The method can be sensitive to outliers in the data.
• Inability to Handle Multicollinearity: If features are highly correlated, LARS might encounter multicollinearity issues.

LARS is valuable in regression tasks where selecting the most informative features and constructing a linear model with a minimal number of features is essential.

2.1.6.1. Code for creating the Lars model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.Lars model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# Lars.py
# The code demonstrates the process of training Lars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "Lars"
onnx_model_filename = data_path + "lars"

# create a Lars Regressor model
lars_regressor_model = Lars()

# fit the model to the data
lars_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = lars_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(lars_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(lars_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  Lars Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  
Python  Lars ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  Lars ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  15

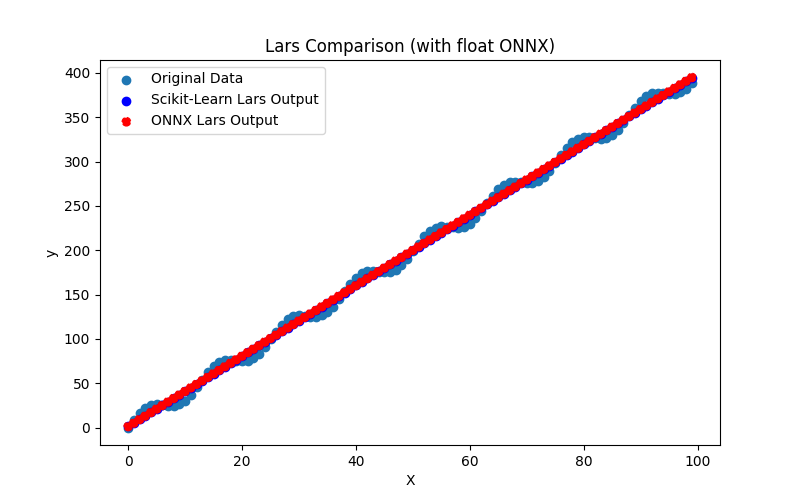
Fig.24. Results of the Lars.py (float ONNX)

2.1.6.2. MQL5 code for executing ONNX Models

This code executes the saved lars_cv_float.onnx and lars_cv_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                         Lars.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "Lars"
#define   ONNXFilenameFloat  "lars_float.onnx"
#define   ONNXFilenameDouble "lars_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

Lars (EURUSD,H1)        Testing ONNX float: Lars (lars_float.onnx)
Lars (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
Lars (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3477377671679385
Lars (EURUSD,H1)        MQL5:   Mean Squared Error: 49.7781414740478638
Lars (EURUSD,H1)        
Lars (EURUSD,H1)        Testing ONNX double: Lars (lars_double.onnx)
Lars (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
Lars (EURUSD,H1)        MQL5:   Mean Absolute Error: 6.3477379263364302
Lars (EURUSD,H1)        MQL5:   Mean Squared Error: 49.7781401712817768

Comparison with the original double model in Python:

Testing ONNX float: Lars (lars_float.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477377671679385

Testing ONNX double: Lars (lars_double.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477379263364302

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.6.3. ONNX representation of the lars_float.onnx and lars_double.onnx

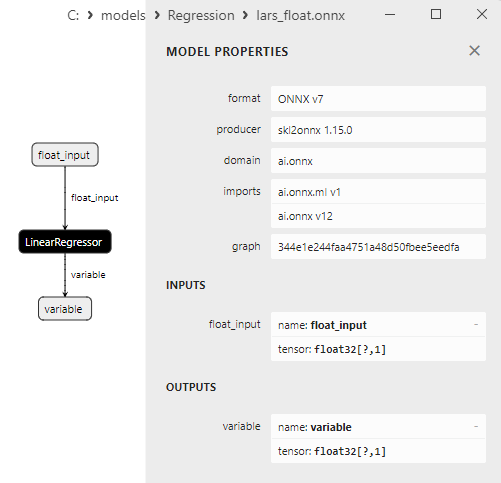
Fig.25. ONNX representation of the lars_float.onnx in Netron

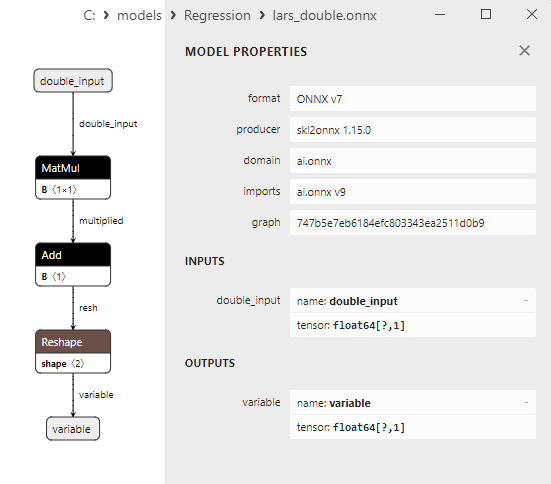
Fig.26. ONNX representation of lars_double.onnx in Netron

2.1.7. sklearn.linear_model.LarsCV

LarsCV is a variation of the LARS (Least Angle Regression) method that automatically selects the optimal number of features to include in the model using cross-validation.

This method helps strike a balance between a model that generalizes data effectively and one that uses a minimal number of features.

Working Principle of LarsCV:

1. Input Data: It begins with the original dataset, comprising features (independent variables) and their corresponding target variable values.
2. Initialization: It starts with a null model, which means no active features. All coefficients are set to zero.
3. Cross-Validation: LarsCV performs cross-validation for different quantities of included features. This evaluates the model's performance with different sets of features.
4. Selecting the Optimal Number of Features: LarsCV chooses the number of features that yields the best model performance, as determined through cross-validation.
5. Model Training: The model is trained using the chosen number of features and their respective coefficients.
6. Prediction: After training, the model can be used to predict target variable values for new data.

Advantages of LarsCV:

• Automatic Feature Selection: LarsCV automatically chooses the optimal number of features, simplifying the model setup process.
• Interpretability: Similar to the regular LARS, LarsCV maintains relatively high model interpretability.
• Efficiency: The method can be efficient, especially when datasets have many features, but only a few are significant.

Limitations of LarsCV:

• Linear Model: LarsCV constructs a linear model, which might be insufficient for modeling complex nonlinear relationships.
• Noise Sensitivity: The method can be sensitive to outliers in the data.
• Inability to Handle Multicollinearity: If features are highly correlated, LarsCV might encounter multicollinearity issues.

LarsCV is useful in regression tasks where automatically choosing the best set of features used in the model and maintaining model interpretability are important.

2.1.7.1. Code for creating the LarsCV model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LarsCV model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LarsCV.py
# The code demonstrates the process of training LarsCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LarsCV"
onnx_model_filename = data_path + "lars_cv"

# create a LarsCV Regressor model
larscv_regressor_model = LarsCV()

# fit the model to the data
larscv_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = larscv_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(larscv_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(larscv_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LarsCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  
Python  LarsCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382640824089
Python  Mean Absolute Error: 6.347737845846069
Python  Mean Squared Error: 49.778142539016564
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LarsCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lars_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  16

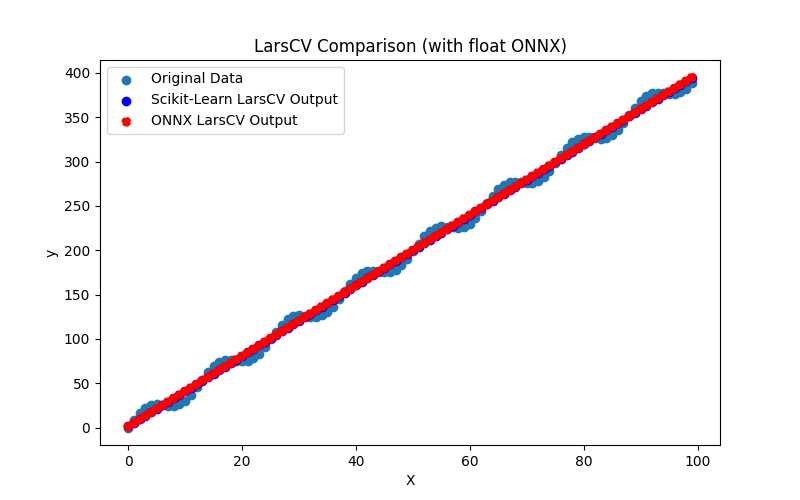
Fig.27. Results of the LarsCV.py (float ONNX)

2.1.7.2. MQL5 code for executing ONNX Models

This code executes the saved lars_cv_float.onnx and lars_cv_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                       LarsCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LarsCV"
#define   ONNXFilenameFloat  "lars_cv_float.onnx"
#define   ONNXFilenameDouble "lars_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

LarsCV (EURUSD,H1)      Testing ONNX float: LarsCV (lars_cv_float.onnx)
LarsCV (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962382640824089
LarsCV (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3477378458460691
LarsCV (EURUSD,H1)      MQL5:   Mean Squared Error: 49.7781425390165566
LarsCV (EURUSD,H1)      
LarsCV (EURUSD,H1)      Testing ONNX double: LarsCV (lars_cv_double.onnx)
LarsCV (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.9962382642612767
LarsCV (EURUSD,H1)      MQL5:   Mean Absolute Error: 6.3477379221400145
LarsCV (EURUSD,H1)      MQL5:   Mean Squared Error: 49.7781401721031642

Comparison with the original double precision model in Python:

Testing ONNX float: LarsCV (lars_cv_float.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477378458460691

Testing ONNX double: LarsCV (lars_cv_double.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477379221400145

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 16 decimal places.

2.1.7.3. ONNX representation of the lars_cv_float.onnx and lars_cv_double.onnx

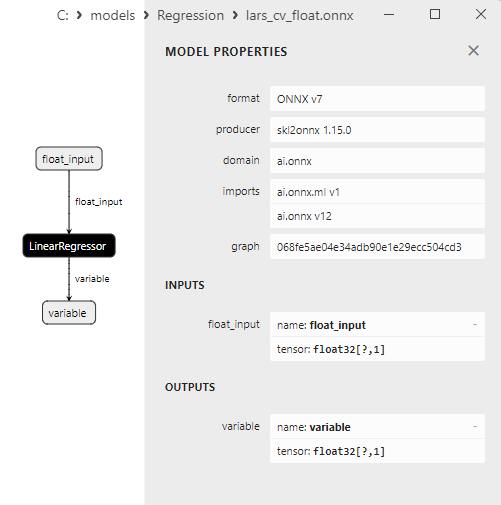
Fig.28. ONNX representation of the lars_cv_float.onnx in Netron

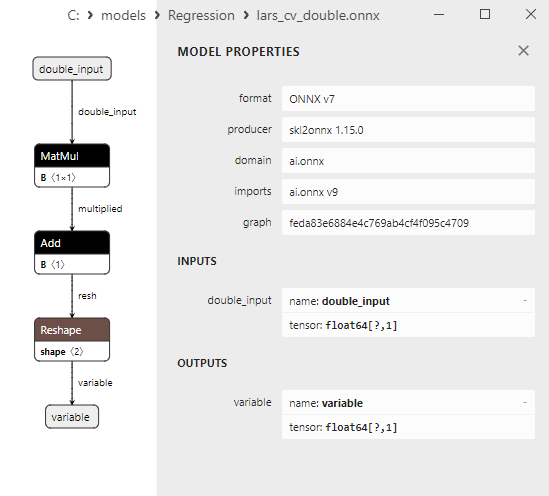
Fig.29. ONNX representation of the lars_cv_double.onnx in Netron

2.1.8. sklearn.linear_model.Lasso

Lasso (Least Absolute Shrinkage and Selection Operator) is a regression method used to select the most important features and reduce model dimensionality.

It achieves this by adding a penalty for the sum of the absolute values of the coefficients (L1 regularization) in the linear regression optimization problem.

Working Principle of Lasso:

1. Input Data: It begins with the original dataset, including features (independent variables) and their corresponding target variable values.
2. Objective Function: The objective function in Lasso includes the sum of squared regression errors and a penalty on the sum of the absolute values of coefficients associated with features.
3. Optimization: The Lasso model is trained by minimizing the objective function, resulting in some coefficients becoming zero, effectively excluding the corresponding features from the model.
4. Selecting the Optimal Penalty Value: Lasso includes a hyperparameter that determines the strength of regularization. Choosing the optimal value for this hyperparameter may require cross-validation.
5. Generating Predictions: After training, the model can be used to predict target variable values for new data.

Advantages of Lasso:

• Feature Selection: Lasso automatically selects the most important features, excluding less significant ones from the model. This reduces data dimensionality and simplifies the model.
• Regularization: The penalty on the sum of the absolute values of coefficients helps prevent model overfitting and enhances its generalization.
• Interpretability: As Lasso excludes some features, the model remains relatively interpretable.

Limitations of Lasso:

• Linear Model: Lasso constructs a linear model, which might be insufficient for modeling complex nonlinear relationships.
• Noise Sensitivity: The method can be sensitive to outliers in the data.
• Inability to Handle Multicollinearity: If features are highly correlated, Lasso might encounter multicollinearity problems.

Lasso is useful in regression tasks where selecting the most important features and reducing the model's dimensionality while maintaining interpretability are essential.

2.1.8.1. Code for creating the Lasso model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.Lasso model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX..

# Lasso.py
# The code demonstrates the process of training Lasso model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "Lasso"
onnx_model_filename = data_path + "lasso"

# create a Lasso model
lasso_model = Lasso()

# fit the model to the data
lasso_model.fit(X, y)

# predict values for the entire dataset
y_pred = lasso_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  Lasso Original model (double)
Python  R-squared (Coefficient of determination): 0.9962381735682287
Python  Mean Absolute Error: 6.346393791922984
Python  Mean Squared Error: 49.77934029129379
Python  
Python  Lasso ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962381720269486
Python  Mean Absolute Error: 6.346395056911361
Python  Mean Squared Error: 49.77936068668213
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  Lasso ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962381735682287
Python  Mean Absolute Error: 6.346393791922984
Python  Mean Squared Error: 49.77934029129379
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

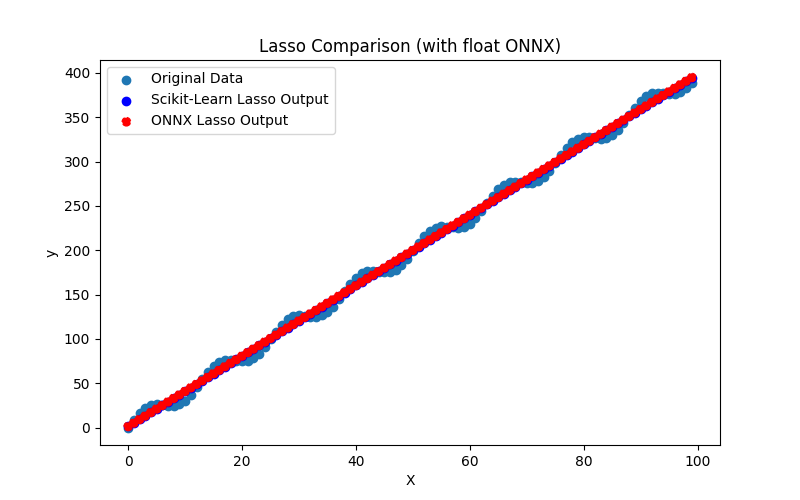
Fig.30. Results of the Lasso.py (float ONNX)

2.1.8.2. MQL5 code for executing ONNX Models

This code executes the saved lasso_float.onnx and lasso_double.onnx and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                        Lasso.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "Lasso"
#define   ONNXFilenameFloat  "lasso_float.onnx"
#define   ONNXFilenameDouble "lasso_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

Lasso (EURUSD,H1)       Testing ONNX float: Lasso (lasso_float.onnx)
Lasso (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962381720269486
Lasso (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3463950569113612
Lasso (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7793606866821037
Lasso (EURUSD,H1)       
Lasso (EURUSD,H1)       Testing ONNX double: Lasso (lasso_double.onnx)
Lasso (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962381735682287
Lasso (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3463937919229840
Lasso (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7793402912937850

Comparison with the original double model in Python:

Testing ONNX float: Lasso (lasso_float.onnx)
Python  Mean Absolute Error: 6.346393791922984
MQL5:   Mean Absolute Error: 6.3463950569113612

Testing ONNX double: Lasso (lasso_double.onnx)
Python  Mean Absolute Error: 6.346393791922984
MQL5:   Mean Absolute Error: 6.3463937919229840

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 15 decimal places.

2.1.8.3. ONNX representation of the lasso_float.onnx and lasso_double.onnx

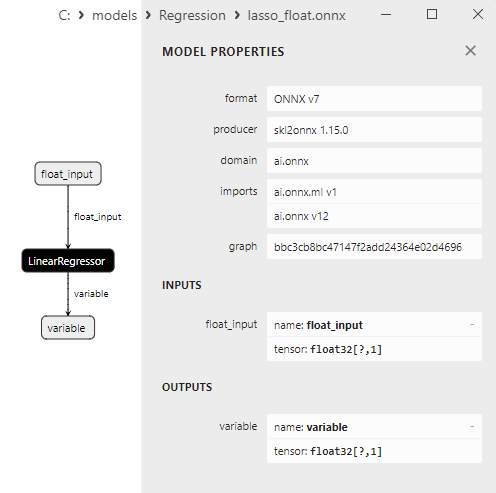
Fig.31. ONNX representation of the lasso_float.onnx in Netron

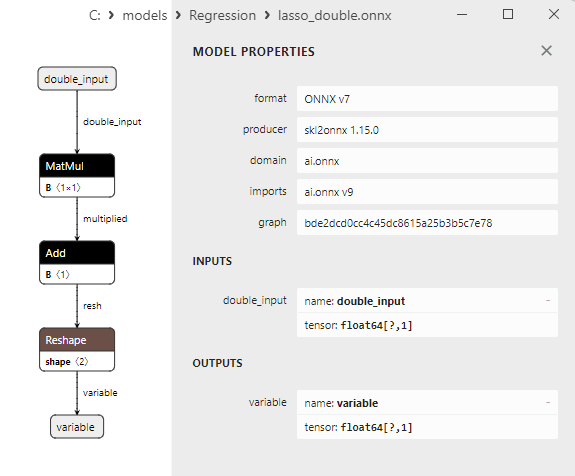
Fig.32. ONNX representation of the lasso_double.onnx in Netron

2.1.9. sklearn.linear_model.LassoCV

LassoCV  is a variant of the Lasso method (Least Absolute Shrinkage and Selection Operator) that automatically selects the optimal value for the regularization hyperparameter (alpha) using cross-validation.

This method enables finding a balance between reducing the model's dimensionality (selecting important features) and preventing overfitting, making it useful for regression tasks.

Working Principle of LassoCV:

1. Input Data: It starts with the original dataset, including features (independent variables) and their corresponding target variable values.
2. Initialization: LassoCV initializes several different values of the regularization hyperparameter (alpha) that cover a range from low to high.
3. Cross-Validation: For each alpha value, LassoCV performs cross-validation to assess the model's performance. Metrics like mean squared error (MSE) or coefficient of determination (R^2) are commonly used.
4. Selecting the Optimal Alpha: LassoCV selects the alpha value where the model achieves the best performance as determined by cross-validation.
5. Model Training: The Lasso model is trained using the chosen alpha value, excluding less important features and applying L1 regularization.
6. Generating Predictions: After training, the model can be used to predict target variable values for new data.

Advantages of LassoCV:

• Automatic Alpha Selection: LassoCV automatically selects the optimal alpha value using cross-validation, simplifying model tuning.
• Feature Selection: LassoCV automatically chooses the most important features, reducing the model's dimensionality and simplifying its interpretation.
• Regularization: The method prevents model overfitting through L1 regularization.

Limitations of LassoCV:

• Linear Model: LassoCV builds a linear model, which might be insufficient for modeling complex nonlinear relationships.
• Noise Sensitivity: The method can be sensitive to outliers in the data.
• Inability to Handle Multicollinearity: When features are highly correlated, LassoCV might face multicollinearity problems.

LassoCV is beneficial in regression tasks where selecting the most important features and reducing the model's dimensionality while maintaining interpretability and preventing overfitting are important.

2.1.9.1. Code for creating the LassoCV model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LassoCV model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LassoCV.py
# The code demonstrates the process of training LassoCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LassoCV"
onnx_model_filename = data_path + "lasso_cv"

# create a LassoCV Regressor model
lassocv_regressor_model = LassoCV()

# fit the model to the data
lassocv_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = lassocv_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(lassocv_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LassoCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962241428413416
Python  Mean Absolute Error: 6.33567334453819
Python  Mean Squared Error: 49.96500551028169
Python  
Python  LassoCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.996224142876629
Python  Mean Absolute Error: 6.335673221332177
Python  Mean Squared Error: 49.96500504333324
Python  R^2 matching decimal places:  10
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  6
Python  float ONNX model precision:  6
Python  
Python  LassoCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962241428413416
Python  Mean Absolute Error: 6.33567334453819
Python  Mean Squared Error: 49.96500551028169
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  14

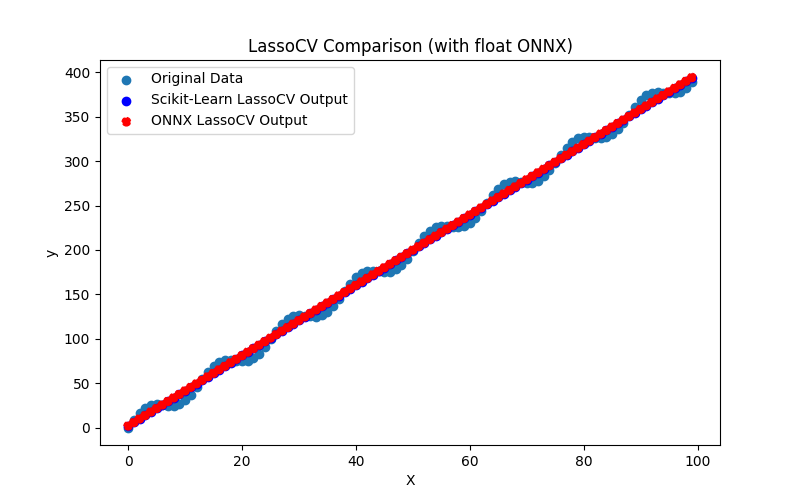
Fig.33. Results of the LassoCV.py (float ONNX)

2.1.9.2. MQL5 code for executing ONNX Models

This code executes the saved lasso_cv_float.onnx and lasso_cv_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                      LassoCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoCV"
#define   ONNXFilenameFloat  "lasso_cv_float.onnx"
#define   ONNXFilenameDouble "lasso_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

2023.10.26 22:14:00.736 LassoCV (EURUSD,H1)     Testing ONNX float: LassoCV (lasso_cv_float.onnx)
2023.10.26 22:14:00.739 LassoCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962241428766290
2023.10.26 22:14:00.739 LassoCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3356732213321800
2023.10.26 22:14:00.739 LassoCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.9650050433332211
2023.10.26 22:14:00.748 LassoCV (EURUSD,H1)     
2023.10.26 22:14:00.748 LassoCV (EURUSD,H1)     Testing ONNX double: LassoCV (lasso_cv_double.onnx)
2023.10.26 22:14:00.753 LassoCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962241428413416
2023.10.26 22:14:00.753 LassoCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3356733445381899
2023.10.26 22:14:00.753 LassoCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.9650055102816992

Comparison with the original double model in Python:

Testing ONNX float: LassoCV (lasso_cv_float.onnx)
Python  Mean Absolute Error: 6.33567334453819
MQL5:   Mean Absolute Error: 6.3356732213321800
        
Testing ONNX double: LassoCV (lasso_cv_double.onnx)
Python  Mean Absolute Error: 6.33567334453819
MQL5:   Mean Absolute Error: 6.3356733445381899

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.9.3. ONNX representation of the lasso_cv_float.onnx and lasso_cv_double.onnx

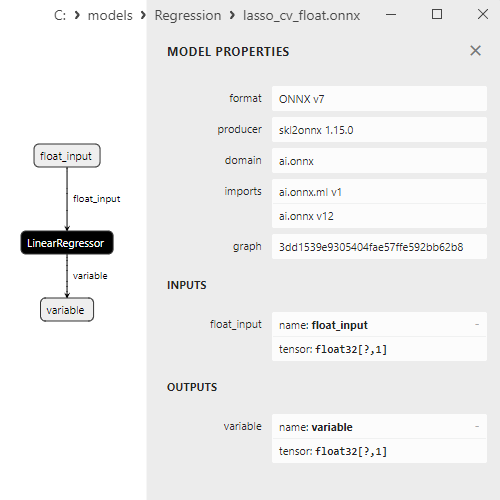
Fig.34. ONNX representation of the lasso_cv_float.onnx in Netron

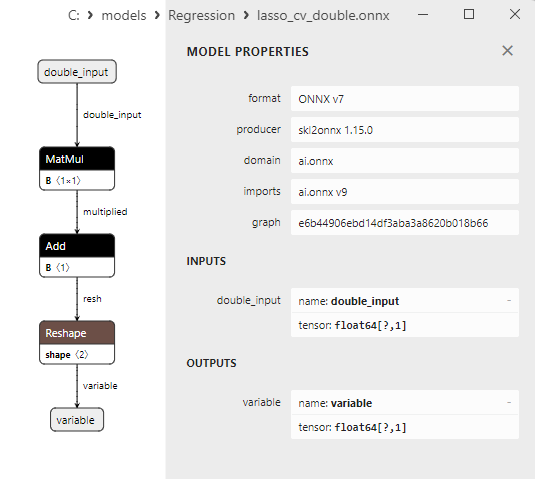
Fig.35. ONNX representation of the lasso_cv_double.onnx in Netron

2.1.10. sklearn.linear_model.LassoLars

LassoLars is a combination of two methods: Lasso (Least Absolute Shrinkage and Selection Operator) and LARS (Least Angle Regression).

This method is used for regression tasks and combines the advantages of both algorithms, allowing simultaneous feature selection and model dimensionality reduction.

Working Principle of LassoLars:

1. Input Data: It starts with the original dataset, including features (independent variables) and their corresponding target variable values.
2. Initialization: LassoLars begins with a null model, meaning no active features. All coefficients are set to zero.
3. Stepwise Feature Selection: Similar to the LARS method, LassoLars selects, at each step, the feature most correlated with the model residuals and adds it to the model. Then, the coefficient of this feature is adjusted using the least squares method.
4. Application of L1 Regularization: Simultaneously with stepwise feature selection, LassoLars applies L1 regularization, adding a penalty for the sum of the absolute values of coefficients. This allows modeling complex relationships and choosing the most important features.
5. Making Predictions: After training, the model can be used to predict target variable values for new data.

Advantages of LassoLars:

• Feature Selection: LassoLars automatically selects the most important features and reduces the model's dimensionality, aiding in avoiding overfitting and simplifying interpretation.
• Interpretability: The method maintains the model's interpretability, making it easy to determine which features are included and how they influence the target variable.
• Regularization: LassoLars applies L1 regularization, preventing overfitting and enhancing the model's generalization.

Limitations of LassoLars:

• Linear Model: LassoLars builds a linear model, which might be insufficient for modeling complex nonlinear relationships.
• Sensitivity to Noise: The method might be sensitive to outliers in the data.
• Computational Complexity: Feature selection at each step and applying regularization might require more computational resources than simple linear regression.

LassoLars is useful in regression tasks where it's important to choose the most important features, reduce the model's dimensionality, and maintain interpretability.

2.1.10.1. Code for creating the LassoLars model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LassoLars model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LassoLars.py
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLars
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LassoLars"
onnx_model_filename = data_path + "lasso_lars"

# create a LassoLars Regressor model
lassolars_regressor_model = LassoLars(alpha=0.1)

# fit the model to the data
lassolars_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = lassolars_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LassoLars Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382633544077
Python  Mean Absolute Error: 6.3476035128950805
Python  Mean Squared Error: 49.778152172481896
Python  
Python  LassoLars ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382635045889
Python  Mean Absolute Error: 6.3476034814795375
Python  Mean Squared Error: 49.77815018516975
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LassoLars ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382633544077
Python  Mean Absolute Error: 6.3476035128950805
Python  Mean Squared Error: 49.778152172481896
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  16

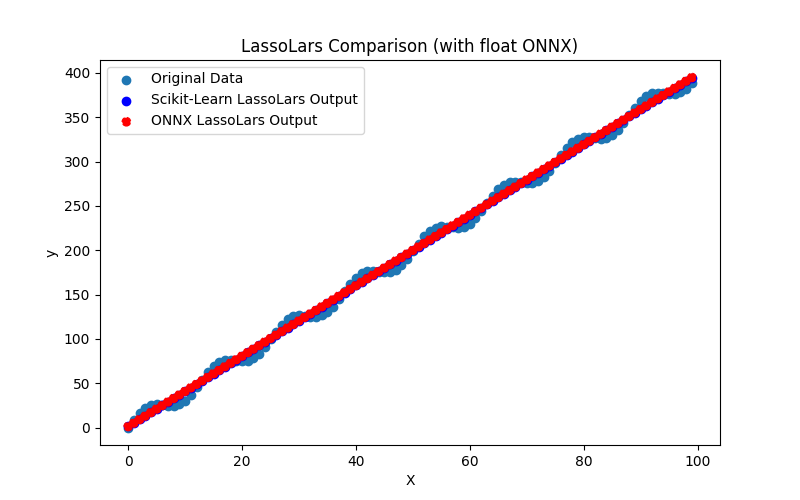
Fig.36. Result of the LassoLars.py (float)

2.1.10.2. MQL5 code for executing ONNX Models

This code executes the saved lasso_lars_float.onnx and lasso_lars_double.onnx and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                    LassoLars.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoLars"
#define   ONNXFilenameFloat  "lasso_lars_float.onnx"
#define   ONNXFilenameDouble "lasso_lars_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

LassoLars (EURUSD,H1)   Testing ONNX float: LassoLars (lasso_lars_float.onnx)
LassoLars (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382635045889
LassoLars (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3476034814795375
LassoLars (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781501851697357
LassoLars (EURUSD,H1)   
LassoLars (EURUSD,H1)   Testing ONNX double: LassoLars (lasso_lars_double.onnx)
LassoLars (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382633544077
LassoLars (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3476035128950858
LassoLars (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781521724819029

Comparison with the original double model in Python:

Testing ONNX float: LassoLars (lasso_lars_float.onnx)
Python  Mean Absolute Error: 6.3476035128950805
MQL5:   Mean Absolute Error: 6.3476034814795375

Testing ONNX double: LassoLars (lasso_lars_double.onnx)
Python  Mean Absolute Error: 6.3476035128950805
MQL5:   Mean Absolute Error: 6.3476035128950858

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.10.3. ONNX representation of the lasso_lars_float.onnx and lasso_lars_double.onnx

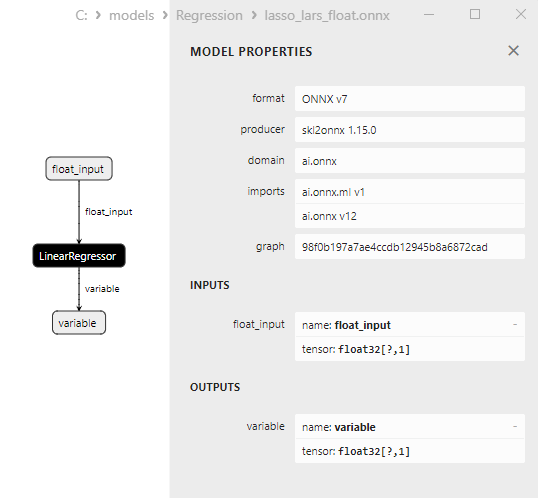
Fig.37. ONNX representation of the lasso_lars_float.onnx in Netron

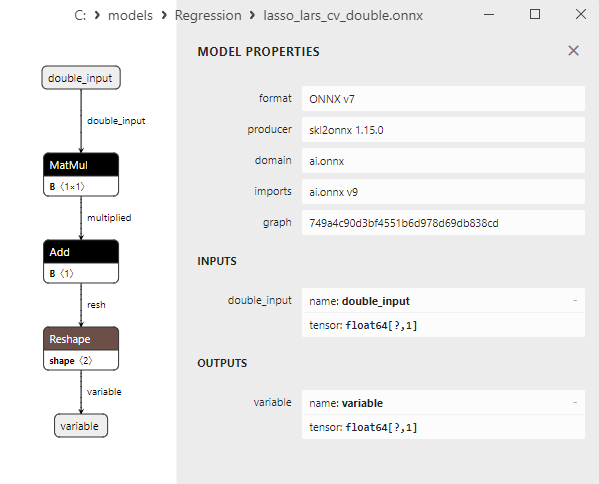
Fig.38. ONNX representation of the lasso_lars_double.onnx in Netron

2.1.11. sklearn.linear_model.LassoLarsCV

LassoLarsCV  is a method that combines Lasso (Least Absolute Shrinkage and Selection Operator) and LARS (Least Angle Regression) with automatic selection of the optimal regularization hyperparameter (alpha) using cross-validation.

This method combines the advantages of both algorithms and allows determining the optimal alpha value for the model, considering feature selection and regularization.

Working Principle of LassoLarsCV:

1. Input Data: It starts with the original dataset, including features (independent variables) and their corresponding target variable values.
2. Initialization: LassoLarsCV begins with a null model, where all coefficients are set to zero.
3. Definition of Alpha Range: A range of values for the hyperparameter alpha is determined, which will be considered during the selection process. Usually, a logarithmic scale of alpha values is used.
4. Cross-Validation: For each alpha value from the chosen range, LassoLarsCV performs cross-validation to evaluate the model's performance with this alpha value. Typically, metrics like mean squared error (MSE) or coefficient of determination (R^2) are used.
5. Selection of Optimal Alpha: LassoLarsCV chooses the alpha value where the model achieves the best performance based on the cross-validation results.
6. Model Training: The LassoLars model is trained using the selected alpha value, excluding less important features and applying L1 regularization.
7. Making Predictions: After training, the model can be used to predict target variable values for new data.

Advantages of LassoLarsCV:

• Automatic Alpha Selection: LassoLarsCV automatically selects the optimal hyperparameter alpha using cross-validation, simplifying model tuning.
• Feature Selection: LassoLarsCV automatically chooses the most important features and reduces the model's dimensionality.
• Regularization: The method applies L1 regularization, preventing overfitting and enhancing the model's generalization.

Limitations of LassoLarsCV:

• Linear Model: LassoLarsCV builds a linear model, which might be insufficient for modeling complex nonlinear relationships.
• Sensitivity to Noise: The method might be sensitive to outliers in the data.
• Computational Complexity: Feature selection at each step and applying regularization might require more computational resources than simple linear regression.

LassoLarsCV is useful in regression tasks where it's essential to choose the most important features, reduce the model's dimensionality, prevent overfitting, and automatically tune the model's hyperparameters.

2.1.11.1. Code for creating the LassoLarsCV model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LassoLarsCV model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LassoLarsCV.py
# The code demonstrates the process of training LassoLars model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LassoLarsCV"
onnx_model_filename = data_path + "lasso_lars_cv"

# create a LassoLarsCV Regressor model
lassolars_cv_regressor_model = LassoLarsCV(cv=5)

# fit the model to the data
lassolars_cv_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = lassolars_cv_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(lassolars_cv_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LassoLarsCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  
Python  LassoLarsCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382640824089
Python  Mean Absolute Error: 6.347737845846069
Python  Mean Squared Error: 49.778142539016564
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LassoLarsCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642612767
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.77814017210321
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  16

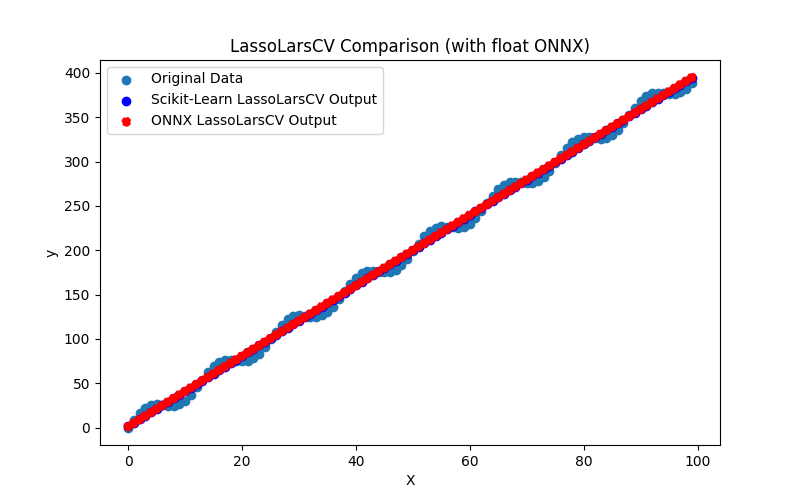
Fig.39. Results of the LassoLarsCV.py (float ONNX)

2.1.11.2. MQL5 code for executing ONNX Models

This code executes the saved lasso_lars_cv_float.onnx and lasso_lars_cv_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                  LassoLarsCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoLarsCV"
#define   ONNXFilenameFloat  "lasso_lars_cv_float.onnx"
#define   ONNXFilenameDouble "lasso_lars_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

LassoLarsCV (EURUSD,H1) Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx)
LassoLarsCV (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382640824089
LassoLarsCV (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477378458460691
LassoLarsCV (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781425390165566
LassoLarsCV (EURUSD,H1) 
LassoLarsCV (EURUSD,H1) Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx)
LassoLarsCV (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382642612767
LassoLarsCV (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477379221400145
LassoLarsCV (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781401721031642

Comparison with the original double model in Python:

Testing ONNX float: LassoLarsCV (lasso_lars_cv_float.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477378458460691
        
Testing ONNX double: LassoLarsCV (lasso_lars_cv_double.onnx)
Python  Mean Absolute Error: 6.3477379221400145
MQL5:   Mean Absolute Error: 6.3477379221400145

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 16 decimal places.

2.1.11.3. ONNX representation of the lasso_lars_cv_float.onnx and lasso_lars_cv_double.onnx

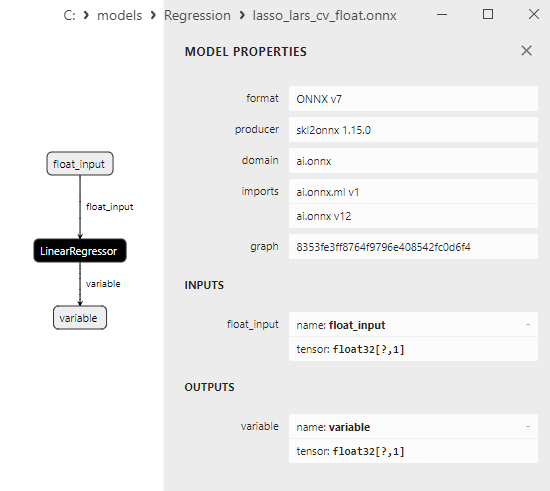
Fig.40. ONNX representation of the lasso_lars_cv_float.onnx in Netron

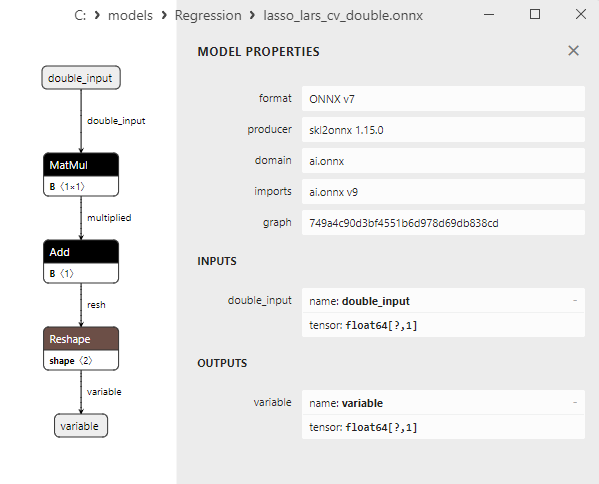
Fig.41. ONNX representation of the lasso_lars_cv_double.onnx in Netron

2.1.12. sklearn.linear_model.LassoLarsIC

LassoLarsIC is a regression method that combines Lasso (Least Absolute Shrinkage and Selection Operator) and Information Criterion (IC) to automatically select the optimal set of features.

It utilizes information criteria such as AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) to determine which features to include in the model and applies L1 regularization to estimate the model coefficients.

Working Principle of LassoLarsIC:

1. Input Data: It starts with the original dataset, including features (independent variables) and their corresponding target variable values.
2. Initialization: LassoLarsIC begins with a null model, meaning no active features. All coefficients are set to zero.
3. Feature Selection using Information Criterion: The method assesses the information criterion (e.g., AIC or BIC) for different feature sets, starting from an empty model and gradually incorporating features into the model. The information criterion evaluates the model's quality, considering the trade-off between fitting the data and model complexity.
4. Selection of Optimal Feature Set: LassoLarsIC chooses the feature set for which the information criterion achieves the best value. This feature set will be included in the model.
5. Application of L1 Regularization: L1 regularization is applied to the selected features, aiding in the estimation of model coefficients.
6. Making Predictions: After training, the model can be used to predict target variable values for new data.

Advantages of LassoLarsIC:

• Automatic Feature Selection: LassoLarsIC automatically chooses the optimal feature set, reducing the model's dimensionality and preventing overfitting.
• Information Criteria: The use of information criteria allows for balancing model quality and complexity.
• Regularization: The method applies L1 regularization, preventing overfitting and enhancing the model's generalization.

Limitations of LassoLarsIC:

• Linear Model: LassoLarsIC builds a linear model, which may be insufficient for modeling complex nonlinear relationships..
• Sensitivity to Noise: The method might be sensitive to outliers in the data.
• Computational Complexity: Evaluating information criteria for various feature sets might require additional computational resources.

LassoLarsIC is valuable in regression tasks where automatically selecting the best feature set and reducing the model's dimensionality based on information criteria is crucial.

2.1.12.1. Code for creating the LassoLarsIC model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LassoLarsIC model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LassoLarsIC.py
# The code demonstrates the process of training LassoLarsIC model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LassoLarsIC
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name="LassoLarsIC"
onnx_model_filename = data_path + "lasso_lars_ic"

# create a LassoLarsIC Regressor model
lasso_lars_ic_regressor_model = LassoLarsIC(criterion='aic')

# fit the model to the data
lasso_lars_ic_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = lasso_lars_ic_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(lasso_lars_ic_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LassoLarsIC Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  
Python  LassoLarsIC ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LassoLarsIC ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\lasso_lars_ic_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336425
Python  Mean Squared Error: 49.778140171281784
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  15

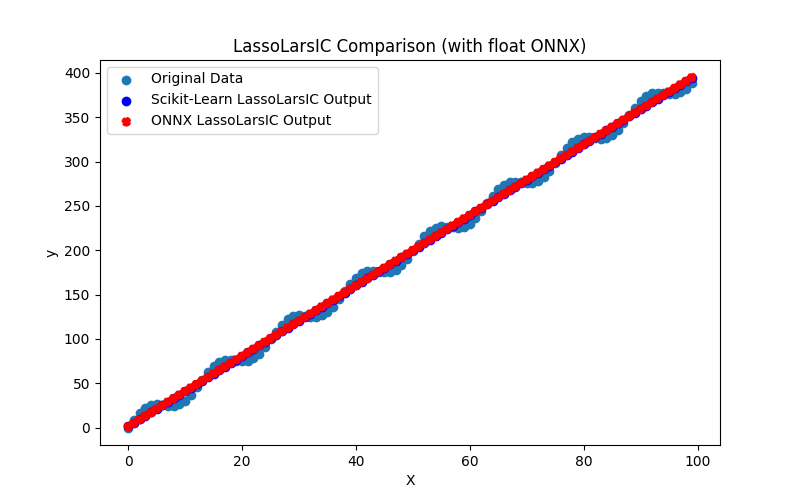
Fig.42. Results of the LassoLarsIC.py (float ONNX)

2.1.12.2. MQL5 code for executing ONNX Models

This code executes the saved lasso_lars_ic_float.onnx and lasso_lars_ic_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                  LassoLarsIC.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LassoLarsIC"
#define   ONNXFilenameFloat  "lasso_lars_ic_float.onnx"
#define   ONNXFilenameDouble "lasso_lars_ic_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

LassoLarsIC (EURUSD,H1) Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx)
LassoLarsIC (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
LassoLarsIC (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477377671679385
LassoLarsIC (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781414740478638
LassoLarsIC (EURUSD,H1) 
LassoLarsIC (EURUSD,H1) Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx)
LassoLarsIC (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
LassoLarsIC (EURUSD,H1) MQL5:   Mean Absolute Error: 6.3477379263364302
LassoLarsIC (EURUSD,H1) MQL5:   Mean Squared Error: 49.7781401712817768

Comparison with the original double precision model in Python:

Testing ONNX float: LassoLarsIC (lasso_lars_ic_float.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477377671679385
 
Testing ONNX double: LassoLarsIC (lasso_lars_ic_double.onnx)
Python  Mean Absolute Error: 6.347737926336425
MQL5:   Mean Absolute Error: 6.3477379263364302

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.12.3. ONNX representation of the lasso_lars_ic_float.onnx and lasso_lars_ic_double.onnx

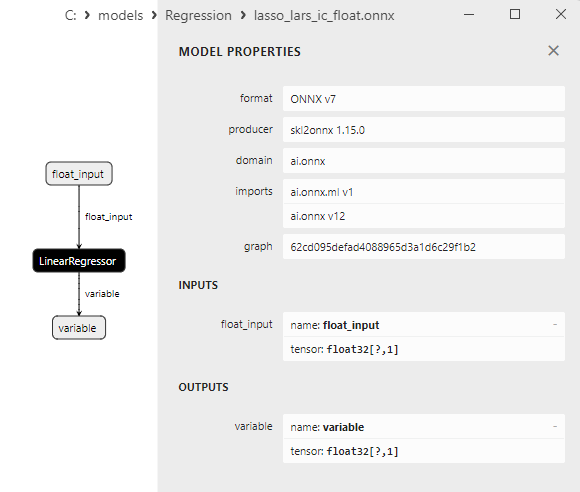
Fig.43. ONNX representation of the lasso_lars_ic_float.onnx in Netron

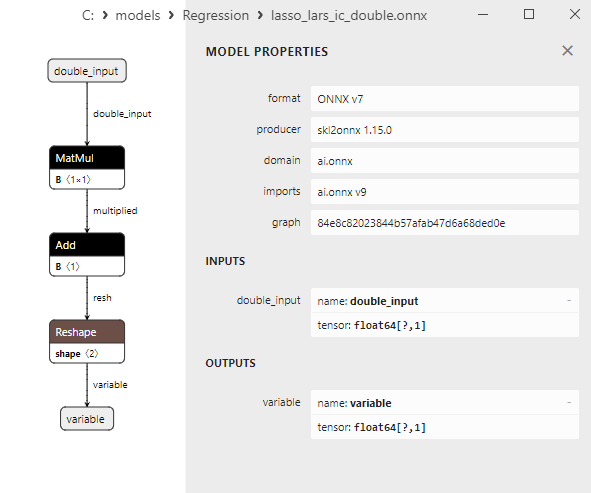
Fig.44. ONNX representation of the lasso_lars_ic_double.onnx in Netron

2.1.13. sklearn.linear_model.LinearRegression

LinearRegression is one of the simplest and most widely used methods in machine learning for regression tasks.

It's used to build linear models that predict numerical values (continuous) of the target variable based on a linear combination of input features.

Working Principle of LinearRegression:

1. Linear Model: The LinearRegression model assumes that there exists a linear relationship between independent variables (features) and the target variable. This relationship can be expressed by the linear regression equation:y = β₀ + β₁x₁ + β₂x₂ + ... + βₚxₚ, where y is the target variable, β₀ -is the intercept coefficient, β₁, β₂, ... βₚ - are the feature coefficients, x₁, x₂, ... xₚ  are the feature values.
2. Parameter Estimation: The goal of LinearRegression is to estimate the coefficients  β₀, β₁, β₂, ... βₚ, that best fit the data. This is typically achieved using the Ordinary Least Squares (OLS) method, minimizing the sum of squared differences between actual and predicted values.
3. Model Evaluation: Various metrics such as Mean Squared Error (MSE), Coefficient of Determination (R²), among others, are used to assess the quality of the LinearRegression model.

Advantages of LinearRegression:

• Simplicity and Interpretability: LinearRegression is a simple method with easy interpretability, allowing the analysis of the influence of each feature on the target variable.
• High Training and Prediction Speed: The linear regression model has high training and prediction speeds, making it a good choice for large datasets.
• Applicability: LinearRegression can be successfully applied to diverse regression tasks.

Limitations of LinearRegression:

• Linearity: This method assumes linearity in the relationship between features and the target variable, which might be insufficient for modeling complex nonlinear dependencies.
• Sensitivity to Outliers: LinearRegression is sensitive to outliers in the data, which can affect the model's quality.

LinearRegression is a simple and widely used regression method that constructs a linear model to predict numerical values of the target variable based on a linear combination of input features. It is well-suited for problems with a linear relationship and when model interpretability is important.

2.1.13.1. Code for creating the LinearRegression model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LinearRegression model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LinearRegression.py
# The code demonstrates the process of training LinearRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LinearRegression"
onnx_model_filename = data_path + "linear_regression"

# create a Linear Regression model
linear_model = LinearRegression()

# fit the model to the data
linear_model.fit(X, y)

# predict values for the entire dataset
y_pred = linear_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LinearRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  
Python  LinearRegression ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  LinearRegression ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_regression_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

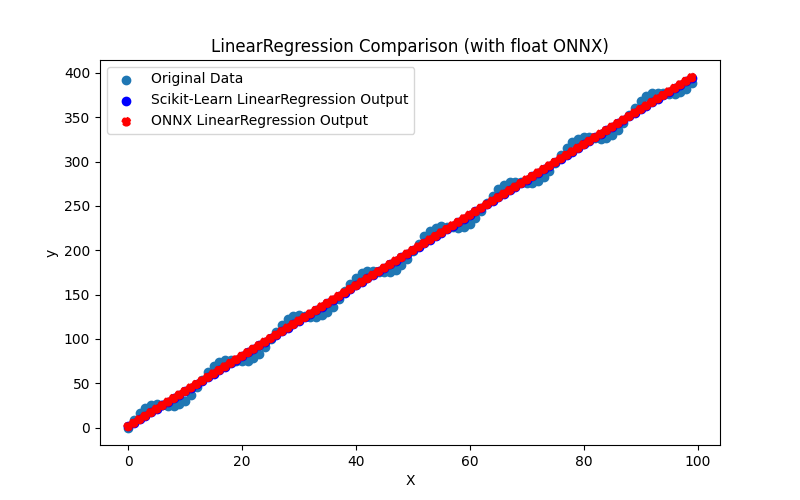
Fig.45.Results of the LinearRegression.py (float ONNX)

2.1.13.2. MQL5 code for executing ONNX Models

This code executes the saved linear_regression_float.onnx and linear_regression_double.onnx and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                             LinearRegression.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LinearRegression"
#define   ONNXFilenameFloat  "linear_regression_float.onnx"
#define   ONNXFilenameDouble "linear_regression_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

LinearRegression (EURUSD,H1)    Testing ONNX float: LinearRegression (linear_regression_float.onnx)
LinearRegression (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
LinearRegression (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3477377671679385
LinearRegression (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7781414740478638
LinearRegression (EURUSD,H1)    
LinearRegression (EURUSD,H1)    Testing ONNX double: LinearRegression (linear_regression_double.onnx)
LinearRegression (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
LinearRegression (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3477379263364266
LinearRegression (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7781401712817768

Comparison with the original double precision model in Python:

Testing ONNX float: LinearRegression (linear_regression_float.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477377671679385

Testing ONNX double: LinearRegression (linear_regression_double.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477379263364266

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.13.3. ONNX representation of the linear_regression_float.onnx and linear_regression_double.onnx

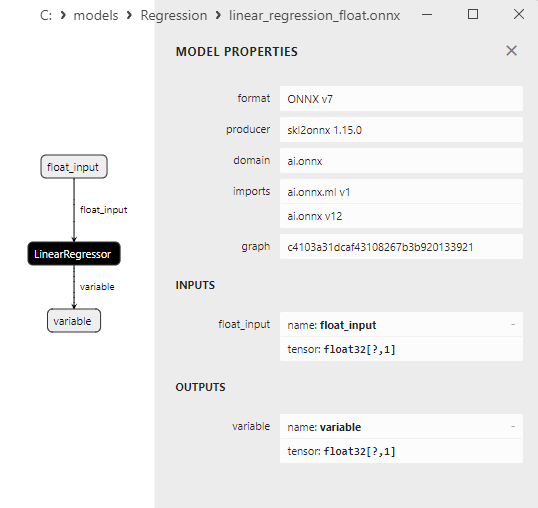
Fig.46. ONNX representation of the linear_regression_float.onnx in Netron

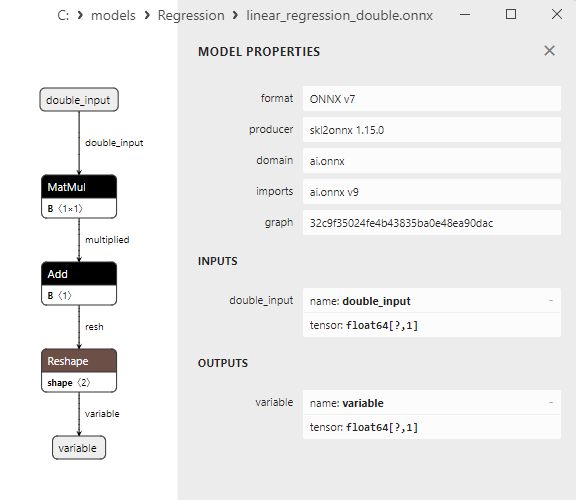
Fig.47. ONNX representation of the linear_regression_double.onnx in Netron

Note on Ridge and RidgeCV Methods

Ridge and RidgeCV are two related methods in machine learning used for regularization in Ridge regression. They share similar functionality but differ in their usage and parameter tuning.

Working Principle of Ridge (Ridge Regression):

• Ridge is a regression method involving L2 regularization. It means that it adds the sum of squared coefficients (L2 norm) to the loss function minimized by the model. This additional regularization term helps reduce the magnitudes of the model's coefficients, thus preventing overfitting.
• Use of the alpha parameter: In the Ridge method, the alpha parameter (also known as regularization strength) is pre-set and not automatically altered. Users need to select a suitable alpha value based on their knowledge of the data and experiments.

Working Principle of RidgeCV (Ridge Cross-Validation):

• RidgeCV is an extension of the Ridge method, which involves automatically selecting the optimal value for the alpha parameter using cross-validation. Instead of manually setting alpha, RidgeCV iterates through different alpha values and chooses the one providing the best performance in cross-validation.
• Advantage of automatic tuning: The primary advantage of RidgeCV is its automatic determination of the optimal alpha value without the need for manual adjustment. This makes the tuning process more convenient and prevents potential errors in alpha selection.

The key difference between Ridge and RidgeCV is that Ridge requires users to explicitly specify the alpha parameter value, whereas RidgeCV automatically finds the optimal alpha value using cross-validation. RidgeCV is typically a more preferred choice when dealing with a large amount of data and aiming to avoid manual parameter tuning.

2.1.14. sklearn.linear_model.Ridge

Ridge is a regression method used in machine learning to solve regression problems. It's part of the family of linear models and represents a regularized linear regression.

The main feature of Ridge regression is adding L2 regularization to the standard ordinary least squares (OLS) method.

How Ridge regression works:

1. Linear regression: Similar to regular linear regression, Ridge regression aims to find a linear relationship between independent variables (features) and the target variable.
2. L2 regularization: The primary distinction of Ridge regression is adding L2 regularization to the loss function. This means a penalty for large values of regression coefficients is added to the sum of squared differences between actual and predicted values.
3. Penalizing coefficients: L2 regularization imposes a penalty on the values of regression coefficients. As a result, some coefficients tend to be closer to zero, reducing overfitting and enhancing model stability.
4. Hyperparameter α: One of the essential parameters in Ridge regression is the hyperparameter α (alpha), determining the degree of regularization. Higher α values lead to stronger regularization, resulting in simpler models with lower coefficient values.

Advantages of Ridge regression:

• Reduction of overfitting: L2 regularization in Ridge helps reduce overfitting, making the model more robust against noise in the data.
• Handling multicollinearity: Ridge regression copes well with multicollinearity issues, particularly when features are highly correlated.
• Addressing the curse of dimensionality: Ridge helps in scenarios with many features, where OLS might be unstable.

Limitations of Ridge regression:

• Doesn't eliminate features: Ridge regression does not zero out feature coefficients, only reducing them, meaning some features might still remain in the model.
• Choosing optimal α: Selecting the correct value for the hyperparameter α may require cross-validation.

Ridge regression is a regression method that introduces L2 regularization to standard linear regression to reduce overfitting, enhance stability, and address multicollinearity issues. This method is useful when balancing accuracy and model stability is needed.

2.1.14.1. Code for creating the Ridge model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.Ridge model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX..

# Ridge.py
# The code demonstrates the process of training Ridge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "Ridge"
onnx_model_filename = data_path + "ridge"

# create a Ridge model
regression_model = Ridge()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  Ridge Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382641178552
Python  Mean Absolute Error: 6.347684462929819
Python  Mean Squared Error: 49.77814206996523
Python  
Python  Ridge ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382634837793
Python  Mean Absolute Error: 6.347684915729416
Python  Mean Squared Error: 49.77815046053819
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  Ridge ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641178552
Python  Mean Absolute Error: 6.347684462929819
Python  Mean Squared Error: 49.77814206996523
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

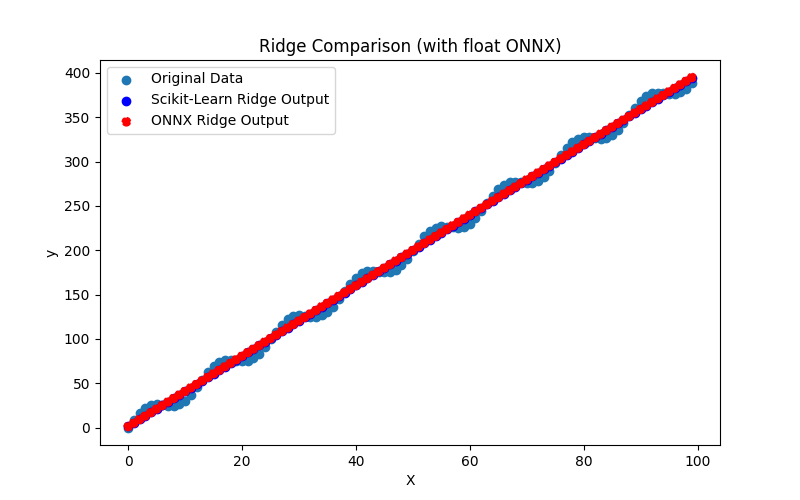
Fig.49. Results of the Ridge.py (float ONNX)

2.1.14.2. MQL5 code for executing ONNX Models

This code executes the saved ridge_float.onnx and ridge_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                        Ridge.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "Ridge"
#define   ONNXFilenameFloat  "ridge_float.onnx"
#define   ONNXFilenameDouble "ridge_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

Ridge (EURUSD,H1)       Testing ONNX float: Ridge (ridge_float.onnx)
Ridge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382634837793
Ridge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3476849157294160
Ridge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781504605381784
Ridge (EURUSD,H1)       
Ridge (EURUSD,H1)       Testing ONNX double: Ridge (ridge_double.onnx)
Ridge (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382641178552
Ridge (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3476844629298235
Ridge (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781420699652131

Comparison with the original double precision model in Python:

Testing ONNX float: Ridge (ridge_float.onnx)
Python  Mean Absolute Error: 6.347684462929819
MQL5:   Mean Absolute Error: 6.3476849157294160
       
Testing ONNX double: Ridge (ridge_double.onnx)
Python  Mean Absolute Error: 6.347684462929819
MQL5:   Mean Absolute Error: 6.3476844629298235

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.14.3. ONNX representation of the ridge_float.onnx and ridge_double.onnx

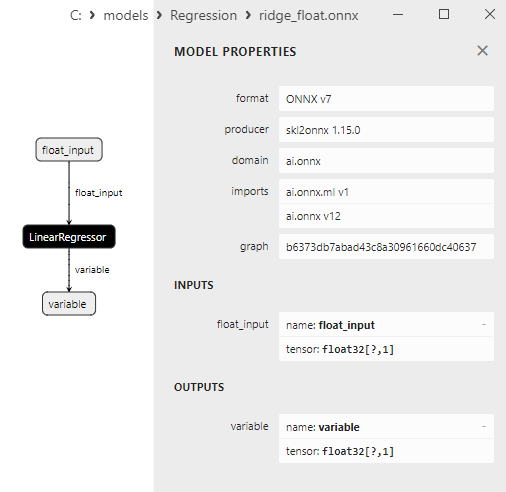
Fig.50. ONNX representation of the ridge_float.onnx in Netron

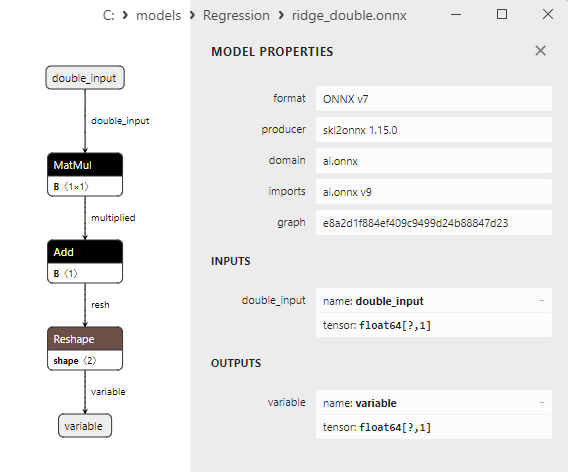
Fig.51. ONNX representation of the ridge_double.onnx in Netron

2.1.15. sklearn.linear_model.RidgeCV

RidgeCV - is an extension of Ridge regression that includes automatic selection of the best hyperparameter α (alpha), which determines the degree of regularization in Ridge regression. The hyperparameter α controls the balance between minimizing the sum of squared errors (as in ordinary linear regression) and minimizing the value of regression coefficients (regularization). RidgeCV automatically selects the optimal value of α based on specified parameters and criteria.

How RidgeCV works:

1. Input data: RidgeCV takes input data consisting of features (independent variables) and the target variable (continuous).
2. Choosing α: Ridge regression requires the selection of the hyperparameter α, which determines the degree of regularization. RidgeCV automatically selects the optimal value of α from the given range.
3. Cross-validation: RidgeCV uses cross-validation, such as k-fold cross-validation, to assess which α value provides the best model generalization on independent data.
4. Optimal α: Upon completing the training process, RidgeCV chooses the α value that delivers the best performance in cross-validation and uses this value to train the final Ridge regression model.

Advantages of RidgeCV:

• Automatic selection of α: RidgeCV allows for automatic selection of the optimal value of the hyperparameter α, simplifying the model tuning process.
• Balance between regularization and performance: This method helps find the optimal balance between regularization (reducing overfitting) and model performance.

Limitations of RidgeCV:

• Computational complexity: Cross-validation may require significant computational resources, especially when using a large range of α values.

RidgeCV is a Ridge regression method with automatic selection of the optimal hyperparameter α using cross-validation. This method streamlines the hyperparameter selection process and enables finding the best balance between regularization and model performance.

2.1.15.1. Code for creating the RidgeCV model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.RidgeCV model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# RidgeCV.py
# The code demonstrates the process of training RidgeCV model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RidgeCV
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RidgeCV"
onnx_model_filename = data_path + "ridge_cv"

# create a RidgeCV model
regression_model = RidgeCV()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  RidgeCV Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382499160807
Python  Mean Absolute Error: 6.34720334999352
Python  Mean Squared Error: 49.77832999861571
Python  
Python  RidgeCV ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382499108485
Python  Mean Absolute Error: 6.3472036427935485
Python  Mean Squared Error: 49.77833006785168
Python  R^2 matching decimal places:  11
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  6
Python  
Python  RidgeCV ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ridge_cv_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382499160807
Python  Mean Absolute Error: 6.34720334999352
Python  Mean Squared Error: 49.77832999861571
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  14

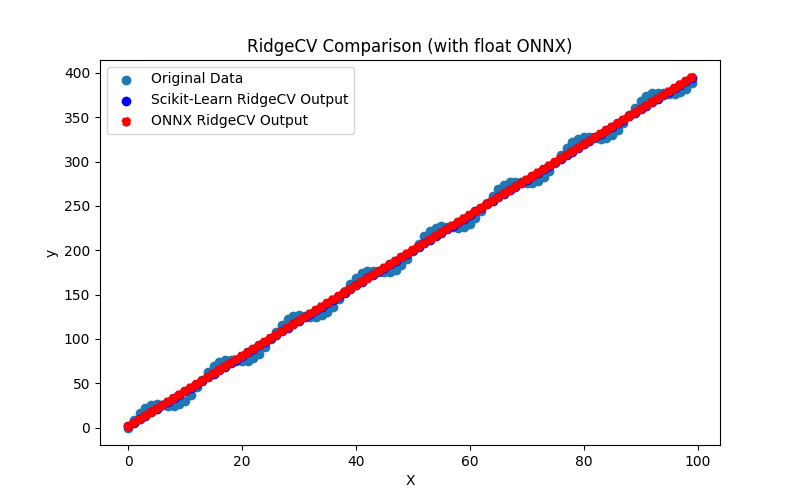
Fig.52. Results of the RidgeCV.py (float ONNX)

2.1.15.2. MQL5 code for executing ONNX Models

This code executes the saved ridge_cv_float.onnx and ridge_cv_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                      RidgeCV.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RidgeCV"
#define   ONNXFilenameFloat  "ridge_cv_float.onnx"
#define   ONNXFilenameDouble "ridge_cv_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

RidgeCV (EURUSD,H1)     Testing ONNX float: RidgeCV (ridge_cv_float.onnx)
RidgeCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382499108485
RidgeCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3472036427935485
RidgeCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7783300678516909
RidgeCV (EURUSD,H1)     
RidgeCV (EURUSD,H1)     Testing ONNX double: RidgeCV (ridge_cv_double.onnx)
RidgeCV (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382499160807
RidgeCV (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3472033499935216
RidgeCV (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7783299986157246

Comparison with the original double precision model in Python:

Testing ONNX float: RidgeCV (ridge_cv_float.onnx)
Python  Mean Absolute Error: 6.34720334999352
MQL5:   Mean Absolute Error: 6.3472036427935485

Testing ONNX double: RidgeCV (ridge_cv_double.onnx)
Python  Mean Absolute Error: 6.34720334999352
MQL5:   Mean Absolute Error: 6.3472033499935216

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.15.3. ONNX representation of the ridge_cv_float.onnx and ridge_cv_double.onnx

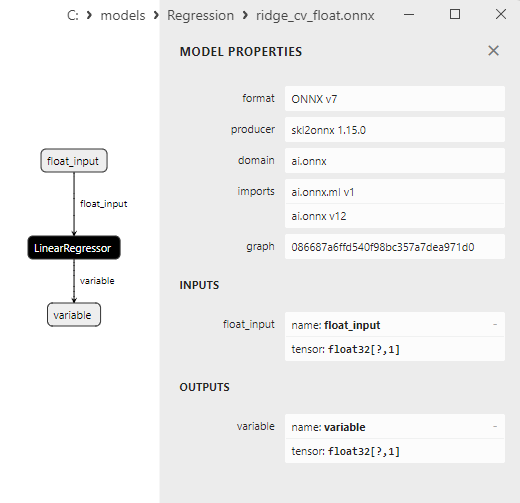
Fig.53. ONNX representation of the ridge_cv_float.onnx in Netron

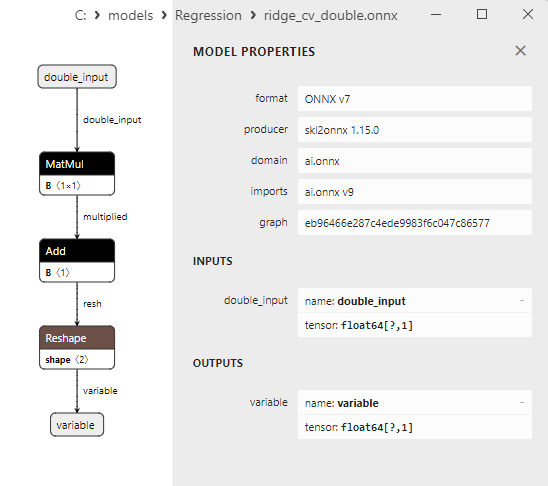
Fig.54. ONNX representation of the ridge_cv_double.onnx in Netron

2.1.16. sklearn.linear_model.OrthogonalMatchingPursuit

OrthogonalMatchingPursuit (OMP) is an algorithm used to solve feature selection and linear regression problems.

It is one of the methods for selecting the most significant features, which can be helpful in reducing data dimensionality and improving the model's generalization ability.

How OrthogonalMatchingPursuit works:

1. Input data: It begins with a dataset containing features (independent variables) and values of the target variable (continuous).
2. Selecting the number of features: One of the initial steps when using OrthogonalMatchingPursuit is determining the number of features you want to include in the model. This number can be predefined or chosen using criteria such as the Akaike Information Criterion (AIC) or minimum error criteria.
3. Iterative feature addition: The algorithm starts with an empty model and iteratively adds features that best explain the model's residuals. In each iteration, a new feature is chosen to be orthogonal to the previously selected features. The optimal feature is selected based on its correlation with the model residuals.
4. Model training: After adding the specified number of features, the model is trained on the data considering only these selected features.
5. Making predictions: After training, the model can predict the values of the target variable on new data.

Advantages of OrthogonalMatchingPursuit:

• Dimensionality reduction: OMP can reduce the data dimensionality by selecting only the most informative features.
• Interpretability: Because OMP selects only a small number of features, models created using it can be more interpretable.

Limitations of OrthogonalMatchingPursuit:

• Sensitivity to the number of selected features: The number of selected features needs to be properly tuned, and incorrect choices may lead to overfitting or underfitting.
• Does not consider multicollinearity: OMP may not account for multicollinearity between features, which could impact the selection of optimal features.
• Computational complexity: OMP is computationally expensive, especially for large datasets.

OrthogonalMatchingPursuit is an algorithm for feature selection and linear regression, allowing the selection of the most informative features for the model. This method can be valuable for reducing data dimensionality and improving model interpretability.

2.1.16.1. Code for creating the OrthogonalMatchingPursuit model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.OrthogonalMatchingPursuit model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# OrthogonalMatchingPursuit.py
# The code demonstrates the process of training OrthogonalMatchingPursuit model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import OrthogonalMatchingPursuit
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "OrthogonalMatchingPursuit"
onnx_model_filename = data_path + "orthogonal_matching_pursuit"

# create an OrthogonalMatchingPursuit model
regression_model = OrthogonalMatchingPursuit()

# fit the model to the data
regression_model.fit(X, y)

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  OrthogonalMatchingPursuit Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281784
Python  
Python  OrthogonalMatchingPursuit ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  OrthogonalMatchingPursuit ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\orthogonal_matching_pursuit_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281784
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  16

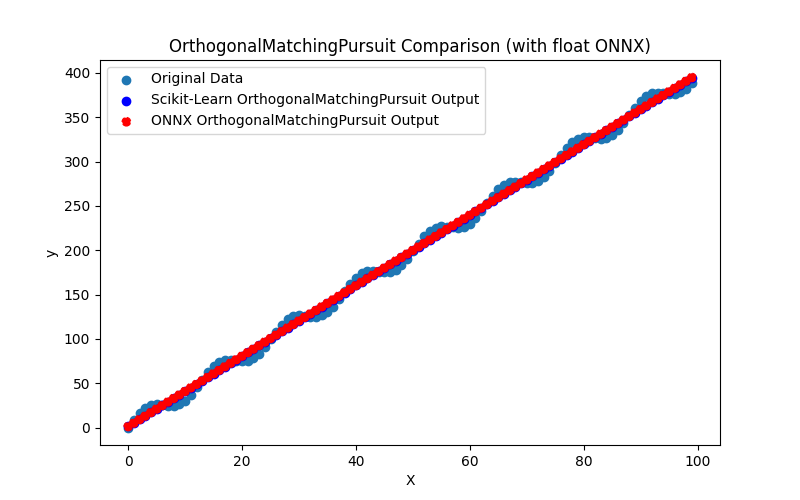
Fig.55. Results of the OrthogonalMatchingPursuit.py (float ONNX)

2.1.16.2. MQL5 code for executing ONNX Models

This code executes the saved orthogonal_matching_pursuit_float.onnx and orthogonal_matching_pursuit_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                    OrthogonalMatchingPursuit.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "OrthogonalMatchingPursuit"
#define   ONNXFilenameFloat  "orthogonal_matching_pursuit_float.onnx"
#define   ONNXFilenameDouble "orthogonal_matching_pursuit_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

OrthogonalMatchingPursuit (EURUSD,H1)   Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx)
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3477377671679385
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781414740478638
OrthogonalMatchingPursuit (EURUSD,H1)   
OrthogonalMatchingPursuit (EURUSD,H1)   Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx)
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3477379263364275
OrthogonalMatchingPursuit (EURUSD,H1)   MQL5:   Mean Squared Error: 49.7781401712817768

Comparison with the original double precision model in Python:

Testing ONNX float: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_float.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477377671679385
        
Testing ONNX double: OrthogonalMatchingPursuit (orthogonal_matching_pursuit_double.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477379263364275

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 16 decimal places.

2.1.16.3. ONNX representation of the orthogonal_matching_pursuit_float.onnx and orthogonal_matching_pursuit_double.onnx

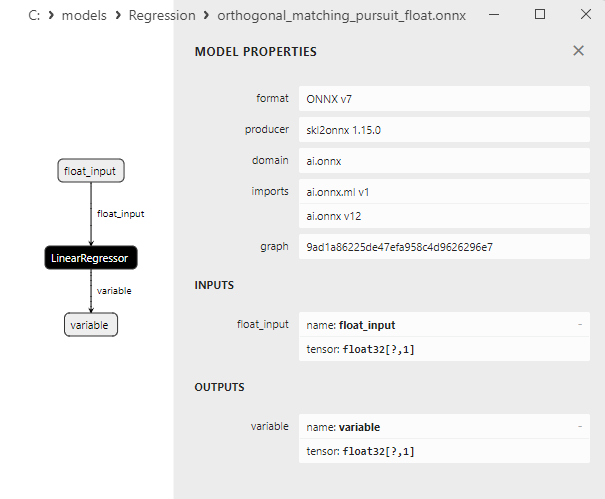
Fig.56. ONNX representation of the orthogonal_matching_pursuit_float.onnx in Netron

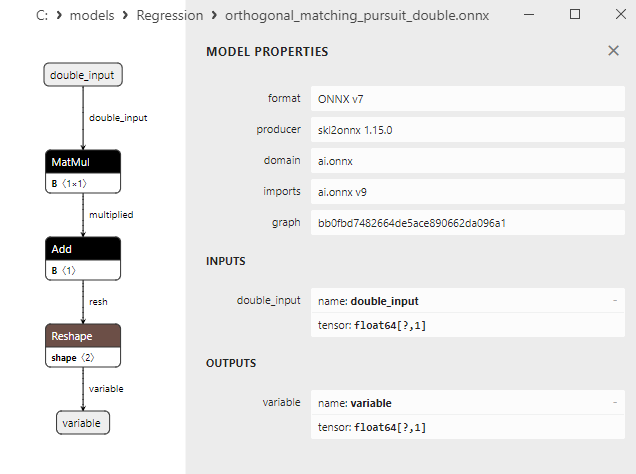
Fig.57. ONNX representation of the orthogonal_matching_pursuit_double.onnx in Netron

2.1.17. sklearn.linear_model.PassiveAggressiveRegressor

PassiveAggressiveRegressor is a machine learning method used for regression tasks.

This method is a variant of the Passive-Aggressive (PA) algorithm that can be employed to train a model capable of predicting continuous values of the target variable.

How PassiveAggressiveRegressor works:

1. Input data: It starts with a dataset comprising features (independent variables) and values of the target variable (continuous).
2. Supervised learning: PassiveAggressiveRegressor is a supervised learning method trained on pairs (X, y), where X represents the features, and y corresponds to the target variable values.
3. Adaptive learning: The primary idea behind the Passive-Aggressive method is the adaptive learning approach. The model learns by minimizing the prediction error on each training example. It updates by correcting the weights to reduce the prediction error.
4. Parameter C: PassiveAggressiveRegressor has a hyperparameter C, which controls how strongly the model adapts to errors. A higher C value means more aggressive weight updates, while a lower C value makes the model less aggressive.
5. Prediction: Once trained, the model can predict target variable values for new data.

Advantages of PassiveAggressiveRegressor:

• Adaptability: The method can adapt to changes in data and update the model to minimize prediction errors.
• Efficiency for large datasets: PassiveAggressiveRegressor can be an effective method for regression, particularly when trained on substantial volumes of data.

Limitations of PassiveAggressiveRegressor:

• Sensitivity to the choice of parameter C: Properly selecting the value of C may require tuning and experimentation.
• Additional features may be needed: In some cases, additional engineered features might be required for successful model training.

PassiveAggressiveRegressor is a machine learning method for regression tasks that learns adaptively by minimizing prediction errors on training data. This method can be valuable for handling large datasets and requires tuning the C parameter for optimal performance.

2.1.17.1. Code for creating the PassiveAggressiveRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.PassiveAggressiveRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# PassiveAggressiveRegressor.py
# The code demonstrates the process of training PassiveAggressiveRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PassiveAggressiveRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PassiveAggressiveRegressor"
onnx_model_filename = data_path + "passive_aggressive_regressor"

# create a PassiveAggressiveRegressor model
regression_model = PassiveAggressiveRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  PassiveAggressiveRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9894376841493092
Python  Mean Absolute Error: 9.64524669506544
Python  Mean Squared Error: 139.76857373191007
Python  
Python  PassiveAggressiveRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9894376801868329
Python  Mean Absolute Error: 9.645248834431873
Python  Mean Squared Error: 139.76862616640122
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  5
Python  
Python  PassiveAggressiveRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\passive_aggressive_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9894376841493092
Python  Mean Absolute Error: 9.64524669506544
Python  Mean Squared Error: 139.76857373191007
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  14

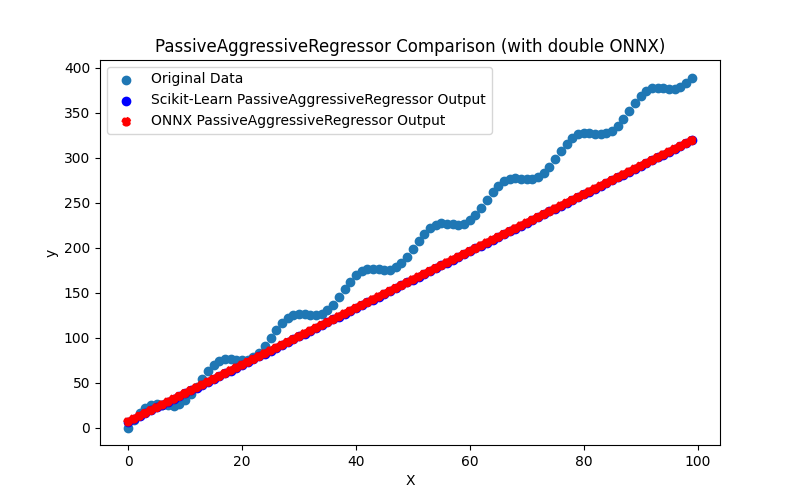
Fig.58. Results of the PassiveAggressiveRegressor.py (double ONNX)

2.1.17.2. MQL5 code for executing ONNX Models

This code executes the saved passive_aggressive_regressor_float.onnx and passive_aggressive_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                   PassiveAggressiveRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "PassiveAggressiveRegressor"
#define   ONNXFilenameFloat  "passive_aggressive_regressor_float.onnx"
#define   ONNXFilenameDouble "passive_aggressive_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

PassiveAggressiveRegressor (EURUSD,H1)  Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx)
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9894376801868329
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Absolute Error: 9.6452488344318716
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Squared Error: 139.7686261664012761
PassiveAggressiveRegressor (EURUSD,H1)  
PassiveAggressiveRegressor (EURUSD,H1)  Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx)
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9894376841493092
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Absolute Error: 9.6452466950654419
PassiveAggressiveRegressor (EURUSD,H1)  MQL5:   Mean Squared Error: 139.7685737319100667

Comparison with the original double precision model in Python:

Testing ONNX float: PassiveAggressiveRegressor (passive_aggressive_regressor_float.onnx)
Python  Mean Absolute Error: 9.64524669506544
MQL5:   Mean Absolute Error: 9.6452488344318716
        
Testing ONNX double: PassiveAggressiveRegressor (passive_aggressive_regressor_double.onnx)
Python  Mean Absolute Error: 9.64524669506544
MQL5:   Mean Absolute Error: 9.6452466950654419

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.17.3. ONNX representation of the passive_aggressive_regressor_float.onnx and passive_aggressive_regressor_double.onnx

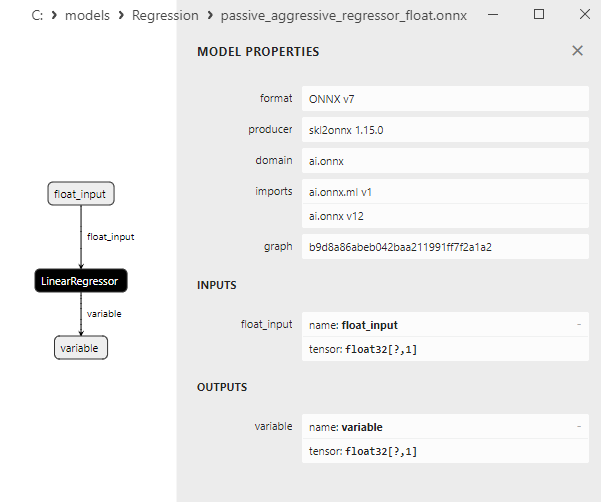
Fig.59. ONNX representation of the passive_aggressive_regressor_float.onnx in Netron

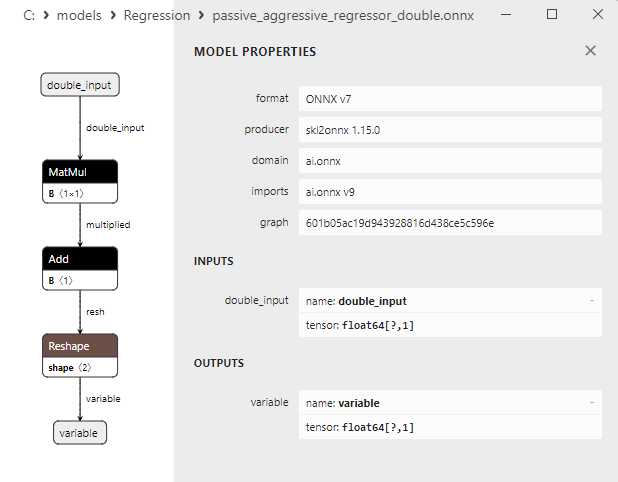
Fig.60. ONNX representation of the passive_aggressive_regressor_double.onnx in Netron

2.1.18. sklearn.linear_model.QuantileRegressor

QuantileRegressor is a machine learning method used to estimate quantiles (specific percentiles) of the target variable in regression tasks.

Instead of predicting the mean value of the target variable, as typically done in regression tasks, QuantileRegressor predicts values corresponding to specified quantiles, such as the median (50th percentile) or the 25th and 75th percentiles.

How QuantileRegressor works:

1. Input data: It begins with a dataset containing features (independent variables) and the target variable (continuous).
2. Quantile focus: Instead of predicting exact values of the target variable, QuantileRegressor models the conditional distribution of the target variable and predicts values for certain quantiles of this distribution.
3. Training for different quantiles: Training a QuantileRegressor model involves training separate models for each desired quantile. Each of these models predicts a value corresponding to its quantile.
4. Quantile parameter: The main parameter for this method is the choice of desired quantiles for which you want to get predictions. For example, if you need predictions for the median, you'll need to train the model on the 50th percentile.
5. Quantile prediction: After training, the model can be used to predict values corresponding to specified quantiles on new data.

Advantages of QuantileRegressor:

• Flexibility: QuantileRegressor provides flexibility in predicting various quantiles, which can be useful in tasks where different percentiles of the distribution are important.
• Robustness to outliers: A quantile-oriented approach can be robust against outliers as it does not consider the mean, which can be heavily influenced by extreme values.

Limitations of QuantileRegressor:

• Need for quantile selection: Choosing optimal quantiles might require some knowledge about the task.
• Increased computational complexity: Training separate models for different quantiles can increase the computational complexity of the task.

QuantileRegressor is a machine learning method designed to predict values corresponding to specified quantiles of the target variable. This method can be useful in tasks where various percentiles of the distribution are of interest and in cases where data may contain outliers.

2.1.18.1. Code for creating the QuantileRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.QuantileRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# QuantileRegressor.py
# The code demonstrates the process of training QuantileRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import QuantileRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "QuantileRegressor"
onnx_model_filename = data_path + "quantile_regressor"

# create a QuantileRegressor model
regression_model = QuantileRegressor(solver='highs')

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  QuantileRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9959915738839231
Python  Mean Absolute Error: 6.3693091850025185
Python  Mean Squared Error: 53.0425343337143
Python  
Python  QuantileRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9959915739158818
Python  Mean Absolute Error: 6.3693091422201125
Python  Mean Squared Error: 53.042533910812814
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  7
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  7
Python  
Python  QuantileRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\quantile_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9959915738839231
Python  Mean Absolute Error: 6.3693091850025185
Python  Mean Squared Error: 53.0425343337143
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  13
Python  double ONNX model precision:  16

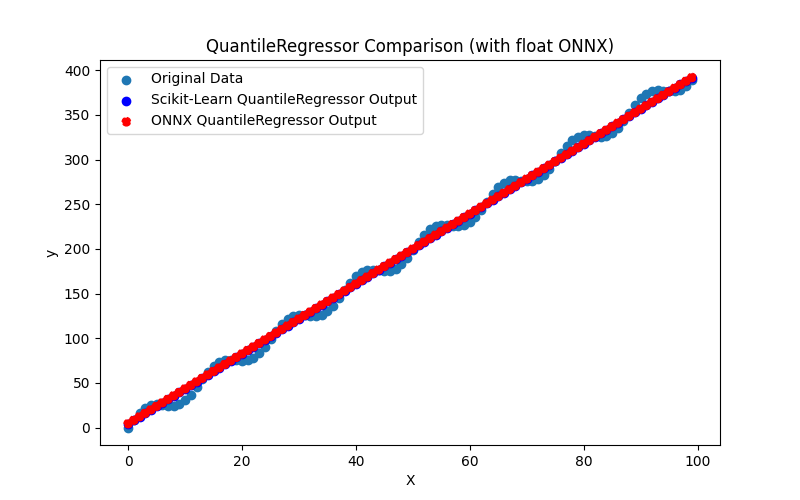
Fig.61. Results of the QuantileRegressor.py (float ONNX)

2.1.18.2. MQL5 code for executing ONNX Models

This code executes the saved quantile_regressor_float.onnx and quantile_regressor_double.onnx and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                            QuantileRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "QuantileRegressor"
#define   ONNXFilenameFloat  "quantile_regressor_float.onnx"
#define   ONNXFilenameDouble "quantile_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

QuantileRegressor (EURUSD,H1)   Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx)
QuantileRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9959915739158818
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3693091422201169
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 53.0425339108128071
QuantileRegressor (EURUSD,H1)   
QuantileRegressor (EURUSD,H1)   Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx)
QuantileRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9959915738839231
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3693091850025185
QuantileRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 53.0425343337142721

Comparison with the original double precision model in Python:

Testing ONNX float: QuantileRegressor (quantile_regressor_float.onnx)
Python  Mean Absolute Error: 6.3693091850025185
MQL5:   Mean Absolute Error: 6.3693091422201169

Testing ONNX double: QuantileRegressor (quantile_regressor_double.onnx)
Python  Mean Absolute Error: 6.3693091850025185
MQL5:   Mean Absolute Error: 6.3693091850025185

Accuracy of ONNX float MAE: 7 decimal places, Accuracy of ONNX double MAE: 16 decimal places.

2.1.18.3. ONNX representation of the quantile_regressor_float.onnx and quantile_regressor_double.onnx

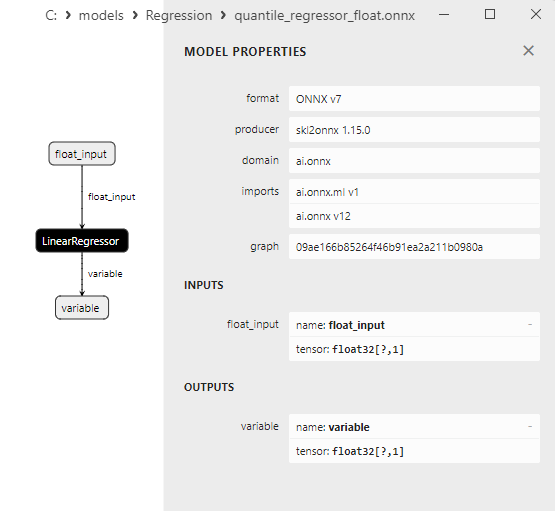
Fig.62. ONNX representation of the quantile_regressor_float.onnx in Netron

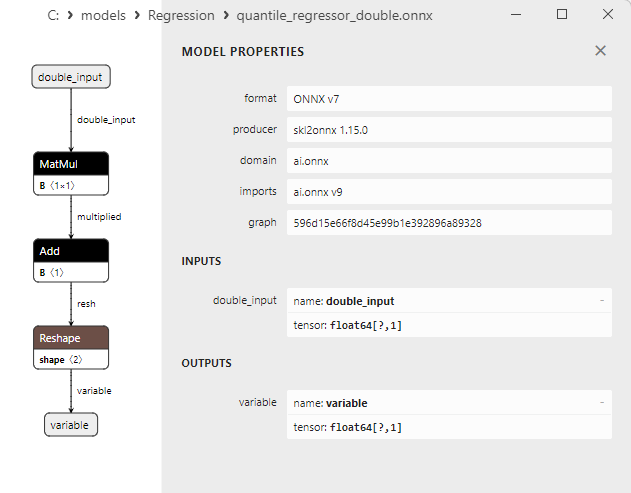
Fig.63. ONNX representation of the quantile_regressor_double.onnx in Netron

2.1.19. sklearn.linear_model.RANSACRegressor

RANSACRegressor is a machine learning method used to solve regression problems using the RANSAC (Random Sample Consensus) method.

The RANSAC method is designed to handle data containing outliers or imperfections, allowing for a more robust regression model by excluding the influence of outliers.

How RANSACRegressor works:

1. Input data: It begins with a dataset containing features (independent variables) and the target variable (continuous).
2. Selection of random subsets: RANSAC starts by choosing random subsets of data used to train the regression model. These subsets are called "hypotheses."
3. Fitting model to hypotheses: For each chosen hypothesis, a regression model is trained. In the case of RANSACRegressor, linear regression is usually used, and the model is fitted to the subset of data.
4. Outlier evaluation: After training the model, its fit to all the data is evaluated. The error between the predicted and actual values is computed for each data point.
5. Outlier identification: Data points with errors exceeding a specified threshold are considered outliers. These outliers can influence model training and distort results.
6. Model update: All data points not considered outliers are used to update the regression model. This process may be repeated multiple times with different random hypotheses.
7. Final model: After several iterations, RANSACRegressor selects the best model trained on the subset of data and returns it as the final regression model.

Advantages of RANSACRegressor:

• Outlier robustness: RANSACRegressor is a robust method against outliers as it excludes them from training.
• Robust regression: This method enables the creation of a more reliable regression model when data contains outliers or imperfections.

Limitations of RANSACRegressor:

• Sensitivity to error threshold: Choosing an error threshold to determine which points are considered outliers might require experimentation.
• Complexity of hypothesis selection: Choosing good hypotheses at the initial stage might not be a straightforward task.

RANSACRegressor is a machine learning method used for regression problems based on the RANSAC method. This method allows the creation of a more robust regression model when data contains outliers or imperfections by excluding their influence on the model.

2.1.19.1. Code for creating the RANSACRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.RANSACRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# RANSACRegressor.py
# The code demonstrates the process of training RANSACRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import RANSACRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RANSACRegressor"
onnx_model_filename = data_path + "ransac_regressor"

# create a RANSACRegressor model
regression_model = RANSACRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  RANSACRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  
Python  RANSACRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382641628886
Python  Mean Absolute Error: 6.3477377671679385
Python  Mean Squared Error: 49.77814147404787
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  ONNX: MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  RANSACRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\ransac_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.347737926336427
Python  Mean Squared Error: 49.77814017128179
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

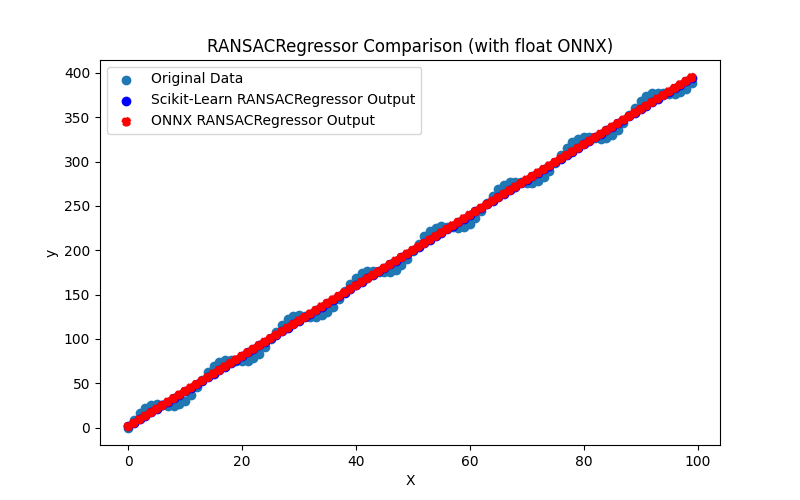
Fig.64. Results of the RANSACRegressor.py (float ONNX)

2.1.19.2. MQL5 code for executing ONNX Models

This code executes the saved ransac_regressor_float.onnx and ransac_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                              RANSACRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RANSACRegressor"
#define   ONNXFilenameFloat  "ransac_regressor_float.onnx"
#define   ONNXFilenameDouble "ransac_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

RANSACRegressor (EURUSD,H1)     Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx)
RANSACRegressor (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382641628886
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3477377671679385
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7781414740478638
RANSACRegressor (EURUSD,H1)     
RANSACRegressor (EURUSD,H1)     Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx)
RANSACRegressor (EURUSD,H1)     MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Absolute Error: 6.3477379263364266
RANSACRegressor (EURUSD,H1)     MQL5:   Mean Squared Error: 49.7781401712817768

Comparison with the original double precision model in Python:

Testing ONNX float: RANSACRegressor (ransac_regressor_float.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477377671679385
     
Testing ONNX double: RANSACRegressor (ransac_regressor_double.onnx)
Python  Mean Absolute Error: 6.347737926336427
MQL5:   Mean Absolute Error: 6.3477379263364266

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.19.3. ONNX representation of the ransac_regressor_float.onnx and ransac_regressor_double.onnx

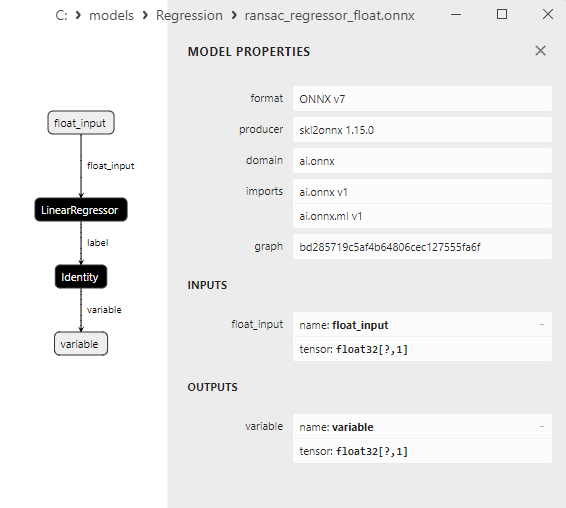
Fig.65. ONNX representation of the ransac_regressor_float.onnx in Netron

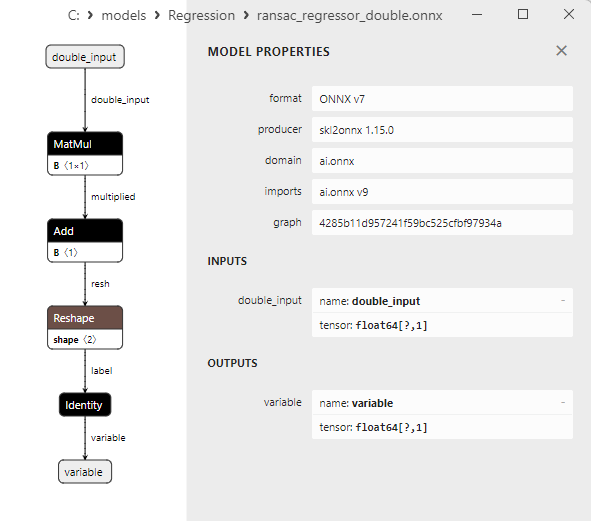
Fig.66. ONNX representation of the ransac_regressor_double.onnx in Netron

2.1.20. sklearn.linear_model.TheilSenRegressor

Theil-Sen regression (Theil-Sen estimator) is a regression estimation method used to approximate linear relationships between independent variables and the target variable.

It offers a more robust estimate compared to ordinary linear regression in the presence of outliers and noise in the data.

How Theil-Sen regression works:

1. Point selection: Initially, Theil-Sen selects random pairs of data points from the training dataset.
2. Slope calculation: For each pair of data points, the method computes the slope of the line passing through these points, creating a set of slopes.
3. Median slope: Then, the method finds the median slope from the set of slopes. This median slope is used as an estimation of the linear regression slope.
4. Median deviations: For each data point, the method computes the deviation (difference between the actual value and the value predicted based on the median slope) and finds the median of these deviations. This creates an estimate for the coefficient of the linear regression intercept.
5. Final estimation: The final estimations of the slope and intercept coefficients are used to build the linear regression model.

Advantages of Theil-Sen regression:

• Outlier resilience: Theil-Sen regression is more robust against outliers and data noise compared to regular linear regression.
• Less strict assumptions: The method does not require strict assumptions about data distribution or dependency form, making it more versatile.
• Suitable for multicollinear data: Theil-Sen regression performs well with data where independent variables are highly correlated (multicollinearity issue).

Limitations of Theil-Sen regression:

• Computational complexity: Computing median slopes for all pairs of data points might be time-consuming, especially for large datasets.
• Intercept coefficient estimation: Median deviations are used for estimating the intercept coefficient, which can lead to bias in the presence of outliers.

Theil-Sen regression is an estimation method for regression that provides a stable assessment of the linear relationship between independent variables and the target variable, particularly in the presence of outliers and data noise. This method is useful when a stable estimate is needed under real-world data conditions.

2.1.20.1. Code for creating the TheilSenRegressor and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.TheilSenRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX..

# TheilSenRegressor.py
# The code demonstrates the process of training TheilSenRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TheilSenRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "TheilSenRegressor"
onnx_model_filename = data_path + "theil_sen_regressor"

# create a TheilSen Regressor model
regression_model = TheilSenRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  TheilSenRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9962329196940459
Python  Mean Absolute Error: 6.338686004537594
Python  Mean Squared Error: 49.84886353898735
Python  
Python  TheilSenRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.996232919516505
Python  Mean Absolute Error: 6.338686370832071
Python  Mean Squared Error: 49.84886588834327
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  6
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  6
Python  
Python  TheilSenRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\theil_sen_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962329196940459
Python  Mean Absolute Error: 6.338686004537594
Python  Mean Squared Error: 49.84886353898735
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

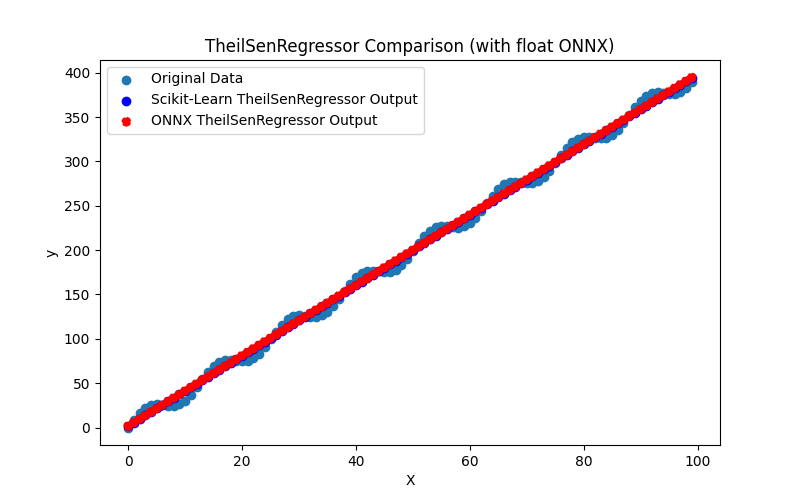
Fig.67. Results of the TheilSenRegressor.py (float ONNX)

2.1.20.2. MQL5 code for executing ONNX Models

This code executes the saved theil_sen_regressor_float.onnx and theil_sen_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                            TheilSenRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "TheilSenRegressor"
#define   ONNXFilenameFloat  "theil_sen_regressor_float.onnx"
#define   ONNXFilenameDouble "theil_sen_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

TheilSenRegressor (EURUSD,H1)   Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx)
TheilSenRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962329195165051
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3386863708320735
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 49.8488658883432691
TheilSenRegressor (EURUSD,H1)   
TheilSenRegressor (EURUSD,H1)   Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx)
TheilSenRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9962329196940459
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 6.3386860045375943
TheilSenRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 49.8488635389873735

Comparison with the original double precision model in Python:

Testing ONNX float: TheilSenRegressor (theil_sen_regressor_float.onnx)
Python  Mean Absolute Error: 6.338686004537594
MQL5:   Mean Absolute Error: 6.3386863708320735
        
Testing ONNX double: TheilSenRegressor (theil_sen_regressor_double.onnx)
Python  Mean Absolute Error: 6.338686004537594
MQL5:   Mean Absolute Error: 6.3386860045375943

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 15 decimal places.

2.1.20.3. ONNX representation of the theil_sen_regressor_float.onnx and theil_sen_regressor_double.onnx

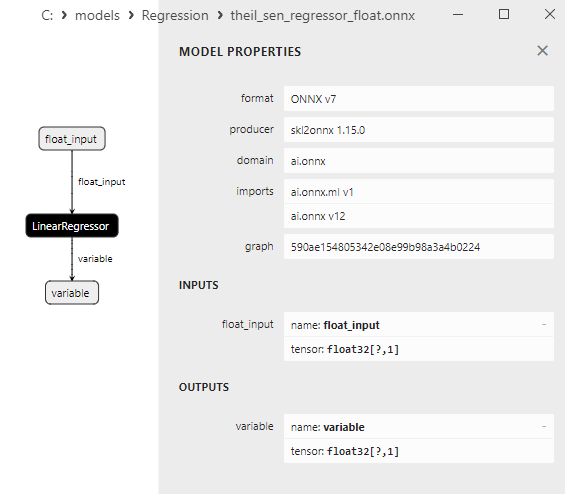
Fig.68. ONNX representation of the theil_sen_regressor_float.onnx in Netron

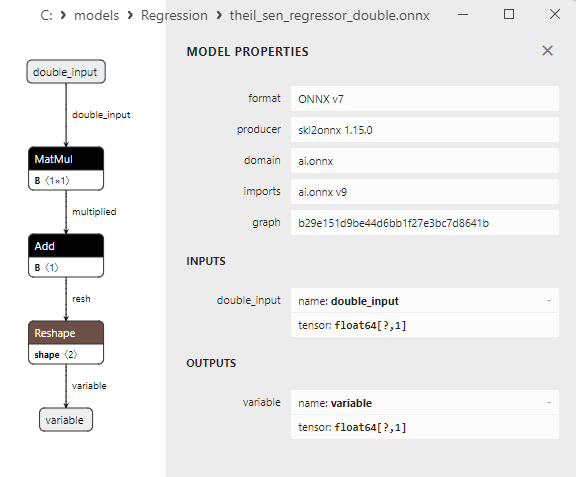
Fig.69. ONNX representation of the theil_sen_regressor_double.onnx in Netron

2.1.21. sklearn.linear_model.LinearSVR

LinearSVR (Linear Support Vector Regression) is a machine learning model for regression tasks based on the Support Vector Machines (SVM) method.

This method is used to find linear relationships between features and the target variable using a linear kernel.

How LinearSVR works:

1. Input data: LinearSVR begins with a dataset that includes features (independent variables) and their corresponding target variable values.
2. Selecting a linear model: The model assumes there's a linear relationship between the features and the target variable, described by a linear regression equation.
3. Model training: LinearSVR finds optimal values for the model's coefficients by minimizing a loss function that considers prediction error and an acceptable error (epsilon).
4. Generating predictions: After training, the model can predict the target variable values for new data based on the discovered coefficients.

Advantages of LinearSVR:

• Support Vector Regression: LinearSVR employs the Support Vector Machines method, which enables finding the optimal separation between data while considering an acceptable error.
• Support for multiple features: The model can handle multiple features and process data in high dimensions.
• Regularization: LinearSVR involves regularization, aiding in combating overfitting and ensuring more stable predictions.

Limitations of LinearSVR:

• Linearity: LinearSVR is constrained by using linear relationships between features and the target variable. In the case of complex, nonlinear relationships, the model might be insufficiently flexible.
• Sensitivity to outliers: The model can be sensitive to outliers in the data and the acceptable error (epsilon).
• Inability to capture complex relationships: LinearSVR, like other linear models, is unable to capture complex nonlinear relationships between features and the target variable.

LinearSVR is a regression machine learning model that utilizes the Support Vector Machines method to find linear relationships between features and the target variable. It supports regularization and can be used in tasks where controlling acceptable error is essential. However, the model is limited by its linear dependence and might be sensitive to outliers.

2.1.21.1. Code for creating the LinearSVR model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.LinearSVR model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# LinearSVR.py
# The code demonstrates the process of training LinearSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "LinearSVR"
onnx_model_filename = data_path + "linear_svr"

# create a Linear SVR model
linear_svr_model = LinearSVR()

# fit the model to the data
linear_svr_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = linear_svr_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(linear_svr_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(linear_svr_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  LinearSVR Original model (double)
Python  R-squared (Coefficient of determination): 0.9944935515149387
Python  Mean Absolute Error: 7.026852359381935
Python  Mean Squared Error: 72.86550241109444
Python  
Python  LinearSVR ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9944935580726729
Python  Mean Absolute Error: 7.026849848037511
Python  Mean Squared Error: 72.86541563418206
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  4
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  4
Python  
Python  LinearSVR ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\linear_svr_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9944935515149387
Python  Mean Absolute Error: 7.026852359381935
Python  Mean Squared Error: 72.86550241109444
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  14
Python  double ONNX model precision:  15

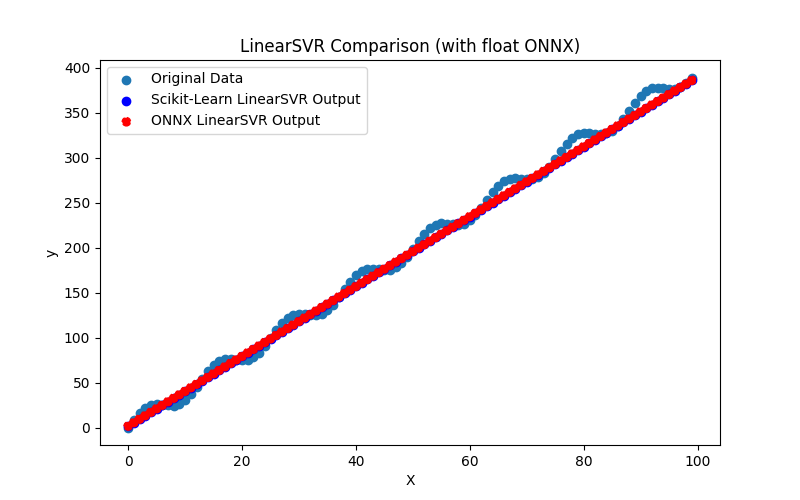
Fig.70. Results of the LinearSVR.py (float ONNX)

2.1.21.2. MQL5 code for executing ONNX Models

This code executes the saved linear_svr_float.onnx and linear_svr_double.onnx and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                    LinearSVR.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "LinearSVR"
#define   ONNXFilenameFloat  "linear_svr_float.onnx"
#define   ONNXFilenameDouble "linear_svr_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

LinearSVR (EURUSD,H1)   Testing ONNX float: LinearSVR (linear_svr_float.onnx)
LinearSVR (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9944935580726729
LinearSVR (EURUSD,H1)   MQL5:   Mean Absolute Error: 7.0268498480375108
LinearSVR (EURUSD,H1)   MQL5:   Mean Squared Error: 72.8654156341820567
LinearSVR (EURUSD,H1)   
LinearSVR (EURUSD,H1)   Testing ONNX double: LinearSVR (linear_svr_double.onnx)
LinearSVR (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9944935515149387
LinearSVR (EURUSD,H1)   MQL5:   Mean Absolute Error: 7.0268523593819374
LinearSVR (EURUSD,H1)   MQL5:   Mean Squared Error: 72.8655024110944680

Comparison with the original double precision model in Python:

Testing ONNX float: LinearSVR (linear_svr_float.onnx)
Python  Mean Absolute Error: 7.026852359381935
MQL5:   Mean Absolute Error: 7.0268498480375108
   
Testing ONNX double: LinearSVR (linear_svr_double.onnx)
Python  Mean Absolute Error: 7.026852359381935
MQL5:   Mean Absolute Error: 7.0268523593819374

Accuracy of ONNX float MAE: 4 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.21.3. ONNX representation of the linear_svr_float.onnx and linear_svr_double.onnx

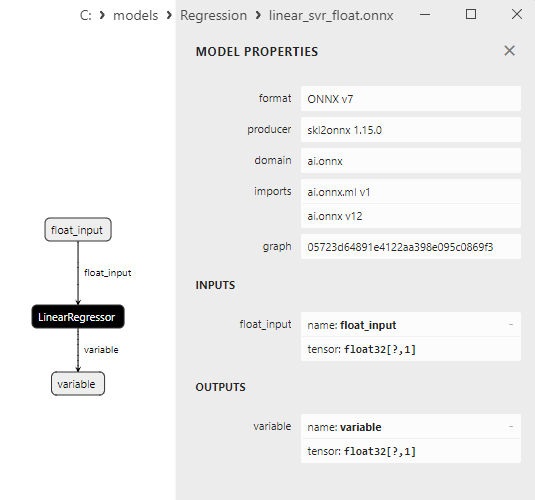
Fig.71. ONNX representation of the linear_svr_float.onnx in Netron

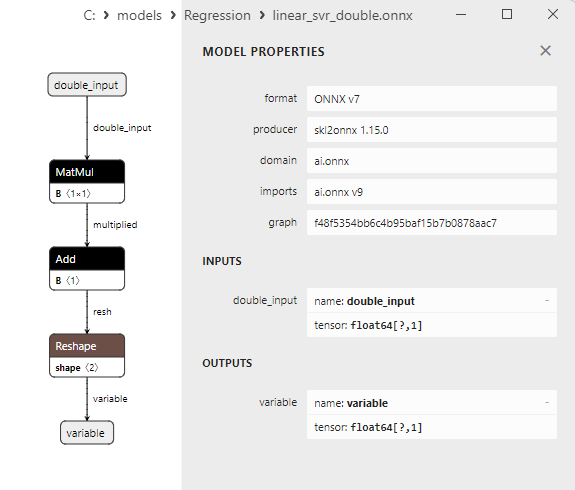
Fig.72. ONNX representation of the linear_svr_double.onnx in Netron

2.1.22. sklearn.neural_network.MLPRegressor

MLPRegressor (Multi-Layer Perceptron Regressor) is a machine learning model that utilizes artificial neural networks for regression tasks.

It's a multi-layer neural network comprising several layers of neurons (including input, hidden, and output layers) that are trained to predict continuous values of the target variable.

How MLPRegressor works:

1. Input data: It starts with a dataset containing features (independent variables) and their corresponding target variable values.
2. Creating a multi-layer neural network: MLPRegressor employs a multi-layer neural network with multiple hidden layers of neurons. These neurons are connected via weighted connections and activation functions.
3. Model training: MLPRegressor trains the neural network by adjusting weights and biases to minimize a loss function that measures the disparity between the network's predictions and the actual target variable values. This is achieved through backpropagation algorithms.
4. Generating predictions: After training, the model can predict target variable values for new data.

Advantages of MLPRegressor:

• Flexibility: Multi-layer neural networks can model complex nonlinear relationships between features and the target variable.
• Versatility: MLPRegressor can be used for various regression tasks, including time series problems, function approximation, and more.
• Generalization ability: Neural networks learn from data and can generalize the dependencies found in the training data to new data.

Limitations of MLPRegressor:

• Complexity of the base model: Large neural networks can be computationally expensive and require extensive data for training.
• Hyperparameter tuning: Choosing optimal hyperparameters (number of layers, number of neurons in each layer, learning rate, etc.) might require experimentation.
• Susceptibility to overfitting: Large neural networks can be prone to overfitting if there's insufficient data or insufficient regularization.

MLPRegressor represents a powerful machine learning model based on multi-layer neural networks and can be used for a wide range of regression tasks. This model is flexible but requires meticulous tuning and training on large volumes of data to achieve optimal results.

2.1.22.1. Code for creating the MLPRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.neural_network.MLPRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# MLPRegressor.py
# The code demonstrates the process of training MLPRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "MLPRegressor"
onnx_model_filename = data_path + "mlp_regressor"

# create an MLP Regressor model
mlp_regressor_model = MLPRegressor(hidden_layer_sizes=(100, 50), activation='relu', max_iter=1000)

# fit the model to the data
mlp_regressor_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = mlp_regressor_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(mlp_regressor_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)
# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(mlp_regressor_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  MLPRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9874070836467945
Python  Mean Absolute Error: 10.62249788982753
Python  Mean Squared Error: 166.63901957615224
Python  
Python  MLPRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9874070821340352
Python  Mean Absolute Error: 10.62249972216809
Python  Mean Squared Error: 166.63903959413219
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  MLPRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\mlp_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9874070836467945
Python  Mean Absolute Error: 10.622497889827532
Python  Mean Squared Error: 166.63901957615244
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  12
Python  double ONNX model precision:  14

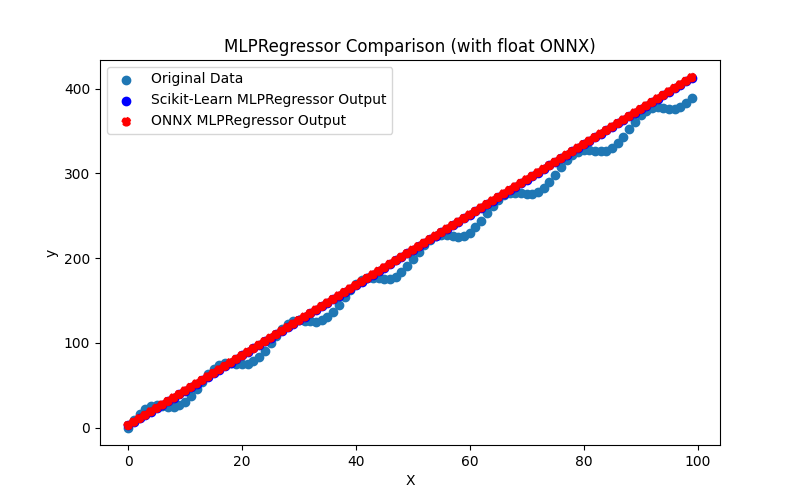
Fig.73. Results of the MLPRegressor.py (float ONNX)

2.1.22.2. MQL5 code for executing ONNX Models

This code executes the saved mlp_regressor_float.onnx and mlp_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                 MLPRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "MLPRegressor"
#define   ONNXFilenameFloat  "mlp_regressor_float.onnx"
#define   ONNXFilenameDouble "mlp_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

MLPRegressor (EURUSD,H1)        Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx)
MLPRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9875198695654352
MLPRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 10.5596681685341309
MLPRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 165.1465507645494597
MLPRegressor (EURUSD,H1)        
MLPRegressor (EURUSD,H1)        Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx)
MLPRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9875198617341387
MLPRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 10.5596715833884609
MLPRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 165.1466543942046599

Comparison with the original double precision model in Python:

Testing ONNX float: MLPRegressor (mlp_regressor_float.onnx)
Python  Mean Absolute Error: 10.62249788982753
MQL5:   Mean Absolute Error: 10.6224997221680901

Testing ONNX double: MLPRegressor (mlp_regressor_double.onnx)
Python  Mean Absolute Error: 10.62249788982753
MQL5:   Mean Absolute Error: 10.6224978898275282

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.22.3. ONNX representation of the mlp_regressor_float.onnx and mlp_regressor_double.onnx

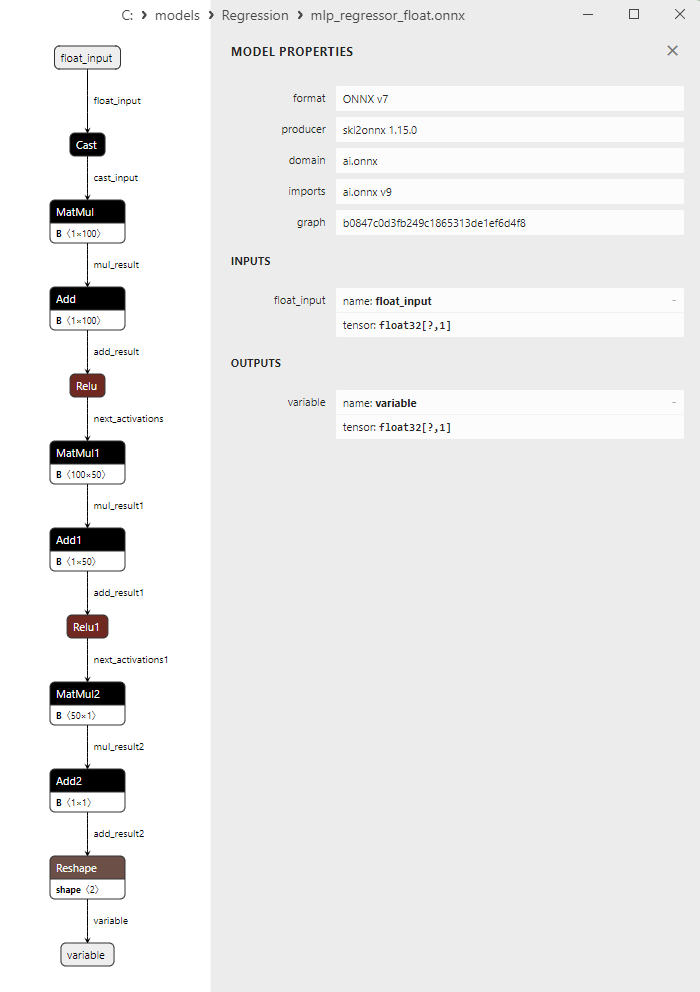
Fig.74. ONNX representation of the mlp_regressor_float.onnx in Netron

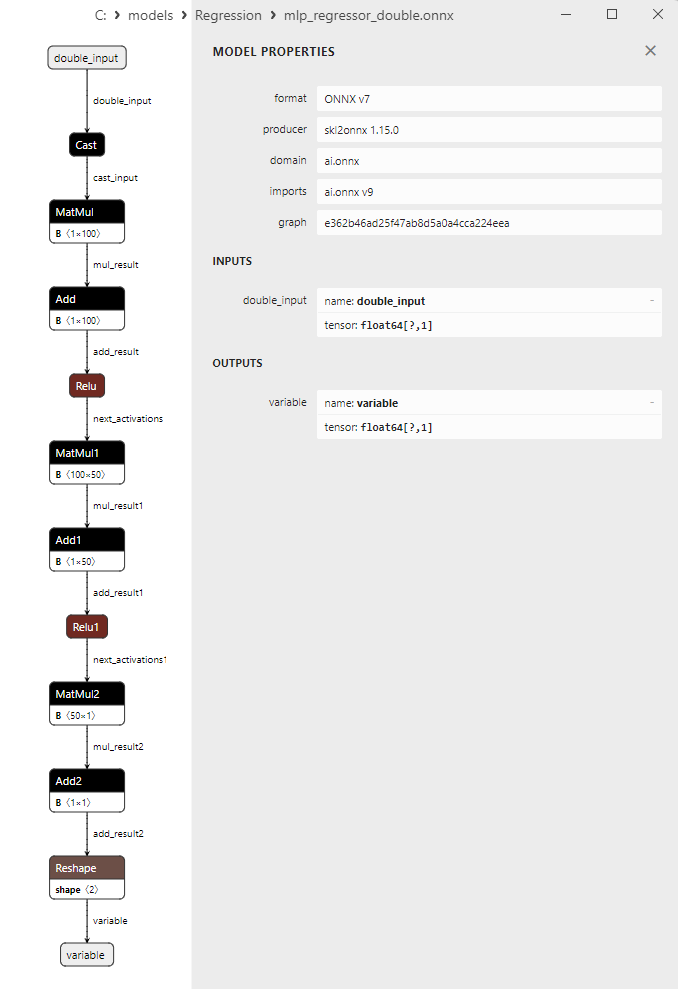
Fig.75. ONNX representation of the mlp_regressor_double.onnx in Netron

2.1.23. sklearn.cross_decomposition.PLSRegression

PLSRegression (Partial Least Squares Regression) is a machine learning method used for solving regression problems.

It is a part of the PLS family of methods and is applied to analyze and model relationships between two sets of variables, where one set serves as predictors, and the other set is the target variables.

How PLSRegression works:

1. Input data: It starts with two sets of data, labeled as X and Y. The X set contains independent variables (predictors), and the Y set contains target variables (dependent).
2. Selection of linear combinations: PLSRegression identifies linear combinations (components) in sets X and Y that maximize the covariance between them. These components are referred to as PLS components.
3. Maximizing covariance: The primary objective of PLSRegression is to find PLS components that maximize the covariance between X and Y. This allows for the extraction of the most informative relationships between predictors and target variables.
4. Model training: Once the PLS components are found, they can be used to create a model that predicts Y values based on X.
5. Generating predictions: After training, the model can be used to predict Y values for new data using corresponding X values.

Advantages of PLSRegression:

• Correlation analysis: PLSRegression enables the analysis and modeling of correlations between two sets of variables, which can be useful for understanding the relationships between predictors and target variables.
• Dimensionality reduction: The method can also be used to reduce the dimensionality of data by identifying the most important PLS components.

Limitations of PLSRegression:

• Sensitivity to the choice of the number of components: Selecting the optimal number of PLS components may require some experimentation.
• Dependency on the data structure: PLSRegression results can heavily rely on the structure of the data and the correlations between them.

PLSRegression is a machine learning method used to analyze and model correlations between two sets of variables, where one set acts as predictors, and the other is the target variables. This method allows for studying relationships within the data and can be useful for reducing data dimensionality and predicting target variable values based on predictors.

2.1.23.1. Code for creating the PLSRegression model and exporting it to ONNX for float and double

This code creates the sklearn.cross_decomposition.PLSRegression model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# PLSRegression.py
# The code demonstrates the process of training PLSRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PLSRegression"
onnx_model_filename = data_path + "pls_regression"

# create a PLSRegression model
pls_model = PLSRegression(n_components=1)

# fit the model to the data
pls_model.fit(X, y)

# predict values for the entire dataset
y_pred = pls_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(pls_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(pls_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  PLSRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281805
Python  
Python  PLSRegression ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382638567003
Python  Mean Absolute Error: 6.3477379221400145
Python  Mean Squared Error: 49.778145525764096
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  8
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  8
Python  
Python  PLSRegression ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\pls_regression_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9962382642613388
Python  Mean Absolute Error: 6.3477379263364275
Python  Mean Squared Error: 49.778140171281805
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  15
Python  double ONNX model precision:  16

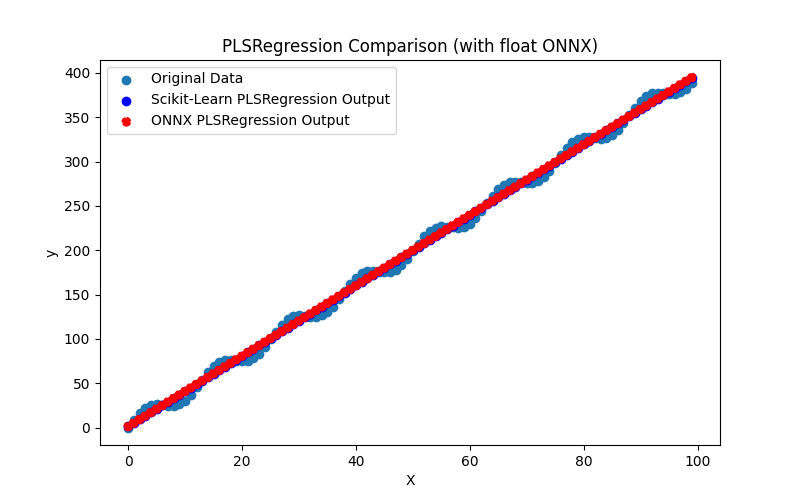
Fig.76. Results of the PLSRegression.py (float ONNX)

2.1.23.2. MQL5 code for executing ONNX Models

This code executes the saved pls_regression_float.onnx and pls_regression_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                PLSRegression.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "PLSRegression"
#define   ONNXFilenameFloat  "pls_regression_float.onnx"
#define   ONNXFilenameDouble "pls_regression_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

PLSRegression (EURUSD,H1)       Testing ONNX float: PLSRegression (pls_regression_float.onnx)
PLSRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382638567003
PLSRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3477379221400145
PLSRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781455257640815
PLSRegression (EURUSD,H1)       
PLSRegression (EURUSD,H1)       Testing ONNX double: PLSRegression (pls_regression_double.onnx)
PLSRegression (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9962382642613388
PLSRegression (EURUSD,H1)       MQL5:   Mean Absolute Error: 6.3477379263364275
PLSRegression (EURUSD,H1)       MQL5:   Mean Squared Error: 49.7781401712817839

Comparison with the original double precision model in Python:

Testing ONNX float: PLSRegression (pls_regression_float.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477379221400145
       
Testing ONNX double: PLSRegression (pls_regression_double.onnx)
Python  Mean Absolute Error: 6.3477379263364275
MQL5:   Mean Absolute Error: 6.3477379263364275

Accuracy of ONNX float MAE: 8 decimal places, Accuracy of ONNX double MAE: 16 decimal places.

2.1.23.3. ONNX representation of the pls_regression_float.onnx and pls_regression_double.onnx

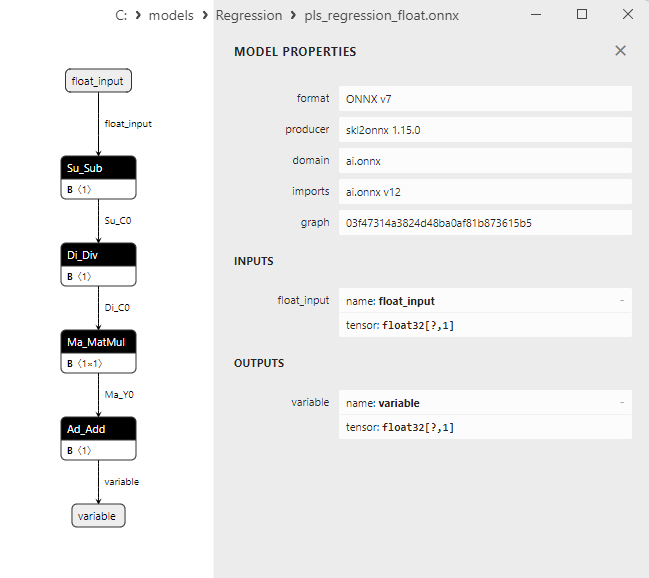
Fig.77. ONNX representation of the pls_regression_float.onnx in Netron

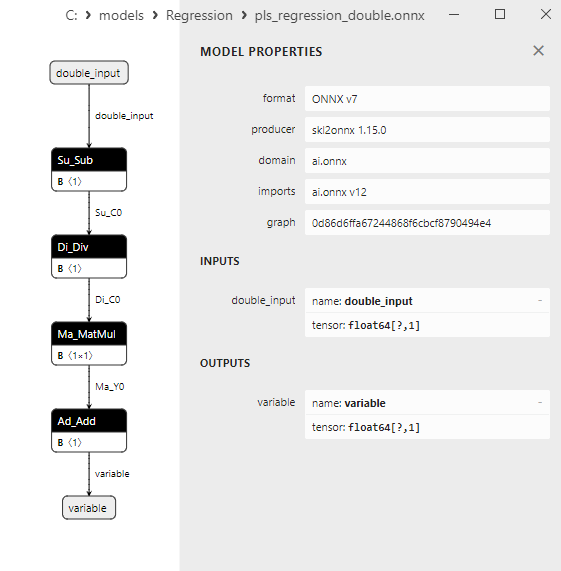
Fig.78. ONNX representation of the pls_regression_double.onnx in Netron

2.1.24. sklearn.linear_model.TweedieRegressor

TweedieRegressor is a regression method designed to solve regression problems using the Tweedie distribution. The Tweedie distribution is a probability distribution that can describe a wide range of data, including data with varying variance structure. TweedieRegressor is applied in regression tasks where the target variable possesses characteristics that align with the Tweedie distribution.

How TweedieRegressor works:

1. Target variable and Tweedie distribution: TweedieRegressor assumes that the target variable follows a Tweedie distribution. The Tweedie distribution depends on the parameter 'p,' which determines the distribution's shape and the degree of variance.
2. Model training: TweedieRegressor trains a regression model to predict the target variable based on independent variables (features). The model maximizes the likelihood for data corresponding to the Tweedie distribution.
3. Choosing the 'p' parameter: Selecting the 'p' parameter is a crucial aspect when using TweedieRegressor. This parameter defines the distribution's shape and variance. Different 'p' values correspond to different types of data; for instance, p=1 corresponds to the Poisson distribution, while p=2 corresponds to the normal distribution.
4. Transforming responses: Sometimes the model may require transformations of responses (target variables) before training. This transformation relates to the 'p' parameter and might involve logarithmic functions or other transformations to conform to the Tweedie distribution.

Advantages of TweedieRegressor:

• Ability to model data with varying variance: The Tweedie distribution can adapt to data with different variance structures, which is valuable for real-world data where variance can vary.
• Variety of 'p' parameters: The ability to choose different 'p' values allows modeling various data types.

Limitations of TweedieRegressor:

• Complexity in choosing the 'p' parameter: Selecting the correct 'p' value may require knowledge about the data and experimentation.
• Conformance to the Tweedie distribution: For successful application of TweedieRegressor, the target variable must correspond to the Tweedie distribution. Non-compliance may lead to poor model performance.

TweedieRegressor is a regression method that uses the Tweedie distribution to model data with varying variance structures. This method is useful in regression tasks where the target variable conforms to the Tweedie distribution and can be tuned with different 'p' parameter values for better data adaptation.

2.1.24.1. Code for creating the TweedieRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.TweedieRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# TweedieRegressor.py
# The code demonstrates the process of training TweedieRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import TweedieRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "TweedieRegressor"
onnx_model_filename = data_path + "tweedie_regressor"

# create a Tweedie Regressor model
regression_model = TweedieRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

2023.10.31 11:39:36.223 Python  TweedieRegressor Original model (double)
2023.10.31 11:39:36.223 Python  R-squared (Coefficient of determination): 0.9962368328117072
2023.10.31 11:39:36.223 Python  Mean Absolute Error: 6.342397897667562
2023.10.31 11:39:36.223 Python  Mean Squared Error: 49.797082198408745
2023.10.31 11:39:36.223 Python  
2023.10.31 11:39:36.223 Python  TweedieRegressor ONNX model (float)
2023.10.31 11:39:36.223 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_float.onnx
2023.10.31 11:39:36.253 Python  Information about input tensors in ONNX:
2023.10.31 11:39:36.253 Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
2023.10.31 11:39:36.253 Python  Information about output tensors in ONNX:
2023.10.31 11:39:36.253 Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
2023.10.31 11:39:36.253 Python  R-squared (Coefficient of determination) 0.9962368338709323
2023.10.31 11:39:36.253 Python  Mean Absolute Error: 6.342397072978867
2023.10.31 11:39:36.253 Python  Mean Squared Error: 49.797068181938165
2023.10.31 11:39:36.253 Python  R^2 matching decimal places:  8
2023.10.31 11:39:36.253 Python  MAE matching decimal places:  6
2023.10.31 11:39:36.253 Python  MSE matching decimal places:  4
2023.10.31 11:39:36.253 Python  float ONNX model precision:  6
2023.10.31 11:39:36.613 Python  
2023.10.31 11:39:36.613 Python  TweedieRegressor ONNX model (double)
2023.10.31 11:39:36.613 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\tweedie_regressor_double.onnx
2023.10.31 11:39:36.613 Python  Information about input tensors in ONNX:
2023.10.31 11:39:36.613 Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
2023.10.31 11:39:36.613 Python  Information about output tensors in ONNX:
2023.10.31 11:39:36.628 Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
2023.10.31 11:39:36.628 Python  R-squared (Coefficient of determination) 0.9962368328117072
2023.10.31 11:39:36.628 Python  Mean Absolute Error: 6.342397897667562
2023.10.31 11:39:36.628 Python  Mean Squared Error: 49.797082198408745
2023.10.31 11:39:36.628 Python  R^2 matching decimal places:  16
2023.10.31 11:39:36.628 Python  MAE matching decimal places:  15
2023.10.31 11:39:36.628 Python  MSE matching decimal places:  15
2023.10.31 11:39:36.628 Python  double ONNX model precision:  15

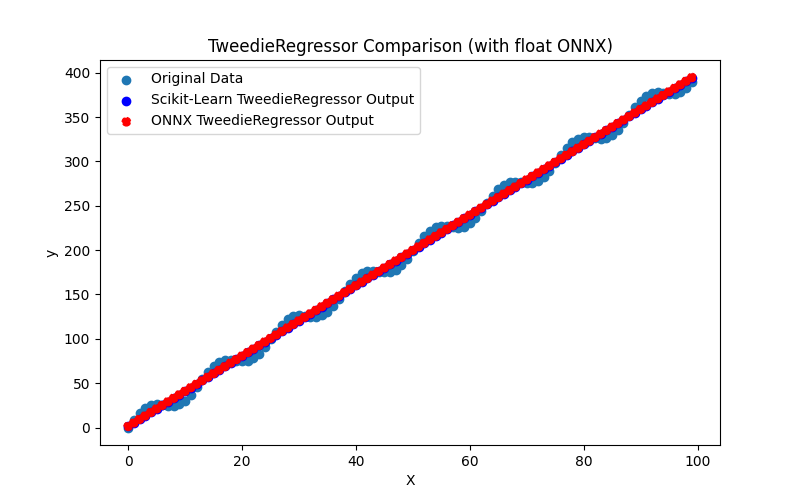
Fig.79. Results of the TweedieRegressor.py (float ONNX)

2.1.24.2. MQL5 code for executing ONNX Models

This code executes the saved tweedie_regressor_float.onnx and tweedie_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                             TweedieRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "TweedieRegressor"
#define   ONNXFilenameFloat  "tweedie_regressor_float.onnx"
#define   ONNXFilenameDouble "tweedie_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

2023.10.31 11:42:20.113 TweedieRegressor (EURUSD,H1)    Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx)
2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962368338709323
2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3423970729788666
2023.10.31 11:42:20.119 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7970681819381653
2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1)    
2023.10.31 11:42:20.125 TweedieRegressor (EURUSD,H1)    Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx)
2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9962368328117072
2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 6.3423978976675608
2023.10.31 11:42:20.130 TweedieRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 49.7970821984087593

Comparison with the original double precision model in Python:

Testing ONNX float: TweedieRegressor (tweedie_regressor_float.onnx)
Python  Mean Absolute Error: 6.342397897667562
MQL5:   Mean Absolute Error: 6.3423970729788666

Testing ONNX double: TweedieRegressor (tweedie_regressor_double.onnx)
Python  Mean Absolute Error: 6.342397897667562
MQL5:   Mean Absolute Error: 6.3423978976675608

Accuracy of ONNX float MAE: 6 decimal places, Accuracy of ONNX double MAE: 14 decimal places.

2.1.24.3. ONNX representation of the tweedie_regressor_float.onnx and tweedie_regressor_double.onnx

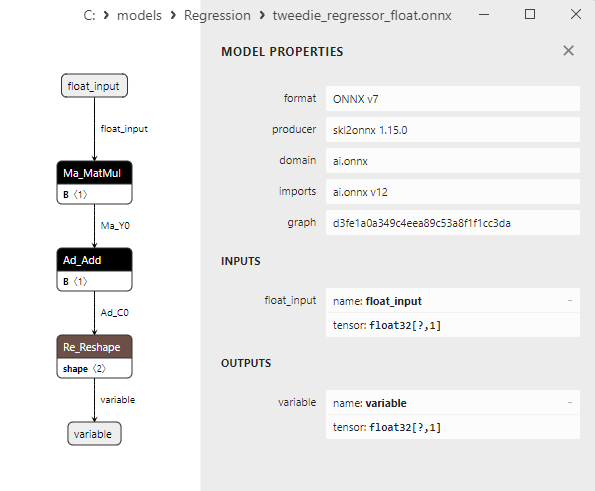
Fig.80. ONNX representation of the tweedie_regressor_float.onnx in Netron

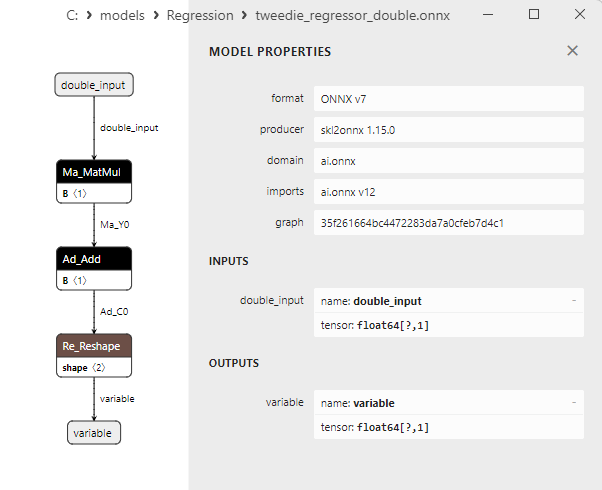
Fig.81. ONNX representation of the tweedie_regressor_double.onnx in Netron

2.1.25. sklearn.linear_model.PoissonRegressor

PoissonRegressor is a machine learning method applied to solve regression tasks based on the Poisson distribution..

This method is suitable when the dependent variable (target variable) is count data, representing the number of events that occurred within a fixed period of time or in a fixed spatial interval. PoissonRegressor models the relationship between predictors (independent variables) and the target variable by assuming that this relationship conforms to the Poisson distribution.

How PoissonRegressor works:

1. Input data: Starting with a dataset that includes features (independent variables) and the target variable, representing the count of events.
2. Poisson distribution: The PoissonRegressor method models the target variable by assuming it follows the Poisson distribution. The Poisson distribution is suitable for modeling events that occur at a fixed mean intensity within a given time interval or spatial range.
3. Model training: PoissonRegressor trains a model that estimates the parameters of the Poisson distribution, considering the predictors. The model attempts to find the best fit for the observed data using the likelihood function that corresponds to the Poisson distribution.
4. Predicting count values: After training, the model can be used to predict count values (the number of events) on new data, and these predictions also follow the Poisson distribution.

Advantages of PoissonRegressor:

• Suitable for count data: PoissonRegressor is suitable for tasks where the target variable represents count data, such as the number of orders, calls, etc.
• Specificity of the distribution: Since the model adheres to the Poisson distribution, it can be more accurate for data that are well described by this distribution.

Limitations of PoissonRegressor:

• Only suitable for count data: PoissonRegressor is not suitable for regression where the target variable is continuous and non-count.
• Dependence on feature selection: The quality of the model can heavily depend on the selection and engineering of features.

PoissonRegressor is a machine learning method used for solving regression tasks when the target variable represents count data and is modeled using the Poisson distribution. This method is beneficial for tasks related to events occurring at a fixed intensity within specific time or spatial intervals.

2.1.25.1. Code for creating the PoissonRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.PoissonRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# PoissonRegressor.py
# The code demonstrates the process of training PoissonRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import PoissonRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PoissonRegressor"
onnx_model_filename = data_path + "poisson_regressor"

# create a PoissonRegressor model
regression_model = PoissonRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  PoissonRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9204304782362495
Python  Mean Absolute Error: 27.59790466048524
Python  Mean Squared Error: 1052.9242570153044
Python  
Python  PoissonRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9204305082536851
Python  Mean Absolute Error: 27.59790825165078
Python  Mean Squared Error: 1052.9238598018305
Python  R^2 matching decimal places:  6
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  2
Python  float ONNX model precision:  5
Python  
Python  PoissonRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\poisson_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9204304782362495
Python  Mean Absolute Error: 27.59790466048524
Python  Mean Squared Error: 1052.9242570153044
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  13
Python  double ONNX model precision:  14

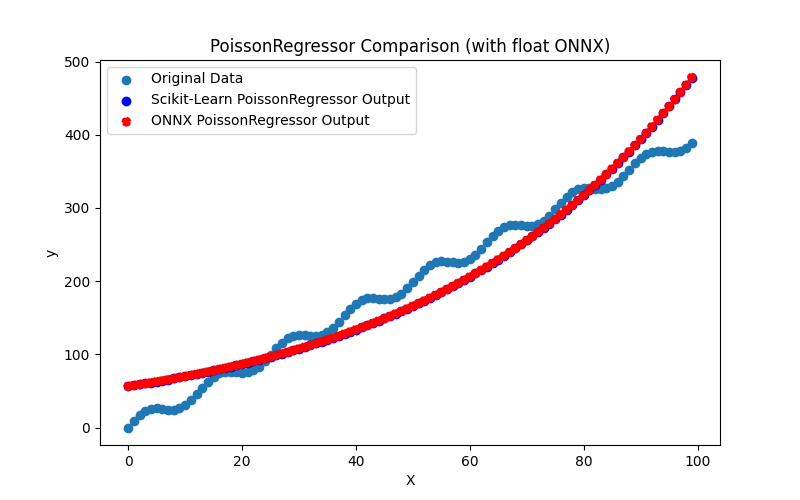
Fig.82. Results of the PoissonRegressor.py (float ONNX)

2.1.25.2. MQL5 code for executing ONNX Models

This code executes the saved poisson_regressor_float.onnx and poisson_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                             PoissonRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "PoissonRegressor"
#define   ONNXFilenameFloat  "poisson_regressor_float.onnx"
#define   ONNXFilenameDouble "poisson_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

PoissonRegressor (EURUSD,H1)    Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx)
PoissonRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9204305082536851
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 27.5979082516507788
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 1052.9238598018305311
PoissonRegressor (EURUSD,H1)    
PoissonRegressor (EURUSD,H1)    Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx)
PoissonRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9204304782362493
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 27.5979046604852343
PoissonRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 1052.9242570153051020

Comparison with the original double precision model in Python:

Testing ONNX float: PoissonRegressor (poisson_regressor_float.onnx)
Python  Mean Absolute Error: 27.59790466048524
MQL5:   Mean Absolute Error: 27.5979082516507788
    
Testing ONNX double: PoissonRegressor (poisson_regressor_double.onnx)
Python  Mean Absolute Error: 27.59790466048524
MQL5:   Mean Absolute Error: 27.5979046604852343

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.25.3. ONNX representation of the poisson_regressor_float.onnx and poisson_regressor_double.onnx

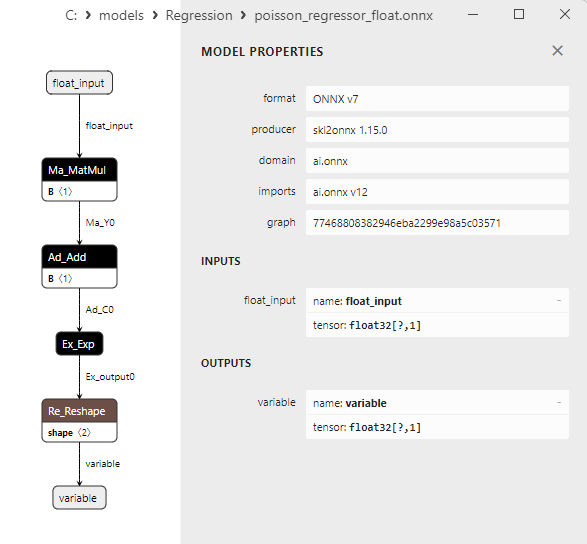
Fig.83. ONNX representation of the poisson_regressor_float.onnx in Netron

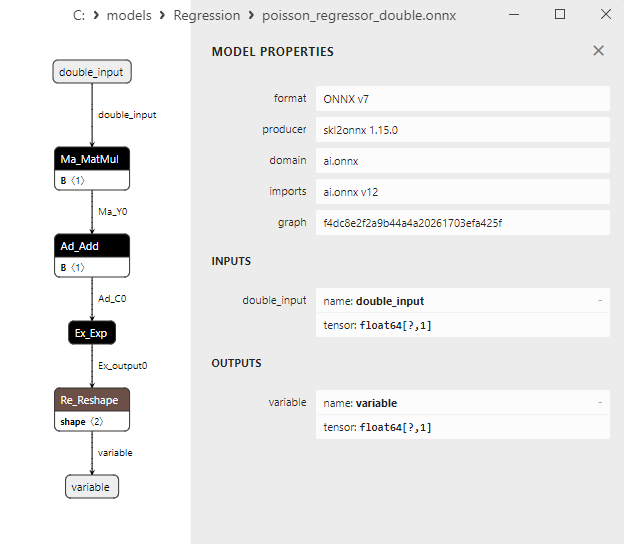
Fig.84. ONNX representation of the poisson_regressor_double.onnx in Netron

2.1.26. sklearn.neighbors.RadiusNeighborsRegressor

RadiusNeighborsRegressor  is a machine learning method used for regression tasks. It's a variant of the k-Nearest Neighbors (k-NN) method designed to predict values of the target variable based on the nearest neighbors in the feature space. However, instead of a fixed number of neighbors (as in the k-NN method), RadiusNeighborsRegressor uses a fixed radius to determine neighbors for each sample.

How RadiusNeighborsRegressor works:

1. Input data: Starting with a dataset that includes features (independent variables) and the target variable (continuous).
2. Setting the radius: RadiusNeighborsRegressor requires setting a fixed radius to determine the closest neighbors for each sample in the feature space.
3. Neighbor definition: For each sample, all data points within the specified radius are determined, becoming neighbors of that sample.
4. Weighted averaging: To predict the value of the target variable for each sample, the values of its neighbors' target variables are used. This is often done using weighted averaging, where weights depend on the distance between samples.
5. Prediction: After training, the model can be used to predict the values of the target variable on new data based on the nearest neighbors in the feature space.

Advantages of RadiusNeighborsRegressor:

• Versatility: RadiusNeighborsRegressor can be used for regression tasks, particularly when the number of neighbors may vary significantly depending on the radius.
• Resilience to outliers: A neighbor-based approach can be resilient to outliers because the model only considers nearby data points.

Limitations of RadiusNeighborsRegressor:

• Dependency on radius selection: Choosing the right radius may require tuning and experimentation.
• Computational complexity: Handling large datasets may require substantial computational resources.

RadiusNeighborsRegressor is a machine learning method used for regression tasks based on the k-Nearest Neighbors method with a fixed radius. This method can be valuable in situations where the number of neighbors can change depending on the radius and in cases where data contains outliers.

2.1.26.1. Code for creating the RadiusNeighborsRegressor and exporting it to ONNX for float and double

This code creates the sklearn.neighbors.RadiusNeighborsRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# RadiusNeighborsRegressor.py
# The code demonstrates the process of training RadiusNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import RadiusNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RadiusNeighborsRegressor"
onnx_model_filename = data_path + "radius_neighbors_regressor"

# create a RadiusNeighborsRegressor model
regression_model = RadiusNeighborsRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  RadiusNeighborsRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9999521132921395
Python  Mean Absolute Error: 0.591458244376554
Python  Mean Squared Error: 0.6336732353950723
Python  
Python  RadiusNeighborsRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999999971
Python  Mean Absolute Error: 4.393654615473253e-06
Python  Mean Squared Error: 3.829042036424747e-11
Python  R^2 matching decimal places:  4
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  RadiusNeighborsRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\radius_neighbors_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 1.0
Python  Mean Absolute Error: 0.0
Python  Mean Squared Error: 0.0
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  double ONNX model precision:  0

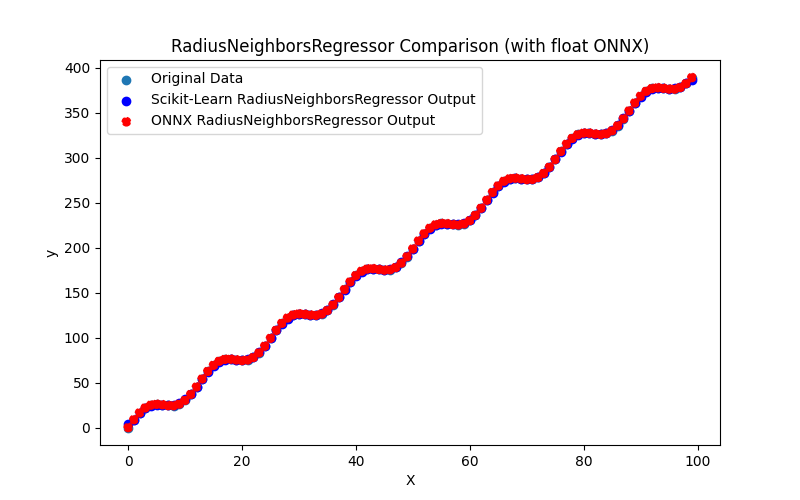
Fig.85. Results of the RadiusNeighborsRegressor.py (float ONNX)

2.1.26.2. MQL5 code for executing ONNX Models

This code executes the saved radius_neighbors_regressor_float.onnx and radius_neighbors_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                     RadiusNeighborsRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RadiusNeighborsRegressor"
#define   ONNXFilenameFloat  "radius_neighbors_regressor_float.onnx"
#define   ONNXFilenameDouble "radius_neighbors_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

RadiusNeighborsRegressor (EURUSD,H1)    Testing ONNX float: RadiusNeighborsRegressor (radius_neighbors_regressor_float.onnx)
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9999999999999971
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000043936546155
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000382904
RadiusNeighborsRegressor (EURUSD,H1)    
RadiusNeighborsRegressor (EURUSD,H1)    Testing ONNX double: RadiusNeighborsRegressor (radius_neighbors_regressor_double.onnx)
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 1.0000000000000000
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000000000000000
RadiusNeighborsRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000000000

2.1.26.3. ONNX representation of the radius_neighbors_regressor_float.onnx and radius_neighbors_regressor_double.onnx

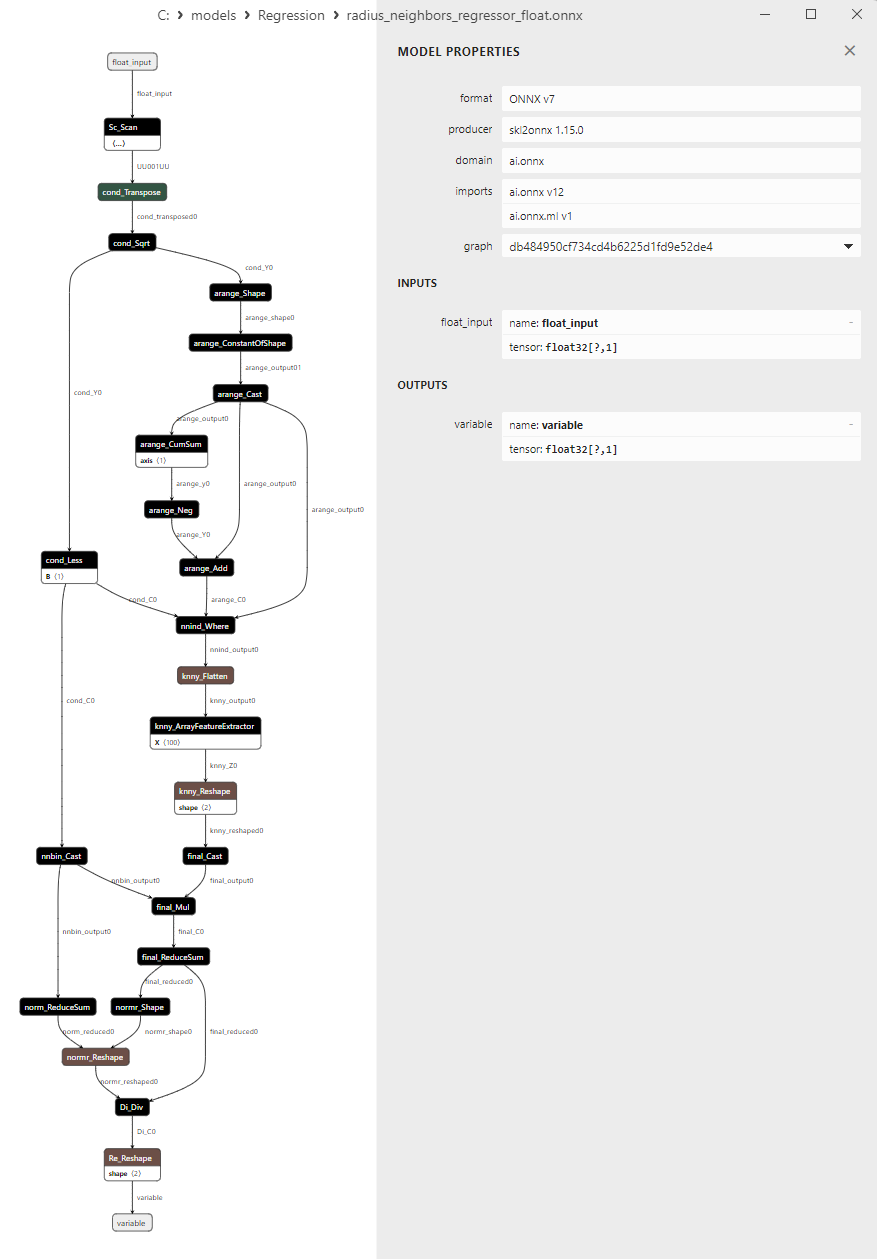
Fig.86. ONNX representation of the radius_neighbors_regressor_float.onnx in Netron

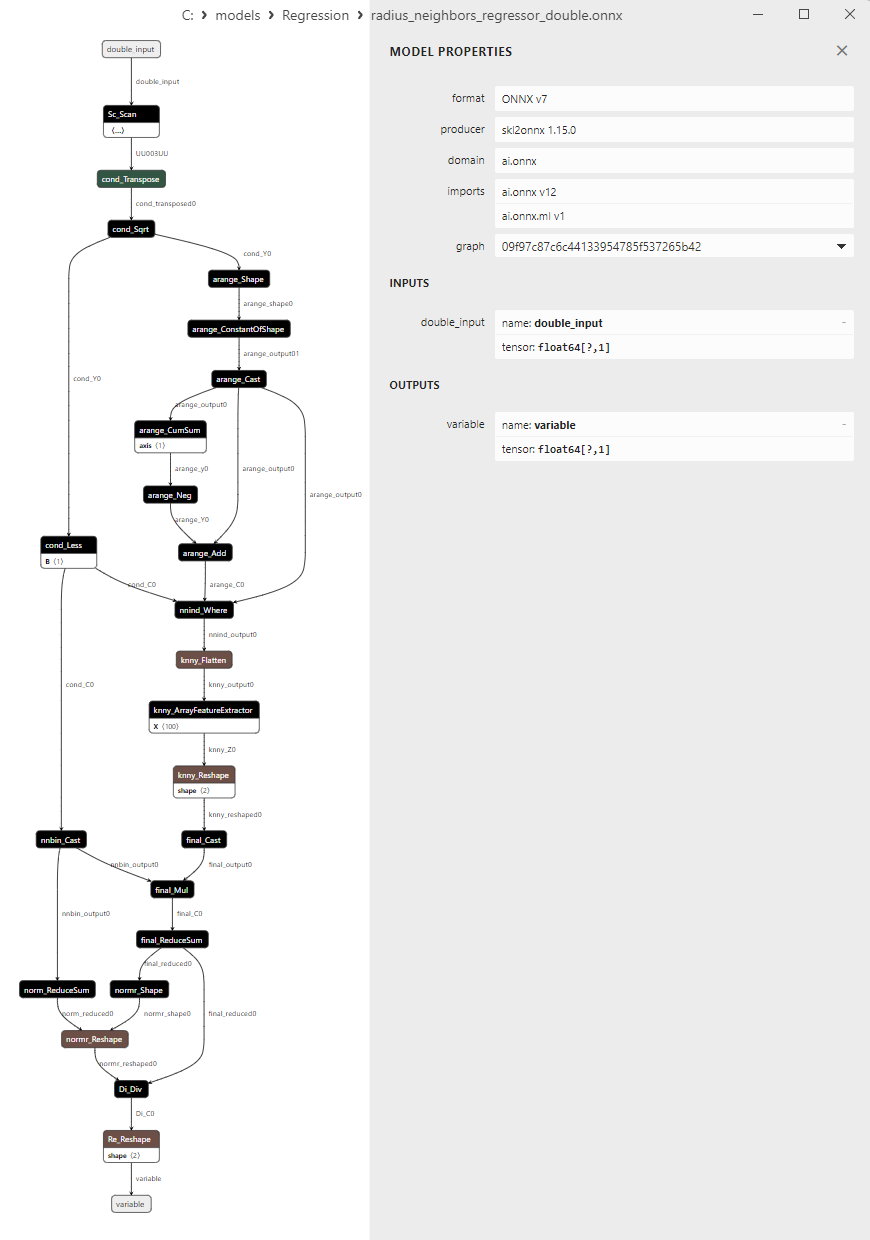
Fig.87. ONNX-representaion of radius_neighbors_regressor_double.onnx in Netron

2.1.27. sklearn.neighbors.KNeighborsRegressor

KNeighborsRegressor is a machine learning method used for regression tasks.

It belongs to the category of k-Nearest Neighbors (k-NN) algorithms and is used to predict numerical values of the target variable based on the proximity (similarity) between objects in the training dataset.

How KNeighborsRegressor works:

1. Input data: It begins with the initial dataset, including features (independent variables) and corresponding values of the target variable.
2. Selecting the number of neighbors (k): You need to choose the number of nearest neighbors (k) to be considered during prediction. This number is one of the model's hyperparameters.
3. Calculating proximity: For new data (points for which predictions are needed), the distance or similarity between this data and all objects in the training dataset is computed.
4. Choosing k nearest neighbors: k objects from the training dataset that are closest to the new data are selected.
5. Prediction: For regression tasks, predicting the value of the target variable for new data is calculated as the average value of the target variables of the k nearest neighbors.

Advantages of KNeighborsRegressor:

• Ease of use: KNeighborsRegressor is a straightforward algorithm that does not require complex preprocessing of data.
• Non-parametric nature: The method does not assume a specific functional form of dependency between features and the target variable, enabling modeling of diverse relationships.
• Reproducibility: Results from KNeighborsRegressor can be reproduced as predictions are based on data proximity.

Limitations of KNeighborsRegressor:

• Computational complexity: Calculating distances to all points in the training dataset can be computationally expensive for large volumes of data.
• Sensitivity to the choice of the number of neighbors: Selecting the optimal value of k requires tuning and can significantly impact the model's performance.
• Sensitivity to noise: The method can be sensitive to data noise and outliers.

KNeighborsRegressor is useful in regression tasks where considering the neighborhood of objects for predicting the target variable is essential. It can be particularly useful in situations where the relationship between features and the target variable is nonlinear and complex.

2.1.27.1. Code for creating the KNeighborsRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.neighbors.KNeighborsRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# KNeighborsRegressor.py
# The code demonstrates the process of training KNeighborsRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "KNeighborsRegressor"
onnx_model_filename = data_path + "kneighbors_regressor"

# create a KNeighbors Regressor model
kneighbors_model = KNeighborsRegressor(n_neighbors=5)

# fit the model to the data
kneighbors_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = kneighbors_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(kneighbors_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(kneighbors_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  KNeighborsRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9995599863346534
Python  Mean Absolute Error: 1.7414210057117578
Python  Mean Squared Error: 5.822594523532273
Python  
Python  KNeighborsRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9995599867417418
Python  Mean Absolute Error: 1.7414195457976402
Python  Mean Squared Error: 5.8225891366283875
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  4
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  4
Python  
Python  KNeighborsRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\kneighbors_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9995599863346534
Python  Mean Absolute Error: 1.7414210057117583
Python  Mean Squared Error: 5.822594523532269
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  14
Python  MSE matching decimal places:  13
Python  double ONNX model precision:  14

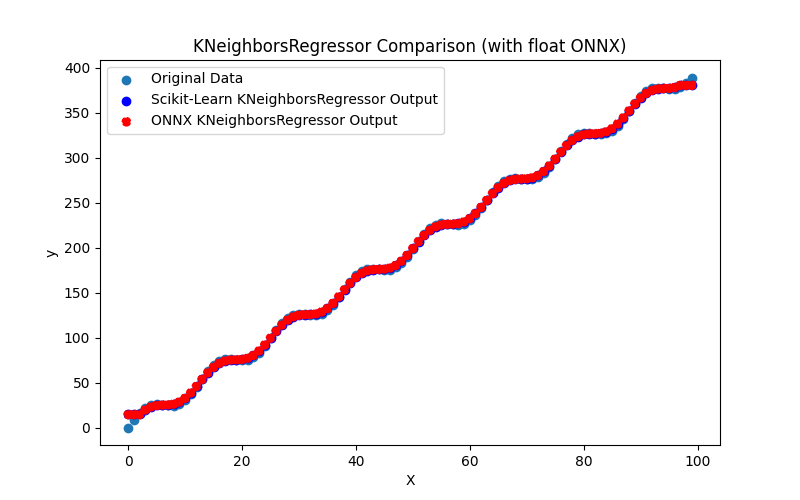
Fig.88. Results of the KNeighborsRegressor.py (float ONNX)

2.1.27.2. MQL5 code for executing ONNX Models

This code executes the saved kneighbors_regressor_float.onnx and kneighbors_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                          KNeighborsRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "KNeighborsRegressor"
#define   ONNXFilenameFloat  "kneighbors_regressor_float.onnx"
#define   ONNXFilenameDouble "kneighbors_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

KNeighborsRegressor (EURUSD,H1) Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx)
KNeighborsRegressor (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9995599860116634
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Absolute Error: 1.7414200607817711
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Squared Error: 5.8225987975798184
KNeighborsRegressor (EURUSD,H1) 
KNeighborsRegressor (EURUSD,H1) Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx)
KNeighborsRegressor (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9995599863346534
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Absolute Error: 1.7414210057117601
KNeighborsRegressor (EURUSD,H1) MQL5:   Mean Squared Error: 5.8225945235322705

Comparison with the original double precision model in Python:

Testing ONNX float: KNeighborsRegressor (kneighbors_regressor_float.onnx)
Python  Mean Absolute Error: 1.7414210057117578
MQL5:   Mean Absolute Error: 1.7414200607817711
 
Testing ONNX double: KNeighborsRegressor (kneighbors_regressor_double.onnx)
Python  Mean Absolute Error: 1.7414210057117578
MQL5:   Mean Absolute Error: 1.7414210057117601

Accuracy of ONNX float MAE: 5 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.27.3. ONNX representation of the kneighbors_regressor_float.onnx and kneighbors_regressor_double.onnx

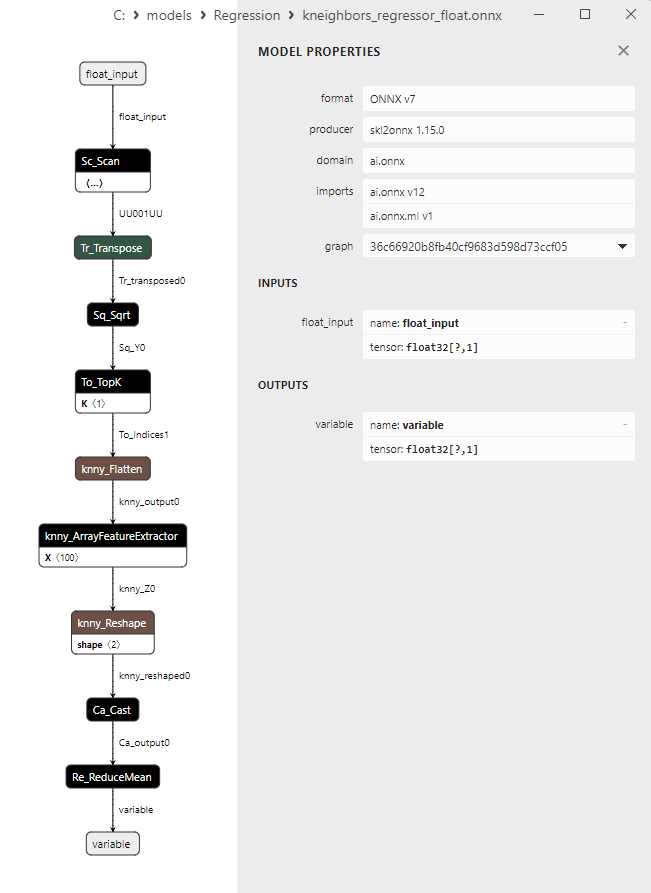
Fig.89. ONNX representation of the kneighbors_regressor_float.onnx in Netron

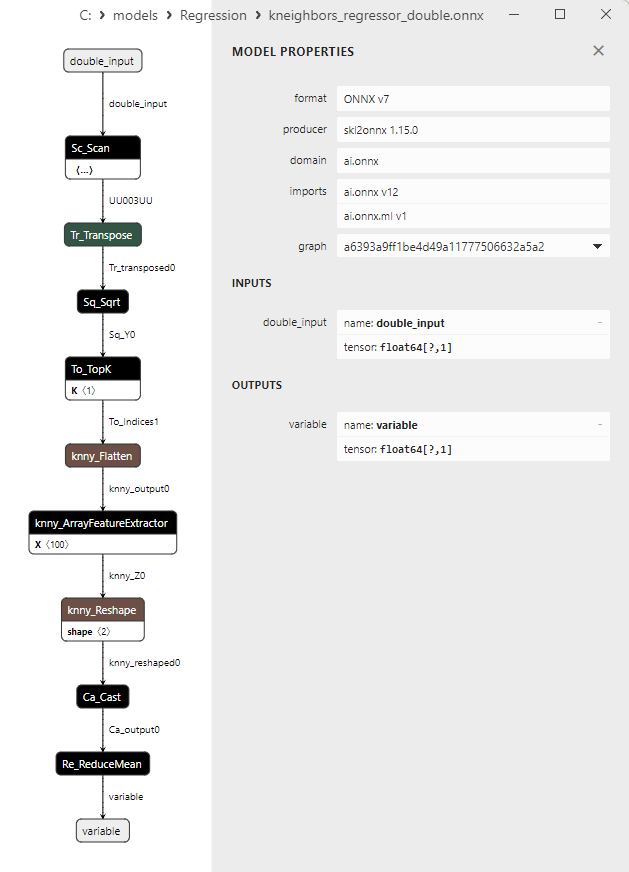
Fig.90. ONNX representation of the kneighbors_regressor_double.onnx in Netron

2.1.28. sklearn.gaussian_process.GaussianProcessRegressor

GaussianProcessRegressor is a machine learning method used for regression tasks that allows modeling uncertainty in predictions.

The Gaussian Process (GP) is a powerful tool in Bayesian machine learning and is used to model complex functions and predict target variable values while accounting for uncertainty.

How GaussianProcessRegressor works:

1. Input data: It begins with the initial dataset, including features (independent variables) and corresponding values of the target variable.
2. Modeling the Gaussian process: Gaussian Process employs a Gaussian process, which is a collection of random variables described by a Gaussian (normal) distribution. GP models not only the mean values for each data point but also the covariance (or similarity) between these points.
3. Choosing the covariance function: A crucial aspect of GP is the selection of the covariance function (or kernel) that determines the interconnectedness and strength among data points. Different covariance functions can be used based on the nature of the data and the task.
4. Model training: GaussianProcessRegressor trains the GP using the training data. During training, the model adjusts the parameters of the covariance function and evaluates uncertainty in predictions.
5. Prediction: After training, the model can be used to predict target variable values for new data. An important feature of GP is that it predicts not only the mean value but also a confidence interval that estimates the level of confidence in the predictions.

Advantages of GaussianProcessRegressor:

• Modeling uncertainty: GP allows for accounting for uncertainty in predictions, which is beneficial in tasks where knowing the confidence in predicted values is crucial.
• Flexibility: GP can model various functions, and its covariance functions can be adapted for different data types.
• Few hyperparameters: GP has a relatively small number of hyperparameters, simplifying model tuning.

Limitations of GaussianProcessRegressor:

• Computational complexity: GP can be computationally expensive, especially with a large volume of data.
• Inefficiency in high-dimensional spaces: GP might lose efficiency in tasks with numerous features due to the curse of dimensionality.

GaussianProcessRegressor is useful in regression tasks where modeling uncertainty and providing reliable predictions are crucial. This method is frequently used in Bayesian machine learning and meta-analysis.

2.1.28.1. Code for creating the GaussianProcessRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.gaussian_process.GaussianProcessRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# GaussianProcessRegressor.py
# The code demonstrates the process of training GaussianProcessRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "GaussianProcessRegressor"
onnx_model_filename = data_path + "gaussian_process_regressor"

# create a GaussianProcessRegressor model
kernel = 1.0 * RBF()
gp_model = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10)

# fit the model to the data
gp_model.fit(X, y)

# predict values for the entire dataset
y_pred = gp_model.predict(X, return_std=False)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(gp_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("ONNX: MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(gp_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  GaussianProcessRegressor Original model (double)
Python  R-squared (Coefficient of determination): 1.0
Python  Mean Absolute Error: 3.504041501400934e-13
Python  Mean Squared Error: 1.6396606443650807e-25
Python  
Python  GaussianProcessRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: GPmean, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999999936
Python  Mean Absolute Error: 6.454076974495848e-06
Python  Mean Squared Error: 8.493606782250733e-11
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  GaussianProcessRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gaussian_process_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: GPmean, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 1.0
Python  Mean Absolute Error: 3.504041501400934e-13
Python  Mean Squared Error: 1.6396606443650807e-25
Python  R^2 matching decimal places:  1
Python  MAE matching decimal places:  19
Python  MSE matching decimal places:  20
Python  double ONNX model precision:  19

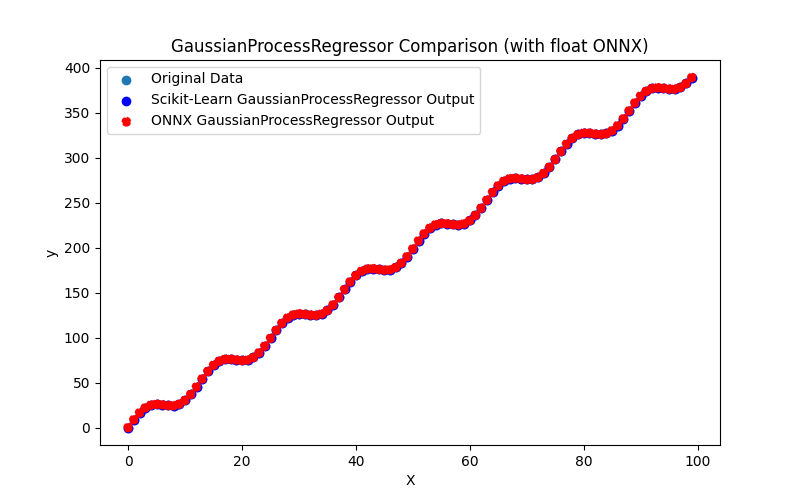
Fig.91. Results of the GaussianProcessRegressor.py (float ONNX)

2.1.28.2. MQL5 code for executing ONNX Models

This code executes the saved gaussian_process_regressor_float.onnx and gaussian_process_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                     GaussianProcessRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "GaussianProcessRegressor"
#define   ONNXFilenameFloat  "gaussian_process_regressor_float.onnx"
#define   ONNXFilenameDouble "gaussian_process_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

GaussianProcessRegressor (EURUSD,H1)    Testing ONNX float: GaussianProcessRegressor (gaussian_process_regressor_float.onnx)
GaussianProcessRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9999999999999936
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000064540769745
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000849361
GaussianProcessRegressor (EURUSD,H1)    
GaussianProcessRegressor (EURUSD,H1)    Testing ONNX double: GaussianProcessRegressor (gaussian_process_regressor_double.onnx)
GaussianProcessRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 1.0000000000000000
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 0.0000000000003504
GaussianProcessRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 0.0000000000000000

2.1.28.3. ONNX representation of the gaussian_process_regressor_float.onnx and gaussian_process_regressor_double.onnx

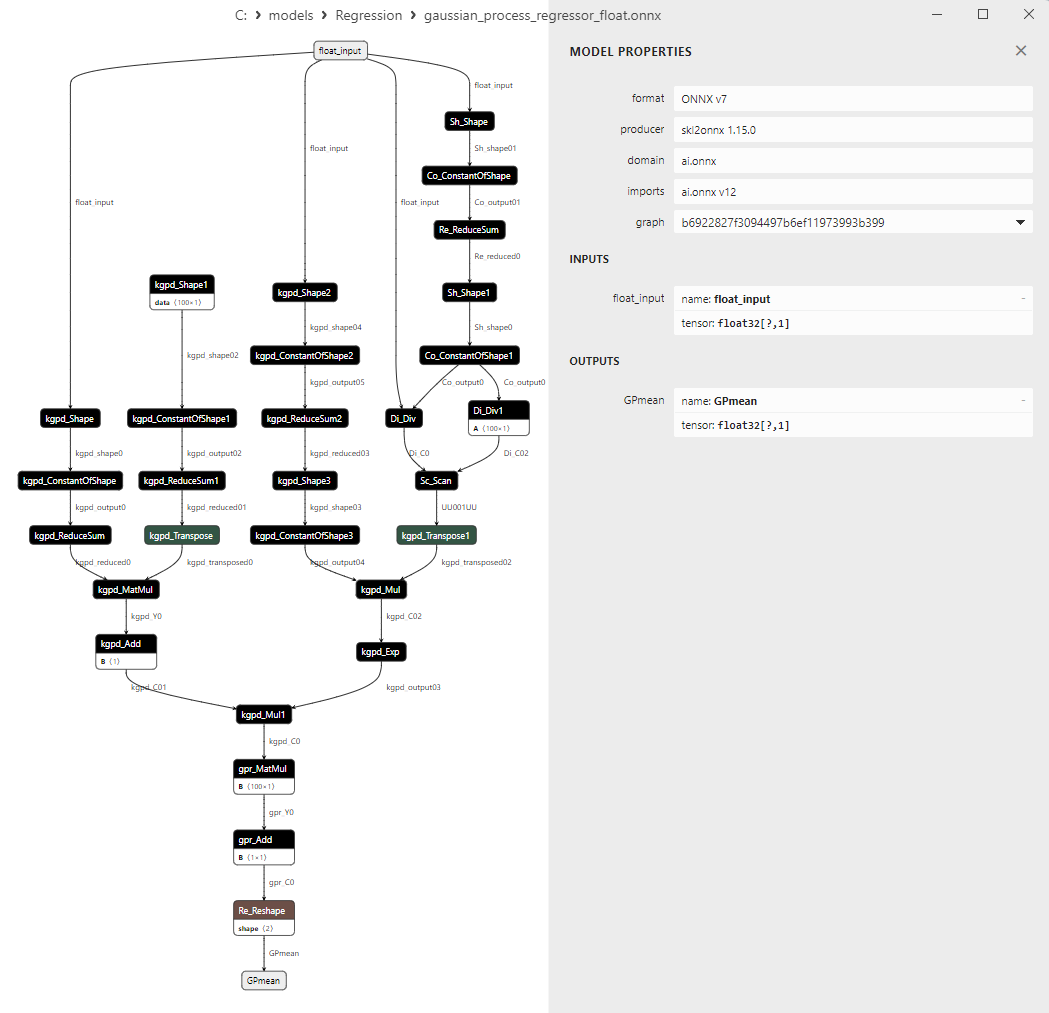
Fig.92. ONNX representation of the gaussian_process_regressor_float.onnx in Netron

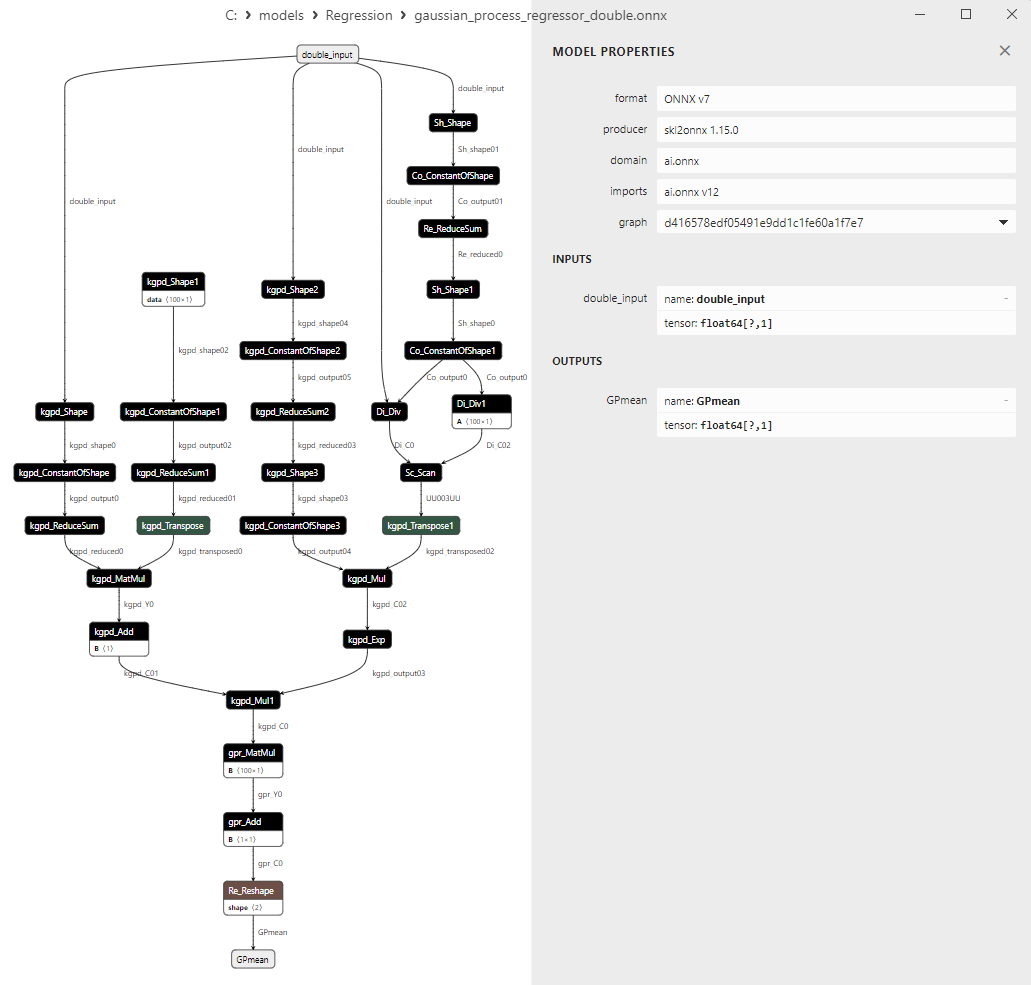
Fig.93. ONNX representation of the gaussian_process_regressor_double.onnx in Netron

2.1.29. sklearn.linear_model.GammaRegressor

GammaRegressor is a machine learning method designed for regression tasks where the target variable follows a gamma distribution.

The gamma distribution is a probability distribution used to model positive, continuous random variables. This method enables modeling and predicting positive numerical values, such as cost, time, or proportions.

How GammaRegressor works:

1. Input data: It starts with the initial dataset, where there are features (independent variables) and corresponding values of the target variable following the gamma distribution.
2. Loss function selection: GammaRegressor utilizes a loss function that corresponds to the gamma distribution and considers the peculiarities of this distribution. This allows modeling data while considering the non-negativity and the right-skew of the gamma distribution.
3. Model training: The model is trained on data using the chosen loss function. During training, it adjusts the model's parameters to minimize the loss function.
4. Prediction: After training, the model can be used to predict the values of the target variable for new data.

Advantages of GammaRegressor:

• Modeling positive values: This method is specifically designed for modeling positive numerical values, which can be useful in tasks where the target variable is lower-bounded.
• Considering the gamma distribution shape: GammaRegressor accounts for the characteristics of the gamma distribution, enabling more accurate modeling of data following this distribution.
• Usefulness in econometrics and medical research: The gamma distribution is frequently used to model cost, waiting time, and other positive random variables in econometrics and medical research.

Limitations of GammaRegressor:

• Limitation on data type: This method is suitable only for regression tasks where the target variable follows the gamma distribution or similar distributions. For data that doesn't conform to such a distribution, this method might not be effective.
• Requires choosing a loss function: Choosing an appropriate loss function might require knowledge about the distribution of the target variable and its characteristics.

GammaRegressor is useful in tasks where modeling and predicting positive numerical values that align with the gamma distribution are needed.

2.1.29.1. Code for creating the GammaRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.GammaRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# GammaRegressor.py
# The code demonstrates the process of training GammaRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import GammaRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 10+4*X + 10*np.sin(X*0.5)

model_name = "GammaRegressor"
onnx_model_filename = data_path + "gamma_regressor"

# create a Gamma Regressor model
regression_model = GammaRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  GammaRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.7963797339354436
Python  Mean Absolute Error: 37.266200319422815
Python  Mean Squared Error: 2694.457784927322
Python  
Python  GammaRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.7963795030042045
Python  Mean Absolute Error: 37.266211754095956
Python  Mean Squared Error: 2694.4608407846144
Python  R^2 matching decimal places:  6
Python  MAE matching decimal places:  4
Python  MSE matching decimal places:  1
Python  float ONNX model precision:  4
Python  
Python  GammaRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gamma_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.7963797339354436
Python  Mean Absolute Error: 37.266200319422815
Python  Mean Squared Error: 2694.457784927322
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  15
Python  MSE matching decimal places:  12
Python  double ONNX model precision:  15

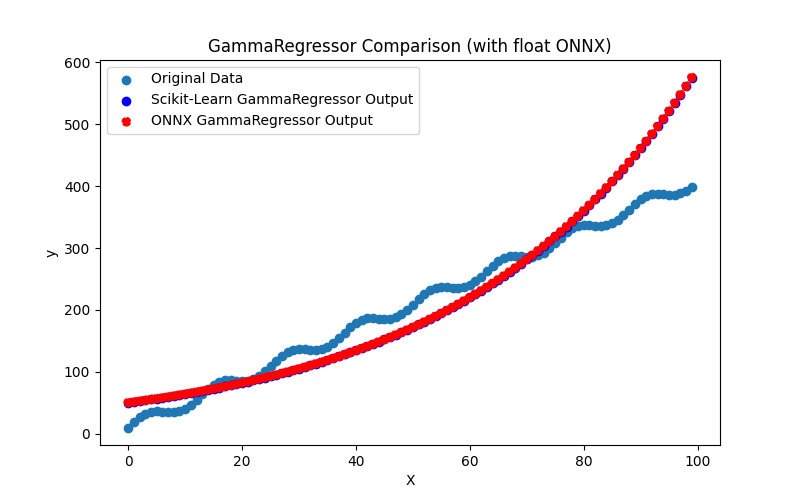
Fig.94. Results of the GammaRegressor.py (float ONNX)

2.1.29.2. MQL5 code for executing ONNX Models

This code executes the saved gamma_regressor_float.onnx and gamma_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                               GammaRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "GammaRegressor"
#define   ONNXFilenameFloat  "gamma_regressor_float.onnx"
#define   ONNXFilenameDouble "gamma_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(10+4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

GammaRegressor (EURUSD,H1)      Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx)
GammaRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.7963795030042045
GammaRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 37.2662117540959628
GammaRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 2694.4608407846144473
GammaRegressor (EURUSD,H1)      
GammaRegressor (EURUSD,H1)      Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx)
GammaRegressor (EURUSD,H1)      MQL5:   R-Squared (Coefficient of determination): 0.7963797339354435
GammaRegressor (EURUSD,H1)      MQL5:   Mean Absolute Error: 37.2662003194228220
GammaRegressor (EURUSD,H1)      MQL5:   Mean Squared Error: 2694.4577849273218817

Comparison with the original double precision model in Python:

Testing ONNX float: GammaRegressor (gamma_regressor_float.onnx)
Python  Mean Absolute Error: 37.266200319422815
MQL5:   Mean Absolute Error: 37.2662117540959628
      
Testing ONNX double: GammaRegressor (gamma_regressor_double.onnx)
Python  Mean Absolute Error: 37.266200319422815
MQL5:   Mean Absolute Error: 37.2662003194228220

Accuracy of ONNX float MAE: 4 decimal places, Accuracy of ONNX double MAE: 13 decimal places.

2.1.29.3. ONNX representation of the gamma_regressor_float.onnx and gamma_regressor_double.onnx

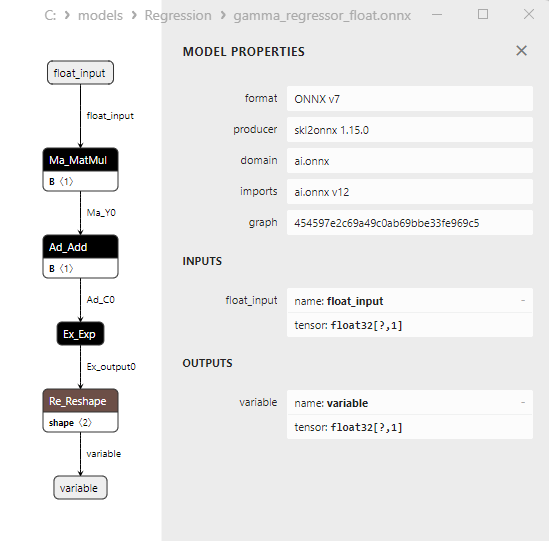
Fig.95. ONNX representation of the gamma_regressor_float.onnx in Netron

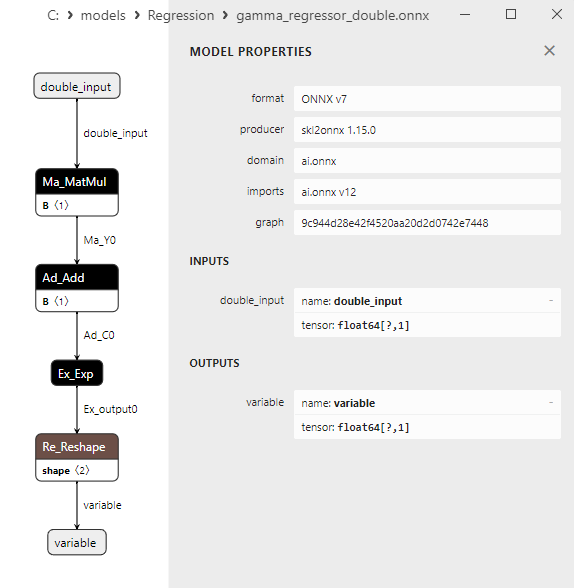
Fig.96. ONNX representation of the gamma_regressor_double.onnx in Netron

2.1.30. sklearn.linear_model.SGDRegressor

SGDRegressor is a regression method that utilizes Stochastic Gradient Descent (SGD) to train a regression model. It is part of the linear models family and can be employed for regression tasks. The key attributes of SGDRegressor are efficiency and its capability to handle large volumes of data.

How SGDRegressor works:

1. Linear regression: Similar to Ridge and Lasso, SGDRegressor aims to find a linear relationship between independent variables (features) and the target variable in a regression problem.
2. Stochastic Gradient Descent: The basis of SGDRegressor is stochastic gradient descent. Instead of computing gradients on the entire training dataset, it updates the model based on randomly selected mini-batches of data. This allows for efficient model training and working with substantial datasets.
3. Regularization: SGDRegressor supports L1 and L2 regularization (Lasso and Ridge). This helps control overfitting and improves model stability.
4. Hyperparameters: Similar to Ridge and Lasso, SGDRegressor allows tuning hyperparameters such as the regularization parameter (α, alpha) and the type of regularization.

Advantages of SGDRegressor:

• Efficiency: SGDRegressor performs well with large datasets and efficiently trains models on extensive data.
• Ability for regularization: The option to apply L1 and L2 regularization makes this method suitable for managing overfitting issues.
• Adaptive gradient descent: Stochastic gradient descent enables adaptation to changing data and the ability to train models on the fly.

Limitations of SGDRegressor:

• Sensitivity to hyperparameter choice: Tuning hyperparameters like learning rate and regularization coefficient might require experimentation.
• Not always converging to global minimum: Due to the stochastic nature of gradient descent, SGDRegressor doesn’t always converge to the global minimum of the loss function.

SGDRegressor is a regression method that uses stochastic gradient descent to train a regression model. It's efficient, capable of handling large datasets, and supports regularization for managing overfitting.

2.1.30.1. Code for creating the SGDRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.SGDRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# SGDRegressor2.py
# The code demonstrates the process of training SGDRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,10,0.1).reshape(-1,1)
y = 4*X + np.sin(X*10)

model_name = "SGDRegressor"
onnx_model_filename = data_path + "sgd_regressor"

# create an SGDRegressor model
regression_model = SGDRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  SGDRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9961197872743282
Python  Mean Absolute Error: 0.6405924406136998
Python  Mean Squared Error: 0.5169867345998348
Python  
Python  SGDRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9961197876338647
Python  Mean Absolute Error: 0.6405924014799271
Python  Mean Squared Error: 0.5169866866963753
Python  R^2 matching decimal places:  9
Python  MAE matching decimal places:  7
Python  MSE matching decimal places:  6
Python  float ONNX model precision:  7
Python  
Python  SGDRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\sgd_regressor_double.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: double_input, Data Type: tensor(double), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(double), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9961197872743282
Python  Mean Absolute Error: 0.6405924406136998
Python  Mean Squared Error: 0.5169867345998348
Python  R^2 matching decimal places:  16
Python  MAE matching decimal places:  16
Python  MSE matching decimal places:  16
Python  double ONNX model precision:  16

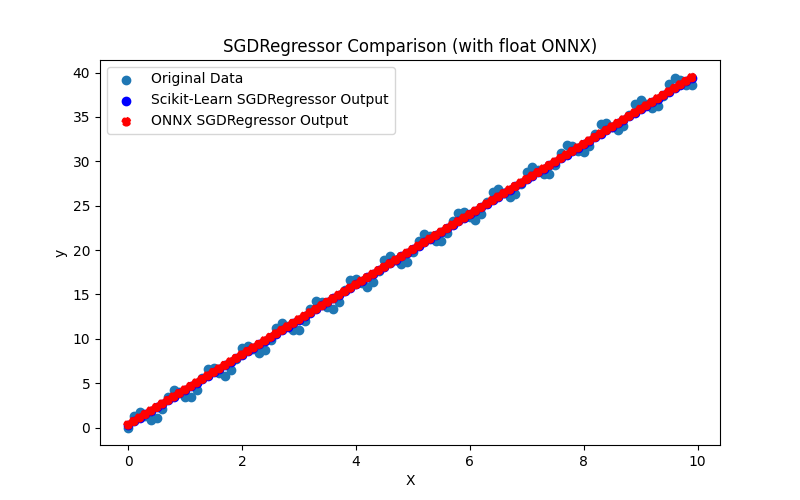
Fig.97. Results of the SGDRegressor.py (float ONNX)

2.1.30.2. MQL5 code for executing ONNX Models

This code executes the saved sgd_regressor_float.onnx and sgd_rgressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                 SGDRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "SGDRegressor"
#define   ONNXFilenameFloat  "sgd_regressor_float.onnx"
#define   ONNXFilenameDouble "sgd_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i*0.1;
      y[i]=(double)(4*x[i] + sin(x[i]*10));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

SGDRegressor (EURUSD,H1)        Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx)
SGDRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9961197876338647
SGDRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 0.6405924014799272
SGDRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 0.5169866866963754
SGDRegressor (EURUSD,H1)        
SGDRegressor (EURUSD,H1)        Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx)
SGDRegressor (EURUSD,H1)        MQL5:   R-Squared (Coefficient of determination): 0.9961197872743282
SGDRegressor (EURUSD,H1)        MQL5:   Mean Absolute Error: 0.6405924406136998
SGDRegressor (EURUSD,H1)        MQL5:   Mean Squared Error: 0.5169867345998348

Comparison with the original double precision model in Python:

Testing ONNX float: SGDRegressor (sgd_regressor_float.onnx)
Python  Mean Absolute Error: 0.6405924406136998
MQL5:   Mean Absolute Error: 0.6405924014799272
        
Testing ONNX double: SGDRegressor (sgd_regressor_double.onnx)
Python  Mean Absolute Error: 0.6405924406136998
MQL5:   Mean Absolute Error: 0.6405924406136998

Accuracy of ONNX float MAE: 7 decimal places, Accuracy of ONNX double MAE: 16 decimal places.

2.1.30.3. ONNX representation of the sgd_regressor_float.onnx and sgd_regressor_double.onnx

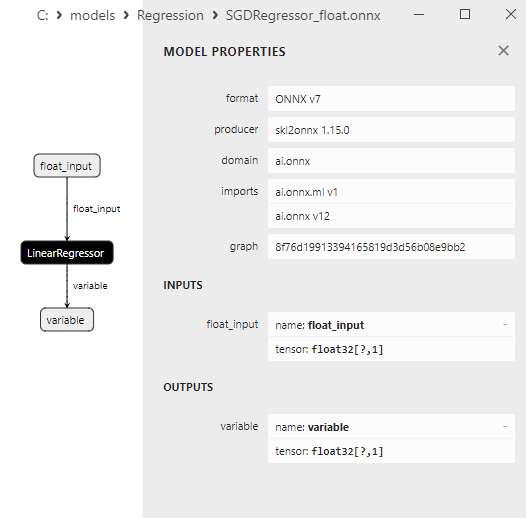
Fig.98. ONNX representation of the sgd_regressor_float.onnx in Netron

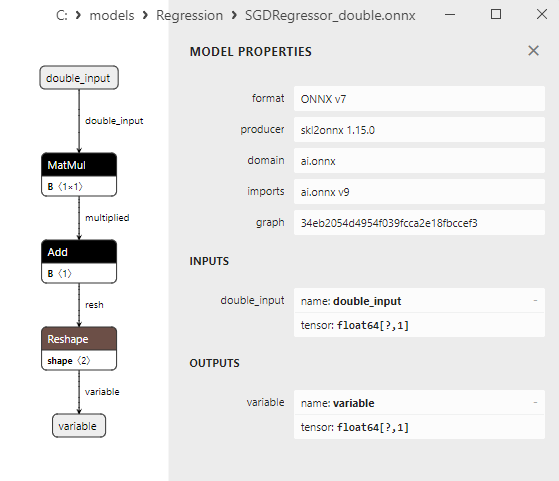
Fig.99. ONNX representation of the sgd_rgressor_double.onnx in Netron

2.2. Regression models from the Scikit-learn library that are converted only into float precision ONNX models

This section covers models that can only function with float precision. Converting them to ONNX with double precision leads to errors related to the limitations of the ai.onnx.ml subset of ONNX operators.

2.2.1. sklearn.linear_model.AdaBoostRegressor

AdaBoostRegressor - is a machine learning method used for regression, which involves predicting numerical values (e.g., real estate prices, sales volumes, etc.).

This method is a variation of the AdaBoost (Adaptive Boosting) algorithm, initially developed for classification tasks.

How AdaBoostRegressor works:

1. Original dataset: It begins with the original dataset containing features (independent variables) and their corresponding target variables (dependent variables we aim to predict).
2. Weight initialization: Initially, each data point (observation) has equal weights, and the model is built based on this weighted dataset.
3. Training weak learners: AdaBoostRegressor constructs several weak regression models (e.g., decision trees) that attempt to predict the target variable. These models are referred to as "weak learners." Each weak learner is trained on data while considering the weights of each observation.
4. Selection of weak learner weights: AdaBoostRegressor computes weights for each weak learner based on how well that learner performed in predictions. Learners making more accurate predictions receive higher weights, and vice versa.
5. Update of observation weights: Observation weights are updated so that observations previously incorrectly predicted receive greater weights, thus increasing their importance for the next model.
6. Final prediction: AdaBoostRegressor combines the predictions of all weak learners, assigning weights based on their performance. This results in the final prediction of the model.

Advantages of AdaBoostRegressor:

• Adaptability: AdaBoostRegressor adapts to complex functions and deals better with nonlinear relationships.
• Overfitting reduction: AdaBoostRegressor uses regularization through the update of observation weights, helping to prevent overfitting.
• Powerful ensemble: By combining multiple weak models, AdaBoostRegressor can create strong models that can predict the target variable fairly accurately.

Limitations of AdaBoostRegressor:

• Sensitivity to outliers: AdaBoostRegressor is sensitive to outliers in the data, affecting prediction quality.
• High computational costs: Constructing multiple weak learners might require more computational resources and time.
• Not always the best choice: AdaBoostRegressor is not always the optimal choice, and in some cases, other regression methods might perform better.

AdaBoostRegressor is a useful machine learning method applicable to various regression tasks, especially in situations where data contains complex dependencies.

2.2.1.1. Code for creating the AdaBoostRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.AdaBoostRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# AdaBoostRegressor.py
# The code demonstrates the process of training AdaBoostRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import AdaBoostRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "AdaBoostRegressor"
onnx_model_filename = data_path + "adaboost_regressor"

# create an AdaBoostRegressor model
regression_model = AdaBoostRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  AdaBoostRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9991257208809748
Python  Mean Absolute Error: 2.3678022748065457
Python  Mean Squared Error: 11.569124350863143
Python  
Python  AdaBoostRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9991257199849699
Python  Mean Absolute Error: 2.36780399225718
Python  Mean Squared Error: 11.569136207480646
Python  R^2 matching decimal places:  7
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  AdaBoostRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx

Here the model was exported into ONNX models for float and double. The ONNX float model executed successfully, while there execution error with the double model (errors in the Errors tab):

AdaBoostRegressor.py started    AdaBoostRegressor.py    1       1
Traceback (most recent call last):      AdaBoostRegressor.py    1       1
    onnx_session = ort.InferenceSession(onnx_filename)  AdaBoostRegressor.py    159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\adaboost_regressor_double.onnx failed:Type Error:       onnxruntime_inference_collection.py     424     1
AdaBoostRegressor.py finished in 3207 ms                5       1

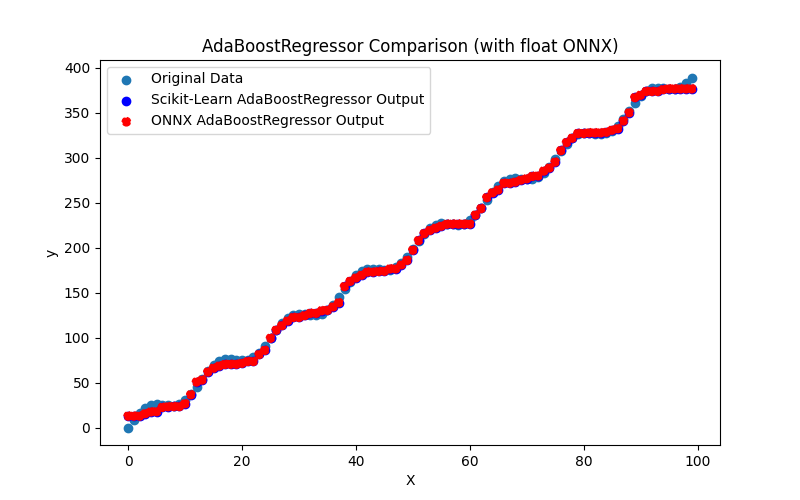
Fig.100. Results of the AdaBoostRegressor.py (float ONNX)

2.2.1.2. MQL5 code for executing ONNX Models

This code executes the saved adaboost_regressor_float.onnx and adaboost_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                            AdaBoostRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "AdaBoostRegressor"
#define   ONNXFilenameFloat  "adaboost_regressor_float.onnx"
#define   ONNXFilenameDouble "adaboost_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

AdaBoostRegressor (EURUSD,H1)   
AdaBoostRegressor (EURUSD,H1)   Testing ONNX float: AdaBoostRegressor (adaboost_regressor_float.onnx)
AdaBoostRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9991257199849699
AdaBoostRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 2.3678039922571803
AdaBoostRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 11.5691362074806463
AdaBoostRegressor (EURUSD,H1)   
AdaBoostRegressor (EURUSD,H1)   Testing ONNX double: AdaBoostRegressor (adaboost_regressor_double.onnx)
AdaBoostRegressor (EURUSD,H1)   ONNX: cannot create session (OrtStatus: 1 'Type Error: Type parameter (T) of Optype (Mul) bound to different types (tensor(float) and tensor(double) in node (Mul).'), inspect code 'Scripts\Regression\AdaBoostRegressor.mq5' (133:16)
AdaBoostRegressor (EURUSD,H1)   model_name=AdaBoostRegressor OnnxCreate error 5800

The ONNX float model executed successfully, while there execution error with the double model.

2.2.1.3. ONNX representation of the adaboost_regressor_float.onnx and adaboost_regressor_double.onnx

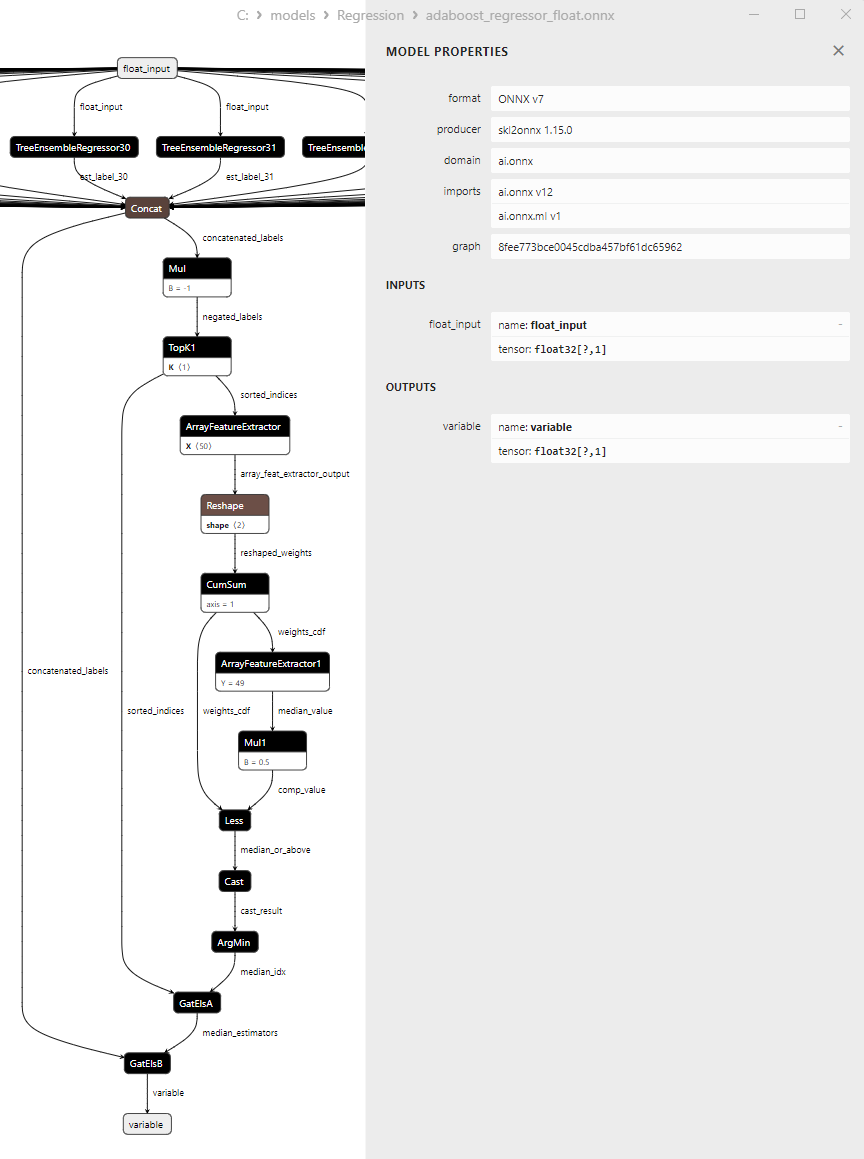
Fig.101. ONNX representation of the adaboost_regressor_float.onnx in Netron

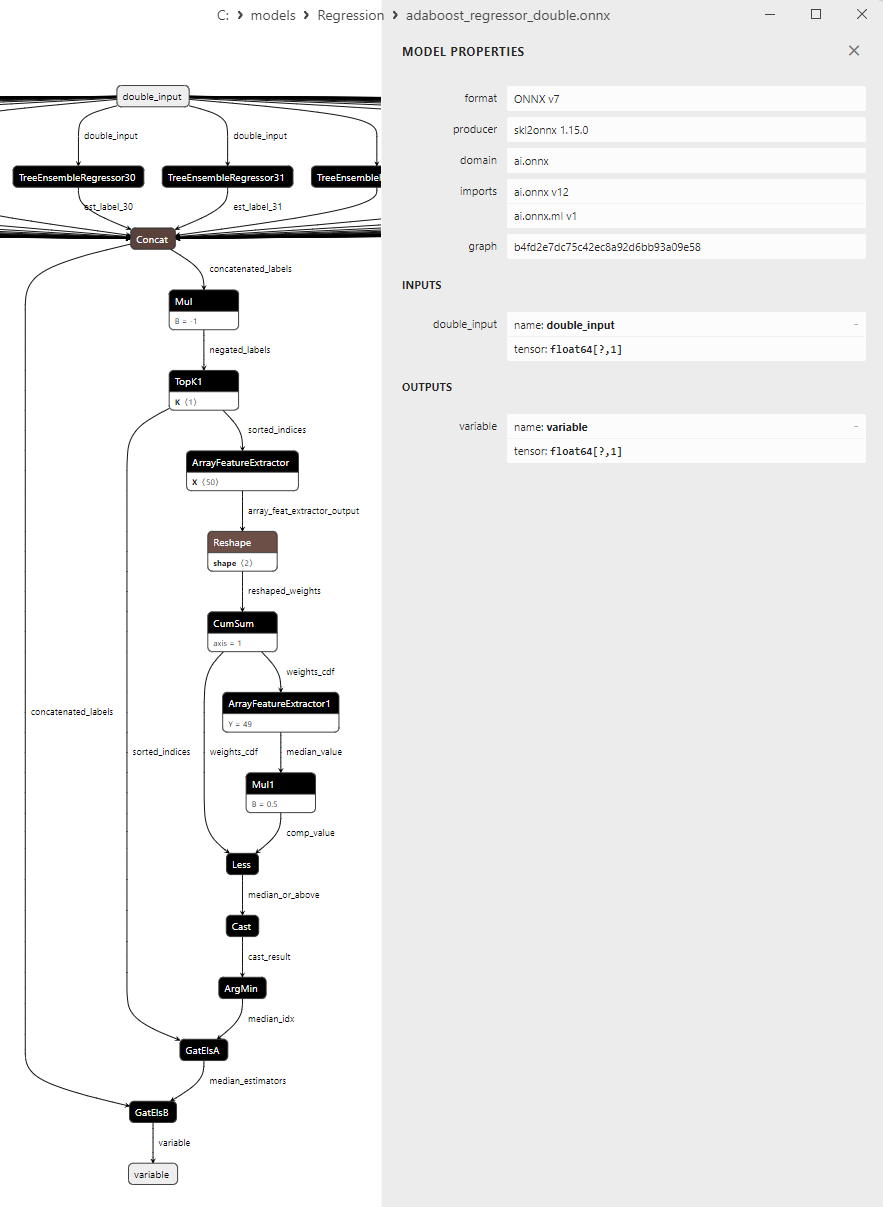
Fig.102. ONNX representation of the adaboost_regressor_double.onnx in Netron

2.2.2. sklearn.linear_model.BaggingRegressor

BaggingRegressor is a machine learning method used for regression tasks.

It represents an ensemble method based on the idea of "bagging" (Bootstrap Aggregating), which involves constructing multiple base regression models and combining their predictions to obtain a more stable and accurate result.

How BaggingRegressor works:

1. Original dataset: It starts with the original dataset containing features (independent variables) and their corresponding target variables (dependent variables we aim to predict).
2. Generation of subsets: BaggingRegressor randomly creates several subsets (samples with replacement) from the original data. Each subset contains a random set of observations from the original data.
3. Training base regression models: For each subset, BaggingRegressor constructs a separate base regression model (e.g., decision tree, random forest, linear regression model, etc.).
4. Predictions from base models: Each base model is used to predict the target variable based on the corresponding subset.
5. Averaging or combination: BaggingRegressor averages or combines the predictions of all base models to obtain the final regression prediction.

Advantages of BaggingRegressor:

• Variance reduction: BaggingRegressor reduces the model's variance, making it more robust to fluctuations in the data.
• Overfitting reduction: As the model is trained on different data subsets, BaggingRegressor usually reduces the risk of overfitting.
• Improved generalization: By combining predictions from multiple models, BaggingRegressor typically provides more accurate and stable forecasts.
• Wide range of base models: BaggingRegressor can use different types of base regression models, making it a flexible method.

Limitations of BaggingRegressor:

• It is not always capable of enhancing performance when the base model already performs well on the data.
• BaggingRegressor might require more computational resources and time compared to training a single model.

BaggingRegressor is a powerful machine learning method that can be beneficial in regression tasks, especially with noisy data, and the need for improved prediction stability.

2.2.2.1. Code for creating the BaggingRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.BaggingRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# BaggingRegressor.py
# The code demonstrates the process of training BaggingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import BaggingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "BaggingRegressor"
onnx_model_filename = data_path + "bagging_regressor"

# create a Bagging Regressor model
regression_model = BaggingRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  
Python  BaggingRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9998128324923137
Python  Mean Absolute Error: 1.0257279210387649
Python  Mean Squared Error: 2.4767424083953005
Python  
Python  BaggingRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9998128317934672
Python  Mean Absolute Error: 1.0257282792130034
Python  Mean Squared Error: 2.4767516560614187
Python  R^2 matching decimal laces:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  4
Python  float ONNX model precision:  5
Python  
Python  BaggingRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx

Errors tab:

BaggingRegressor.py started     BaggingRegressor.py     1       1
Traceback (most recent call last):      BaggingRegressor.py     1       1
    onnx_session = ort.InferenceSession(onnx_filename)  BaggingRegressor.py     161     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\bagging_regressor_double.onnx failed:Type Error: T      onnxruntime_inference_collection.py     424     1
BaggingRegressor.py finished in 3173 ms         5       1

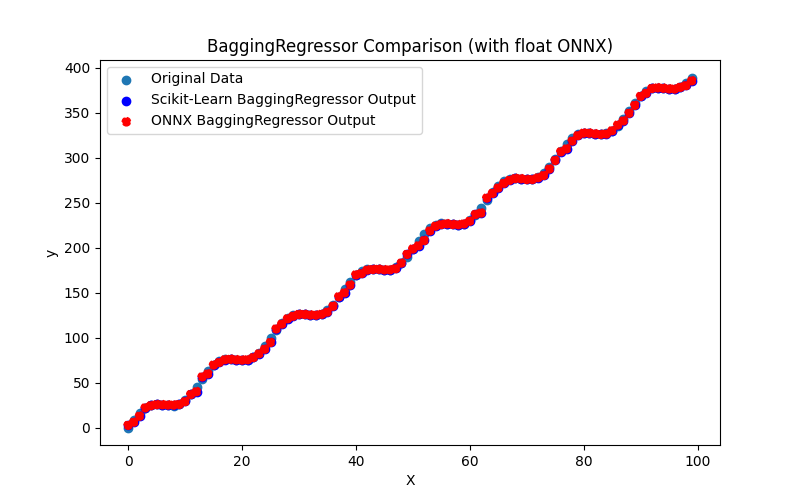
Fig.103. Results of the BaggingRegressor.py (float ONNX)

2.2.2.2. MQL5 code for executing ONNX Models

This code executes the saved bagging_regressor_float.onnx and bagging_regressor_double.onnx and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                             BaggingRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "BaggingRegressor"
#define   ONNXFilenameFloat  "bagging_regressor_float.onnx"
#define   ONNXFilenameDouble "bagging_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

BaggingRegressor (EURUSD,H1)    Testing ONNX float: BaggingRegressor (bagging_regressor_float.onnx)
BaggingRegressor (EURUSD,H1)    MQL5:   R-Squared (Coefficient of determination): 0.9998128317934672
BaggingRegressor (EURUSD,H1)    MQL5:   Mean Absolute Error: 1.0257282792130034
BaggingRegressor (EURUSD,H1)    MQL5:   Mean Squared Error: 2.4767516560614196
BaggingRegressor (EURUSD,H1)    
BaggingRegressor (EURUSD,H1)    Testing ONNX double: BaggingRegressor (bagging_regressor_double.onnx)
BaggingRegressor (EURUSD,H1)    ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (ReduceMean) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\BaggingRegressor.mq5' (133:16)
BaggingRegressor (EURUSD,H1)    model_name=BaggingRegressor OnnxCreate error 5800

The ONNX model calculated in float executed normally, but an error occurred when executing the model in double.

2.2.2.3. ONNX representation of the bagging_regressor_float.onnx and bagging_regressor_double.onnx

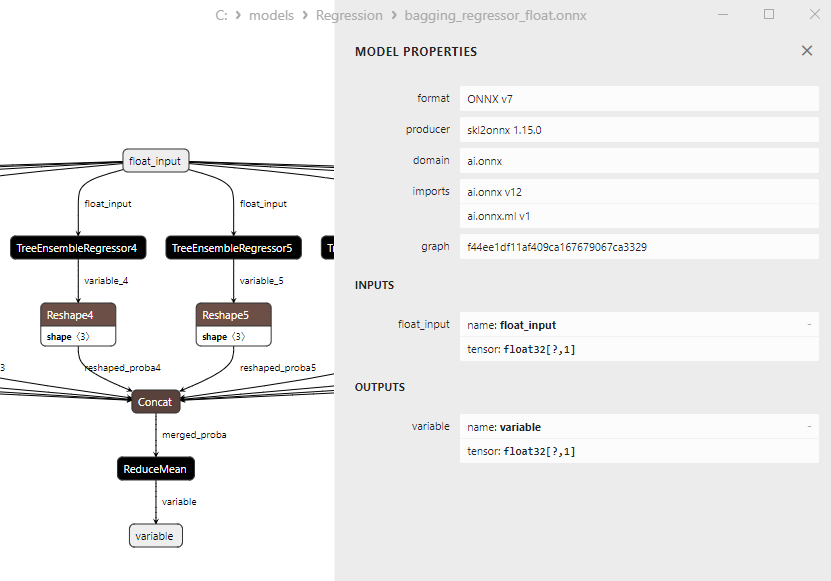
Fig.104. ONNX representation of the bagging_regressor_float.onnx in Netron

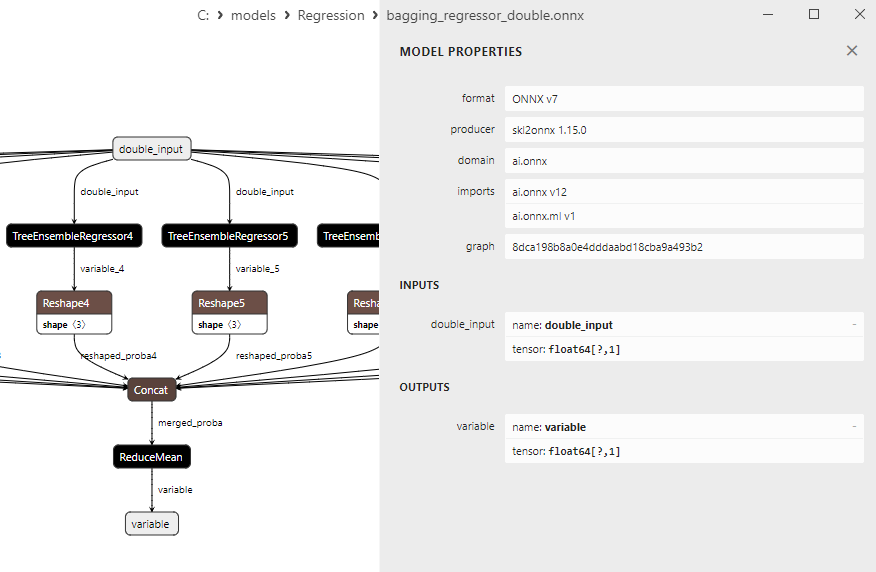
Fig.105. ONNX representation of the bagging_regressor_double.onnx in Netron

2.2.3. sklearn.linear_model.DecisionTreeRegressor

DecisionTreeRegressor is a machine learning method used for regression tasks, predicting numerical values of the target variable based on a set of features (independent variables).

This method is based on building decision trees that partition feature space into intervals and predict the target variable's value for each interval.

Working principle of DecisionTreeRegressor:

1. Beginning construction: Starting with the initial dataset containing features (independent variables) and corresponding values of the target variable.
2. Feature selection and splitting: The decision tree selects a feature and a threshold value that divides the data into two or more subgroups. This split is performed to minimize the mean squared error (the average squared deviation between predicted and actual values of the target variable) within each subgroup.
3. Recursive building: The process of feature selection and splitting is repeated for each subgroup, creating sub-trees. This process is done recursively until certain stopping criteria are met, such as maximum tree depth or minimum samples in a node.
4. Leaf nodes: When stopping criteria are met, leaf nodes are created, predicting numerical values of the target variable for samples that fall into a given leaf node.
5. Prediction: For new data, the decision tree is applied, and new observations traverse the tree until they reach a leaf node that predicts the numerical value of the target variable.

Advantages of DecisionTreeRegressor:

• Interpretability: Decision trees are easy to understand and visualize, making them useful for explaining model decision-making.
• Outlier robustness: Decision trees can be robust to data outliers.
• Handling both numeric and categorical data: Decision trees can process both numeric and categorical features without additional preprocessing.
• Automated feature selection: Trees can automatically select important features, ignoring less relevant ones.

Limitations of DecisionTreeRegressor:

• Overfitting vulnerability: Decision trees can be prone to overfitting, especially if they are too deep.
• Generalization issues: Decision trees may not generalize well to data not included in the training set.
• Not always an optimal choice: In some cases, other regression methods like linear regression or k-nearest neighbors might perform better.

DecisionTreeRegressor is a valuable method for regression tasks, especially when understanding the model's decision-making logic and visualizing the process is crucial.

2.2.3.1. Code for creating the DecisionTreeRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.linear_model.DecisionTreeRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# DecisionTreeRegressor.py
# The code demonstrates the process of training DecisionTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "DecisionTreeRegressor"
onnx_model_filename = data_path + "decision_tree_regressor"

# create a Decision Tree Regressor model
regression_model = DecisionTreeRegressor()

# fit the model to the data
regression_model.fit(X, y)

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  DecisionTreeRegressor Original model (double)
Python  R-squared (Coefficient of determination): 1.0
Python  Mean Absolute Error: 0.0
Python  Mean Squared Error: 0.0
Python  
Python  DecisionTreeRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999999971
Python  Mean Absolute Error: 4.393654615473253e-06
Python  Mean Squared Error: 3.829042036424747e-11
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  DecisionTreeRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx

Errors tab:

DecisionTreeRegressor.py started        DecisionTreeRegressor.py        1       1
Traceback (most recent call last):      DecisionTreeRegressor.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  DecisionTreeRegressor.py        160     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\decision_tree_regressor_double.onnx failed:Type Er      onnxruntime_inference_collection.py     424     1
DecisionTreeRegressor.py finished in 2957 ms            5       1

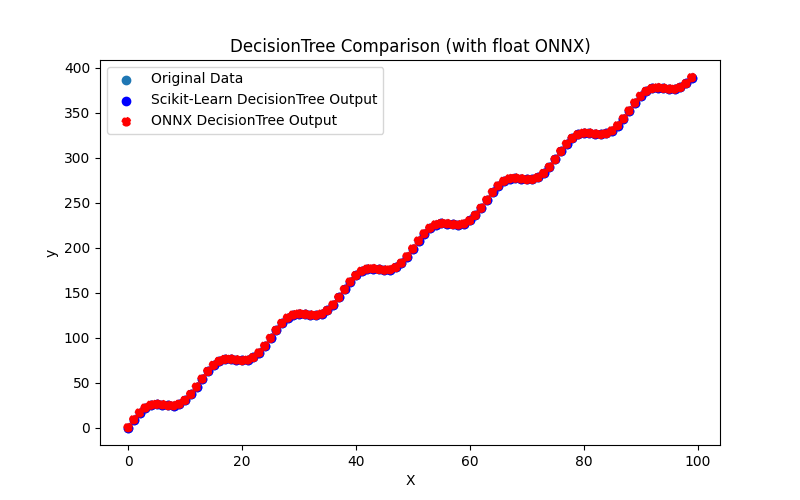
Fig.106. Results of the DecisionTreeRegressor.py (float ONNX)

2.2.3.2. MQL5 code for executing ONNX Models

This code executes the saved decision_tree_regressor_float.onnx and decision_tree_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                        DecisionTreeRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "DecisionTreeRegressor"
#define   ONNXFilenameFloat  "decision_tree_regressor_float.onnx"
#define   ONNXFilenameDouble "decision_tree_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

DecisionTreeRegressor (EURUSD,H1)       Testing ONNX float: DecisionTreeRegressor (decision_tree_regressor_float.onnx)
DecisionTreeRegressor (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9999999999999971
DecisionTreeRegressor (EURUSD,H1)       MQL5:   Mean Absolute Error: 0.0000043936546155
DecisionTreeRegressor (EURUSD,H1)       MQL5:   Mean Squared Error: 0.0000000000382904
DecisionTreeRegressor (EURUSD,H1)       
DecisionTreeRegressor (EURUSD,H1)       Testing ONNX double: DecisionTreeRegressor (decision_tree_regressor_double.onnx)
DecisionTreeRegressor (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\DecisionTreeRegressor.mq5' (133:16)
DecisionTreeRegressor (EURUSD,H1)       model_name=DecisionTreeRegressor OnnxCreate error 5800

The ONNX model calculated in float executed normally, but an error occurred when executing the model in double.

2.2.3.3. ONNX representation of the decision_tree_regressor_float.onnx and decision_tree_regressor_double.onnx

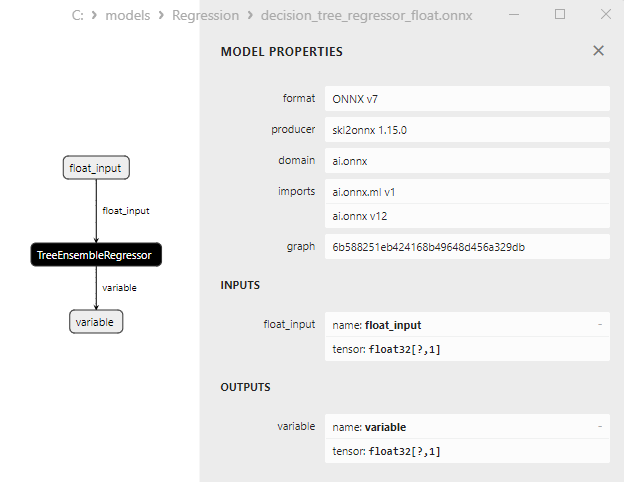
Fig.107. ONNX representation of the decision_tree_regressor_float.onnx in Netron

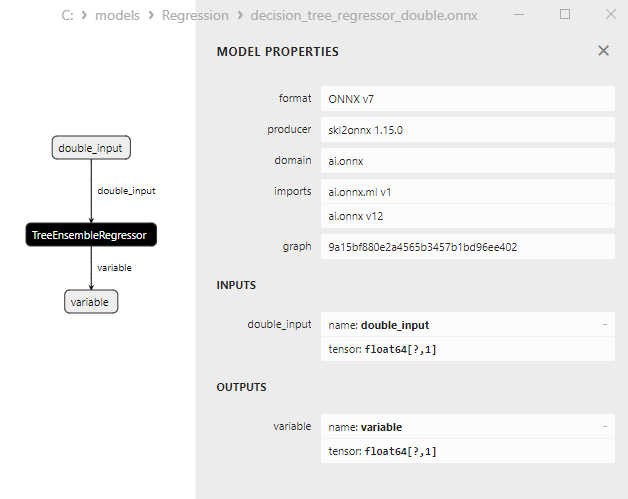
Fig.108. ONNX representation of the decision_tree_regressor_double.onnx in Netron

2.2.4. sklearn.tree.ExtraTreeRegressor

ExtraTreeRegressor, or Extremely Randomized Trees Regressor, is a regression ensemble method based on decision trees.

This method is a variation of random forests and differs in that instead of choosing the best split for each tree node, it uses random splits for each node. This makes it more random and faster, which can be advantageous in certain situations.

Working principle of ExtraTreeRegressor:

1. Beginning construction: Starting with the initial dataset containing features (independent variables) and corresponding values of the target variable.
2. Randomness in splits: Unlike regular decision trees where the best split is chosen, ExtraTreeRegressor uses random threshold values to split the tree nodes. This makes the splitting process more random and less prone to overfitting.
3. Tree construction: The tree is built by splitting nodes based on random features and threshold values. This process continues until certain stopping criteria are met, such as maximum tree depth or minimum number of samples in a node.
4. Ensemble of trees: ExtraTreeRegressor constructs multiple such random trees, the number of which is controlled by the "n_estimators" hyperparameter.
5. Prediction: To predict the target variable for new data, ExtraTreeRegressor simply averages the predictions of all trees in the ensemble.

Advantages of ExtraTreeRegressor:

• Reduction in overfitting: Using random node splits makes the method less prone to overfitting compared to regular decision trees.
• High parallelization: Since the trees are built independently, ExtraTreeRegressor can be easily parallelized for training on multiple processors.
• Fast training: Compared to some other methods like gradient boosting, ExtraTreeRegressor can be trained faster.

Limitations of ExtraTreeRegressor:

• May be less accurate: In some cases, especially with small datasets, ExtraTreeRegressor may be less accurate compared to more complex methods.
• Less interpretable: Compared to linear models, decision trees, and other simpler methods, ExtraTreeRegressor is typically less interpretable.

ExtraTreeRegressor can be a useful method for regression in situations where reducing overfitting and quick training are needed.

2.2.4.1. Code for creating the ExtraTreeRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.tree.ExtraTreeRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# ExtraTreeRegressor.py
# The code demonstrates the process of training ExtraTreeRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import ExtraTreeRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ExtraTreeRegressor"
onnx_model_filename = data_path + "extra_tree_regressor"

# create an ExtraTreeRegressor model
regression_model = ExtraTreeRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression data
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

2023.10.30 14:40:57.665 Python  ExtraTreeRegressor Original model (double)
2023.10.30 14:40:57.665 Python  R-squared (Coefficient of determination): 1.0
2023.10.30 14:40:57.665 Python  Mean Absolute Error: 0.0
2023.10.30 14:40:57.665 Python  Mean Squared Error: 0.0
2023.10.30 14:40:57.681 Python  
2023.10.30 14:40:57.681 Python  ExtraTreeRegressor ONNX model (float)
2023.10.30 14:40:57.681 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_float.onnx
2023.10.30 14:40:57.681 Python  Information about input tensors in ONNX:
2023.10.30 14:40:57.681 Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
2023.10.30 14:40:57.681 Python  Information about output tensors in ONNX:
2023.10.30 14:40:57.681 Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
2023.10.30 14:40:57.681 Python  R-squared (Coefficient of determination) 0.9999999999999971
2023.10.30 14:40:57.681 Python  Mean Absolute Error: 4.393654615473253e-06
2023.10.30 14:40:57.681 Python  Mean Squared Error: 3.829042036424747e-11
2023.10.30 14:40:57.681 Python  R^2 matching decimal places:  0
2023.10.30 14:40:57.681 Python  MAE matching decimal places:  0
2023.10.30 14:40:57.681 Python  MSE matching decimal places:  0
2023.10.30 14:40:57.681 Python  float ONNX model precision:  0
2023.10.30 14:40:58.011 Python  
2023.10.30 14:40:58.011 Python  ExtraTreeRegressor ONNX model (double)
2023.10.30 14:40:58.011 Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx

Errors tab:

ExtraTreeRegressor.py started   ExtraTreeRegressor.py   1       1
Traceback (most recent call last):      ExtraTreeRegressor.py   1       1
    onnx_session = ort.InferenceSession(onnx_filename)  ExtraTreeRegressor.py   159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_tree_regressor_double.onnx failed:Type Error      onnxruntime_inference_collection.py     424     1
ExtraTreeRegressor.py finished in 2980 ms               5       1

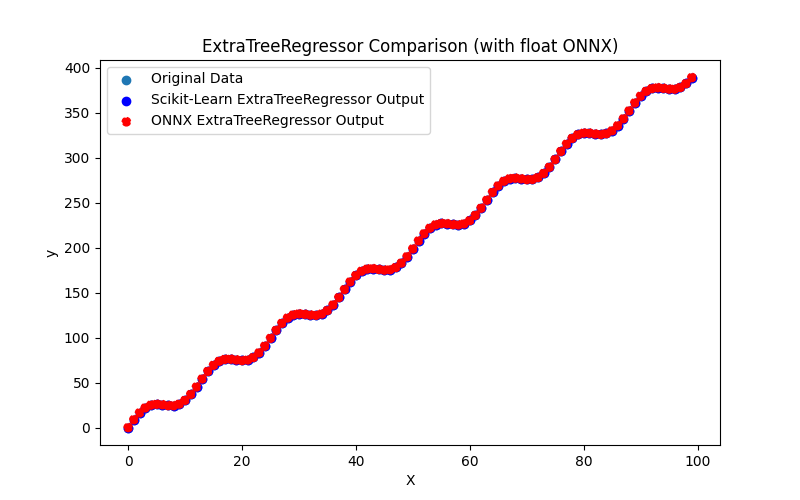
Fig.109. Results of the ExtraTreeRegressor.py (float ONNX)

2.2.4.2. MQL5 code for executing ONNX Models

This code executes the saved extra_tree_regressor_float.onnx and extra_tree_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                           ExtraTreeRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ExtraTreeRegressor"
#define   ONNXFilenameFloat  "extra_tree_regressor_float.onnx"
#define   ONNXFilenameDouble "extra_tree_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

ExtraTreeRegressor (EURUSD,H1)  Testing ONNX float: ExtraTreeRegressor (extra_tree_regressor_float.onnx)
ExtraTreeRegressor (EURUSD,H1)  MQL5:   R-Squared (Coefficient of determination): 0.9999999999999971
ExtraTreeRegressor (EURUSD,H1)  MQL5:   Mean Absolute Error: 0.0000043936546155
ExtraTreeRegressor (EURUSD,H1)  MQL5:   Mean Squared Error: 0.0000000000382904
ExtraTreeRegressor (EURUSD,H1)  
ExtraTreeRegressor (EURUSD,H1)  Testing ONNX double: ExtraTreeRegressor (extra_tree_regressor_double.onnx)
ExtraTreeRegressor (EURUSD,H1)  ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreeRegressor.mq5' (133:16)
ExtraTreeRegressor (EURUSD,H1)  model_name=ExtraTreeRegressor OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double.

2.2.4.3. ONNX representation extra_tree_regressor_float.onnx and extra_tree_regressor_double.onnx

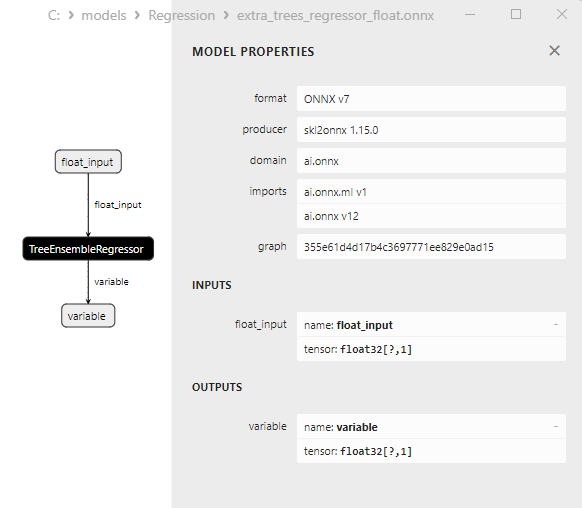
Fig.110. ONNX representation of the extra_tree_regressor_float.onnx in Netron

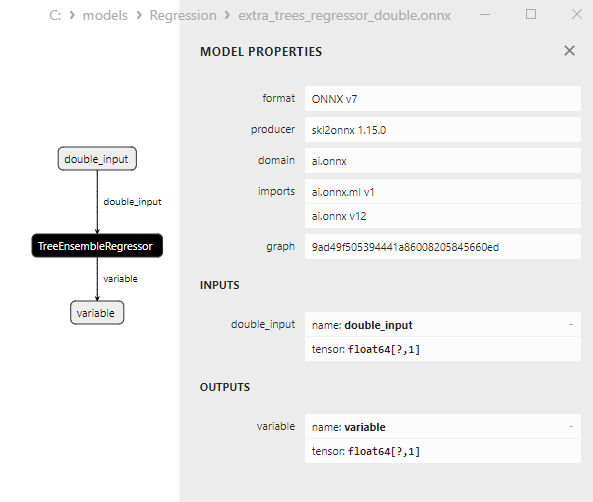
Fig.111. ONNX representation of the extra_tree_regressor_double.onnx in Netron

2.2.5. sklearn.ensemble.ExtraTreesRegressor

ExtraTreesRegressor (Extremely Randomized Trees Regressor) is a machine learning method that represents a variation of Random Forests for regression tasks.

This method employs an ensemble of decision trees to predict numerical values of the target variable based on a set of features.

How ExtraTreesRegressor works:

1. Beginning Construction: It starts with the original dataset, including features (independent variables) and their corresponding values of the target variable.
2. Randomness in Splits: Unlike regular decision trees where the best split is selected to divide nodes, ExtraTreesRegressor uses random threshold values to split tree nodes. This randomness makes the splitting process more arbitrary and less prone to overfitting.
3. Tree Building: ExtraTreesRegressor constructs multiple decision trees in the ensemble. The number of trees is controlled by the "n_estimators" hyperparameter. Each tree is trained on a random subsample of data (with replacement) and random subsets of features.
4. Prediction: For predicting the target variable for new data, ExtraTreesRegressor aggregates the predictions of all trees in the ensemble (usually by averaging).

Advantages of ExtraTreesRegressor:

• Reduction in Overfitting: Using random node splits and data subsampling makes the method less prone to overfitting compared to conventional decision trees.
• High Parallelization: As trees are built independently, ExtraTreesRegressor can be easily parallelized for training on multiple processors.
• Robustness to Outliers: The method typically shows resilience to outliers in the data.
• Handling Numerical and Categorical Data: ExtraTreesRegressor can handle both numerical and categorical features without additional preprocessing.

Limitations of ExtraTreesRegressor:

• May Require Fine-Tuning of Hyperparameters: Although ExtraTreesRegressor usually works well with default parameters, fine-tuning of hyperparameters might be needed for achieving maximum performance.
• Less Interpretability: Like other ensemble methods, ExtraTreesRegressor is less interpretable compared to simpler models such as linear regression.

ExtraTreesRegressor can be a beneficial method for regression across various tasks, particularly when reducing overfitting and improving the model's generalization is necessary.

2.2.5.1. Code for creating the ExtraTreesRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.ensemble.ExtraTreesRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# ExtraTreesRegressor.py
# The code demonstrates the process of training ExtraTreesRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "ExtraTreesRegressor"
onnx_model_filename = data_path + "extra_trees_regressor"

# create an Extra Trees Regressor model
regression_model = ExtraTreesRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  ExtraTreesRegressor Original model (double)
Python  R-squared (Coefficient of determination): 1.0
Python  Mean Absolute Error: 2.2302160118670144e-13
Python  Mean Squared Error: 8.41048471722451e-26
Python  
Python  ExtraTreesRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999999999998015
Python  Mean Absolute Error: 3.795239380975701e-05
Python  Mean Squared Error: 2.627067474763585e-09
Python  R^2 matching decimal places:  0
Python  MAE matching decimal places:  0
Python  MSE matching decimal places:  0
Python  float ONNX model precision:  0
Python  
Python  ExtraTreesRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx

Errors tab:

ExtraTreesRegressor.py started  ExtraTreesRegressor.py  1       1
Traceback (most recent call last):      ExtraTreesRegressor.py  1       1
    onnx_session = ort.InferenceSession(onnx_filename)  ExtraTreesRegressor.py  160     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\extra_trees_regressor_double.onnx failed:Type Erro      onnxruntime_inference_collection.py     424     1
ExtraTreesRegressor.py finished in 4654 ms              5       1

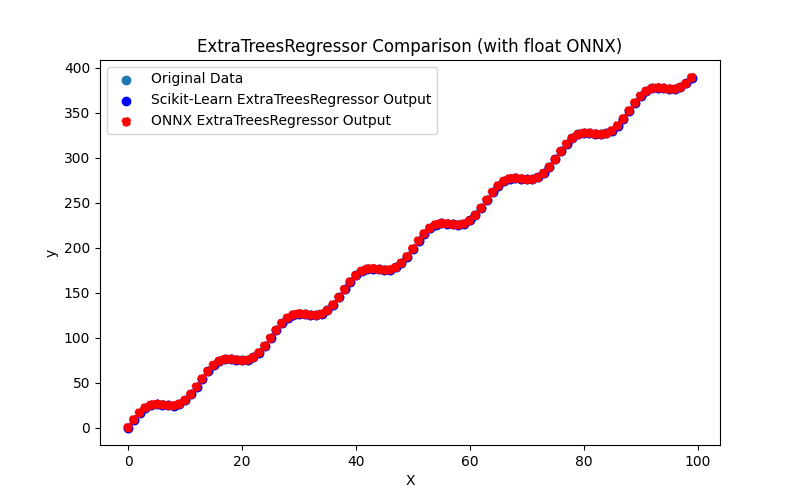
Fig.112. Results of the ExtraTreesRegressor.py (float ONNX)

2.2.5.2. MQL5 code for executing ONNX Models

This code creates the extra_trees_regressor_float.onnx and extra_trees_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                          ExtraTreesRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "ExtraTreesRegressor"
#define   ONNXFilenameFloat  "extra_trees_regressor_float.onnx"
#define   ONNXFilenameDouble "extra_trees_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

ExtraTreesRegressor (EURUSD,H1) Testing ONNX float: ExtraTreesRegressor (extra_trees_regressor_float.onnx)
ExtraTreesRegressor (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.9999999999998015
ExtraTreesRegressor (EURUSD,H1) MQL5:   Mean Absolute Error: 0.0000379523938098
ExtraTreesRegressor (EURUSD,H1) MQL5:   Mean Squared Error: 0.0000000026270675
ExtraTreesRegressor (EURUSD,H1) 
ExtraTreesRegressor (EURUSD,H1) Testing ONNX double: ExtraTreesRegressor (extra_trees_regressor_double.onnx)
ExtraTreesRegressor (EURUSD,H1) ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\ExtraTreesRegressor.mq5' (133:16)
ExtraTreesRegressor (EURUSD,H1) model_name=ExtraTreesRegressor OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double.

2.2.5.3. ONNX representation of the extra_trees_regressor_float.onnx and extra_trees_regressor_double.onnx

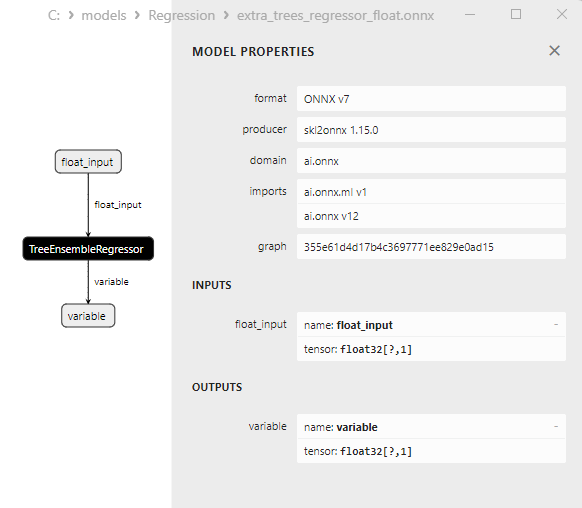
Fig.113. ONNX representation of the extra_trees_regressor_float.onnx in Netron

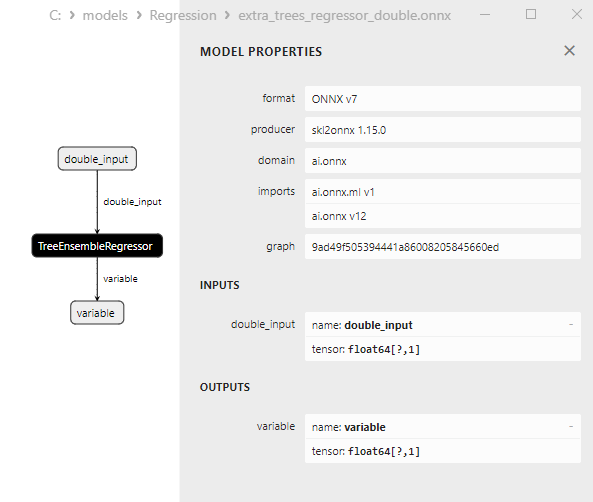
Fig.114. ONNX representation of the extra_trees_regressor_double.onnx in Netron

2.2.6. sklearn.svm.NuSVR

NuSVR is a machine learning method used for regression tasks. This method is based on Support Vector Machine (SVM) but is applied to regression tasks instead of classification tasks.

NuSVR is a variation of SVM designed to solve regression tasks by predicting continuous values of the target variable.

How NuSVR works:

1. Input Data: It starts with a dataset that includes features (independent variables) and values of the target variable (continuous).
2. Kernel Selection: NuSVR uses kernels such as linear, polynomial, or radial basis function (RBF) to transform the data into a higher-dimensional space where a linear separating hyperplane can be found.
3. Defining the Nu parameter: The Nu parameter controls model complexity and defines how many training examples will be considered as outliers. The Nu value should range from 0 to 1, influencing the number of support vectors.
4. Support Vector Construction: NuSVR aims to find an optimal separating hyperplane that maximizes the gap between this hyperplane and the nearest sample points.
5. Model Training: The model is trained to minimize regression error and meet the constraints associated with the Nu parameter.
6. Making Predictions: After training, the model can be used to predict the values of the target variable on new data.

Advantages of NuSVR:

• Outlier Handling: NuSVR allows controlling outliers using the Nu parameter, regulating the number of training examples considered as outliers.
• Multiple Kernels: The method supports various types of kernels, enabling the modeling of complex nonlinear relationships.

Limitations of NuSVR:

• Nu Parameter Selection: Choosing the correct value for the Nu parameter may require some experimentation.
• Data Scale Sensitivity: SVM, including NuSVR, can be sensitive to data scale, so feature standardization or normalization might be necessary.
• Computational Complexity: For large datasets and complex kernels, NuSVR can be computationally expensive.

NuSVR is a machine learning method for regression tasks based on the Support Vector Machine (SVM) method. It allows the prediction of continuous values of the target variable and provides the capability to manage outliers using the Nu parameter.

2.2.6.1. Code for creating the NuSVR model and exporting it to ONNX for float and double

This code creates the sklearn.svm.NuSVR model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# NuSVR.py
# The code demonstrates the process of training NuSVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import NuSVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "NuSVR"
onnx_model_filename = data_path + "nu_svr"

# create a NuSVR model
nusvr_model = NuSVR()

# fit the model to the data
nusvr_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = nusvr_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(nusvr_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(nusvr_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  NuSVR Original model (double)
Python  R-squared (Coefficient of determination): 0.2771437770527445
Python  Mean Absolute Error: 83.76666411704255
Python  Mean Squared Error: 9565.381751764757
Python  
Python  NuSVR ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_float.onnx
Python  Information about input tensors in ONNX:
1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.27714379657935495
Python  Mean Absolute Error: 83.766663385322
Python  Mean Squared Error: 9565.381493373838
Python  R^2 matching decimal places:  7
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  5
Python  
Python  NuSVR ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\nu_svr_double.onnx

Errors tab:

NuSVR.py started        NuSVR.py        1       1
Traceback (most recent call last):      NuSVR.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  NuSVR.py        159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess.initialize_session(providers, provider_options, disabled_optimizers)   onnxruntime_inference_collection.py     435     1
onnxruntime.capi.onnxruntime_pybind11_state.NotImplemented: [ONNXRuntimeError] : 9 : NOT_IMPLEMENTED : Could not find an implementation for SVMRegressor(1) node with name 'SVM'        onnxruntime_inference_collection.py     435     1
NuSVR.py finished in 2925 ms            5       1

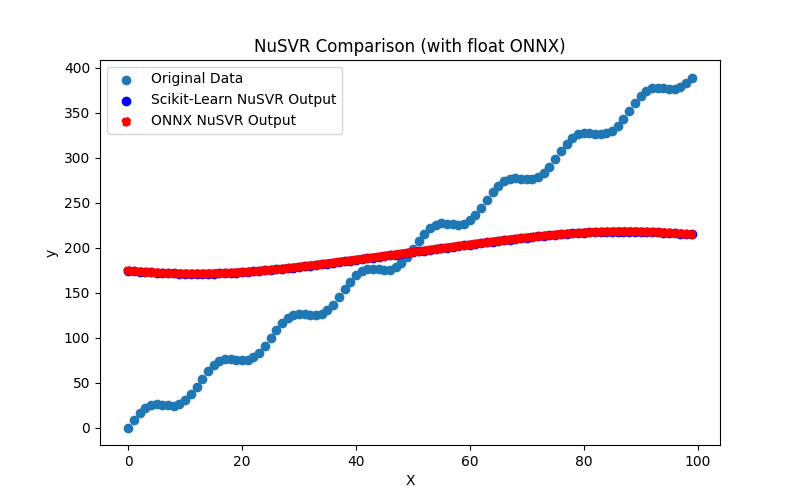
Fig.115. Results of the NuSVR.py (float ONNX)

2.2.6.2. MQL5 code for executing ONNX Models

This code executes the saved nu_svr_float.onnx and nu_svr_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                        NuSVR.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "NuSVR"
#define   ONNXFilenameFloat  "nu_svr_float.onnx"
#define   ONNXFilenameDouble "nu_svr_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

NuSVR (EURUSD,H1)       Testing ONNX float: NuSVR (nu_svr_float.onnx)
NuSVR (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.2771437965793548
NuSVR (EURUSD,H1)       MQL5:   Mean Absolute Error: 83.7666633853219906
NuSVR (EURUSD,H1)       MQL5:   Mean Squared Error: 9565.3814933738358377
NuSVR (EURUSD,H1)       
NuSVR (EURUSD,H1)       Testing ONNX double: NuSVR (nu_svr_double.onnx)
NuSVR (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\Regression\NuSVR.mq5' (133:16)
NuSVR (EURUSD,H1)       model_name=NuSVR OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double.

Comparison with the original double precision model in Python:

Testing ONNX float: NuSVR (nu_svr_float.onnx)
Python  Mean Absolute Error: 83.76666411704255
MQL5:   Mean Absolute Error: 83.7666633853219906

2.2.6.3. ONNX representation of the nu_svr_float.onnx and nu_svr_double.onnx

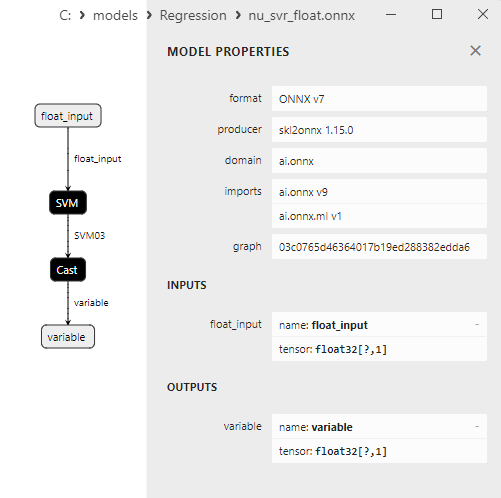
Fig.116. ONNX representation of the nu_svr_float.onnx in Netron

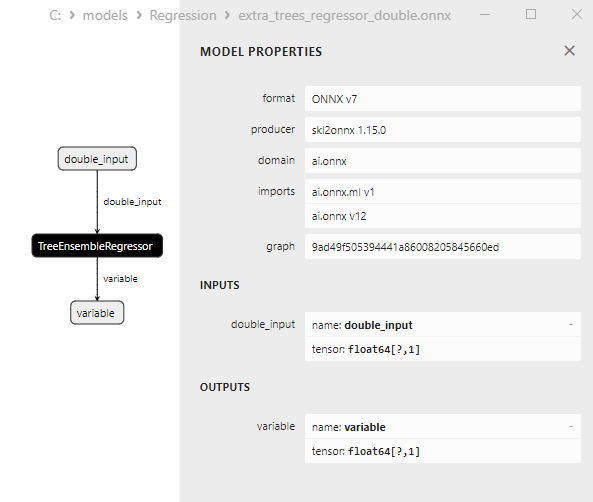
Fig.117. ONNX representation of the nu_svr_double.onnx in Netron

2.2.7. sklearn.ensemble.RandomForestRegressor

RandomForestRegressor is a machine learning method used to solve regression tasks.

It's one of the most popular methods based on ensemble learning and employs the Random Forest algorithm to create powerful and robust regression models.

Here's how RandomForestRegressor works:

1. Input Data: It begins with a dataset that includes features (independent variables) and a target variable (continuous).
2. Random Forest: RandomForestRegressor uses an ensemble of decision trees to solve the regression task. Each tree in the forest works on predicting the target variable values.
3. Bootstrap Sampling: Each tree is trained using bootstrap samples, which means random sampling with replacement from the training dataset. This allows diversity in the data each tree learns from.
4. Random Feature Selection: When building each tree, a random subset of features is also selected, making the model more robust and reducing correlations between trees.
5. Averaging Predictions: Once all the trees are constructed, RandomForestRegressor averages or combines their predictions to get the final regression prediction.

Advantages of RandomForestRegressor:

• Power and Robustness: RandomForestRegressor is a powerful regression method that often delivers good performance.
• Handling Large Data: It handles large datasets well and can handle a multitude of features.
• Resilience to Overfitting: Due to bootstrap sampling and random feature selection, the random forest is typically robust against overfitting.
• Feature Importance Estimation: Random Forest can provide information about the importance of each feature in the regression task.

Limitations of RandomForestRegressor:

• Lack of Interpretability: The model might be less interpretable compared to linear models.
• Not Always the Most Accurate Model: In some tasks, more complex ensembles might be unnecessary, and linear models could be more suitable.

RandomForestRegressor is a powerful machine learning method for regression tasks that uses an ensemble of random decision trees to create a stable and high-performing regression model. This method is particularly useful for tasks with large datasets and for evaluating feature importance.

2.2.7.1. Code for creating the RandomForestRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.ensemble.RandomForestRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# RandomForestRegressor.py
# The code demonstrates the process of training RandomForestRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "RandomForestRegressor"
onnx_model_filename = data_path + "random_forest_regressor"

# create a RandomForestRegressor model
regression_model = RandomForestRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  RandomForestRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9998854509605539
Python  Mean Absolute Error: 0.9186485980852603
Python  Mean Squared Error: 1.5157997632401086
Python  
Python  RandomForestRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9998854516013125
Python  Mean Absolute Error: 0.9186420704511761
Python  Mean Squared Error: 1.515791284236419
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  5
Python  
Python  RandomForestRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx

Errors tab:

RandomForestRegressor.py started        RandomForestRegressor.py        1       1
Traceback (most recent call last):      RandomForestRegressor.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  RandomForestRegressor.py        159     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     383     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     424     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\random_forest_regressor_double.onnx failed:Type Er      onnxruntime_inference_collection.py     424     1
RandomForestRegressor.py finished in 4392 ms            5       1

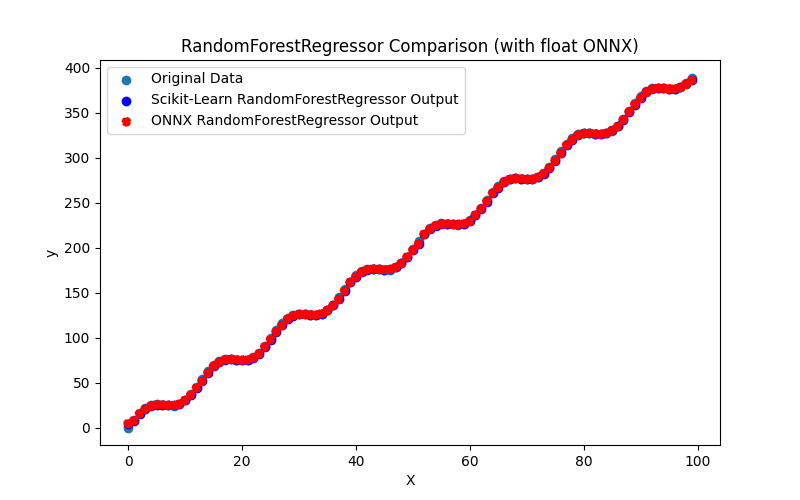
Fig.118. Results of the RandomForestRegressor.py (float ONNX)

2.2.7.2. MQL5 code for executing ONNX Models

This code executes the saved random_forest_regressor_float.onnx and random_forest_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                        RandomForestRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "RandomForestRegressor"
#define   ONNXFilenameFloat  "random_forest_regressor_float.onnx"
#define   ONNXFilenameDouble "random_forest_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

RandomForestRegressor (EURUSD,H1)       
RandomForestRegressor (EURUSD,H1)       Testing ONNX float: RandomForestRegressor (random_forest_regressor_float.onnx)
RandomForestRegressor (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9998854516013125
RandomForestRegressor (EURUSD,H1)       MQL5:   Mean Absolute Error: 0.9186420704511761
RandomForestRegressor (EURUSD,H1)       MQL5:   Mean Squared Error: 1.5157912842364190
RandomForestRegressor (EURUSD,H1)       
RandomForestRegressor (EURUSD,H1)       Testing ONNX double: RandomForestRegressor (random_forest_regressor_double.onnx)
RandomForestRegressor (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\RandomForestRegressor.mq5' (133:16)
RandomForestRegressor (EURUSD,H1)       model_name=RandomForestRegressor OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double..

2.2.7.3. ONNX representation of the random_forest_regressor_float.onnx and random_forest_regressor_double.onnx

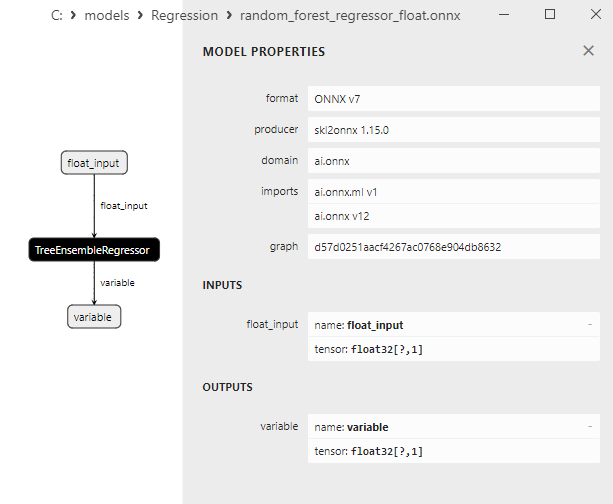
Fig.119. ONNX representation of the random_forest_regressor_float.onnx in Netron

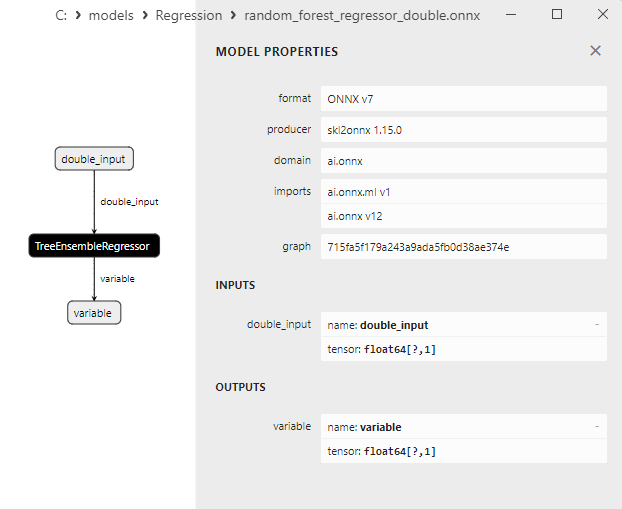
Fig.120. ONNX representation of the random_forest_regressor_double.onnx in Netron

2.2.8. sklearn.ensemble.GradientBoostingRegressor

GradientBoostingRegressor is a machine learning method used for regression tasks. It's part of the ensemble methods family and is based on the idea of building weak models and combining them into a strong model using gradient boosting..

Gradient boosting is a technique to enhance models by iteratively adding weak models and correcting the errors of previous models.

Here's how GradientBoostingRegressor works:

1. Initialization: It starts with the original dataset containing features (independent variables) and their corresponding target values.
2. First Model: It begins by training the first model, often chosen as a simple regression model (e.g., decision tree) on the original data.
3. Residuals and Anti-Gradient: Residuals, the difference between the predicted values of the first model and the actual target variable values, are computed. Then, the anti-gradient of this loss function is calculated, indicating the direction to improve the model.
4. Building the Next Model: The next model is constructed, focusing on predicting the anti-gradient (errors of the first model). This model is trained on residuals and added to the first model.
5. Iterations: The process of constructing new models and correcting residuals is repeated multiple times. Each new model takes into account the residuals of the previous models and aims to enhance predictions.
6. Model Combination: Predictions of all models are combined into the final prediction through averaging or weighting them according to their importance.

Advantages of GradientBoostingRegressor:

• High Performance: Gradient boosting is a powerful method capable of achieving high performance in regression tasks.
• Robustness to Outliers: It handles outliers in data and constructs models considering this uncertainty.
• Automatic Feature Selection: It automatically selects the most important features for predicting the target variable.
• Handling Various Loss Functions: The method allows the use of different loss functions depending on the task.

Limitations of GradientBoostingRegressor:

• Hyperparameter Tuning Required: Achieving maximum performance necessitates tuning hyperparameters such as learning rate, tree depth, and model count.
• Computationally Expensive: Gradient boosting can be computationally expensive, especially with large volumes of data and a high number of trees.

GradientBoostingRegressor is a powerful regression method often used in practical tasks to achieve high performance with the correct hyperparameter tuning.

2.2.8.1. Code for creating the GradientBoostingRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.ensemble.GradientBoostingRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# GradientBoostingRegressor.py
# The code demonstrates the process of training GradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "GradientBoostingRegressor"
onnx_model_filename = data_path + "gradient_boosting_regressor"

# create a Gradient Boosting Regressor model
regression_model = GradientBoostingRegressor()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  GradientBoostingRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9999959514652565
Python  Mean Absolute Error: 0.15069342754017417
Python  Mean Squared Error: 0.053573282108575676
Python  
Python  GradientBoostingRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9999959514739537
Python  Mean Absolute Error: 0.15069457426101718
Python  Mean Squared Error: 0.05357316702127665
Python  R^2 matching decimal places:  10
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  6
Python  float ONNX model precision:  5
Python  
Python  GradientBoostingRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx

Errors tab:

GradientBoostingRegressor.py started    GradientBoostingRegressor.py    1       1
Traceback (most recent call last):      GradientBoostingRegressor.py    1       1
    onnx_session = ort.InferenceSession(onnx_filename)  GradientBoostingRegressor.py    161     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     419     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     452     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\gradient_boosting_regressor_double.onnx failed:Typ      onnxruntime_inference_collection.py     452     1
GradientBoostingRegressor.py finished in 3073 ms                5       1

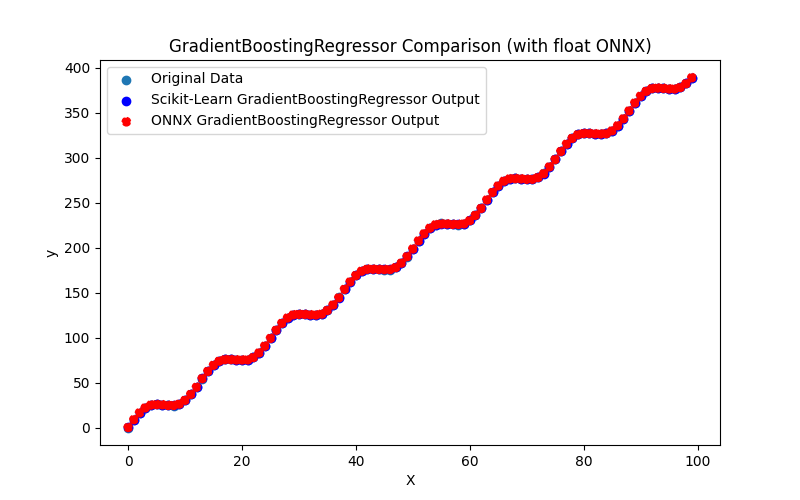
Fig.121. Results of the GradientBoostingRegressor.py (float ONNX)

2.2.8.2. MQL5 code for executing ONNX Models

This code executes the gradient_boosting_regressor_float.onnx and gradient_boosting_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                    GradientBoostingRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "GradientBoostingRegressor"
#define   ONNXFilenameFloat  "gradient_boosting_regressor_float.onnx"
#define   ONNXFilenameDouble "gradient_boosting_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

GradientBoostingRegressor (EURUSD,H1)   Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx)
GradientBoostingRegressor (EURUSD,H1)   MQL5:   R-Squared (Coefficient of determination): 0.9999959514739537
GradientBoostingRegressor (EURUSD,H1)   MQL5:   Mean Absolute Error: 0.1506945742610172
GradientBoostingRegressor (EURUSD,H1)   MQL5:   Mean Squared Error: 0.0535731670212767
GradientBoostingRegressor (EURUSD,H1)   
GradientBoostingRegressor (EURUSD,H1)   Testing ONNX double: GradientBoostingRegressor (gradient_boosting_regressor_double.onnx)
GradientBoostingRegressor (EURUSD,H1)   ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\GradientBoostingRegressor.mq5' (133:16)
GradientBoostingRegressor (EURUSD,H1)   model_name=GradientBoostingRegressor OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double.

Comparison with the original double precision model in Python:

Testing ONNX float: GradientBoostingRegressor (gradient_boosting_regressor_float.onnx)
Python  Mean Absolute Error: 0.15069342754017417
MQL5:   Mean Absolute Error: 0.1506945742610172

Accuracy of ONNX float MAE: 5 decimal places.

2.2.8.3. ONNX representation of the gradient_boosting_regressor_float.onnx and gradient_boosting_regressor_double.onnx

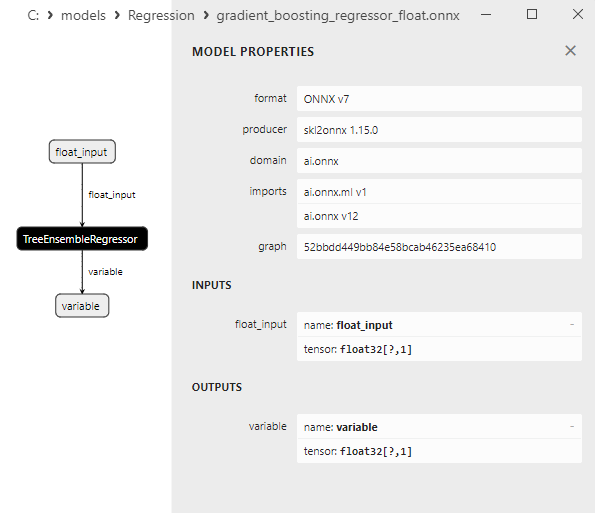
Fig.122. ONNX-representastion of the gradient_boosting_regressor_float.onnx in Netron

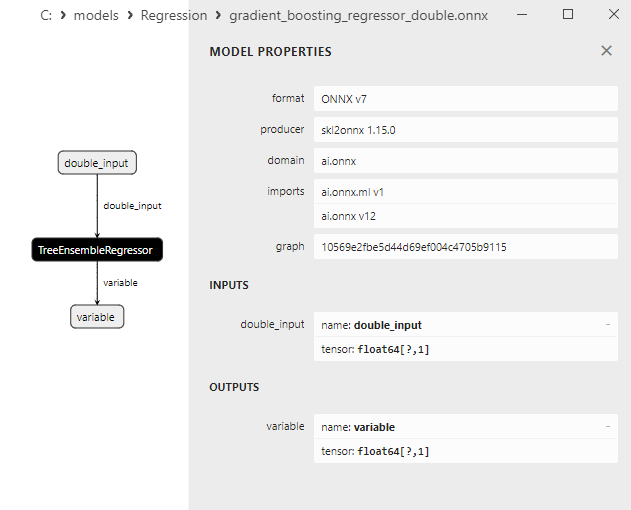
Fig.123. ONNX representation of the gradient_boosting_regressor_double.onnx in Netron

2.2.9. sklearn.ensemble.HistGradientBoostingRegressor

HistGradientBoostingRegressor is a machine learning method that represents a variation of gradient boosting optimized for working with large datasets.

This method is used for regression tasks, and its name "Hist" signifies that it employs histogram-based methods to expedite the training process.

How HistGradientBoostingRegressor Works:

1. Initialization: It starts with the original dataset containing features (independent variables) and their corresponding target values.
2. Histogram-Based Methods: Instead of exact data splitting at tree nodes, HistGradientBoostingRegressor uses histogram-based methods to efficiently represent data in the form of histograms. This significantly speeds up the training process, especially on large datasets.
3. Building Base Trees: The method constructs a set of base decision trees referred to as "histogram decision trees" using the histogram representations of the data. These trees are built based on gradient boosting and adjusted to residuals of the previous model.
4. Gradual Training: HistGradientBoostingRegressor incrementally adds new trees to the ensemble, with each tree correcting the residuals of the previous trees.
5. Model Combination: After building the base trees, predictions from all trees are combined to obtain the final prediction.

Advantages of HistGradientBoostingRegressor:

• High Performance: This method is optimized to handle large volumes of data and can achieve high performance.
• Noise Robustness: HistGradientBoostingRegressor generally performs well even in the presence of noise in data.
• High-Dimensional Efficiency: The method can handle tasks with a high number of features (high-dimensional data).
• Excellent Parallelization: It can efficiently parallelize training across multiple processors.

Limitations of HistGradientBoostingRegressor:

• Requires Hyperparameter Tuning: Achieving maximum performance demands tuning hyperparameters such as tree depth and model count.
• Less Interpretability Than Linear Models: Like other ensemble methods, HistGradientBoostingRegressor is less interpretable than simpler models like linear regression.

HistGradientBoostingRegressor can be a useful regression method for tasks involving large datasets where high performance and high-dimensional data efficiency are essential.

2.2.9.1. Code for creating the HistGradientBoostingRegressor model and exporting it to ONNX for float and double

This code creates the sklearn.ensemble.HistGradientBoostingRegressor model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# HistGradientBoostingRegressor.py
# The code demonstrates the process of training HistGradientBoostingRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import HistGradientBoostingRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "HistGradientBoostingRegressor"
onnx_model_filename = data_path + "hist_gradient_boosting_regressor"

# create a Histogram-Based Gradient Boosting Regressor model
hist_gradient_boosting_model = HistGradientBoostingRegressor()

# fit the model to the data
hist_gradient_boosting_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = hist_gradient_boosting_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(hist_gradient_boosting_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  HistGradientBoostingRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.9833421349506157
Python  Mean Absolute Error: 9.070567104488434
Python  Mean Squared Error: 220.4295035561544
Python  
Python  HistGradientBoostingRegressor ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.9833421351962779
Python  Mean Absolute Error: 9.07056497799043
Python  Mean Squared Error: 220.42950030536645
Python  R^2 matching decimal places:  8
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  5
Python  float ONNX model precision:  5
Python  
Python  HistGradientBoostingRegressor ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx

Errors tab:

HistGradientBoostingRegressor.py started        HistGradientBoostingRegressor.py        1       1
Traceback (most recent call last):      HistGradientBoostingRegressor.py        1       1
    onnx_session = ort.InferenceSession(onnx_filename)  HistGradientBoostingRegressor.py        161     1
    self._create_inference_session(providers, provider_options, disabled_optimizers)    onnxruntime_inference_collection.py     419     1
    sess = C.InferenceSession(session_options, self._model_path, True, self._read_config_from_model)    onnxruntime_inference_collection.py     452     1
onnxruntime.capi.onnxruntime_pybind11_state.Fail: [ONNXRuntimeError] : 1 : FAIL : Load model from C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\hist_gradient_boosting_regressor_double.onnx faile      onnxruntime_inference_collection.py     452     1
HistGradientBoostingRegressor.py finished in 3100 ms            5       1

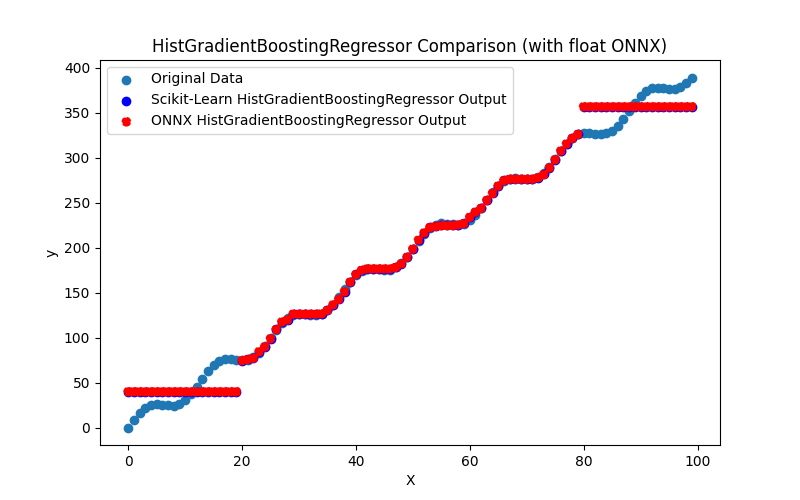
Fig.124. Results of the HistGradientBoostingRegressor.py (float ONNX)

2.2.9.2. MQL5 code for executing ONNX Models

This code executes the saved hist_gradient_boosting_regressor_float.onnx and hist_gradient_boosting_regressor_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                HistGradientBoostingRegressor.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "HistGradientBoostingRegressor"
#define   ONNXFilenameFloat  "hist_gradient_boosting_regressor_float.onnx"
#define   ONNXFilenameDouble "hist_gradient_boosting_regressor_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

HistGradientBoostingRegressor (EURUSD,H1)       Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx)
HistGradientBoostingRegressor (EURUSD,H1)       MQL5:   R-Squared (Coefficient of determination): 0.9833421351962779
HistGradientBoostingRegressor (EURUSD,H1)       MQL5:   Mean Absolute Error: 9.0705649779904292
HistGradientBoostingRegressor (EURUSD,H1)       MQL5:   Mean Squared Error: 220.4295003053665312
HistGradientBoostingRegressor (EURUSD,H1)       
HistGradientBoostingRegressor (EURUSD,H1)       Testing ONNX double: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_double.onnx)
HistGradientBoostingRegressor (EURUSD,H1)       ONNX: cannot create session (OrtStatus: 1 'Type Error: Type (tensor(double)) of output arg (variable) of node (TreeEnsembleRegressor) does not match expected type (tensor(float)).'), inspect code 'Scripts\Regression\HistGradientBoostingRegressor.mq5' (133:16)
HistGradientBoostingRegressor (EURUSD,H1)       model_name=HistGradientBoostingRegressor OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double.

Comparison with the original double precision model in Python:

Testing ONNX float: HistGradientBoostingRegressor (hist_gradient_boosting_regressor_float.onnx)
Python  Mean Absolute Error: 9.070567104488434
MQL5:   Mean Absolute Error: 9.0705649779904292

Accuracy of ONNX float MAE: 5 decimal places

2.2.9.3. ONNX representation of the hist_gradient_boosting_regressor_float.onnx and hist_gradient_boosting_regressor_double.onnx  

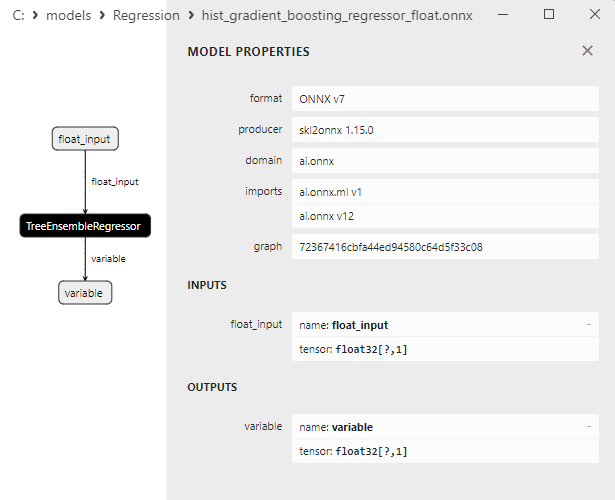
Fig.125. ONNX representation of the hist_gradient_boosting_regressor_float.onnx in Netron

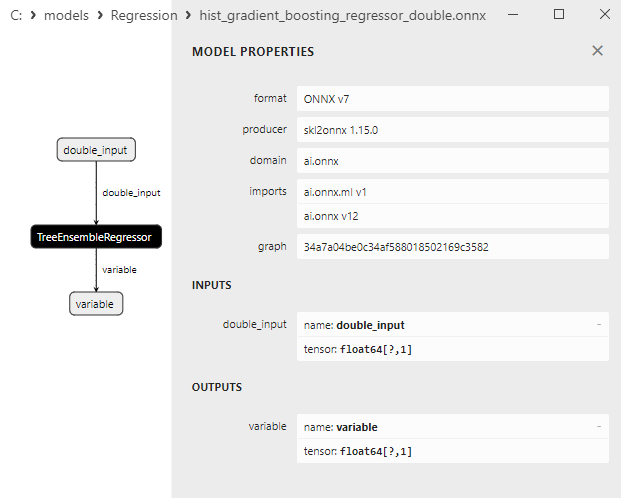
Fig.126. ONNX representation of the hist_gradient_boosting_regressor_double.onnx in Netron

2.2.10. sklearn.svm.SVR

SVR (Support Vector Regression) is a machine learning method used for regression tasks. It is based on the same concept as the Support Vector Machine (SVM) for classification but is adapted for regression. The primary goal of SVR is to predict continuous values of the target variable by relying on the maximum average distance between data points and the regression line.

How SVR Works:

1. Boundary Definition: Similar to SVM, SVR constructs boundaries that separate different classes of data points. Instead of class separation, SVR aims to build a "tube" around data points, where the tube's width is controlled by a hyperparameter.
2. Target Variable and Loss Function: Instead of using classes as in classification, SVR deals with continuous values of the target variable. It minimizes the prediction error measured using a loss function, such as the squared difference between the predicted and actual values.
3. Regularization: SVR also supports regularization, aiding in controlling model complexity and preventing overfitting.
4. Kernel Functions: SVR typically employs kernel functions that allow it to handle nonlinear dependencies between features and the target variable. Popular kernel functions include the radial basis function (RBF), polynomial, and linear functions.

Advantages of SVR:

• Robustness to Outliers: SVR can handle outliers in data as it aims to minimize prediction error.
• Support for Nonlinear Dependencies: The use of kernel functions enables SVR to model complex and nonlinear dependencies between features and the target variable.
• High Prediction Quality: In regression tasks that require precise predictions, SVR can provide high-quality results.

Limitations of SVR:

• Sensitivity to Hyperparameters: Choosing the kernel function and model parameters, such as the tube width (hyperparameters), may require careful tuning and optimization.
• Computational Complexity: Training the SVR model, especially when using complex kernel functions and large datasets, can be computationally intensive.

SVR is a machine learning method for regression tasks based on the idea of constructing a "tube" around data points to minimize prediction errors. It exhibits robustness to outliers and the ability to handle nonlinear dependencies, making it useful in various regression tasks.

2.2.10.1. Code for creating the SVR model and exporting it to ONNX for float and double

This code creates the sklearn.svm.SVR model, trains it on synthetic data, saves the model in the ONNX format, and performs predictions using both float and double input data. It also evaluates the accuracy of both the original model and the models exported to ONNX.

# SVR.py
# The code demonstrates the process of training SVR model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "SVR"
onnx_model_filename = data_path + "svr"

# create an SVR model
regression_model = SVR()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  SVR Original model (double)
Python  R-squared (Coefficient of determination): 0.398243655775797
Python  Mean Absolute Error: 73.63683696034649
Python  Mean Squared Error: 7962.89631509593
Python  
Python  SVR ONNX model (float)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_float.onnx
Python  Information about input tensors in ONNX:
Python  1. Name: float_input, Data Type: tensor(float), Shape: [None, 1]
Python  Information about output tensors in ONNX:
Python  1. Name: variable, Data Type: tensor(float), Shape: [None, 1]
Python  R-squared (Coefficient of determination) 0.3982436352100983
Python  Mean Absolute Error: 73.63683840363255
Python  Mean Squared Error: 7962.896587236852
Python  R^2 matching decimal places:  7
Python  MAE matching decimal places:  5
Python  MSE matching decimal places:  3
Python  float ONNX model precision:  5
Python  
Python  SVR ONNX model (double)
Python  ONNX model saved to C:\Users\user\AppData\Roaming\MetaQuotes\Terminal\D0E8209F77C8CF37AD8BF550E51FF075\MQL5\Scripts\Regression\svr_double.onnx

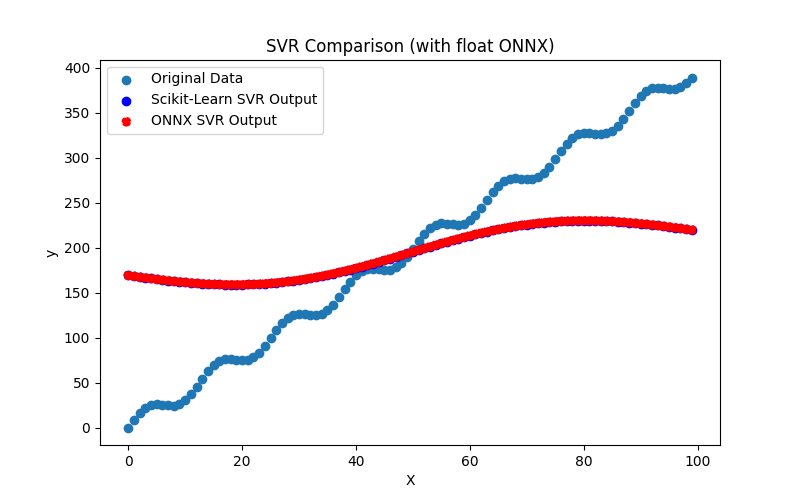
Fig.127. Results of the SVR.py (float ONNX)

2.2.10.2. MQL5 code for executing ONNX Models

This code executes the saved  svr_float.onnx and svr_double.onnx models and demonstrating the use of regression metrics in MQL5.

//+------------------------------------------------------------------+
//|                                                          SVR.mq5 |
//|                                  Copyright 2023, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"

#define   ModelName          "SVR"
#define   ONNXFilenameFloat  "svr_float.onnx"
#define   ONNXFilenameDouble "svr_double.onnx"

#resource ONNXFilenameFloat  as const uchar ExtModelFloat[];
#resource ONNXFilenameDouble as const uchar ExtModelDouble[];

#define   TestFloatModel  1
#define   TestDoubleModel 2

//+------------------------------------------------------------------+
//| Calculate regression using float values                          |
//+------------------------------------------------------------------+
bool RunModelFloat(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   float input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=(float)input_vector[k];
//--- prepare output tensor
   float output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }
//+------------------------------------------------------------------+
//| Calculate regression using double values                         |
//+------------------------------------------------------------------+
bool RunModelDouble(long model,vector &input_vector, vector &output_vector)
  {
//--- check number of input samples
   ulong batch_size=input_vector.Size();
   if(batch_size==0)
      return(false);
//--- prepare output array
   output_vector.Resize((int)batch_size);
//--- prepare input tensor
   double input_data[];
   ArrayResize(input_data,(int)batch_size);
//--- set input shape
   ulong input_shape[]= {batch_size, 1};
   OnnxSetInputShape(model,0,input_shape);
//--- copy data to the input tensor
   for(int k=0; k<(int)batch_size; k++)
      input_data[k]=input_vector[k];
//--- prepare output tensor
   double output_data[];
   ArrayResize(output_data,(int)batch_size);
//--- set output shape
   ulong output_shape[]= {batch_size,1};
   OnnxSetOutputShape(model,0,output_shape);
//--- run the model
   bool res=OnnxRun(model,ONNX_DEBUG_LOGS,input_data,output_data);
//--- copy output to vector
   if(res)
     {
      for(int k=0; k<(int)batch_size; k++)
         output_vector[k]=output_data[k];
     }
//---
   return(res);
  }

//+------------------------------------------------------------------+
//| Generate synthetic data                                          |
//+------------------------------------------------------------------+
bool GenerateData(const int n,vector &x,vector &y)
  {
   if(n<=0)
      return(false);
//--- prepare arrays
   x.Resize(n);
   y.Resize(n);
//---
   for(int i=0; i<n; i++)
     {
      x[i]=(double)1.0*i;
      y[i]=(double)(4*x[i] + 10*sin(x[i]*0.5));
     }
//---
   return(true);
  }

//+------------------------------------------------------------------+
//| TestRegressionModel                                              |
//+------------------------------------------------------------------+
bool TestRegressionModel(const string model_name,const int model_type)
  {
//---
   long  model=INVALID_HANDLE;
   ulong flags=ONNX_DEFAULT;

   if(model_type==TestFloatModel)
     {
      PrintFormat("\nTesting ONNX float: %s (%s)",model_name,ONNXFilenameFloat);
      model=OnnxCreateFromBuffer(ExtModelFloat,flags);
     }
   else
      if(model_type==TestDoubleModel)
        {
         PrintFormat("\nTesting ONNX double: %s (%s)",model_name,ONNXFilenameDouble);
         model=OnnxCreateFromBuffer(ExtModelDouble,flags);
        }
      else
        {
         PrintFormat("Model type is not incorrect.");
         return(false);
        }
//--- check
   if(model==INVALID_HANDLE)
     {
      PrintFormat("model_name=%s OnnxCreate error %d",model_name,GetLastError());
      return(false);
     }
//---
   vector x_values= {};
   vector y_true= {};
   vector y_predicted= {};
//---
   int n=100;
   GenerateData(n,x_values,y_true);
//---
   bool run_result=false;
   if(model_type==TestFloatModel)
     {
      run_result=RunModelFloat(model,x_values,y_predicted);
     }
   else
      if(model_type==TestDoubleModel)
        {
         run_result=RunModelDouble(model,x_values,y_predicted);
        }
//---
   if(run_result)
     {
      PrintFormat("MQL5:   R-Squared (Coefficient of determination): %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_R2));
      PrintFormat("MQL5:   Mean Absolute Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MAE));
      PrintFormat("MQL5:   Mean Squared Error: %.16f",y_predicted.RegressionMetric(y_true,REGRESSION_MSE));
     }
   else
      PrintFormat("Error %d",GetLastError());
//--- release model
   OnnxRelease(model);
//---
   return(true);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart(void)
  {
//--- test ONNX regression model for float
   TestRegressionModel(ModelName,TestFloatModel);
//--- test ONNX regression model for double
   TestRegressionModel(ModelName,TestDoubleModel);
//---
   return(0);
  }
//+------------------------------------------------------------------+

Output:

SVR (EURUSD,H1) Testing ONNX float: SVR (svr_float.onnx)
SVR (EURUSD,H1) MQL5:   R-Squared (Coefficient of determination): 0.3982436352100981
SVR (EURUSD,H1) MQL5:   Mean Absolute Error: 73.6368384036325523
SVR (EURUSD,H1) MQL5:   Mean Squared Error: 7962.8965872368517012
SVR (EURUSD,H1) 
SVR (EURUSD,H1) Testing ONNX double: SVR (svr_double.onnx)
SVR (EURUSD,H1) ONNX: cannot create session (OrtStatus: 9 'Could not find an implementation for SVMRegressor(1) node with name 'SVM''), inspect code 'Scripts\R\SVR.mq5' (133:16)
SVR (EURUSD,H1) model_name=SVR OnnxCreate error 5800

The float ONNX model executed normally, but an error occurred when executing the ONNX model in double.

Comparison with the original double precision model in Python:

Testing ONNX float: SVR (svr_float.onnx)
Python  Mean Absolute Error: 73.63683696034649
MQL5:   Mean Absolute Error: 73.6368384036325523

Accuracy of ONNX float MAE: 5 decimal places

2.2.10.3. ONNX representation of svr_float.onnx and svr_double.onnx

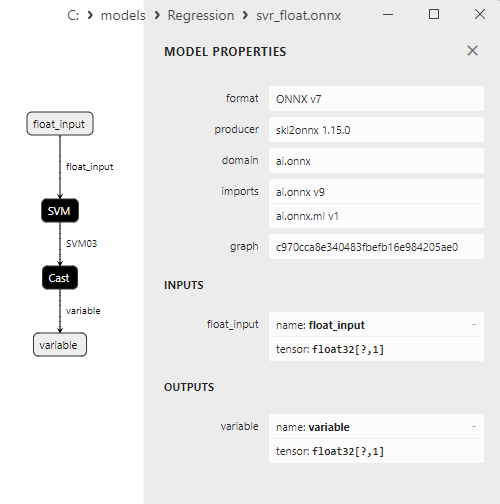
Fig.128. ONNX representation of svr_float.onnx in Netron

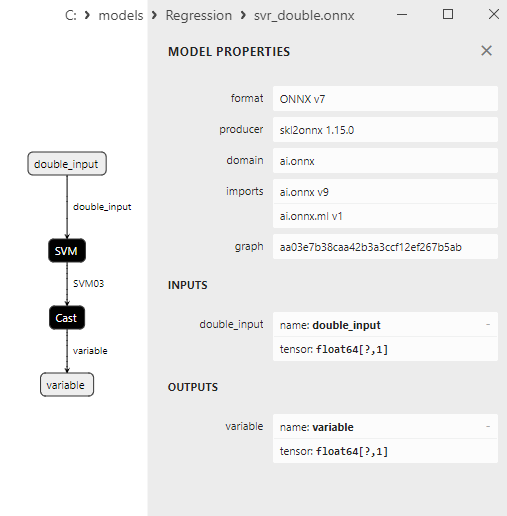
Fig.129. ONNX representation of the svr_double.onnx in Netron

2.3. Regression Models that Encountered Problems When Converting to ONNX

Some regression models couldn't be converted into the ONNX format by the sklearn-onnx converter.

2.3.1. sklearn.dummy.DummyRegressor

The DummyRegressor is a machine learning method used in regression tasks to create a baseline model that predicts the target variable using simple rules. It's valuable for comparison with other more complex models and evaluating their performance. This method is often used in the context of assessing the quality of other regression models.

The DummyRegressor offers several strategies for prediction:

1. "mean" (default): DummyRegressor predicts the mean value of the target variable from the training dataset. This strategy is useful to determine how much better another model is compared to simply predicting the mean.
2. "median": DummyRegressor predicts the median value of the target variable from the training dataset.
3. "quantile": DummyRegressor predicts the quantile value of the target variable (specified by the quantile parameter) from the training dataset.
4. "constant": DummyRegressor predicts a constant value set by the user (using the strategy parameter).

Advantages of DummyRegressor:

• Performance Assessment: DummyRegressor is useful for evaluating the performance of other more complex models. If your model can't outperform predictions made by DummyRegressor, it might indicate issues in the model.
• Comparison with Baseline Models: DummyRegressor allows for comparing the performance of more complex models against a baseline (e.g., mean or median value).
• User-Friendly: DummyRegressor is easy to implement and use for comparative analysis.

Limitations of DummyRegressor:

• Not for Accurate Prediction: DummyRegressor provides only basic baseline predictions and is not intended for accurate forecasting.
• Ignores Complex Dependencies: DummyRegressor disregards complex data structures and feature dependencies.
• Not Suitable for Tasks Requiring Accurate Prediction: In real-world prediction tasks, using DummyRegressor for forecasting the target variable is insufficient.

DummyRegressor is valuable as a tool for a quick assessment and performance comparison of other regression models, but it isn't a standalone serious regression model.

2.3.1.1. Code for creating the DummyRegressor model

# DummyRegressor.py
# The code demonstrates the process of training DummyRegressor model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.dummy import DummyRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "DummyRegressor"
onnx_model_filename = data_path + "dummy_regressor"

# create an Dummy Regressor model
regression_model = DummyRegressor(strategy="mean")

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  DummyRegressor Original model (double)
Python  R-squared (Coefficient of determination): 0.0
Python  Mean Absolute Error: 100.00329851715793
Python  Mean Squared Error: 13232.758393867645

Errors tab:

DummyRegressor.py started       DummyRegressor.py       1       1
Traceback (most recent call last):      DummyRegressor.py       1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     DummyRegressor.py       87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.dummy.DummyRegressor'>'. _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
DummyRegressor.py finished in 2565 ms           19      1

2.3.2. sklearn.kernel_ridge.KernelRidge

KernelRidge is a machine learning method used for regression tasks. It combines the kernel method of Support Vector Machines (Kernel SVM) and regression. KernelRidge enables the modeling of complex, nonlinear relationships between features and the target variable using kernel functions.

Working principle of KernelRidge:

• Input data: It starts with the original dataset containing features (independent variables) and their corresponding target variable values.
• Kernel functions: KernelRidge uses kernel functions (such as polynomial, RBF - radial basis function, and others) that transform data into a high-dimensional space, allowing the modeling of more complex nonlinear relationships.
• Model training: The model is trained on the data by minimizing the mean squared error between predicted values and the actual target variable values. Kernel functions are used to account for complex dependencies.
• Prediction: After training, the model can be used to predict target variable values for new data, using the same kernel functions.

Advantages of KernelRidge:

• Modeling complex nonlinear relationships: KernelRidge allows the modeling of complex and nonlinear dependencies between features and the target variable.
• Selection of different kernels: You can choose different kernels depending on the nature of the data and the task.
• Regularization: The method includes regularization, helping prevent model overfitting.

Limitations of KernelRidge:

• Lack of interpretability: Like many nonlinear methods, KernelRidge is less interpretable than linear models.
• Computational complexity: Using kernel functions can be computationally expensive with large volumes of data and/or high dimensionality.
• Parameter tuning requirement: Choosing the appropriate kernel and model parameters requires tuning and expertise.

KernelRidge is useful in regression tasks where data exhibits complex, nonlinear dependencies, and a model capable of considering these relationships is required. It is also helpful in tasks where kernel functions can be utilized to transform data into a more informative representation.

2.3.2.1. Code for creating the KernelRidge model

# KernelRidge.py
# The code demonstrates the process of training KernelRidge model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.kernel_ridge import KernelRidge
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "KernelRidge"
onnx_model_filename = data_path + "kernel_ridge"

# create an KernelRidge model
regression_model = KernelRidge(alpha=1.0, kernel='linear')

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  KernelRidge Original model (double)
Python  R-squared (Coefficient of determination): 0.9962137909675411
Python  Mean Absolute Error: 6.36977985227399
Python  Mean Squared Error: 50.10198935520715

Errors tab:

KernelRidge.py started  KernelRidge.py  1       1
Traceback (most recent call last):      KernelRidge.py  1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     KernelRidge.py  87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.kernel_ridge.KernelRidge'>'.     _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
KernelRidge.py finished in 2516 ms              19      1

2.3.3. sklearn.isotonic.IsotonicRegression

IsotonicRegression - is a machine learning method used for regression tasks that models a monotonic relationship between features and the target variable. In this context, "monotonicity" means that an increase in the value of one of the features leads to an increase or decrease in the value of the target variable, while preserving the direction of change.

Working principle of IsotonicRegression:

1. Input data: It starts with the original dataset containing features (independent variables) and their corresponding target variable values.
2. Monotonic regression: IsotonicRegression aims to find the best monotonic function that describes the relationship between the features and the target variable. This function can be linear or nonlinear but must maintain monotonicity.
3. Model training: The model is trained on the data to determine the parameters of the monotonic function. During training, the model tries to minimize the sum of squared errors between predictions and the actual target variable values.
4. Prediction: After training, the model can be used to predict target variable values for new data while maintaining the monotonic relationship.

Advantages of IsotonicRegression:

• Modeling monotonic relationships: This method is an ideal choice when data demonstrates monotonic dependencies, and it's important to maintain this characteristic in the model.
• Interpretability: Monotonic models can be more interpretable as they allow a clear definition of the influence direction of each feature on the target variable.

Limitations of IsotonicRegression:

• Not suitable for complex, nonlinear relationships: This method is limited to modeling monotonic relationships and, therefore, is not suitable for modeling complex nonlinear dependencies.
• Parameter tuning: Some IsotonicRegression implementations might have parameters that require tuning to achieve optimal performance.

IsotonicRegression is useful in tasks where the monotonicity of the relationship between features and the target variable is considered an important factor, and there is a need to build a model that preserves this characteristic.

2.3.3.1. Code for creating the IsotonicRegression models

# IsotonicRegression.py
# The code demonstrates the process of training IsotonicRegression model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.isotonic import IsotonicRegression
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "IsotonicRegression"
onnx_model_filename = data_path + "isotonic_regression"

# create an IsotonicRegression model
regression_model = IsotonicRegression()

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  IsotonicRegression Original model (double)
Python  R-squared (Coefficient of determination): 0.9999898125037958
Python  Mean Absolute Error: 0.20093409873424467
Python  Mean Squared Error: 0.13480867590911208

Errors tab:

IsotonicRegression.py started   IsotonicRegression.py   1       1
Traceback (most recent call last):      IsotonicRegression.py   1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     IsotonicRegression.py   87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.isotonic.IsotonicRegression'>'.  _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
IsotonicRegression.py finished in 2499 ms               19      1

2.3.4. sklearn.cross_decomposition.PLSCanonical

PLSCanonical (Partial Least Squares Canonical) is a machine learning method used to solve canonical correlation problems. It is an extension of the Partial Least Squares (PLS) method and is applied to analyze and model relationships between two sets of variables.

Working principle of PLSCanonical:

1. Input data: It starts with two datasets (X and Y), where each set represents a collection of variables (features). Usually, X and Y contain correlated data, and the task is to find linear combinations of features that maximize the correlation between them.
2. Selection of linear combinations: PLSCanonical finds linear combinations (components) in both X and Y to maximize the correlation between the components of the two datasets. These components are called canonical variables.
3. Maximum correlation search: The primary goal of PLSCanonical is to find canonical variables that maximize the correlation between X and Y, highlighting the most informative relationships between the two datasets.
4. Model training: Once the canonical variables are found, they can be used to create a model that predicts Y values based on X.
5. Generating predictions: After training, the model can be used to predict Y values in new data using corresponding X values.

Advantages of PLSCanonical:

• Correlation analysis: PLSCanonical allows the analysis and modeling of correlations between two datasets, which can be useful for understanding the relationships between variables.
• Dimensionality reduction: The method can also be used to reduce the data dimensionality, highlighting the most important components.

Limitations of PLSCanonical:

• Sensitivity to the choice of the number of components: Selecting the optimal number of canonical variables may require some experimentation.
• Dependency on data structure: The results of PLSCanonical can heavily depend on the data structure and correlations between them.

PLSCanonical is a machine learning method used to analyze and model correlations between two sets of variables. This method enables studying relationships between data and can be useful for reducing data dimensionality and predicting values based on correlated components.

2.3.4.1. Code for creating the PLSCanonical

# PLSCanonical.py
# The code demonstrates the process of training PLSCanonical model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import PLSCanonical
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name = "PLSCanonical"
onnx_model_filename = data_path + "pls_canonical"

# create an PLSCanonical model
regression_model = PLSCanonical(n_components=1)

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8, 5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  
Python  PLSCanonical Original model (double)
Python  R-squared (Coefficient of determination): 0.9962347199278333
Python  Mean Absolute Error: 6.3561407034365995
Python  Mean Squared Error: 49.82504148022689

Errors tab:

PLSCanonical.py started PLSCanonical.py 1       1
Traceback (most recent call last):      PLSCanonical.py 1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     PLSCanonical.py 87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.PLSCanonical'>'.        _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
PLSCanonical.py finished in 2513 ms             19      1

2.3.5. sklearn.cross_decomposition.CCA

Canonical Correlation Analysis (CCA)is a multivariate statistical analysis method used to study the relationships between two sets of variables (set X and set Y). The main goal of CCA is to find linear combinations of variables X and Y that maximize the correlation between them. These linear combinations are called canonical variables.

Working principle of CCA:

1. Input data: It starts with two sets of variables X and Y. There can be any number of variables in these sets, and CCA attempts to find linear combinations that maximize the correlation between them.
2. Construction of canonical variables: CCA identifies canonical variables in X and Y that maximize their correlation. These canonical variables are linear combinations of the original variables, one for each canonical indicator.
3. Correlation assessment: CCA evaluates the correlation between pairs of canonical variables. Canonical variables are usually ordered by decreasing correlation, so the first pair has the highest correlation, the second has the next highest, and so on.
4. Interpretation: Canonical variables can be interpreted considering their correlation and variable weights. This allows understanding which variables from sets X and Y are most strongly related.

Advantages of CCA:

• Reveals hidden connections: CCA can help discover hidden correlations between two sets of variables that may not be obvious during initial analysis.
• Robust to noise: CCA can account for noise in data and focus on the most significant correlations.
• Multiple applications: CCA can be used in various fields including statistics, bioinformatics, finance, among others, to study relationships between sets of variables.

Limitations of CCA:

• Requires more data: CCA might require a larger amount of data than other analysis methods to reliably estimate correlations.
• Linear relationships: CCA assumes linear relationships between variables, which might be insufficient in some cases.
• Interpretation complexity: Interpreting canonical variables can be complex, especially when there are many variables in sets X and Y.

CCA is beneficial in tasks where studying the relationship between two sets of variables and uncovering hidden correlations is required.

2.3.5.1. Code for creating the CCA model

# CCA.py
# The code demonstrates the process of training CCA model, exporting it to ONNX format (both float and double), and making predictions using the ONNX models.
# Copyright 2023, MetaQuotes Ltd.
# https://www.mql5.com

# function to compare matching decimal places
def compare_decimal_places(value1, value2):
    # convert both values to strings
    str_value1 = str(value1)
    str_value2 = str(value2)

    # find the positions of the decimal points in the strings
    dot_position1 = str_value1.find(".")
    dot_position2 = str_value2.find(".")

    # if one of the values doesn't have a decimal point, return 0
    if dot_position1 == -1 or dot_position2 == -1:
        return 0

    # calculate the number of decimal places
    decimal_places1 = len(str_value1) - dot_position1 - 1
    decimal_places2 = len(str_value2) - dot_position2 - 1

    # find the minimum of the two decimal places counts
    min_decimal_places = min(decimal_places1, decimal_places2)

    # initialize a count for matching decimal places
    matching_count = 0

    # compare characters after the decimal point
    for i in range(1, min_decimal_places + 1):
        if str_value1[dot_position1 + i] == str_value2[dot_position2 + i]:
            matching_count += 1
        else:
            break

    return matching_count

# import necessary libraries
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_decomposition import CCA
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
import onnx
import onnxruntime as ort
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType
from skl2onnx.common.data_types import DoubleTensorType
from sys import argv

# define the path for saving the model
data_path = argv[0]
last_index = data_path.rfind("\\") + 1
data_path = data_path[0:last_index]

# generate synthetic data for regression
X = np.arange(0,100,1).reshape(-1,1)
y = 4*X + 10*np.sin(X*0.5)

model_name="CCA"
onnx_model_filename = data_path + "cca"

# create an CCA model
regression_model = CCA(n_components=1)

# fit the model to the data
regression_model.fit(X, y.ravel())

# predict values for the entire dataset
y_pred = regression_model.predict(X)

# evaluate the model's performance
r2 = r2_score(y, y_pred)
mse = mean_squared_error(y, y_pred)
mae = mean_absolute_error(y, y_pred)

print("\n"+model_name+" Original model (double)")
print("R-squared (Coefficient of determination):", r2)
print("Mean Absolute Error:", mae)
print("Mean Squared Error:", mse)

# convert to ONNX-model (float)
# define the input data type as FloatTensorType
initial_type_float = [('float_input', FloatTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_float.onnx"
onnx.save_model(onnx_model_float, onnx_filename)

print("\n"+model_name+" ONNX model (float)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as FloatTensorType
initial_type_float = X.astype(np.float32)

# predict values for the entire dataset using ONNX
y_pred_onnx_float = onnx_session.run([output_name], {input_name: initial_type_float})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_float = r2_score(y, y_pred_onnx_float)
mse_onnx_float = mean_squared_error(y, y_pred_onnx_float)
mae_onnx_float = mean_absolute_error(y, y_pred_onnx_float)
print("R-squared (Coefficient of determination)", r2_onnx_float)
print("Mean Absolute Error:", mae_onnx_float)
print("Mean Squared Error:", mse_onnx_float)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_float))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_float))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_float))
print("float ONNX model precision: ",compare_decimal_places(mae, mae_onnx_float))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with float ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_float.png')

# convert to ONNX-model (double)
# define the input data type as DoubleTensorType
initial_type_double = [('double_input', DoubleTensorType([None, X.shape[1]]))]

# export the model to ONNX format
onnx_model_double = convert_sklearn(regression_model, initial_types=initial_type_double, target_opset=12)

# save the model to a file
onnx_filename=onnx_model_filename+"_double.onnx"
onnx.save_model(onnx_model_double, onnx_filename)

print("\n"+model_name+" ONNX model (double)")
# print model path
print(f"ONNX model saved to {onnx_filename}")

# load the ONNX model and make predictions
onnx_session = ort.InferenceSession(onnx_filename)
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name

# display information about input tensors in ONNX
print("Information about input tensors in ONNX:")
for i, input_tensor in enumerate(onnx_session.get_inputs()):
    print(f"{i + 1}. Name: {input_tensor.name}, Data Type: {input_tensor.type}, Shape: {input_tensor.shape}")

# display information about output tensors in ONNX
print("Information about output tensors in ONNX:")
for i, output_tensor in enumerate(onnx_session.get_outputs()):
    print(f"{i + 1}. Name: {output_tensor.name}, Data Type: {output_tensor.type}, Shape: {output_tensor.shape}")

# define the input data type as DoubleTensorType
initial_type_double = X.astype(np.float64)

# predict values for the entire dataset using ONNX
y_pred_onnx_double = onnx_session.run([output_name], {input_name: initial_type_double})[0]

# calculate and display the errors for the original and ONNX models
r2_onnx_double = r2_score(y, y_pred_onnx_double)
mse_onnx_double = mean_squared_error(y, y_pred_onnx_double)
mae_onnx_double = mean_absolute_error(y, y_pred_onnx_double)
print("R-squared (Coefficient of determination)", r2_onnx_double)
print("Mean Absolute Error:", mae_onnx_double)
print("Mean Squared Error:", mse_onnx_double)
print("R^2 matching decimal places: ",compare_decimal_places(r2, r2_onnx_double))
print("MAE matching decimal places: ",compare_decimal_places(mae, mae_onnx_double))
print("MSE matching decimal places: ",compare_decimal_places(mse, mse_onnx_double))
print("double ONNX model precision: ",compare_decimal_places(mae, mae_onnx_double))

# set the figure size
plt.figure(figsize=(8,5))
# plot the original data and the regression line
plt.scatter(X, y, label='Original Data', marker='o')
plt.scatter(X, y_pred, color='blue', label='Scikit-Learn '+model_name+' Output', marker='o')
plt.scatter(X, y_pred_onnx_float, color='red', label='ONNX '+model_name+' Output', marker='o', linestyle='--')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.title(model_name+' Comparison (with double ONNX)')
#plt.show()
plt.savefig(data_path + model_name+'_plot_double.png')

Output:

Python  CCA Original model (double)
Python  R-squared (Coefficient of determination): 0.9962347199278333
Python  Mean Absolute Error: 6.3561407034365995
Python  Mean Squared Error: 49.82504148022689

Errors tab:

CCA.py started  CCA.py  1       1
Traceback (most recent call last):      CCA.py  1       1
    onnx_model_float = convert_sklearn(regression_model, initial_types=initial_type_float, target_opset=12)     CCA.py  87      1
    onnx_model = convert_topology(      convert.py      208     1
    topology.convert_operators(container=container, verbose=verbose)    _topology.py    1532    1
    self.call_shape_calculator(operator)        _topology.py    1348    1
    operator.infer_types()      _topology.py    1163    1
    raise MissingShapeCalculator(       _topology.py    629     1
skl2onnx.common.exceptions.MissingShapeCalculator: Unable to find a shape calculator for type '<class 'sklearn.cross_decomposition._pls.CCA'>'. _topology.py    629     1
It usually means the pipeline being converted contains a        _topology.py    629     1
transformer or a predictor with no corresponding converter      _topology.py    629     1
implemented in sklearn-onnx. If the converted is implemented    _topology.py    629     1
in another library, you need to register        _topology.py    629     1
the converted so that it can be used by sklearn-onnx (function  _topology.py    629     1
update_registered_converter). If the model is not yet covered   _topology.py    629     1
by sklearn-onnx, you may raise an issue to      _topology.py    629     1
https://github.com/onnx/sklearn-onnx/issues     _topology.py    629     1
to get the converter implemented or even contribute to the      _topology.py    629     1
project. If the model is a custom model, a new converter must   _topology.py    629     1
be implemented. Examples can be found in the gallery.   _topology.py    629     1
CCA.py finished in 2543 ms              19      1

Conclusion

The article reviewed 45 regression models available in the Scikit-learn library version 1.3.2.

1. Out of this set, 5 models faced difficulties when converting to the ONNX format:

1. DummyRegressor (Dummy regressor);
2. KernelRidge (Kernel Ridge Regression);
3. IsotonicRegression (Isotonic Regression);
4. PLSCanonical (Partial Least Squares Canonical Analysis);
5. CCA (Canonical Correlation Analysis).

These models might be too complex in their structure or logic and could use specific data structures or algorithms that are not fully compatible with the ONNX format..

2. The remaining 40 models were successfully converted to ONNX with computations in float precision.

1. ARDRegression: Automatic Relevance Determination Regression (ARD);
2. BayesianRidge: Bayesian Ridge Regression with regularization;
3. ElasticNet: Combination of L1 and L2 regularization for mitigating overfitting;
4. ElasticNetCV: Elastic Net with automatic regularization parameter selection;
5. HuberRegressor: Regression with decreased sensitivity to outliers;
6. Lars: Least Angle Regression;
   
7. LarsCV: Cross-validated Least Angle Regression;
8. Lasso: L1-regularized regression for feature selection;
   
9. LassoCV: Cross-validated Lasso regression;
10. LassoLars: Combination of Lasso and LARS for regression;
    
11. LassoLarsCV: Cross-validated LassoLars regression;
12. LassoLarsIC: Information criteria for LassoLars parameter selection;
13. LinearRegression: Simple linear regression;
14. Ridge: Linear regression with L2 regularization;
    
15. RidgeCV: Cross-validated Ridge regression;
16. OrthogonalMatchingPursuit: Regression with orthogonal feature selection;
17. PassiveAggressiveRegressor: Regression with a passive-aggressive learning approach;
18. QuantileRegressor: Quantile regression;
19. RANSACRegressor: Regression with the RANdom SAmple Consensus method;
20. TheilSenRegressor: Non-linear regression based on Theil-Sen method.
21. LinearSVR: Linear support vector regression;
22. MLPRegressor: Regression using a multi-layer perceptron;
23. PLSRegression: Partial Least Squares Regression;
24. TweedieRegressor: Tweedie distribution-based regression;
25. PoissonRegressor: Regression for modeling Poisson-distributed data;
26. RadiusNeighborsRegressor: Regression based on radius neighbors;
    
27. KNeighborsRegressor: Regression based on k-nearest neighbors;
28. GaussianProcessRegressor: Gaussian process-based regression;
29. GammaRegressor: Regression for modeling gamma-distributed data;
30. SGDRegressor: Regression based on stochastic gradient descent;
31. AdaBoostRegressor: Regression using the AdaBoost algorithm;
32. BaggingRegressor: Regression using the Bagging method;
33. DecisionTreeRegressor: Decision tree-based regression;
34. ExtraTreeRegressor: Extra decision tree-based regression;
35. ExtraTreesRegressor: Regression with extra decision trees;
36. NuSVR: Continuous linear support vector regression (SVR);
37. RandomForestRegressor: Regression with an ensemble of decision trees (Random Forest);
38. GradientBoostingRegressor: Regression with gradient boosting;
39. HistGradientBoostingRegressor: Regression with histogram gradient boosting;
40. SVR: Support vector regression method.
    

3. The possibility of converting regression models into ONNX with calculations in double precision was also explored.

A serious issue encountered during the conversion of models to double precision in ONNX is the limitation of ML operators ai.onnx.ml.LinearRegressor, ai.onnx.ml.SVMRegressor, ai.onnx.ml.TreeEnsembleRegressor: their parameters and output values are of float type. Essentially, these are precision reduction components and their execution in double precision calculations is doubtful. For this reason, the ONNX Runtime library did not implement some operators for ONNX models in double precision (errors of NOT_IMPLEMENTED nature might occur: 'Could not find an implementation for the node LinearRegressor:LinearRegressor(1)', 'Could not find an implementation for SVMRegressor(1) node with name 'SVM', and so on). Thus, within the current ONNX specification, complete double precision operation for these ML operators is impossible.

For linear regression models, the sklearn-onnx converter managed to bypass the LinearRegressor limitation: MatMul() and Add() ONNX operators are used instead. Thanks to this approach, the first 30 models from the previous list were successfully converted into ONNX models with calculations in double precision, and these models retained the accuracy of the original models in double precision.

However, for more complex ML operators like SVMRegressor and TreeEnsembleRegressor, this was not achieved. Therefore, models like AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor, and SVR are currently available only in ONNX models with calculations in float.

Summary

The article covered 45 regression models from the Scikit-learn library version 1.3.2 and their conversion results into ONNX format for both float and double precision computations.

Out of all the reviewed models, 5 proved to be complex for ONNX conversion. These models include DummyRegressor, KernelRidge, IsotonicRegression, PLSCanonical, and CCA. Their complex structure or logic may require additional adaptation for successful ONNX conversion.

The remaining 40 regression models were successfully transformed into ONNX format for float. Among them, 30 models were also successfully converted into ONNX format for double precision, retaining their accuracy

Due to the limitation in ML operators for SVMRegressor and TreeEnsembleRegressor, the modles AdaBoostRegressor, BaggingRegressor, DecisionTreeRegressor, ExtraTreeRegressor, ExtraTreesRegressor, NuSVR, RandomForestRegressor, GradientBoostingRegressor, HistGradientBoostingRegressor and SVR are currently only available in ONNX models with computations in float.

All the scripts from the article are also available in the public project MQL5\Shared Projects\Scikit.Regression.ONNX.