MQL5 中的统计分布 - 充分利用 R 并使其更快

MQL5 标准库已经补充了大量的来自 R 语言的数学函数。此外, 与 R 语言的初始版本相比, 处理速度提升了 3 到 7 倍。与此同时, 修正了 R 语言中已发现的某些函数的实现错误。

目录

1. 用于计算数组元素统计特性的函数
   
   
   • 1.1. MathMean()
   • 1.2. MathVariance()
   • 1.3. MathSkewness()
   • 1.4. MathKurtosis()
   • 1.5. MathMoments()
   • 1.6. MathMedian()
   • 1.7. MathStandardDeviation()
   • 1.8. MathAverageDeviation()


2. 使用统计分布的函数
   
   2.1. 正态分布
   
   • 2.1.1. MathProbabilityDensityNormal()
   • 2.1.2. MathCumulativeDistributionNormal()
   • 2.1.3. MathQuantileNormal()
   • 2.1.4. MathRandomNormal()
   • 2.1.5. MathMomentsNormal()
   
   2.2. 对数正态分布
   
   • 2.2.1. MathProbabilityDensityLognormal()
   • 2.2.2. MathCumulativeDistributionLognormal()
   • 2.2.3. MathQuantileLognormal()
   • 2.2.4. MathRandomLognormal()
   • 2.2.5. MathMomentsLognormal()
   
   2.3. β 分布
   
   • 2.3.1. MathProbabilityDensityBeta()
   • 2.3.2. MathCumulativeDistributionBeta()
   • 2.3.3. MathQuantileBeta()
   • 2.3.4. MathRandomBeta()
   • 2.3.5. MathMomentsBeta()
   
   2.4. 非中心 β 分布
   
   • 2.4.1. MathProbabilityDensityNoncentralBeta()
   • 2.4.2. MathCumulativeDistributionNoncentralBeta()
   • 2.4.3. MathQuantileNoncentralBeta()
   • 2.4.4. MathRandomNoncentralBeta()
   • 2.4.5. MathMomentsNoncentralBeta()
   
   2.5. γ 分布
   
   • 2.5.1. MathProbabilityDensityGamma()
   • 2.5.2. MathCumulativeDistributionGamma()
   • 2.5.3. MathQuantileGamma()
   • 2.5.4. MathRandomGamma()
   • 2.5.5. MathMomentsGamma()
   
   2.6. 卡方分布
   
   • 2.6.1. MathProbabilityDensityChiSquare()
   • 2.6.2. MathCumulativeDistributionChiSquare()
   • 2.6.3. MathQuantileChiSquare()
   • 2.6.4. MathRandomChiSquare()
   • 2.6.5. MathMomentsChiSquare()
   
   2.7. 非中心卡方分布
   
   • 2.7.1. MathProbabilityDensityNoncentralChiSquare()
   • 2.7.2. MathCumulativeDistributionNoncentralChiSquare()
   • 2.7.3. MathQuantileNoncentralChiSquare()
   • 2.7.4. MathRandomNoncentralChiSquare()
   • 2.7.5. MathMomentsNoncentralChiSquare()
   
   2.8. 指数分布
   
   • 2.8.1. MathProbabilityDensityExponential()
   • 2.8.2. MathCumulativeDistributionExponential()
   • 2.8.3. MathQuantileExponential()
   • 2.8.4. MathRandomExponential()
   • 2.8.5. MathMomentsExponential()
   
   2.9. F-分布
   
   • 2.9.1. MathProbabilityDensityF()
   • 2.9.2. MathCumulativeDistributionF()
   • 2.9.3. MathQuantileF()
   • 2.9.4. MathRandomF()
   • 2.9.5. MathMomentsF()
   
   2.10. 非中心 F-分布
   
   • 2.10.1. MathProbabilityDensityNoncentralF()
   • 2.10.2. MathCumulativeDistributionNoncentralF()
   • 2.10.3. MathQuantileNoncentralF()
   • 2.10.4. MathRandomNoncentralF()
   • 2.10.5. MathMomentsNoncentralF()
   
   2.11. t-分布
   
   • 2.11.1. MathProbabilityDensityT()
   • 2.11.2. MathCumulativeDistributionT()
   • 2.11.3. MathQuantileT()
   • 2.11.4. MathRandomT()
   • 2.11.5. MathMomentsT()
   
   2.12. 非中心 t-分布
   
   • 2.12.1. MathProbabilityDensityNoncentralT()
   • 2.12.2. MathCumulativeDistributionNoncentralT()
   • 2.12.3. MathQuantileNoncentralT()
   • 2.12.4. MathRandomNoncentralT()
   • 2.12.5. MathMomentsNoncentralT()
   
   2.13. 逻辑斯谛分布
   
   • 2.13.1. MathProbabilityDensityLogistic()
   • 2.13.2. MathCumulativeDistributionLogistic()
   • 2.13.3. MathQuantileLogistic()
   • 2.13.4. MathRandomLogistic()
   • 2.13.5. MathMomentsLogistic()
   
   2.14. 柯西分布
   
   • 2.14.1. MathProbabilityDensityCauchy()
   • 2.14.2. MathCumulativeDistributionCauchy()
   • 2.14.3. MathQuantileCauchy()
   • 2.14.4. MathRandomCauchy()
   • 2.14.5. MathMomentsCauchy()
   
   2.15. 均匀分布
   
   • 2.15.1. MathProbabilityDensityUniform()
   • 2.15.2. MathCumulativeDistributionUniform()
   • 2.15.3. MathQuantileUniform()
   • 2.15.4. MathRandomUniform()
   • 2.15.5. MathMomentsUniform()
   
   2.16. 威布尔分布
   
   • 2.16.1. MathProbabilityDensityWeibull()
   • 2.16.2. MathCumulativeDistributionWeibull()
   • 2.16.3. MathQuantileWeibull()
   • 2.16.4. MathRandomWeibull()
   • 2.16.5. MathMomentsWeibull()
   
   2.17. 二项式分布
   
   • 2.17.1. MathProbabilityDensityBinomial()
   • 2.17.2. MathCumulativeDistributionBinomial()
   • 2.17.3. MathQuantileBinomial()
   • 2.17.4. MathRandomBinomial()
   • 2.17.5. MathMomentsBinomial()
   
   2.18. 负二项式分布
   
   • 2.18.1. MathProbabilityDensityNegativeBinomial()
   • 2.18.2. MathCumulativeDistributionNegativeBinomial()
   • 2.18.3. MathQuantileNegativeBinomial()
   • 2.18.4. MathRandomNegativeBinomial()
   • 2.18.5. MathMomentsNegativeBinomial()
   
   2.19. 几何分布
   
   • 2.19.1. MathProbabilityDensityGeometric()
   • 2.19.2. MathCumulativeDistributionGeometric()
   • 2.19.3. MathQuantileGeometric()
   • 2.19.4. MathRandomGeometric()
   • 2.19.5. MathMomentsGeometric()
   
   2.20. 超几何分布
   
   • 2.20.1. MathProbabilityDensityHypergeometric()
   • 2.20.2. MathCumulativeDistributionHypergeometric()
   • 2.20.3. MathQuantileHypergeometric()
   • 2.20.4. MathRandomHypergeometric()
   • 2.20.5. MathMomentsHypergeometric()
   
   2.21. 泊松分布
   
   • 2.21.1. MathProbabilityDensityPoisson()
   • 2.21.2. MathCumulativeDistributionPoisson()
   • 2.21.3. MathQuantilePoisson()
   • 2.21.4. MathRandomPoisson()
   • 2.21.5. MathMomentsPoisson()
   
   
3. 对应于 R 语言的统计函数列表
   
   
4. 函数使用例程
   
   
5. 计算速度比较
   
   
6. 已检测到的 R 语言中的计算误差
   
   
7. 参考文献

概论

R 语言 是统计处理和数据分析的最佳工具之一。

得益于可用性以及对多种统计分布的支持, 它已在各种数据分析和处理中变得普遍。使用概率理论和数学统计的装置, 可以重新审视金融市场数据, 并提供创造交易策略的新机会。运用统计库, 所有这些功能现在均可于 MQL5 中使用。

统计库包含用于计算数据统计特性的函数, 以及用于处理统计分布的函数。

本文研究软件库的主要函数和它们的实际运用例程。

1. 用于计算数组元素统计特性的函数

这组函数计算数组元素的标准特征 (平均值, 方差, 偏度, 峰度, 中值, 均方根和标准偏差)。

1.1. MathMean

函数计算数组元素的平均值 (第一力矩)。出错情况下它返回 NaN (非数字)。R 语言的 mean() 模拟。

double MathMean(
  const double   &array[]         // [输入] 数据数组
);

1.2. MathVariance

函数计算数组元素的方差 (第二力矩)。出错情况下它返回 NaN。R 语言的 var() 模拟。

double MathVariance(
  const double   &array[]         // [输入] 数据数组
);

1.3. MathSkewness

函数计算数组元素的偏斜度 (第三力矩)。出错情况下它返回 NaN。R (e1071 库) 语言的 skewness() 模拟。

double MathSkewness(
  const double   &array[]         // [输入] 数据数组
);

1.4. MathKurtosis

函数计算数组元素的峰度 (第四力矩)。出错情况下它返回 NaN。R (e1071 库) 语言的 kurtosis() 模拟。

double MathKurtosis(
  const double   &array[]         // [输入] 数据数组
);

1.5. MathMoments

函数计算数组元素的前 4 个力矩 (均值, 方差, 偏度, 峰度)。如果力矩已计算成功则返回 true, 否则 false。

bool MathMoments(
  const double   &array[],         // [输入] 数据数组
  double         &mean,            // [输出] 均值变量 (第一力矩)
  double         &variance,        // [输出] 方差变量 (第二力矩)
  double         &skewness,        // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,        // [输出] 峰度变量 (第四力矩)
  const int      start=0,          // [输入] 初始计算索引
  const int      count=WHOLE_ARRAY // [输入] 用于计算的元素数量

);

1.6. MathMedian

函数计算数组元素的中值。出错情况下它返回 NaN。R 语言的 median() 模拟。

double MathMedian(
  double         &array[]         // [输入] 数据数组
);

1.7. MathStandardDeviation

函数计算数组元素的标准偏差。出错情况下它返回 NaN。R 语言的 sd() 模拟。

double MathStandardDeviation(
  const double   &array[]         // [输入] 数据数组
);

1.8. MathAverageDeviation

函数计算数组元素的平均绝对偏差。出错情况下它返回 NaN。R 语言的 aad() 模拟。

double MathAverageDeviation(
  const double   &array[]         // [输入] 数据数组
);

所有计算峰度的函数都使用围绕正态分布的过量峰度 (过量峰度=峰度-3), 即正态分布的过量峰度为零。

如果分布峰值围绕期望值很尖锐, 则为正, 而峰值很平坦, 则为负。

2. 统计分布

MQL5 的统计库包含 5 个用于处理统计分布的函数:

1. 计算概率密度 (MathProbabilityDensityX() 函数);
   
2. 计算概率 (MathCumulativeDistributionX() 函数);
   概率分布函数等于随机变量落在范围内 (-inf; x) 的概率。
   
3. 计算分布四分位数 (MathQuantileX() 函数);
   对于给定的分布参数, 分布的四分位数 x 对应于一个落在具有指定概率的 (-int, x) 范围内的随机值。
   
4. 生成具有指定分布的随机数 (MathRandomX() 函数);
5. 计算分布的理论力矩 (MathMomentsX() 函数);

2.1. 正态分布

2.1.1. MathProbabilityDensityNormal

函数以 mu 和 sigma 为参数, 计算随机变量 x 的正态分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数均值 (期望值)
  const double   sigma,       // [输入] 分布参数的 sigma (均方根)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量 x 的正态分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数均值 (期望值)
  const double   sigma,       // [输入] 分布参数的 sigma (均方根)
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的正态分布概率密度函数值。出错情况下它返回 false。R 语言的 dnorm() 模拟。

bool MathProbabilityDensityNormal(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数均值 (期望值)
  const double   sigma,       // [输入] 分布参数的 sigma (均方根)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的正态分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityNormal(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数均值 (期望值)
  const double   sigma,       // [输入] 分布参数的 sigma (均方根)
  double         &result[]    // [输出] 概率密度值的数组
);

2.1.2. MathCumulativeDistributionNormal

函数以 mu 和 sigma 为参数, 计算随机变量 x 的正态分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量 x 的正态分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的正态分布函数值。出错情况下它返回 false。R 语言的 pnorm() 模拟。

bool MathCumulativeDistributionNormal(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的正态分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionNormal(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.1.3. MathQuantileNormal

对于指定概率, 函数以 mu 和 sigma 为参数, 计算随机变量 x 的逆正态分布函数值。出错情况下它返回 NaN。

double MathQuantileNormal(
  const double   probability, // [输入] 随机变量概率值
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  const bool     tail,        // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,    // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code  // [输出] 错误代码变量
);

对于指定概率, 函数以 mu 和 sigma 为参数, 计算随机变量 x 的逆正态分布函数值。出错情况下它返回 NaN。

double MathQuantileNormal(
  const double   probability, // [输入] 随机变量概率值
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  int            &error_code  // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 mu 和 sigma 为参数, 计算逆正态分布函数值。出错情况下它返回 false。R 语言的 qnorm() 模拟。

bool MathQuantileNormal(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   mu,            // [输入] 期望值
  const double   sigma,         // [输入] 均方根偏离
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 mu 和 sigma 为参数, 计算逆正态分布函数值。出错情况下它返回 false。

bool MathQuantileNormal(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   mu,            // [输入] 期望值
  const double   sigma,         // [输入] 均方根偏离
  double         &result[]      // [输出] 具有分位数值的数组
);

2.1.4. MathRandomNormal

函数根据参数为 mu 和 sigma 的正态定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomNormal(
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 mu 和 sigma 的正态定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rnorm() 模拟。

bool MathRandomNormal(
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.1.5. MathMomentsNormal

函数计算正态分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsNormal(
  const double   mu,          // [输入] 期望值
  const double   sigma,       // [输入] 均方根偏离
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.2. 对数正态分布

2.2.1. MathProbabilityDensityLognormal

函数以 mu 和 sigma 为参数, 计算随机变量 x 的对数正态分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityLognormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量 x 的对数正态分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityLognormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的对数正态分布概率密度函数值。出错情况下它返回 NaN。R 语言的 dlnorm() 模拟。

bool MathProbabilityDensityLognormal(
  const double   &x[],        // [输入] 随机变量值数组
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的对数正态分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityLognormal(
  const double   &x[],        // [输入] 随机变量值数组
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  double         &result[]    // [输出] 概率密度值的数组
);

2.2.2. MathCumulativeDistributionLognormal

函数以 mu 和 sigma 为参数, 计算随机变量 x 的对数正态分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionLognormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量 x 的对数正态分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionLognormal(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的对数正态分布函数值。出错情况下它返回 false。R 语言的 plnorm() 模拟。

bool MathCumulativeDistributionLognormal(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的对数正态分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionLognormal(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.2.3. MathQuantileLognormal

函数以 mu 和 sigma 为参数, 计算指定概率的逆对数正态分布函数值。出错情况下它返回 NaN。

double MathQuantileLognormal(
  const double   probability, // [输入] 随机变量发生概率值
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  const bool     tail,        // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,    // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算指定概率的逆对数正态分布函数值。出错情况下它返回 NaN。

double MathQuantileLognormal(
  const double   probability, // [输入] 随机变量发生概率值
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  int            &error_code  // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 mu 和 sigma 为参数, 计算逆对数正态分布函数值。出错情况下它返回 false。R 语言的 qlnorm() 模拟。

bool MathQuantileLognormal(
  const double   &probability[], // [输入] 随机变量概率值数组
  const double   mu,             // [输入] 期望值的对数 (对数均值)
  const double   sigma,          // [输入] 均方根偏离的对数 (对数标准偏离)
  const bool     tail,           // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,       // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]       // [输出] 分位数值数组
);

对于指定的概率值数组 'probability[]', 函数以 mu 和 sigma 为参数, 计算逆对数正态分布函数值。出错情况下它返回 false。

bool MathQuantileLognormal(
  const double   &probability[], // [输入] 随机变量概率值数组
  const double   mu,             // [输入] 期望值的对数 (对数均值)
  const double   sigma,          // [输入] 均方根偏离的对数 (对数标准偏离)
  double         &result[]       // [输出] 分位数值数组
);

2.2.4. MathRandomLognormal

函数根据参数为 mu 和 sigma 的对数正态定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomLognormal(
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 mu 和 sigma 的对数正态定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rlnorm() 模拟。

bool MathRandomLognormal(
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.2.5. MathMomentsLognormal

函数计算对数正态分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsLognormal(
  const double   mu,          // [输入] 期望值的对数 (对数均值)
  const double   sigma,       // [输入] 均方根偏离的对数 (对数标准偏离)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.3. β 分布

2.3.1. MathProbabilityDensityBeta

函数以 a 和 b 为参数, 计算随机变量 x 的 β 分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的 β 分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 β 分布概率密度函数值。出错情况下它返回 false。R 语言的 dbeta() 模拟。

bool MathProbabilityDensityBeta(
  const double   &x[],        // [输入] 随机变量值数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 β 分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityBeta(
  const double   &x[],        // [输入] 随机变量值数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  double         &result[]    // [输出] 概率密度值的数组
);

2.3.2. MathCumulativeDistributionlBeta

函数以 a 和 b 为参数, 计算随机变量 x 的 β 分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的 β 分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 β 分布概率密度函数值。出错情况下它返回 false。R 语言的 pbeta() 模拟。

bool MathCumulativeDistributionBeta(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 β 分布概率密度函数值。出错情况下它返回 false。

bool MathCumulativeDistributionBeta(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.3.3. MathQuantileBeta

对于指定概率, 函数以 a 和 b 为参数, 计算随机变量 x 的逆 β 分布函数值。出错情况下它返回 NaN。

double MathQuantileBeta(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 a 和 b 为参数, 计算随机变量 x 的逆 β 分布函数值。出错情况下它返回 NaN。

double MathQuantileBeta(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆 β 分布函数值。出错情况下它返回 false。R 语言的 qbeta() 模拟。

bool MathQuantileBeta(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆 β 分布函数值。出错情况下它返回 false。

bool MathQuantileBeta(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.3.4. MathRandomBeta

函数根据参数为 a 和 b 的 β 分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomBeta(
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 a 和 b 的 β 分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rbeta() 模拟。

bool MathRandomBeta(
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.3.5. MathMomentsBeta

函数计算 β 分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsBeta(
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.4. 非中心 β 分布

2.4.1. MathProbabilityDensityNoncentralBeta

函数以 a 和 b 为参数, 计算随机变量 x 的非中心 β 分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的非中心 β 分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的非中心 β 分布概率密度函数值。出错情况下它返回 false。R 语言的 dbeta() 模拟。

bool MathProbabilityDensityNoncentralBeta(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的非中心 β 分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityNoncentralBeta(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  double         &result[]    // [输出] 概率密度值的数组
);

2.4.2. MathCumulativeDistributionNoncentralBeta

函数以 a 和 b 为参数, 计算随机变量 x 的非中心 β 分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的非中心 β 分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralBeta(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的非中心 β 分布概率密度函数值。出错情况下它返回 false。R 语言的 pbeta() 模拟。

bool MathCumulativeDistributionNoncentralBeta(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的非中心 β 分布概率密度函数值。出错情况下它返回 false。

bool MathCumulativeDistributionNoncentralBeta(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.4.3. MathQuantileNoncentralBeta

函数以 a 和 b 为参数, 计算随机变量 x 的非中心 β 分布逆概率分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralBeta(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,        // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的非中心 β 分布逆概率分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralBeta(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,        // [输入] 非中心参数
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 a, b 和 lambda 为参数, 计算非中心 β 分布逆概率分布函数值。出错情况下它返回 false。R 语言的 qbeta() 模拟。

bool MathQuantileNoncentralBeta(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,        // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 a, b 和 lambda 为参数, 计算非中心 β 分布逆概率分布函数值。出错情况下它返回 false。

bool MathQuantileNoncentralBeta(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] β 分布的第一个参数 (shape1)
  const double   b,             // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,        // [输入] 非中心参数
  double         &result[]      // [输出] 具有分位数值的数组
);

2.4.4. MathRandomNoncentralBeta

函数根据参数为 a, b, lambda 的非中心 β 分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomNoncentralBeta(
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 a, b 和 lambda 的非中心 β 分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rbeta() 模拟。

bool MathRandomNoncentralBeta(
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.4.5. MathMomentsNoncentralBeta

函数计算参数为 a, b, lambda 的非中心 β 分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

double MathMomentsNoncentralBeta(
  const double   a,           // [输入] β 分布的第一个参数 (shape1)
  const double   b,           // [输入] β 分布的第二个参数 (shape2)
  const double   lambda,      // [输入] 非中心参数
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.5. γ 分布

2.5.1. MathProbabilityDensityGamma

函数以 a 和 b 为参数, 计算随机变量 x 的 γ 分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityGamma(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的 γ 分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityGamma(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 γ 分布概率密度函数值。出错情况下它返回 false。R 语言的 dgamma() 模拟。

bool MathProbabilityDensityGamma(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 γ 分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityGamma(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  double         &result[]    // [输出] 概率密度值的数组
);

2.5.2. MathCumulativeDistributionGamma

函数以 a 和 b 为参数, 计算随机变量 x 的 γ 分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionGamma(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的 γ 分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionGamma(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 γ 分布函数值。出错情况下它返回 false。R 语言的 pgamma() 模拟。

bool MathCumulativeDistributionGamma(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的 γ 分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionGamma(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.5.3. MathQuantileGamma

对于指定概率, 函数以 a 和 b 为参数, 计算随机变量 x 的逆 γ 分布函数值。出错情况下它返回 NaN。

double MathQuantileGamma(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] 第一个 分布参数 (shape)
  const double   b,             // [输入] 第二个分布参数 (scale)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 a 和 b 为参数, 计算随机变量 x 的逆 γ 分布函数值。出错情况下它返回 NaN。

double MathQuantileGamma(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] 第一个 分布参数 (shape)
  const double   b,             // [输入] 第二个分布参数 (scale)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆 γ 分布函数值。出错情况下它返回 false。R 语言的 qgamma() 模拟。

bool MathQuantileGamma(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 第一个 分布参数 (shape)
  const double   b,             // [输入] 第二个分布参数 (scale)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆 γ 分布函数值。出错情况下它返回 false。

bool MathQuantileGamma(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 第一个 分布参数 (shape)
  const double   b,             // [输入] 第二个分布参数 (scale)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.5.4. MathRandomGamma

函数根据参数为 a 和 b 的 γ 分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomGamma(
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 a 和 b 的 γ 分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rgamma() 模拟。

bool MathRandomGamma(
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.5.5. MathMomentsGamma

函数计算参数为 a, b, lambda 的非中心 γ 分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsGamma(
  const double   a,           // [输入] 第一个 分布参数 (shape)
  const double   b,           // [输入] 第二个分布参数 (scale)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.6. 卡方分布

2.6.1. MathProbabilityDensityChiSquare

函数以 nu 为参数, 计算随机变量 x 的卡方分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量 x 的卡方分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量数组 x[] 的卡方分布概率密度函数值。出错情况下它返回 false。R 语言的 dchisq() 模拟。

bool MathProbabilityDensityChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 nu 为参数, 计算随机变量数组 x[] 的卡方分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  double         &result[]    // [输出] 概率密度值的数组
);

2.6.2. MathCumulativeDistributionChiSquare

函数以 nu 为参数, 计算随机变量 x 的卡方分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量 x 的卡方分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量数组 x[] 的卡方分布概率密度函数值。出错情况下它返回 false。R 语言的 pchisq() 模拟。

bool MathCumulativeDistributionChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 nu 为参数, 计算随机变量数组 x[] 的卡方分布概率密度函数值。出错情况下它返回 false。

bool MathCumulativeDistributionChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.6.3. MathQuantileChiSquare

对于指定概率, 函数计算逆卡方分布函数值。出错情况下它返回 NaN。

double MathQuantileChiSquare(  
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数计算逆卡方分布函数值。出错情况下它返回 NaN。

double MathQuantileChiSquare(  
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu,            // [输入] 分布参数 (自由度数值)
  int            &error_code    // [输出] 错误代码变量
);

对于指定数组 'probability[]', 函数计算逆卡方分布函数值。出错情况下它返回 false。R 语言的 qchisq() 模拟。

bool MathQuantileChiSquare(  
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定数组 'probability[]', 函数计算逆卡方分布函数值。出错情况下它返回 false。

bool MathQuantileChiSquare(  
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.6.4. MathRandomChiSquare

函数根据参数为 nu 的卡方分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomChiSquare(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 nu 的卡方分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rchisq() 模拟。

bool MathRandomChiSquare(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.6.5. MathMomentsChiSquare

函数计算参数为 nu 的卡方分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsChiSquare(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.7. 非中心卡方分布

2.7.1. MathProbabilityDensityNoncentralChiSquare

函数以 nu 和 sigma 为参数, 计算随机变量 x 的非中心卡方分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 和 sigma 为参数, 计算随机变量 x 的非中心卡方分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 和 sigma 为参数, 计算随机变量数组 x[] 的非中心卡方分布概率密度函数值。出错情况下它返回 false。R 语言的 dchisq() 模拟。

bool MathProbabilityDensityNoncentralChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 nu 和 sigma 为参数, 计算随机变量数组 x[] 的非中心卡方分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityNoncentralChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  double         &result[]    // [输出] 概率密度值的数组
);

2.7.2. MathCumulativeDistributionNoncentralChiSquare

函数以 nu 和 sigma 为参数, 计算随机变量 x 的非中心卡方分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 和 sigma 为参数, 计算随机变量 x 的非中心卡方分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralChiSquare(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 和 sigma 为参数, 计算随机变量数组 x[] 的非中心卡方分布概率密度函数值。出错情况下它返回 false。R 语言的 pchisq() 模拟。

bool MathCumulativeDistributionNoncentralChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 nu 和 sigma 为参数, 计算随机变量数组 x[] 的非中心卡方分布概率密度函数值。出错情况下它返回 false。

bool MathCumulativeDistributionNoncentralChiSquare(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.7.3. MathQuantileNoncentralChiSquare

对于指定概率, 函数以 nu 和 sigma 为参数, 计算逆非中心卡方分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralChiSquare(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 nu 和 sigma 为参数, 计算逆非中心卡方分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralChiSquare(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  int            &error_code    // [输出] 错误代码变量
);

对于指定 'probability[]', 函数以 nu 和 sigma 为参数, 计算逆非中心卡方分布函数值。出错情况下它返回 false。R 语言的 qchisq() 模拟。

bool MathQuantileNoncentralChiSquare(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定 'probability[]', 函数以 nu 和 sigma 为参数, 计算逆非中心卡方分布函数值。出错情况下它返回 false。

bool MathQuantileNoncentralChiSquare(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  double         &result[]      // [输出] 具有分位数值的数组
);

2.7.4. MathRandomNoncentralChiSquare

函数根据参数为 nu 和 sigma 的非中心卡方分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomNoncentralChiSquare(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 nu 和 sigma 的非中心卡方分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rchisq() 模拟。

bool MathRandomNoncentralChiSquare(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.7.5. MathMomentsNoncentralChiSquare

函数计算参数为 nu 和 sigma 的非中心卡方分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsNoncentralChiSquare(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.8. 指数分布

2.8.1. MathProbabilityDensityExponential

函数以 mu 为参数, 计算随机变量 x 的指数分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityExponential(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 (期望值)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 为参数, 计算随机变量 x 的指数分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityExponential(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 (期望值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 为参数, 计算随机变量数组 x[] 的指数分布概率密度函数值。出错情况下它返回 false。R 语言的 dexp() 模拟。

bool MathProbabilityDensityExponential(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 (期望值)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 mu 为参数, 计算随机变量数组 x[] 的指数分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityExponential(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 (期望值)
  double         &result[]    // [输出] 概率密度值的数组
);

2.8.2. MathCumulativeDistributionExponential

函数以 mu 为参数, 计算随机变量 x 的概率指数分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionExponential(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 (期望值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 为参数, 计算随机变量 x 的概率指数分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionExponential(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 (期望值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 为参数, 计算随机变量 x 的概率指数分布函数值。出错情况下它返回 false。R 语言的 pexp() 模拟。

bool MathCumulativeDistributionExponential(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 (期望值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 mu 为参数, 计算随机变量 x 的概率指数分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionExponential(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 (期望值)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.8.3. MathQuantileExponential

对于指定概率, 函数以 mu 为参数, 计算逆指数分布函数值。出错情况下它返回 NaN。

double MathQuantileExponential(
  const double   probability,   // [输入] 随机变量发生概率
  const double   mu,            // [输入] 分布参数 (期望值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 mu 为参数, 计算逆指数分布函数值。出错情况下它返回 NaN。

double MathQuantileExponential(
  const double   probability,   // [输入] 随机变量发生概率
  const double   mu,            // [输入] 分布参数 (期望值)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 mu 为参数, 计算逆指数分布函数值。出错情况下它返回 false。R 语言的 qexp() 模拟。

bool MathQuantileExponential(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   mu,            // [输入] 分布参数 (期望值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 mu 为参数, 计算逆指数分布函数值。出错情况下它返回 false。

bool MathQuantileExponential(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   mu,            // [输入] 分布参数 (期望值)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.8.4. MathRandomExponential

函数根据参数为 mu 的指数分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomExponential(
  const double   mu,          // [输入] 分布参数 (期望值)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 mu 的指数分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rexp() 模拟。

bool MathRandomExponential(
  const double   mu,          // [输入] 分布参数 (期望值)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.8.5. MathMomentsExponential

函数计算参数为 mu 的指数分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsExponential(
  const double   mu,          // [输入] 分布参数 (期望值)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.9. F-分布

2.9.1. MathProbabilityDensityF

函数以 nu1 和 nu2 为参数, 计算随机变量 x 的费舍尔 F-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1 和 nu2 为参数, 计算随机变量 x 的费舍尔 F-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1 和 nu2 为参数, 计算随机变量数组 x[] 的费舍尔 F-分布概率密度函数值。出错情况下它返回 false。R 语言的 df() 模拟。

bool MathProbabilityDensityF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 nu1 和 nu2 为参数, 计算随机变量数组 x[] 的费舍尔 F-分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  double         &result[]    // [输出] 概率密度值的数组
);

2.9.2. MathCumulativeDistributionF

函数以 nu1 和 nu2 为参数, 计算随机变量 x 的费舍尔 F-分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1 和 nu2 为参数, 计算随机变量 x 的费舍尔 F-分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1 和 nu2 为参数, 计算随机变量数组 x[] 的费舍尔 F-分布概率密度函数值。出错情况下它返回 false。R 语言的 pf() 模拟。

bool MathCumulativeDistributionF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 nu1 和 nu2 为参数, 计算随机变量数组 x[] 的费舍尔 F-分布概率密度函数值。出错情况下它返回 false。

bool MathCumulativeDistributionF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.9.3. MathQuantileF

对于指定概率, 函数以 mu 为参数, 计算逆费舍尔 F-分布函数值。出错情况下它返回 NaN。

double MathQuantileF(
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 mu 为参数, 计算逆费舍尔 F-分布函数值。出错情况下它返回 NaN。

double MathQuantileF(
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 mu 为参数, 计算逆费舍尔 F-分布函数值。出错情况下它返回 false。R 语言的 qf() 模拟。

bool MathQuantileF(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 分位数值的数组
);

对于指定概率, 函数以 mu 为参数, 计算逆费舍尔 F-分布函数值。出错情况下它返回 false。

bool MathQuantileF(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  double         &result[]      // [输出] 分位数值的数组
);

2.9.4. MathRandomF

函数根据参数为 nu1 和 nu2 的费舍尔 F-分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomF(
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 nu1 和 nu2 的费舍尔 F-分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rf() 模拟。

bool MathRandomF(
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.9.5. MathMomentsF

函数计算参数为 nu1 和 nu2 的费舍尔 F-分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsF(
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.10. 非中心 F-分布

2.10.1. MathProbabilityDensityNoncentralF

函数以 nu1 和 nu2 为参数, 计算随机变量 x 的非中心费舍尔 F-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1 和 nu2 为参数, 计算随机变量 x 的非中心费舍尔 F-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1, nu2 和 sigma 为参数, 计算随机变量数组 x[] 的非中心费舍尔 F-分布概率密度函数值。出错情况下它返回 false。R 语言的 df() 模拟。

double MathProbabilityDensityNoncentralF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 nu1, nu2 和 sigma 为参数, 计算随机变量数组 x[] 的非中心费舍尔 F-分布概率密度函数值。出错情况下它返回 false。

double MathProbabilityDensityNoncentralF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  double         &result[]    // [输出] 概率密度值的数组
);

2.10.2. MathCumulativeDistributionlNoncentralF

函数以 nu1, nu2, 和 sigma 为参数, 计算随机变量 x 的非中心费舍尔 F-分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1, nu2, 和 sigma 为参数, 计算随机变量 x 的非中心费舍尔 F-分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralF(
  const double   x,           // [输入] 随机变量值
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu1, nu2, 和 sigma 为参数, 计算随机变量 x 的非中心费舍尔 F-分布概率分布函数值。出错情况下它返回 false。R 语言的 pf() 模拟。

bool MathCumulativeDistributionNoncentralF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 nu1, nu2, 和 sigma 为参数, 计算随机变量 x 的非中心费舍尔 F-分布概率分布函数值。出错情况下它返回 NaN。

bool MathCumulativeDistributionNoncentralF(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.10.3. MathQuantileNoncentralF

对于指定概率, 函数以 nu1, nu2 和 sigma 为参数, 计算逆非中心费舍尔 F-分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralF(
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 nu1, nu2 和 sigma 为参数, 计算逆非中心费舍尔 F-分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralF(
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 nu1, nu2 和 sigma 为参数, 计算逆非中心费舍尔 F-分布函数值。出错情况下它返回 false。R 语言的 qf() 模拟。

bool MathQuantileNoncentralF(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定概率, 函数以 nu1, nu2 和 sigma 为参数, 计算逆非中心费舍尔 F-分布函数值。出错情况下它返回 false。

bool MathQuantileNoncentralF(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  double         &result[]      // [输出] 具有分位数值的数组
);

2.10.4. MathRandomNoncentralF

函数根据参数为 nu1, nu2 和 sigma 的非中心费舍尔 F-分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomNoncentralF(
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  int            &error_code    // [输出] 错误代码变量
);

函数根据参数为 nu1, nu2 和 sigma 的非中心费舍尔 F-分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rf() 模拟。

bool MathRandomNoncentralF(
  const double   nu1,           // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,           // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,         // [输入] 非中心参数
  double         &result[]      // [输出] 具有分位数值的数组
);

2.10.5. MathMomentsNoncentralF

函数计算参数为 nu1, nu2 和 sigma 的非中心费舍尔 F-分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsNoncentralF(
  const double   nu1,         // [输入] 第一个分布参数 (自由度数值)
  const double   nu2,         // [输入] 第二个分布参数 (自由度数值)
  const double   sigma,       // [输入] 非中心参数
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
e.)

2.11. t-分布

2.11.1. MathProbabilityDensityT

函数以 nu 为参数, 计算随机变量 x 的学生 t-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityT(
  const double   x,             // [输入] 随机变量值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const bool     log_mode,      // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code    // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量 x 的学生 t-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityT(
  const double   x,             // [输入] 随机变量值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  int            &error_code    // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量数组 x[] 的学生 t-分布概率密度函数值。出错情况下它返回 false。R 语言的 dt() 模拟。

bool MathProbabilityDensityT(
  const double   &x[],          // [输入] 随机变量值的数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const bool     log_mode,      // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]      // [输出] 概率密度值的数组
);

函数以 nu 为参数, 计算随机变量数组 x[] 的学生 t-分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityT(
  const double   &x[],          // [输入] 随机变量值的数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  double         &result[]      // [输出] 概率密度值的数组
);

2.11.2. MathCumulativeDistributionT

函数以 nu 为参数, 计算随机变量 x 的学生 t-分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionT(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量 x 的学生 t-分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionT(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量数组 x[] 的学生 t-分布函数值。出错情况下它返回 false。R 语言的 pt() 模拟。

bool MathCumulativeDistributionT(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 nu 为参数, 计算随机变量数组 x[] 的学生 t-分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionT(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.11.3. MathQuantileT

对于指定概率, 函数以 nu 为参数, 计算逆学生 t-分布函数值。出错情况下它返回 NaN。

double MathQuantileT(
  const double   probability,   // [输入] 随机变量发生概率
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 nu 为参数, 计算逆学生 t-分布函数值。出错情况下它返回 NaN。

double MathQuantileT(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的 'probability[]' 数组, 函数以 nu 为参数, 计算逆学生 t-分布函数值。出错情况下它返回 false。R 语言的 qt() 模拟。

bool MathQuantileT(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的 'probability[]' 数组, 函数以 nu 为参数, 计算逆学生 t-分布函数值。出错情况下它返回 false。

bool MathQuantileT(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.11.4. MathRandomT

函数根据参数为 nu 的学生 t-分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomT(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 nu 的学生 t-分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rt() 模拟。

bool MathRandomT(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.11.5. MathMomentsT

函数计算参数为 nu 的学生 t-分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

double MathMomentsT(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.12. 非中心 t-分布

2.12.1. MathProbabilityDensityNoncentralT

函数以 nu 为参数, 计算随机变量 x 的非中心学生 t-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralT(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量 x 的非中心学生 t-分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNoncentralT(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 为参数, 计算随机变量数组 x[] 的非中心学生 t-分布概率密度函数值。出错情况下它返回 false。R 语言的 dt() 模拟。

bool MathProbabilityDensityNoncentralT(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 nu 为参数, 计算随机变量数组 x[] 的非中心学生 t-分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityNoncentralT(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  double         &result[]    // [输出] 概率密度值的数组
);

2.12.2. MathCumulativeDistributionlNoncentralT

函数以 nu 和 delta 为参数, 计算随机变量 x 的非中心学生 t-分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralT(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 和 delta 为参数, 计算随机变量 x 的非中心学生 t-分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNoncentralT(
  const double   x,           // [输入] 随机变量值
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  int            &error_code  // [输出] 错误代码变量
);

函数以 nu 和 delta 为参数, 计算随机变量数组 x[] 的非中心学生 t-分布概率分布函数值。出错情况下它返回 false。R 语言的 pt() 模拟。

bool MathCumulativeDistributionNoncentralT(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 nu 和 delta 为参数, 计算随机变量数组 x[] 的非中心学生 t-分布概率分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionNoncentralT(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.12.3. MathQuantileNoncentralT

对于指定概率, 函数以 nu 和 delta 为参数, 计算逆非中心学生 t-分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralT(
  const double   probability,   // |输入] 随机变量发生概率值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   delta,         // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 nu 和 delta 为参数, 计算逆非中心学生 t-分布函数值。出错情况下它返回 NaN。

double MathQuantileNoncentralT(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   delta,         // [输入] 非中心参数
  int            &error_code    // [输出] 错误代码变量
);

对于指定 'probability[]', 函数以 nu 和 sigma 为参数, 计算逆非中心学生 t-分布函数值。出错情况下它返回 false。R 语言的 qt() 模拟。

bool MathQuantileNoncentralT(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   delta,         // [输入] 非中心参数
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定 'probability[]', 函数以 nu 和 sigma 为参数, 计算逆非中心学生 t-分布函数值。出错情况下它返回 false。

bool MathQuantileNoncentralT(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   delta,         // [输入] 非中心参数
  double         &result[]      // [输出] 具有分位数值的数组
);

2.12.4. MathRandomNoncentralT

函数根据参数为 nu 和 delta 的非中心学生 t-分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomNoncentralT(
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   delta,         // [输入] 非中心参数
  int            &error_code    // [输出] 错误代码变量
);

函数根据参数为 nu 和 delta 的非中心学生 t-分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rt() 模拟。

bool MathRandomNoncentralT(
  const double   nu,            // [输入] 分布参数 (自由度数值)
  const double   delta,         // [输入] 非中心参数
  const int      data_count,    // [输入] 所需数据数量
  double         &result[]      // [输出] 伪随机变量值数组
);

2.12.5. MathMomentsNoncentralT

函数计算参数为 nu 和 delta 的非中心学生 t-分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

double MathMomentsNoncentralT(
  const double   nu,          // [输入] 分布参数 (自由度数值)
  const double   delta,       // [输入] 非中心参数
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.13. 逻辑斯谛分布

2.13.1. MathProbabilityDensityLogistic

函数以 mu 和 sigma 为参数, 计算随机变量 x 的逻辑斯谛分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityLogistic(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量 x 的逻辑斯谛分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityLogistic(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的逻辑斯谛分布概率密度函数值。出错情况下它返回 false。R 语言的 dlogis() 模拟。

bool MathProbabilityDensityLogistic(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的逻辑斯谛分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityLogistic(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  double         &result[]    // [输出] 概率密度值的数组
);

2.13.2. MathCumulativeDistributionlLogistic

函数以 mu 和 sigma 为参数, 计算随机变量 x 的逻辑斯谛分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionLogistic(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量 x 的逻辑斯谛分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionLogistic(
  const double   x,           // [输入] 随机变量值
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  int            &error_code  // [输出] 错误代码变量
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的逻辑斯谛分布函数值。出错情况下它返回 false。R 语言的 plogis() 模拟。

bool MathCumulativeDistributionLogistic(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 mu 和 sigma 为参数, 计算随机变量数组 x[] 的逻辑斯谛分布函数值。出错情况下它返回 false。R 语言的 plogis() 模拟。

bool MathCumulativeDistributionLogistic(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.13.3. MathQuantileLogistic

对于指定概率, 函数以 mu 和 sigma 为参数, 计算随机变量 x 的逆逻辑斯谛分布函数值。出错情况下它返回 NaN。

double MathQuantileLogistic(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   mu,            // [输入] 分布参数 mean
  const double   sigma,         // [输入] 分布参数 scale
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 mu 和 sigma 为参数, 计算随机变量 x 的逆逻辑斯谛分布函数值。出错情况下它返回 NaN。

double MathQuantileLogistic(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   mu,            // [输入] 分布参数 mean
  const double   sigma,         // [输入] 分布参数 scale
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 mu 和 sigma 为参数, 计算逆逻辑斯谛分布函数值。出错情况下它返回 false。R 语言的 qlogis() 模拟。

bool MathQuantileLogistic(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   mu,            // [输入] 分布参数 mean
  const double   sigma,         // [输入] 分布参数 scale
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 mu 和 sigma 为参数, 计算逆逻辑斯谛分布函数值。出错情况下它返回 false。

bool MathQuantileLogistic(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   mu,            // [输入] 分布参数 mean
  const double   sigma,         // [输入] 分布参数 scale
  double         &result[]      // [输出] 具有分位数值的数组
);

2.13.4. MathRandomLogistic

函数根据参数为 mu 和 sigma 的逻辑斯谛分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomLogistic(
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 mu 和 sigma 的逻辑斯谛分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rlogis() 模拟。

bool MathRandomLogistic(
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.13.5. MathMomentsLogistic

函数计算参数为 mu 和 sigma 的逻辑斯谛分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsLogistic(
  const double   mu,          // [输入] 分布参数 mean
  const double   sigma,       // [输入] 分布参数 scale
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.14. 柯西分布

2.14.1. MathProbabilityDensityCauchy

函数以 a 和 b 为参数, 计算随机变量 x 的柯西分布概率分布函数值。出错情况下它返回 NaN。

double MathProbabilityDensityCauchy(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的柯西分布概率分布函数值。出错情况下它返回 NaN。

double MathProbabilityDensityCauchy(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的柯西分布概率密度函数值。出错情况下它返回 false。R 语言的 dcauchy() 模拟。

bool MathProbabilityDensityCauchy(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则计算概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的柯西分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityCauchy(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  double         &result[]    // [输出] 概率密度值的数组
);

2.14.2. MathCumulativeDistributionCauchy

函数以 a 和 b 为参数, 计算随机变量 x 的柯西分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionCauchy(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的柯西分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionCauchy(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的柯西分布概率密度函数值。出错情况下它返回 false。R 语言的 pcauchy() 模拟。

bool MathCumulativeDistributionCauchy(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的柯西分布概率密度函数值。出错情况下它返回 false。

bool MathCumulativeDistributionCauchy(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  double         &result[]    // [输出] 概率密度值的数组
);

2.14.3. MathQuantileCauchy

对于指定概率, 函数以 a 和 b 为参数, 计算逆柯西分布函数值。出错情况下它返回 NaN。

double MathQuantileCauchy(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   a,             // [输入] 分布参数 mean
  const double   b,             // [输入] 分布参数 scale
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 a 和 b 为参数, 计算逆柯西分布函数值。出错情况下它返回 NaN。

double MathQuantileCauchy(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   a,             // [输入] 分布参数 mean
  const double   b,             // [输入] 分布参数 scale
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆柯西分布函数值。出错情况下它返回 false。R 语言的 qcauchy() 模拟。

bool MathQuantileCauchy(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 分布参数 mean
  const double   b,             // [输入] 分布参数 scale
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆柯西分布函数值。出错情况下它返回 false。

bool MathQuantileCauchy(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 分布参数 mean
  const double   b,             // [输入] 分布参数 scale
  double         &result[]      // [输出] 具有分位数值的数组
);

2.14.4. MathRandomCauchy

函数根据参数为 a 和 b 的柯西分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomCauchy(
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 a 和 b 的柯西分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rcauchy() 模拟。

double MathRandomCauchy(
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.14.5. MathMomentsCauchy

函数计算柯西分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsCauchy(
  const double   a,           // [输入] 分布参数 mean
  const double   b,           // [输入] 分布参数 scale
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.15. 均匀分布

2.15.1. MathProbabilityDensityUniform

函数以 a 和 b 为参数, 计算随机变量 x 的均匀分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityUniform(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的均匀分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityUniform(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的均匀分布概率密度函数值。出错情况下它返回 false。R 语言的 dunif() 模拟。

bool MathProbabilityDensityUniform(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的均匀分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityUniform(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  double         &result[]    // [输出] 概率密度值的数组
);

2.15.2. MathCumulativeDistributionUniform

函数以 a 和 b 为参数, 计算随机变量 x 的均匀分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionUniform(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的均匀分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionUniform(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的均匀分布函数值。出错情况下它返回 false。R 语言的 punif() 模拟。

bool MathCumulativeDistributionUniform(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的均匀分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionUniform(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  double         &result[]    // [输出] 概率密度值的数组
);

2.15.3. MathQuantileUniform

对于指定概率, 函数以 a 和 b 为参数, 计算逆均匀分布函数值。出错情况下它返回 NaN。

double MathQuantileUniform(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   a,             // [输入] 分布参数 a (下边界)
  const double   b,             // [输入] 分布参数 b (上边界)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 a 和 b 为参数, 计算逆均匀分布函数值。出错情况下它返回 NaN。

double MathQuantileUniform(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] 分布参数 a (下边界)
  const double   b,             // [输入] 分布参数 b (上边界)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆均匀分布函数值。出错情况下它返回 false。R 语言的 qunif() 模拟。

bool MathQuantileUniform(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 分布参数 a (下边界)
  const double   b,             // [输入] 分布参数 b (上边界)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆均匀分布函数值。出错情况下它返回 false。

bool MathQuantileUniform(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 分布参数 a (下边界)
  const double   b,             // [输入] 分布参数 b (上边界)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.15.4. MathRandomUniform

函数根据参数为 a 和 b 的均匀分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomUniform(
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 a 和 b 的均匀分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 runif() 模拟。

bool MathRandomUniform(
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.15.5. MathMomentsUniform

函数计算均匀分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsUniform(
  const double   a,           // [输入] 分布参数 a (下限)
  const double   b,           // [输入] 分布参数 b (上限)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.16. 威布尔分布

2.16.1. MathProbabilityDensityWeibull

函数以 a 和 b 为参数, 计算随机变量 x 的威布尔分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityWeibull(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的威布尔分布概率密度函数值。出错情况下它返回 NaN。

double MathProbabilityDensityWeibull(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的威布尔分布概率密度函数值。出错情况下它返回 false。R 语言的 dweibull() 模拟。

bool MathProbabilityDensityWeibull(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量数组 x[] 的威布尔分布概率密度函数值。出错情况下它返回 false。

bool MathProbabilityDensityWeibull(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  double         &result[]    // [输出] 概率密度值的数组
);

2.16.2. MathCumulativeDistributionWeibull

函数以 a 和 b 为参数, 计算随机变量 x 的威布尔分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionWeibull(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的威布尔分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionWeibull(
  const double   x,           // [输入] 随机变量值
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  int            &error_code  // [输出] 错误代码变量
);

函数以 a 和 b 为参数, 计算随机变量 x 的威布尔分布函数值。出错情况下它返回 false。R 语言的 pweibull() 模拟。

bool MathCumulativeDistributionWeibull(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 a 和 b 为参数, 计算随机变量 x 的威布尔分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionWeibull(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  double         &result[]    // [输出] 概率密度值的数组
);

2.16.3. MathQuantileWeibull

对于指定概率, 函数以 a 和 b 为参数, 计算逆威布尔分布函数值。出错情况下它返回 NaN。

double MathQuantileWeibull(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] 分布参数  (shape)
  const double   b,             // [输入] 分布参数  (scale)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 a 和 b 为参数, 计算逆威布尔分布函数值。出错情况下它返回 NaN。

double MathQuantileWeibull(
  const double   probability,   // [输入] 随机变量发生概率
  const double   a,             // [输入] 分布参数  (shape)
  const double   b,             // [输入] 分布参数 (scale)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆威布尔分布函数值。出错情况下它返回 false。R 语言的 qweibull() 模拟。

bool MathQuantileWeibull(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 分布参数  (shape)
  const double   b,             // [输入] 分布参数  (scale)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 a 和 b 为参数, 计算逆威布尔分布函数值。出错情况下它返回 false。

bool MathQuantileWeibull(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   a,             // [输入] 分布参数  (shape)
  const double   b,             // [输入] 分布参数  (scale)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.16.4. MathRandomWeibull

函数根据参数为 a 和 b 的威布尔分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomWeibull(
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 a 和 b 的威布尔分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rweibull() 模拟。

bool MathRandomWeibull(
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.16.5. MathMomentsWeibull

函数计算威布尔分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsWeibull(
  const double   a,           // [输入] 分布参数 (shape)
  const double   b,           // [输入] 分布参数 (scale)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.17. 二项式分布

2.17.1. MathProbabilityDensityBinomial

函数以 n 和 p 为参数, 计算随机变量 x 的二项式分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 n 和 p 为参数, 计算随机变量 x 的二项式分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  int            &error_code  // [输出] 错误代码变量
);

函数以 n 和 p 为参数, 计算随机变量数组 x[] 的二项式分布概率规模函数值。出错情况下它返回 false。R 语言的 dbinom() 模拟。

bool MathProbabilityDensityBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 n 和 p 为参数, 计算随机变量数组 x[] 的二项式分布概率规模函数值。出错情况下它返回 false。

bool MathProbabilityDensityBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  double         &result[]    // [输出] 概率密度值的数组
);

2.17.2. MathCumulativeDistributionBinomial

函数以 n 和 p 为参数, 计算随机变量 x 的二项式分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 n 和 p 为参数, 计算随机变量 x 的二项式分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  int            &error_code  // [输出] 错误代码变量
);

函数以 n 和 p 为参数, 计算随机变量数组 x[] 的二项式分布概率分布函数值。出错情况下它返回 false。R 语言的 pbinom() 模拟。

bool MathCumulativeDistributionBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 n 和 p 为参数, 计算随机变量数组 x[] 的二项式分布概率分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  double         &result[]    // [输出] 概率密度值的数组
);

2.17.3. MathQuantileBinomial

对于指定概率, 函数以 n 和 p 为参数, 计算逆二项定律分布函数值。出错情况下它返回 NaN。

double MathQuantileBinomial(
  const double   probability,   // [输入] 随机变量发生概率
  const double   n,             // [输入] 分布参数 (测试次数)
  const double   p,             // [输入] 分布参数 (每次测试的成功概率)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 n 和 p 为参数, 计算逆二项定律分布函数值。出错情况下它返回 NaN。

double MathQuantileBinomial(
  const double   probability,   // [输入] 随机变量发生概率
  const double   n,             // [输入] 分布参数 (测试次数)
  const double   p,             // [输入] 分布参数 (每次测试的成功概率)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 n 和 p 为参数, 计算二项定律逆分布函数值。出错情况下它返回 false。R 语言的 qbinom() 模拟。

bool MathQuantileBinomial(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   n,             // [输入] 分布参数 (测试次数)
  const double   p,             // [输入] 分布参数 (每次测试的成功概率)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 n 和 p 为参数, 计算二项定律逆分布函数值。出错情况下它返回 false。

bool MathQuantileBinomial(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   n,             // [输入] 分布参数 (测试次数)
  const double   p,             // [输入] 分布参数 (每次测试的成功概率)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.17.4. MathRandomBinomial

函数根据参数为 n 和 p 的二项式分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomBinomial(
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 n 和 p 的二项式分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rbinom() 模拟。

bool MathRandomBinomial(
  const double   n,           // [输入] 分布参数 (测试次数)
  const double   p,           // [输入] 分布参数 (每次测试的成功概率)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.17.5. MathMomentsBinomial

函数计算参数为 n 和 p 的二项式分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsBinomial(
  const double   n,           // [输入] 测试次数
  const double   p,           // [输入] 每次测试的成功概率
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.18. 负二项式分布

2.18.1. MathProbabilityDensityNegativeBinomial

函数以 r 和 p 为参数, 计算随机变量 x 的负二项式分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNegativeBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 r 和 p 为参数, 计算随机变量 x 的负二项式分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityNegativeBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  int            &error_code  // [输出] 错误代码变量
);

函数以 n 和 p 为参数, 计算随机变量数组 x[] 的负二项式分布概率规模函数值。出错情况下它返回 false。R 语言的 dnbinom() 模拟。

bool MathProbabilityDensityNegativeBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 n 和 p 为参数, 计算随机变量数组 x[] 的负二项式分布概率规模函数值。出错情况下它返回 false。

bool MathProbabilityDensityNegativeBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  double         &result[]    // [输出] 概率密度值的数组
);

2.18.2. MathCumulativeDistributionNegativeBinomial

函数以 r 和 p 为参数, 计算随机变量 x 的负二项式分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNegativeBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 r 和 p 为参数, 计算随机变量 x 的负二项式分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionNegativeBinomial(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  int            &error_code  // [输出] 错误代码变量
);

函数以 r 和 p 为参数, 计算随机变量数组 x[] 的负二项式分布概率分布函数值。出错情况下它返回 false。R 语言的 pnbinom() 模拟。

bool MathCumulativeDistributionNegativeBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 r 和 p 为参数, 计算随机变量数组 x[] 的负二项式分布概率分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionNegativeBinomial(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.18.3. MathQuantileNegativeBinomial

对于指定概率, 函数以 r 和 p 为参数, 计算负二项定律逆分布函数值。出错情况下它返回 NaN。

double MathQuantileNegativeBinomial(
  const double   probability,   // [输入] 随机变量发生概率值 
  const double   r,             // [输入] 测试成功次数
  double         p,             // [输入] 成功概率
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 r 和 p 为参数, 计算负二项定律逆分布函数值。出错情况下它返回 NaN。

double MathQuantileNegativeBinomial(
  const double   probability,   // [输入] 随机变量发生概率值 
  const double   r,             // [输入] 测试成功次数
  double         p,             // [输入] 成功概率
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 r 和 p 为参数, 计算负二项定律逆分布函数值。出错情况下它返回 false。R 语言的 qnbinom() 模拟。

bool MathQuantileNegativeBinomial(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   r,             // [输入] 测试成功次数
  double         p,             // [输入] 成功概率
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 r 和 p 为参数, 计算负二项定律逆分布函数值。出错情况下它返回 false。

bool MathQuantileNegativeBinomial(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   r,             // [输入] 测试成功次数
  double         p,             // [输入] 成功概率
  double         &result[]      // [输出] 具有分位数值的数组
);

2.18.4. MathRandomNegativeBinomial

函数根据参数为 r 和 p 的负二项式分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomNegativeBinomial(
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 r 和 p 的负二项式分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rnbinom() 模拟。

bool MathRandomNegativeBinomial(
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.18.5. MathMomentsNegativeBinomial

函数计算参数为 r 和 p 的负二项式分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsNegativeBinomial(
  const double   r,           // [输入] 成功测试数
  double         p,           // [输入] 成功的概率
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.19. 几何分布

2.19.1. MathProbabilityDensityGeometric

函数以 p 为参数, 计算随机变量 x 的几何分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityGeometric(
  const double   x,           // [输入] 随机变量值
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 p 为参数, 计算随机变量 x 的几何分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityGeometric(
  const double   x,           // [输入] 随机变量值
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  int            &error_code  // [输出] 错误代码变量
);

函数以 p 为参数, 计算随机变量数组 x[] 的几何分布概率规模函数值。出错情况下它返回 false。R 语言的 dgeom() 模拟。

bool MathProbabilityDensityGeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 p 为参数, 计算随机变量数组 x[] 的几何分布概率规模函数值。出错情况下它返回 false。

bool MathProbabilityDensityGeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  double         &result[]    // [输出] 概率密度值的数组
);

2.19.2. MathCumulativeDistributionGeometric

函数以 p 为参数, 计算随机变量 x 的几何分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionGeometric(
  const double   x,           // [输入] 随机变量值
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  const bool     tail,        // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,    // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code  // [输出] 错误代码变量
);

函数以 p 为参数, 计算随机变量 x 的几何分布概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionGeometric(
  const double   x,           // [输入] 随机变量值
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  int            &error_code  // [输出] 错误代码变量
);

函数以 p 为参数, 计算随机变量数组 x[] 的几何定律概率分布函数值。出错情况下它返回 false。R 语言的 pgeom() 模拟。

bool MathCumulativeDistributionGeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  const bool     tail,        // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,    // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 p 为参数, 计算随机变量数组 x[] 的几何定律概率分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionGeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  double         &result[]    // [输出] 概率密度值的数组
);

2.19.3. MathQuantileGeometric

对于指定概率, 函数以 p 为参数, 计算几何定律逆分布函数值。出错情况下它返回 NaN。

double MathQuantileGeometric(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   p,             // [输入] 分布参数 (一次测试中的事件发生概率)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 p 为参数, 计算几何定律逆分布函数值。出错情况下它返回 NaN。

double MathQuantileGeometric(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   p,             // [输入] 分布参数 (一次测试中的事件发生概率)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 p 为参数, 计算几何定律逆分布函数值。出错情况下它返回 false。R 语言的 qgeom() 模拟。

bool MathQuantileGeometric(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   p,             // [输入] 分布参数 (一次测试中的事件发生概率)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 p 为参数, 计算几何定律逆分布函数值。出错情况下它返回 false。

bool MathQuantileGeometric(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   p,             // [输入] 分布参数 (一次测试中的事件发生概率)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.19.4. MathRandomGeometric

函数根据参数为 p 的几何分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomGeometric(
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 p 的几何分布定律产生伪随机变量分布。出错情况下它返回 false。Analog of the rgeom() in R.

bool MathRandomGeometric(
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.19.5. MathMomentsGeometric

函数计算参数为 p 的几何分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsGeometric(
  const double   p,           // [输入] 分布参数 (一次测试中的事件发生概率)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.20. 超几何分布

2.20.1. MathProbabilityDensityHypergeometric

函数以 m, k 和 n 为参数, 计算随机变量 x 的超几何分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityHypergeometric(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 m, k 和 n 为参数, 计算随机变量 x 的超几何分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityHypergeometric(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  int            &error_code  // [输出] 错误代码变量
);

函数以 m, k 和 n 为参数, 计算随机变量数组 x 的超几何分布概率规模函数值。出错情况下它返回 false。R 语言的 dhyper() 模拟。

bool MathProbabilityDensityHypergeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 m, k 和 n 为参数, 计算随机变量数组 x 的超几何分布概率规模函数值。出错情况下它返回 false。

bool MathProbabilityDensityHypergeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.20.2. MathCumulativeDistributionHypergeometric

函数以 m, k 和 n 为参数, 计算随机变量 x 的超几何定律概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionHypergeometric(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  const bool     tail,        // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,    // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code  // [输出] 错误代码变量
);

函数以 m, k 和 n 为参数, 计算随机变量 x 的超几何定律概率分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionHypergeometric(
  const double   x,           // [输入] 随机变量值 (整数)
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  int            &error_code  // [输出] 错误代码变量
);

函数以 m, k 和 n 为参数, 计算随机变量数组 x[] 的超几何定律概率分布函数值。出错情况下它返回 false。R 语言的 phyper() 模拟。

bool MathCumulativeDistributionHypergeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  const bool     tail,        // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,    // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]    // [输出] 分布函数值的数组
);

函数以 m, k 和 n 为参数, 计算随机变量数组 x[] 的超几何定律概率分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionHypergeometric(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  double         &result[]    // [输出] 分布函数值数组
);

2.20.3. MathQuantileHypergeometric

对于指定概率, 函数以 m, k 和 n 为参数, 计算超几何定律的逆分布函数值。出错情况下它返回 NaN。

double MathQuantileHypergeometric(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   m,             // [输入] 对象总数 (整数)
  const double   k,             // [输入] 具有所需特性的对象数量 (整数)
  const double   n,             // [输入] 绘制对象数量 (整数)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 m, k 和 n 为参数, 计算超几何定律的逆分布函数值。出错情况下它返回 NaN。

double MathQuantileHypergeometric(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   m,             // [输入] 对象总数 (整数)
  const double   k,             // [输入] 具有所需特性的对象数量 (整数)
  const double   n,             // [输入] 绘制对象数量 (整数)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 m, k 和 n 为参数, 计算超几何定律逆分布函数值。出错情况下它返回 false。R 语言的 qhyper() 模拟。

bool MathQuantileHypergeometric(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   m,             // [输入] 对象总数 (整数)
  const double   k,             // [输入] 具有所需特性的对象数量 (整数)
  const double   n,             // [输入] 绘制对象数量 (整数)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 m, k 和 n 为参数, 计算超几何定律逆分布函数值。出错情况下它返回 false。

bool MathQuantileHypergeometric(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   m,             // [输入] 对象总数 (整数)
  const double   k,             // [输入] 具有所需特性的对象数量 (整数)
  const double   n,             // [输入] 绘制对象数量 (整数)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.20.4. MathRandomHypergeometric

函数根据参数为 m, n 和 k 的超几何分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomHypergeometric(
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 m, n 和 k 的超几何分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rhyper() 模拟。

bool MathRandomHypergeometric(
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  const int      data_count,  // [输入] 所需数据数量
  double         &result[]    // [输出] 伪随机变量值数组
);

2.20.5. MathMomentsHypergeometric

函数计算参数为 m, n 和 k 的超几何分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsHypergeometric(
  const double   m,           // [输入] 对象总数 (整数)
  const double   k,           // [输入] 具有所需特性的对象数量 (整数)
  const double   n,           // [输入] 绘制对象数量(整数)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

2.21. 泊松分布

2.21.1. MathProbabilityDensityPoisson

函数以 lambda 为参数, 计算随机变量 x 的泊松分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityPoisson(
  const double   x,           // [输入] 随机变量值
  const double   lambda,      // [输入] 分布参数 (mean)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 lambda 为参数, 计算随机变量 x 的泊松分布概率规模函数值。出错情况下它返回 NaN。

double MathProbabilityDensityPoisson(
  const double   x,           // [输入] 随机变量值
  const double   lambda,      // [输入] 分布参数 (mean)
  int            &error_code  // [输出] 错误代码变量
);

函数以 lambda 为参数, 计算随机变量数组 x[] 的泊松分布概率规模函数值。出错情况下它返回 false。R 语言的 dpois() 模拟。

bool MathProbabilityDensityPoisson(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   lambda,      // [输入] 分布参数 (mean)
  const bool     log_mode,    // [输入] 计算对数值的标志, 如果 log_mode = true, 则返回概率密度的自然对数
  double         &result[]    // [输出] 概率密度值的数组
);

函数以 lambda 为参数, 计算随机变量数组 x[] 的泊松分布概率规模函数值。出错情况下它返回 false。

bool MathProbabilityDensityPoisson(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   lambda,      // [输入] 分布参数 (mean)
  double         &result[]    // [输出] 概率密度值的数组
);

2.21.2. MathCumulativeDistributionPoisson

函数以 lambda 为参数, 计算随机变量 x 的泊松分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionPoisson(
  const double   x,           // [输入] 随机变量值
  const double   lambda,      // [输入] 分布参数 (mean)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  int            &error_code  // [输出] 错误代码变量
);

函数以 lambda 为参数, 计算随机变量 x 的泊松分布函数值。出错情况下它返回 NaN。

double MathCumulativeDistributionPoisson(
  const double   x,           // [输入] 随机变量值
  const double   lambda,      // [输入] 分布参数 (mean)
  int            &error_code  // [输出] 错误代码变量
);

函数以 lambda 为参数, 计算随机变量数组 x[] 的泊松分布函数值。出错情况下它返回 false。R 语言的 ppois() 模拟。

bool MathCumulativeDistributionPoisson(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   lambda,      // [输入] 分布参数 (mean)
  const bool     tail,        // [输入] 计算标志, 如果 true, 则计算不超过随机变量 x 的概率
  const bool     log_mode,    // [输入] 计算数值对数的标志, 如果 log_mode=true, 则计算概率的自然对数
  double         &result[]    // [输出] 概率函数密度值的数组
);

函数以 lambda 为参数, 计算随机变量数组 x[] 的泊松分布函数值。出错情况下它返回 false。

bool MathCumulativeDistributionPoisson(
  const double   &x[],        // [输入] 随机变量值的数组
  const double   lambda,      // [输入] 分布参数 (mean)
  double         &result[]    // [输出] 概率函数密度值的数组
);

2.21.3. MathQuantilePoisson

对于指定概率, 函数以 lambda 为参数, 计算逆泊松分布函数值。出错情况下它返回 NaN。

double MathQuantilePoisson(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   lambda,        // [输入] 分布参数 (mean)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  int            &error_code    // [输出] 错误代码变量
);

对于指定概率, 函数以 lambda 为参数, 计算逆泊松分布函数值。出错情况下它返回 NaN。

double MathQuantilePoisson(
  const double   probability,   // [输入] 随机变量发生概率值
  const double   lambda,        // [输入] 分布参数 (mean)
  int            &error_code    // [输出] 错误代码变量
);

对于指定的概率值数组 'probability[]', 函数以 lambda 为参数, 计算逆泊松分布函数值。出错情况下它返回 false。R 语言的 qpois() 模拟。

double MathQuantilePoisson(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   lambda,        // [输入] 分布参数 (mean)
  const bool     tail,          // [输入] 计算标志, 如果 false, 则执行 1.0-概率的计算
  const bool     log_mode,      // [输入] 计算标志, 如果 log_mode=true, 执行 Exp(probability) 计算
  double         &result[]      // [输出] 具有分位数值的数组
);

对于指定的概率值数组 'probability[]', 函数以 lambda 为参数, 计算逆泊松分布函数值。出错情况下它返回 false。

double MathQuantilePoisson(
  const double   &probability[],// [输入] 随机变量概率值数组
  const double   lambda,        // [输入] 分布参数 (mean)
  double         &result[]      // [输出] 具有分位数值的数组
);

2.21.4. MathRandomPoisson

函数根据参数为 lambda 的泊松分布定律产生伪随机变量分布。出错情况下它返回 NaN。

double MathRandomPoisson(
  const double   lambda,      // [输入] 分布参数 (mean)
  int            &error_code  // [输出] 错误代码变量
);

函数根据参数为 lambda 的泊松分布定律产生伪随机变量分布。出错情况下它返回 false。R 语言的 rpois() 模拟。

double MathRandomPoisson(
  const double   lambda,      // [输入] 分布参数 (mean)
  int            &error_code  // [输出] 错误代码变量
);

2.21.5. MathMomentsPoisson

函数计算参数为 lambda 的泊松分布前 4 个力矩的理论值。如果力矩计算已成功, 则返回 true, 否则返回 false。

bool MathMomentsPoisson(
  const double   lambda,      // [输入] 分布参数 (均值)
  double         &mean,       // [输出] 均值变量 (第一力矩)
  double         &variance,   // [输出] 方差变量 (第二力矩)
  double         &skewness,   // [输出] 偏度变量 (第三力矩)
  double         &kurtosis,   // [输出] 峰度变量 (第四力矩)
  int            &error_code  // [输出] 错误代码变量
);

3. 对应于 R 语言的统计函数列表

处于便利, 表 1-2 包括统计库的函数, 以及对应于 R 语言的函数。

编号	计算值	在 MQL5 中的函数	在 R 语言中的函数
1	均值	MathMean	mean
2	方差	MathVariance	var
3	偏度	MathSkewness	skewness
60	峰度	MathKurtosis	kurtosis
5	中间值	MathMedian	median
6	标准偏差	MathStandardDeviation	sd
7	平均偏差	MathAverageDeviation	aad

表 1. 用于计算数组数据的统计特性的函数

编号	分布	密度函数	在 MQL5 中的函数	在 R 语言中的函数
1	正态		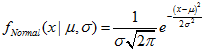MathProbabilityDensityNormal MathCumulativeDistributionNormal MathQuantileNormal MathRandomNormal	dnorm pnorm qnorm rnorm
2	β		MathProbabilityDensityBeta MathCumulativeDistributionBeta MathQuantileBeta MathRandomBeta	dbeta pbeta qbeta rbeta
3	二项		MathProbabilityDensityBinomial MathCumulativeDistributionBinomial MathQuantileBinomial MathRandomBinomial	dbinom pbinom qbinom rbinom
60	柯西		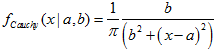MathProbabilityDensityCauchy MathCumulativeDistributionCauchy MathQuantileCauchy MathRandomCauchy	dcauchy pcauchy qcauchy rcauchy
5	卡方		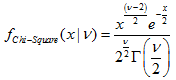MathProbabilityDensityChiSquare MathCumulativeDistributionChiSquare MathQuantileChiSquare MathRandomChiSquare	dchisq pchisq qchisq rchisq
6	指数		MathProbabilityDensityExponential MathCumulativeDistributionExponential MathQuantileExponential MathRandomExponential	dexp pexp qexp rexp
7	F-分布		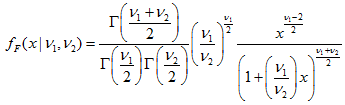MathProbabilityDensityF MathCumulativeDistributionF MathQuantileF MathRandomF	df pf qf rf
8	γ		MathProbabilityDensityGamma MathCumulativeDistributionGamma MathQuantileGamma MathRandomGamma	dgamma pgamma qgamma rgamma
9	几何		MathProbabilityDensityGeometric MathCumulativeDistributionGeometric MathQuantileGeometric MathRandomGeometric	dgeom pgeom qgeom rgeom
10	超几何		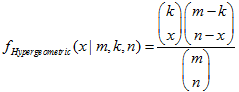MathProbabilityDensityHypergeometric MathCumulativeDistributionHypergeometric MathQuantileHypergeometric MathRandomHypergeometric	dhyper phyper qhyper rhyper
11	逻辑斯谛		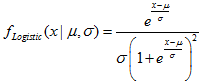MathProbabilityDensityLogistic MathCumulativeDistributionLogistic MathQuantileLogistic MathRandomLogistic	dlogis plogis qlogis rlogis
12	对数正态		MathProbabilityDensityLognormal MathCumulativeDistributionLognormal MathQuantileLognormal MathRandomLognormal	dlnorm plnorm qlnorm rlnorm
13	负二项		MathProbabilityDensityNegativeBinomial MathCumulativeDistributionNegativeBinomial MathQuantileNegativeBinomial MathRandomNegativeBinomial	dnbinom pnbinom qnbinom rnbinom
14	非中心 β		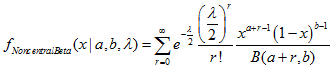MathProbabilityDensityNoncentralBeta MathCumulativeDistributionNoncentralBeta MathQuantileNoncentralBeta MathRandomNoncentralBeta	dbeta pbeta qbeta rbeta
15	非中心卡方		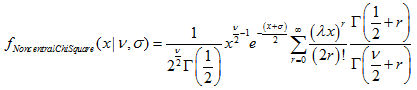MathProbabilityDensityNoncentralChiSquare MathCumulativeDistributionNoncentralChiSquare MathQuantileNoncentralChiSquare MathRandomNoncentralChiSquare	dchisq pchisq qchisq rchisq
16	非中心 F-分布		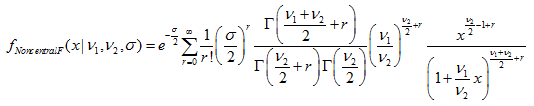MathProbabilityDensityNoncentralF() MathCumulativeDistributionNoncentralF() MathQuantileNoncentralF() MathRandomNoncentralF()	df pf qf rf
17	非中心 t-分布		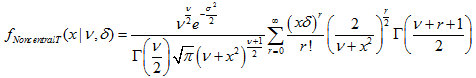MathProbabilityDensityNoncentralT MathCumulativeDistributionNoncentralT MathQuantileNoncentralT MathRandomNoncentralT	dt pt qt rt
18	泊松		MathProbabilityDensityPoisson MathCumulativeDistributionPoisson MathQuantilePoisson MathRandomPoisson	dpois ppois qpois rpois
19	t-分布		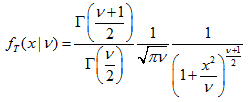MathProbabilityDensityT MathCumulativeDistributionT MathQuantileT MathRandomT	dt pt qt rt
20	均匀		MathProbabilityDensityUniform MathCumulativeDistributionUniform MathQuantileUniform MathRandomUniform	dunif punif qunif runif
21	威布尔		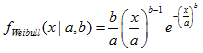MathProbabilityDensityWeibull MathCumulativeDistributionWeibull MathQuantileWeibull MathRandomWeibull	dweibull pweibull qweibull rweibull

表 2. 使用统计分布的函数

MQL5 统计库还提供了用来计算数组的数学函数, 它们列于下表 3。

描述	MQL5	R
生成数值序列	bool MathSequence(const double from,const double to,const double step,double &result[]) bool MathSequenceByCount(const double from,const double to,const int count,double &result[]) bool MathSequence(const int from,const int to,const int step,int &result[]) bool MathSequenceByCount(const int from,const int to,const int count,int &result[])	seq()
生成重复序列	bool MathReplicate(const double &array[],const int count,double &result[]) bool MathReplicate(const int &array[],const int count,int &result[])	rep()
生成逆向元素的数组	bool MathReverse(const double &array[],double &result[]) bool MathReverse(const int &array[],int &result[])	rev(x)
比较数组, 如果所有元素匹配, 则返回 true	bool MathIdentical(const double &array1[],const double &array2[]) bool MathIdentical(const int &array1[],const int &array2[])	identical()
生成含有唯一值的数组	bool MathUnique(const double &array[],double &result[]) bool MathUnique(const int &array[],int &result[])	unique()
根据排序数组元素的顺序生成具有排列的整数数组	bool MathOrder(const double &array[],int &result[]) bool MathOrder(const int &array[],int &result[])	order()
从数组元素生成随机样本。参数 replace=true 允许使用原始序列替换的元素执行随机抽样。数组 probabilities[] 定义了对元素进行抽样的概率。	bool MathSample(const double &array[],const int count,double &result[]) bool MathSample(const double &array[],const int count,const bool replace,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,double &result[]) bool MathSample(const double &array[],double &probabilities[],const int count,const bool replace,double &result[]) bool MathSample(const int &array[],const int count,int &result[]) bool MathSample(const int &array[],const int count,const bool replace,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,int &result[]) bool MathSample(const int &array[],double &probabilities[],const int count,const bool replace,int &result[])	sample()
返回数组元素合计	double MathSum(const double &array[])	sum()
返回数组元素的乘积	double MathProduct(const double &array[])	prod()
生成累加和的数组	bool MathCumulativeSum(const double &array[],double &result[]) bool MathCumulativeSum(double &array[])	cumsum()
生成累加乘积的数组	bool MathCumulativeProduct(const double &array[],double &result[]) bool MathCumulativeProduct(double &array[])	cumprod()
生成最小值累加数组	bool MathCumulativeMin(const double &array[],double &result[]) bool MathCumulativeMin(double &array[])	cummin()
生成最大值累加数组	bool MathCumulativeMax(const double &array[],double &result[]) bool MathCumulativeMax(double &array[])	cummax()
生成 y[i]=x[i+lag]-x[i] 元素差值数组	bool MathDifference(const double &array[],const int lag,double &result[]) bool MathDifference(const double &array[],const int lag,const int differences,double &result[]) bool MathDifference(const int &array[],const int lag,int &result[]) bool MathDifference(const int &array[],const int lag,const int differences,int &result[])	diff()
返回数组元素最小值	double MathMin(const double &array[])	min()
返回数组元素最大值	double MathMax(const double &array[])	max()
计算数组元素的最小值和最大值	bool MathRange(const double &array[],double &min,double &max)	range()
计算数组元素的平均值	double MathMean(const double &array[])	mean()
计算数组元素的标准偏差	double MathStandardDeviation(const double &array[])	sd()
计算数组元素的中值	double MathMedian(double &array[])	median()
计算数组元素的排位	bool MathRank(const int &array[],double &rank[]) bool MathRank(const double &array[],double &rank[])	rank()
计算Pearson', pearman 和 Kendall 的相关系数	bool MathCorrelationPearson(const double &array1[],const double &array2[],double &r) bool MathCorrelationPearson(const int &array1[],const int &array2[],double &r) bool MathCorrelationSpearman(const double &array1[],const double &array2[],double &r) bool MathCorrelationSpearman(const int &array1[],const int &array2[],double &r) bool MathCorrelationKendall(const double &array1[],const double &array2[],double &tau) bool MathCorrelationKendall(const int &array1[],const int &array2[],double &tau)	corr()
计算与指定概率相对应的样本分位数	bool MathQuantile(const double &array[],const double &probs[],double &quantile[])	qunatile()
计算数组元素 Tukey 的五个数字合计 (最小值, 下铰链, 中值, 上铰链, 最大值)	bool MathTukeySummary(const double &array[],const bool removeNAN,double &minimum,double &lower_hinge,double &median,double &upper_hinge,double &maximum)	fivenum()
计算数组元素的对数 (自然数和给定底数)	bool MathLog(const double &array[],double &result[]) bool MathLog(const double &array[],const double base,double &result[]) bool MathLog(double &array[]) bool MathLog(double &array[],const double base)	log()
计算数组元素的以 2 为底的对数	bool MathLog2(const double &array[],double &result[]) bool MathLog2(double &array[])	log2()
计算数组元素的以10 为底的对数	bool MathLog10(const double &array[],double &result[]) bool MathLog10(double &array[])	log10()
计算数组元素的 log(1 + x) 函数值	bool MathLog1p(const double &array[], double &result[]) bool MathLog1p(double &array[])	log1p()
计算数组元素的 exp(x) 函数值	bool MathExp(const double &array[], double &result[]) bool MathExp(double &array[])	exp()
计算数组元素的 ex(x)-1 函数值	bool MathExpm1(const double &array[], double &result[]) bool MathExpm1(double &array[])	expm1()
计算数组元素的 sin(x) 函数值	bool MathSin(const double &array[], double &result[]) bool MathSin(double &array[])	sin()
计算数组元素的 cos(x) 函数值	bool MathCos(const double &array[], double &result[]) bool MathCos(double &array[])	cos()
计算数组元素的 tan(x) 函数值	bool MathTan(const double &array[], double &result[]) bool MathTan(double &array[])	tan()
计算数组元素的 arcsin(x) 函数值	bool MathArcsin(const double &array[], double &result[]) bool MathArcsin(double &array[])	arcsin()
计算数组元素的 arccos(x) 函数值	bool MathArccos(const double &array[], double &result[]) bool MathArccos(double &array[])	arccos()
计算数组元素的 arctan(x) 函数值	bool MathArctan(const double &array[], double &result[]) bool MathArctan(double &array[])	arctan()
计算数组元素的 arctan(y/x) 函数值	bool MathArctan2(const double &array1[], const double &array2[], double &result[])	arctan2()
计算数组元素的 sin(pi*x) 函数值	bool MathSinPi(const double &array[], double &result[]) bool MathSinPi(double &array[])	sinpi()
计算数组元素的 cos(pi*x) 函数值	bool MathCosPi(const double &array[], double &result[]) bool MathCosPi(const double &array[])	cospi()
计算数组元素的 tan(pi*x) 函数值	bool MathTanPi(const double &array[], double &result[]) bool MathTanPi(double &array[])	tanpi()
计算数组元素的绝对值	bool MathAbs(const double &array[], double &result[]) bool MathAbs(double &array[])	abs()
计算数组元素的平方根	bool MathSqrt(const double &array[], double &result[]) bool MathSqrt(double &array[])	sqrt()
返回最接近数组元素的较大整数	bool MathCeil(const double &array[], double &result[]) bool MathCeil(double &array[])	ceil()
返回最接近数组元素的较小整数	bool MathFloor(const double &array[], double &result[]) bool MathFloor(double &array[])	floor()
计算数组元素的整数部分	bool MathTrunc(const double &array[], const int digits, double &result[]) bool MathTrunc(double &array[])	trunc()
计算数组元素的舍入值	bool MathRound(const double &array[], const int digits, double &result[]) bool MathRound(double &array[],int digits)	round()
对于数组元素, 计算指定尾数位数的四舍五入值	bool MathSignif(const double &array[], const int digits, double &result[]) bool MathSignif(double &array[], const int digits)	signinf()
计算数组元素的 sinh(x) 函数值	bool MathSinh(const double &array[],double &result[]) bool MathSinh(double &array[])	sinh()
计算数组元素的 cosh(x) 函数值	bool MathCosh(const double &array[],double &result[]) bool MathCosh(double &array[])	cosh()
计算数组元素的 tanh(x) 函数值	bool MathTanh(const double &array[],double &result[]) bool MathTanh(double &array[])	tanh()
计算数组元素的 arcsinh(x) 函数值	bool MathArcsinh(const double &array[],double &result[]) bool MathArcsinh(double &array[])	asinh()
计算数组元素的 arccosh(x) 函数值	bool MathArccosh(const double &array[],double &result[]) bool MathArccosh(double &array[])	acosh()
计算数组元素的 arctanh(x) 函数值	bool MathArctanh(const double &array[],double &result[]) bool MathArctanh(double &array[])	atanh()
计算数组元素的按位取非运算结果	bool MathBitwiseNot(const int &array[],int &result[]) bool MathBitwiseNot(int &array[])	bitwNot()
计算数组元素的逻辑与运算结果	bool MathBitwiseAnd(const int &array1[],const int &array2[],int &result[])	bitwAnd()
计算数组元素的逻辑或运算结果	bool MathBitwiseOr(const int &array1[],const int &array2[],int &result[])	bitwOr()
计算数组元素的逻辑异或运算结果	bool MathBitwiseXor(const int &array1[],const int &array2[],int &result[])	bitwXor()
计算数组元素的按位左移运算结果	bool MathBitwiseShiftL(const int &array[],const int n,int &result[]) bool MathBitwiseShiftL(int &array[],const int n)	bitwShiftL()
计算数组元素的按位右移运算结果	bool MathBitwiseShiftR(const int &array[],const int n,int &result[]) bool MathBitwiseShiftR(int &array[],const int n)	bitwShiftR()

表 3. 计算数组内数值的数学函数

4. 函数使用例程

我们在正态分布的例子上研究统计函数的实际应用。

假设有以下问题需要解决:

1. 根据参数为 mu 和 sigma 的正态定律分布, 计算落于 [mu-sigma,mu+sigma] 范围内的随机变量概率。
2. 根据参数为 mu 和 sigma 的正态定律分布, 搜索随机变量 x 的数值范围, 其与 mu 对称并且对应于 95％的置信率。
3. 生成 1000000 个随机数, 根据参数为 mu 和 sigma 的正态定律分布, 计算所得值的直方图, 前 4 个力矩, 并与理论值进行比较。

解决方案示例在 NormalExample 脚本:

//+------------------------------------------------------------------+
//|                                                NormalExample.mq5 |
//|                                 版权所有 2016, MetaQuotes 软件公司|
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "版权所有 2016, MetaQuotes 软件公司"
#property link      "https://www.mql5.com"
#property version   "1.00"
//--- 包含用于计算正态分布的函数
#include <Math\Stat\Normal.mqh>
//+------------------------------------------------------------------+
//| 计算直方图                                                        |
//+------------------------------------------------------------------+
void CalculateHistogram(double &data[],const int ncells=200,const string filename="normal.csv")
  {
   if(ArraySize(data)<=0)
      return;

   int n=ArraySize(data);
//--- 在 'data' 数组里搜索最小值和最大值
   double minv,maxv,range;
   minv=data[0];
   maxv=data[0];
   for(int i=1; i<n; i++)
     {
      minv=MathMin(minv,data[i]);
      maxv=MathMax(maxv,data[i]);
     }
//--- 计算范围
   range=maxv-minv;
//   Print("最小=",minv," 最大=",maxv," 范围=",range," 大小=",n);
   if(range==0)
      return;
//--- 直方图计算数组
   double x[];
   double y[];
//--- 设置直方图值
   ArrayResize(x,ncells);
   ArrayResize(y,ncells);
   for(int i=0; i<ncells; i++)
     {
      x[i]=minv+i*range/(ncells-1);
      y[i]=0;
     }
//--- 计算直方图
   for(int i=0; i<n; i++)
     {
      double v=(maxv-data[i])/range;
      int ind=int((v*(ncells-1)));
      y[ind]++;
     }
//--- 检查文件名
   if(filename=="")
      return;
//--- 打开文件写入
   ResetLastError();
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_TXT|FILE_ANSI);
//--- 数据写入文件
   if(filehandle!=INVALID_HANDLE)
     {
      for(int i=0; i<ncells; i++)
        {
         string str=StringFormat("%6.20f;%6.20f",x[i],y[i]);
         FileWrite(filehandle,str);
        }
      FileClose(filehandle);
      PrintFormat("直方图保存于文件 %s",filename);
     }
   else
      PrintFormat("调用 FileOpen 错误, 错误代码=%d",GetLastError());
  }
//+------------------------------------------------------------------+
//| 脚本程序开始函数                                                  |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- 1. 计算随机变量概率, 
//--- 根据参数为 mu 和 sigma 的正态定律分布, 落于 [mu-sigma,mu+sigma] 范围
//--- 设置分布参数
   double mu=5.0;
   double sigma=1.0;
//--- 设置间隔
   double x1=mu-sigma;
   double x2=mu+sigma;
//--- 概率计算变量
   double cdf1,cdf2,probability;
//--- 错误代码变量
   int error_code1,error_code2;
//--- 计算分布函数值
   cdf1=MathCumulativeDistributionNormal(x1,mu,sigma,error_code1);
   cdf2=MathCumulativeDistributionNormal(x2,mu,sigma,error_code2);
//--- 检查错误代码
   if(error_code1==ERR_OK && error_code2==ERR_OK)
     {
      //--- 计算概率
      probability=cdf2-cdf1;
      //--- 输出结果
      PrintFormat("x1=%5.8f, x2=%5.8f, 概率=%5.8f",x1,x2,probability);
     }
//--- 2. 根据参数为 mu 和 sigma 的正态定律分布, 搜索随机变量范围值, 
//--- 其与 mu 对称, 且对应于 95% 的置信率。
//--- 设置置信率
   probability=0.95;
//--- 在间隔界限处设置概率
   double p1=(1.0-probability)*0.5;
   double p2=probability+(1.0-probability)*0.5;
//--- 计算间隔界限
   x1=MathQuantileNormal(p1,mu,sigma,error_code1);
   x2=MathQuantileNormal(p2,mu,sigma,error_code2);
//--- 检查错误代码
   if(error_code1==ERR_OK && error_code2==ERR_OK)
     {
      //--- 输出结果  
      PrintFormat("x1=%5.8f, x2=%5.8f",x1,x2);
     }
//--- 3. 根据参数为 mu 和 sigma 的正态定律分布, 生成 1000000 个随机数,
//--- 在所获数值上计算直方图, 前 4 个力矩并, 与理论值比较
//--- 设置数值数量并准备数组
   int data_count=1000000;
   double data[];
   ArrayResize(data,data_count);
//--- 生成随机值并将它们保存到数组
   for(int i=0; i<data_count; i++)
     {
      data[i]=MathRandomNormal(mu,sigma,error_code1);
     }
//--- 设置初始值索引, 以及用于计算的数据量
   int start=0;
   int count=data_count;
//--- 计算所生成数值的前 4 个力矩
   double mean=MathMean(data,start,count);
   double variance=MathVariance(data,start,count);
   double skewness=MathSkewness(data,start,count);
   double kurtosis=MathKurtosis(data,start,count);
//--- 理论力矩的变量
   double normal_mean=0;
   double normal_variance=0;
   double normal_skewness=0;
   double normal_kurtosis=0;
//--- 显示计算的力矩值
   PrintFormat("              均值=%.10f,         方差=%.10f         偏度=%.10f         峰度=%.10f",mean,variance,skewness,kurtosis);
//--- 计算力矩的理论值, 并将它们与所获值比较
   if(MathMomentsNormal(mu,sigma,normal_mean,normal_variance,normal_skewness,normal_kurtosis,error_code1))
     {
      PrintFormat("正态均值=%.10f,  正态方差=%.10f  正态偏度=%.10f  正态峰度=%.10f",normal_mean,normal_variance,normal_skewness,normal_kurtosis);
      PrintFormat("增量均值=%.4f, 增量方差=%.4f  增量偏度=%.4f  增量峰度=%.4f",mean-normal_mean,variance-normal_variance,skewness-normal_skewness,kurtosis-normal_kurtosis);
     }
//--- 计算分布直方图, 并将其保存到 normal.csv 文件
   int ncells=50;
   CalculateHistogram(data,ncells,"normal.csv");
  }

Script execution results:

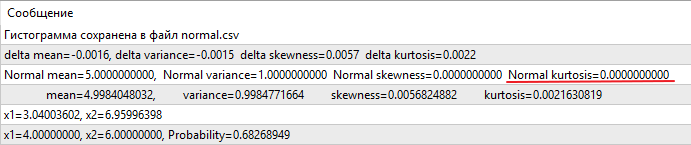
图例. 1. TestNormal.mq5 脚本操作结果

注意, "峰度" 参数值的所有计算均使用 "过量峰度=峰度-3", 即, 对于正态分布等于零。

计算过的直方图保存到 normal.csv 文件 (图例. 2)

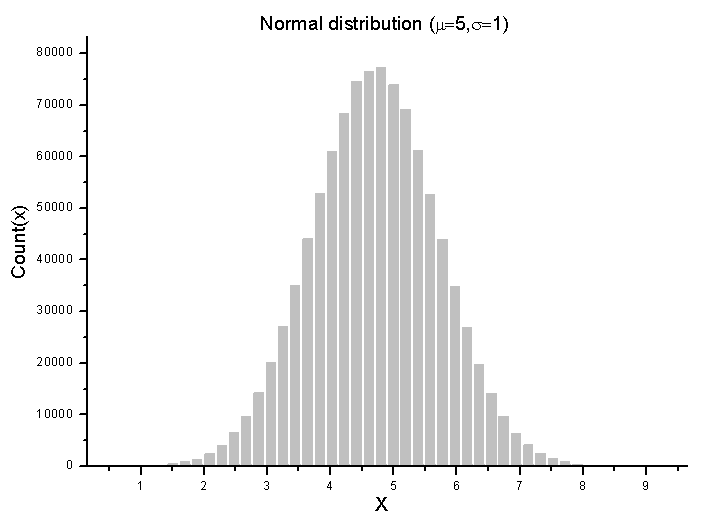
图例. 2. 随机数的分布直方图, 是根据参数为 mu=5 he1 sigma=1 的正态分布生成

5. 计算速度比较

为了比较统计函数的计算速度, 用来测量概率密度函数(pdf), 累加分布函数(cdf), 分位数计算函数和伪随机数生成函数计算时间的脚本已经准备就绪。

计算已在 51 个值的数组上执行。对于连续分布, 函数值的计算在 0 到 1 的范围内执行; 对于离散分布 - 从 0 到 50。R 语言统计函数的计算时间已经使用 microbenchmark 库得到。MQL5 函数的计算时间已经利用 GetMicrosecondCount() 函数测量。计算脚本 TestStatBenchmark.mq5 可在 终端_数据_文件夹\MQL5\Scripts\UnitTests\Stat 下找到。R 语言版的脚本和计算速度测量的结果在附录中提供。

计算已在 Intel Core i7-4790, CPU 3.6 Ghz, 16 GB RAM, Windows 10 x64 的电脑上进行。

计算时间测量的结果 (微秒, μs) 示于表 3 中。

编号	分布	MQL5 计算 PDF 时间 (µs)	R time for calculating PDF 时间 (µs)	PDF R/MQL5	MQL5 计算 CDF 时间 (µs)	R time for calculating CDF 时间 (µs)	CDF R/MQL5	MQL5 time for calculating 分位数 时间 (µs)	R time for calculating 分位数 时间 (µs)	Quantile R/MQL5	MQL5 time for generating 随机数 时间 (µs)	R time for generating random numbers (µs)	Random R/MQL5
1	二项	4.39	11.663	2.657	13.65	25.316	1.855	50.18	66.845	1.332	318.73	1816.463	5.699
2	β	1.74	17.352	9.972	4.76	15.076	3.167	48.72	129.992	2.668	688.81	1723.45	2.502
3	γ	1.31	8.251	6.347	8.09	14.792	1.828	50.83	64.286	1.265	142.84	1281.707	8.973
60	柯西	0.45	1.423	3.162	1.33	15.078	11.34	1.37	2.845	2.077	224.19	588.517	2.625
5	指数	0.85	3.13	3.682	0.77	2.845	3.695	0.53	2.276	4.294	143.18	389.406	2.72
6	均匀	0.42	2.561	6.098	0.45	1.423	3.162	0.18	2.846	15.81	40.3	247.467	6.141
7	几何	2.3	5.121	2.227	2.12.	4.552	2.147	0.81	5.407	6.675	278	1078.045	3.879
8	超几何	1.85	11.095	5.997	0.9	8.819	9.799	0.75	9.957	13.28	302.55	880.356	2.91
9	逻辑斯谛	1.27	4.267	3.36	1.11	4.267	3.844	0.71	3.13	4.408	178.65	626.632	3.508
10	威布尔	2.99	5.69	1.903	2.74	4.268	1.558	2.64	6.828	2.586	536.37	1558.472	2.906
11	泊松	2.91	5.974	2.053	6.26	8.534	1.363	3.43	13.085	3.815	153.59	303.219	1.974
12	F	3.86	10.241	2.653	9.94	22.472	2.261	65.47	135.396	2.068	1249.22	1801.955	1.442
13	卡方	2.47	5.974	2.419	7.71	13.37	1.734	44.11	61.725	1.399	210.24	1235.059	5.875
14	非中心卡方	8.05	14.223	1.767	45.61	209.068	4.584	220.66	10342.96	46.873	744.45	1997.653	2.683
15	非中心 F	19.1	28.446	1.489	14.67	46.935	3.199	212.21	2561.991	12.073	1848.9	2912.141	1.575
16	非中心 β	16.3	26.739	1.64	10.48	43.237	4.126	153.66	2290.915	14.909	2686.82	2839.893	1.057
17	负二项	6.13	11.094	1.81	12.21	19.627	1.607	14.05	60.019	4.272	1130.39	1936.498	1.713
18	正态	1.15	4.267	3.71	0.81	3.983	4.917	0.7	2.277	3.253	293.7	696.321	2.371
19	对数正态	1.99	5.406	2.717	3.19	8.819	2.765	3.18	6.259	1.968	479.75	1269.761	2.647
20	T	2.32	11.663	5.027	8.01	19.059	2.379	50.23	58.596	1.167	951.58	1425.92	1.498
21	非中心 T	38.47	86.757	2.255	27.75	39.823	1.435	1339.51	1930.524	1.441	1550.27	1699.84	1.096
			<PDF R/MQL5>	3.474		<CDF R/MQL5>	3.465		<Quantile R/MQL5>	7.03		<Random R/MQL5>	3.13

Table 4. R 语言和 MQL5 中的统计函数计算时间 (单位微秒)

R 语言取用最小时间值, 对于 MQL5 取用了平均值 (pdf_mean, cdf_mean, quantile_mean, random_mean)。

表 3 所示即使在这样的条件下, MQL5 中统计库函数的计算仍然比 R 语言中的统计库函数的计算快若干倍。平均而言, MQL5 的计算比 R 语言快 3 至 7 倍, 甚至考虑到较新版本的 R 语言函数实际上是用C++ 编写的。

实际上, MQL5 编译器比 R 语言函数的 C++ 实现要快得多, 这表明我们的开发具有极高品质。将程序从 R 语言转换为 MQL5 可以显著提高速度, 并且不需要使用第三方 DLL。

6. 已检测到的 R 语言中的计算误差

在 R 语言的测试期间, 已检测到非中心 t-分布的分位数计算中的误差。

例如:

> n <- 10
> k <- seq(0,1,by=1/n)
> nt_pdf<-dt(k, 10,8, log = FALSE)
> nt_cdf<-pt(k, 10,8, log = FALSE)
> nt_quantile<-qt(nt_cdf, 10,8, log = FALSE)
> nt_pdf
 [1] 4.927733e-15 1.130226e-14 2.641608e-14 6.281015e-14 1.516342e-13 3.708688e-13 9.166299e-13
 [8] 2.283319e-12 5.716198e-12 1.433893e-11 3.593699e-11
> nt_cdf
 [1] 6.220961e-16 1.388760e-15 3.166372e-15 7.362630e-15 1.742915e-14 4.191776e-14 1.021850e-13
 [8] 2.518433e-13 6.257956e-13 1.563360e-12 3.914610e-12
> k
 [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
> nt_quantile
 [1]           -Inf -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154 -1.340781e+154
 [7] -1.340781e+154   7.000000e-01   8.000000e-01   9.000000e-01   1.000000e+00

在 R 语言中学生 t-分布的计算使用 Lenth [6] 提出的 AS 243 算法。该方法的优点是具有不完全 β 函数的无限系列成员的快速递归计算。但文献 [7] 中已经表明, 由于在序列成员求和期间精度评估中的错误, 该算法导致错误 (文献 [7] 中的表 2), 特别是对于非中心 delta 参数的大数值。文献 [7] 的作者提出了一种非中心 t-分布概率递归计算的校正算法。

MQL5 统计库使用文献 [7] 中提出的正确算法来计算概率, 这提供了准确的结果。

应当注意, 在 R 语言中, γ、卡方和非中心卡方分布在点 x = 0 处的概率密度的定义会导致无限表达式:

> dgamma(0,0.5,1)
[1] Inf
> dchisq(0,df=0.5,ncp=1)
[1] Inf
> dchisq(0,df=0.5,ncp=0)
[1] Inf

因此, 在 R 语言中, 在点 x = 0 处, 概率密度的定义使用极限值。尽管在点 x = 0 处无穷大, 在此情况下, 在积分期间不发生偏差, 并且密度的积分是有限的。

当计算概率时 (例如, for x=0.1), 它们与来自 Wolfram Alpha (γ, 卡方, 非中心卡方) 的值相匹配。

> pgamma(0.1,0.5,1)
[1] 0.3452792
> pchisq(0.1,df=0.5,ncp=0)
[1] 0.5165553
> pchisq(0.1,df=0.5,ncp=1)
[1] 0.3194965

Wolfram Alpha (数值) 和 Matlab 在点 point x=0 出的密度定义不一样:

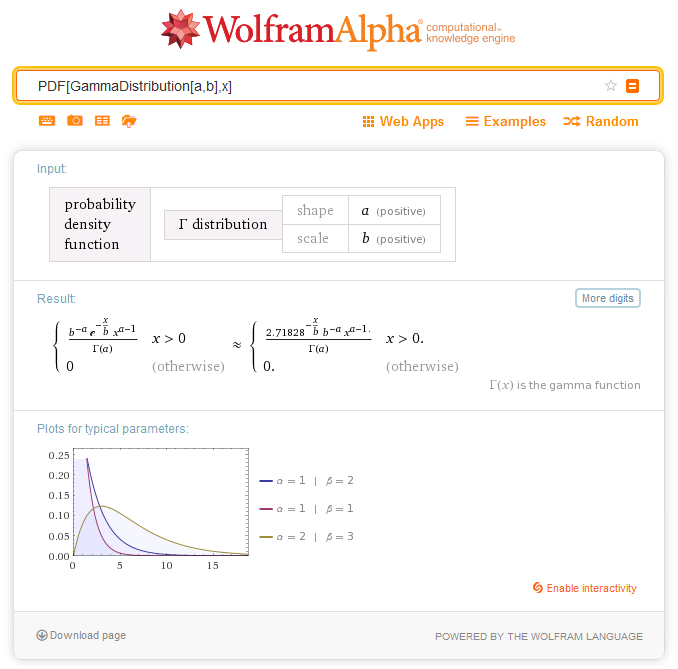
图例. 3. 在 Wolfram Alpha 中的 γ 分布概率密度定义

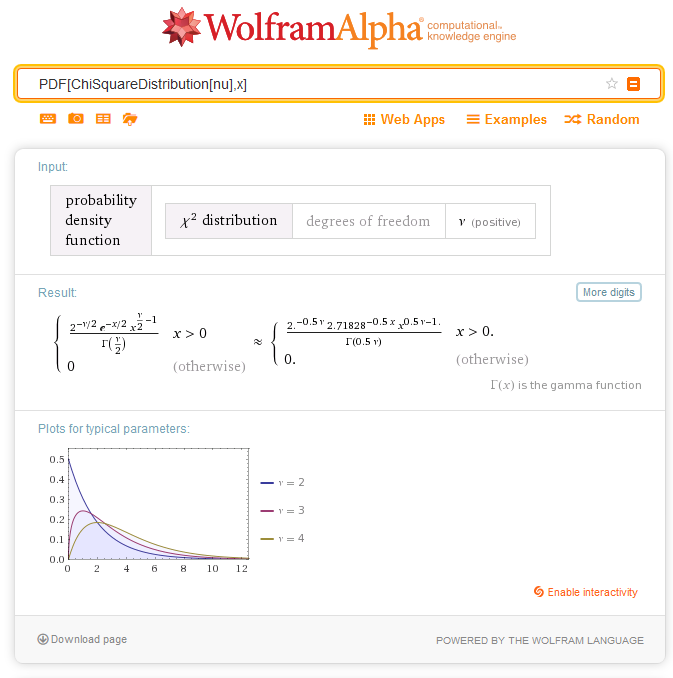
图例. 4. 在 Wolfram Alpha 中的卡方分布概率密度定义

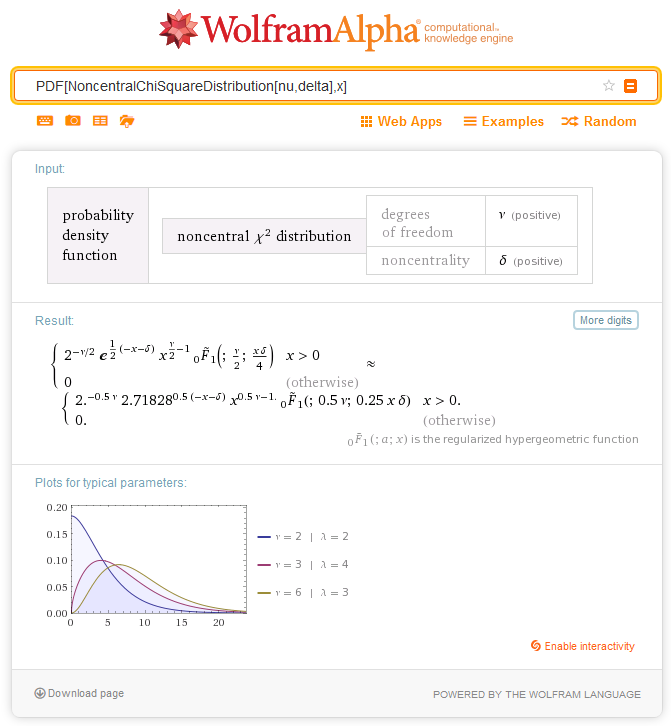
图例. 5. 在 Wolfram Alpha 中的非中心卡方分布概率密度定义

在 MQL5 统计库中, 根据定义, 在点 x = 0 处这些分布的密度被认为等于零。

为了确保计算精度, 并允许第三方开发人员测试库的质量, 在标准发布版中含有多个单元测试脚本。它们可以在 /Scripts/UnitTests/Stat 文件夹中找到。

结论

本文研究 MQL5 统计库的主要函数。

它们可以进行数据统计特性的计算, 并可处理 R 语言实现的基本统计分布。此外, 软件库还包含用于计算理论分布力矩的函数, 可评估真实分布到建模的一致性程度。

由于 MQL5 的新 64-位编译器 的极高性能, 复杂的数学计算比 R 语言中快若干倍, 这显著促进了研究进程。

参考文献

1. 用于统计计算的 R 项目。
2. N. Balakrishnan, N. L. Johnson, S. Kotz  "Continuous Univariate Distributions: Volume 1." Wiley-Interscience, 1994.
3. N. Balakrishnan, N. L. Johnson, S. Kotz  "Continuous Univariate Distributions: Volume 2." Wiley-Interscience, 2000.
4. N. L. Johnson, S. Kotz, A. W. Kemp  "Univariate Discrete Distributions", Wiley-Interscience, 2005.
5. Forbes C., Evans M., Hastings N., Peacock B., "Statistical Distributions", 4th Edition, John Wiley and Sons, 2011.
6. Lenth, R.V., "Cumulative distribution function of the noncentral t distribution", Appled Statistics,  vol. 38 (1989), 185–189.
7. D. Benton, K. Krishnamoorthy, "Computing discrete mixtures of continuous distributions: noncentral chisquare, noncentral t and the distribution of the square of the sample multiple correlation coefficient",  Computational Statistics & Data Analysis, 43, (2003), 249-267

附录。统计函数计算时间的测量结果

评估 R 语言中统计函数计算时间及其操作结果的脚本在附录中提供, 以及 TestStatBenchmark.mq5 脚本操作的结果。

R 语言脚本:

library(microbenchmark)
n <- 50
k <- seq(0,n,by=1)
binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
print(binomial_pdf)
print(binomial_cdf)
print(binomial_quantile)
print(binomial_random)

n <- 50
k <- seq(0,1,by=1/n)
beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
print(beta_pdf)
print(beta_cdf)
print(beta_quantile)
print(beta_random)

n <- 50
k <- seq(0,1,by=1/n)
gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
print(gamma_pdf)
print(gamma_cdf)
print(gamma_quantile)
print(gamma_random)

n <- 50
k <- seq(0,1,by=1/n)
cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
print(cauchy_pdf)
print(cauchy_cdf)
print(cauchy_quantile)
print(cauchy_random)

n <- 50
k <- seq(0,1,by=1/n)
exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
exponential_random <- microbenchmark(random<-rexp(10000, 2))
print(exponential_pdf)
print(exponential_cdf)
print(exponential_quantile)
print(exponential_random)


n <- 50
k <- seq(0,1,by=1/n)
uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
print(uniform_pdf)
print(uniform_cdf)
print(uniform_quantile)
print(uniform_random)


n <- 50
k <- seq(0,n,by=1)
geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
print(geometric_pdf)
print(geometric_cdf)
print(geometric_quantile)
print(geometric_random)

n <- 50
k <- seq(0,n,by=1)
hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
print(hypergeometric_pdf)
print(hypergeometric_cdf)
print(hypergeometric_quantile)
print(hypergeometric_random)

n <- 50
k <- seq(0,1,by=1/n)
logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
print(logistic_pdf)
print(logistic_cdf)
print(logistic_quantile)
print(logistic_random)

n <- 50
k <- seq(0,1,by=1/n)
weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
print(weibull_pdf)
print(weibull_cdf)
print(weibull_quantile)
print(weibull_random)

n <- 50
k <- seq(0,n,by=1)
poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
poisson_random <- microbenchmark(random<-rpois(10000, 1))
print(poisson_pdf)
print(poisson_cdf)
print(poisson_quantile)
print(poisson_random)

n <- 50
k <- seq(0,1,by=1/n)
f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
f_random <- microbenchmark(random<-rf(10000, 10,20))
print(f_pdf)
print(f_cdf)
print(f_quantile)
print(f_random)

n <- 50
k <- seq(0,1,by=1/n)
chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
print(chisquare_pdf)
print(chisquare_cdf)
print(chisquare_quantile)
print(chisquare_random)

n <- 50
k <- seq(0,1,by=1/n)
nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
print(nchisquare_pdf)
print(nchisquare_cdf)
print(nchisquare_quantile)
print(nchisquare_random)

n <- 50
k <- seq(0,1,by=1/n)
nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
print(nf_pdf)
print(nf_cdf)
print(nf_quantile)
print(nf_random)

n <- 50
k <- seq(0,1,by=1/n)
nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
print(nbeta_pdf)
print(nbeta_cdf)
print(nbeta_quantile)
print(nbeta_random)

n <- 50
k <- seq(0,n,by=1)
nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
print(nbinom_pdf)
print(nbinom_cdf)
print(nbinom_quantile)
print(nbinom_random)

n <- 50
k <- seq(0,1,by=1/n)
normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
print(normal_pdf)
print(normal_cdf)
print(normal_quantile)
print(normal_random)

n <- 50
k <- seq(0,1,by=1/n)
lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
print(lognormal_pdf)
print(lognormal_cdf)
print(lognormal_quantile)
print(lognormal_random)

n <- 50
k <- seq(0,1,by=1/n)
t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
t_random <- microbenchmark(random<-rt(10000, 8))
print(t_pdf)
print(t_cdf)
print(t_quantile)
print(t_random)

n <- 50
k <- seq(0,1,by=1/n)
nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
nt_random <- microbenchmark(random<-rt(10000, 10,1))
print(nt_pdf)
print(nt_cdf)
print(nt_quantile)
print(nt_random)

Result:

R version 3.2.5 (2016-04-14) -- "Very, Very Secure Dishes"
Copyright (C) 2016 The R Foundation for Statistical Computing
Platform: x86_64-w64-mingw32/x64 (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under certain conditions.
Type 'license()' or 'licence()' for distribution details.

R is a collaborative project with many contributors.
Type 'contributors()' for more information and
'citation()' on how to cite R or R packages in publications.

Type 'demo()' for some demos, 'help()' for on-line help, or
'help.start()' for an HTML browser interface to help.
Type 'q()' to quit R.

[Workspace loaded from ~/Test/111/.RData]

> library(microbenchmark)
> n <- 50
> k <- seq(0,n,by=1)
> binomial_pdf <- microbenchmark(pdf<-dbinom(k, 50, 0.6, log = FALSE))
> binomial_cdf <- microbenchmark(cdf<-pbinom(k, 50, 0.6, log = FALSE))
> binomial_quantile <- microbenchmark(quantile<-qbinom(cdf, 50, 0.6, log = FALSE))
> binomial_random <- microbenchmark(random<-rbinom(10000, 50, 0.6))
> print(binomial_pdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 pdf <- dbinom(k, 50, 0.6, log = FALSE) 11.663 11.948 13.37888 12.233 12.233 47.503   100
> print(binomial_cdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 cdf <- pbinom(k, 50, 0.6, log = FALSE) 25.316 25.602 29.63195 25.886 35.557 93.868   100
> print(binomial_quantile)
Unit: microseconds
                                          expr    min    lq     mean median     uq     max neval
 quantile <- qbinom(cdf, 50, 0.6, log = FALSE) 66.845 67.13 72.09098 67.699 73.672 130.276   100
> print(binomial_random)
Unit: milliseconds
                             expr      min      lq     mean   median       uq      max neval
 random <- rbinom(10000, 50, 0.6) 1.816463 1.89056 1.948185 1.929814 1.989262 2.308835   100
> 
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> beta_pdf <- microbenchmark(pdf<-dbeta(k, 2, 4, log = FALSE))
> beta_cdf <- microbenchmark(cdf<-pbeta(k, 2, 4, log = FALSE))
> beta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2, 4, log = FALSE))
> beta_random <- microbenchmark(random<-rbeta(10000, 2, 4,))
> print(beta_pdf)
Unit: microseconds
                               expr    min     lq     mean median     uq     max neval
 pdf <- dbeta(k, 2, 4, log = FALSE) 17.352 17.637 19.99512 17.638 18.206 109.797   100
> print(beta_cdf)
Unit: microseconds
                               expr    min     lq     mean median      uq    max neval
 cdf <- pbeta(k, 2, 4, log = FALSE) 15.076 15.361 16.83489 15.646 15.9295 75.379   100
> print(beta_quantile)
Unit: microseconds
                                      expr     min      lq     mean   median     uq     max neval
 quantile <- qbeta(cdf, 2, 4, log = FALSE) 129.992 130.277 140.8325 131.4145 143.93 201.672   100
> print(beta_random)
Unit: milliseconds
                           expr     min       lq     mean   median       uq      max neval
 random <- rbeta(10000, 2, 4, ) 1.72345 1.794132 1.862292 1.836515 1.901226 2.823963   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> gamma_pdf <- microbenchmark(pdf<-dgamma(k, 1,1, log = FALSE))
> gamma_cdf <- microbenchmark(cdf<-pgamma(k, 1,1, log = FALSE))
> gamma_quantile <- microbenchmark(quantile<-qgamma(cdf, 1, 1, log = FALSE))
> gamma_random <- microbenchmark(random<-rgamma(10000, 1,1))
> print(gamma_pdf)
Unit: microseconds
                                expr   min     lq     mean median    uq     max neval
 pdf <- dgamma(k, 1, 1, log = FALSE) 8.251 8.8195 10.92684  9.104 9.389 122.312   100
> print(gamma_cdf)
Unit: microseconds
                                expr    min     lq     mean median     uq     max neval
 cdf <- pgamma(k, 1, 1, log = FALSE) 14.792 15.646 20.43306 20.055 21.334 106.099   100
> print(gamma_quantile)
Unit: microseconds
                                       expr    min     lq     mean median    uq     max neval
 quantile <- qgamma(cdf, 1, 1, log = FALSE) 64.286 64.854 70.09419 65.139 67.13 162.988   100
> print(gamma_random)
Unit: milliseconds
                          expr      min       lq     mean   median       uq      max neval
 random <- rgamma(10000, 1, 1) 1.281707 1.330347 1.410961 1.362631 1.421226 2.322204   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> cauchy_pdf <- microbenchmark(pdf<-dcauchy(k, 2,1, log = FALSE))
> cauchy_cdf <- microbenchmark(cdf<-pgamma(k, 2,1, log = FALSE))
> cauchy_quantile <- microbenchmark(quantile<-qcauchy(cdf, 2, 1, log = FALSE))
> cauchy_random <- microbenchmark(random<-rcauchy(10000, 2, 1))
> print(cauchy_pdf)
Unit: microseconds
                                 expr   min    lq   mean median    uq    max neval
 pdf <- dcauchy(k, 2, 1, log = FALSE) 1.423 1.708 2.8431  1.709 2.278 67.415   100
> print(cauchy_cdf)
Unit: microseconds
                                expr    min     lq     mean median     uq    max neval
 cdf <- pgamma(k, 2, 1, log = FALSE) 15.078 15.646 16.51914  15.93 16.215 33.281   100
> print(cauchy_quantile)
Unit: microseconds
                                        expr   min   lq   mean median    uq    max neval
 quantile <- qcauchy(cdf, 2, 1, log = FALSE) 2.845 3.13 3.8044  3.131 3.415 56.606   100
> print(cauchy_random)
Unit: microseconds
                           expr     min      lq     mean   median      uq      max neval
 random <- rcauchy(10000, 2, 1) 588.517 615.823 663.8658 637.7255 674.845 1520.356   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> exponential_pdf <- microbenchmark(pdf<-dexp(k, 2, log = FALSE))
> exponential_cdf <- microbenchmark(cdf<-pexp(k, 2, log = FALSE))
> exponential_quantile <- microbenchmark(quantile<-qexp(cdf, 2, log = FALSE))
> exponential_random <- microbenchmark(random<-rexp(10000, 2))
> print(exponential_pdf)
Unit: microseconds
                           expr  min    lq    mean median    uq    max neval
 pdf <- dexp(k, 2, log = FALSE) 3.13 3.414 4.08887  3.415 3.415 67.699   100
> print(exponential_cdf)
Unit: microseconds
                           expr   min   lq    mean median     uq    max neval
 cdf <- pexp(k, 2, log = FALSE) 2.845 3.13 4.38756  3.414 3.5565 58.597   100
> print(exponential_quantile)
Unit: microseconds
                                  expr   min    lq    mean median    uq    max neval
 quantile <- qexp(cdf, 2, log = FALSE) 2.276 2.561 3.80729 2.5615 2.846 44.659   100
> print(exponential_random)
Unit: microseconds
                     expr     min       lq     mean   median       uq      max neval
 random <- rexp(10000, 2) 389.406 408.8895 440.9583 418.4185 444.8715 1371.875   100
> 
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> uniform_pdf <- microbenchmark(pdf<-dunif(k, 0, 10, log = FALSE))
> uniform_cdf <- microbenchmark(cdf<-punif(k, 0, 10, log = FALSE))
> uniform_quantile <- microbenchmark(quantile<-qunif(cdf, 0, 10, log = FALSE))
> uniform_random <- microbenchmark(random<-runif(10000, 0, 10))
> print(uniform_pdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 pdf <- dunif(k, 0, 10, log = FALSE) 2.561 2.846 3.78734   3.13 3.131 66.277   100
> print(uniform_cdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 cdf <- punif(k, 0, 10, log = FALSE) 1.423 1.708 2.41635  1.992 1.993 53.477   100
> print(uniform_quantile)
Unit: microseconds
                                       expr   min    lq    mean median     uq    max neval
 quantile <- qunif(cdf, 0, 10, log = FALSE) 2.846 3.131 5.13561  3.415 3.6995 82.774   100
> print(uniform_random)
Unit: microseconds
                          expr     min       lq     mean   median       uq      max neval
 random <- runif(10000, 0, 10) 247.467 258.7035 317.1567 279.6095 357.2635 1267.769   100
> 
> 
> n <- 50
> k <- seq(0,n,by=1)
> geometric_pdf <- microbenchmark(pdf<-dgeom(k, 0.3, log = FALSE))
> geometric_cdf <- microbenchmark(cdf<-pgeom(k, 0.3, log = FALSE))
> geometric_quantile <- microbenchmark(quantile<-qgeom(cdf, 0.3, log = FALSE))
> geometric_random <- microbenchmark(random<-rgeom(10000, 0.3))
> print(geometric_pdf)
Unit: microseconds
                              expr   min    lq    mean median    uq    max neval
 pdf <- dgeom(k, 0.3, log = FALSE) 5.121 5.122 6.14258  5.406 5.406 60.304   100
> print(geometric_cdf)
Unit: microseconds
                              expr   min    lq    mean median     uq    max neval
 cdf <- pgeom(k, 0.3, log = FALSE) 4.552 4.836 5.50548  4.837 5.1215 46.081   100
> print(geometric_quantile)
Unit: microseconds
                                     expr   min    lq    mean median    uq    max neval
 quantile <- qgeom(cdf, 0.3, log = FALSE) 5.407 5.974 7.12107  5.975 6.259 71.681   100
> print(geometric_random)
Unit: milliseconds
                        expr      min       lq     mean   median       uq      max neval
 random <- rgeom(10000, 0.3) 1.078045 1.127681 1.192608 1.156125 1.199361 1.604267   100
> 
> n <- 50
> k <- seq(0,n,by=1)
> hypergeometric_pdf <- microbenchmark(pdf<-dhyper(k, 12,38,11, log = FALSE))
> hypergeometric_cdf <- microbenchmark(cdf<-phyper(k, 12,38,11, log = FALSE))
> hypergeometric_quantile <- microbenchmark(quantile<-qhyper(cdf, 12,38,11, log = FALSE))
> hypergeometric_random <- microbenchmark(random<-rhyper(10000, 12,38,11))
> print(hypergeometric_pdf)
Unit: microseconds
                                      expr    min     lq     mean median     uq     max neval
 pdf <- dhyper(k, 12, 38, 11, log = FALSE) 11.095 13.939 17.07667 14.224 14.935 101.548   100
> print(hypergeometric_cdf)
Unit: microseconds
                                      expr   min    lq     mean median     uq   max neval
 cdf <- phyper(k, 12, 38, 11, log = FALSE) 8.819 9.387 12.60515  9.672 12.517 62.01   100
> print(hypergeometric_quantile)
Unit: microseconds
                                             expr   min      lq     mean median     uq    max neval
 quantile <- qhyper(cdf, 12, 38, 11, log = FALSE) 9.957 10.3835 13.00618  10.81 11.948 64.286   100
> print(hypergeometric_random)
Unit: microseconds
                                expr     min       lq     mean   median       uq      max neval
 random <- rhyper(10000, 12, 38, 11) 880.356 938.9515 993.8324 963.9835 996.8365 1375.289   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> logistic_pdf <- microbenchmark(pdf<-dlogis(k, 1,2, log = FALSE))
> logistic_cdf <- microbenchmark(cdf<-plogis(k, 1,2, log = FALSE))
> logistic_quantile <- microbenchmark(quantile<-qlogis(cdf, 1,2, log = FALSE))
> logistic_random <- microbenchmark(random<-rlogis(10000, 1,2))
> print(logistic_pdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 pdf <- dlogis(k, 1, 2, log = FALSE) 4.267 4.552 5.94354  4.553 4.837 53.477   100
> print(logistic_cdf)
Unit: microseconds
                                expr   min    lq    mean median    uq    max neval
 cdf <- plogis(k, 1, 2, log = FALSE) 4.267 4.552 5.96056  4.837 4.837 96.428   100
> print(logistic_quantile)
Unit: microseconds
                                       expr  min    lq   mean median    uq    max neval
 quantile <- qlogis(cdf, 1, 2, log = FALSE) 3.13 3.415 4.1742  3.415 3.699 56.036   100
> print(logistic_random)
Unit: microseconds
                          expr     min      lq     mean   median      uq      max neval
 random <- rlogis(10000, 1, 2) 626.632 649.956 696.2128 675.2725 715.805 1589.191   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> weibull_pdf <- microbenchmark(pdf<-dweibull(k, 5,1, log = FALSE))
> weibull_cdf <- microbenchmark(cdf<-pweibull(k, 5,1, log = FALSE))
> weibull_quantile <- microbenchmark(quantile<-qweibull(cdf, 5,1, log = FALSE))
> weibull_random <- microbenchmark(random<-rweibull(10000, 5,1))
> print(weibull_pdf)
Unit: microseconds
                                  expr  min    lq    mean median    uq    max neval
 pdf <- dweibull(k, 5, 1, log = FALSE) 5.69 5.974 7.21775  5.975 6.259 85.619   100
> print(weibull_cdf)
Unit: microseconds
                                  expr   min    lq    mean median    uq    max neval
 cdf <- pweibull(k, 5, 1, log = FALSE) 4.268 4.552 7.83782 4.8365 7.966 90.455   100
> print(weibull_quantile)
Unit: microseconds
                                         expr   min    lq    mean median    uq    max neval
 quantile <- qweibull(cdf, 5, 1, log = FALSE) 6.828 7.112 7.96587  7.113 7.397 48.641   100
> print(weibull_random)
Unit: milliseconds
                            expr      min      lq     mean   median       uq      max neval
 random <- rweibull(10000, 5, 1) 1.558472 1.59744 1.659753 1.632853 1.679502 2.616603   100
> 
> n <- 50
> k <- seq(0,n,by=1)
> poisson_pdf <- microbenchmark(pdf<-dpois(k, 1, log = FALSE))
> poisson_cdf <- microbenchmark(cdf<-ppois(k, 1, log = FALSE))
> poisson_quantile <- microbenchmark(quantile<-qpois(cdf, 1, log = FALSE))
> poisson_random <- microbenchmark(random<-rpois(10000, 1))
> print(poisson_pdf)
Unit: microseconds
                            expr   min    lq    mean median    uq    max neval
 pdf <- dpois(k, 1, log = FALSE) 5.974 6.543 7.30316  6.544 6.828 54.046   100
> print(poisson_cdf)
Unit: microseconds
                            expr   min    lq     mean median    uq    max neval
 cdf <- ppois(k, 1, log = FALSE) 8.534 8.819 10.25846  9.104 9.388 64.286   100
> print(poisson_quantile)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 quantile <- qpois(cdf, 1, log = FALSE) 13.085 13.086 14.37438  13.37 13.654 61.157   100
> print(poisson_random)
Unit: microseconds
                      expr     min       lq     mean  median      uq     max neval
 random <- rpois(10000, 1) 303.219 314.8815 327.5787 324.552 341.335 373.477   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> f_pdf <- microbenchmark(pdf<-df(k, 10,20, log = FALSE))
> f_cdf <- microbenchmark(cdf<-pf(k, 10,20, log = FALSE))
> f_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,log = FALSE))
> f_random <- microbenchmark(random<-rf(10000, 10,20))
> print(f_pdf)
Unit: microseconds
                              expr    min    lq     mean median     uq    max neval
 pdf <- df(k, 10, 20, log = FALSE) 10.241 10.81 12.43159 10.811 11.095 71.112   100
> print(f_cdf)
Unit: microseconds
                              expr    min     lq     mean median      uq    max neval
 cdf <- pf(k, 10, 20, log = FALSE) 22.472 22.757 25.66972 23.041 23.3265 86.189   100
> print(f_quantile)
Unit: microseconds
                                     expr     min     lq     mean   median      uq     max neval
 quantile <- qf(cdf, 10, 20, log = FALSE) 135.396 136.25 166.7057 157.7255 186.171 255.717   100
> print(f_random)
Unit: milliseconds
                        expr      min       lq     mean   median      uq      max neval
 random <- rf(10000, 10, 20) 1.801955 1.889706 1.947645 1.929528 1.98272 2.725546   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> chisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,log = FALSE))
> chisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2, log = FALSE))
> chisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2, log = FALSE))
> chisquare_random <- microbenchmark(random<-rchisq(10000, 2))
> print(chisquare_pdf)
Unit: microseconds
                             expr   min    lq    mean median    uq    max neval
 pdf <- dchisq(k, 2, log = FALSE) 5.974 6.259 7.06416 6.4015 6.544 52.339   100
> print(chisquare_cdf)
Unit: microseconds
                             expr   min     lq     mean median    uq    max neval
 cdf <- pchisq(k, 2, log = FALSE) 13.37 13.655 15.46392 13.655 13.94 99.841   100
> print(chisquare_quantile)
Unit: microseconds
                                    expr    min      lq     mean  median    uq     max neval
 quantile <- qchisq(cdf, 2, log = FALSE) 61.725 62.2945 68.40176 62.7215 72.25 132.553   100
> print(chisquare_random)
Unit: milliseconds
                       expr      min      lq    mean   median       uq      max neval
 random <- rchisq(10000, 2) 1.235059 1.29408 1.38993 1.333903 1.401743 2.205582   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nchisquare_pdf <- microbenchmark(pdf<-dchisq(k, 2,1, log = FALSE))
> nchisquare_cdf <- microbenchmark(cdf<-pchisq(k, 2,1,log = FALSE))
> nchisquare_quantile <- microbenchmark(quantile<-qchisq(cdf, 2,1, log = FALSE))
> nchisquare_random <- microbenchmark(random<-rchisq(10000, 2,1))
> print(nchisquare_pdf)
Unit: microseconds
                                expr    min     lq    mean median      uq    max neval
 pdf <- dchisq(k, 2, 1, log = FALSE) 14.223 14.509 17.3866 14.793 15.6455 37.548   100
> print(nchisquare_cdf)
Unit: microseconds
                                expr     min     lq     mean   median      uq     max neval
 cdf <- pchisq(k, 2, 1, log = FALSE) 209.068 210.49 231.6357 223.1475 240.499 309.193   100
> print(nchisquare_quantile)
Unit: milliseconds
                                       expr      min       lq     mean   median       uq      max neval
 quantile <- qchisq(cdf, 2, 1, log = FALSE) 10.34296 10.65955 10.90239 10.83733 11.02563 12.31558   100
> print(nchisquare_random)
Unit: milliseconds
                          expr      min       lq     mean   median       uq      max neval
 random <- rchisq(10000, 2, 1) 1.997653 2.073457 2.187417 2.114845 2.183111 3.134576   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nf_pdf <- microbenchmark(pdf<-df(k, 10,20,2, log = FALSE))
> nf_cdf <- microbenchmark(cdf<-pf(k, 10,20,2, log = FALSE))
> nf_quantile <- microbenchmark(quantile<-qf(cdf, 10,20,2, log = FALSE))
> nf_random <- microbenchmark(random<-rf(10000, 10,20,2))
> print(nf_pdf)
Unit: microseconds
                                 expr    min     lq     mean median     uq    max neval
 pdf <- df(k, 10, 20, 2, log = FALSE) 28.446 30.153 34.12338 30.438 31.291 68.836   100
> print(nf_cdf)
Unit: microseconds
                                 expr    min      lq     mean median     uq     max neval
 cdf <- pf(k, 10, 20, 2, log = FALSE) 46.935 61.8685 64.53899 63.433 65.708 106.953   100
> print(nf_quantile)
Unit: milliseconds
                                        expr      min       lq     mean  median       uq      max neval
 quantile <- qf(cdf, 10, 20, 2, log = FALSE) 2.561991 2.640355 2.719223 2.68999 2.744461 3.737598   100
> print(nf_random)
Unit: milliseconds
                           expr      min       lq     mean   median       uq      max neval
 random <- rf(10000, 10, 20, 2) 2.912141 2.989225 3.100073 3.035163 3.110825 4.062433   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nbeta_pdf <- microbenchmark(pdf<-dbeta(k, 2,4,1, log = FALSE))
> nbeta_cdf <- microbenchmark(cdf<-pbeta(k, 2,4,1, log = FALSE))
> nbeta_quantile <- microbenchmark(quantile<-qbeta(cdf, 2,4,1, log = FALSE))
> nbeta_random <- microbenchmark(random<-rbeta(10000, 2,4,1))
> print(nbeta_pdf)
Unit: microseconds
                                  expr    min     lq     mean median      uq    max neval
 pdf <- dbeta(k, 2, 4, 1, log = FALSE) 26.739 27.308 31.31301 27.592 30.5795 56.891   100
> print(nbeta_cdf)
Unit: microseconds
                                  expr    min     lq     mean median      uq     max neval
 cdf <- pbeta(k, 2, 4, 1, log = FALSE) 43.237 43.806 55.11814 56.321 57.7435 167.255   100
> print(nbeta_quantile)
Unit: milliseconds
                                         expr      min       lq     mean   median      uq      max neval
 quantile <- qbeta(cdf, 2, 4, 1, log = FALSE) 2.290915 2.375111 2.440959 2.431146 2.49927 2.644764   100
> print(nbeta_random)
Unit: milliseconds
                            expr      min       lq     mean   median       uq      max neval
 random <- rbeta(10000, 2, 4, 1) 2.839893 3.002737 3.143906 3.073848 3.150932 4.302789   100
> 
> n <- 50
> k <- seq(0,n,by=1)
> nbinom_pdf <- microbenchmark(pdf<-dnbinom(k, 2, 0.5, log = FALSE))
> nbinom_cdf <- microbenchmark(cdf<-pnbinom(k, 2, 0.5, log = FALSE))
> nbinom_quantile <- microbenchmark(quantile<-qnbinom(cdf, 2, 0.5, log = FALSE))
> nbinom_random <- microbenchmark(random<-rnbinom(10000, 2, 0.5))
> print(nbinom_pdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq    max neval
 pdf <- dnbinom(k, 2, 0.5, log = FALSE) 11.094 11.379 13.37031 11.664 11.948 78.508   100
> print(nbinom_cdf)
Unit: microseconds
                                   expr    min     lq     mean median     uq     max neval
 cdf <- pnbinom(k, 2, 0.5, log = FALSE) 19.627 19.913 22.94469 20.197 20.482 130.277   100
> print(nbinom_quantile)
Unit: microseconds
                                          expr    min     lq     mean median     uq     max neval
 quantile <- qnbinom(cdf, 2, 0.5, log = FALSE) 60.019 60.588 69.73866 61.442 74.099 122.028   100
> print(nbinom_random)
Unit: milliseconds
                             expr      min       lq     mean   median       uq      max neval
 random <- rnbinom(10000, 2, 0.5) 1.936498 2.029226 2.086237 2.072035 2.125084 2.354061   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> normal_pdf <- microbenchmark(pdf<-dnorm(k, 1, 1, log = FALSE))
> normal_cdf <- microbenchmark(cdf<-pnorm(k, 1, 1, log = FALSE))
> normal_quantile <- microbenchmark(quantile<-qnorm(cdf, 1,1, log = FALSE))
> normal_random <- microbenchmark(random<-rnorm(10000, 1,1))
> print(normal_pdf)
Unit: microseconds
                               expr   min    lq   mean median    uq    max neval
 pdf <- dnorm(k, 1, 1, log = FALSE) 4.267 4.552 5.7927  4.553 4.837 75.663   100
> print(normal_cdf)
Unit: microseconds
                               expr   min    lq    mean median    uq    max neval
 cdf <- pnorm(k, 1, 1, log = FALSE) 3.983 4.269 5.94911  4.553 4.979 50.632   100
> print(normal_quantile)
Unit: microseconds
                                      expr   min    lq    mean median    uq    max neval
 quantile <- qnorm(cdf, 1, 1, log = FALSE) 2.277 2.561 3.42042  2.845 2.846 45.227   100
> print(normal_random)
Unit: microseconds
                         expr     min      lq     mean   median       uq     max neval
 random <- rnorm(10000, 1, 1) 696.321 728.747 779.1994 749.7965 778.3835 1541.12   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> lognormal_pdf <- microbenchmark(pdf<-dlnorm(k, 0.5,0.6, log = FALSE))
> lognormal_cdf <- microbenchmark(cdf<-plnorm(k, 0.5,0.6, log = FALSE))
> lognormal_quantile <- microbenchmark(quantile<-qlnorm(cdf, 0.5,0.6, log = FALSE))
> lognormal_random <- microbenchmark(random<-rlnorm(10000, 0.5,0.6))
> print(lognormal_pdf)
Unit: microseconds
                                    expr   min   lq    mean median    uq    max neval
 pdf <- dlnorm(k, 0.5, 0.6, log = FALSE) 5.406 5.69 6.89638  5.975 6.259 50.917   100
> print(lognormal_cdf)
Unit: microseconds
                                    expr   min    lq    mean median      uq    max neval
 cdf <- plnorm(k, 0.5, 0.6, log = FALSE) 8.819 9.387 12.3463 9.3885 12.6595 71.681   100
> print(lognormal_quantile)
Unit: microseconds
                                           expr   min    lq    mean median    uq    max neval
 quantile <- qlnorm(cdf, 0.5, 0.6, log = FALSE) 6.259 6.544 7.38277  6.544 6.828 58.881   100
> print(lognormal_random)
Unit: milliseconds
                              expr      min       lq     mean   median       uq      max neval
 random <- rlnorm(10000, 0.5, 0.6) 1.269761 1.329209 1.380386 1.362632 1.401743 2.247395   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> t_pdf <- microbenchmark(pdf<-dt(k, 8, log = FALSE))
> t_cdf <- microbenchmark(cdf<-pt(k, 8, log = FALSE))
> t_quantile <- microbenchmark(quantile<-qt(cdf, 8, log = FALSE))
> t_random <- microbenchmark(random<-rt(10000, 8))
> print(t_pdf)
Unit: microseconds
                         expr    min     lq     mean median      uq    max neval
 pdf <- dt(k, 8, log = FALSE) 11.663 12.233 15.71413 12.517 16.0725 76.517   100
> print(t_cdf)
Unit: microseconds
                         expr    min      lq     mean median     uq     max neval
 cdf <- pt(k, 8, log = FALSE) 19.059 20.6235 23.23485  21.05 21.619 127.717   100
> print(t_quantile)
Unit: microseconds
                                expr    min     lq     mean median    uq     max neval
 quantile <- qt(cdf, 8, log = FALSE) 58.596 58.882 64.84339 59.166 62.01 151.611   100
> print(t_random)
Unit: milliseconds
                   expr     min       lq     mean  median       uq     max neval
 random <- rt(10000, 8) 1.42592 1.480676 1.553132 1.51424 1.569565 2.44679   100
> 
> n <- 50
> k <- seq(0,1,by=1/n)
> nt_pdf <- microbenchmark(pdf<-dt(k, 10,1, log = FALSE))
> nt_cdf <- microbenchmark(cdf<-pt(k, 10,1, log = FALSE))
> nt_quantile <- microbenchmark(quantile<-qt(cdf, 10,1, log = FALSE))
> nt_random <- microbenchmark(random<-rt(10000, 10,1))
> print(nt_pdf)
Unit: microseconds
                             expr    min     lq     mean median      uq     max neval
 pdf <- dt(k, 10, 1, log = FALSE) 86.757 88.037 92.88671 89.317 91.4505 130.276   100
> print(nt_cdf)
Unit: microseconds
                             expr    min      lq     mean  median     uq    max neval
 cdf <- pt(k, 10, 1, log = FALSE) 39.823 40.2505 44.51695 40.6765 49.352 70.829   100
> print(nt_quantile)
Unit: milliseconds
                                    expr      min       lq     mean median       uq      max neval
 quantile <- qt(cdf, 10, 1, log = FALSE) 1.930524 1.981866 2.038755 2.0224 2.079715 2.594987   100
> print(nt_random)
Unit: milliseconds
                       expr     min       lq     mean   median       uq      max neval
 random <- rt(10000, 10, 1) 1.69984 1.764693 1.867469 1.814044 1.893263 2.856959   100

脚本 TestStatBenchmark.mq5 的操作结果:

IG    0    13:06:15.252    TestStatBenchmark (EURUSD,H1)    Unit tests for Package Statistic Benchmark
PP    0    13:06:15.252    TestStatBenchmark (EURUSD,H1)   
KJ    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds):      pdf_mean=4.39,      pdf_median=4.00,      pdf_min=3.00,      pdf_max=40.00,       pdf_stddev=2.21,       pdf_avgdev=0.95
MS    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds):      cdf_mean=13.65,      cdf_median=12.00,      cdf_min=11.00,      cdf_max=54.00,       cdf_stddev=4.09,       cdf_avgdev=2.37
GF    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds): quantile_mean=50.18, quantile_median=45.00, quantile_min=43.00, quantile_max=108.00,  quantile_stddev=9.97,  quantile_avgdev=7.41
QO    0    13:06:15.639    TestStatBenchmark (EURUSD,H1)    Binomial time (microseconds):   random_mean=318.73,   random_median=312.00,   random_min=284.00,   random_max=478.00,    random_stddev=28.74,    random_avgdev=22.22
LP    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds):      pdf_mean=1.74,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=18.00,       pdf_stddev=1.07,       pdf_avgdev=0.53
EI    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds):      cdf_mean=4.76,      cdf_median=4.00,      cdf_min=3.00,      cdf_max=68.00,       cdf_stddev=3.07,       cdf_avgdev=1.19
LM    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds): quantile_mean=48.72, quantile_median=44.00, quantile_min=43.00, quantile_max=111.00,  quantile_stddev=10.21,  quantile_avgdev=6.96
QG    0    13:06:16.384    TestStatBenchmark (EURUSD,H1)    Beta time (microseconds):   random_mean=688.81,   random_median=680.00,   random_min=625.00,   random_max=976.00,    random_stddev=43.92,    random_avgdev=31.81
HE    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds):      pdf_mean=1.31,      pdf_median=1.00,      pdf_min=1.00,      pdf_max=13.00,       pdf_stddev=0.82,       pdf_avgdev=0.47
GL    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds):      cdf_mean=8.09,      cdf_median=7.00,      cdf_min=7.00,      cdf_max=92.00,       cdf_stddev=3.67,       cdf_avgdev=1.40
CF    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds): quantile_mean=50.83, quantile_median=46.00, quantile_min=45.00, quantile_max=106.00,  quantile_stddev=9.27,  quantile_avgdev=6.72
GR    0    13:06:16.587    TestStatBenchmark (EURUSD,H1)    Gamma time (microseconds):   random_mean=142.84,   random_median=132.00,   random_min=128.00,   random_max=260.00,    random_stddev=19.73,    random_avgdev=15.32
QD    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds):      pdf_mean=0.45,      pdf_median=0.00,      pdf_min=0.00,      pdf_max=11.00,       pdf_stddev=0.85,       pdf_avgdev=0.54
QK    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds):      cdf_mean=1.33,      cdf_median=1.00,      cdf_min=1.00,      cdf_max=12.00,       cdf_stddev=0.81,       cdf_avgdev=0.48
MR    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds): quantile_mean=1.37, quantile_median=1.00, quantile_min=1.00, quantile_max=14.00,  quantile_stddev=0.89,  quantile_avgdev=0.51
IK    0    13:06:16.815    TestStatBenchmark (EURUSD,H1)    Cauchy time (microseconds):   random_mean=224.19,   random_median=215.00,   random_min=200.00,   random_max=352.00,    random_stddev=26.86,    random_avgdev=20.34
PQ    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds):      pdf_mean=0.85,      pdf_median=1.00,      pdf_min=0.00,      pdf_max=18.00,       pdf_stddev=1.40,       pdf_avgdev=0.54
GK    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds):      cdf_mean=0.77,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=16.00,       cdf_stddev=0.94,       cdf_avgdev=0.47
HE    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds): quantile_mean=0.53, quantile_median=0.00, quantile_min=0.00, quantile_max=10.00,  quantile_stddev=0.78,  quantile_avgdev=0.54
HL    0    13:06:16.960    TestStatBenchmark (EURUSD,H1)    Exponential time (microseconds):   random_mean=143.18,   random_median=130.00,   random_min=128.00,   random_max=272.00,    random_stddev=21.58,    random_avgdev=16.98
LK    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds):      pdf_mean=0.42,      pdf_median=0.00,      pdf_min=0.00,      pdf_max=12.00,       pdf_stddev=0.82,       pdf_avgdev=0.52
CE    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds):      cdf_mean=0.45,      cdf_median=0.00,      cdf_min=0.00,      cdf_max=16.00,       cdf_stddev=0.96,       cdf_avgdev=0.55
LO    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds): quantile_mean=0.18, quantile_median=0.00, quantile_min=0.00, quantile_max=1.00,  quantile_stddev=0.38,  quantile_avgdev=0.29
GE    0    13:06:17.002    TestStatBenchmark (EURUSD,H1)    Uniform time (microseconds):   random_mean=40.30,   random_median=36.00,   random_min=35.00,   random_max=83.00,    random_stddev=7.61,    random_avgdev=5.41
OP    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds):      pdf_mean=2.30,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=14.00,       pdf_stddev=1.30,       pdf_avgdev=0.52
DK    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds):      cdf_mean=2.12,      cdf_median=2.00,      cdf_min=1.00,      cdf_max=18.00,       cdf_stddev=1.69,       cdf_avgdev=0.53
NE    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds): quantile_mean=0.81, quantile_median=1.00, quantile_min=0.00, quantile_max=10.00,  quantile_stddev=0.68,  quantile_avgdev=0.39
IL    0    13:06:17.286    TestStatBenchmark (EURUSD,H1)    Geometric time (microseconds):   random_mean=278.00,   random_median=271.00,   random_min=251.00,   random_max=429.00,    random_stddev=28.23,    random_avgdev=21.62
PG    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds):      pdf_mean=1.85,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=15.00,       pdf_stddev=1.07,       pdf_avgdev=0.48
CM    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds):      cdf_mean=0.90,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=17.00,       cdf_stddev=0.85,       cdf_avgdev=0.32
NP    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds): quantile_mean=0.75, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00,  quantile_stddev=0.96,  quantile_avgdev=0.48
FE    0    13:06:17.592    TestStatBenchmark (EURUSD,H1)    Hypergeometric time (microseconds):   random_mean=302.55,   random_median=295.00,   random_min=272.00,   random_max=466.00,    random_stddev=30.20,    random_avgdev=22.99
ML    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds):      pdf_mean=1.27,      pdf_median=1.00,      pdf_min=0.00,      pdf_max=91.00,       pdf_stddev=3.04,       pdf_avgdev=0.56
DR    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds):      cdf_mean=1.11,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=17.00,       cdf_stddev=1.34,       cdf_avgdev=0.40
IH    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds): quantile_mean=0.71, quantile_median=1.00, quantile_min=0.00, quantile_max=12.00,  quantile_stddev=0.79,  quantile_avgdev=0.47
GL    0    13:06:17.774    TestStatBenchmark (EURUSD,H1)    Logistic time (microseconds):   random_mean=178.65,   random_median=164.00,   random_min=162.00,   random_max=309.00,    random_stddev=24.09,    random_avgdev=17.94
MJ    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds):      pdf_mean=2.99,      pdf_median=3.00,      pdf_min=2.00,      pdf_max=17.00,       pdf_stddev=1.63,       pdf_avgdev=0.57
GD    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds):      cdf_mean=2.74,      cdf_median=3.00,      cdf_min=2.00,      cdf_max=19.00,       cdf_stddev=1.23,       cdf_avgdev=0.58
FO    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds): quantile_mean=2.64, quantile_median=2.00, quantile_min=2.00, quantile_max=19.00,  quantile_stddev=1.64,  quantile_avgdev=0.76
DJ    0    13:06:18.319    TestStatBenchmark (EURUSD,H1)    Weibull time (microseconds):   random_mean=536.37,   random_median=526.00,   random_min=483.00,   random_max=759.00,    random_stddev=46.99,    random_avgdev=34.40
HR    0    13:06:18.485    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds):      pdf_mean=2.91,      pdf_median=3.00,      pdf_min=2.00,      pdf_max=15.00,       pdf_stddev=1.40,       pdf_avgdev=0.58
IL    0    13:06:18.486    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds):      cdf_mean=6.26,      cdf_median=6.00,      cdf_min=5.00,      cdf_max=23.00,       cdf_stddev=2.38,       cdf_avgdev=1.07
HE    0    13:06:18.486    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds): quantile_mean=3.43, quantile_median=3.00, quantile_min=2.00, quantile_max=20.00,  quantile_stddev=1.48,  quantile_avgdev=0.68
DL    0    13:06:18.486    TestStatBenchmark (EURUSD,H1)    Poisson time (microseconds):   random_mean=153.59,   random_median=144.00,   random_min=138.00,   random_max=265.00,    random_stddev=18.57,    random_avgdev=13.99
IH    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds):      pdf_mean=3.86,      pdf_median=4.00,      pdf_min=3.00,      pdf_max=21.00,       pdf_stddev=1.78,       pdf_avgdev=0.76
GS    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds):      cdf_mean=9.94,      cdf_median=9.00,      cdf_min=7.00,      cdf_max=36.00,       cdf_stddev=3.82,       cdf_avgdev=2.15
OI    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds): quantile_mean=65.47, quantile_median=59.00, quantile_min=57.00, quantile_max=147.00,  quantile_stddev=12.99,  quantile_avgdev=9.64
DE    0    13:06:19.814    TestStatBenchmark (EURUSD,H1)    F time (microseconds):   random_mean=1249.22,   random_median=1213.00,   random_min=1127.00,   random_max=1968.00,    random_stddev=117.69,    random_avgdev=72.17
EL    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds):      pdf_mean=2.47,      pdf_median=2.00,      pdf_min=2.00,      pdf_max=13.00,       pdf_stddev=1.32,       pdf_avgdev=0.65
JK    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds):      cdf_mean=7.71,      cdf_median=7.00,      cdf_min=7.00,      cdf_max=23.00,       cdf_stddev=1.91,       cdf_avgdev=0.88
KQ    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds): quantile_mean=44.11, quantile_median=41.00, quantile_min=40.00, quantile_max=120.00,  quantile_stddev=8.17,  quantile_avgdev=5.38
CL    0    13:06:20.079    TestStatBenchmark (EURUSD,H1)    ChiSquare time (microseconds):   random_mean=210.24,   random_median=196.00,   random_min=190.00,   random_max=437.00,    random_stddev=29.14,    random_avgdev=21.00
HD    0    13:06:21.098    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds):      pdf_mean=8.05,      pdf_median=8.00,      pdf_min=7.00,      pdf_max=24.00,       pdf_stddev=2.41,       pdf_avgdev=1.09
MR    0    13:06:21.098    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds):      cdf_mean=45.61,      cdf_median=42.00,      cdf_min=41.00,      cdf_max=97.00,       cdf_stddev=8.25,       cdf_avgdev=5.70
FN    0    13:06:21.098    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds): quantile_mean=220.66, quantile_median=211.50, quantile_min=196.00, quantile_max=362.00,  quantile_stddev=24.71,  quantile_avgdev=19.45
LI    0    13:06:21.099    TestStatBenchmark (EURUSD,H1)    Noncentral ChiSquare time (microseconds):   random_mean=744.45,   random_median=728.00,   random_min=672.00,   random_max=1082.00,    random_stddev=62.42,    random_avgdev=43.24
RE    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds):      pdf_mean=19.10,      pdf_median=18.00,      pdf_min=16.00,      pdf_max=50.00,       pdf_stddev=4.67,       pdf_avgdev=2.64
FS    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds):      cdf_mean=14.67,      cdf_median=13.00,      cdf_min=12.00,      cdf_max=39.00,       cdf_stddev=3.94,       cdf_avgdev=2.44
EN    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds): quantile_mean=212.21, quantile_median=203.00, quantile_min=189.00, quantile_max=347.00,  quantile_stddev=24.37,  quantile_avgdev=19.30
EF    0    13:06:23.194    TestStatBenchmark (EURUSD,H1)    Noncentral F time (microseconds):   random_mean=1848.90,   random_median=1819.00,   random_min=1704.00,   random_max=2556.00,    random_stddev=118.75,    random_avgdev=78.66
EN    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds):      pdf_mean=16.30,      pdf_median=15.00,      pdf_min=14.00,      pdf_max=43.00,       pdf_stddev=4.32,       pdf_avgdev=2.43
EP    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds):      cdf_mean=10.48,      cdf_median=10.00,      cdf_min=8.00,      cdf_max=32.00,       cdf_stddev=3.02,       cdf_avgdev=1.72
ME    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds): quantile_mean=153.66, quantile_median=141.00, quantile_min=135.00, quantile_max=283.00,  quantile_stddev=20.83,  quantile_avgdev=16.16
QJ    0    13:06:26.061    TestStatBenchmark (EURUSD,H1)    Noncentral Beta time (microseconds):   random_mean=2686.82,   random_median=2649.00,   random_min=2457.00,   random_max=3753.00,    random_stddev=150.32,    random_avgdev=98.23
OO    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds):      pdf_mean=6.13,      pdf_median=6.00,      pdf_min=5.00,      pdf_max=24.00,       pdf_stddev=2.38,       pdf_avgdev=1.22
DG    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds):      cdf_mean=12.21,      cdf_median=11.00,      cdf_min=11.00,      cdf_max=33.00,       cdf_stddev=3.07,       cdf_avgdev=1.58
LJ    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds): quantile_mean=14.05, quantile_median=13.00, quantile_min=12.00, quantile_max=82.00,  quantile_stddev=4.81,  quantile_avgdev=2.28
EM    0    13:06:27.225    TestStatBenchmark (EURUSD,H1)    Negative Binomial time (microseconds):   random_mean=1130.39,   random_median=1108.00,   random_min=1039.00,   random_max=1454.00,    random_stddev=69.41,    random_avgdev=51.70
GP    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds):      pdf_mean=1.15,      pdf_median=1.00,      pdf_min=0.00,      pdf_max=19.00,       pdf_stddev=1.34,       pdf_avgdev=0.45
OI    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds):      cdf_mean=0.81,      cdf_median=1.00,      cdf_min=0.00,      cdf_max=17.00,       cdf_stddev=1.16,       cdf_avgdev=0.49
CN    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds): quantile_mean=0.70, quantile_median=1.00, quantile_min=0.00, quantile_max=13.00,  quantile_stddev=0.82,  quantile_avgdev=0.49
EG    0    13:06:27.521    TestStatBenchmark (EURUSD,H1)    Normal time (microseconds):   random_mean=293.70,   random_median=281.00,   random_min=256.00,   random_max=537.00,    random_stddev=43.28,    random_avgdev=31.62
FD    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds):      pdf_mean=1.99,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=18.00,       pdf_stddev=1.48,       pdf_avgdev=0.48
PN    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds):      cdf_mean=3.19,      cdf_median=3.00,      cdf_min=2.00,      cdf_max=17.00,       cdf_stddev=1.61,       cdf_avgdev=0.64
DH    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds): quantile_mean=3.18, quantile_median=3.00, quantile_min=2.00, quantile_max=19.00,  quantile_stddev=1.77,  quantile_avgdev=0.64
NR    0    13:06:28.010    TestStatBenchmark (EURUSD,H1)    Lognormal time (microseconds):   random_mean=479.75,   random_median=468.00,   random_min=428.00,   random_max=754.00,    random_stddev=48.26,    random_avgdev=34.30
FL    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds):      pdf_mean=2.32,      pdf_median=2.00,      pdf_min=1.00,      pdf_max=15.00,       pdf_stddev=1.29,       pdf_avgdev=0.54
QE    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds):      cdf_mean=8.01,      cdf_median=7.00,      cdf_min=6.00,      cdf_max=39.00,       cdf_stddev=3.13,       cdf_avgdev=1.73
MM    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds): quantile_mean=50.23, quantile_median=45.00, quantile_min=44.00, quantile_max=113.00,  quantile_stddev=10.28,  quantile_avgdev=7.73
KG    0    13:06:29.022    TestStatBenchmark (EURUSD,H1)    T time (microseconds):   random_mean=951.58,   random_median=931.00,   random_min=859.00,   random_max=1439.00,    random_stddev=78.14,    random_avgdev=49.72
CQ    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds):      pdf_mean=38.47,      pdf_median=35.00,      pdf_min=32.00,      pdf_max=164.00,       pdf_stddev=9.66,       pdf_avgdev=6.38
OO    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds):      cdf_mean=27.75,      cdf_median=25.00,      cdf_min=24.00,      cdf_max=80.00,       cdf_stddev=7.02,       cdf_avgdev=4.63
PF    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds): quantile_mean=1339.51, quantile_median=1306.00, quantile_min=1206.00, quantile_max=2262.00,  quantile_stddev=128.18,  quantile_avgdev=74.83
OR    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    Noncentral T time (microseconds):   random_mean=1550.27,   random_median=1520.00,   random_min=1418.00,   random_max=2317.00,    random_stddev=112.08,    random_avgdev=73.74
LQ    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)   
GH    0    13:06:31.979    TestStatBenchmark (EURUSD,H1)    21 of 21 passed