MQL5 Wizard Techniques you should know (Part 45): Reinforcement Learning with Monte-Carlo

Introduction

This article continues our look at reinforcement learning by considering another algorithm, namely the Monte-Carlo. This algorithm is very similar and in fact arguably encompasses both Q-Learning and SARSA in that it can be either on-policy or off-policy. What sets it apart though is the emphasis on episodes. These simply are a way of batching the reinforcement learning cycle updates, that we introduced in this article, such that the updating of the Q-Values of the Q-Map happens less frequently.

With the Monte Carlo algorithm, Q-Values are only updated after the completion of an episode. An episode is a batch of cycles. For this article, we have assigned this number of cycles the input parameter ‘m_episodes_size’ and it is optimizable or adjustable. Monte Carlo is attributed to being quite robust to market variability because it can better simulate a wide range of possible market scenarios, allowing traders to determine how different strategies perform under a variety of conditions. This variability helps traders understand potential tradeoffs, risks and returns, enabling them to make more informed decisions.

This edge, it is argued, stems from its ‘long-term performance insight’ which contrasts with traditional methods that tend to focus on short-term outcomes. By this what’s meant is the infrequent updates Monte Carlo simulations performs, given that they only happen once in an episode, do evade market noise which Q-Learning & SARSA are bound to run into since they execute their updates more frequently. Assessment of the long-term performance of trading strategies by evaluating cumulative rewards over time is therefore what Monte Carlo strives to achieve. By analysing multiple episodes of this, traders can gain insights into the overall profitability and sustainability of their strategies.

The Monte Carlo algorithm computes action-value estimates based on average returns of state-action pairs across multiple cycles within a single episode. This better allows traders to assess which actions (e.g., buying or selling) are most likely to yield favourable outcomes based on historical performance. This updating of the Q-Values stems from having the reward component of these Q-Values determined as follows:

Where:

• R t+1 , R t+2 ,…,R T  are the rewards received at each step after time t.
• γ /gamma is the discount factor (0 ≤ γ ≤ 1), which sets by how much future rewards are "discounted" (i.e., valued less than immediate rewards).
• T represents the time step at which the episode ends (terminal state or episode size in cycles).

These over-arching reward considerations, implied by the updating of Q-Values indicated above, tend to make Monte Carlo more adaptable, as already alluded to. This inherent adaptability, allows traders to adjust their strategies based on evolving market conditions. This adaptability is crucial in financial markets, where trends can change rapidly, and past performance may not always predict future results. In the last reinforcement learning article that covered SARSA we looked at reinforcement learning as an independent model that was trained to forecast price action and not just assist in the training of other machine learning models as would traditionally be the case if we were to consider it as a 3^rd form of training besides supervised and unsupervised learning. We follow a similar approach for this article.

The strategies therefore that would be adaptable under Monte Carlo would in many ways be informed by the choice of Q-Map, and states. For the last article seeing as the reinforcement learning algorithm was also the main forecasting model for the Expert Advisor, via a custom signal class, we used 3 environment states crossed across a short term-horizon and long-term horizon to create a grid/ matrix of 9 options. What these states captured was simply bullishness, flatness and bearishness, and it is relatively simple/ crude. However, it has potential to be made more elaborate and sensitive to the markets by not just increasing its overall dimensions, but also by adding more factors for it to consider. When this is then married to Monte Carlo, then the adaptability will be enhanced.

Recap on Reinforcement Learning (RL) in Trading

Reinforcement learning (RL) is intended to operate in dynamic environments such as financial markets, where it continually interacts with its ‘surroundings’ by taking actions (such as buying, selling, holding) based on its current state (where these states are defined by market prices or indicators etc.). Each action taken by the agent influences the state of the environment, leading to new observations and potential rewards.

Additional examples of state-sets that can be adopted by traders for their Q-Maps can include Technical Indicator-Based States. These can include Moving Averages where if the Short-term MA is more than the Long-term MA is a Bullish state while a Short-term MA being below the Long-term MA would imply a Bearish state and equality meaning a neutral state.

Since we have combined both short-term and long-term outlooks on a single axis, it means we now have the opportunity of introducing another axis that covers different metrics besides MA indicator readings. Another indicator reading that could be used for this is the Relative Strength Index (RSI). With it, we would consider the states of Overbought (RSI > 70) that could potentially be a sell signal, and the state of Oversold (RSI < 30) that would potentially be a buy signal, plus an additional transient state that offers no signal.

Or still within the indicator-based states we could look at the Bollinger-Bands where price being near or above the upper band could be a bearish state, while price at or below the lower band could be a bullish state with again a 3^rd neutral state being implied for any other position.

Besides technical indicator states, market volatility could also present an alternative axis to the environment states matrix. With this, measurement would be based on indicators like the standard deviation of price, or the ATR and while one could use three possible states of high volatility, low volatility, and mild; many more gradations could be added to better make the algorithm more sensitive to the markets. This state setup (or axis) would help guide the agent on whether to trade aggressively or conservatively. Volume-based states can also be considered for equities, with a similar gradation.

Besides the bearish and bullish trends in price action that we have used in the past articles and are considering as states for this one as well, more specific price-action patterns like breakouts through support/ resistance levels. Alternatively, it could be for head and shoulders patterns for both the bullish and bearish signals, with any other pattern being a whipsaw. The recognizing of such patterns in recent price action would enable the agent to anticipate continuation or reversal.

Another possible axis to the Q-Map states could be time-based states. Recall this axis would then be paired with another axis such as price action above or the mentioned technical indicators such that inference can be drawn to which price action is more dependable in each time period. Possible time states can include market open/ close, the trading sessions, or even days of the week. Sentiment-based states are another axis that could form the environment states matrix. Measuring of these sentiments would be dependent on economic news calendar readings for a specific indicator, given the variety that is available. The gradation of these states should range from positive to neutral to negative, with intra states addable depending on the granularity one is interested in. Incorporating sentiment states, particularly with these methods, could help the agent respond to external events affecting the market.

Similar and alternative to this would be economic event-based states. However, something different from these two that could also be considered is portfolio-based-states. This category is very applicable outside of forex, and it does present a number of potential axes. First up is exposure-levels, where one’s portfolio is graded on relative exposure of say equities to bonds. The gradation could range from 90-10 on one end up to 10-90 on the other end respectively. Such an axis can be paired with time or any other different but related metric such that portfolio performance (which would be aligned to the agent-rewards) can guide the Q-Value update process.

Another option in portfolio-based-states is risk-level. This could consider capital allocation percentages, for each investment, with the state gradations ranging from a small amount < 0.5% to a cap of say 10%. Again, comparison or the pairing of this could be with another portfolio specific metric and an optimization over a decent data set should provide a Q-Map that guides on what risk-levels to use when. Another alternative could be drawdown states, and in summary these portfolio-based-states would allow the agent to account for the broader financial context, and not just isolated market signals.

I could also mention macro-trend-states, the principles are similar but more importantly the examples shared here are not exhaustive. The choice of environment-states can go a long way in defining one’s strategy and therefore delivering his edge depending on how unique it is as well as the effort put into not just testing but also in cross-validating it.

Besides environment states, the reward signals after each action, provide the agent with feedback in the form that indicates the success or failure of its action. Rewards can be quantified in terms of profit/loss (as we have been applying so far), risk-adjusted returns, or any other relevant performance metric, that can guide the agent toward more favourable actions. Recall, the rewards are a key component in updating the Q-Values of the Q-Map.

RL is perhaps better known for balancing exploration vs. exploitation when making forecasts. On paper, the agent often employs exploration strategies to discover new actions that might yield better rewards, while alternately exploiting known actions that have previously proven successful. The balancing of exploration and exploitation, which is controlled by an input parameter epsilon, is crucial for the agent to avoid local optima and continue improving its decision-making over time.

Through trial and error therefore, since the epsilon-greedy approach in selecting suitable actions incorporates random selection; the agent learns from its experiences in the environment, and adjusts its action selection policy by basing on past outcomes. With each experience, the agent’s understanding of which actions lead to positive rewards, enabling it to make better choices in similar future situations; improves.

This improvement is thanks to the agent’s Q-Map values or policy. The map represents a strategy that pairs states to actions, and continuously updates each state’s actions by basing on the observed rewards. The improvement of the policy is guided by reinforcement learning algorithms that aim to maximize cumulative rewards over time.

Those are the basic aspects we had looked at in the last three articles on RL; however there are more innovative concepts still within RL. One such is value function estimation, where the agent often estimates the value function, that can predict the expected return from a given state or state-action pair. By approximating the value function, the agent can assess the potential long-term benefits of different actions, thus facilitating better decisions.

Temporal Credit Assignment is another concept where the agent connects actions taken in the past with rewards received in the future. This approach on paper does allow the agent to understand how its previous actions affect future outcomes, which can lead to better planning or the pre-emptive setting of certain policies that override default action-state pairing.

Another one is adaptive learning rates, a theme we considered in this past article when we were dealing with Multi-Layer-Perceptrons. These too can be engaged as alpha when performing Q-Value updates. The agent can employ them whereby they adjust based on the uncertainty of state-action values, enabling more aggressive updates when the agent is uncertain and more conservative updates as it gains confidence. This adaptability could help the agent learn efficiently in varying market conditions.

Other RL related noteworthy ideas include Generalization Across States to improve efficiency and Long-Term Strategy Development that looks beyond immediate rewards.

The Monte Carlo Algorithm

The Learning Approach adopted by Monte Carlo methods is different from the earlier RL algorithms we considered in that it learns from complete episodes of experience, waiting until the end of an episode to ‘learn’ but taking a wholistic approach across multiple reward points that were received in the interim. This therefore calls for the need to have reward values buffered across multiple times so that when the episode is concluded, all past reward values are accessible. We implement this in MQL5 as follows, from within the get output function of our custom signal class:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalMC::GetOutput(Cql *QL, vector &Rewards)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      for(int i = m_episode_cycles - 1; i > 0; i--)
      {  Rewards[i] = Rewards[i - 1];
      }
      Rewards[0] = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.transition_act = 1;
      if(Rewards[m_episode_cycles - 1] != -1.0)
      {  double _reward = Rewards[m_episode_cycles - 1];
         for(int i = m_episode_cycles - 2; i >= 0; i--)
         {  _reward += pow(QL.THIS.gamma, m_episode_cycles - 1 - i) * Rewards[i];
         }
         if(m_policy)
         {  QL.SetOnPolicy(_reward, _in_e);
         }
         else if(!m_policy)
         {  QL.SetOffPolicy(_reward, _in_e);
         }
      }
   }
}

Q-Learning by contrast uses a temporal-difference (TD) learning method that updates the value estimates after each action taken (or after each cycle), using bootstrapping from subsequent state-action values. This is similar to SARSA but here updates to the value estimates are done using the action taken in the next state, providing an on-policy learning approach.

Monte Carlo update mechanism is based on the average return observed after taking actions from a state across multiple cycles in an episode. Each state-action pair is updated only once the episode is complete, so as to reflect the true long-term return. The reward value used in this update is therefore a weighted sum as shown in the formula already shared above, as well as the MQL5 code in the get output function above.

Q-Learning, however, uses the maximum future reward from the next state (off-policy) to make updates on the current state's action value, which can lead to more aggressive learning as it considers the best possible outcome on each cycle step within an episode. Similarly, SARSA does update the value based on actual action taken in the next state (on-policy), merging the agent's current policy into the learning process, which can lead to slightly more conservative updates than Q-Learning but still more aggressive than Monte Carlo.

Monte Carlo, as a rule, relies on complete exploration of the environment through multiple cycles in an episode, to learn optimal actions, allowing for thorough sampling of state-action pairs before making updates. This is via an ε-greedy approach, which we introduced with our introductory article on Q-Learning, where updates were influenced by actions not taken by the agent.

SARSA is also ε-greedy in its approach to balancing exploration and exploitation, however it updates values based on the action actually taken in the next state, making it more responsive to the agent's current policy and exploration choices. Monte Carlo’s difference from these two, besides having updates done only once in an episode, is that it can be either on-policy or off-policy. To this end, our custom signal class for Monte Carlo has an input parameter m_on_policy which is boolean, and as its name suggests would guide whether it is being used in an on or off policy state.

The class interface for this custom signal class is presented below:

//+------------------------------------------------------------------+
//| MCs CSignalMC.                                                   |
//| Purpose: MonteCarlo for Reinforcement-Learning.                  |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
class CSignalMC   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   int                           m_episode_cycles;    // Episode Size

public:
   void                          CSignalMC(void);
   void                          ~CSignalMC(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }
   void                          QL_EpisodeCycles(int value)
   {  m_episode_cycles = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   void              GetOutput(Cql *QL, vector &Rewards);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   vector            REWARDS_BUY, REWARDS_SELL;
};

Monte Carlo convergence tends to be slower as it requires complete episodes for updates, which may not necessarily be efficient in environments with long episodes or sparse rewards. This contrasts with the Q-Learning algorithm that for the most part converges faster due to its bootstrapping nature, however is bound to be unstable since it can oscillate or diverge in environments with non-stationary rewards or high variance. SARSA is touted as more stable than Q-Learning in certain situations since it accounts for the agent's actual policy during updates, which tends to result in smoother learning curves.

When it comes to sampling efficiency, Monte Carlo is typically less sample-efficient due to its requirements for full episodes to obtain updates, which can be a major drawback in environments with a large state-action space. Q-Learning, on the other hand, is more sample-efficient as it updates values at every step, allowing for quicker modifications based on immediate feedback. In fact, it is arguably even more efficient than SARSA, since the later may require more samples than Q-Learning because it is sensitive to the current policy and the exploration strategy used.

Monte Carlo is well-suited for environments where episodes can be defined clearly, and the long-term returns tend to be more crucial than short run spurts, such as in trading simulations. This clearly sets it up as a key strategy for value or long-term ‘traders’. Q-Learning is effective in environments with a clear reward structure and well-defined state transitions, making it ideal for tasks like day trading. While SARSA is beneficial in situations where learning needs to reflect the agent's policy closely, such as in dynamic or partially observable environments where adaptation is crucial like swing trading.

Implementing Monte Carlo in a Custom Signal Class

We implement our custom signal that uses Monte Carlo RL as the root model and signal generator. Main steps in realizing this are already shared above with the class interface and the get output function. Below are the long and short condition functions:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalMC::LongCondition(void)
{  int result = 0;
   GetOutput(QL_BUY, REWARDS_BUY);
   if(QL_BUY.transition_act == 0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalMC::ShortCondition(void)
{  int result = 0;
   GetOutput(QL_SELL, REWARDS_SELL);
   if(QL_SELL.transition_act == 2)
   {  result = 100;//printf(__FUNCSIG__);
   }
   return(result);
}

Complete source code for this implementation is attached at the bottom, and guides on using it to assemble a wizard assembled Expert Advisor can be found here and here. The Markov decision process is inherent in using Q-Maps, nonetheless there is an input parameter that present the option to use Markov weighting when performing Q-Value updates. In addition, we can optimize for whether to use on policy or not, the size of epsilon our parameter that guides the extent to which we explore vs exploit and the number of cycles in an episode. We perform optimization runs on the pair GBP USD for the year 2022 on the one-hour time frame. Below are our results:

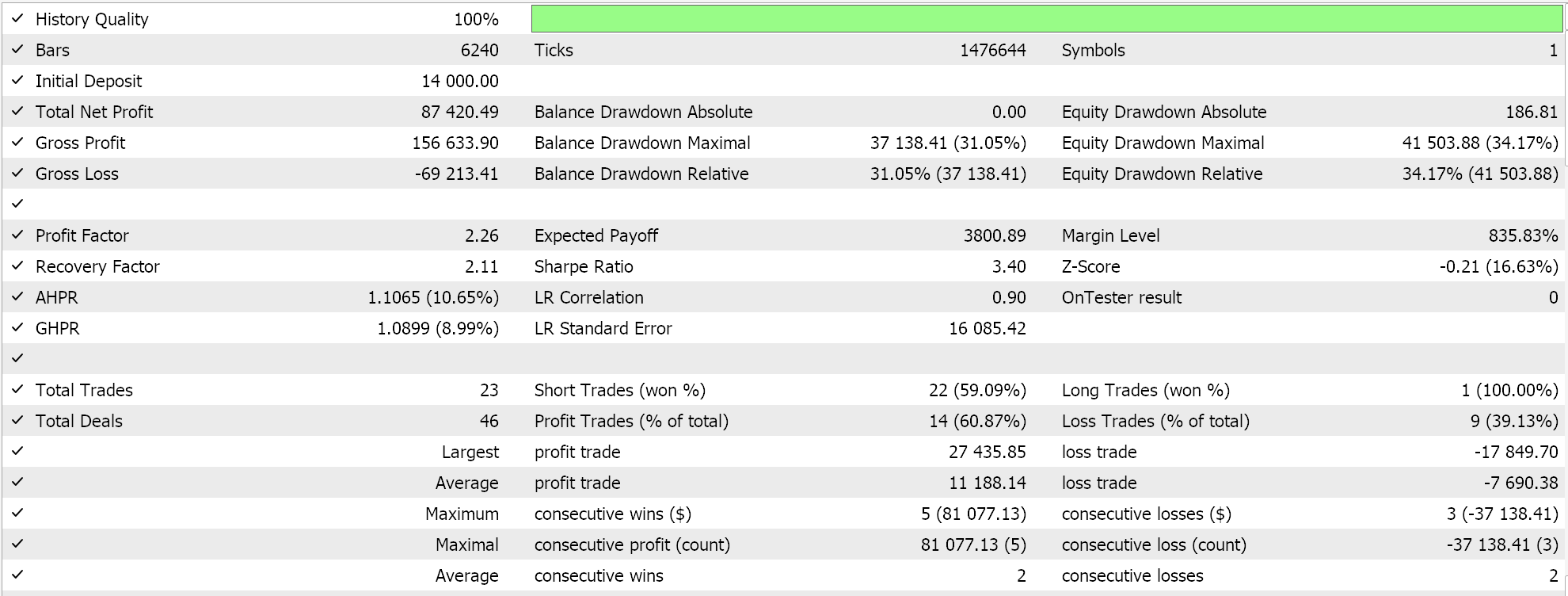
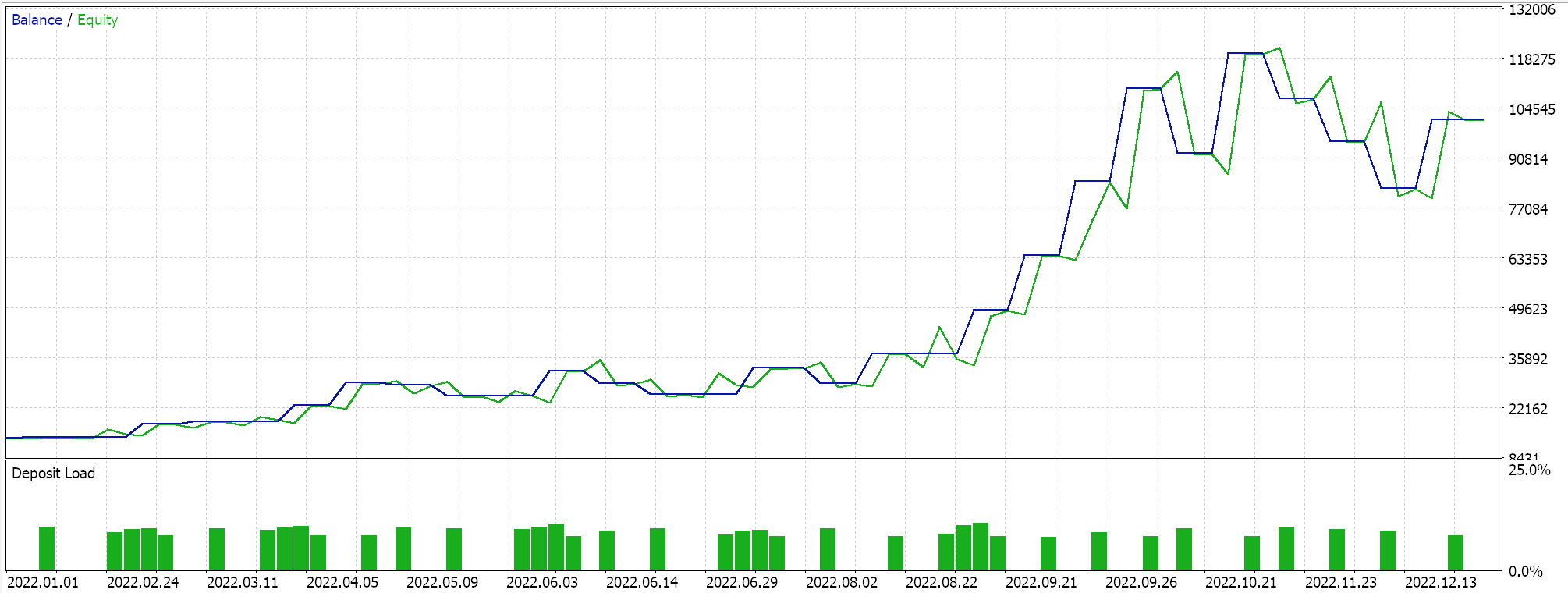
Conclusion and Additional Considerations

In summary, we have looked at the Monte Carlo algorithm of Reinforcement Learning which takes a lot of features from Q-Learning and SARSA, two algorithms we had previously covered here and here respectively, and presents an even more dynamic and adaptable way of learning that remains focused on long-term traits and attributes if its environment. Besides using a more customized environment matrix as highlighted in some of the alternatives listed in this article, an alternative action scale, with more than 3 options, can also be exploited.

There are also some additional considerations when implementing Monte Carlo (MC) that bear mentioning. MC balances the tradeoff between bias and variance in the way the update reward value is calculated. In instances where the number of cycles in an episode are few, there tends to be a high bias and low variance, while longer episodes with high count of cycles tend to feature the opposite. Therefore, depending on one’s objectives, this is something to consider when developing the Q-Map because a high bias will tend to make the model more adaptable to short-term action while high variance will seat better with the algorithm’s intent of capturing long-term traits and attributes.

The more granular exploration of the state-action space that is afforded from having multiple rewards from different time points when using multiple n-step returns means by varying horizons of possible returns (which in our custom signal class was controlled by the input parameter m_episode_cycles), we can fine tune the signal strength for trading strategies. This granularity leads to more nuanced decisions when determining entry and exit points, allowing for the optimizing of both and adjustments to the timing and intensity of their signals.