Most notable Artificial Cooperative Search algorithm modifications (ACSm)

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

1. Introduction

In the previous article, we got acquainted with an interesting and promising optimization algorithm known as Artificial Cooperative Search (ACS). This algorithm is inspired by observations of the interaction and cooperation of living organisms in nature, where they unite to achieve common goals and obtain mutual benefit. The basic idea of ACS is to model such mutualistic relationships between "predators" and "preys" in order to optimize complex multidimensional problems.

Now that we have become familiar with the basic version of ACS, we will try to expand its capabilities using modified versions of the algorithm. These enhanced versions of ACS will use additional mechanisms inspired by observations of natural ecosystems to improve the efficiency of finding optimal solutions.

Studying known modified versions of ACS will allow us to gain a deeper understanding of how the principles of cooperation and mutually beneficial coexistence of living organisms can be successfully adapted to solve complex optimization problems, and will help to reveal new perspectives in the field of artificial intelligence and inspire further developments in this exciting domain.

2. Algorithm implementation

The first and minor modification of the ACS (Modified Artificial Cooperative Search Algorithms) includes two major changes:

1. Using augmented forms of A and B matrices (populations):
   - In this modification, A and B matrices have additional columns. Each row of the matrix contains N variables and an additional column that stores the function value calculated based on the first N variables. This makes it easier to track function values and improves the accuracy of solutions.

2. Changing the way the M binary matrix is created:
   - In the original algorithm, the M matrix is filled with "0" values, and then some elements are selected and set to "1". This change results in a small improvement in the accuracy of the solutions, at least for the test functions the experiments were conducted on.

Thus, these changes in the first and minor modification of the ACS algorithm are aimed at improving the accuracy of solutions and the efficiency of the algorithm in solving optimization problems. Instead of adding an additional column to store the fitness values of individuals, as the authors suggest, we will use the already familiar "f" field in the structure of agents that describe individuals in the population.

The second and significant modification of the ACS algorithm includes the following changes that differ from the original version:

1. Change an approach to filling the Predator and Prey matrices:
- In this modification, each row in the augmented A and B matrices is sorted by the fitness function value. The rows from the sorted A and B matrices are then compared, and based on this comparison it is determined which rows will go into the Predator and Prey matrices. This approach allows selecting candidates for update based on their merit (feature value) rather than random selection.

2. Random comparisons to update A and B matrices:
- At the end of each iteration of the main loop in this modification, the A and B matrices are updated through random comparisons. This means that both matrices have the same probability of being updated. This approach allows both populations to be updated evenly and improves diversity in the search for the optimal solution.

Thus, the second modification of the ACS algorithm improves the selection of candidates and updating the A and B populations making them more efficient and diverse in finding the optimal solution. It differs from the original version of the algorithm in the way the Predator and Prey populations are formed and in the use of random comparisons to update the matrices.

The third major modification of the ACS algorithm represents a completely different approach to the formation of the Predator and Prey matrices. Detailed description of changes made in the third modification:

1. Pop population:
   - This modification creates a new matrix Pop combining the augmented A and B matrices. Pop contains all rows from A and B matrices. Then it is sorted by fitness function values. The first popSize rows in Pop become the Predator population, while the last popSize rows become the Prey population.

2. Updating Predator and Prey:
   - After forming Predator and Prey populations, the algorithm continues updating based on the fitness of individuals. Preference is given to the best solutions selected as Predator, which helps improve the accuracy and convergence speed of the algorithm.

3. Using random comparisons:
   - Similar to the second modification, at the end of each iteration of the main loop, the A and B matrices are updated through random comparisons. This approach ensures equal chances for renewal of both populations and promotes diversity in the search for the optimal solution.

Thus, the third modification of the ACS algorithm focuses on using fitness to form the Predator and Prey populations. It represents a more advanced and efficient approach to selecting candidates and updating populations while searching for an optimal solution.

Having reviewed the possible modifications to the basic version of the algorithm (ACS), we are now ready to move on to implementing the first improved version of this promising optimization method. Our goal is to increase the efficiency of finding optimal solutions. Step by step, we will introduce new elements into the basic structure of ACS, carefully analyzing their impact on the performance and convergence of the algorithm.

Let's start implementing the first modified version of the algorithm and explore its potential. In each subsequent version of the algorithm, sections of the code that differ from the previous version are indicated in green.

C_AO_ACSm1 class code description:

1. C_AO_ACSm1 is a class derived from the C_AO base class.
2. The class has a public constructor and destructor.
3. The following data members are initialized in the constructor:

• ao_name, ao_desc, ao_link - descriptive rows regarding the algorithm
• popSize - population size
• bioProbab - probability of biological interaction
• params - array of algorithm parameters, in this case we have two parameters: popSize and bioProbab

4. SetParams() - method sets the popSize and bioProbab values based on the parameters from the params array.
5. Init() - method takes as input the ranges and search steps, as well as the number of epochs, and returns a logical value indicating the success of the initialization.
6. Moving() and Revision() - methods contain the basic logic of the algorithm for moving and revising the agents.
7. Private data members include arrays of structures of S_AO_Agent and S_C types, as well as Key and phase variables used in the algorithm.
8. ArrayShuffle() - private method shuffles array elements.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm1 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm1 () { }
  C_AO_ACSm1 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m1";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];

  S_C M               [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

The Init method of the C_AO_ACSm1 class performs object initialization:

1. Init() - method declaration. It takes four arguments: minimum search range "rangeMinP", maximum search range "rangeMaxP", "rangeStepP" search step and the number of epochs "epochsP", which is 0 by default.
2. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false - call the StandardInit function, which performs standard initialization of the base class. If StandardInit returns false, the Init method terminates immediately and returns false.
3. In the loop for (int i = 0; i < popSize; i++), each element of the A, B, Predator, Prey and M arrays is initialized using the Init method.
4. ArrayResize (A, popSize) and similar rows change the size of the A, B, Predator, Prey and M arrays to popSize.
5. In the nested loop for (int j = 0; j < coords; j++), each c element (individual coordinates) of each object in the A and B arrays is initialized using a random value in the given range.
6. phase = 0 sets phase to 0.
7. The method returns true if initialization is successful.

The code is responsible for the initial setup and preparation of data required for further algorithm operation. It creates arrays of objects, initializes their values, and sets the initial state of the algorithm.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm1::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method of the C_AO_ACSm1 class implements the basic logic of moving individuals in the algorithm:

1. if (phase == 0) - here individuals are copied from the A population to the a array (the "а" array is used to pass individuals for fitness function calculation).

• For each element in the loop for (int i = 0; i < popSize; i++), individual coordinates are copied from A to a array.
• The phase variable value is increased by 1 and the method is returned.

2. if (phase == 1) - here fitness is assigned to individuals of the A population and individuals from the B population are copied.

• For each element in the loop for (int i = 0; i < popSize; i++), the a [i].f fitness value is copied to A [i].f.
• Next, for each element in the loop for (int i = 0; i < popSize; i++), individual coordinates are copied from B to a array for further calculation of the fitness of individuals.
  
• The phase value is increased by 1 and the method is returned.

3. if (phase == 2) - here fitness is returned to B population individuals.

• For each element in the loop for (int i = 0; i < popSize; i++), the a [i].f fitness value is copied to B [i].f.
  
• The phase value is increased by 1 and the further algorithm logic is executed.

4. Selection - selection is performed here.

• If the u.RNDprobab() random value is less than 0.5, for each element in the loop for (int i = 0; i < popSize; i++), A [i] individual is copied to Predator [i], while Key is set to 1.
• Otherwise, for each element in the loop for (int i = 0; i < popSize; i++), B [i] individual is copied to Predator [i], while Key is set to 2.
• The selection for the Prey array is executed in a similar manner.

5. Permutation of Prey - here the coordinates are permuted randomly in each individual of the Prey population.

• For each individual in the loop for (int i = 0; i < popSize; i++), ArrayShuffle (Prey [i].c) is executed by mixing individual coordinates (the coordinates of each individual are mixed separately, while the coordinates between individuals are not mixed).

6. Mutation and Crossover - mutation and crossover are executed here.

• R value is calculated depending on a random number.
• The M binary matrix is filled with ones.
• Additional operations are performed on the M matrix by changing some of its elements to 0 or 1, depending on the bioProbab probability of biological interaction.
• For each individual in the loop for (int i = 0; i < popSize; i++), mutation and crossover are performed, updating the values in the a population array.

7. Boundary control - block performs boundary control, in which the a population individuals coordinates outside the specified range of optimized parameters are replaced with random values within the range.

This method implements the basic operations of the algorithm, such as selection, mutation, crossover, and boundary control, which are applied to a population of individuals to find the optimal solution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = A [i];                                                       
    }

    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Predator [i] = B [i];                             
    }

    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = A [i];                                 
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      Prey [i] = B [i];                                 
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Next, let's consider the Revision method code of the C_AO_ACSm1 class. It performs the following operations:

1. Check if phase populations preparation phase is already complete phase >= 3. If this condition is not met, the method returns without performing further actions.

2. Update the selection of Selection update individuals:

• For each individual in the a population, check whether its f fitness value exceeds the corresponding value in the Predator array. If yes, the value in Predator is updated.
• Depending on the Key variable value, Predator population individuals are copied to the A or B population.

3. Determine the Ybest best fitness value and its Ibest index in the Predator array:

• Iterate over the Predator array, find the maximum fitness value and its index.

4. Update the fB best global solution:

• If Ybest exceeds the current best fB value, fB is updated, while the appropriate a and cB array elements are copied from the Predator array.

This method updates individual selection, determines the best solution and updates the global best solution within the optimization algorithm.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Predator [i].f)
    {                      
      Predator [i] = a [i];
    }                                    
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      A [i] = Predator [i];
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      B [i] = Predator [i];
    }
  }

  double Ybest = -DBL_MAX;
  int Ibest = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (Predator [i].f > Ybest)
    {
      Ybest = Predator [i].f;
      Ibest = i;
    }
  }

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

The ArrayShuffle method of the C_AO_ACS class is applied in all three modifications, as well as performs a random shuffle of elements in the array:

1. Define the "arr" array size using the ArraySize function.
2. Iterate over arr array in reverse order, starting from the last element.
3. For each i element, generates a random index j from 0 to i.
4. Swaps arr[i] and arr[j] elements using the tmp temporary variable.

As a result, the arr array elements are shuffled randomly.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm1::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Now it is time to analyze the code of the second modification of the ACS algorithm. The Moving method code of the C_AO_ACSm2 class in accordance with the changes:

1. Phase 0:

• If the phase is equal to 0, each individual in the a population gets the values from the A population.
• The phase value is incremented and the method is returned.

2. Phase 1:

• If the phase is 1, each individual in the a population gets f fitness values in the A population.
• Each individual in the a population gets the values from the B population.
• The phase value is incremented and the method is returned.

3. Phase 2:

• If the phase is 2, each individual in the B population gets "f" fitness values from the a population.
• The phase value increases and the further algorithm logic continues.

4. Selection:

• For each individual in the A and B populations, f fitness values are compared.
• If f value in A exceeds B, an individual from A is copied to Predator, while an individual from B is copied to Prey. Otherwise, it is the other way around (the fittest individuals are designated as "predators" and the least fit ones become "prey").

5. Permutation of Prey:

• The coordinates of each individual in the Prey population is permuted using the ArrayShuffle function.

6. Mutation and Crossover:

• R value is defined depending on a random number.
• The M binary matrix is filled with zeros.
• Additional operations are performed on the M matrix, where some elements are set to 1 depending on the bioProbab probability.

   For each individual in the a population:

• Mutation is performed: a[i].c[j] element is calculated as the sum of Predator[i].c[j] and the product of R by the difference between Prey[i].c[j] and Predator[i].c[j].
• Crossover is performed: if M[i].c[j] is equal to 1, a[i].c[j] is replaced with Predator[i].c[j].
• Boundary check: if a[i].c[j] is out of rangeMin[j] and rangeMax[j], it is replaced with a random value within this range.

7. Checking coordinates:

• For each individual in the a population, coordinates are checked using the SeInDiSp function.
  

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm2::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection                     
  for (int i = 0; i < popSize; i++)
  {                                
    if (A [i].f > B [i].f)         
    {                              
      Predator [i] = A [i];        
      Prey     [i] = B [i];        
    }                              
    else                           
    {                              
      Predator [i] = B [i];        
      Prey     [i] = A [i];        
    }                              
  }                                

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 0s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 0;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

I will not consider the Revision method of the second algorithm modification here since it has remained intact.

Let's move on to the third modification. The following changes have been made in the definition of the C_AO_ACSm3 third modification class derived from the C_AO base class:

The list of data members has changed:

• bioProbab - probability of biological interaction.
• A[], B[], Predator[], Prey[], Pop[], pTemp[] - arrays storing different populations of individuals.
• M[] - array storing additional data associated with individuals.
• phase - algorithm current phase.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACSm3 : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACSm3 () { }
  C_AO_ACSm3 ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search m3";
    ao_link = "https://www.mql5.com/ru/articles/15014";

    popSize   = 10;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_AO_Agent A        [];
  S_AO_Agent B        [];
  S_AO_Agent Predator [];
  S_AO_Agent Prey     [];
  S_AO_Agent Pop      [];
  S_AO_Agent pTemp    [];

  S_C M               [];

  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

The following changes have been made to the Init initialization method of the C_AO_ACSm3 class:

1. Memory is allocated for arrays A, B, Predator, Prey, Pop, pTemp and M of popSize or popSize * 2.

2. Each element of the A, B, Predator, Prey, Pop and M arrays is initialized using the Init method.

The authors of the original version of the algorithm do not have a division of logic into phases. I have added a division into phases to implement the algorithm in the style I have adopted for all population algorithms. This was necessary because the ACS uses a pre-calculation of the agent fitness for А and B populations. These operations should be performed sequentially in methods.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACSm3::Init (const double &rangeMinP [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,        popSize);
  ArrayResize (B,        popSize);
  ArrayResize (Predator, popSize);
  ArrayResize (Prey,     popSize);
  ArrayResize (Pop,      popSize * 2);
  ArrayResize (pTemp,    popSize * 2);

  ArrayResize (M,        popSize);

  for (int i = 0; i < popSize; i++)
  {
    A        [i].Init (coords);
    B        [i].Init (coords);
    Predator [i].Init (coords);
    Prey     [i].Init (coords);

    M        [i].Init (coords);
  }

  for (int i = 0; i < popSize * 2; i++) Pop [i].Init (coords);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
    }
  }

  phase = 0;

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Now let's have a look at the code of the Moving method within the C_AO_ACSm3 class of the third modification. The changes have affected the following code areas:

• Merging A and B populations into a single Pop population.
• Sorting the Pop population by the fitness values of individuals.
• Filling in Predator and Prey populations from the Pop sorted array where the best half of the population becomes "predators" and the other half becomes "prey", respectively.
• Filling in the M binary matrix with ones.
• Additional operations with the M matrix, in which some elements change to 0 or 1 depending on a random number and the bioProbab probability of biological interaction.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACSm3::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) A [i].f = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) B [i].f = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Merge matrices A and B to create matrix Pop      
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Pop [i]           = A [i];                        
    Pop [i + popSize] = B [i];                        
  }                                                   
                                                      
  // Sort matrix Pop using column N as sort key values
  u.Sorting (Pop, pTemp, popSize * 2);                
                                                      
  // Populate Predator and Prey matrices              
  for (int i = 0; i < popSize; i++)                   
  {                                                   
    Predator [i] = Pop [i];                           
    Prey     [i] = Pop [i + popSize];                 
  }                                                   

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;                
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;              
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        if (u.RNDprobab() < bioProbab)
        {                             
          M[i].c[j] = 1;              
        }                             
        else                          
        {                             
          M[i].c[j] = 0;              
        }                             
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test results

We have carefully reviewed and analyzed all known versions of this algorithm. Now it is time to focus on their practical results and the conclusions we can draw. I propose to dwell in detail on how each of the modifications affected productivity, accuracy and efficiency. This will allow us to better understand which changes have been most successful and where we should move next.

The first version of the modification showed approximately comparable results in the overall score, but the results improved significantly on the Hilly function with 1000 variables and on the Forest function with 50 and 1000 variables.

ACS|Artificial Cooperative Search m1|1.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7130880902279995
25 Hilly's; Func runs: 10000; result: 0.7565145335137569
500 Hilly's; Func runs: 10000; result: 0.31899537529427235
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999866176
25 Forest's; Func runs: 10000; result: 0.9555551824899264
500 Forest's; Func runs: 10000; result: 0.24186829565864398
=============================
5 Megacity's; Func runs: 10000; result: 0.6607692307692307
25 Megacity's; Func runs: 10000; result: 0.5038461538461539
500 Megacity's; Func runs: 10000; result: 0.13922307692307825
=============================
All score: 5.28986 (58.78%)

The second version of the algorithm showed a noticeable improvement in results on all test functions with 50 and 1000 variables, but the results became significantly worse on Megacity with 10 variables (extremely large spread of results) compared to the basic version. This indicates that the movement in this direction is promising (although there are controversial points), and it is worth continuing to work on further modifications.

ACS|Artificial Cooperative Search m2|2.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.7682797921658492
25 Hilly's; Func runs: 10000; result: 0.7664893907210706
500 Hilly's; Func runs: 10000; result: 0.31831672493319296
=============================
5 Forest's; Func runs: 10000; result: 0.9999997349437437
25 Forest's; Func runs: 10000; result: 0.9534110489423269
500 Forest's; Func runs: 10000; result: 0.24425762117784502
=============================
5 Megacity's; Func runs: 10000; result: 0.6176923076923077
25 Megacity's; Func runs: 10000; result: 0.5384615384615385
500 Megacity's; Func runs: 10000; result: 0.14057692307692446
=============================
All score: 5.34749 (59.42%)

Unfortunately, the third modification, which seemed to be the most promising, did not live up to expectations and showed an overall result somewhat worse than the basic version of the algorithm. Although it is worth noting that the results on the smooth Hilly function with 10 variables have improved significantly. The algorithm demonstrates higher convergence accuracy precisely on smooth functions with a small number of variables.

ACS|Artificial Cooperative Search m3|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8836798635515516
25 Hilly's; Func runs: 10000; result: 0.715438105666966
500 Hilly's; Func runs: 10000; result: 0.3011611038405591
=============================
5 Forest's; Func runs: 10000; result: 0.9893902762645717
25 Forest's; Func runs: 10000; result: 0.7954795408759185
500 Forest's; Func runs: 10000; result: 0.21910399769909533
=============================
5 Megacity's; Func runs: 10000; result: 0.6315384615384615
25 Megacity's; Func runs: 10000; result: 0.49876923076923074
500 Megacity's; Func runs: 10000; result: 0.12683076923077044
=============================
All score: 5.16139 (57.35%)

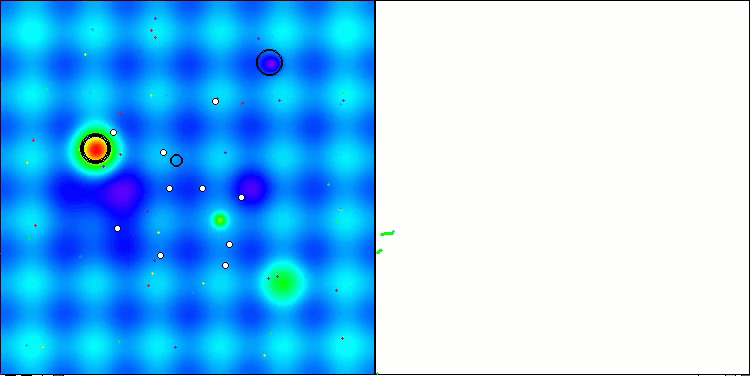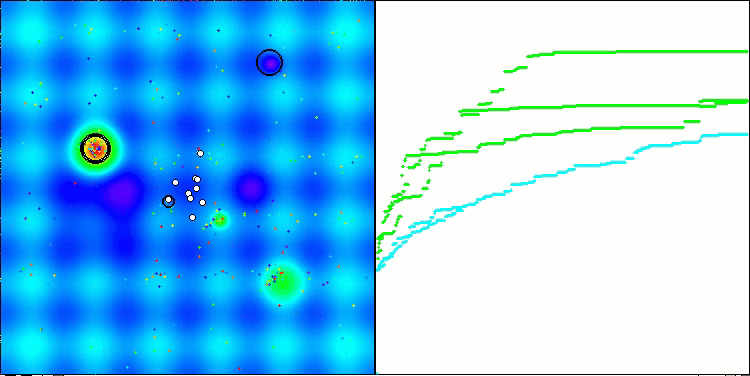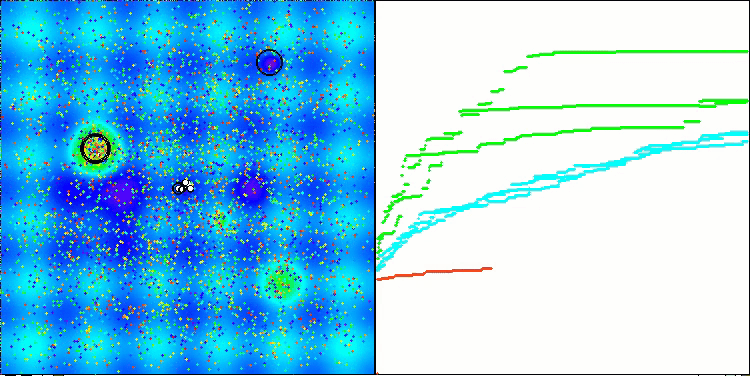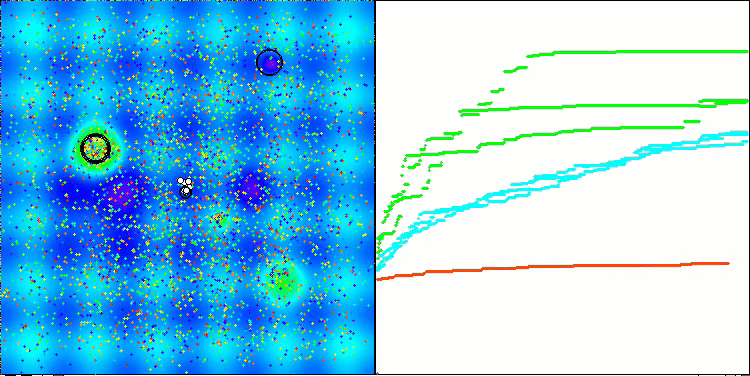
Visualization of the second modification of the algorithm. With a small number of variables, there is quite a large spread in the results on the Hilly and Megacity functions, while the algorithm feels excellent on the spiky smooth Forest function.

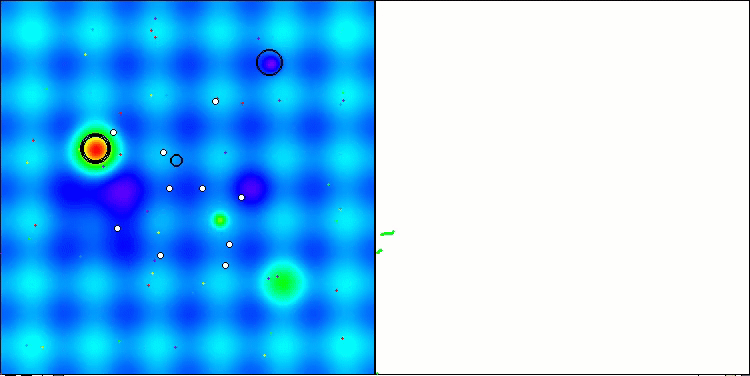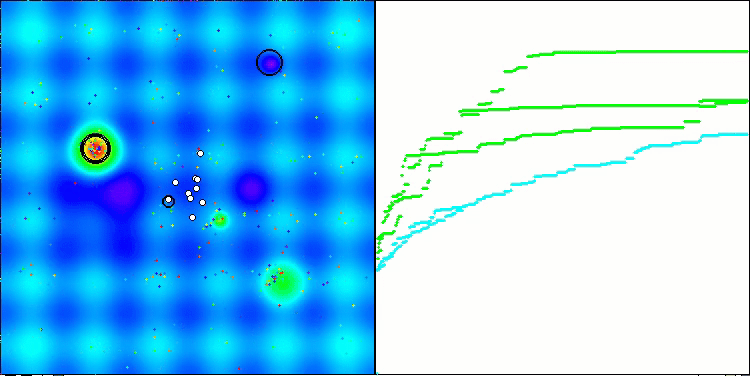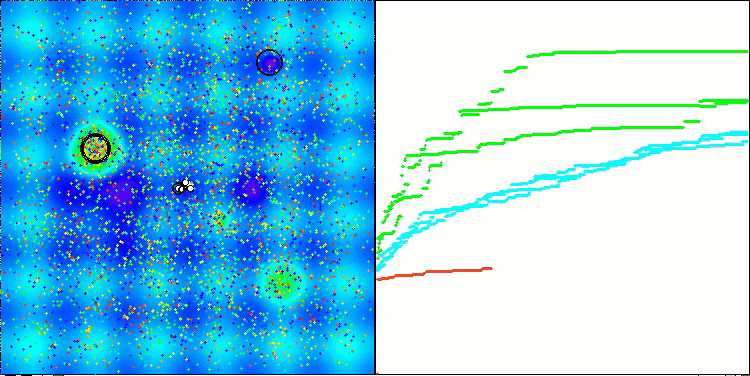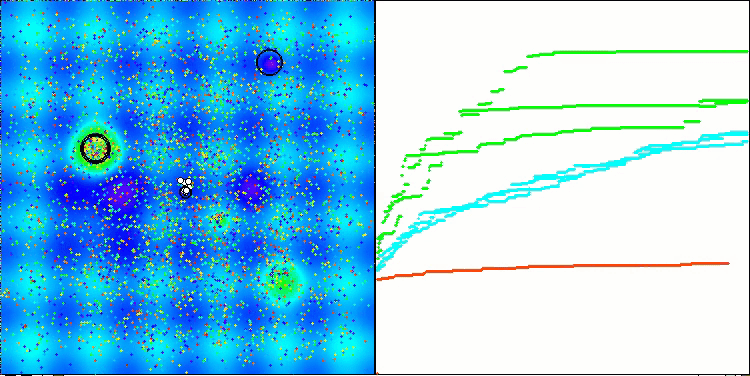
  ACSm2 on the Hilly test function

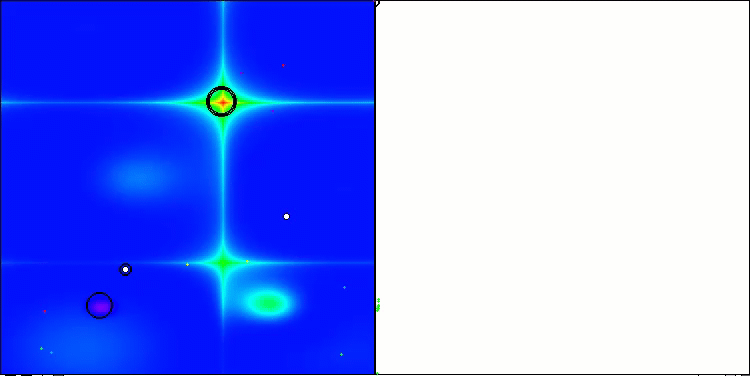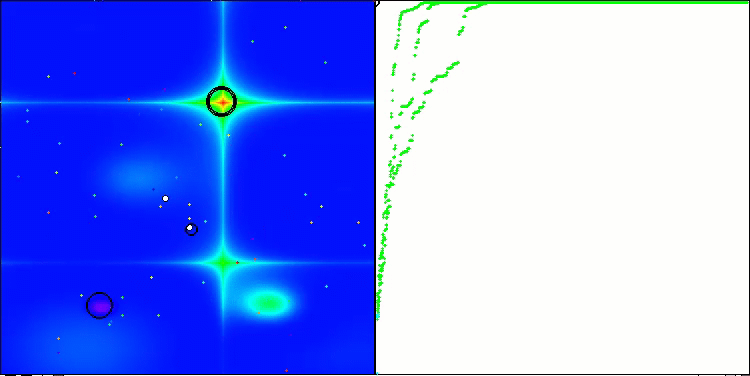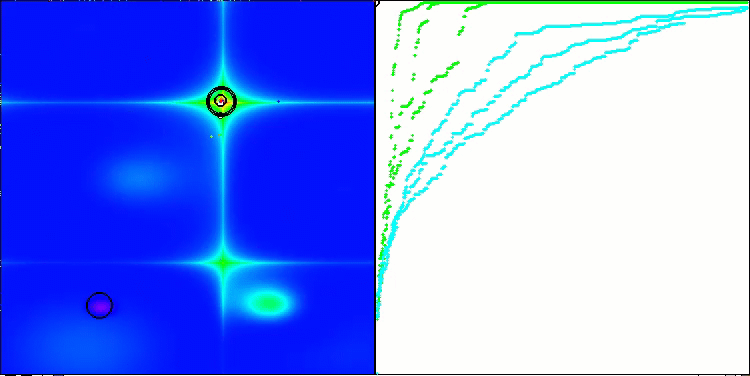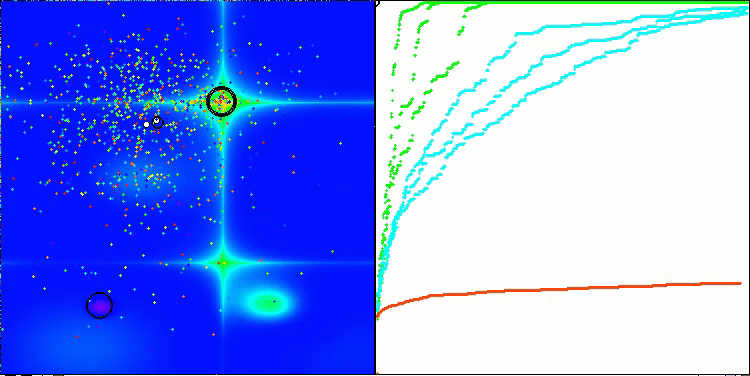
ACSm2 on the Forest test function

  ACSm2 on the Megacity test function

Summary

The overall conclusions are as follows:

1. The first modification of the ACS algorithm, with the addition of augmented forms of the A and B matrices, improved the accuracy of solutions, especially on Hilly functions with 1000 variables and Forest functions with 50 and 1000 variables.

2. The second modification, which changes the approach to filling the Predator and Prey matrices and uses random comparisons to update the matrices, showed a noticeable improvement in results on all test functions with 50 and 1000 variables, but led to a greater spread of results on the Megacity function with 10 variables.

3. The third modification, with a focus on using fitness to form the Predator and Prey populations, did not live up to expectations, showing an overall result somewhat worse than the basic version of the algorithm, although it improved the accuracy of convergence on smooth functions with a small number of variables.

Thus, each modification has its own strengths and weaknesses, and for further development of the algorithm it is necessary to take these features into account in order to create a more efficient and universal version of the ACS algorithm.

Possible areas for improvement:

1. Modification of search mechanisms:

• Analyze the current search mechanisms used in the algorithm and consider the possibility of their further optimization.
• Explore whether additional mechanisms such as adaptive search steps can be introduced to improve search efficiency.

2. Exploring hybrid approaches:

• Consider combining the current algorithm with other optimization methods to take advantage of the strengths of different approaches. For example, we can try to integrate elements of evolutionary algorithms or swarm intelligence methods to increase diversity and convergence speed.

3. Analysis and improvement of the mechanism of interaction between populations:

• Find out how the way A and B populations interact can be improved so that they complement each other more effectively during the search. It may be worth considering more complex structures of information sharing or cooperative learning between populations.

Figure 1. Color gradation of the algorithm modifications according to relevant tests for comparison with the basic version. Results greater than or equal to 0.99 are highlighted in white

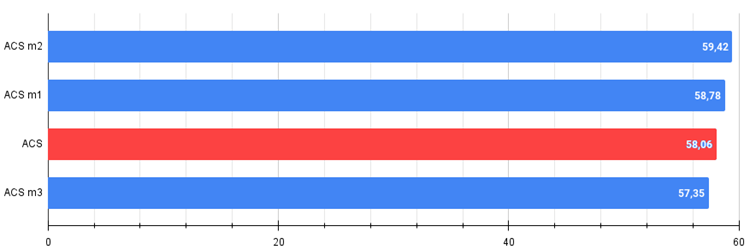
Figure 2. The histogram of the algorithm modification results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

General pros and cons of the modified ACS algorithm versions:

Advantages:

1. Small number of external parameters (only one).
   
2. Good convergence on various types of functions.

Disadvantages:

1. Scatter of results on low-dimensional functions.
   

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355