
Neural networks made easy (Part 70): Closed-Form Policy Improvement Operators (CFPI)
Introduction
The approach to optimizing the Agent policy with constraints on its behavior turned out to be promising in solving offline reinforcement learning problems. By exploiting historical transitions, the Agent policy is trained to maximize a learned value function.
Behavior constrained policy can help to avoid a significant distribution shift in relation to Agent actions, which provides sufficient confidence in the assessment of the action costs. In the previous article we got acquainted with the SPOT method, which exploits this approach. As a continuation of the topic, I propose to get acquainted with the Closed-Form Policy Improvement (CFPI) algorithm, which was presented in the paper "Offline Reinforcement Learning with Closed-Form Policy Improvement Operators".
1. Closed-Form Policy Improvement (CFPI) algorithm
A closed-form expression is a mathematical function expressed using a finite number of standard operations. It may contain constants, variables, standard operators and functions, but usually does not contain limits, differential or integration expressions. Thus, the CFPI method we are considering introduces some analytical grains into the Agent's policy learning algorithm.
Most existing offline Reinforcement Learning models use Stochastic Gradient Descent (SGD) to optimize their strategies, which can lead to instability in the training process and requires careful tuning of the learning rate. Additionally, the performance of strategies trained offline may depend on the specific evaluation point. This often leads to significant variations in the final stage of learning. This instability presents a significant challenge in offline reinforcement learning, as limited access to interaction with the environment makes it difficult to tune hyperparameters. In addition to variations across different evaluation points, using SGD to improve a strategy can lead to significant variations in performance under different random initial conditions.
In their work, the authors of the CFPI method aim to reduce the mentioned instability of offline RL learning. They develop stable strategy improvement operators. In particular, they note that the need to limit distributional shift motivates the use of a first-order Taylor approximation, leading to a linear approximation of the Agent's policy objective function that is accurate within a sufficiently small neighborhood of the behavior strategy. Based on this key observation, the authors of the method construct strategy improvement operators that return closed-form solutions.
By modeling behavior strategies as a single Gaussian distribution, the strategy improvement operator proposed by the authors of CFPI deterministically shifts the behavior policy in the direction of improving the value. As a result, the proposed Closed-Form Policy Improvement method avoids the learning instability of strategy improvement because it only uses learning the basic behavior strategies of a given dataset.
The authors of the CFPI method also note that practical data sets are often collected using heterogeneous strategies. This can lead to a multi-modal distribution of Agent actions. A Single Gaussian distribution will not be able to capture many of the modes of the underlying distribution, limiting the potential for improvement of the strategy. Modeling the behavior policy as a mixture of Gaussian distributions provides better expressiveness but entails additional optimization difficulties. The authors of the method solve this problem by using a lower bound on LogSumExp and Jensen's inequality, which also leads to a closed-form strategy improvement operator applicable to multimodal behavior strategies.
The authors highlight the following contributions of the Closed-Form Policy Improvement method:
- CFPI operators that are compatible with single-mode and multi-mode behavior strategies and can improve upon strategies learned by other algorithms.
- Empirical evidence of the benefits of modeling behavioral strategy as a mixture of Gaussian distributions.
- Single-step and iterative variants of the proposed algorithm outperform existing algorithms on a standard benchmark.
The authors of CFPI create an analytical strategy improvement operator without training to avoid instability in offline scenarios. They note that optimization with respect to the objective function generates a strategy that allows constrained deviation from the behavior strategy in the offline sample. Therefore, it will only query the Q-value in the vicinity of the behavior during training. This naturally motivates the use of first-order linear approximation.
At the same time, the evaluation of actions in the updated policy provides an accurate linear approximation of the learned value function only in a sufficiently small neighborhood of the distribution of the training sample. Therefore, the choice of the State-Action pair from the training dataset is critical to the final learning result.
To solve the problem, the authors propose to solve the following approximate problem for any state S:
![]()
It should be noted that D(•,•) does not have to be a mathematically defined divergence function. We can consider any general D(•,•), which can constrain the deviation of the Agent's behavior policy from the distribution of the training dataset.
In general, the above problem does not always have a closed-form solution. The authors of the CFPI method analyze a special case:
- The use a Gaussian strategy to collect the training dataset.
- Then, they train the deterministic behavior policy of the Agent.
- D(•,•) is the negative likelihood function.
In such a scenario, a reasonable choice for policy training is to concentrate around the distribution of the training dataset. Then the proposed optimization problem can be represented as a closed-form expression:
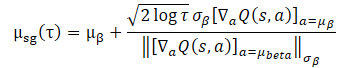
Using this closed-form expression to improve Agent policy brings beneficial computational efficiency and avoids potential instability caused by SGD. However, its applicability depends on the assumption of a Single Gaussian for the training dataset collection strategy. In practice, historical datasets are typically collected by heterogeneous strategies with varying levels of expertise. A one-dimensional Gaussian may not capture the entire distribution picture, so it seems reasonable to use a mixture of Gaussians to represent the data collection policy.
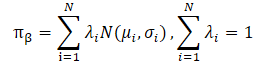
However, direct substitution of a mixture of Gaussians for training data collection policies violates the applicability of the problem presented above, since it leads to a non-convex objective function. Here we face two major challenges in solving the optimization problem.
First, it is unclear how to select the appropriate action from the training dataset. Here, it is also necessary to ensure that the solution to the target policy is located in a small neighborhood of the selected action.
Secondly, the use of a mixture of Gaussians does not admit a convex form, which results on optimization difficulties.
The use of LogSumExp allows you to transform the optimization problem.
![]()
This can be represented as a closed-form expression.
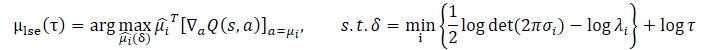
The use of Jensen's inequality allows us to obtain the following optimization problem:
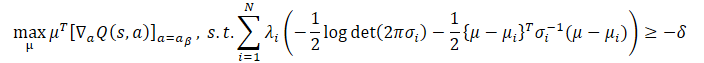
The closed-form solution for this problem looks like this:
![]()
Compared to the original optimization problem, both proposed extensions impose stricter confidence interval constraints. This is achieved by providing a lower bound on the log-likelihoods of the mixture of Gaussians above a certain threshold value. At the same time, the parameter τ controls the size of the confidence interval.
Both optimization problems have their pros and cons. When the training dataset distribution exhibits obvious multimodality, the lower bound on the logarithm of the data collection policy constructed by Jensen's inequality cannot capture different modes due to its concavity, losing the advantage of modeling the data collection policy as a Gaussian Mixture. In this case, the LogSumExp optimization problem can serve as a reasonable replacement for the original optimization problem because the lower bound of LogSumExp preserves the multimodality of the logarithm of the data collection policy.
When the distribution of the training dataset is reduced to a Single Gaussian, the approximation by Jensen's inequality becomes an equality. Thus, µjensen accurately solves the given optimization problem. However, in this case, the degree of accuracy of the lower bound of LogSumExp largely depends on the weights λi=1...N.
Fortunately, we can combine the best qualities of both approaches and obtain a CFPI operator that takes into account all the above scenarios, which returns a behavior policy that selects the higher ranked action from µlse and µjensen:
![]()
In the original paper, you can find detailed calculations and evidence of the applicability of all the presented expressions.
The authors of the CFPI method note that the proposed method is also applicable to non-Gaussian distributions of the training dataset. At the same time, the presented CFPI operators allow you to create a general template for offline learning with the ability to obtain single-step, multi-step and iterative methods.
A pre-trained Critic model is used to evaluate actions. It can be trained on the training dataset in any known way. This is actually the first stage of the model training algorithm.
Next, a certain packet of States is sampled from the training dataset. Actions are generated for this package taking into account the current Agent policy. Then the resulting actions are evaluated taking into account the above proposed CFPI operators.
Based on the results of this assessment, optimal states are selected, at which the Agent policy is updated.
When constructing multi-step and iterative methods, the process is repeated.
Although the design of CFPI operators is inspired by the behavioral Agent policy constraint paradigm, the proposed approaches are compatible with common basic reinforcement learning methods. The authors in their paper demonstrated examples where CFPI operators increased the efficiency of strategies learned using other algorithms.
2. Implementation using MQL5
The above is a theoretical description of the Closed-Form Policy Improvement method. I agree that the presented mathematical equations may seem quite complicated. So, let's try to understand them in more detail in the process of implementing the proposed approaches.
It should immediately be noted that the model training algorithm proposed by the authors of the article provides for sequential training of the Critic and the Actor. The Critic model is trained first. We can begin to train the Actor politics only after that.
With this approach, our technique when the Critic uses the Actor model for preliminary processing of the source data becomes irrelevant. Because at the stage of training the Critic, the Actor model has not yet been formed. Of course, we could generate an Actor model and use it as before. But in this case, we encounter the following problem: at the policy training stage, the CFPI algorithm does not provide for updating the Critic model. Changing the parameters of the Actor will necessarily lead to changing the parameters of preliminary processing of the source data. In this case, the distribution at the Critic input changes. This generally leads to a distortion in the assessment of the Actor actions.
To correct the described situation, we can avoid using the common Initial State Encoder or move it into a separate model.
We cannot transfer the Encoder to the Critic model, since the feed-forward pass of the Critic requires actions generated by the Actor. Also, the feed-forward pass of the Actor requires the results of the Encoder. The circle closed up.
2.1 Model architecture
In my implementation, I decided to create the Environmental State Encoder as a separate model. This, in turn, affected the architecture of the models. The description of the model architecture is given in the CreateDescriptions method. Despite the consistent training of the Actor and Critic models, I did not divide the description of the model architecture into 2 methods. Therefore, in the parameters, the method receives pointers to 3 dynamic arrays of objects for recording the model architecture.
In the body of the method, we check the relevance of the received pointers and, if necessary, create new array object instances.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
The first is a description of the architecture of the Current State Encoder. The architecture of the model begins with a layer of source data, the size of which must be sufficient to record information about price movement and indicator values for the entire depth of the analyzed history.
//--- State Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
The resulting "raw" data is preprocessed in the batch normalization layer.
Next comes the convolutional block, which allows us to reduce the data dimensionality while also identifying stable patterns in the data.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; int prev_wout = descr.window_out = BarDescr / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; prev_wout = descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
The results of the convolutional block are processed by 2 fully connected neural layers.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
The data processed in this way is supplemented with information about the state of the account, which includes the timestamp harmonics.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 2 * LatentCount; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; }
We create stochasticity at the output of the Encoder. This allows us to both reduce the possibility of model overfitting and increase the stability of our model in a stochastic external environment.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = LatentCount; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
This is followed by a description of the Actor architecture. It receives as input the results of the environmental encoder described above.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
As you can see, all the preparatory work to prepare the initial data is performed in the encoder. This allows us to make the Actor model as simple as possible. Here we create 3 fully connected layers.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
At the model output, we form a stochastic policy in a continuous action space.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
The Critic model also uses the results of the Encoder as input. But unlike the Actor model, it supplements the results with a vector of evaluated Actions. Therefore, after the source data layer, we use a concatenation layer that combines 2 source data tensors.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; }
Next comes the decision-making block from fully connected neural layers.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
With this, we complete the description of the model architecture and move on to constructing a model learning algorithm.
Of course, before we start training the models, we need to collect a training dataset. Now please pay attention to the following. This time I can't use the environmental interaction Expert Advisors from previous works in unchanged forms. The model architecture has changed, and the environment state encoder has been separated into an external model. This has affected the algorithms of our Expert Advisors. However, these changes have only been made to certain points, with which you familiarize yourself in the files "...\Experts\CFPI\Research.mq5" and "...\Experts\CFPI\Test.mq5". These files are provided in the attachment. We now move on to building a learning algorithm for the Critic.
2.2 Critic training
The Critic model training algorithm is implemented in the EA "...\Experts\CFPI\StudyCritic.mq5". In this EA, we have two Critic models trained in parallel. As you know, the use of two Critics allows us to increase the stability and efficiency of subsequent training of the Actor behavior policy. Together with the Critics models, we will train a general Encoder for the environment state.
//+------------------------------------------------------------------+ //| Input parameters | //+------------------------------------------------------------------+ input int Iterations = 1e6; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ STrajectory Buffer[]; CNet StateEncoder; CNet Critic1; CNet Critic2;
In the EA initialization method, we first try to load the training dataset.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
Then we load the necessary models. If it is not possible to load pre-trained models, we generate new ones filled with random parameters.
//--- load models float temp; if(!StateEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); if(!CreateDescriptions(actor, critic, encoder)) { delete actor; delete critic; delete encoder; return INIT_FAILED; } if(!Critic1.Create(critic) || !Critic2.Create(critic) || !StateEncoder.Create(encoder)) { delete actor; delete critic; delete encoder; return INIT_FAILED; } delete actor; delete critic; delete encoder; //--- }
We transfer all models into a single OpenCL context, which enables data exchange between models without unnecessary transfer of information to the main program memory and back.
//---
OpenCL = Critic1.GetOpenCL();
Critic2.SetOpenCL(OpenCL);
StateEncoder.SetOpenCL(OpenCL);
To eliminate possible errors in data transfer between models, we check their compliance with the uniform layout of the data used.
//--- StateEncoder.getResults(Result); if(Result.Total() != LatentCount) { PrintFormat("The scope of the State Encoder does not match the latent size count (%d <> %d)", LatentCount, Result.Total()); return INIT_FAILED; } //--- StateEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- Critic1.GetLayerOutput(0, Result); if(Result.Total() != LatentCount) { PrintFormat("Input size of Critic1 doesn't match State Encoder output (%d <> %d)", Result.Total(), LatentCount); return INIT_FAILED; } //--- Critic2.GetLayerOutput(0, Result); if(Result.Total() != LatentCount) { PrintFormat("Input size of Critic2 doesn't match State Encoder output (%d <> %d)", Result.Total(), LatentCount); return INIT_FAILED; }
After successfully passing all controls, we initialize the auxiliary data buffer.
//--- Gradient.BufferInit(AccountDescr, 0);
We also initialize a custom event to start the model training process.
//--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
After that, we complete the operation of the EA initialization method.
In the EA deinitialization method, we save the trained models and clear the memory.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { StateEncoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); Critic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true); Critic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
The actual process of training models is implemented in the Train method. In the body of the method, we first calculate the weighted probabilities of selecting trajectories from the experience replay buffer.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Then we declare local variables and create a training loop with the number of iterations equal to the value specified by the user in the EA's external parameters.
vector<float> rewards, rewards1, rewards2, target_reward; uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) {
In the training loop body, we sample a trajectory and the state on it.
int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3)); if(i < 0) { iter--; continue; }
After that, we fill the source data buffers. First, we fill the buffer for describing the state of the environment with data on price movement and values of the analyzed indicators from the experience replay buffer.
//--- Q-function study
State.AssignArray(Buffer[tr].States[i].state);
Then we will fill the buffer describing the account status and open positions.
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Supplement the buffer with timestamp harmonics.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
The collected data is sufficient for a feed-forward pass of the environment state Encoder.
//--- if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
As mentioned above, at this stage we are not using the Actor model. Critics are trained by supervised learning methods using the evaluation of actual actions and rewards received from the environment, which were previously stored in the training dataset. Therefore, for a feed-forward pass of both Critics, we use the results of the environmental state Encoder and the action vector from the training dataset.
//--- Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
We check the correctness of the operations and load the results of the feed-forward pass of both Critics.
//---
Critic1.getResults(rewards1);
Critic2.getResults(rewards2);
The next step is to generate target values for training the models. As mentioned above, we will train the actual values from the training dataset. At this stage, we use a reward for one transition to a new state. To improve convergence, we adjust the direction of the error gradient vector using the CAGrad method.
The parameters of the models are adjusted one by one. First, we adjust the parameters of the first Critic and then call the backpropagation pass method of the environment state Encoder.
rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards); rewards = rewards - target_reward * DiscFactor; Result.AssignArray(CAGrad(rewards - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !StateEncoder.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Then we repeat the operations for the second Critic.
Result.AssignArray(CAGrad(rewards - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !StateEncoder.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Please note that after updating each Critic, the Encoder parameters are adjusted. Thus, we are trying to make environmental embedding as informative and accurate as possible.
After successfully updating the model parameters, we only need to inform the user about the training progress and move on to the next iteration of the loop.
//--- if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
After completing all iterations of the learning loop system, we clear the comments field on the chart. We also output information about the training results to the log and initiate EA termination.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); ExpertRemove(); //--- }
The full Expert Advisor code can be found in the attachment.
2.3 Behavior Policy Training
After training the Critics, we move on to the next stage - training the Actor behavior policy. We implement this functionality in the EA "...\Experts\CFPI\Study.mq5". First, to external parameters, we add the size of the packet in which we will select the optimal point for training.
//+------------------------------------------------------------------+ //| Input parameters | //+------------------------------------------------------------------+ input int Iterations = 10000; input int BatchSize = 256;
In this EA we will use 4 models, but we will only train the Actor.
CNet Actor; CNet Critic1; CNet Critic2; CNet StateEncoder;
In the EA initialization method, we first upload the training set.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
After that, we load the models. We first load the pre-trained environment state Encoder and Critic models. If these models are not available, we cannot run the learning process further. So, if an error occurs while loading models, we terminate the EA operation.
//--- load models float temp; if(!StateEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Can't load Critic models"); return INIT_FAILED; }
If there is no pre-trained Actor, we initialize a new model filled with random parameters.
if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Actor.Create(actor)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; }
We transfer all models to one OpenCL context and disable the training mode for the Encoder and Critics.
OpenCL = Actor.GetOpenCL(); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); StateEncoder.SetOpenCL(OpenCL); //--- StateEncoder.TrainMode(false); Critic1.TrainMode(false); Critic2.TrainMode(false);
After that, we check the compatibility of the model architectures.
//--- Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
StateEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
StateEncoder.getResults(Result); int latent_state = Result.Total(); Critic1.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic1 doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Critic2.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic2 doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Actor.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Actor doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
If the check block is completed successfully, we can move on to the next step. We initialize the auxiliary buffer and generate a custom event to start the learning process.
Gradient.BufferInit(AccountDescr, 0); //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
This completes the operations of the EA initialization method. In the EA deinitialization method, we save the trained models and clear the memory.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); delete Result; delete OpenCL; }
The Actor model training process is implemented in the Train method. In the body of the method, we first determine the probabilities of choosing trajectories from the training dataset.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
After that, we will create the necessary local variables.
//--- vector<float> rewards, rewards1, rewards2, target_reward; vector<float> action, action_beta; float Improve = 0; int bar = (HistoryBars - 1) * BarDescr; uint ticks = GetTickCount();
Next, we create a model training loop with the number of iterations specified in the EA's external parameters.
//--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) {
In the body of the loop to train the Actor's behavior policy, we will use the approaches of the CFPI method. First, we need to sample a batch of data from the training dataset. We need to generate and evaluate the actions of the current Actor policy in selected states. To perform these operations, let's create a nested loop with a number of iterations equal to the size of the package being analyzed. We will save the results of the operations into the local mBatch matrix.
matrix<float> mBatch = matrix<float>::Zeros(BatchSize, 4); for(int b = 0; b < BatchSize; b++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { b--; continue; }
Sampling operations are similar to those we performed earlier.
We fill the environment state describing buffers with data from each selected state.
//--- State
State.AssignArray(Buffer[tr].States[i].state);
Add account status buffers.
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Add timestamp harmonics.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
Run the State Encoder feed-forward method.
//--- State embedding if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
After generating the environmental state embedding, we generate the Agent actions taking into account the current policy.
//--- Action if(!Actor.feedForward(GetPointer(StateEncoder), -1, NULL, 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
The generated actions are evaluated by both Critics.
//--- Cost if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
After successfully completing all operations, we upload the results to local vectors. Then form similar data vectors from the training dataset.
Critic1.getResults(rewards1); Critic2.getResults(rewards2); Actor.getResults(action); action_beta.Assign(Buffer[tr].States[i].action); rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards);
The coordinates of the analyzed state are saved to the result matrix in the form of indexes of the trajectory and the state in it. We also save the deviation of the action vector and its impact on the result.
//--- Collect mBatch[b, 0] = float(tr); mBatch[b, 1] = float(i); mBatch[b, 2] = MathMin(rewards1.Sum(), rewards2.Sum()) - (rewards - target_reward * DiscFactor).Sum(); mBatch[b, 3] = MathSqrt(MathPow(action - action_beta, 2).Sum()); }
After that, we move on to sampling and assessing the next state.
After processing and collecting data from the entire package, we need to select the optimal state to optimize the Actor behavior policy. At this stage, we need to select a state with a reliable Critic assessment and maximum influence on the model result.
Regarding the reliability of the action evaluation, we have already said that the assessment of actions from the Critic is more accurate when the deviations from the training dataset distribution are minimal. As the deviation increases, the accuracy of the Critic's assessment decreases. Following this logic, the criterion for the accuracy of action assessment can be the distance between actions, which we stored in the column with index 3 of our analytical matrix.
Now we need to choose a confidence interval. In the original paper, the authors of the CFPI method used the variance of the distribution. However, we cannot take the variance for the vector of action deviations. The fact is that variance is considered as the standard deviation from the middle of the distribution. In our case, we kept the absolute values of the deviations. Thus, the zero deviation, in which the Critic's estimate is most accurate, can only be an extreme. The average value of the distribution is far from this point. Consequently, the use of variance in this case does not guarantee the desired accuracy of action estimates.
But here we can use the "3 sigma" rule: in a normal distribution, 68% of the data does not deviate from the mathematical expectation by more than 1 standard deviation. This means that we can use the quantile function to determine the confidence range. Using quite simple mathematical operations, we create the weights vector with zero values for actions with deviations greater than the confidence interval and "1" for the rest.
action = mBatch.Col(3); float quant = action.Quantile(0.68); vector<float> weights = action - quant - FLT_EPSILON; weights.Clip(weights.Min(), 0); weights = weights / weights; weights.ReplaceNan(0);
We have decided on the confidence interval. Now, we can select an array of states with an adequate assessment of actions. We need to choose the most optimal state to optimize the Actor behavior policy. In order to simplify the entire algorithm and speed up the model training process, I decided not to use the analytical methods proposed by the CFPI algorithm authors and used a simpler one instead.
Obviously, in our case, the most optimal direction of optimization is the one in which the profitability of the Agent behavior policy changes with a minimum shift in the action subspace. Because we want to maximize the profitability of our policy, and minimal deviations suggest a more accurate assessment of the actions by the Critic. Of course, in our analytical matrix there are both positive and negative deviations in the assessment of actions. The increase in overall profitability is equally influenced by both an increase in profits and a decrease in losses. Therefore, to calculate the optimal selection criterion, we use the absolute value of the transition reward deviation.
rewards = mBatch.Col(2); weights = MathAbs(rewards) * weights / action;
In the resulting vector, we select the element with the highest value. Its index will point to the optimal state to use in the model optimization algorithm.
ulong pos = weights.ArgMax(); int sign = (rewards[pos] >= 0 ? 1 : -1);
Here we will save the sign of the reward deviation into a local variable.
Looking ahead a little, I must say that we will update the Actor behavior policy using error gradients passed through the Critic model. In this learning mode, we cannot calculate the error in the Actor predictions. To control the learning process, I introduced a coefficient of average improvement of the states used.
Improve = (Improve * iter + weights[pos]) / (iter + 1);
Next comes the familiar algorithm for optimizing the policy model. But this time we are not using a random state, but one in which we can maximize the performance of the model.
int tr = int(mBatch[pos, 0]); int i = int(mBatch[pos, 1]);
As before, we fill the buffers for describing the state of the environment and the state of the account.
//--- Policy study State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Add timestamp state.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Generate environment state embedding.
//--- State if(Account.GetIndex() >= 0) Account.BufferWrite(); if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Agent action taking into account the current policy.
//--- Action if(!Actor.feedForward(GetPointer(StateEncoder), -1, NULL, 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Estimate the cost of the Agent actions.
//--- Cost if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
To optimize the Agent behavior policy, we use the Critic with a minimum score. To increase convergence, we adjust the gradient direction vector using the CAGrad method.
Critic1.getResults(rewards1); Critic2.getResults(rewards2); //--- rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards); rewards = rewards - target_reward * DiscFactor; CNet *critic = NULL; if(rewards1.Sum() <= rewards2.Sum()) { Result.AssignArray(CAGrad((rewards1 - rewards)*sign) + rewards1); critic = GetPointer(Critic1); } else { Result.AssignArray(CAGrad((rewards2 - rewards)*sign) + rewards2); critic = GetPointer(Critic2); }
We perform the Critic and Actor backpropagation passes sequentially.
if(!critic.backProp(Result, GetPointer(Actor), -1) || !Actor.backPropGradient((CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Please note that at this stage we are not optimizing the Critic model. Therefore, there is no need for a backpropagation pass through the environment state Encoder.
This completes the operations of one iteration of updating the Agent behavior policy. We inform the user about the progress of the learning process and move on to the next iteration of the cycle.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> %15.8f\n", "Mean Improvement", iter * 100.0 / (double)(Iterations), Improve); Comment(str); ticks = GetTickCount(); } }
After completing all iterations of the training cycle, we clear the comments field on the chart, display information about the training results in the log, and initiate the EA shutdown.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Mean Improvement", Improve); ExpertRemove(); //--- }
Here we complete our consideration of the algorithms used in the article. The full code of all programs is attached below. We move on to checking the results of the work done.
3. Test
Above, we have seen the Closed-Form Policy Improvement method and done quite a lot of work on implementing its approaches using MQL5. We used the ideas proposed by the method authors. However, the analytical method used for selecting the optimal state was different from that proposed in the paper. In addition, in our work we used developments from our previous experience. Therefore, the results obtained may differ significantly from what the method authors presented in their paper. Naturally, our test environment differs from the experiments described in the original paper.
As always, the models are trained and tested using historical data for EURUSD H1. The model is trained using data for the first 7 months of 2023. To test the trained model, we use historical data from August 2023. All indicators are used with default parameters.
The implementation of the CFPI method required some changes in the model architecture but did not affect the structure of the source data. Therefore, at the first stage of training, we can use the training dataset created earlier when testing one of the previously discussed learning algorithms. I used the training data set from the previous articles. For the current article, I created a copy of a file called "CFPI.bd". But you can also create a completely new training dataset using one of the previously discussed methods. In this part, the CFPI method does not impose restrictions.
However, changes in the architecture did not allow us to use previously trained models. Therefore, the entire learning process was implemented "from scratch".
First, we trained the State Encoder and Critic models using the EA "...\Experts\CFPI\StudyCritic.mq5".
The training dataset includes 500 trajectories with 3591 environmental states in each. This in total amounts to almost 1.8 million "State-Action-Reward" sets. Primary training of Critics models was performed for 1 million iterations, which theoretically allows us to analyze almost every second state. For continuous trajectories, when not every new state of the environment makes fundamental changes in the market situation, this is a pretty good result. Given the emphasis on trajectories with maximum profitability, this will allow Critics to almost completely study such trajectories and expand their "horizon" to less profitable passes.
The next step is to train the Actor behavior policy in the EA "...\Experts\CFPI\Study.mq5". Here we execute 10 thousand training iterations with a package of 256 states. In total, this allows us to analyze more than 2.5 million states, which is larger than our training dataset.
I must say that after the first training iteration in test passes, you can notice some prerequisites for creating profitable strategies. The balance charts have some profitable intervals. In the process of additional collection of training trajectories, out of 200 passes, 3 completed with a profit. Of course, this may be either my subjective opinion or the result of a confluence of certain factors independent of the method. For example, we were lucky, and random initialization of models generated fairly good results. Anyway, we can say for sure that as a result of subsequent iterations of training models and collecting additional passes, there is a clear tendency towards an increase in the average profitability and profit factor of passes.
After several model training iterations, we obtained an Actor behavior policy that was capable of generating profit both on the historical data of the training dataset and on test data not included in the training dataset. The model testing results are shown below.
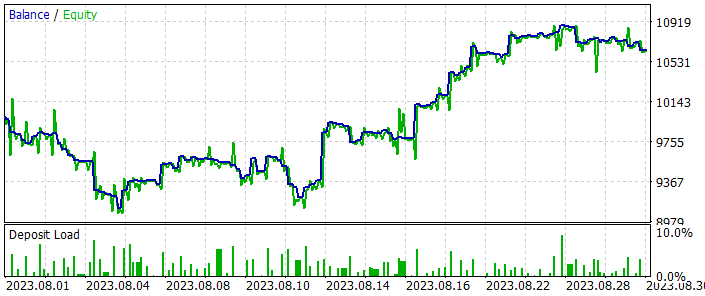
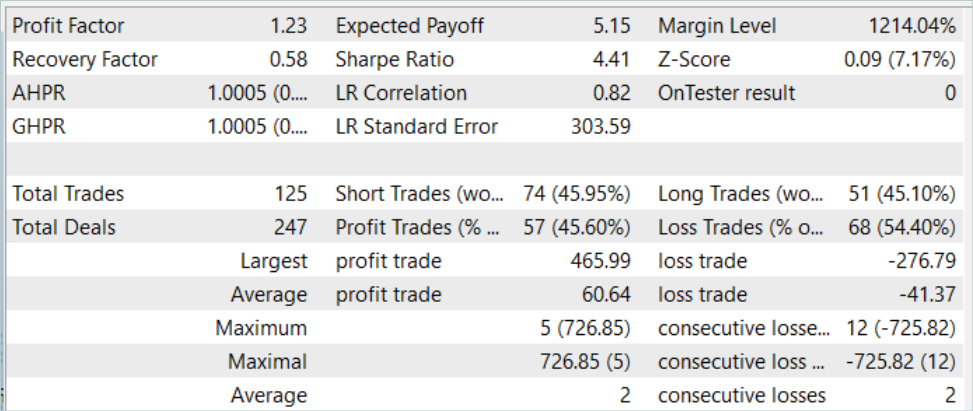
On the balance chart, you can notice some drawdown at the beginning of the testing period. But then the model demonstrates a fairly even tendency towards balance growth. This allows us to both regain what we lost and increase profits. In total, during the testing period, the model made 125 transactions, 45.6% of which were closed with a profit. The highest profitable and average profitable trade are 50% higher than the corresponding loss metrics. This resulted in the profit factor of 1.23.
Conclusion
In this article, we got acquainted with another model training algorithm: Closed-Form Policy Improvement. Probably the main contribution of this method is the addition of analytical approaches for choosing the direction of optimization of the trained model. Well, this process requires additional computational costs. However, oddly enough, this approach reduces the model training cost as a whole. This is because we are not trying to completely repeat the best of the presented trajectories. Instead, we focus on areas of maximum efficiency and do not waste time searching for optimal noise phenomena.
In the practical part of our article, we implemented the ideas proposed by the authors of the CFPI method, although with some changes compared to the authors' original mathematical calculations. Nevertheless, we received positive experience and good testing results.
My personal opinion is that the Closed-Form Policy Improvement method is worth considering. We can use its approaches to build our own trading strategies.
References
Programs used in the article
| # | Issued to | Type | Description |
|---|---|---|---|
| 1 | Research.mq5 | EA | Example collection EA |
| 2 | ResearchRealORL.mq5 | EA | EA for collecting examples using the Real-ORL method |
| 3 | Study.mq5 | EA | Actor Training EA |
| 4 | StudyCritic.mq5 | EA | Critics Training EA |
| 5 | Test.mq5 | EA | Model testing EA |
| 6 | Trajectory.mqh | Class library | System state description structure |
| 7 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 8 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/13982
 Modified Grid-Hedge EA in MQL5 (Part IV): Optimizing Simple Grid Strategy (I)
Modified Grid-Hedge EA in MQL5 (Part IV): Optimizing Simple Grid Strategy (I)
 Causal inference in time series classification problems
Causal inference in time series classification problems
 Trailing stop in trading
Trailing stop in trading
 DRAW_ARROW drawing type in multi-symbol multi-period indicators
DRAW_ARROW drawing type in multi-symbol multi-period indicators
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use