
Neural networks made easy (Part 69): Density-based support constraint for the behavioral policy (SPOT)
Introduction
Offline reinforcement learning allows the training of models based on data collected from interactions with the environment. This allows a significant reduction of the process of interacting with the environment. Moreover, given the complexity of environmental modeling, we can collect real-time data from multiple research agents and then train the model using this data.
At the same time, using a static training dataset significantly reduces the environment information available to us. Due to the limited resources, we cannot preserve the entire diversity of the environment in the training dataset.
However, in the process of learning the Agent's optimal policy, there is a high probability of its actions going beyond the distribution of the training dataset. Obviously, due to the lack of feedback from the environment, we cannot get a real assessment of such actions. Due to the lack of data in the training dataset, our Critic also cannot generate an adequate assessment. In this case, we can get both high and low expectations.
It must be said that high expectations are much more dangerous than low ones. With underestimated estimates, the model may refuse to perform these actions, which will lead to learning a suboptimal Agent policy. In case of overestimation, the model will tend to repeat similar actions, which can lead to significant losses during operation. Therefore, maintaining the Agent's policy within the training dataset becomes an important aspect to ensure the reliability of offline training.
Various offline reinforcement learning methods for solving this problem use parameterization or regularization, which constrain the Agent's policy to perform actions within the support set of the training dataset. Detailed constructions usually interfere with Agent models, which can lead to additional operational costs and prevent the full use of established online reinforcement learning methods. Regularization methods reduce the discrepancy between the learned policy and the training dataset, which may not meet the definition of density-based support and thus ineffectively avoid acting outside the distribution.
In this context, I suggest considering the applicability of the Supported Policy OpTimization (SPOT) method, which was presented in the article "Supported Policy Optimization for Offline Reinforcement Learning". Its approaches follow directly from a theoretical formalization of policy constraint based on the density distribution of the training dataset. SPOT uses a density estimator based on a Variational AutoEncoder (VAE), which is a simple yet effective regularization element. It can be built into ready-made reinforcement learning algorithms. SPOT achieves best-in-class performance on standard offline RL benchmarks. Thanks to its flexible design, models pre-trained offline using SPOT can also be fine-tuned online.
1. Supported Policy OpTimization (SPOT) algorithm
Performing support constraint is the typical method to mitigate errors in offline reinforcement learning. In turn, support constraint can be formalized based on the density of the behavioral strategy. The authors of the Supported Policy OpTimization method propose a regularization algorithm from the perspective of explicit estimation of the behavior density. SPOT includes a regularization term that follows directly from the theoretical formalization of the density support constraint. The regularization element uses a conditional variational auto-encoder (CVAE) that learns the density of the training dataset.
Similar to how an optimal strategy can be extracted from an optimal Q-function, a supported optimal strategy can also be recovered using greedy selection:
![]()
In the case of function approximation, this corresponds to a constrained strategy optimization problem.
Unlike specific Agent policy parameterization or divergence penalties used in other methods to constrain support, the authors of SPOT propose to use the density of the training dataset directly as a constraint:
![]()
where ϵ'=log ϵ for ease of notation.
Behavior density-based constraint is simple and straightforward in the context of support constraint. The authors of the method suggest using the log-likelihood function instead of the probabilistic one because of its mathematical convenience.
In turn, this imposes the additional constraint in that the density of the behavioral strategy is constrained below at each point in the state space. It is practically impossible to solve such a problem due to a large, even infinite number of constraints. Instead, the SPOT algorithm authors use a heuristic approximation that considers the average behavior density:
![]()
Let's convert the constrained optimization problem into an unconstrained one. For this, we treat the constraint term as a penalty. Thus, we obtain the policy learning objective as:
![]()
where λ is a Lagrangian multiplier.
The straightforward regularization term in the loss function presented above requires access to the behavioral policy used in collecting the training dataset. But we only have offline data generated by this policy. We can explicitly estimate the probability density at an arbitrary point using various density estimation methods. Variational autoencoder (VAE) is one of the best neural-density estimation models. The authors of the method decided to use a conditional variational autoencoder as their density estimator. After training the VAE, we can simply use it as the lower bound.
The general framework presented above can be built on various reinforcement learning algorithms with minimal modifications. In their paper, the authors of the method use TD3 as a base algorithm.
2. Implementation using MQL5
After considering the theoretical aspects of the Supported Policy Optimization method, we move on to its implementation using MQL5. We will implement our model based on the Expert Advisors from the article concerning the Real-ORL method. Let me remind you that the basic model used is based on the Soft Actor-Critic method close to TD3 which is utilized by the SPOT authors. However, our model will be complemented by a number of approaches that were discussed in previous articles.
First of all, we should note that the SPOT method adds regularization of the Agent's policy based on the data density in the training set. This regularization is applied at the stage of Agent policy offline training. It does not affect the process of interaction with the environment. Consequently, the training dataset collecting and testing Expert Advisors will be used without changes. You can familiarize yourself with them in the attachment.
Thus, we can immediately move on to the model training Expert Advisor. However, it should be noted that before we start training the policy, we need to train the autoencoder of the training dataset density function. Therefore, we will divide the learning process into 2 phases. The autoencoder will be trained in a separate Expert Advisor "...\SPOT\StudyCVAE.mq5".
2.1 Density model training
Before we start building the density model training EA, let's first discuss what and how we will train. The authors of the SPOT method proposed using an extended autoencoder to study the density of the training dataset. What does this mean from a practical point of view?
We have already discussed the properties of the autoencoder that compresses and recovers data. We also mentioned that neural networks can only operate stably in an environment similar to the training dataset. Consequently, when we feed into the model initial data that is far from the distribution of the training dataset, the results of its operation will be close to random values. Therefore, this leads to a significant increase in the data decoding error. We will exploit the combination of these properties of the autoencoder model.
We train the autoencoder on the distribution of Agent actions from the training dataset. In the process of training the Agent, we will feed into the autoencoder the actions proposed by the updated Agent policy. The error in data decoding will indirectly indicate the distance of predictive actions from the distribution of the training dataset.
So, now we have some understanding of the functionality, and it fits into the architecture of the autoencoder. But is it enough for us to understand the presence of an Agent's action in the training dataset? We understand perfectly well that the same action in different environmental conditions can give completely opposite results. Therefore, we have to train the autoencoder to extract the distributions of actions in different environmental states. Thus, we come to the conclusion that we have to feed a "State-Action" pair into the autoencoder input. In this case, at the output of the autoencoder we expect to receive the Agent Action that was fed to the input.
Note that when we feed the "State-Action" pair to the input of the autoencoder, we expect that in its latent state there will be compressed information about the State and Action. However, by training the autoencoder to decode only the action, there is a high probability that we will train the autoencoder to ignore information about the State of the environment. It will also use the entire size of the latent state to transmit the desired Action. This ultimately brings us back to the situation of encoding and decoding stateless Actions, which is extremely undesirable. Therefore, it is important for us to focus the attention of the Autoencoder on both components of the original State-Action data. To achieve this result, the authors of the method use an extended autoencoder, the architecture of which provides for the input of a certain Key for decoding data. This Key, together with the latent representation, is fed to the input of the decoder. In our case, we will use the state of the environment as the Key.
Thus, we have to build an autoencoder model, which should receive 3 tensors for the input of the feed-forward pass:
- Environment state (Encoder input)
- Agent action (Encoder input)
- Environment state (Decoder input Key)
Previously, we built models with only initial data from 2 tensors. Now we have to implement the initial data from 3 tensors. This problem can be solved in several ways.
First, we can combine the State-Action pair into a single tensor. Then the Key will be the second tensor of the source data, and this fits into the model we used earlier with 2 tensors of the source data. But combining disparate environmental data and Agent actions can have a negative impact on model performance and limit our ability to preprocess raw environmental data.
The second option is to add a method for working with the model with 3 tensors of the original data. This is a labor-intensive process that can lead to endless creation of methods for each specific task. This will make our library cumbersome and difficult to understand and maintain.
In this article, I chose the third option, which seems the simplest to me. We will create separate Encoder and Decoder models. Each will work with 2 tensors of the initial data. Their implementation fully complies with the methods we previously developed.
This is a theoretical decision. Now let's move on to describing the architecture of our Autoencoder models. This will be done in the CreateCVAEDescriptions method. We feed into the method pointers to 2 dynamic arrays, in which we will assemble the architecture of 2 models, Encoder and Decoder. In the body of the method, we check the received pointers and, if necessary, create new instances of dynamic array objects.
bool CreateCVAEDescriptions(CArrayObj *encoder, CArrayObj *decoder) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!decoder) { decoder = new CArrayObj(); if(!decoder) return false; }
First we describe the Encoder architecture. We feed the model with historical price movement data and analyzed indicator values. The input data fed to the model is raw and unprocessed. Therefore, next we carry out the primary preprocessing in the batch data normalization layer.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Next, we compress the data and simultaneously extract established patterns using a block of convolutional layers.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; int prev_wout = descr.window_out = BarDescr / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; prev_wout = descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
The environment state embedding obtained in this way is combined with the vector of the Agent's actions.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!encoder.Add(descr)) { delete descr; return false; }
Then, using 2 fully connected layers, we compress the data.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * EmbeddingSize; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
At the output of the Encoder, we create a stochastic latent representation using the internal layer of the variational autoencoder.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = EmbeddingSize; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
The following is a description of the Decoder architecture. The model input is a latent representation generated by the Encroder.
//--- Decoder decoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = EmbeddingSize; descr.activation = None; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; }
We immediately concatenate the resulting tensor with the environmental state vector.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = EmbeddingSize; descr.window = prev_count; descr.step = (HistoryBars * BarDescr); descr.optimization = ADAM; descr.activation = LReLU; if(!decoder.Add(descr)) { delete descr; return false; }
We input into the Encoder raw unprocessed data describing the state of the environment and performed their primary processing in the batch normalization layer. But in the Decoder, we do not have the opportunity to carry out such normalization. I decided not to normalize the data 2 times. Instead, in the process of training and operation, I will take data from the Encoder after normalization. This will allow us to make the Decoder a little simpler and reduce data processing time.
Next, we use fully connected layers to reconstruct the action vector from the received initial data.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!decoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NActions; descr.optimization = ADAM; descr.activation = SIGMOID; if(!decoder.Add(descr)) { delete descr; return false; } //--- return true; }
After describing the architecture of our Autoencoder, we move on to constructing an Expert Advisor to train this autoencoder. As mentioned above, we will train 2 models: Encoder and Decoder.
CNet Encoder; CNet Decoder;
In the program's OnInit initialization method, we first load the training dataset. Do not forget to check the operation result, as in case of data loading error, there will be nothing to train the model on.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
Next, we try to load pre-trained models and, if necessary, generate new models initialized with random parameters.
//--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Decoder.Load(FileName + "Dec.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new CVAE"); CArrayObj *encoder = new CArrayObj(); CArrayObj *decoder = new CArrayObj(); if(!CreateCVAEDescriptions(encoder,decoder)) { delete encoder; delete decoder; return INIT_FAILED; } if(!Encoder.Create(encoder) || !Decoder.Create(decoder)) { delete encoder; delete decoder; return INIT_FAILED; } delete encoder; delete decoder; }
We then move both models into a single OpenCL context, which allows us to exchange data between models without dumping them into the main program's memory.
OpenCL = Encoder.GetOpenCL(); Decoder.SetOpenCL(OpenCL);
Here we carry out minimally necessary control over the architecture of loaded (or created) models. Make sure to check the results of the operations.
Encoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- Encoder.getResults(Result); int latent_state = Result.Total(); Decoder.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Decoder doesn't match result of Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
We then initialize the creation of an event for starting the model training process. After that, we complete the program initialization method with the INIT_SUCCEEDED result.
if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
In the OnDeinit program deinitialization method, we save the trained models and clear the memory of objects created in the program.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Encoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); Decoder.Save(FileName + "Dec.nnw", Decoder.getRecentAverageError(), 0, 0, TimeCurrent(), true); delete Result; delete OpenCL; }
Note that we save all models in the general terminal catalog. This makes them available both when using programs in the terminal and in the strategy tester.
The model training process is implemented in the Train method. In the method body, we first create the required local variables.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); int bar = (HistoryBars - 1) * BarDescr;
Then we create a training loop.
for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = int((MathRand() * MathRand() / MathPow(32767, 2)) * (total_tr)); int i = int((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) continue;
Note that, unlike our recent work, we do not use trajectory prioritization here. This is a completely conscious and intentional step. This is because at this stage, we strive to study the true data density in the training dataset. While the use of trajectory prioritization can distort information in favor of trajectories with higher priority. Therefore, we use uniform sampling of trajectories and states in them.
After sampling the trajectory and state, we fill the description buffers of the environment State and the Agent's Actions from the training dataset.
State.AssignArray(Buffer[tr].States[i].state); Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite();
I remember that usually in the concept of "environment description" we include a vector describing the state of the account and open positions. Here I did not focus on the state of the account, since the direction of the position being opened or held is determined by the state of the market. Analysis of the account status is performed to manage risks and determine the size of the position. At this stage, I decided to limit the process to studying the density of actions in individual market situations and did not focus on the risk management model.
After preparing the initial data buffers, we run a feed-forward pass of the autoencoder. As discussed above, we feed a pointer to the Encoder twice at the Decoder input. In this case, we use the model output as the main input data stream. For an additional stream of input data, we remove the results from the Encoder batch normalization layer. Make sure to monitor the entire process.
if(!Encoder.feedForward(GetPointer(State), 1,false, GetPointer(Actions)) || !Decoder.feedForward(GetPointer(Encoder), -1, GetPointer(Encoder),1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
In the process of training the Autoencoder, we do not need to analyze or process the results of its operation. We just need to specify the target values, for which we use the Agent's action vector. This is the same vector that we previously fed into the Encoder. In other words, we already have a result buffer prepared, and we call the backpropagation methods of both autoencoder models.
if(!Decoder.backProp(GetPointer(Actions), GetPointer(Encoder), 1) || !Encoder.backPropGradient(GetPointer(Actions), GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Note that the Encoder updates its parameters based on the error gradient received from the Decoder. And we don't need to generate a separate target buffer for the Encoder.
This completes the operations of one iteration of autoencoder training. All we have to do is inform the user about the progress of the operations and move on to the next iteration of the model training loop.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Decoder", iter * 100.0 / (double)(Iterations), Decoder.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Here we display error information only for the Decoder, since the error is not calculated for the Encoder.
After successful completion of all iterations of the autoencoder training loop, we clear the comment field of the chart and initiate the process of terminating the EA.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Decoder", Decoder.getRecentAverageError()); ExpertRemove(); //--- }
The full Expert Advisor code can be found in the attachment. All programs used in this article are also presented there.
2.2 Agent Policy Training
After training the density model, we proceed to the Agent policy training Expert Advisor "...\SPOT\Study.mq5". The Agent training process is virtually unchanged. It was only slightly supplemented in terms of regularizing its behavior policy. The architecture of all trained models was also copied without changes. Therefore, let's only look at some of the methods of the EA "...\SPOT\Study.mq5". You can find its full code in the attachment.
No matter how small the changes in the Agent's policy training algorithm are, they involve higher-trained autoencoder models. We need to add them to the program.
STrajectory Buffer[]; CNet Actor; CNet Critic1; CNet Critic2; CNet TargetCritic1; CNet TargetCritic2; CNet Convolution; CNet Encoder; CNet Decoder;
In the OnInit program initialization method, we, as before, load the training dataset and control the execution of operations.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
Then, even before loading the trained models, we load the Autoencoder. If it is impossible to load models, we inform the user and terminate the initialization method with the INIT_FAILED result.
//--- load models float temp; if(!Encoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Decoder.Load(FileName + "Dec.nnw", temp, temp, temp, dtStudied, true)) { Print("Cann't load CVAE"); return INIT_FAILED; }
Note that in the absence of pre-trained models, we do not create new ones with random parameters. Since untrained models will only distort the learning process, and the results of such training will be unpredictable.
On the other hand, we could add a flag and, in the absence of trained Autoencoder models, train the Agent's policy without regularizing its actions, as was done previously. When working on a real problem, I would probably do this. But in this case, we want to evaluate the work of regularization. Therefore, interrupting the program serves as an additional point of control for the "human factor".
Next, we load the trained models and, if necessary, create new ones initialized with random parameters.
if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !TargetCritic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *convolution = new CArrayObj(); if(!CreateDescriptions(actor, critic, convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } if(!Actor.Create(actor) || !Critic1.Create(critic) || !Critic2.Create(critic) || !Convolution.Create(convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } if(!TargetCritic1.Create(critic) || !TargetCritic2.Create(critic)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } delete actor; delete critic; delete convolution; //--- TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1.0f); TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1.0f); StartTargetIter = StartTargetIteration; } else StartTargetIter = 0; if(!Convolution.Load(FileName + "CNN.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new Encoder model"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *convolution = new CArrayObj(); if(!CreateDescriptions(actor, critic, convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } if(!Convolution.Create(convolution)) { delete actor; delete critic; delete convolution; return INIT_FAILED; } delete actor; delete critic; delete convolution; }
Once new models are successfully loaded and/or initialized, we move them into a single OpenCL context. Also, in learning models, we disable the parameter updating mode. That is, we will not perform additional downstream training of the Autoencoder at this stage.
OpenCL = Actor.GetOpenCL(); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); TargetCritic1.SetOpenCL(OpenCL); TargetCritic2.SetOpenCL(OpenCL); Convolution.SetOpenCL(OpenCL); Encoder.SetOpenCL(OpenCL); Decoder.SetOpenCL(OpenCL); Encoder.TrainMode(false); Decoder.TrainMode(false);
One thing to note here is that although the random encoder is not trained either, we did not change its training mode flag. There is no need for this. The learning mode change method does not remove unused buffers. Therefore, it does not clear memory. It just changes the flag that controls the backpropagation algorithm. We do not call the encoder's backpropagation method in the program. This means that the effect of changing the random encoder training flag is close to zero. In the case of an autoencoder, the situation is slightly different. We will consider it later, in the Train model training method. Now let's return to the method of initializing the EA.
After creating models and transferring them into a single OpenCL context, we perform minimal control over the compliance of their architecture with the constants used in the program.
First, we check whether the size of the Actor's results layer matches the size of the Agent's action vector.
Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
The size of the Actor's initial data must correspond to the size of the vector describing the state of the environment.
Actor.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Actor doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
We also make sure to check the correspondence between the size of the Actor's latent layer and the Critic's source data buffer.
Actor.GetLayerOutput(LatentLayer, Result); int latent_state = Result.Total(); Critic1.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic doesn't match latent state Actor (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
We do similar checks for the Encoder and Decoder models of the autoencoder.
Decoder.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the Decoder does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; } Encoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } Encoder.getResults(Result); latent_state = Result.Total(); Decoder.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Decoder doesn't match result of Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
This concludes the work on preparing the models. Let's initialize the auxiliary buffer and generate an event to start the learning process.
Gradient.BufferInit(AccountDescr, 0); //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
Then we complete the method of initializing the Expert Advisor with a positive result.
Since we will not change the parameters of the autoencoder models during the training process, we do not need to save them after the program is completed. Therefore, the OnDeinit method remains unchanged. You can find its code in the attachment. Next, we move on to the process of training models. So, let's consider the Train method.
The algorithm of the Actor policy training method is more comprehensive and complex compared to the density model training method discussed above. Let's dwell on it in more detail.
At the beginning of the method, we prepare several local variables and matrices, which we will use later in the process of training models.
void Train(void) { int total_tr = ArraySize(Buffer); uint ticks = GetTickCount(); //--- int total_states = Buffer[0].Total; for(int i = 1; i < total_tr; i++) total_states += Buffer[i].Total; vector<float> temp, next; Convolution.getResults(temp); matrix<float> state_embedding = matrix<float>::Zeros(total_states, temp.Size()); matrix<float> rewards = matrix<float>::Zeros(total_states, NRewards); matrix<float> actions = matrix<float>::Zeros(total_states, NActions);
Next, we create a system of loops for generating embeddings of all states from the experience replay buffer. The outer loop of our system will iterate over the trajectories in the training dataset. The nested loop will iterate over the environmental states that the Agent visited while passing the trajectory.
int state = 0; for(int tr = 0; tr < total_tr; tr++) { for(int st = 0; st < Buffer[tr].Total; st++) { State.AssignArray(Buffer[tr].States[st].state);
In the body of the loop system, we load a vector describing a particular state of the environment from the training sample. Supplement it with a description of the account status and open positions.
float PrevBalance = Buffer[tr].States[MathMax(st - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(st - 1, 0)].account[1]; State.Add((Buffer[tr].States[st].account[0] - PrevBalance) / PrevBalance); State.Add(Buffer[tr].States[st].account[1] / PrevBalance); State.Add((Buffer[tr].States[st].account[1] - PrevEquity) / PrevEquity); State.Add(Buffer[tr].States[st].account[2]); State.Add(Buffer[tr].States[st].account[3]); State.Add(Buffer[tr].States[st].account[4] / PrevBalance); State.Add(Buffer[tr].States[st].account[5] / PrevBalance); State.Add(Buffer[tr].States[st].account[6] / PrevBalance);
Here we add the harmonics of the timestamp into the buffer.
double x = (double)Buffer[tr].States[st].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_MN1); State.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_W1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[st].account[7] / (double)PeriodSeconds(PERIOD_D1); State.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); State.AddArray(vector<float>::Zeros(NActions));
In order to evaluate states regardless of the actions taken by the Agent, we fill the rest of the buffer with zero values.
After successfully filling the source data buffer, we call the random encoder's feed-forward pass method.
if(!Convolution.feedForward((CBufferFloat *)GetPointer(State), 1, false, (CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); ExpertRemove(); return; }
We save the results of its work in the embedding matrix.
Convolution.getResults(temp); if(!state_embedding.Row(temp, state)) continue;
At the same time, we save completed actions and rewards received as a result of subsequent transitions.
if(!temp.Assign(Buffer[tr].States[st].action) || !actions.Row(temp, state)) continue; if(!temp.Assign(Buffer[tr].States[st].rewards) || !next.Assign(Buffer[tr].States[st + 1].rewards) || !rewards.Row(temp - next * DiscFactor, state)) continue;
After successfully adding all entities to the local matrices, we increment the counter of processed states. We inform the user about the progress of the state embedding process and move on to the next iteration of the loop system.
state++; if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %6.2f%%", "Embedding ", state * 100.0 / (double)(total_states)); Comment(str); ticks = GetTickCount(); } } }
After all iterations of the loop system have successfully completed, we adjust the sizes of the local matrices, if necessary, to the actual size of the data being used.
if(state != total_states)
{
rewards.Resize(state, NRewards);
actions.Resize(state, NActions);
state_embedding.Reshape(state, state_embedding.Cols());
total_states = state;
}
Then, we move on to the next stage of the preparatory work, in which we prepare a number of local variables and determine the priority of sampling trajectories from the training dataset in the model training process.
vector<float> rewards1, rewards2, target_reward; STarget target; int bar = (HistoryBars - 1) * BarDescr; //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
At this point, the preparatory work is completed, and we move directly to training the models. To do this, we create a training loop with the number of iterations specified in the EA's external parameters.
In the body of the loop, we sample the trajectory taking into account priorities and randomly select a state on it.
for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { iter--; continue; }
Next, according to the SAC method, we need to calculate the expected reward until the end of the episode. To do this, we use target models of Critics. However, we will perform these operations only using pre-trained models. Therefore, before starting operations, we check whether the minimum required number of preliminary training iterations have been completed.
target_reward = vector<float>::Zeros(NRewards); //--- Target if(iter >= StartTargetIter) { State.AssignArray(Buffer[tr].States[i + 1].state);
After successfully passing the control, we fill the initial data buffer with a description of the subsequent state of the environment.
Separately, we populate the buffer describing the account status and open positions.
float PrevBalance = Buffer[tr].States[i].account[0]; float PrevEquity = Buffer[tr].States[i].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i + 1].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i + 1].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i + 1].account[2]); Account.Add(Buffer[tr].States[i + 1].account[3]); Account.Add(Buffer[tr].States[i + 1].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i + 1].account[6] / PrevBalance);
Also, we add timestamp harmonics to the same buffer.
double x = (double)Buffer[tr].States[i + 1].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i + 1].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); //--- if(Account.GetIndex() >= 0) Account.BufferWrite();
The collected data is sufficient to complete the Actor's feed-forward pass.
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Note that we are calling the feed-forward pass method on the Actor model being trained with the following state of the environment. This generates an Actor action according to the updated policy. Thus, target Critics evaluate the expected reward from the updated policy until the end of the episode.
if(!TargetCritic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor)) || !TargetCritic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
We use the minimum score received from the 2 target Critics as the expected value in subsequent operations.
TargetCritic1.getResults(rewards1); TargetCritic2.getResults(rewards2); target_reward.Assign(Buffer[tr].States[i + 1].rewards); if(rewards1.Sum() <= rewards2.Sum()) target_reward = rewards1 - target_reward; else target_reward = rewards2 - target_reward; target_reward *= DiscFactor; target_reward[NRewards - 1] = EntropyLatentState(Actor); }
In the next step, we train our Critics. To ensure the correctness of their assessments, training is based on a comparison of actual actions and rewards from the training dataset. Let me remind you that in our model, we use the Actor to pre-process the environment state. Therefore, as before, we populate the initial data buffers with a description of the sampled state of the environment.
//--- Q-function study
State.AssignArray(Buffer[tr].States[i].state);
We fill the buffer describing the account status and open positions.
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Add timestamp state.
double x = (double)Buffer[tr].States[i].account[7] / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = (double)Buffer[tr].States[i].account[7] / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
Next, execute the feed-forward pass for the Actor.
if(!Actor.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Please note that at this stage we have a complete set of data to perform a feed-forward pass of the Autoencoder. We do not put off until later what can be done now. So, we call the feed-forward methods of Encoder and Decoder.
if(!Encoder.feedForward((CBufferFloat *)GetPointer(State), 1, false, (CNet *)GetPointer(Actor)) || !Decoder.feedForward(GetPointer(Encoder), -1, GetPointer(Encoder), 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
As mentioned above, the Critics are trained on the actual actions of the Actor from the training dataset. So we'll load them into the data buffer and call the feed-forward methods of both Critics.
Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Next, we supplement the current state description buffer with the necessary data and perform the embedding of the analyzed state using a random encoder.
if(!State.AddArray(GetPointer(Account)) || !State.AddArray(vector<float>::Zeros(NActions)) || !Convolution.feedForward((CBufferFloat *)GetPointer(State), 1, false, (CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Based on the embedding results, we generate target values for Actor and Critics.
Convolution.getResults(temp); target = GetTargets(Quant, temp, state_embedding, rewards, actions);
After that, we update the parameters of our Critics. As we have seen before, the CAGrad method is used to adjust the gradient vector to improve model convergence.
Critic1.getResults(rewards1); Result.AssignArray(CAGrad(target.rewards + target_reward - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } Critic2.getResults(rewards2); Result.AssignArray(CAGrad(target.rewards + target_reward - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient), LatentLayer)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
After successfully updating the Critic models, we move on to optimizing the Actor policy. This process can be divided into 3 blocks. In the first block, we adjust the Agent's policy to repeat a certain action collected from actions in the training dataset performed in similar states and weighted by the reward received.
//--- Policy study Actor.getResults(rewards1); Result.AssignArray(CAGrad(target.actions - rewards1) + rewards1); if(!Actor.backProp(Result, GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
At the second stage, we use the results of the Autoencoder and check the deviation of the generated Agent actions from the training data. If the Action's decoding error threshold is exceeded, we attempt to return the Actor's policy to the training dataset distribution. To do this, we run the backpropagation pass of the Autoencoder, and the encoding error is passed directly to the Actor as an error gradient, similar to passing the error gradient from the Critic. It is for the safe implementation of this operation that we disabled the learning mode in the Encoder and Decoder at the stage of program initialization.
Decoder.getResults(rewards2); if(rewards2.Loss(rewards1, LOSS_MSE) > MeanCVAEError) { Actions.AssignArray(rewards1); if(!Decoder.backProp(GetPointer(Actions), GetPointer(Encoder), 1) || !Encoder.backPropGradient((CNet*)GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } }
At the next stage of training the Actor's policy, we check the reliability of the forecasts of our Critics. IF the forecasts are confident enough, we adjust the Actor's policy towards the most likely maximum reward. At this stage, we also disable the Critic parameter update mode to avoid the effect of mutual adaptation of models.
CNet *critic = NULL; if(Critic1.getRecentAverageError() <= Critic2.getRecentAverageError()) critic = GetPointer(Critic1); else critic = GetPointer(Critic2); if(MathAbs(critic.getRecentAverageError()) <= MaxErrorActorStudy) { if(!critic.feedForward(GetPointer(Actor), LatentLayer, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; } critic.getResults(rewards1); Result.AssignArray(CAGrad(target.rewards + target_reward - rewards1) + rewards1); critic.TrainMode(false); if(!critic.backProp(Result, GetPointer(Actor)) || !Actor.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); critic.TrainMode(true); break; } critic.TrainMode(true); }
Next, we need to update the target Critic models.
//--- Update Target Nets if(iter >= StartTargetIter) { TargetCritic1.WeightsUpdate(GetPointer(Critic1), Tau); TargetCritic2.WeightsUpdate(GetPointer(Critic2), Tau); } else { TargetCritic1.WeightsUpdate(GetPointer(Critic1), 1); TargetCritic2.WeightsUpdate(GetPointer(Critic2), 1); }
We also need to inform the user about the progress of the learning process.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); str += StringFormat("%-14s %5.2f%% -> Error %15.8f\n", "Actor", iter * 100.0 / (double)(Iterations), Actor.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
After completing all iterations of the model training cycle, we clear the comments field on the chart. We also output information about the model training results to the log and initiate EA termination.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); ExpertRemove(); //--- }
This concludes our work on implementing the Supported Policy Optimization method using MQL5. Find the complete code of all programs used in the article in the attachment. Now we move on to the next part of our article, in which we will check the results using a practical case.
3. Test
We have implemented the Supported Policy OpTimization (SPOT) method using MQL5 tools. Now it's time to test the results of our work in practice. As always, I would like to draw your attention to the fact that this work presents my own vision of the approaches proposed by the authors of the method. Furthermore, they are superimposed on previously created developments using other methods. As a result, we built a model as some conglomerate of various ideas collected by my vision of the process. Consequently, all possibly observed shortcomings cannot be completely projected onto any of the methods used.
As before, the models are trained and tested using historical data for EURUSD H1. All indicators are used with default parameters. The model is trained using data for the first 7 months of 2023. To test the trained model, we use historical data from August 2023.
As mentioned above, the models of interaction with the environment are used without changes. Therefore, for the first stage of training we can use the training dataset collected as part of the article on Real-ORL, which served as the donor of the models. I copied the training dataset and saved it as "SPOT.bd".
At the first stage, we train the Autoencoder. The training dataset includes 500 trajectories with 3591 environmental states in each. This in total amounts to almost 1.8 million "State-Action-Reward" sets. I have run 5 Autoencoder training loops, each having 0.5 million iterations, which is 40% greater than the size of the training dataset.
After the initial training of the Autoencoder, we start the process of training models in the EA "...\SPOT\Study.mq5". Note that the duration of the model training process significantly exceeds the Autoencoder training time.
It should also be noted that keeping the Agent's policy within the training dataset leaves no hope of obtaining results that are superior to the passes in the training dataset. Therefore, to obtain more optimal policies, we need to iteratively update the experience replay buffer and update the models, including the autoencoder.
Therefore, in parallel with the model training process, I run the optimization of the "ResearchExORL.mq5" EA in the strategy tester to study strategies beyond the training set.
After completing the model training loop, we perform the 200-pass optimization of the "Research.mq5" EA, which explores the environment in some environment of learned Actor policies.
Based on the updated training set, we repeat the Autoencoder training for 0.5 million iterations. Then perform the downstream training of the Actor policy.
As a result of several training loops, I managed to train the Actor policy capable of generating profit during the training and test historical period. Model results for August 2023 are presented below.
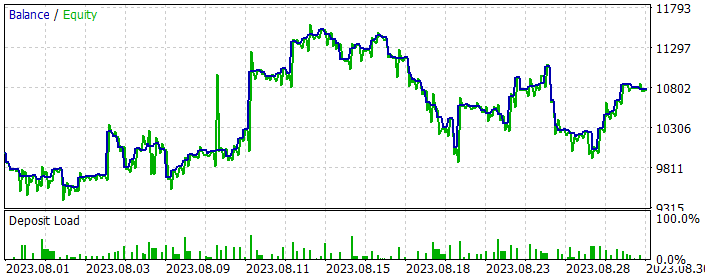
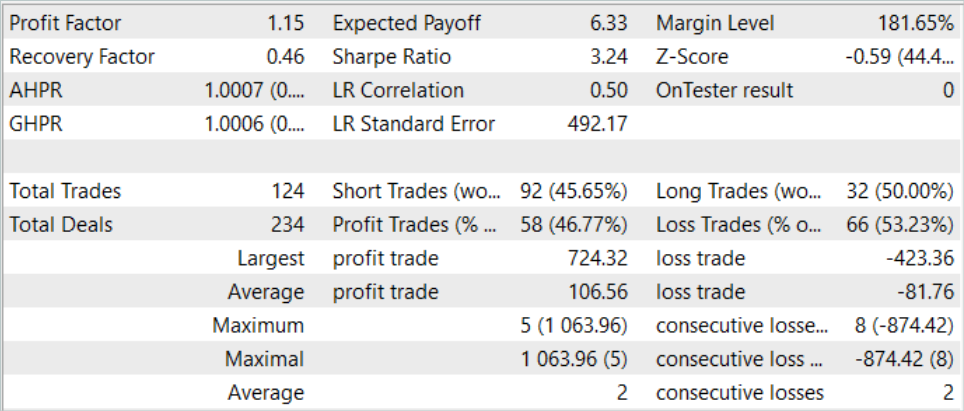
As you can see from the data presented, during the month of testing the strategy, the model made 124 trades (92 short and 32 long). Of these, almost 47% were closed with a profit. It is noteworthy that the share of profitable long and short positions is close (50% and 46%, respectively). Moreover, the average profitable trade is 25% higher than the average loss. The largest profitable trade is almost 2 times greater than the largest loss. In general, based on the trading results, the profit factor was 1.15.
Conclusion
In this article we got acquainted with the Supported Policy OpTimization (SPOT) method, which represents a successful solution to the problem of offline learning under conditions of a limited training dataset. Its ability to adjust policy given estimated behavioral strategy density demonstrates superior performance on standard test scenarios. SPOT easily integrates into existing offline RL algorithms, providing flexibility for application in different contexts. Its modular structure allows its use with different learning approaches.
A unique feature of SPOT is its use of regularization based on an explicit estimate of the density of the training set data. This provides precise control of acceptable policy actions and effectively prevents extrapolation beyond the training dataset.
In the practical part, we implemented our vision of the proposed approaches using MQL5. Based on the test results, we can draw a conclusion about the effectiveness of this method. During the training process, we can also note the stability of the process. Based on the training results, we managed to find a profitable strategy for the Actor's behavior.
However, please note that keeping the Actor's policy within the training dataset limits the stimulation of research outside of it. On the one hand, this makes the learning process more stable. On the other hand, it limits the possibilities of exploring unknown subspaces of the environment. Based on this, we can conclude that the most effective use of this method is possible when the training dataset has suboptimal passes.
At the same time, to stimulate exploration of the environment, you can try to "flip" the method and stimulate the study of actions outside the training dataset. But this is a topic for future research.
References
Programs used in the article
| # | Issued to | Type | Description |
|---|---|---|---|
| 1 | Research.mq5 | EA | Example collection EA |
| 2 | ResearchRealORL.mq5 | EA | EA for collecting examples using the Real-ORL method |
| 3 | ResearchExORL.mq5 | EA | EA for collecting examples using the ExORL method |
| 4 | Study.mq5 | EA | Agent training EA |
| 5 | StudyCVAE.mq5 | EA | Autoencoder learning Expert Advisor |
| 6 | Test.mq5 | EA | Model testing EA |
| 7 | Trajectory.mqh | Class library | System state description structure |
| 8 | NeuroNet.mqh | Class library | A library of classes for creating a neural network |
| 9 | NeuroNet.cl | Code Base | OpenCL program code library |
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/13954
 Triangular arbitrage with predictions
Triangular arbitrage with predictions
 Developing an MQL5 RL agent with RestAPI integration (Part 3): Creating automatic moves and test scripts in MQL5
Developing an MQL5 RL agent with RestAPI integration (Part 3): Creating automatic moves and test scripts in MQL5
 Learn how to trade the Fair Value Gap (FVG)/Imbalances step-by-step: A Smart Money concept approach
Learn how to trade the Fair Value Gap (FVG)/Imbalances step-by-step: A Smart Money concept approach
 Population optimization algorithms: Binary Genetic Algorithm (BGA). Part I
Population optimization algorithms: Binary Genetic Algorithm (BGA). Part I
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Is it intentional that there are no attachments to this article?
Is it intentional that there are no attachments to this article?
This is an unfortunate error and a working version of the article has been published. Corrected.