Neural networks made easy (Part 35): Intrinsic Curiosity Module

Contents

• Introduction
• 1. Curiosity is the urge to learn
• 2. Intrinsic curiosity block using MQL5
• 2.1. Experience replay block
• 2.2. Intrinsic Curiosity Module (ICM)
• 3. Testing
• Conclusion
• References
• Programs used in the article

Introduction

We continue to study reinforcement learning algorithms. As we have previously learned, all reinforcement learning algorithms are built on the paradigm of getting a reward from the environment for each time the agent transits from one environment state to another by performing some action. In turn, the agent strives to construct its action policy in such a way as to maximize the reward received. When starting considering reinforcement learning methods, we mentioned the importance of building a clear reward policy which plays one of the key roles in achieving the model training goal.

But in most real life situations, rewards don't follow every action. There can be a time lag between an action and a reward, varying in length. Sometimes receiving one reward depends on a number of actions. In such cases, we split the total reward into component parts and placed them along the entire path of the agent from the action to the reward. This is a pretty complicated process, full of conventions and compromises.

Trading is one of these tasks. The agent must open a position in the right direction at an opportune moment. Then it should wait for the moment when the profitability of the open position is at its maximum. After that it should close the position and lock the operation result. Thus, we receive the reward inly at the point the position is closed, in the form of the account balance change. In the previously considered algorithms, we distributed this reward among steps (one step is the time interval of one candlestick) in the amount equal to a multiple of a change in the symbol price. But how correct is that? At each step, the agent performed an action, such a trading operation or a decision not to perform a trading operation. So, the decision not to trade is also the agent's action which it chooses to implement. So, there is the question of how much each action contributes to the overall result. 

Are there other approaches to organizing the reward policy and the model training process?

1. Curiosity is the urge to learn

Look at the behavior of living beings. Animals and birds are able to travel long distances before they receive a reward in the form of food. Humans do not receive rewards for each of their actions. Human learning principles are multifaceted. One of the driving forces of learning is curiosity. When there is a closed door in front of you, it is curiosity that makes you open and look inside. This is the human nature.

Our brain is designed so that when we perform some action, we already predict the result of its impact 1-2 steps forward. Sometimes even more. Well, we perform any action in an effort to obtain the desired result. Then, by comparing the result with our expectations, we correct our actions. We also know that we can repeat an attempt only if it's a game. In real life, there is no possibility to take a step back and repeat the same situation. Each new attempt is a new result. Therefore, before committing any action, we analyze all our previously gained experience. Based on the experience, we select the action that seems correct to us.

When we get into an unfamiliar situation, we try to explore it and to remember the environment. In doing so, we may not think about which benefit this can bring in the future. We do not receive immediate rewards for our actions. We only gain the experience which may be useful in the future.

We have previously mentioned the need to explore the environment as much as possible, as well as the balance between the use of previously gained experience and the study of the environment. We have even introduced the novelty hyperparameter in the ɛ-greedy strategy. But the hyperparameter is a constant. Our purpose now is to train the model to manage the level of novelty on its own, depending on the situation.

The authors of the article "Curiosity-driven Exploration by Self-supervised Prediction" tried to apply such approaches when creating their algorithm. This article was published in May 2017. The method is based on the formation of curiosity as an error in the model's ability to predict the consequences of its actions. The curiosity is higher for previously not committed actions. The article explores three big challenges:

1. Rare extrinsic reward. Curiosity allows the agent to reach its goal with fewer interactions with the environment.
2. Training without extrinsic rewards. Curiosity pushes the agent to explore the environment efficiently even when there is no extrinsic reward from the environment.
3. Generalization to invisible scenarios. Knowledge gained from previous experience helps the agent to explore new places much faster than starting from scratch.

The authors proposed a rather simple idea: To an external reward re, we add some intrinsic reward ri, which will be a measure of curiosity and which will encourage the exploration of the environment. This cocktail will then be provided to the agent for training. Reward scaling factors can be used to adjust the impact of extrinsic and intrinsic rewards. Such factors are hyperparameters of the model.

The main novelty lies in the architecture of the ICM block which generates this intrinsic reward. The Intrinsic Curiosity Module contains three separate models:

• Encoder
• Inverse Model
• Forward Model

Two subsequent system states and the performed action are input into the module. The action is encoded as a one-hot vector. The action can be encoded both outside the module and inside it. The system states input into the module are encoded using an encoder. The encoder aims at reducing the dimension of the tensor which describes the system state as well as at filtering the data. The authors divide all features describing the system state into three groups:

1. Those affected by the agent.
2. Unaffected by the agent but affecting the agent.
3. Unaffected by the agent and not affecting the agent.

The encoder should help focus on the first two groups and neutralize the influence of the third group.

The Inverse Model receives the encoded state of 2 subsequent states and learns to determine the action performed to transit between states. The training of the inverse model together with the encoder should distinguish the first 2 groups of features. LogLoss is used as the loss function for the Inverse Model.

The Forward Model learns to predict the next state based on the encoded current state and the performed action. The measure of curiosity is the quality of the prediction. The prediction error computed by MSE is an intrinsic reward.

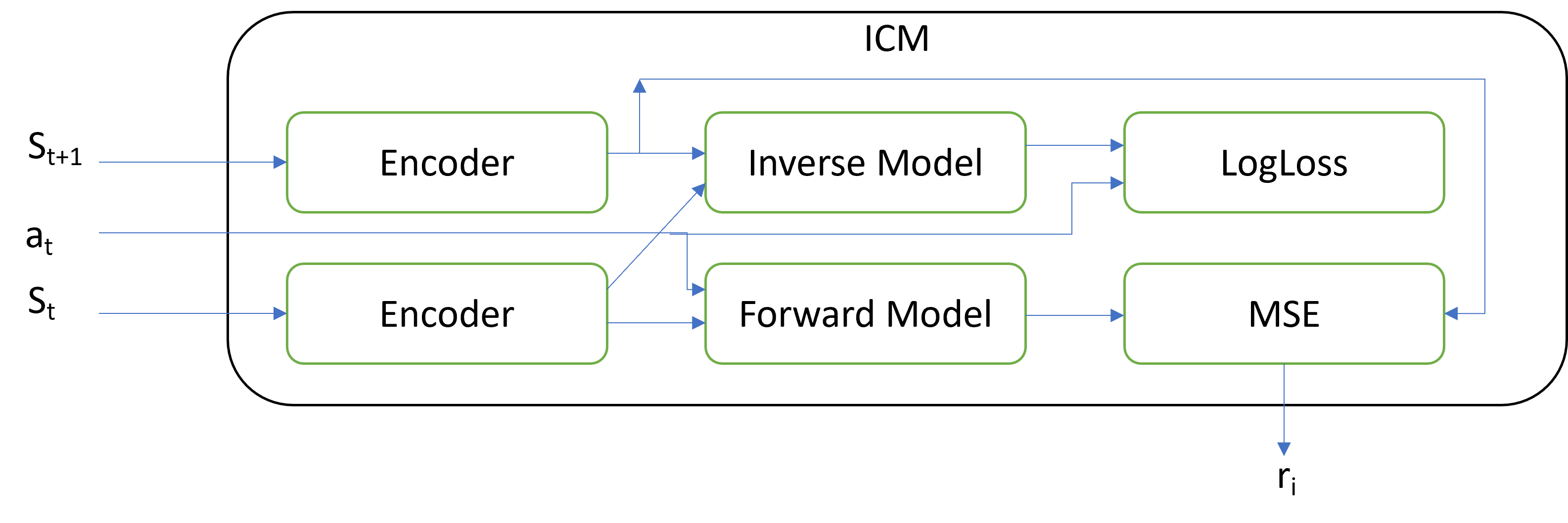
It may seem strange but as the Forward Model error grows, the intrinsic reward of the DQN model we are training also grows. The idea is to encourage the model to perform more actions, the results of which are unknown. Thus, the model will explore the environment. As we explore the environment, the model's curiosity decreases and DQN maximizes the extrinsic reward.

The Intrinsic Curiosity Module can be used with any of the models we have discussed so far. And we don't forget to use all previously studied architectural solutions to improve the model convergence.

The practical tests conducted by the methodology authors show the effectiveness of the algorithm in computer games with a reward at the end of the game level. In addition, the model demonstrates the ability to generalize — it can use previously gained experience when moving to a new game level. Especially interesting is the model's ability to perform well when textures change and noise is added. That is, the model learns to identify the main things and to ignore various noises. This increases the model stability in various environment states.

2. Intrinsic curiosity block using MQL5

We have briefly considered the theoretical aspects of the methodology. Now let's move on to the practical part of our article. In this part, we will implement the method using MQL5. Before proceeding with the implementation, please note that we will not use the previously considered approaches for a number of reasons.

The first thing that will change is the reward policy. I decided to get closer to the real situation. The extrinsic reward will be a change in the account balance. Please note it is the balance, not the equity change. I understand that such a reward can be quite rare, but we apply the new method in an effort to this problem.

Since we are limited to rewards in the form of a balance change, but at the same time, each agent action can be expressed as trading operations, we have to add variables that characterize the trading account state to the system state description. We will also have to monitor the opening and closing of positions, as well as accumulated floating profit for each position.

In order not to implement tracking of each position in the EA code, I decided to move the model training process to the strategy tester. We will let the model perform operations in the strategy tester. Then, by using the account status and open position polling functions, we can get all the necessary information from the strategy tester.

Therefore, we need to create a memory buffer for the experience replay. We talked about the reasons for creating such a buffer in the article "Neural networks made easy (Part 27): Deep Q-learning (DQN)". Previously, we used the entire symbol history for the training period as a buffer. But it is not possible now, since we add the account state data. So, we will implement a cumulative experience buffer inside the program.

In addition, we will enable the EA to open several positions at the same time, Including oppositely directed ones. This changes the space of possible agent actions. The agent will be able to perform four actions:

0 — buy

1 — sell

2 — close all open positions

3 — skip a turn, wait for a suitable state

Let us start the development by implementing the experience replay buffer.

2.1. Experience replay block

The experience replay buffer should allow a constant addition of records. Every time we will be adding a whole data package which includes:

• environment state description tensor
• action being taken
• extrinsic reward received

And the most appropriate approach to implement the buffer would be to use a dynamic object array. Each individual record will contain an object with the above information.

To organize each individual record in the buffer, we will create the CReplayState class derived from the CObject base class. In the class, we use a static data buffer object and two variables to store the data, the action taken, and the reward.

Note that the agent performs the action from the current state. And it receives a reward for transiting to this state. I.e. this is a reward for transiting from the previous state to the current due to the action performed in the previous step. Although the reward and the action are added to the buffer in the same record, they actually belong to different intervals.

class CReplayState : public CObject
  {
protected:
   CBufferFloat      cState;
   int               iAction;
   double            dReaward;

public:
                     CReplayState(CBufferFloat *state, int action, double reward);
                    ~CReplayState(void) {};
   bool              GetCurrent(CBufferFloat *&state, int &action);
   bool              GetNext(CBufferFloat *&state, double &reward);
  };

In the class constructor, we get all the necessary information and copy it to class variables and internal objects.

CReplayState::CReplayState(CBufferFloat *state, int action, double reward)
  {
   cState.AssignArray(state);
   iAction = action;
   dReaward = reward;
  }

Since we are using a static data buffer object, our class destructor remains empty.

Let's add two more methods to our class to access the saved data GetCurrent and GetNext. In the first case, we return the state and the action. And in the second we return the action and the reward.

bool CReplayState::GetCurrent(CBufferFloat *&state, int &action)
  {
   action = iAction;
   double reward;
   return GetNext(state, reward);
  }

The algorithm of both methods is quite simple. And we will look at their use a little later.

bool CReplayState::GetNext(CBufferFloat *&state, double &reward)
  {
   reward = dReaward;
   if(!state)
     {
      state = new CBufferFloat();
      if(!state)
         return false;
     }
   return state.AssignArray(GetPointer(cState));
  }

After creating a single record object, we move on to creating our experience buffer CReplayBuffer as an inheritor of the CArrayObj class of objects dynamic array. This class will be constantly updated with new states during the EA operation. And to avoid memory overflow, we will limit the maximum size to the iMaxSize variable value. We will also add the SetMaxSize method to manage the buffer size. We do not create other objects and variables in the class body. That is why the constructor and the destructor are empty.

class CReplayBuffer : protected CArrayObj
  {
protected:
   uint              iMaxSize;
public:
                     CReplayBuffer(void) : iMaxSize(500) {};
                    ~CReplayBuffer(void) {};
   //---
   void              SetMaxSize(uint size)   {  iMaxSize = size; }
   bool              AddState(CBufferFloat *state, int action, double reward);
   bool              GetRendomState(CBufferFloat *&state1, int &action, double &reward, CBufferFloat*& state2);
   bool              GetState(int position, CBufferFloat *&state1, int &action, double &reward, CBufferFloat*& state2);
   int               Total(void) { return CArrayObj::Total(); }
  };

To add records to the buffer, we will use the AddState method. The method receives in parameters new record data, including the state tensor, the action and the extrinsic reward.

In the method body, we check the pointer to the object of the system state buffer. If the pointer check is successful, we create a new record object and add it to the dynamic array. The main operations with the dynamic arrays are implemented using the parent class methods.

After that we check the current buffer size. If necessary, we delete the oldest objects to bring the buffer size in line with the specified buffer size maximum.

bool CReplayBuffer::AddState(CBufferFloat *state, int action, double reward)
  {
   if(!state)
      return false;
//---
   if(!Add(new CReplayState(state, action, reward)))
      return false;
   while(Total() > (int)iMaxSize)
      Delete(0);
//---
   return true;
  }

To get data from the buffer, we will create two methods: GetRendomState and GetState. The first one returns a random state from the buffer, and the second method returns the states at the specified index in the buffer. In the body of the first method, we only generate a random number within the buffer size and call the second method to get the data with the generated index.

bool CReplayBuffer::GetRendomState(CBufferFloat *&state1, int &action, double &reward, CBufferFloat *&state2)
  {
   int position = (int)(MathRand() * MathRand() / pow(32767.0, 2.0) * (Total() - 1));
   return GetState(position, state1, action, reward, state2);
  }

If you look at the algorithm of the second method GetState, you will notice the difference in the number of requested and previously saved data. When saving, we received one system state, while now two environment state tensors are requested.

Let's remember how the Q-learning process is organized. Training is based on four data objects:

• the current state of the environment
• the action taken by the agent
• the next state of the environment
• reward for the transition between the states of the environment

Therefore, we need to extract two subsequent states of the system from the experience buffer. Also, we were saving the action form the analyzed state and the reward for transition to the same state. Therefore, we need to extract the state and action from one record and extract the environment state and the reward from the next record. This is how we organized the GetCurrent and GetNext methods above.

Now let's look at the implementation of the GetState method. First of all, in the method body, we check the specified index of the entry to be retrieved. It must be at least 0 and at most the index of the penultimate record in the buffer. This is because we need the data of two subsequent records.

Next, we call GetCurrent for the record with the specified index. Then we move on to the next record and call the GetNext method. The operation result is returned to the caller program.

bool CReplayBuffer::GetState(int position, CBufferFloat *&state1, int &action, double &reward, CBufferFloat *&state2)
  {
   if(position < 0 || position >= (Total() - 1))
      return false;
   CReplayState* element = m_data[position];
   if(!element || !element.GetCurrent(state1, action))
      return false;
   element = m_data[position + 1];
   if(!element.GetNext(state2, reward))
      return false;
//---
   return true;
  }

The experience buffer is specific to a particular training session and there is no value in storing its data. Therefore, there is no need to create file operation methods for the classes discussed above.

2.2. Intrinsic Curiosity Module (ICM)

After creating the experience buffer, we proceed to the implementation of the Intrinsic Curiosity Module algorithm. As mentioned earlier in the theoretical part, the module uses three models: encoder, inverse and direct models. In my implementation, I did not stick to the architecture presented by the authors. To save resources, I did not create a separate encoder for the Intrinsic Curiosity Module.

The original architecture implies the creation of an encoder similar to the one used in the training DQN-model. I decided to use the existing encoder of the training model to encode the signal. Of course, this requires the synchronization of the models and some additions to the backpropagation method of the model. However, this will reduce the consumption of memory and computing resources which would be required to create and train the additional encoder.

In addition, I expect to get additional profit in the form of finer tuning of the DQN-model's encoder.

To implement the algorithm, let us create a new CICM neural network dispatcher class which inherits our base CNet neural network dispatcher class. Three internal variables are added in the class body:

• iMinBufferSize — the minimum size of the experience buffer required to start training models.
• iStateEmbedingLayer — the number of the neural layer of the model we are training, from which we will read the encoded state of the environment. This is the neural layer that completes the encoder of the model.
• dPrevBalance — a variable to record the last state of the account balance. We will use it to determine the extrinsic reward.

In addition, we will declare four internal objects. These include one object of the experience accumulation buffer and three neural network objects: cTargetNet, cInverseNet and cForwardNet.

We are using Q-learning, and Target Net is one of the main pillars of this learning method.

class CICM : protected CNet
  {
protected:
   uint              iMinBufferSize;
   uint              iStateEmbedingLayer;
   double            dPrevBalance;
   //---
   CReplayBuffer     cReplay;
   CNet              cTargetNet;
   CNet              cInverseNet;
   CNet              cForwardNet;

   virtual bool      AddInputData(CArrayFloat *inputVals);

public:
                     CICM(void);
                     CICM(CArrayObj *Description, CArrayObj *Forward, CArrayObj *Inverse);
   bool              Create(CArrayObj *Description, CArrayObj *Forward, CArrayObj *Inverse);
   int               feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true, bool sample = true); 
   bool              backProp(int batch, float discount = 0.9f);
   int               getAction(void);      
   int               getSample(void);
   float             getRecentAverageError() { return recentAverageError; }
   bool              Save(string file_name, bool common = true);
   bool              Save(string dqn, string forward, string invers, bool common = true);
   virtual bool      Load(string file_name, bool common = true);
   bool              Load(string dqn, string forward, string invers, uint state_layer, bool common = true);
   //---
   virtual int       Type(void)   const   {  return defICML;   }
   virtual bool      TrainMode(bool flag)
            { return (CNet::TrainMode(flag) && cForwardNet.TrainMode(flag) && cInverseNet.TrainMode(flag)); } 
   virtual bool      GetLayerOutput(uint layer, CBufferFloat *&result) 
     { return        CNet::GetLayerOutput(layer, result); }
   //---
   virtual bool      UpdateTarget(string file_name);
   virtual void      SetStateEmbedingLayer(uint layer) { iStateEmbedingLayer = layer; }
   virtual void      SetBufferSize(uint min, uint max);
  };

In previous articles, we have already created similar child class of our base dispatcher class for the neural network model operation, and the set of methods of the new class is almost the same as the previously overridden methods. Let's dwell on the main changes that have been made to the overridden methods. Let's start with the model creation method Create. The previously created procedure for passing the model architecture description does not provide the creation of nested models. In order not to make global changes to this subprocess, I decided to add a description of two more models in the Create method parameters. In the method body, we will sequentially call the relevant methods for all models used. Each model will receive the required architecture description. Remember to control the execution of the called methods.

bool CICM::Create(CArrayObj *Description, CArrayObj *Forward, CArrayObj *Inverse)
  {
   if(!CNet::Create(Description))
      return false;
   if(!cForwardNet.Create(Forward))
      return false;
   if(!cInverseNet.Create(Inverse))
      return false;
   cTargetNet.Create(NULL);
//---
   return true;
  }

Please note that after calling this method, it is necessary to specify the number of the main model's neural layer in order to read the state embedding. This operation is implemented by calling the SetStateEmbedingLayer method.

   virtual void      SetStateEmbedingLayer(uint layer) { iStateEmbedingLayer = layer; }

Unlike previous similar classes, in which we used the feed forward pass of the parent class, in this case we needed to modify the organization of the feed forward pass.

We have changed the return type. Previously the method returned a boolean value of the execution of the method operations and we used the CNet::getResults method to get feed forward results. This is because a tensor of the results was returned. This time, the new class feed forward method will return the discrete value of the selected action. The user can still select either a greedy strategy or the sampling of an action from a probability distribution. An additional sample parameter is responsible for it.

int CICM::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true, bool sample = true)
  {
   if(!AddInputData(inputVals))
      return -1;
//---
   if(!CNet::feedForward(inputVals, window, tem))
      return -1;
   double balance = AccountInfoDouble(ACCOUNT_BALANCE);
   double reward = (dPrevBalance == 0 ? 0 : balance - dPrevBalance);
   dPrevBalance = balance;
   int action = (sample ? getSample() : getAction());
   if(!cReplay.AddState(inputVals, action, reward))
      return -1;
//---
   return action;
  }

To keep the general approach to the model operation, in the current state description tensor, we expect to receive only indications of the symbol's market state from the calling program. But our new model also requires information about the account state. We will add this information to the resulting tensor in the AddInputData method. Only after successfully adding the necessary information, we call the feed forward method of the parent class.

We still have some more innovations. Next, we should add new data to the experience buffer. To do this, we first define an extrinsic reward for transition to the current state. As mentioned above, we use balance changes as extrinsic rewards.

Next, we determine the next action of the agent in accordance with the strategy chosen by the user. Then we pass all this data to the experience accumulation buffer. Once all of the above operations are completed, we return the selected agent action to the calling program.

Pay attention that we control the process at each step. If an error occurs at any of the steps, the method returns -1 to the caller program. Therefore, when organizing the space of possible agent actions, take this into account or change the return value so that the caller can clearly separate the error state from the agent's action.

The next step is to modify the backProp method. This method has undergone the most dramatic changes. First of all, we have a completely changed set of parameters. They no longer contain the target value tensor. The new method receives only the size of the update package and the discount factor in parameters.

In the method body, we first check the size of the experience buffer. Further method operations are only possible if the model has accumulated enough experience.

Note that if the experience is not enough, we exit with the true result. The false value should only be returned if an operation execution error has occurred. This allows the model to execute further operations as normal.

bool CICM::backProp(int batch, float discount = 0.900000f)
  {
//---
   if(cReplay.Total() < (int)iMinBufferSize)
      return true;
   if(!UpdateTarget(TargetNetFile))
      return false;

In addition, before starting the model training process, make sure to update Target Net. Because its encoder will be used to get the environment state embedding after transition.

Next, we will do a little preparatory work and declare several internal variables and objects that will serve as an intermediate data storage.

   CLayer *currentLayer, *nextLayer, *prevLayer;
   CNeuronBaseOCL *neuron;
   CBufferFloat *state1, *state2, *targetVals = new CBufferFloat();
   vector<float> target, actions, st1, st2, result;
   double reward;
   int action;

After the preparatory work, implement the model training loop. The number of loop iterations is equal to the model update batch size specified in the parameters.

In the loop body, we first randomly extract one dataset from the experience buffer, consisting of two consecutive system states, the selected action and the reward received. After that implement the feed forward pass of the model being trained.

//--- training loop in the batch size
   for(int i = 0; i < batch; i++)
     {
      //--- get a random state and the buffer replay
      if(!cReplay.GetRendomState(state1, action, reward, state2))
         return false;
      //--- feed forward pass of the training model ("current" state)
      if(!CNet::feedForward(state1, 1, false))
         return false;

Following the successful execution of the feed forward pass of the main model, we will implement preparatory work to run the feed forward pass of the Forward Model. Here we extract the embedding of the current system state and create a one-hot vector of the performed action.

      //--- unload state embedding
      if(!GetLayerOutput(iStateEmbedingLayer, state1))
         return false;
      //--- prepare a one-hot action vector and concatenate with the current state vector
      getResults(target);
      actions = vector<float>::Zeros(target.Size());
      actions[action] = 1;
      if(!targetVals.AssignArray(actions) || !targetVals.AddArray(state1))
         return false;

After that run the feed forward pass of the Forward Model, with prediction of the next state embedding.

      //--- forward net feed forward pass - next state prediction
      if(!cForwardNet.feedForward(targetVals, 1, false))
         return false;

Next we implement the Target Net feed forward and extract the next state embedding.

      //--- feed forward
      if(!cTargetNet.feedForward(state2, 1, false))
         return false;
      //--- unload the state embedding and concatenate with the "current" state embedding
      if(!cTargetNet.GetLayerOutput(iStateEmbedingLayer, state2))
         return false;

We combine the resulting two embeddings of successive states into a single tensor and call the feed forward pass method of Inverse Model.

      //--- inverse net feed forward - defining the performed action.
      if(!state1.AddArray(state2) || !cInverseNet.feedForward(state1, 1, false))
         return false;

Next run backpropagation methods for Forward Model and Inverse Model. We have already prepared the target values for them in the form of the next state embedding and a one-hot performed action vector.

      //--- inverse net backpropagation
      if(!targetVals.AssignArray(actions) || !cInverseNet.backProp(targetVals))
         return false;
      //--- forward net backpropagation
      if(!cForwardNet.backProp(state2))
         return false;

Next, we return to operations with the main model. Here we adjust the reward by adding to it the intrinsic curiosity reward and the expected future reward predicted by Target Net.

      //--- reward adjustment
      cForwardNet.getResults(st1);
      state2.GetData(st2);
      reward += (MathPow(st2 - st1, 2)).Sum();
      cTargetNet.getResults(targetVals);
      target[action] = (float)(reward + discount * targetVals.Maximum());
      if(!targetVals.AssignArray(target))
         return false;

After preparing the target reward, we can run the backward pass of the main DQN-model. But there is one caveat. In addition to propagating the error gradient from the predictive reward, we also need to add the error gradient of the inverse model to the state embedding block. To do this, we should copy the error gradient data from the source data layer of the inverse model to the error gradient buffer of the main model's embedding layer before running the backpropagation pass of the main model. This is because the whole algorithm is built in such a way that with each backward pass, we simply overwrite the data in the buffers. So, we need to drive a wedge into the error gradient propagation process. For this, we have to completely rewrite the code of the main model's backpropagation pass.

Here we first determine the model's reward prediction error and call the calcOutputGradients method of the last neural layer, which determines the error gradient at the model output.

      //--- backpropagation pass of the model being trained
        {
         getResults(result);
         float error = result.Loss(target, LOSS_MSE);
         //---
         currentLayer = layers.At(layers.Total() - 1);
         if(CheckPointer(currentLayer) == POINTER_INVALID)
            return false;
         neuron = currentLayer.At(0);
         if(!neuron.calcOutputGradients(targetVals, error))
            return false;
         //---
         backPropCount++;
         recentAverageError += (error - recentAverageError) / fmin(recentAverageSmoothingFactor, (float)backPropCount);

Here we will calculate the model's average prediction error.

The next step is to propagate the error gradient over to all neural layers of the model. To do this, we will create a loop with a reverse iteration over all neural layers of the model and the sequential call of the calcHiddenGradients method for all neural layers. As you remember, this method is responsible for propagating the error gradient through the neural layer.

         //--- Calc Hidden Gradients
         int total = layers.Total();
         for(int layerNum = total - 2; layerNum >= 0; layerNum--)
           {
            nextLayer = currentLayer;
            currentLayer = layers.At(layerNum);
            neuron = currentLayer.At(0);
            if(!neuron.calcHiddenGradients(nextLayer.At(0)))
               return false;

In the main model training subprocess, we have been completely repeating the algorithm of the same parent class method up to this step. At this point, we have to make a small adjustment to the algorithm.

We will add a condition to check if the analyzed neural layer is the output of the system state encoder. If the check is successful, we will add the values of the error gradient from the inverse model to the error gradient obtained from the next neural layer.

I used the previously created MatrixSum kernel to add two tensors. To read more about this kernel, please see the article "Neural networks made easy (Part 8): Attention mechanisms".

            if(layerNum == iStateEmbedingLayer)
              {
               CLayer* temp = cInverseNet.layers.At(0);
               CNeuronBaseOCL* inv = temp.At(0);
               uint global_work_offset[1] = {0};
               uint global_work_size[1];
               global_work_size[0] = neuron.Neurons();
               opencl.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix1, neuron.getGradientIndex());
               opencl.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix2, inv.getGradientIndex());
               opencl.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix_out, neuron.getGradientIndex());
               opencl.SetArgument(def_k_MatrixSum, def_k_sum_dimension, 1);
               opencl.SetArgument(def_k_MatrixSum, def_k_sum_multiplyer, 1);
               if(!opencl.Execute(def_k_MatrixSum, 1, global_work_offset, global_work_size))
                 {
                  printf("Error of execution kernel MatrixSum: %d", GetLastError());
                  return false;
                 }
              }
           }

For the correct execution of this action, pay attention to two points.

First, the backpropagation method of the inverse model must propagate the error gradient to the source data layer. For this purpose, the condition layerNum >= 0 must be used in the loop propagating the gradient through hidden layers.

         //--- Calc Hidden Gradients
         int total = layers.Total();
         for(int layerNum = total - 2; layerNum >= 0; layerNum--)
           {

Second, when declaring the architecture of the inverse model, we specify the results level activation method similar to the activation method of the state embedding receiving layer. This action has no effect during the feed forward pass, but it adjusts the error gradient by the derivative of the activation function during the backpropagation pass.

Further steps are similar to the parent class's backpropagation algorithm. After propagating the error gradient, we update the weight matrices of all neural layers of the main model.

         //---
         prevLayer = layers.At(total - 1);
         for(int layerNum = total - 1; layerNum > 0; layerNum--)
           {
            currentLayer = prevLayer;
            prevLayer = layers.At(layerNum - 1);
            neuron = currentLayer.At(0);
            if(!neuron.UpdateInputWeights(prevLayer.At(0)))
               return false;
           }
         //---
         for(int layerNum = 0; layerNum < total; layerNum++)
           {
            currentLayer = layers.At(layerNum);
            CNeuronBaseOCL *temp = currentLayer.At(0);
            if(!temp.TrainMode())
               continue;
            if((layerNum + 1) == total && !temp.getGradient().BufferRead())
               return false;
            break;
           }
        }
     }

Note that we are only updating the weight matrices of the main learning model. Forward Model and Inverse Model parameters are updated when executing backpropagation methods of the corresponding models.

At the end, remove the auxiliary objects created inside the method and complete the method operation with a positive result.

   delete state1;
   delete state2;
   delete targetVals;
//---
   return true;
  }

I would like to say a few words about the file operation methods. Since we are using several models in this algorithm, a question arises about how to save the trained models. I see two options here. We can save all models in one file or save each model in a separate file. I suggest saving models in separate files, as this provides more freedom of action. We can download the trained DQN model to a separate file and then use along with the models discussed earlier. We can also load all the three models and use the method discussed in this article. The only inconvenience is the need to specify the state embedding layer in the main model each time. But we can experiment with the architecture of each individual model in training in an effort to achieve optimal results.

I will not dwell on the description of the algorithms for working with files here. You can find the code of all used programs and classes, as well as their methods, in the attachment.

3. Testing

We have created a class for organizing the Q-learning model using the intrinsic curiosity method. Now we will create an Expert Advisor to train and test the model. As mentioned above, the new model will be trained in the strategy tester. This is fundamentally different from the previously used methods. Therefore, the model training Expert Advisor has undergone significant changes.

The ICM-learning.mq5 EA has been created for testing. To describe the market situation, we used the same indicators with similar parameters. Therefore, the EA's external parameters remained practically unchanged. The same refers to the declaration of global variables and classes.

The EA initialization method is almost the same as was used in previous EAs. The only difference is that there is no generation of the learning process start event. This is because we have completely removed the 'Train' model training function which was used in all previous EAs.

The whole process of training the model is transferred to the methodOnTick. Since our model is trained to analyze the market based on closed candles, we will run the learning process only at the opening of a new candlestick. To do this, in the OnTick method body, we first check the new candlestick opening event. And if the result is positive, we proceed to further actions.

void OnTick()
  {
   if(!IsNewBar())
      return;

Next, load historical data; its amount is equal to the analyzed window size.

   int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), HistoryBars, Rates);
   if(!ArraySetAsSeries(Rates, true))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

Create a description of the current market situation. This process follows the algorithm of a similar process we used in previously considered EAs.

   State1.Clear();
   for(int b = 0; b < (int)HistoryBars; b++)
     {
      float open = (float)Rates[b].open;
      TimeToStruct(Rates[b].time, sTime);
      float rsi = (float)RSI.Main(b);
      float cci = (float)CCI.Main(b);
      float atr = (float)ATR.Main(b);
      float macd = (float)MACD.Main(b);
      float sign = (float)MACD.Signal(b);
      if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
         continue;
      //---
      if(!State1.Add((float)Rates[b].close - open) || !State1.Add((float)Rates[b].high - open) ||
         !State1.Add((float)Rates[b].low - open) || !State1.Add((float)Rates[b].tick_volume / 1000.0f) ||
         !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
         !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
     }

Once the history has been loaded and the market situation description has been generated, call the model's feed forward method and check the result.

In our new implementation, the feedForward method returns the agent action. In accordance with the result, execute a trading operation.

   switch(StudyNet.feedForward(GetPointer(State1), 12, true, true))
     {
      case 0:
         Trade.Buy(Symb.LotsMin(), Symb.Name());
         break;
      case 1:
         Trade.Sell(Symb.LotsMin(), Symb.Name());
         break;
      case 2:
         for(int i=PositionsTotal()-1;i>=0;i--)
            if(PositionGetSymbol(i)==Symb.Name())
              Trade.PositionClose(PositionGetInteger(POSITION_IDENTIFIER));
         break;
     }

Pay attention that when building the model, we talked about four agent actions. Here we see the analysis of only three actions and the execution of the corresponding trading operation. The fact is that the fourth action is waiting for a more suitable market situation, without executing trading operations. Therefore, we do not handle this action.

At the end of the method, call the model's backpropagation method.

   StudyNet.backProp(Batch, DiscountFactor);
//---
  }

You probably noticed that in the training process we never saved the trained model. The trained model saving process has been moved to the EA's deinitialization method.

void OnDeinit(const int reason)
  {
//---
   StudyNet.Save(FileName + ".nnw", FileName + ".fwd", FileName + ".inv", true);
  }

To enable model training in the EA optimization mode, I repeated a similar saving procedure after the completion of each optimizer pass.

void OnTesterPass()
  {
   StudyNet.Save(FileName + ".nnw", FileName + ".fwd", FileName + ".inv", true);
  }

Note that the optimization process should run only on one active core. Otherwise, parallel threads would delete the data of other agents. This would completely eliminate the use of multiple agents.

To train the EA, all models were created using the NetCreator tool. It should be added that to enable EA operation in the strategy tester, the model files must be located in the terminal common directory 'Terminal\Common\Files', since each agent operates in its own sandbox, so they can exchange data only via the common terminals folder.

Training in the strategy tester takes a little longer than the previous virtual training approach. For this reason, I reduced the model training period to 10 months. The rest of the test parameters remained unchanged. Again, I used EURUSD on the H1 timeframe. Indicators were used with default parameters.

To be honest, I expected that the learning process would begin with the deposit loss. But during the first pass, the model showed a result close to 0. Then it even received some profit in the second pass. The model performed 330 trades with more than 98% of operations being profitable.

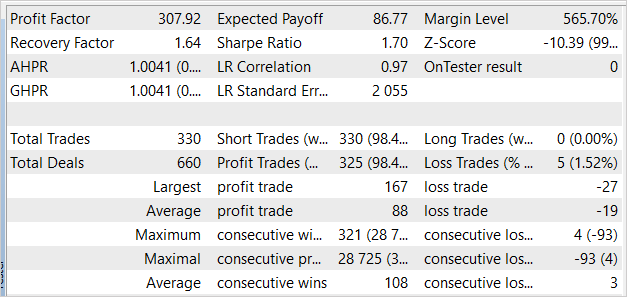
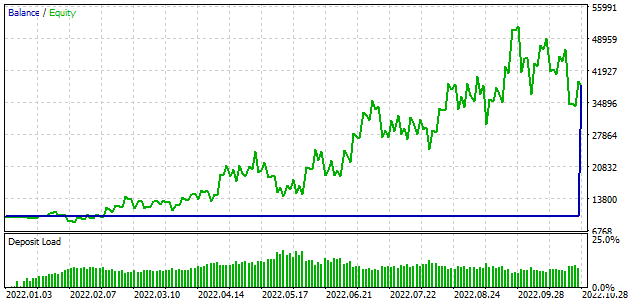
Conclusion

In this article, we discussed the operation of the Intrinsic Curiosity Model. This technology makes enables successful model training with reinforcement learning methods under conditions when extrinsic rewards are rare. This refers to financial trading. The Intrinsic Curiosity technology allows the model to thoroughly explore the environment and find the best ways to achieve the goal. This works even when the environment returns one reward for multiple consecutive actions.

In the practical part of this article, we implemented the presented technology using MQL5. Based on the above work, we can conclude that this approach can generate desired results in trading.

Although the presented EA can perform trading operations, it is not ready for use in real trading. The EA is presented for evaluation purposes only. Significant refinement and comprehensive testing in all possible conditions are required before real life use.

References

1. Neural networks made easy (Part 26): Reinforcement learning
2. Neural networks made easy (Part 27): Deep Q-Learning (DQN)
3. Neural networks made easy (Part 28): Policy gradient algorithm
4. Neural networks made easy (Part 32): Distributed Q-Learning
5. Neural networks made easy (Part 33): Quantile regression in distributed Q-learning
6. Neural networks made easy (Part 34): Fully parameterized quantile function
7. Curiosity-driven Exploration by Self-supervised Prediction

Programs used in the article

#	Issued to	Type	Description
1	ICM-learning.mq5	EA	Model training EA
2	ICM.mqh	Class library	Model organization class library
3	NeuroNet.mqh	Class library	A library of classes for creating a neural network
4	NeuroNet.cl	Code Base	OpenCL program code library