Neuronale Netze leicht gemacht (Teil 35): Modul für intrinsische Neugier

Inhalt

• Einführung
• 1. Neugierde ist der Drang zu lernen
• 2. Der Block der intrinsischer Neugier mit MQL5
• 2.1. Erfahrungswiedergabepuffer (Experience replay)
• 2.2. Intrinsisches Neugiermodul (Intrinsic Curiosity Module, ICM)
• 3. Tests
• Schlussfolgerung
• Referenzen
• Programme, die im diesem Artikel verwendet werden

Einführung

Wir untersuchen weiterhin Algorithmen für das verstärkte Lernen. Wie wir bereits gelernt haben, basieren alle Algorithmen des Verstärkungslernens auf dem Paradigma, dass der Agent jedes Mal eine Belohnung von der Umwelt erhält, wenn er durch die Ausführung einer Aktion von einem Umweltzustand in einen anderen wechselt. Im Gegenzug ist der Agent bestrebt, seine Handlungspolitik so zu gestalten, dass die erhaltene Belohnung maximiert wird. Bei der Betrachtung von Methoden des Reinforcement Learning haben wir bereits erwähnt, wie wichtig es ist, eine klare Belohnungspolitik zu entwickeln, die eine der Schlüsselrollen bei der Erreichung des Modelltrainingsziels spielt.

Aber in den meisten Situationen des wirklichen Lebens folgt nicht auf jede Handlung eine Belohnung. Zwischen einer Handlung und einer Belohnung kann eine Zeitspanne liegen, die unterschiedlich lang sein kann. Manchmal hängt der Erhalt einer Belohnung von einer Reihe von Aktionen ab. In solchen Fällen haben wir die Gesamtbelohnung in einzelne Komponenten aufgeteilt und sie entlang des gesamten Weges des Agenten von der Aktion zur Belohnung platziert. Dies ist ein ziemlich komplizierter Prozess, der von Konventionen und Kompromissen geprägt ist.

Der Handel ist eine dieser Aufgaben. Der Agent muss zum richtigen Zeitpunkt eine Position in der richtigen Richtung eröffnen. Dann sollte er den Moment abwarten, in dem die Rentabilität der offenen Position am höchsten ist. Danach sollte er die Position schließen und das Ergebnis der Operation festhalten. So erhalten wir die Belohnung erst dann, wenn die Position geschlossen wird, und zwar in Form der Veränderung des Kontostands. In den zuvor betrachteten Algorithmen haben wir diese Belohnung auf Schritte verteilt (ein Schritt ist das Zeitintervall einer Kerze), die einem Vielfachen der Veränderung des Symbolpreises entsprechen. Aber wie richtig ist das? Bei jedem Schritt führte der Agent eine Aktion durch, z. B. eine Handelsoperation oder eine Entscheidung, keine Handelsoperation durchzuführen. Die Entscheidung, nicht zu handeln, ist also auch eine Handlung des Agenten, die er ausführen möchte. Es stellt sich also die Frage, wie viel jede einzelne Maßnahme zum Gesamtergebnis beiträgt. 

Gibt es noch andere Ansätze, um die Belohnungspolitik und den Modellbildungsprozess zu organisieren?

1. Neugierde ist der Drang zu lernen

Das Verhalten von Lebewesen dienst als Beispiel. Tiere und Vögel sind in der Lage, weite Strecken zurückzulegen, bevor sie eine Belohnung in Form von Nahrung erhalten. Der Mensch erhält nicht für jede seiner Handlungen eine Belohnung. Die menschlichen Lernprinzipien sind vielschichtig. Eine der treibenden Kräfte des Lernens ist die Neugierde. Wenn man eine geschlossene Tür vor sich hat, ist es die Neugier, die einen dazu bringt, sie zu öffnen und hineinzuschauen. Das ist die menschliche Natur.

Unser Gehirn ist so konzipiert, dass wir, wenn wir eine Handlung ausführen, das Ergebnis ihrer Auswirkung bereits 1-2 Schritte voraussehen. Manchmal sogar mehr. Nun, wir führen jede Handlung aus, um das gewünschte Ergebnis zu erzielen. Durch den Vergleich des Ergebnisses mit unseren Erwartungen korrigieren wir dann unser Handeln. Wir wissen auch, dass wir einen Versuch nur dann wiederholen können, wenn es ein Spiel ist. Im wirklichen Leben gibt es keine Möglichkeit, einen Schritt zurückzutreten und dieselbe Situation zu wiederholen. Jeder neue Versuch ist ein neues Ergebnis. Bevor wir etwas unternehmen, analysieren wir daher alle unsere bisherigen Erfahrungen. Auf der Grundlage unserer Erfahrungen wählen wir die Handlung, die uns richtig erscheint.

Wenn wir in eine ungewohnte Situation kommen, versuchen wir, sie zu erkunden und uns an die Umgebung zu erinnern. Dabei denken wir vielleicht nicht daran, welchen Nutzen dies in der Zukunft bringen kann. Wir erhalten keine unmittelbare Belohnung für unser Handeln. Wir sammeln nur die Erfahrungen, die uns in der Zukunft nützlich sein können.

Wir haben bereits erwähnt, dass es notwendig ist, die Umwelt so weit wie möglich zu erkunden und ein Gleichgewicht zwischen der Nutzung früherer Erfahrungen und dem Studium der Umwelt herzustellen. Wir haben sogar den Neuheits-Hyperparameter in die ɛ-greedy-Strategie eingeführt. Der Hyperparameter ist jedoch eine Konstante. Unser Ziel ist es nun, das Modell so zu trainieren, dass es den Grad der Neuartigkeit je nach Situation selbständig steuern kann.

Die Autoren des Artikels „Curiosity-driven Exploration by Self-supervised Prediction“ haben bei der Entwicklung ihres Algorithmus versucht, solche Ansätze zu verwenden. Dieser Artikel wurde im Mai 2017 veröffentlicht. Die Methode basiert auf der Entstehung von Neugier als Fehler in der Fähigkeit des Modells, die Folgen seiner Handlungen vorherzusagen. Die Neugierde ist bei zuvor nicht begangenen Handlungen größer. Der Artikel befasst sich mit drei großen Herausforderungen:

1. Seltene extrinsische Belohnung. Neugierde ermöglicht es dem Agenten, sein Ziel mit weniger Interaktionen mit der Umwelt zu erreichen.
2. Training ohne extrinsische Belohnungen. Die Neugier treibt den Agenten dazu, die Umgebung effizient zu erkunden, selbst wenn es keine extrinsische Belohnung durch die Umgebung gibt.
3. Verallgemeinerung auf unsichtbare Szenarien. Die aus früheren Erfahrungen gewonnenen Kenntnisse helfen dem Agenten, neue Orte viel schneller zu erkunden, als wenn er ganz von vorne anfängt.

Die Autoren schlugen eine recht einfache Idee vor: Zu einer externen Belohnung re fügen wir eine intrinsische Belohnung ri hinzu, die ein Maß für die Neugierde ist und die Erkundung der Umwelt fördert. Dieser Cocktail wird dann dem Agenten zur Schulung zur Verfügung gestellt. Belohnungsskalierungsfaktoren können verwendet werden, um die Auswirkungen von extrinsischen und intrinsischen Belohnungen anzupassen. Diese Faktoren sind Hyperparameter des Modells.

Die wichtigste Neuerung liegt in der Architektur des ICM-Blocks, der diese intrinsische Belohnung erzeugt. Das Modul Intrinsische Neugier enthält drei separate Modelle:

• Encoder
• Inverses Modell
• Vorwärtsmodell

Zwei nachfolgende Systemzustände und die durchgeführte Aktion werden in das Modul eingegeben. Die Aktion wird als One-Hot-Vektor kodiert. Die Aktion kann sowohl außerhalb des Moduls als auch innerhalb des Moduls kodiert werden. Die in das Modul eingegebenen Systemzustände werden mit Hilfe eines Encoders codiert. Der Encoder zielt darauf ab, die Dimension des Tensors, der den Systemzustand beschreibt, zu reduzieren und die Daten zu filtern. Die Autoren unterteilen alle Merkmale, die den Systemzustand beschreiben, in drei Gruppen:

1. Diejenigen, die von dem Mittel betroffen sind.
2. Die, die nicht durch den Erreger beeinflusst werden, aber den Erreger beeinflussen.
3. Die, die unbeeinflusst sind durch den Wirkstoff und ohne Auswirkungen auf den Wirkstoff.

Der Encoder soll helfen, sich auf die ersten beiden Gruppen zu konzentrieren und den Einfluss der dritten Gruppe zu neutralisieren.

Das inverse Modell empfängt den kodierten Zustand von 2 aufeinanderfolgenden Zuständen und lernt, die Aktion zu bestimmen, die durchgeführt wird, um zwischen den Zuständen zu wechseln. Das Training des inversen Modells zusammen mit dem Encoder sollte die ersten beiden Gruppen von Merkmalen unterscheiden. LogLoss wird als Verlustfunktion für das Inverse Modell verwendet.

Das Vorwärtsmodell lernt, den nächsten Zustand auf der Grundlage des kodierten aktuellen Zustands und der durchgeführten Aktion vorherzusagen. Das Maß der Neugier ist die Qualität der Vorhersage. Der durch MSE berechnete Vorhersagefehler ist eine intrinsische Belohnung.

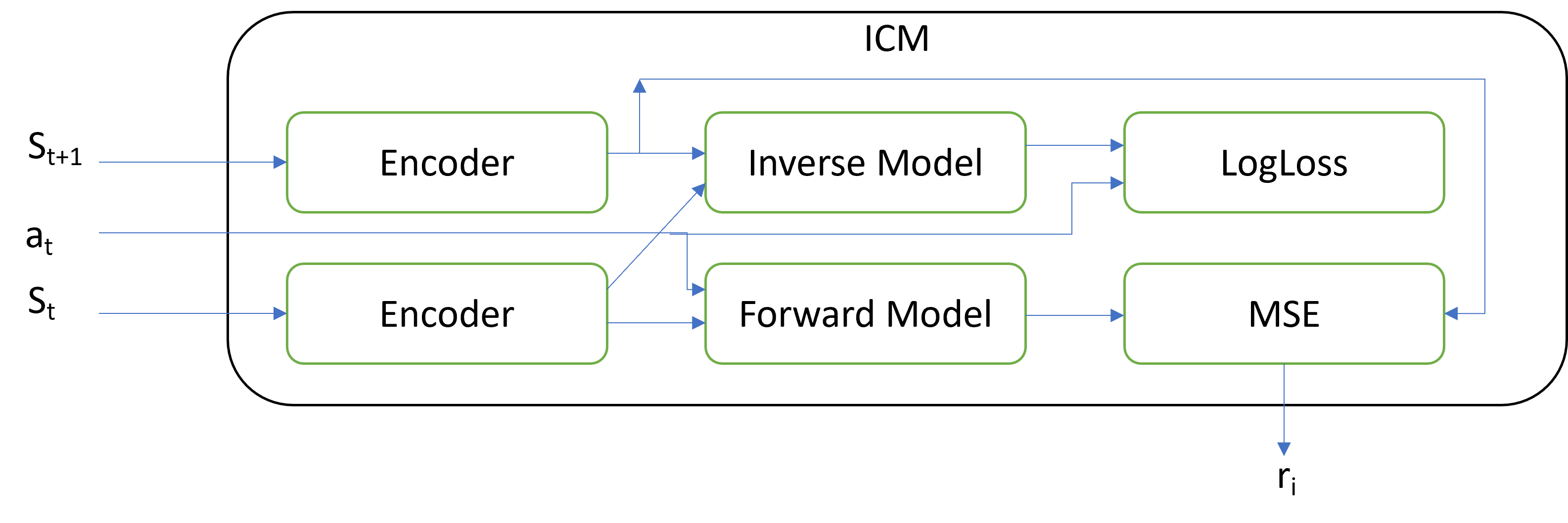
Es mag seltsam erscheinen, aber wenn der Fehler des Vorwärtsmodells zunimmt, wächst auch die intrinsische Belohnung des DQN-Modells, das wir trainieren. Die Idee ist, das Modell dazu zu bringen, mehr Aktionen durchzuführen, deren Ergebnisse unbekannt sind. Das Modell wird also die Umgebung erkunden. Wenn wir die Umgebung erkunden, nimmt die Neugier des Modells ab und DQN maximiert die extrinsische Belohnung.

Das Intrinsic Curiosity Module kann mit jedem der bisher besprochenen Modelle verwendet werden. Und wir vergessen nicht, alle zuvor untersuchten architektonischen Lösungen zu verwenden, um die Modellkonvergenz zu verbessern.

Die von den Autoren der Methodik durchgeführten praktischen Tests zeigen die Wirksamkeit des Algorithmus in Computerspielen mit einer Belohnung am Ende des Spiellevels. Darüber hinaus beweist das Modell die Fähigkeit zur Verallgemeinerung — es kann die zuvor gesammelten Erfahrungen nutzen, wenn es auf eine neue Spielebene wechselt. Besonders interessant ist die Fähigkeit des Modells, gut zu funktionieren, wenn sich Strukturen ändern und Rauschen hinzugefügt wird. Das heißt, das Modell lernt, die wichtigsten Dinge zu erkennen und verschiedene Nebeneinflüssen (Rauschen) zu ignorieren. Dies erhöht die Stabilität des Modells in verschiedenen Umweltzuständen.

2. Intrinsisches Neugiermodul mit MQL5

Wir haben uns kurz mit den theoretischen Aspekten der Methodik befasst. Kommen wir nun zum praktischen Teil unseres Artikels. In diesem Teil werden wir die Methode mit MQL5 implementieren. Bevor wir mit der Umsetzung fortfahren, möchten wir darauf hinweisen, dass wir aus verschiedenen Gründen nicht die zuvor erwogenen Ansätze verwenden werden.

Das erste, was sich ändern wird, ist die Prämienpolitik. Ich beschloss, mich näher mit der tatsächlichen Situation zu befassen. Die extrinsische Belohnung ist eine Veränderung des Kontostands. Bitte beachten Sie, dass es sich um den Saldo (balance) handelt, nicht um die Veränderung des Kapitals (equity). Ich verstehe, dass eine solche Belohnung recht selten sein kann, aber wir wenden die neue Methode an, um dieses Problem zu lösen.

Da wir uns auf Belohnungen in Form einer Saldoänderung beschränken, gleichzeitig aber jede Agentenaktion als Handelsoperationen ausgedrückt werden kann, müssen wir der Systemzustandsbeschreibung Variablen hinzufügen, die den Zustand des Handelskontos charakterisieren. Wir müssen auch die Eröffnung und Schließung von Positionen sowie den kumulierten gleitenden Gewinn für jede Position überwachen.

Um das Tracking der einzelnen Positionen nicht im EA-Code zu implementieren, habe ich beschlossen, das Modelltraining in den Strategietester zu verlagern. Wir lassen das Modell Operationen im Strategietester durchführen. Mit Hilfe der Funktionen zur Abfrage des Kontostands und der offenen Positionen können wir dann alle erforderlichen Informationen vom Strategietester erhalten.

Deshalb müssen wir einen Pufferspeicher für die Wiedergabe der Erfahrung anlegen. Über die Gründe für die Erstellung eines solchen Puffers sprachen wir in dem Artikel „Neuronale Netze leicht gemacht (Teil 27) Deep Q-learning(DQN)“. Bisher haben wir die gesamte Symbolhistorie des Trainingszeitraums als Puffer verwendet. Aber das ist jetzt nicht möglich, da wir die Kontostandsdaten hinzufügen. Wir werden also einen kumulativen Erfahrungspuffer in das Programm einbauen.

Darüber hinaus werden wir den EA in die Lage versetzen, mehrere Positionen gleichzeitig zu eröffnen, einschließlich gegenläufiger Positionen. Dadurch ändert sich der Raum der möglichen Aktionen des Agenten. Der Agent wird vier Aktionen durchführen können:

0 — kaufen

1 — verkaufen

2 — alle offenen Positionen schließen

3 — überspringen eines Zuges, warten auf eine geeignete Bedingung.

Beginnen wir die Entwicklung mit der Implementierung des Erfahrungswiedergabepuffers.

2.1. Erfahrungswiedergabepuffer

Der Erfahrungswiedergabepuffer sollte ein ständiges Hinzufügen von Datensätzen ermöglichen. Jedes Mal werden wir ein ganzes Datenpaket hinzufügen, das Folgendes umfasst:

• Umweltzustandsbeschreibungstensor
• eingeleitete Maßnahmen
• erhaltene extrinsische Belohnung

Und der geeignetste Ansatz zur Implementierung des Puffers wäre die Verwendung eines dynamischen Objektarrays. Jeder einzelne Datensatz enthält ein Objekt mit den oben genannten Informationen.

Um jeden einzelnen Datensatz im Puffer zu organisieren, erstellen wir die Klasse CReplayState, die von der Basisklasse CObject abgeleitet ist. In der Klasse verwenden wir ein statisches Datenpufferobjekt und zwei Variablen, um die Daten, die durchgeführte Aktion und die Belohnung zu speichern.

Beachten Sie, dass der Agent die Aktion vom aktuellen Zustand aus durchführt. Und er erhält eine Belohnung für den Übergang in diesen Zustand. D.h. es handelt sich um eine Belohnung für den Übergang vom vorherigen Zustand zum aktuellen aufgrund der im vorherigen Schritt durchgeführten Aktion. Obwohl die Belohnung und die Aktion im selben Datensatz in den Puffer aufgenommen werden, gehören sie eigentlich zu verschiedenen Intervallen.

class CReplayState : public CObject
  {
protected:
   CBufferFloat      cState;
   int               iAction;
   double            dReaward;

public:
                     CReplayState(CBufferFloat *state, int action, double reward);
                    ~CReplayState(void) {};
   bool              GetCurrent(CBufferFloat *&state, int &action);
   bool              GetNext(CBufferFloat *&state, double &reward);
  };

Im Klassenkonstruktor erhalten wir alle notwendigen Informationen und kopieren sie in Klassenvariablen und interne Objekte.

CReplayState::CReplayState(CBufferFloat *state, int action, double reward)
  {
   cState.AssignArray(state);
   iAction = action;
   dReaward = reward;
  }

Da wir ein statisches Datenpufferobjekt verwenden, bleibt der Destruktor unserer Klasse leer.

Fügen wir unserer Klasse zwei weitere Methoden hinzu, um auf die gespeicherten Daten zuzugreifen: GetCurrent und GetNext. Im ersten Fall geben wir den Zustand und die Aktion zurück. Und in der zweiten geben wir die Aktion und die Belohnung zurück.

bool CReplayState::GetCurrent(CBufferFloat *&state, int &action)
  {
   action = iAction;
   double reward;
   return GetNext(state, reward);
  }

Der Algorithmus beider Methoden ist recht einfach. Auf ihre Verwendung werden wir etwas später eingehen.

bool CReplayState::GetNext(CBufferFloat *&state, double &reward)
  {
   reward = dReaward;
   if(!state)
     {
      state = new CBufferFloat();
      if(!state)
         return false;
     }
   return state.AssignArray(GetPointer(cState));
  }

Nachdem wir ein einzelnes Datensatzobjekt erstellt haben, machen wir uns an die Arbeit und erstellen unseren Erfahrungspuffer mit Hilfe der dynamischen Objekt-Array-Klasse CArrayObj-Klasse. Diese Klasse wird während des EA-Betriebs ständig mit neuen Zuständen aktualisiert. Um einen Speicherüberlauf zu vermeiden, wird die maximale Größe auf den Wert der Variablen iMaxSize begrenzt. Wir werden auch die Methode SetMaxSize hinzufügen, um die Puffergröße zu verwalten. Wir erstellen keine anderen Objekte und Variablen im Klassenkörper. Aus diesem Grund sind der Konstruktor und der Destruktor leer.

class CReplayBuffer : protected CArrayObj
  {
protected:
   uint              iMaxSize;
public:
                     CReplayBuffer(void) : iMaxSize(500) {};
                    ~CReplayBuffer(void) {};
   //---
   void              SetMaxSize(uint size)   {  iMaxSize = size; }
   bool              AddState(CBufferFloat *state, int action, double reward);
   bool              GetRendomState(CBufferFloat *&state1, int &action, double &reward, CBufferFloat*& state2);
   bool              GetState(int position, CBufferFloat *&state1, int &action, double &reward, CBufferFloat*& state2);
   int               Total(void) { return CArrayObj::Total(); }
  };

Um dem Puffer Datensätze hinzuzufügen, wird die Methode AddState verwendet. Die Methode erhält als Parameter neue Aufzeichnungsdaten, einschließlich des Zustandstensors, der Aktion und der extrinsischen Belohnung.

Im Methodenrumpf wird der Zeiger auf das Objekt des Systemstatuspuffers überprüft. Wenn die Zeigerprüfung erfolgreich ist, wird ein neues Datensatzobjekt erstellt und dem dynamischen Array hinzugefügt. Die wichtigsten Operationen mit den dynamischen Arrays werden mit den Methoden der Elternklasse durchgeführt.

Danach überprüfen wir die aktuelle Puffergröße. Falls erforderlich, löschen wir die ältesten Objekte, um die Puffergröße an die angegebene maximale Puffergröße anzupassen.

bool CReplayBuffer::AddState(CBufferFloat *state, int action, double reward)
  {
   if(!state)
      return false;
//---
   if(!Add(new CReplayState(state, action, reward)))
      return false;
   while(Total() > (int)iMaxSize)
      Delete(0);
//---
   return true;
  }

Um Daten aus dem Puffer zu erhalten, werden wir zwei Methoden erstellen: GetRendomState und GetState. Die erste Methode gibt einen zufälligen Zustand aus dem Puffer zurück, und die zweite Methode gibt die Zustände am angegebenen Index im Puffer zurück. Im Hauptteil der ersten Methode erzeugen wir nur eine Zufallszahl innerhalb der Puffergröße und rufen die zweite Methode auf, um die Daten mit dem erzeugten Index zu erhalten.

bool CReplayBuffer::GetRendomState(CBufferFloat *&state1, int &action, double &reward, CBufferFloat *&state2)
  {
   int position = (int)(MathRand() * MathRand() / pow(32767.0, 2.0) * (Total() - 1));
   return GetState(position, state1, action, reward, state2);
  }

Wenn Sie sich den Algorithmus der zweiten Methode GetState ansehen, werden Sie den Unterschied in der Anzahl der angeforderten und der zuvor gespeicherten Daten feststellen. Beim Speichern erhielten wir einen Systemzustand, während jetzt zwei Umgebungszustandstensoren angefordert werden.

Erinnern wir uns daran, wie der Q-Learning-Prozess organisiert ist. Das Training basiert auf vier Datenobjekten:

• der aktuelle Zustand der Umwelt
• die vom Agenten vorgenommene Handlung
• der nächste Zustand der Umwelt
• Belohnung für den Übergang zwischen den Zuständen der Umwelt

Daher müssen wir zwei nachfolgende Zustände des Systems aus dem Erfahrungspuffer extrahieren. Außerdem haben wir die Aktion aus dem analysierten Zustand und die Belohnung für den Übergang in denselben Zustand gespeichert. Daher müssen wir den Zustand und die Aktion aus einem Datensatz extrahieren und den Umgebungszustand und die Belohnung aus dem nächsten Datensatz extrahieren. So haben wir oben die Methoden GetCurrent und GetNext organisiert.

Schauen wir uns nun die Implementierung der Methode GetState an. Zunächst wird im Hauptteil der Methode der angegebene Index des abzurufenden Eintrags überprüft. Er muss mindestens 0 und darf höchstens der Index des vorletzten Datensatzes im Puffer sein. Das liegt daran, dass wir die Daten von zwei aufeinander folgenden Datensätzen benötigen.

Als Nächstes rufen wir GetCurrent für den Datensatz mit dem angegebenen Index auf. Dann gehen wir zum nächsten Datensatz über und rufen die Methode GetNext auf. Das Ergebnis der Operation wird an das aufrufende Programm zurückgegeben.

bool CReplayBuffer::GetState(int position, CBufferFloat *&state1, int &action, double &reward, CBufferFloat *&state2)
  {
   if(position < 0 || position >= (Total() - 1))
      return false;
   CReplayState* element = m_data[position];
   if(!element || !element.GetCurrent(state1, action))
      return false;
   element = m_data[position + 1];
   if(!element.GetNext(state2, reward))
      return false;
//---
   return true;
  }

Der Erfahrungspuffer ist spezifisch für eine bestimmte Trainingseinheit und es ist nicht sinnvoll, seine Daten zu speichern. Daher ist es nicht erforderlich, für die oben genannten Klassen Methoden für eine Dateiverwaltung zu erstellen.

2.2. Intrinsisches Neugiermodul (ICM)

Nach der Erstellung des Erfahrungspuffers gehen wir zur Implementierung des Algorithmus des Intrinsic Curiosity Module über. Wie bereits im theoretischen Teil erwähnt, verwendet das Modul drei Modelle: Encoder-, inverse und direkte Modelle. Bei meiner Implementierung habe ich mich nicht an die von den Autoren vorgestellte Architektur gehalten. Um Ressourcen zu sparen, habe ich keinen separaten Encoder für das intrinsische Neugiermodul erstellt.

Die ursprüngliche Architektur sieht die Erstellung eines Encoders vor, der dem im DQN-Trainingsmodell verwendeten Encoder ähnelt. Ich beschloss, den vorhandenen Encoder des Trainingsmodells zu verwenden, um das Signal zu kodieren. Dies erfordert natürlich die Synchronisierung der Modelle und einige Ergänzungen der Backpropagation-Methode des Modells. Dadurch werden jedoch weniger Speicher- und Rechenressourcen verbraucht, die für die Erstellung und das Training des zusätzlichen Encoders erforderlich wären.

Darüber hinaus erwarte ich den zusätzlichen Nutzen einer Feinabstimmung des Encoders des lernfähigen DQN-Modells.

Um den Algorithmus zu implementieren, erstellen wir eine neue CICM-Dispatcher-Klasse für neuronale Netze, die von unserer Basisklasse CNet-Dispatcher für neuronale Netze erbt. Drei interne Variablen werden in den Klassenkörper eingefügt:

• iMinBufferSize — die Mindestgröße des Erfahrungspuffers, die erforderlich ist, um mit dem Training von Modellen zu beginnen.
• iStateEmbedingLayer — die Nummer der neuronalen Schicht des zu trainierenden Modells, aus der wir den kodierten Zustand der Umgebung lesen. Dies ist die neuronale Schicht, die den Encoder des Modells vervollständigt.
• dPrevBalance — eine Variable, die den letzten Stand des Kontostands aufzeichnet. Wir werden sie verwenden, um die extrinsische Belohnung zu bestimmen.

Darüber hinaus werden wir vier interne Objekte deklarieren. Dazu gehören ein Objekt des Erfahrungssammelpuffers und drei neuronale Netzobjekte: cTargetNet, cInverseNet und cForwardNet.

Wir verwenden Q-Learning, und Target Net ist eine der Hauptsäulen dieser Lernmethode.

class CICM : protected CNet
  {
protected:
   uint              iMinBufferSize;
   uint              iStateEmbedingLayer;
   double            dPrevBalance;
   //---
   CReplayBuffer     cReplay;
   CNet              cTargetNet;
   CNet              cInverseNet;
   CNet              cForwardNet;

   virtual bool      AddInputData(CArrayFloat *inputVals);

public:
                     CICM(void);
                     CICM(CArrayObj *Description, CArrayObj *Forward, CArrayObj *Inverse);
   bool              Create(CArrayObj *Description, CArrayObj *Forward, CArrayObj *Inverse);
   int               feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true, bool sample = true); 
   bool              backProp(int batch, float discount = 0.9f);
   int               getAction(void);      
   int               getSample(void);
   float             getRecentAverageError() { return recentAverageError; }
   bool              Save(string file_name, bool common = true);
   bool              Save(string dqn, string forward, string invers, bool common = true);
   virtual bool      Load(string file_name, bool common = true);
   bool              Load(string dqn, string forward, string invers, uint state_layer, bool common = true);
   //---
   virtual int       Type(void)   const   {  return defICML;   }
   virtual bool      TrainMode(bool flag)
            { return (CNet::TrainMode(flag) && cForwardNet.TrainMode(flag) && cInverseNet.TrainMode(flag)); } 
   virtual bool      GetLayerOutput(uint layer, CBufferFloat *&result) 
     { return        CNet::GetLayerOutput(layer, result); }
   //---
   virtual bool      UpdateTarget(string file_name);
   virtual void      SetStateEmbedingLayer(uint layer) { iStateEmbedingLayer = layer; }
   virtual void      SetBufferSize(uint min, uint max);
  };

In früheren Artikeln haben wir bereits eine ähnliche Unterklasse unserer Dispatcher-Basisklasse für den Betrieb des neuronalen Netzes erstellt, und der Methodensatz der neuen Klasse ist fast derselbe wie die zuvor überschriebenen Methoden. Betrachten wir nun die wichtigsten Änderungen, die an den überschriebenen Methoden vorgenommen wurden. Beginnen wir mit der Modellerstellungsmethode Create. Die zuvor erstellte Prozedur zur Übergabe der Modellarchitekturbeschreibung ermöglicht nicht die Erstellung von verschachtelten Modellen. Um keine globalen Änderungen an diesem Teilprozess vorzunehmen, habe ich beschlossen, eine Beschreibung von zwei weiteren Modellen in die Parameter der Methode Create aufzunehmen. Im Methodenrumpf werden wir nacheinander die entsprechenden Methoden für alle verwendeten Modelle aufrufen. Jedes Modell erhält die erforderliche Architekturbeschreibung. Denken Sie daran, die Ausführung der aufgerufenen Methoden zu kontrollieren.

bool CICM::Create(CArrayObj *Description, CArrayObj *Forward, CArrayObj *Inverse)
  {
   if(!CNet::Create(Description))
      return false;
   if(!cForwardNet.Create(Forward))
      return false;
   if(!cInverseNet.Create(Inverse))
      return false;
   cTargetNet.Create(NULL);
//---
   return true;
  }

Bitte beachten Sie, dass Sie nach dem Aufruf dieser Methode die Nummer der neuronalen Schicht des Hauptmodells angeben müssen, um die Zustandseinbettung zu lesen. Dieser Vorgang wird durch den Aufruf der Methode SetStateEmbedingLayer realisiert.

   virtual void      SetStateEmbedingLayer(uint layer) { iStateEmbedingLayer = layer; }

Im Gegensatz zu früheren ähnlichen Klassen, in denen wir den Vorwärtsdurchgang der übergeordneten Klasse verwendet haben, mussten wir in diesem Fall die Organisation des Vorwärtsdurchgänge ändern.

Wir haben den Rückgabetyp geändert. Zuvor gab die Methode einen booleschen Wert für die Ausführung der Methodenoperationen zurück, und wir verwendeten die Methode CNet::getResults, um die Ergebnisse der Weiterleitung zu erhalten. Dies liegt daran, dass ein Tensor der Ergebnisse zurückgegeben wurde. Diesmal wird die neue Klassenvorwärtsmethode den diskreten Wert der ausgewählten Aktion zurückgeben. Der Nutzer kann weiterhin entweder eine gierige Strategie oder die Auswahl einer Aktion aus einer Wahrscheinlichkeitsverteilung wählen. Ein zusätzlicher Parameter der Stichprobe ist dafür verantwortlich.

int CICM::feedForward(CArrayFloat *inputVals, int window = 1, bool tem = true, bool sample = true)
  {
   if(!AddInputData(inputVals))
      return -1;
//---
   if(!CNet::feedForward(inputVals, window, tem))
      return -1;
   double balance = AccountInfoDouble(ACCOUNT_BALANCE);
   double reward = (dPrevBalance == 0 ? 0 : balance - dPrevBalance);
   dPrevBalance = balance;
   int action = (sample ? getSample() : getAction());
   if(!cReplay.AddState(inputVals, action, reward))
      return -1;
//---
   return action;
  }

Um den allgemeinen Ansatz für den Modellbetrieb beizubehalten, erwarten wir im aktuellen Zustandsbeschreibungstensor nur Angaben über den Marktzustand des Symbols vom aufrufenden Programm. Unser neues Modell erfordert jedoch auch Informationen über den Kontostand. Wir werden diese Informationen dem resultierenden Tensor in der Methode AddInputData hinzufügen. Erst nachdem wir die notwendigen Informationen erfolgreich hinzugefügt haben, rufen wir die Feed-Forward-Methode der übergeordneten Klasse auf.

Wir haben noch einige weitere Innovationen. Als Nächstes sollten wir dem Erfahrungspuffer neue Daten hinzufügen. Zu diesem Zweck definieren wir zunächst eine extrinsische Belohnung für den Übergang zum aktuellen Zustand. Wie bereits erwähnt, verwenden wir Veränderungen des Guthabens als extrinsische Belohnungen.

Als Nächstes bestimmen wir die nächste Aktion des Agenten in Übereinstimmung mit der vom Nutzer gewählten Strategie. Dann übergeben wir alle diese Daten an den Erfahrungsspeicher. Sobald alle oben genannten Vorgänge abgeschlossen sind, geben wir die ausgewählte Agentenaktion an das aufrufende Programm zurück.

Wir müssen darauf, den Prozess bei jedem Schritt zu kontrollieren. Wenn bei einem der Schritte ein Fehler auftritt, gibt die Methode -1 an das aufrufende Programm zurück. Daher berücksichtigen wir bei der Organisation des Raums möglicher Agentenaktionen diesen Umstand oder ändern den Rückgabewert so, dass der Aufrufer den Fehlerzustand eindeutig von der Aktion des Agenten trennen kann.

Der nächste Schritt ist die Änderung der backProp-Methode. Diese Methode hat sich am stärksten verändert. Zunächst einmal haben wir einen völlig neuen Satz von Parametern. Sie enthalten nicht mehr den Zielwert-Tensor. Die neue Methode erhält als Parameter nur die Größe des Aktualisierungspakets und den Abzinsungsfaktor.

Im Hauptteil der Methode wird zunächst die Größe des Erfahrungspuffers überprüft. Weitere Methodenoperationen sind nur möglich, wenn das Modell genügend Erfahrung gesammelt hat.

Wenn die Erfahrung nicht ausreicht, verlassen wir das Programm mit dem Ergebnis true. Der Wert false sollte nur zurückgegeben werden, wenn ein Fehler bei der Ausführung der Operation aufgetreten ist. Dadurch kann das Modell weitere Operationen wie gewohnt ausführen.

bool CICM::backProp(int batch, float discount = 0.900000f)
  {
//---
   if(cReplay.Total() < (int)iMinBufferSize)
      return true;
   if(!UpdateTarget(TargetNetFile))
      return false;

Bevor wir mit dem Modelltraining beginnen, sollten wir außerdem Target Net aktualisieren. Denn sein Encoder wird verwendet, um die Einbettung des Umgebungszustands nach dem Übergang zu erhalten.

Als Nächstes werden wir ein wenig Vorarbeit leisten und mehrere interne Variablen und Objekte deklarieren, die als Zwischenspeicher für Daten dienen werden.

   CLayer *currentLayer, *nextLayer, *prevLayer;
   CNeuronBaseOCL *neuron;
   CBufferFloat *state1, *state2, *targetVals = new CBufferFloat();
   vector<float> target, actions, st1, st2, result;
   double reward;
   int action;

Nach den vorbereitenden Arbeiten implementieren wir die Modelltrainingsschleife. Die Anzahl der Schleifeniterationen entspricht der in den Parametern angegebenen Größe der Modellaktualisierungscharge.

Im Körper der Schleife extrahieren wir zunächst zufällig einen Datensatz aus dem Erfahrungspuffer, der aus zwei aufeinanderfolgenden Systemzuständen, der gewählten Aktion und der erhaltenen Belohnung besteht. Danach implementieren wir den Vorwärtsdurchlauf des zu trainierenden Modells.

//--- training loop in the batch size
   for(int i = 0; i < batch; i++)
     {
      //--- get a random state and the buffer replay
      if(!cReplay.GetRendomState(state1, action, reward, state2))
         return false;
      //--- feed forward pass of the training model ("current" state)
      if(!CNet::feedForward(state1, 1, false))
         return false;

Nach der erfolgreichen Durchführung des Feed-Forward-Durchgangs des Hauptmodells werden wir vorbereitende Arbeiten durchführen, um den Feed-Forward-Durchgang des Forward-Modells durchzuführen. Hier extrahieren wir die Einbettung des aktuellen Systemzustands und erstellen einen One-Hot-Vektor der durchgeführten Aktion.

      //--- unload state embedding
      if(!GetLayerOutput(iStateEmbedingLayer, state1))
         return false;
      //--- prepare a one-hot action vector and concatenate with the current state vector
      getResults(target);
      actions = vector<float>::Zeros(target.Size());
      actions[action] = 1;
      if(!targetVals.AssignArray(actions) || !targetVals.AddArray(state1))
         return false;

Danach wird der Vorwärtsdurchlauf des Vorwärtsmodellsmit der Vorhersage des nächsten Zustands durch.

      //--- forward net feed forward pass - next state prediction
      if(!cForwardNet.feedForward(targetVals, 1, false))
         return false;

Als Nächstes implementieren wir den Vorwärtsdurchlauf des Target Net und extrahieren die nächste Zustandseinbettung.

      //--- feed forward
      if(!cTargetNet.feedForward(state2, 1, false))
         return false;
      //--- unload the state embedding and concatenate with the "current" state embedding
      if(!cTargetNet.GetLayerOutput(iStateEmbedingLayer, state2))
         return false;

Wir kombinieren die beiden resultierenden Einbettungen aufeinanderfolgender Zustände zu einem einzigen Tensor und rufen den Vorwärtsdurchlauf von Inverse Model auf.

      //--- inverse net feed forward - defining the performed action.
      if(!state1.AddArray(state2) || !cInverseNet.feedForward(state1, 1, false))
         return false;

Anschließend führen wir die Backpropagation-Methoden für das Vorwärtsmodell und das inverse Modell aus. Für sie haben wir bereits die Zielwerte in Form der nächsten Zustandseinbettung und eines One-Hot ausgeführten Aktionsvektors vorbereitet.

      //--- inverse net backpropagation
      if(!targetVals.AssignArray(actions) || !cInverseNet.backProp(targetVals))
         return false;
      //--- forward net backpropagation
      if(!cForwardNet.backProp(state2))
         return false;

Anschließend kehren wir zu den Operationen mit dem Hauptmodell zurück. Hier passen wir die Belohnung an, indem wir die Belohnung der intrinsischen Neugier und die erwartete zukünftige Belohnung, die von Target Net vorhergesagt wird, zu ihr addieren.

      //--- reward adjustment
      cForwardNet.getResults(st1);
      state2.GetData(st2);
      reward += (MathPow(st2 - st1, 2)).Sum();
      cTargetNet.getResults(targetVals);
      target[action] = (float)(reward + discount * targetVals.Maximum());
      if(!targetVals.AssignArray(target))
         return false;

Nachdem wir die Belohnung von Taget vorbereitet haben, können wir den Rückwärtsdurchlauf des Haupt-DQN-Modells durchführen. Es gibt jedoch einen Vorbehalt. Zusätzlich zur Weitergabe des Fehlergradienten aus der prädiktiven Belohnung müssen wir auch den Fehlergradienten des inversen Modells zum State Embedding Block hinzufügen. Zu diesem Zweck sollten wir die Fehlergradientendaten aus der Quelldatenschicht des inversen Modells in den Fehlergradientenpuffer der Einbettungsschicht des Hauptmodells kopieren, bevor wir den Backpropagation-Durchgang des Hauptmodells ausführen. Das liegt daran, dass der gesamte Algorithmus so aufgebaut ist, dass wir bei jedem Rückwärtsdurchlauf die Daten in den Puffern einfach überschreiben. Wir müssen also einen Keil in den Prozess der Ausbreitung des Fehlergradienten treiben. Dazu müssen wir den Code des Backpropagation-Durchgangs des Hauptmodells komplett neu schreiben.

Hier bestimmen wir zunächst den Belohnungsvorhersagefehler des Modells und rufen die Methode calcOutputGradients der letzten neuronalen Schicht auf, die den Fehlergradienten am Modellausgang bestimmt.

      //--- backpropagation pass of the model being trained
        {
         getResults(result);
         float error = result.Loss(target, LOSS_MSE);
         //---
         currentLayer = layers.At(layers.Total() - 1);
         if(CheckPointer(currentLayer) == POINTER_INVALID)
            return false;
         neuron = currentLayer.At(0);
         if(!neuron.calcOutputGradients(targetVals, error))
            return false;
         //---
         backPropCount++;
         recentAverageError += (error - recentAverageError) / fmin(recentAverageSmoothingFactor, (float)backPropCount);

Hier berechnen wir den durchschnittlichen Vorhersagefehler des Modells.

Der nächste Schritt besteht darin, den Fehlergradienten auf alle neuronalen Schichten des Modells zu übertragen. Zu diesem Zweck erstellen wir eine Schleife mit einer umgekehrten Iteration über alle neuronalen Schichten des Modells und dem sequentiellen Aufruf der Methode calcHiddenGradients für alle neuronalen Schichten. Wie Sie sich erinnern, ist diese Methode für die Weitergabe des Fehlergradienten durch die neuronale Schicht verantwortlich.

         //--- Calc Hidden Gradients
         int total = layers.Total();
         for(int layerNum = total - 2; layerNum >= 0; layerNum--)
           {
            nextLayer = currentLayer;
            currentLayer = layers.At(layerNum);
            neuron = currentLayer.At(0);
            if(!neuron.calcHiddenGradients(nextLayer.At(0)))
               return false;

Im Hauptteil des Modelltrainings haben wir den Algorithmus der gleichen übergeordneten Klassenmethode bis zu diesem Schritt vollständig wiederholt. An dieser Stelle müssen wir eine kleine Anpassung des Algorithmus vornehmen.

Wir werden eine Bedingung hinzufügen, um zu prüfen, ob die analysierte neuronale Schicht die Ausgabe des Systemzustands-Encoders ist. Wenn die Prüfung erfolgreich ist, addieren wir die Werte des Fehlergradienten aus dem inversen Modell zu dem Fehlergradienten, der aus der nächsten neuronalen Schicht stammt.

Ich habe den zuvor erstellten Kernel MatrixSum verwendet, um zwei Tensoren zu addieren. Mehr über diesen Kernel erfahren Sie in dem Artikel „Neuronale Netze leicht gemacht (Teil 8): Attention-Mechanismen“.

            if(layerNum == iStateEmbedingLayer)
              {
               CLayer* temp = cInverseNet.layers.At(0);
               CNeuronBaseOCL* inv = temp.At(0);
               uint global_work_offset[1] = {0};
               uint global_work_size[1];
               global_work_size[0] = neuron.Neurons();
               opencl.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix1, neuron.getGradientIndex());
               opencl.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix2, inv.getGradientIndex());
               opencl.SetArgumentBuffer(def_k_MatrixSum, def_k_sum_matrix_out, neuron.getGradientIndex());
               opencl.SetArgument(def_k_MatrixSum, def_k_sum_dimension, 1);
               opencl.SetArgument(def_k_MatrixSum, def_k_sum_multiplyer, 1);
               if(!opencl.Execute(def_k_MatrixSum, 1, global_work_offset, global_work_size))
                 {
                  printf("Error of execution kernel MatrixSum: %d", GetLastError());
                  return false;
                 }
              }
           }

Für die korrekte Durchführung dieser Aktion sind zwei Punkte zu beachten.

Zunächst muss die Backpropagation-Methode des inversen Modells den Fehlergradienten auf die Quelldatenebene übertragen. Zu diesem Zweck muss die Bedingung layerNum >= 0 in der Schleife verwendet werden, die den Gradienten durch die versteckten Schichten propagiert.

         //--- Calc Hidden Gradients
         int total = layers.Total();
         for(int layerNum = total - 2; layerNum >= 0; layerNum--)
           {

Zweitens legen wir bei der Deklaration der Architektur des inversen Modells die Aktivierungsmethode der Ergebnisebene fest, die der Aktivierungsmethode der zustandseinbettenden Empfangsschicht ähnelt. Diese Aktion hat während des Feedforward-Durchgangs keine Auswirkungen, passt aber den Fehlergradienten durch die Ableitung der Aktivierungsfunktion während des Backpropagation-Durchgangs an.

Die weiteren Schritte sind ähnlich wie beim Backpropagation-Algorithmus der Elternklasse. Nach der Weitergabe des Fehlergradienten werden die Gewichtsmatrizen aller neuronalen Schichten des Hauptmodells aktualisiert.

         //---
         prevLayer = layers.At(total - 1);
         for(int layerNum = total - 1; layerNum > 0; layerNum--)
           {
            currentLayer = prevLayer;
            prevLayer = layers.At(layerNum - 1);
            neuron = currentLayer.At(0);
            if(!neuron.UpdateInputWeights(prevLayer.At(0)))
               return false;
           }
         //---
         for(int layerNum = 0; layerNum < total; layerNum++)
           {
            currentLayer = layers.At(layerNum);
            CNeuronBaseOCL *temp = currentLayer.At(0);
            if(!temp.TrainMode())
               continue;
            if((layerNum + 1) == total && !temp.getGradient().BufferRead())
               return false;
            break;
           }
        }
     }

Beachten Sie, dass wir nur die Gewichtsmatrizen des Hauptlernmodells aktualisieren. Die Parameter von Vorwärtsmodell und Inverses Modell werden bei der Ausführung der Backpropagation-Methoden der entsprechenden Modelle aktualisiert.

Am Ende entfernen wir die in der Methode erstellten Hilfsobjekte und schließen den Methodenvorgang mit einem positiven Ergebnis ab.

   delete state1;
   delete state2;
   delete targetVals;
//---
   return true;
  }

Ich möchte noch ein paar Worte zu den Dateiverarbeitungsmethoden sagen. Da wir in diesem Algorithmus mehrere Modelle verwenden, stellt sich die Frage, wie wir die trainierten Modelle speichern können. Ich sehe hier zwei Möglichkeiten. Wir können alle Modelle in einer Datei speichern oder jedes Modell in einer separaten Datei speichern. Ich schlage vor, die Modelle in separaten Dateien zu speichern, da dies mehr Handlungsspielraum bietet. Wir können das trainierte DQN-Modell in eine separate Datei herunterladen und dann zusammen mit den zuvor besprochenen Modellen verwenden. Wir können auch alle drei Modelle laden und die in diesem Artikel beschriebene Methode anwenden. Die einzige Unannehmlichkeit besteht darin, dass die Zustandseinbettungsebene jedes Mal im Hauptmodell angegeben werden muss. Aber wir können mit der Architektur jedes einzelnen Modells beim Training experimentieren, um optimale Ergebnisse zu erzielen.

Ich werde mich hier nicht mit der Beschreibung der Algorithmen für die Arbeit mit Dateien aufhalten. Den Code aller verwendeten Programme und Klassen sowie deren Methoden finden Sie im Anhang.

3. Tests

Wir haben eine Klasse für die Organisation des Q-Learning-Modells unter Verwendung der Methode der intrinsischen Neugier geschaffen. Nun werden wir einen Expert Advisor erstellen, um das Modell zu trainieren und zu testen. Wie bereits erwähnt, wird das neue Modell im Strategietester trainiert. Dies ist ein grundlegender Unterschied zu den bisher verwendeten Methoden. Aus diesem Grund wurde die Modellschulung Expert Advisor erheblich verändert.

Der EA ICM-learning.mq5 wurde zum Testen erstellt. Zur Beschreibung der Marktsituation haben wir die gleichen Indikatoren mit ähnlichen Parametern verwendet. Daher blieben die äußeren Parameter des EA praktisch unverändert. Das Gleiche gilt für die Deklaration von globalen Variablen und Klassen.

Die EA-Initialisierungsmethode ist fast dieselbe wie in früheren EAs. Der einzige Unterschied besteht darin, dass das Startereignis des Lernprozesses nicht erzeugt wird. Dies liegt daran, dass wir die Funktion „Train“ zum Trainieren des Modells, die in allen früheren EAs verwendet wurde, vollständig entfernt haben.

Der gesamte Prozess der Ausbildung des Modells wird in die Methode OnTick übertragen. Da unser Modell darauf trainiert ist, den Markt auf der Grundlage abgeschlossener Kerzen zu analysieren, führen wir den Lernprozess nur bei der Eröffnung einer neuen Kerze durch. Zu diesem Zweck überprüfen wir im Körper der MethodeOnTick zunächst das neue Eröffnungsereignis der Kerze. Und wenn das Ergebnis positiv ist, werden wir weitere Maßnahmen ergreifen.

void OnTick()
  {
   if(!IsNewBar())
      return;

Als Nächstes laden wir die historische Daten, deren Menge der Größe des analysierten Fensters entspricht.

   int bars = CopyRates(Symb.Name(), TimeFrame, iTime(Symb.Name(), TimeFrame, 1), HistoryBars, Rates);
   if(!ArraySetAsSeries(Rates, true))
     {
      PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
      return;
     }
//---
   RSI.Refresh();
   CCI.Refresh();
   ATR.Refresh();
   MACD.Refresh();

Erstellen einer Beschreibung der aktuellen Marktsituation. Dieser Prozess folgt dem Algorithmus eines ähnlichen Prozesses, den wir in den zuvor betrachteten EAs verwendet haben.

   State1.Clear();
   for(int b = 0; b < (int)HistoryBars; b++)
     {
      float open = (float)Rates[b].open;
      TimeToStruct(Rates[b].time, sTime);
      float rsi = (float)RSI.Main(b);
      float cci = (float)CCI.Main(b);
      float atr = (float)ATR.Main(b);
      float macd = (float)MACD.Main(b);
      float sign = (float)MACD.Signal(b);
      if(rsi == EMPTY_VALUE || cci == EMPTY_VALUE || atr == EMPTY_VALUE || macd == EMPTY_VALUE || sign == EMPTY_VALUE)
         continue;
      //---
      if(!State1.Add((float)Rates[b].close - open) || !State1.Add((float)Rates[b].high - open) ||
         !State1.Add((float)Rates[b].low - open) || !State1.Add((float)Rates[b].tick_volume / 1000.0f) ||
         !State1.Add(sTime.hour) || !State1.Add(sTime.day_of_week) || !State1.Add(sTime.mon) ||
         !State1.Add(rsi) || !State1.Add(cci) || !State1.Add(atr) || !State1.Add(macd) || !State1.Add(sign))
        {
         PrintFormat("%s -> %d", __FUNCTION__, __LINE__);
         break;
        }
     }

Nachdem die Historie geladen und die Beschreibung der Marktsituation erstellt wurde, rufen wir die Feed-Forward-Methode des Modells auf und überprüfen das Ergebnis.

In unserer neuen Implementierung gibt die Methode feedForward die Agentenaktion zurück. Entsprechend dem Ergebnis führen wir eine Handelsoperation durch.

   switch(StudyNet.feedForward(GetPointer(State1), 12, true, true))
     {
      case 0:
         Trade.Buy(Symb.LotsMin(), Symb.Name());
         break;
      case 1:
         Trade.Sell(Symb.LotsMin(), Symb.Name());
         break;
      case 2:
         for(int i=PositionsTotal()-1;i>=0;i--)
            if(PositionGetSymbol(i)==Symb.Name())
              Trade.PositionClose(PositionGetInteger(POSITION_IDENTIFIER));
         break;
     }

Beachten Sie, dass wir bei der Erstellung des Modells von vier Agentenaktionen gesprochen haben. Hier sehen wir die Analyse von nur drei Aktionen und die Ausführung der entsprechenden Handelsoperation. Die vierte Maßnahme besteht darin, auf eine geeignetere Marktsituation zu warten, ohne Handelsoperationen auszuführen. Daher bearbeiten wir diese Aktion nicht.

Am Ende der Methode rufen wir die Backpropagation-Methode des Modells auf.

   StudyNet.backProp(Batch, DiscountFactor);
//---
  }

Sie haben wahrscheinlich bemerkt, dass wir das trainierte Modell während des Trainings nie gespeichert haben. Das Speichern des trainierten Modells wurde in die Deinitialisierungsmethode des EA verlagert.

void OnDeinit(const int reason)
  {
//---
   StudyNet.Save(FileName + ".nnw", FileName + ".fwd", FileName + ".inv", true);
  }

Um das Modelltraining im EA-Optimierungsmodus zu ermöglichen, wiederholte ich einen ähnlichen Speichervorgang nach Abschluss jedes Optimierungsdurchgangs.

void OnTesterPass()
  {
   StudyNet.Save(FileName + ".nnw", FileName + ".fwd", FileName + ".inv", true);
  }

Beachten Sie, dass der Optimierungsprozess nur auf einem aktiven Kern laufen sollte. Andernfalls würden die parallelen Threads die Daten anderer Agenten löschen. Dies würde den Einsatz von Mehrfachagenten vollständig überflüssig machen.

Um den EA zu trainieren, wurden alle Modelle mit NetCreator erstellt. Es sollte hinzugefügt werden, dass sich die Modelldateien im gemeinsamen Terminalverzeichnis „Terminal\Common\Files“ befinden müssen, um den EA-Betrieb im Strategietester zu ermöglichen, da jeder Agent in seiner eigenen Sandbox arbeitet, sodass sie Daten nur über den gemeinsamen Terminalordner austauschen können.

Das Training mit dem Strategietester dauert etwas länger als das bisherige virtuelle Training. Aus diesem Grund habe ich den Trainingszeitraum des Modells auf 10 Monate reduziert. Die übrigen Prüfparameter blieben unverändert. Auch hier habe ich EURUSD auf dem H1-Zeitrahmen verwendet. Die Indikatoren wurden mit Standardparametern verwendet.

Um ehrlich zu sein, hatte ich erwartet, dass der Lernprozess mit dem Verlust der Einlage beginnen würde. Beim ersten Durchgang zeigte das Modell jedoch ein Ergebnis nahe 0 an. Im zweiten Durchgang wurde dann sogar ein Gewinn erzielt. Das Modell führte 330 Transaktionen durch, wobei mehr als 98 % der Positionen gewinnbringend waren.

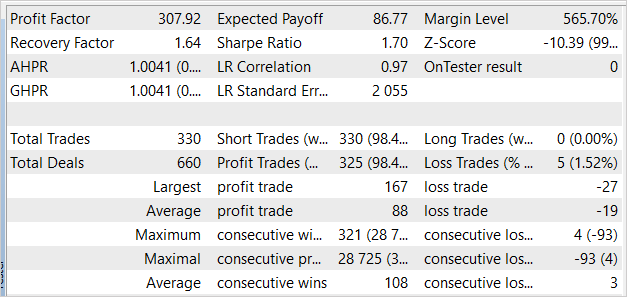
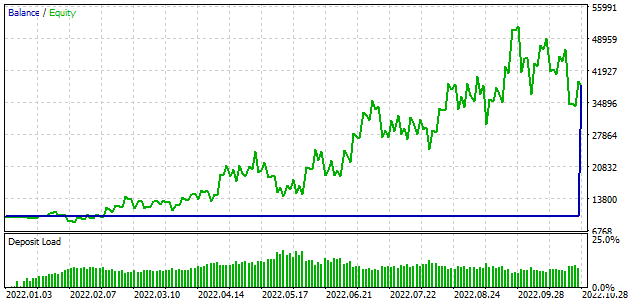
Schlussfolgerung

In diesem Artikel haben wir die Funktionsweise des Modells der intrinsischen Neugierde erörtert. Diese Technologie ermöglicht ein erfolgreiches Modelltraining mit Methoden des Reinforcement Learning unter Bedingungen, in denen extrinsische Belohnungen selten sind. Dies bezieht sich auf den Finanzhandel. Die Technologie der intrinsischen Neugier ermöglicht es dem Modell, die Umgebung gründlich zu erkunden und die besten Wege zu finden, um das Ziel zu erreichen. Dies funktioniert auch dann, wenn die Umgebung eine Belohnung für mehrere aufeinanderfolgende Aktionen ausgibt.

Im praktischen Teil dieses Artikels haben wir die vorgestellte Technologie mit MQL5 umgesetzt. Auf der Grundlage der obigen Arbeit können wir schlussfolgern, dass dieser Ansatz die gewünschten Ergebnisse im Handel erzielen kann.

Obwohl der vorgestellte EA Handelsoperationen durchführen kann, ist er nicht für den Einsatz im realen Handel geeignet. Der EA wird nur zu Bewertungszwecken vorgelegt. Vor dem Einsatz in der Praxis sind erhebliche Verbesserungen und umfassende Tests unter allen möglichen Bedingungen erforderlich.

Referenzen

1. Neuronale Netze leicht gemacht (Teil 26): Reinforcement-Learning
2. Neuronale Netze leicht gemacht (Teil 27): Tiefes Q-Learning (DQN)
3. Neuronale Netze leicht gemacht (Teil 28): Policy Gradient Algorithmus
4. Neuronale Netze leicht gemacht (Teil 32): Verteiltes Q-Learning
5. Neuronale Netze leicht gemacht (Teil 33): Quantilsregression im verteilten Q-Learning
6. Neuronale Netze leicht gemacht (Teil 34): Vollständig parametrisierte Quantilsfunktion
7. Curiosity-driven Exploration by Self-supervised Prediction

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	ICM-learning.mq5	EA	Modelltraining EA
2	ICM.mqh	Klassenbibliothek	Modellorganisation Klassenbibliothek
3	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
4	NeuroNet.cl	Code Base	Die Bibliothek des Programmcodes von OpenCL