MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 20): Symbolische Regression

Einführung

Wir setzen diese Serie fort, in der wir uns Algorithmen ansehen, die schnell kodiert, getestet und vielleicht sogar eingesetzt werden können, und zwar dank des MQL5-Assistenten, der nicht nur über eine Bibliothek von Standard-Handelsfunktionen und -klassen verfügt, die einen kodierten Expert Advisor begleiten, sondern auch über alternative Handelssignale und -methoden, die parallel zu jeder nutzerdefinierten Klassenimplementierung verwendet werden können.

Symbolische Regression ist eine Variante der Regressionsanalyse, die von einem größeren „weißen Fleck“ ausgeht als ihr traditioneller Verwandter, die klassische Regression. Am besten lässt sich dies anhand eines typischen Regressionsproblems veranschaulichen, bei dem die Steigung und der y-Achsenabschnitt einer Linie gesucht werden, die am besten zu einer Reihe von Datenpunkten passt.

source

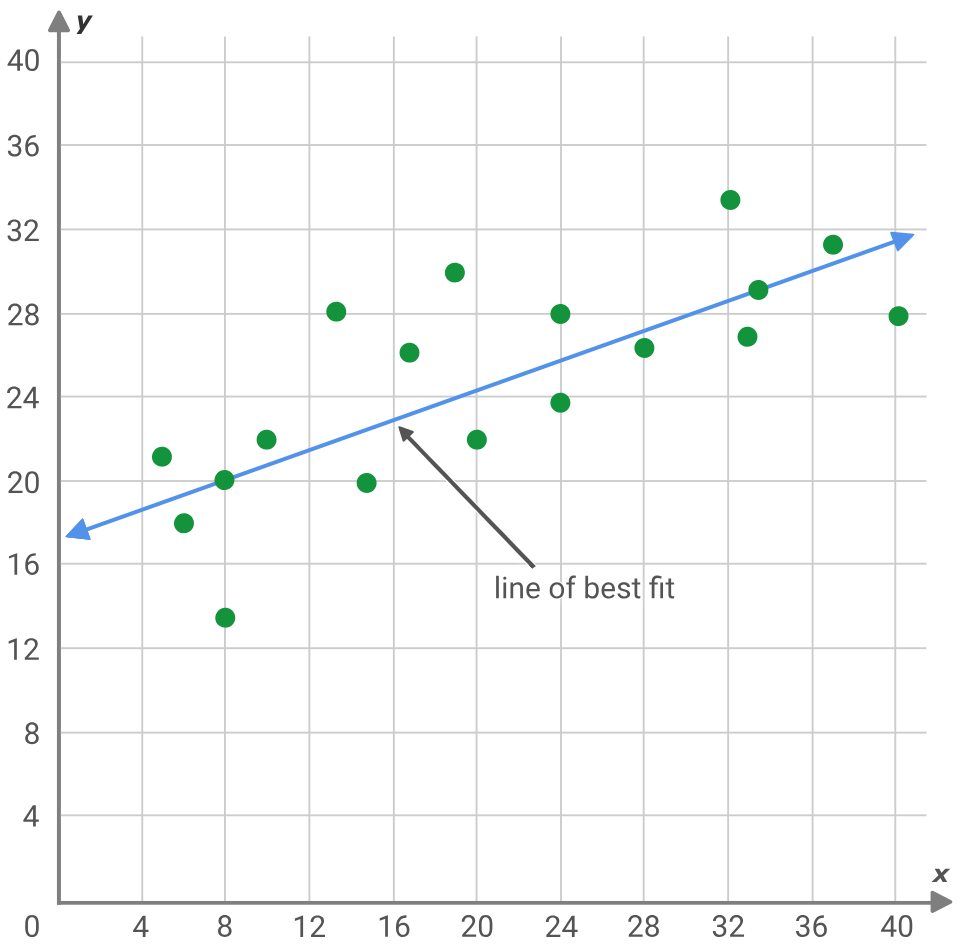
y = mx + c

Wobei:

• y ist der prognostizierte und abhängige Wert
• m ist die Steigung der besten Anpassungslinie
• c ist der y-Achsenabschnitt
• und x ist die unabhängige Variable

Bei der obigen Aufgabe wird davon ausgegangen, dass die Datenpunkte idealerweise auf einer Geraden liegen sollten, weshalb die Lösung(en) für den y-Achsenabschnitt und die Steigung gesucht werden. Alternativ dazu wird auch bei neuronalen Netzen im Wesentlichen versucht, die komplizierte oder quadratische Gleichung zu finden, die 2 Datensätze am besten abbildet (auch bekannt als das Modell), indem ein Netz mit einer vorgegebenen Architektur (Anzahl der Schichten, Schichtgrößen, Aktivierungsarten usw.) angenommen wird. Diese und ähnliche Ansätze weisen zu Beginn alle diese Verzerrung auf, und es gibt Fälle, in denen dies aufgrund von Deep Learning und (oder) Erfahrung gerechtfertigt ist. Die symbolische Regression ermöglicht es jedoch, das beschreibende Modell, das zwei Datensätze abbildet, als Ausdrucksbaum zu konstruieren und dabei mit zufällig zugewiesenen Knoten zu beginnen.

Dadurch könnten theoretisch komplexe Marktzusammenhänge besser aufgedeckt werden, die mit herkömmlichen Mitteln übersehen werden könnten. Die Vorteile der symbolischen Regression (SR) gegenüber alternativen präsumtiven Ansätzen lassen sich wie folgt zusammenfassen: Sie ist anpassungsfähiger an neue Marktdaten und sich ändernde Bedingungen. Dies ist möglich, da jede Analyse ohne Voreingenommenheit beginnt, aber mit einer zufälligen Zuweisung von Ausdrucksbaumknoten, die mit der Optimierung trainiert/verbessert werden, aber nicht nur das. Sie ist auch in der Lage, mehrere Datenquellen zu verwenden, im Gegensatz zu unserem obigen Beispiel der linearen Regression, bei der „x“ die einzige Variable ist, von der angenommen wird, dass sie den „y“-Wert beeinflusst. Die Anpassungsfähigkeit sieht mehr Variablen als nur das einzige „x“, das in einem Ausdrucksbaum eingefügt wurde, um den Wert „y“ besser zu bestimmen; sie ist flexibler, da der Ausdrucksbaum mehr Kontrolle über die Trainingsdaten ausübt, indem er systematische Knoten entwickelt, die die Daten in einer festgelegten Reihenfolge mit definierten Koeffizienten verarbeiten, die es ihm ermöglichen, komplexere Beziehungen zu erfassen, im Gegensatz zu einer linearen Regression (wie oben), bei der nur lineare Beziehungen erfasst werden. Selbst wenn „y“ ausschließlich von „x“ abhängt, ist diese Beziehung möglicherweise nicht linear, sondern könnte quadratisch sein, und die SR ermöglicht es, dies durch genetische Optimierung festzustellen; und schließlich wird die Beziehung zu einem Black-Box-Modell zwischen untersuchten Datensätzen entmystifiziert, indem Erklärbarkeit eingeführt wird, da die konstruierten Ausdrucksbäume inhärent genauer „erklären“, wie die Eingabedaten tatsächlich dem Ziel zugeordnet werden. Die Erklärbarkeit ist den meisten Gleichungen inhärent, aber was SR hinzufügt, ist vielleicht die „Einfachheit“, indem sie genetische Entwicklungen von komplexeren Ausdrücken durchführt und sich zu den einfacheren entwickelt, sofern ihre besten Anpassungsergebnisse besser sind.

Definition

SR stellt das Mapping-Modell zwischen den unabhängigen Variablen und der abhängigen (oder vorhergesagten) Variable als binären Expressionsbaum dar. Also eine schematische Darstellung wie die folgende:

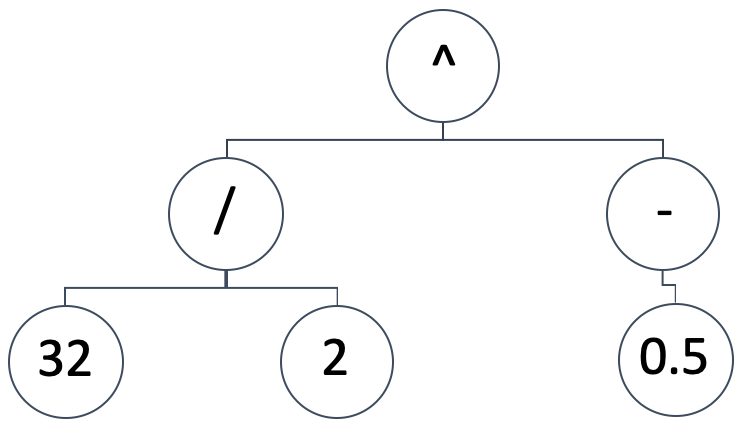
Das würde folgenden mathematischen Ausdruck implizieren:

(32/2) ^ (-0.5)

Das wäre gleichbedeutend mit: 0,25. Ausdrucksbäume können eine Vielzahl von Formen und Muster annehmen, wir wollen die grundlegende Prämisse der SR beibehalten, die darin besteht, mit einer zufälligen und unvoreingenommenen Konfiguration zu beginnen. Gleichzeitig müssen wir in der Lage sein, genetische Optimierungen für jede beliebige Größe eines ursprünglich generierten Ausdrucksbaums durchzuführen und dabei das Ergebnis (oder die Best-Fit-Metrik) mit Ausdrucksbäumen unterschiedlicher Größe zu vergleichen.

Um dies zu erreichen, werden wir unsere genetischen Optimierungen in „Epochen“ durchführen. Während Epochen im Fachjargon des maschinellen Lernens üblich sind, wenn es um das Stapeln von Trainingssitzungen wie bei neuronalen Netzen geht, verwenden wir den Begriff hier, um verschiedene Iterationen der genetischen Optimierung zu bezeichnen, bei denen jeder Durchlauf Ausdrucksbäume der gleichen Größe verwendet. Warum behalten wir die Größe innerhalb jeder Epoche bei? Da bei der genetischen Optimierung Kreuzungen verwendet werden und die Ausdrucksbäume unterschiedlich lang sind, wird der Prozess dadurch unnötig erschwert. Wie können wir dann die anfänglichen Ausdrucksbäume zufällig halten? Indem jede Epoche eine bestimmte Größe von Bäumen repräsentiert. Auf diese Weise optimieren wir über alle Epochen hinweg und vergleichen sie alle mit derselben Benchmark oder Best-Fit-Metrik.

Die in den Vektor-/Matrix-Datentypen von MQL5 verfügbaren Optionen zur Messung der Fitnessfunktion, die wir verwenden können, sind Regression und Verlustfunktionen. Diese integrierten Funktionen sind anwendbar, weil wir die ideale Ausgabe des Trainingsdatensatzes als einen Vektor mit den Ausgaben des getesteten Ausdrucksbaums, ebenfalls in einem Vektorformat, vergleichen werden. Je länger bzw. je größer der Testdatensatz ist, desto größer sind also unsere Vergleichsvektoren. Diese großen Datensätze bedeuten, dass es sehr schwierig sein wird, den idealen Best-Fit-Wert von Null zu erreichen, weshalb in jeder Epoche genügend Optimierungsgenerationen berücksichtigt werden müssen.

Um den besten Expressionsbaum auf der Grundlage der besten Anpassungsbewertung zu ermitteln, werden wir die Expressionsbäume vom längsten (und daher komplexesten) bis zum einfachsten und vermutlich am einfachsten zu „erklärenden“ Baum bewerten. Unsere Ausdrucksbaumformate können eine Fülle von Formen annehmen, wir werden uns jedoch auf die grundlegenden beschränken:

coeff, x-exponent, sign, coeff, x-exponent, sign, …

Wobei:

• coeff für den Koeffizienten von x steht,
• x-exponent die Potenz von x ist und
• sign ein Operator im Ausdruck ist, der -, +, *, / sein kann.

Der letzte Wert eines Ausdrucks ist kein Vorzeichen, da ein solches Vorzeichen keine Verbindung zu irgendetwas herstellt, d. h. die Vorzeichen sind immer kleiner als die x-Werte in einem Ausdruck. Die Größe eines solchen Ausdrucks reicht von 1, wenn wir nur einen x-Koeffizienten und einen Exponenten ohne Vorzeichen angeben, bis zu 16 (16 wird hier nur zu Testzwecken verwendet). Wie bereits erwähnt, steht diese maximale Größe in direktem Zusammenhang mit der Anzahl der Epochen, die bei der genetischen Optimierung verwendet werden. Das bedeutet einfach, dass wir die Optimierung für den idealen Ausdruck mit einem Ausdrucksbaum beginnen, der 16 Einheiten lang ist. Diese 16 Einheiten bedeuten, wie oben erwähnt, 15 Vorzeichen, und „jede Einheit“ ist einfach ein x-Koeffizient und der Exponent des x.

Bei der Auswahl der ersten zufälligen Ausdrucksbäume halten wir uns also immer an das Format von 2 zufälligen Ziffern „Knoten“, gefolgt von einem zufälligen Zeichen „Knoten“, wenn der Ausdrucksbaum mehr als eine Einheit lang ist und wir den Ausdruck nicht beenden, d. h. wir haben eine Einheit zu folgen. Die Auflistung, die uns dabei hilft, dies zu erreichen, finden Sie unten:

//+------------------------------------------------------------------+
// Get Expression Tree
//+------------------------------------------------------------------+
void CSignalSR::GetExpressionTree(int Size, string &ExpressionTree[])
{  if(Size < 1)
   {  return;
   }
   ArrayFree(ExpressionTree);
   ArrayResize(ExpressionTree, (2 * Size) + Size - 1);
   int _digit[];
   GetDigitNode(2 * Size, _digit);
   string _sign[];
   if(Size >= 2)
   {  GetSignNode(Size - 1, _sign);
   }
   int _di = 0, _si = 0;
   for(int i = 0; i < (2 * Size) + Size - 1; i += 3)
   {  ExpressionTree[i] = IntegerToString(_digit[_di]);
      ExpressionTree[i + 1] = IntegerToString(_digit[_di + 1]);
      _di += 2;
      if(Size >= 2 && _si < Size - 1)
      {  ExpressionTree[i + 2] = _sign[_si];
         _si ++;
      }
   }
}

Unsere obige Funktion prüft zunächst, ob die Größe des Ausdrucksbaums mindestens eins beträgt. Wenn dieser Test bestanden ist, müssen wir die tatsächliche Größe des Baums bestimmen. Wie wir oben gesehen haben, folgen die Bäume dem Format coefficient, exponent und dann gegebenenfalls sign. Dies bedeutet, dass bei einer Größe s die Gesamtzahl der Ziffernknoten in diesem Baum 2 x s beträgt, da jede Größeneinheit einen Koeffizienten- und einen Exponentenwert tragen muss. Diese Knoten werden nach dem Zufallsprinzip über die Funktion „GetDigitNode“ ausgewählt, deren Auflistung unten zu sehen ist:

//+------------------------------------------------------------------+
// Get Digit
//+------------------------------------------------------------------+
void CSignalSR::GetDigitNode(int Count, int &Digit[])
{  ArrayFree(Digit);
   ArrayResize(Digit, Count);
   for(int i = 0; i < Count; i++)
   {  Digit[i] = __DIGIT_NODE[MathRand() % __DIGITS];
   }
}

Die Zahlen werden nach dem Zufallsprinzip aus dem statischen globalen Ziffernknotenfeld ausgewählt. Die Vorzeichenknoten variieren jedoch, je nachdem, ob die Größe des Baumes eins übersteigt. Bei einem eindimensionalen Baum wäre kein Vorzeichen anwendbar, da dies nur Platz für einen x-Koeffizienten und seinen Exponenten lässt. Wenn wir mehr als einen haben, dann entspricht die Anzahl der Vorzeichenknoten der Eingabegröße minus eins. Unsere Funktion zur zufälligen Auswahl eines Vorzeichens, um den Vorzeichenplatz im Ausdruck zu füllen, ist unten angegeben:

//+------------------------------------------------------------------+
// Get Sign
//+------------------------------------------------------------------+
void CSignalSR::GetSignNode(int Count, string &Sign[])
{  ArrayFree(Sign);
   ArrayResize(Sign, Count);
   for(int i = 0; i < Count; i++)
   {  Sign[i] = __SIGN_NODE[MathRand() % __SIGNS];
   }
}

Die Vorzeichen (signs) werden wie bei den Ziffernknoten nach dem Zufallsprinzip aus dem Knotenfeld der Vorzeichen ausgewählt. Dieses Array kann jedoch eine Reihe von Varianten annehmen, aber der Kürze halber kürzen wir es auf die Zeichen „+“ und „-“ ab. Das Multiplikationszeichen „*“ könnte hinzugefügt werden, aber das Divisionszeichen „/“ wurde ausdrücklich weggelassen, weil wir keine Division durch Null abfangen, was ziemlich heikel sein kann, wenn wir mit der genetischen Optimierung beginnen und Kreuzungen usw. vornehmen müssten. Es steht dem Leser frei, dies zu erforschen, vorausgesetzt, der Fehler einer Teilung durch Null wird richtig angegangen, da es die Optimierungsergebnisse verfälschen könnte.

Sobald wir eine Anfangspopulation von Zufallsausdrucksbäumen haben, können wir mit dem genetischen Optimierungsprozess für diese bestimmte Epoche beginnen. Bemerkenswert ist auch die einfache Struktur, die wir zum Speichern und Zugreifen auf die Informationen des Ausdrucksbaums verwenden. Es handelt sich im Wesentlichen um eine String-Matrix mit zusätzlicher Flexibilität bei der Größenanpassung (Funktionen, die von einem Standard-Datentyp wie der Matrix zur Verfügung stellen sollte, der Doubles verarbeitet). Dies ist ebenfalls unten aufgeführt:

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
struct Stree
{  string   tree[];

   Stree()
   {  ArrayFree(tree);
   };
   ~Stree() {};
};
struct Spopulation
{  Stree   population[];

   Spopulation() {};
   ~Spopulation() {};
};

Wir verwenden diese Struktur, um Populationen in jeder Optimierungsgeneration zu erstellen und zu verfolgen. Jede Epoche verwendet eine bestimmte Anzahl von Generationen für die Optimierung. Wie bereits erwähnt, werden umso mehr Optimierungsgenerationen benötigt, je größer der Testdatensatz ist. Wenn die Testdaten jedoch zu klein sind, kann dies zu Expressionsbäumen führen, die hauptsächlich von weißem Rauschen und nicht von den zugrunde liegenden Mustern in den getesteten Datensätzen abgeleitet sind.

Sobald wir mit der Optimierung jeder Generation beginnen, müssen wir die Fitness jedes Baumes ermitteln, und da wir mehrere Bäume haben, werden diese Fitnesswerte in einem Vektor gespeichert. Sobald wir diesen Vektor haben, besteht der nächste Schritt darin, einen Schwellenwert für die Beschneidung dieser Population festzulegen, da dieser Baum mit jeder nachfolgenden Generation innerhalb einer bestimmten Epoche verfeinert und verkleinert wird. Wir haben diesen Schwellenwert „_fit“ genannt und er basiert auf einem ganzzahligen Eingabeparameter, der als Perzentilmarkierung dient. Der Parameter reicht von 0 bis 100.

Aus dieser Ausgangspopulation wird eine weitere Stichprobenpopulation gebildet, aus der nur die Expressionsbäume ausgewählt werden, deren Fitness unter oder gleich dem Schwellenwert liegt. Die oben verwendete Funktion zur Berechnung unserer Fitnessbewertung hätte die unten angegebene Auflistung:

//+------------------------------------------------------------------+
// Get Fitness
//+------------------------------------------------------------------+
double CSignalSR::GetFitness(matrix &XY, vector &Y, string &ExpressionTree[])
{  Y.Init(XY.Rows());
   for(int r = 0; r < int(XY.Rows()); r++)
   {  Y[r] = 0.0;
      string _sign = "";
      for(int i = 0; i < int(ExpressionTree.Size()); i += 3)
      {  double _yy = pow(XY[r][0], StringToDouble(ExpressionTree[i + 1]));
         _yy *= StringToDouble(ExpressionTree[i]);
         if(_sign == "+")
         {  Y[r] += _yy;
         }
         else if(_sign == "-")
         {  Y[r] -= _yy;
         }
         else if(_sign == "/" && _yy != 0.0)//un-handled
         {  Y[r] /= _yy;
         }
         else if(_sign == "*")
         {  Y[r] *= _yy;
         }
         else if(_sign == "")
         {  Y[r] = _yy;
         }
         if(i + 2 < int(ExpressionTree.Size()))
         {  _sign = ExpressionTree[i + 2];
         }
      }
   }
   return(Y.RegressionMetric(XY.Col(1), m_regressor));
   //return(_y.Loss(XY.Col(1),LOSS_MAE));
}

Die Funktion „GetFitness“ nimmt die Matrix des Eingabedatensatzes „XY“ und konzentriert sich auf die Spalte x der Matrix (wir verwenden eindimensionale Daten sowohl für die Eingaben als auch für die Ausgaben), um den Prognosewert des Eingabe-Ausdrucksbaums zu ermitteln. Die Eingabematrix hat mehrere Datenzeilen, sodass auf der Grundlage des x-Wertes in jeder Zeile (der ersten Spalte) eine Projektion vorgenommen wird, und alle diese Projektionen werden für jede Zeile in einem Vektor „Y“ gespeichert. Nachdem alle Zeilen verarbeitet wurden, wird dieser Vektor „Y“ mit den tatsächlichen Werten in der zweiten Spalte verglichen, indem entweder die integrierte Regressionsfunktion oder die Verlustfunktion verwendet wird. Wir entscheiden uns für die Regression, wobei der mittlere quadratische Fehler als Regressionsmaß verwendet wird.

Die Größe dieses Wertes ist der Fitnesswert des eingegebenen Ausdrucksbaums. Je kleiner er ist, desto besser passt er. Nachdem wir diesen Wert für jede der Stichprobenpopulationen erhalten haben, müssen wir zunächst prüfen, ob der Stichprobenumfang gerade ist; wenn nicht, reduzieren wir den Umfang um eins. Die Größe muss gleichmäßig sein, weil wir in der nächsten Phase diese Bäume kreuzen und die erzeugten Kreuzungen paarweise hinzugefügt werden, und sie sollten mit der Elternpopulation (den Proben) übereinstimmen, da wir die Population nur reduzieren, wenn wir bei jeder Generation Proben nehmen. Die Kreuzung der Expressionsbäume innerhalb der Proben erfolgt zufällig durch Indexauswahl. Die für die Kreuzung zuständige Funktion ist unten aufgeführt:

//+------------------------------------------------------------------+
// Set Crossover
//+------------------------------------------------------------------+
void CSignalSR::SetCrossover(string &ParentA[], string &ParentB[], string &ChildA[], string &ChildB[])
{  if(ParentA.Size() != ParentB.Size() || ParentB.Size() == 0)
   {  return;
   }
   int _length = int(ParentA.Size());
   ArrayResize(ChildA, _length);
   ArrayResize(ChildB, _length);
   int _cross = 0;
   if(_length > 1)
   {  _cross = rand() % (_length - 1) + 1;
   }
   for(int c = 0; c < _cross; c++)
   {  ChildA[c] = ParentA[c];
      ChildB[c] = ParentB[c];
   }
   for(int l = _cross; l < _length; l++)
   {  ChildA[l] = ParentB[l];
      ChildB[l] = ParentA[l];
   }
}

Diese Funktion prüft zunächst, ob die beiden übergeordneten Ausdrücke die gleiche Größe haben und keiner von ihnen Null ist. Wird dies angegeben, so werden die beiden untergeordneten Arrays in der Größe an die übergeordneten Arrays angepasst und der Kreuzungspunkt ausgewählt. Diese Kreuzung ist ebenfalls zufällig und ist nur relevant, wenn die Größe der Eltern mehr als eins beträgt. Sobald der Kreuzungspunkt gesetzt ist, werden die Werte der beiden Elternfelder vertauscht und in die beiden Kindfelder ausgegeben. Hier sind die übereinstimmenden Längen sehr nützlich, denn wenn sie unterschiedlich wären, wäre zusätzlicher Code erforderlich, um Fälle zu behandeln (oder zu vermeiden), in denen Ziffern mit Zeichen vertauscht werden. Offensichtlich unnötige Komplikationen, wenn alle Größen unabhängig voneinander in ihrer eigenen Epoche getestet werden können, um die beste Anpassung zu erreichen.

Wenn wir die Kreuzung abgeschlossen haben, können wir die Kinder mutieren. „Können“, weil wir für diese Mutationen eine Wahrscheinlichkeitsschwelle von 5 % ansetzen, womit sie nicht garantiert passieren, aber doch Teil des typischen, genetischen Optimierungsprozesses sind. Anschließend kopieren wir diese neue gekreuzte Population, um unsere Ausgangspopulation zu überschreiben, aus der wir zu Beginn eine Stichprobe gezogen hatten, und als Marker protokollieren wir den Best Fit Score des besten Expressionsbaums aus dieser neu gekreuzten Population. Wir verwenden die protokollierte Punktzahl nicht nur, um den am besten passenden Baum zu bestimmen, sondern auch, um in einigen seltenen Fällen die Optimierung zu stoppen, falls wir einen Nullwert erhalten.

Nutzerdefinierte Signalklasse

Bei der Entwicklung der Signalklasse unterscheiden sich unsere Hauptschritte nicht wesentlich von denen, die wir in früheren nutzerdefinierten Signalklassen in dieser Reihe durchgeführt haben. Zunächst müssen wir den Datensatz für unser Modell vorbereiten. Dies sind die Daten, die unsere „XY“-Eingabematrix für die oben betrachtete Funktion „GetFitness“ füllen. Er ist auch eine Eingabe für die Funktion „GetBestTree“, die alle oben beschriebenen Schritte zusammenfasst. Der Quellcode für diese Funktion ist unten angegeben:

//+------------------------------------------------------------------+
// Get Best Fit
//+------------------------------------------------------------------+
void CSignalSR::GetBestTree(matrix &XY, vector &Y, string &BestTree[])
{  double _best_fit = DBL_MAX;
   for(int e = 1 + m_epochs; e >= 1; e--)
   {  Spopulation _p;
      ArrayResize(_p.population, m_population);
      int _e_size = 2 * e;
      for(int p = 0; p < m_population; p++)
      {  string _tree[];
         GetExpressionTree(e, _tree);
         _e_size = int(_tree.Size());
         ArrayResize(_p.population[p].tree, _e_size);
         for(int ee = 0; ee < _e_size; ee++)
         {  _p.population[p].tree[ee] = _tree[ee];
         }
      }
      for(int g = 0; g < m_generations; g++)
      {  vector _fitness;
         _fitness.Init(int(_p.population.Size()));
         for(int p = 0; p < int(_p.population.Size()); p++)
         {  _fitness[p] = GetFitness(XY, Y, _p.population[p].tree);
         }
         double _fit = _fitness.Percentile(m_fitness);
         Spopulation _s;
         int _samples = 0;
         for(int p = 0; p < int(_p.population.Size()); p++)
         {  if(_fitness[p] <= _fit)
            {  _samples++;
               ArrayResize(_s.population, _samples);
               ArrayResize(_s.population[_samples - 1].tree, _e_size);
               for(int ee = 0; ee < _e_size; ee++)
               {  _s.population[_samples - 1].tree[ee] = _p.population[p].tree[ee];
               }
            }
         }
         if(_samples % 2 == 1)
         {  _samples--;
            ArrayResize(_s.population, _samples);
         }
         if(_samples == 0)
         {  break;
         }
         Spopulation _g;
         ArrayResize(_g.population, _samples);
         for(int s = 0; s < _samples - 1; s += 2)
         {  int _a  = rand() % _samples;
            int _b  = rand() % _samples;
            SetCrossover(_s.population[_a].tree, _s.population[_b].tree, _g.population[s].tree, _g.population[s + 1].tree);
            if (rand() % 100 < 5)   // 5% chance
            {  SetMutation(_g.population[s].tree);
            }
            if (rand() % 100 < 5)
            {  SetMutation(_g.population[s + 1].tree);
            }
         }
         // Replace old population
         ArrayResize(_p.population, _samples);
         for(int s = 0; s < _samples; s ++)
         {  for(int ee = 0; ee < _e_size; ee++)
            {  _p.population[s].tree[ee] = _g.population[s].tree[ee];
            }
         }
         // Print best individual
         for(int s = 0; s < _samples; s ++)
         {  _fit = GetFitness(XY, Y, _p.population[s].tree);
            if (_fit < _best_fit)
            {  _best_fit = _fit;
               ArrayCopy(BestTree,_p.population[s].tree);
            }
         }
      }
   }
}

Die Eingabematrix besteht aus eindimensionalen x-Werten und eindimensionalen y-Werten. Unabhängige Variablen und abhängige Variablen. Der Mehrdimensionalität könnte auch dadurch Rechnung getragen werden, dass der „Y“-Eingangsvektor in eine Matrix und ein Ausdrucksbaum für jeden x-Wert im Eingangsvektor und jeden y-Wert im Ausgangsvektor umgewandelt wird. Diese Ausdrucksbäume müssten auch in einem Matrix- oder höherdimensionalen Speicherformat vorliegen.

Wir verwenden jedoch einzelne Dimensionen, und unsere Datenreihe besteht einfach aus aufeinanderfolgenden Schlusskursen. In der obersten oder jüngsten Datenzeile hätten wir also den vorletzten Schlusskurs als x-Wert und den aktuellen Schlusskurs als y-Wert. Die Vorbereitungen und das Füllen unserer „XY“-Matrix mit diesen Daten werden durch den nachstehenden Quellcode übernommen:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   matrix _xy;
   _xy.Init(m_data_set, 2);
   for(int i = 0; i < m_data_set; i++)
   {  _xy[i][0] = m_close.GetData(StartIndex()+i+1);
      _xy[i][1] = m_close.GetData(StartIndex()+i);
   }

...

   return(result);
}

Sobald die Datenaufbereitung abgeschlossen ist, ist es sinnvoll, sich über die Methode zur Bewertung der Eignung klar zu werden, die in unserem Modell verwendet werden soll. Wir entscheiden uns für die Regression im Gegensatz zu einer Verlustfunktion, aber selbst innerhalb der Regression gibt es eine ganze Reihe von Metriken, aus denen man wählen kann. Um eine optimale Auswahl zu ermöglichen, ist die Art der zu verwendenden Regressionsmetrik ein Eingangsparameter, der optimiert werden kann, um besser zu den getesteten Datensätzen zu passen. Unser Standardwert ist jedoch der übliche mittlere quadratische Fehler (Root-Mean-Square-Error).

Die Implementierung des genetischen Algorithmus wird von der Funktion „GetBestTree“ übernommen, deren Quellcode bereits oben aufgeführt ist. Es liefert eine Reihe von Ergebnissen, von denen der beste Ausdrucksbaum am besten ist. Mit diesem Baum können wir den aktuellen Schlusskurs als Eingabe (x-Wert) verarbeiten, um unseren nächsten Schlusskurs (y-Wert) zu erhalten, indem wir die Funktion „GetFitness“ verwenden, da sie auch mehr als nur die Fitness eines abgefragten Ausdrucks zurückgibt, da der Eingabevektor „Y“ unsere Zielprognose enthält. Dies wird im folgenden Code behandelt:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{ 
        ...

   vector _y;
   string _best_fit[];
   GetBestTree(_xy, _y, _best_fit);

        ...

   return(result);
}

Nachdem ein indikativer nächster Schlusskurs ermittelt wurde, besteht der nächste Schritt darin, diesen Kurs in ein brauchbares Signal für den Expert Advisor umzuwandeln. Die Prognosewerte deuten oft nur auf einen Anstieg oder einen Rückgang hin, aber ihr absoluter Wert liegt außerhalb der Spanne, wenn man ihn mit den letzten Schlusskursen vergleicht. Das bedeutet, dass wir sie normalisieren müssen, bevor sie verwendet werden können. Die Normalisierung und die Signalerzeugung werden in unserem Code unten durchgeführt:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{  int result = 0;
   
        ...

   double _cond = (_y[0]-m_close.GetData(StartIndex()))/fmax(fabs(_y[0]),m_close.GetData(StartIndex()));
   _cond *= 100.0;
   //printf(__FUNCSIG__ + " cond: %.2f", _cond);
   //return(result);
   if(_cond > 0.0)
   {  result = int(fabs(_cond));
   }
   return(result);
}

Die Integer-Ausgabe der Kauf- und Verkaufs-Bedingungen in einer Standard-Expert-Signalklasse muss im Bereich 0 - 100 liegen, und das ist es, was wir im obigen Code in unser Signal umwandeln.

Die Bedingungsfunktionen jeweils für Kauf und Verkauf spiegeln sich gegenseitig, und die Zusammenstellung von Signalklassen in Expert Advisors wird in folgenden Artikeln behandelt hier und hier.

Backtests und Optimierung

Bei einem Testlauf mit einigen der „besten Einstellungen“ des zusammengestellten Expert Advisors erhalten wir den folgenden Bericht und die folgende Aktienkurve:

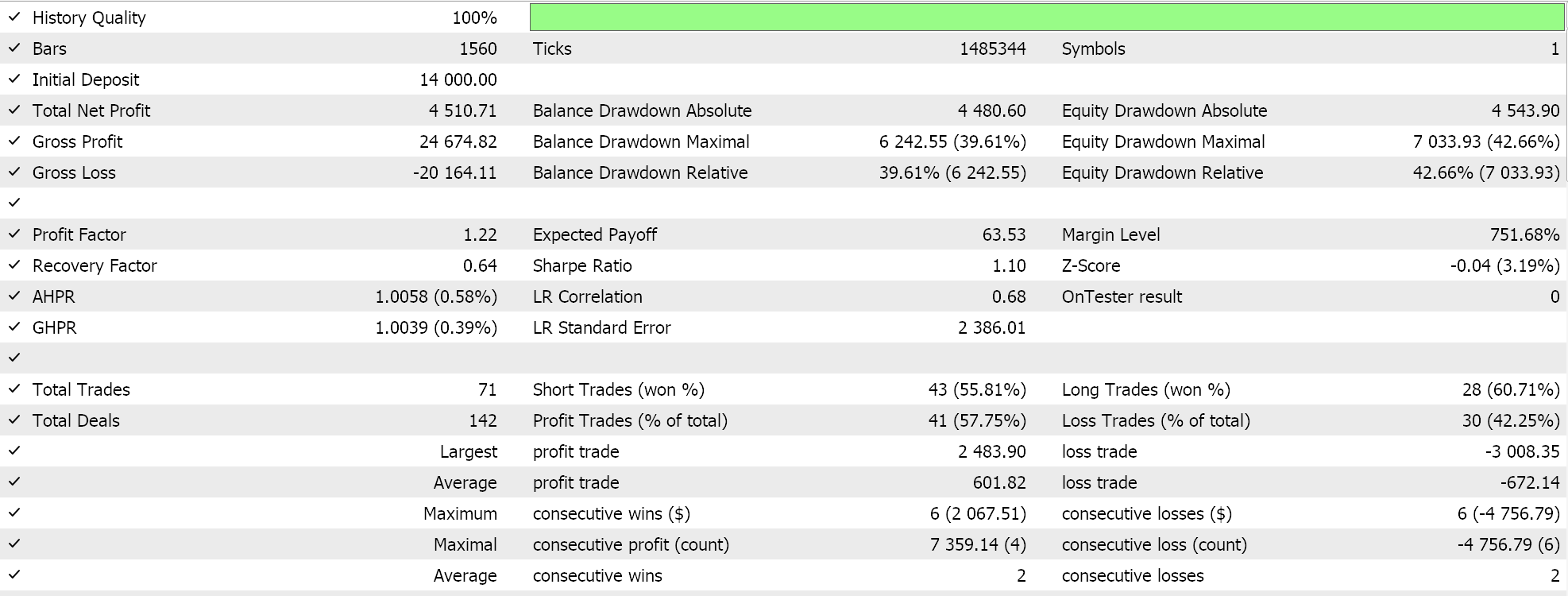
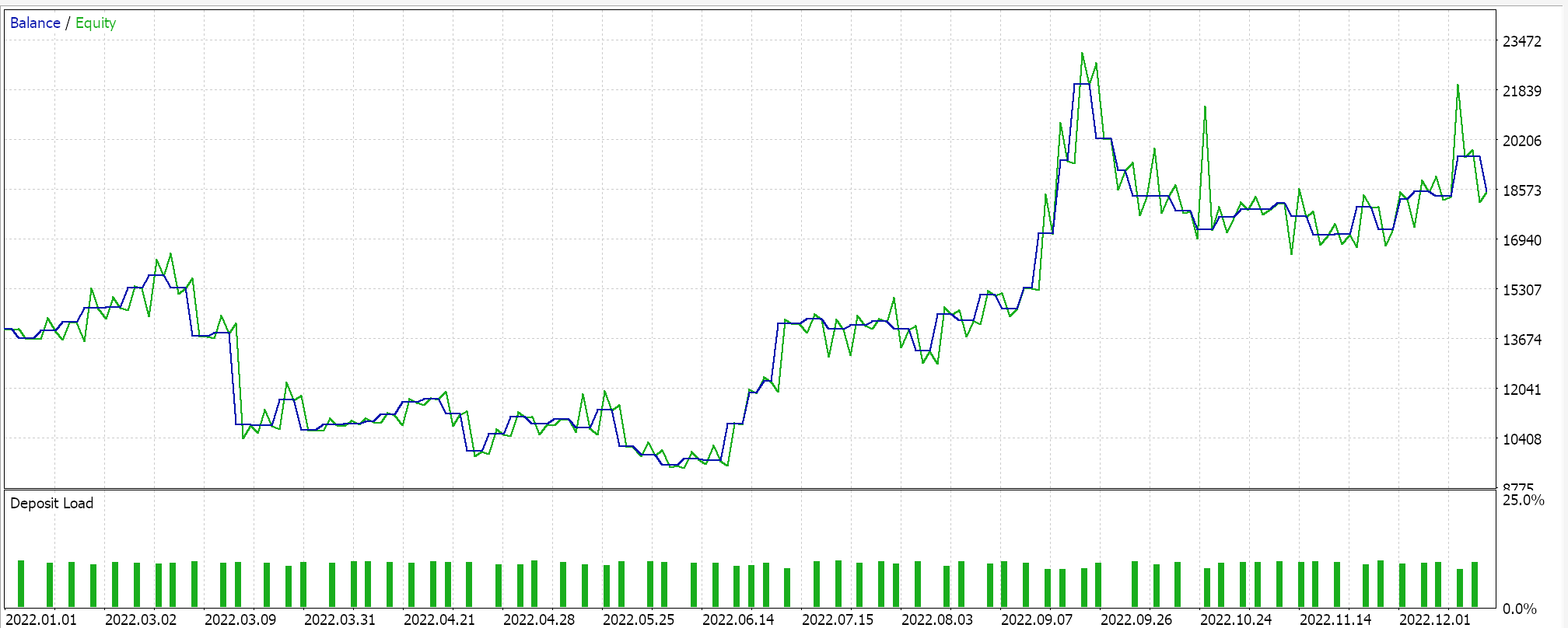
Da die Expressionsbäume zufällig ausgewählt, gekreuzt und mutiert werden, ist es unwahrscheinlich, dass ein bestimmter Testlauf seine Ergebnisse exakt reproduzieren kann. Unser Test wird für das Jahr 2022 für das Paar EUR JPY auf dem 4-Stunden-Zeitrahmen durchgeführt. Wie immer führen wir Tests ohne Preisangaben für SL oder TP durch, da dies helfen kann, die idealen Einstellungen der Experten besser zu ermitteln.

Schlussfolgerung

Zusammenfassend haben wir die symbolische Regression als ein Modell eingeführt, das in einer nutzerdefinierten Instanz einer Signalklasse Expert verwendet werden kann, um Kauf- und Verkaufs-Bedingungen abzuwägen. Wir haben bei dieser Analyse einen sehr bescheidenen Datensatz verwendet, da sowohl die Eingangs- als auch die Ausgangswerte des Modells eindimensional waren. Das bedeutet nicht, dass das Modell nicht erweitert werden kann, um mehrdimensionale Datensätze aufzunehmen. Darüber hinaus ist es aufgrund der genetischen Optimierung des Modells schwierig, bei jedem Testlauf identische Ergebnisse zu erzielen. Dies bedeutet, dass Expert Advisors, die auf diesem Modell basieren, auf relativ großen Zeitrahmen und in Verbindung mit anderen Handelssignalen verwendet werden sollten, damit sie als Bestätigung für bereits unabhängig generierte Signale dienen können.