MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 23): CNNs

Einführung

Wir setzen diese Serie fort, in der wir Ideen zum maschinellen Lernen und zur Statistik betrachten, die für Händler angesichts der schnellen Test- und Prototyping-Umgebung, die der MQL5-Assistent bietet, von Nutzen sein könnten. Das Ziel ist nach wie vor, eine einzige Idee in einem Artikel zu behandeln, und für diesen Beitrag hatte ich ursprünglich gedacht, dass dafür mindestens 2 Artikel nötig wären, aber es scheint, dass wir es in einen einzigen quetschen können. Convolutional Neural Networks (CNNs) verarbeiten, wie der Name schon sagt, mehrdimensionale Daten mit Hilfe von Kerneln in Form von Faltungen.

Diese Kernel enthalten die Netzgewichte und liegen wie die mehrdimensionalen Eingabedaten in der Regel im Matrixformat vor. Sie haben im Vergleich zu den Eingabedaten eine geringere Gesamtgröße, und durch die Iteration über die Eingabedatenmatrix während eines Vorwärtsdurchgangs, wie wir weiter unten sehen werden, durchläuft jede Iteration im Wesentlichen die Eingabedaten. Dieser „Zyklus“ ist der Grund für die Bezeichnung „convolutional“ (Faltung).

In diesem Artikel werden wir eine Einführung in die wichtigsten Schritte eines CNN geben, eine einfache MQL5-Klasse erstellen, die diese Schritte implementiert, diese Klasse in eine nutzerdefinierte MQL5-Assistenten-Signalklasse integrieren und schließlich Testläufe mit einem Expert Advisor durchführen, der aus dieser Signalklasse zusammengestellt wurde.

CNNs sind in der Regel komplexe neuronale Netze, die vor allem in der Video- und Bildverarbeitung eingesetzt werden, wie wir im vorherigen Artikel bei den GANs gesehen haben. Im Gegensatz zu GANs, die darauf trainiert sind, echte Bilder oder Personen auf den Bildern von Fälschungen zu unterscheiden, arbeiten CNNs jedoch eher wie ein Klassifikator, indem sie die Eingabedaten (häufig Bildpixel) in verschiedene Untergruppen von Daten aufteilen, wobei jede Untergruppe eine wichtige Eigenschaft der Eingabedaten erfassen soll. Diese erzeugten Untergruppen werden oft als „Feature Maps“ (Merkmalskarten) bezeichnet.

Die Schritte, die zur ErstEs ist unvermeidlich, dass die Feature-Map oder die Ausgabebilder jeder Iteration weniger Pixel und damit weniger Abmessungen haben als das Eingabebild, sodass in diesem Fall eine anfängliche Auffüllung oder Vergrößerung des Eingabebildes sinnlos sein könnte. Padding (füllen), Feeding Forward (Vorwärtsdurchgang), Activation (Aktivierung), Pooling (Zusammenfassen) und schließlich, wenn das Netz trainiert wird, Backpropagation (Rückwärtsdurchgänge). Im Folgenden wird jeder dieser Schritte anhand eines sehr einfachen CNN mit nur einer Ebene erläutert. Unter einer einzigen Schicht verstehen wir, dass die Eingabedaten durch eine einzige Schicht von Kerneln verarbeitet werden. Dies ist bei CNNs nicht immer der Fall, da sie sich über viele Schichten erstrecken können, sodass jeder der vier oben erwähnten Schritte des Auffüllens, Vorwärtsdurchgangs, Aktivierens und Zusammenfassens für jede Schicht wiederholt wird. Bei einem mehrschichtigen Aufbau bedeutet dies, dass für jede aus einer höheren Schicht erstellte Feature-Map andere wichtige Komponenteneigenschaften vorhanden sind, die in der Folge in neue Feature-Maps aufgeteilt werden.

Padding

Dies markiert den Beginn einer CNN und kann fakultativ sein, unabhängig davon, ob dieser spezielle Schritt enthalten ist oder nicht. Was ist also Padding (Auffüllung)? Wie der Name schon sagt, handelt es sich dabei um das Hinzufügen eines Randes von Daten entlang der Kanten der Eingabedaten. Im Wesentlichen werden die Eingabedaten aufgefüllt. Erinnern Sie sich daran, dass die Eingabedaten in der Regel mehr als eine Dimension haben, oft sind sie sogar zweidimensional, weshalb eine Matrixdarstellung oft angemessen ist. Bilder bestehen aus Pixeln in einer XY-Ebene, sodass ihre Klassifizierung mit einem CNN einfach ist.

Warum müssen wir also „auffüllen“? Die Notwendigkeit ergibt sich aus der Art der Faltung mit den Kerneln während des Vorwärtsschritts. Die Kernel liegen wie die Eingabedaten ebenfalls im Matrixformat vor. Sie tragen die Gewichte des Netzes. Normalerweise hat eine Schicht mehr als einen Kernel, da jeder Kernel für die Ausgabe einer bestimmten Feature-Map verantwortlich ist.

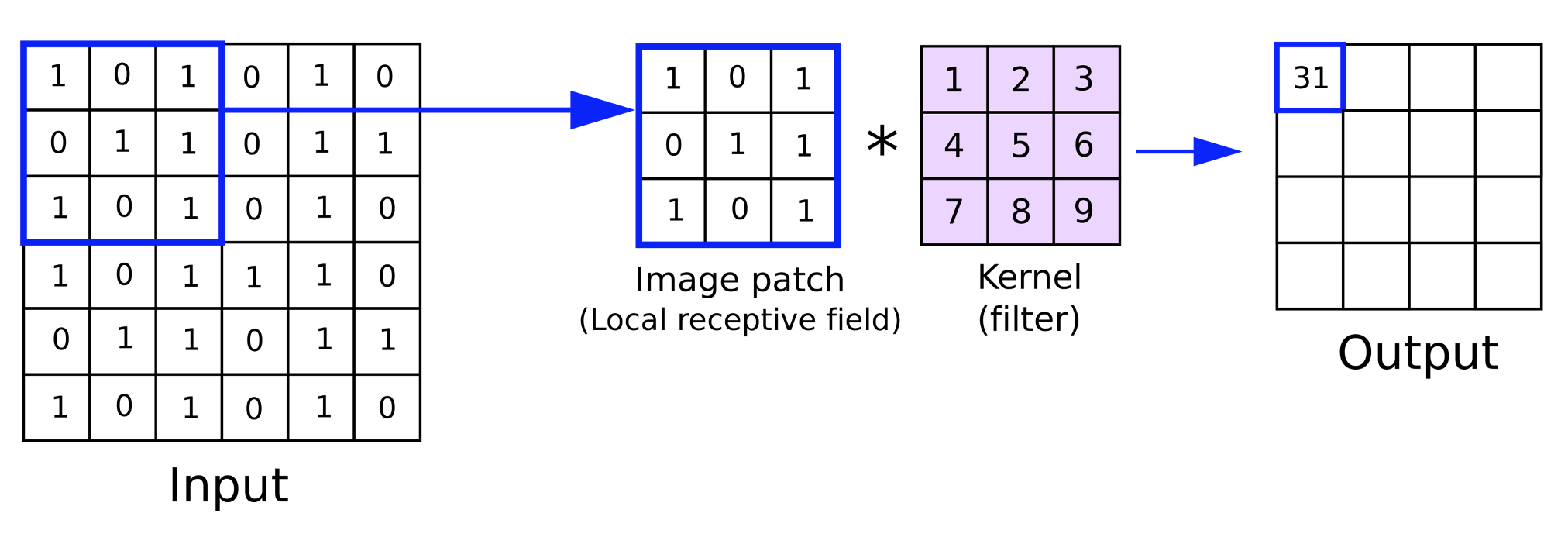
Der Prozess der Multiplikation der Gewichte im Kernel mit den Eingabedaten erfolgt über eine Iteration oder einen Zyklus, was synonym als Faltung bezeichnet wird. Das Endprodukt dieser Multiplikation ist eine Matrix der Feature-Maps, deren Dimensionen immer kleiner sind als die Eingabedaten. Der Sinn des Padding liegt also darin, dass den Eingabedaten zusätzliche Datenränder hinzugefügt werden müssen, wenn der Benutzer möchte, dass die Feature-Map dieselben Abmessungen wie die Roheingabedaten hat.

Quelle

Um dies zu verstehen, betrachten wir eine Eingabedatenmatrix der Größe 6 x 6 und einen Gewichtskern der Größe 3 x 3, dann ergibt eine direkte Multiplikation der Gewichte eine 4 x 4-Matrix wie oben angegeben. Die Formel für die Größe der Ausgabematrix bei gegebener Größe der Eingabedaten und der Kernelmatrix lautet:

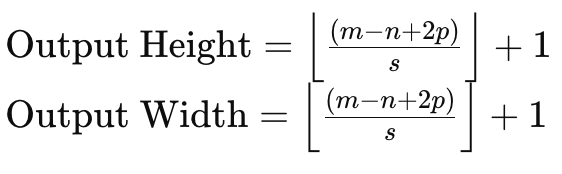
wobei:

• m die Dimension der Eingangsdatenmatrix ist,
• n die Dimension des Gewichtungskernels ist,
• p die Padding.Größe ist,
• und s die Schrittweite ist.

Wenn wir also die Größe einer Eingabedatenmatrix in den Feature-Maps beibehalten wollen, müssen wir die Eingabedatenmatrix um einen Betrag auffüllen, der nicht nur die Größe der Eingabematrix und der Kernelmatrizen berücksichtigt, sondern auch den Betrag der zu verwendenden Schrittweite.

Es gibt im Wesentlichen 3 Methoden des Padding. Die erste ist das Padding mit Nullen, bei dem entlang des Randes der Eingabematrix Nullen hinzugefügt werden, um die erforderliche Breite zu erreichen. Die zweite Form des Padding ist das Randauffüllen, bei dem die Zahlen am Rand der Matrix entlang der neuen Grenze wiederholt werden, um auch der neuen Zielgröße zu entsprechen. Und schließlich gibt es ein reflektiertes Padding, bei dem die Zahlen auf dem neuen vergrößerten Rand aus der Eingabedatenmatrix stammen, wobei die Zahlen entlang des Randes als Spiegellinie fungieren.

<

Quelle

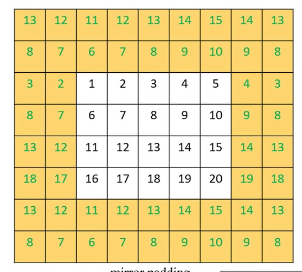
Sobald das Padding abgeschlossen ist, kann der Vorwärtsdurchgang durchgeführt werden. Diese Padding ist jedoch, wie bereits erwähnt, optional, d. h., wenn der Nutzer keine Feature-Maps in passender Größe benötigt, kann sie ganz weggelassen werden. Nehmen wir zum Beispiel eine Situation, in der ein CNN viele Bilder durchkämmen und Fotos von menschlichen Gesichtern aus diesen Bildern extrahieren soll.

Es ist unvermeidlich, dass die Feature-Map oder die Ausgabebilder jeder Iteration weniger Pixel und damit weniger Abmessungen haben als das Eingabebild, sodass in diesem Fall eine anfängliche Auffüllung oder Vergrößerung des Eingabebildes sinnlos sein könnte. Wir implementieren Padding in dieser Form:

//+------------------------------------------------------------------+
//| Pad                                                              |
//+------------------------------------------------------------------+
void Ccnn::Pad()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(padding != PADDING_NONE)
   {  matrix _padded;
      _padded.Init(inputs.Rows() + 2, inputs.Cols() + 2);
      _padded.Fill(0.0);
      for(int i = 0; i < int(_padded.Cols()); i++)
      {  for(int j = 0; j < int(_padded.Rows()); j++)
         {  if(i == 0 || i == int(_padded.Cols()) - 1 || j == 0 || j == int(_padded.Rows()) - 1)
            {  if(padding == PADDING_ZERO)
               {  _padded[j][i] = 0.0;
               }
               else if(padding == PADDING_EDGE)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[0][0];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][0];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[0][inputs.Cols() - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][inputs.Cols() - 1];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][i];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[j][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 1];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 1][i - 1];
                  }
               }
               else if(padding == PADDING_REFLECT)
               {  if(i == 0 && j == 0)
                  {  _padded[j][i] = inputs[1][1];
                  }
                  else if(i == 0 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][1];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == 0)
                  {  _padded[j][i] = inputs[1][inputs.Cols() - 2];
                  }
                  else if(i == int(_padded.Cols()) - 1 && j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][inputs.Cols() - 2];
                  }
                  else if(i == 0)
                  {  _padded[j][i] = inputs[j - 1][1];
                  }
                  else if(j == 0)
                  {  _padded[j][i] = inputs[1][i - 1];
                  }
                  else if(i == int(_padded.Cols()) - 1)
                  {  _padded[j][i] = inputs[j - 1][inputs.Cols() - 2];
                  }
                  else if(j == int(_padded.Rows()) - 1)
                  {  _padded[j][i] = inputs[inputs.Rows() - 2][i - 1];
                  }
               }
            }
            else
            {  _padded[j][i] = inputs[j - 1][i - 1];
            }
         }
      }
      //
      Set(_padded, false);
   }
}

Für unsere Zwecke als Händler und nicht als Bildwissenschaftler werden wir eine Eingabedatenmatrix von Indikatorwerten haben. Diese Indikatorwerte können an eine Vielzahl von Optionen angepasst werden, wir haben jedoch enge Kurslücken aus verschiedenen gleitenden Durchschnittsindikatoren ausgewählt.

Vorwärtsdurchgang (Convolve)

Sobald die Eingabedaten vorbereitet sind, wird eine Multiplikation der Gewichte mit den Eingabedaten für jeden Kernel in der Schicht durchgeführt, um eine Feature-Map zu erstellen. Neben der Multiplikation der Gewichte, die eine kleinere Matrix ergibt, wird zu jedem Matrixwert ein Bias addiert, die ebenso wie die jeweiligen Gewichte für jeden Kernel einzigartig ist.

Jeder Kernel hat die Gewichte und die Biase, die auf die Extraktion eines Schlüsselmerkmals oder einer Eigenschaft der Eingabedaten spezialisiert sind. Je mehr Merkmale man also sammeln möchte, desto mehr Kerne würde man im Netz einsetzen. Die Weiterleitung erfolgt über die Funktion „Convolve“, die hier aufgeführt ist:

//+------------------------------------------------------------------+
//| Convolve through all kernels                                     |
//+------------------------------------------------------------------+
void Ccnn::Convolve()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
// Loop through kernel at set padding_stride
   for (int f = 0; f < kernels; f++)
   {  bool _stop = false;
      int _stride_row = 0, _stride_col = 0;
      output[f].Fill(0.0);
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  output[f][h][g] += (kernel[f].weights[j][i] * inputs[_stride_row + j][_stride_col + i]);
               }
            }
            output[f][h][g] += kernel[f].bias;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(inputs.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(inputs.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Aktivierung

Nach der Faltung (convolving) würden die erzeugten Matrizen ähnlich wie bei der Aktivierung in typischen mehrschichtigen Wahrnehmungen aktiviert werden. In der Bildverarbeitung besteht der häufigste Zweck der Aktivierung jedoch darin, innerhalb eines Modells die Fähigkeit zur Abbildung nichtlinearer Daten einzuführen, sodass auch komplexere Zusammenhänge (z. B. quadratische Gleichungen) erfasst werden können. Gängige Aktivierungsalgorithmen sind ReLU, leaky ReLU, Sigmoid und Tanh.

ReLU ist wohl der populärere Aktivierungsalgorithmus, der in der Regel verwendet wird, da er mit Problemen des verschwindenden Gradienten viel besser zurechtkommt, allerdings gibt es ein Problem mit toten Neuronen, das durch „undichte“ ReLUs verschwindet. Ein totes Neuron bezieht sich auf Situationen, in denen die Ausgaben des Netzes unabhängig von den Änderungen der Eingaben auf konstante Werte aktualisiert werden. Dies kann bei Netzen, die mit Gewichten initialisiert werden und negative Eingaben erhalten, ein großes Problem darstellen, da dann statische Ausgaben unabhängig von der Variabilität der negativen Eingaben erhalten werden. Dies würde sogar durch Training geschehen, was unweigerlich zu verzerrten Gewichten führen würde. Dies wäre ein Verlust an Darstellungskapazität, der das Modell unfähig macht, komplexere Muster darzustellen. Bei dem Rückwärtsdurchgang würde der Fluss der Gradienten durch das Netz mit einer langsameren Konvergenz oder sogar einer vollständigen Stagnation erfolgen.

Das „undichte“ ReLU entschärft dies daher teilweise, indem esPooling (Zusammenfassen) werd einen kleinen, optimierbaren, positiven Wert mit der Bezeichnung „alpha“ als kleine Steigung für negative Eingaben zuweist, sodass Neuronen mit negativen Eingaben nicht absterben, sondern weiterhin zum Lernprozess beitragen. Ein glatterer Gradientenfluss in der Backpropagation führt auch zu einem stabileren und effizienteren Trainingsprozess als das typische ReLU.

Pooling

Nachdem die Merkmalsbilder, die die Ausgänge der Faltung sind, aktiviert wurden, werden sie in einem Prozess, der als Pooling bezeichnet wird, auf Rauschen untersucht. Beim Pooling werden die Abmessungen der Feature-Map in Höhe und Breite reduziert. Der Sinn des Poolings besteht darin, die Rechenlast zu verringern und die Anzahl der Parameter zu reduzieren, mit denen sich das Netz auseinandersetzen muss. Das Pooling trägt auch zur Übersetzungsinvarianz bei, da es in der Lage ist, Schlüsseleigenschaften jeder Feature-Map mit minimalen Daten zu erkennen. m

Es gibt hauptsächlich 3 Arten von Pooling, nämlich: Max-Pooling, Durchschnitts-Pooling und Global-Pooling. Beim Max-Pooling wird der maximale Wert in jedem Merkmalsmatrixfeld an einem Faltungspunkt ausgewählt. Und jeder der ausgewählten Punkte wird in einer neuen Matrix zusammengeführt, die dann die zusammengefasste Matrix ist. Seine Befürworter argumentieren, dass es die meisten kritischen Eigenschaften der gepoolten Feature-Map bewahrt und gleichzeitig die Wahrscheinlichkeit einer Überanpassung verringert.

Beim Average-Pooling wird der Durchschnittswert jedes Feldes während der Faltung berechnet und wie beim Max-Pooling in die gepoolte Matrix zurückgeführt. Die Größe der gepoolten Matrix wird nicht nur durch die Größe des Pooling-Fensters und dessen Größenunterschied zur Feature-Map beeinflusst, sondern auch durch den Pooling-Schritt. Häufig werden Pooling-Schritte mit einem Wert von mehr als 1 verwendet, was zwangsläufig dazu führt, dass die „gepoolte“ Matrix deutlich kleiner ist als die Feature-Map. Für diesen Artikel wollen wir die Dinge einfach halten, da wir davon ausgehen, dass dieser Artikel eine Einführung in CNN ist, verwenden wir einen Pooling-Schritt von eins. Befürworter des Average-Pooling behaupten, dass es differenzierter und weniger aggressiv ist als das maximale Pooling und daher weniger wahrscheinlich ist, dass kritische Merkmale beim Pooling übersehen werden.

Die dritte Art des Poolings, die häufig in CNNs verwendet wird, ist das globale Pooling. Bei dieser Art des Poolings werden keine Faltungen durchgeführt, sondern die gesamte Feature-Map wird auf einen einzigen Wert reduziert, indem entweder der Durchschnitt der Feature-Map gebildet oder ihr Maximum ausgewählt wird. Es handelt sich um eine Art von Pooling, das in der letzten Schicht von mehrschichtigen CNNs angewendet werden kann, wobei für jeden Kernel ein einziger Wert angestrebt wird.

Die Größe des Pooling-Fensters und die Größe des Pooling-Schrittes sind die wichtigsten Determinanten für die Größe der gepoolten Daten: Größere Schritte führen tendenziell zu kleineren gepoolten Daten, während die Größe der Feature-Map und die Größe des Pooling-Fensters in umgekehrtem Verhältnis zueinander stehen. Kleinere zusammengefasste Datenmengen verringern die Netzaktivierungen und den Speicherbedarf erheblich. Unser Pooling ist in MQL5 wie folgt implementiert:

//+------------------------------------------------------------------+
//| Pool                                                             |
//+------------------------------------------------------------------+
void Ccnn::Pool()
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   if(pooling != POOLING_NONE)
   {  for(int f = 0; f < int(output.Size()); f++)
      {  matrix _pooled;
         if(output[f].Cols() > 2 && output[f].Rows() > 2)
         {  _pooled.Init(output[f].Rows() - 2, output[f].Cols() - 2);
            _pooled.Fill(0.0);
            for (int g = 0; g < int(_pooled.Cols()); g++)
            {  for (int h = 0; h < int(_pooled.Rows()); h++)
               {  if(pooling == POOLING_MAX)
                  {  _pooled[h][g] = DBL_MIN;
                  }
                  for (int i = 0; i < int(output[f].Cols()); i++)
                  {  for (int j = 0; j < int(output[f].Rows()); j++)
                     {  if(pooling == POOLING_MAX)
                        {  _pooled[h][g] = fmax(output[f][j][i], _pooled[h][g]);
                        }
                        else if(pooling == POOLING_AVERAGE)
                        {  _pooled[h][g] += output[f][j][i];
                        }
                     }
                  }
                  if(pooling == POOLING_AVERAGE)
                  {  _pooled[h][g] /= double(output[f].Cols()) * double(output[f].Rows());
                  }
               }
            }
            output[f].Copy(_pooled);
         }
      }
   }
}

Rückwärtsdurchgang (Evolve)

Wie bei jedem neuronalen Netz ist der Rückwärtsdurchgang die Phase, in der die Netzgewichte und die Biase „lernen“, indem sie angepasst werden. Sie wird während des Trainingsprozesses durchgeführt, und die Häufigkeit dieses Trainings wird zwangsläufig durch das verwendete Modell bestimmt. Bei Finanzmodellen, die von Händlern verwendet werden, können einige Modelle so programmiert werden, dass sie ihre Netze einmal im Quartal trainieren, z. B. um sich an die neuesten Nachrichten über die Unternehmensgewinne anzupassen, während andere Modelle ihr Training einmal im Monat an den Tagen nach der Veröffentlichung wichtiger Wirtschaftsnachrichten durchführen könnten. Der Punkt ist, dass es zwar wichtig ist, die richtigen Netzgewichte und Biase zu haben, aber vielleicht noch wichtiger ist es, ein klares, voreingestelltes System für das Training und die Aktualisierung dieser Gewichte und Biase zu haben.

Gibt es Netze, für die eine einmalige Schulung ausreicht und die danach ohne Weiterbildungsbedarf genutzt werden können? Ja, das ist möglich, wenn auch in vielen Fällen unwahrscheinlich. Daher ist es ratsam, immer einen Trainingskalender für das Netzwerk zu haben, wenn man mit einem neuronalen Netzwerk handeln möchte.

Die typischen Schritte bei dem Rückwärtsdurchgang sind also immer drei: Berechnung des Fehlers und Verwendung dieses Fehlerdeltas zur Berechnung der Gradienten und anschließend Verwendung dieser Gradienten zur Aktualisierung der Gewichte und Biase. Wir führen alle drei Schritte in unserer Funktion „Evolve“ aus, deren Code weiter unten zu sehen ist:

//+------------------------------------------------------------------+
//| Evolve pass through the neural network to update kernel          |
//| and biases using gradient descent                                |
//+------------------------------------------------------------------+
void Ccnn::Evolve(double LearningRate = 0.05)
{  if(!validated)
   {  printf(__FUNCSIG__ + " network invalid! ");
      return;
   }
   
   for(int f = 0; f < kernels; f++)
   {  matrix _output_error = target[f] - output[f];
      // Calculate output layer gradients
      matrix _output_gradients;
      _output_gradients.Init(output[f].Rows(),output[f].Cols());
      for (int g = 0; g < int(output[f].Rows()); g++)
      {  for (int h = 0; h < int(output[f].Cols()); h++)
         {  _output_gradients[g][h] =  LeakyReLUDerivative(output[f][g][h]) * _output_error[g][h];
         }
      }
      
      // Update output layer kernel weights and biases
      int _stride_row = 0, _stride_col = 0;
      for (int g = 0; g < int(output[f].Cols()); g++)
      {  for (int h = 0; h < int(output[f].Rows()); h++)
         {  double _bias_sum = 0.0;
            for (int i = 0; i < int(kernel[f].weights.Cols()); i++)
            {  for (int j = 0; j < int(kernel[f].weights.Rows()); j++)
               {  kernel[f].weights[j][i] += (LearningRate * _output_gradients[_stride_row + j][_stride_col + i]); // output[f][_stride_row + j][_stride_col + i]);
                  _bias_sum += _output_gradients[_stride_row + j][_stride_col + i];
               }
            }
            kernel[f].bias += LearningRate * _bias_sum;
            _stride_col += padding_stride;
            if(_stride_col + int(kernel[f].weights.Cols()) > int(_output_gradients.Cols()))
            {  _stride_col = 0;
               _stride_row += padding_stride;
               if(_stride_row + int(kernel[f].weights.Rows()) > int(_output_gradients.Rows()))
               {  _stride_col = 0;
                  _stride_row = 0;
               }
            }
         }
      }
   }
}

Unsere Ausgaben am Ende sind Matrizen, und daher werden die Fehlerdeltas zwangsläufig auch im Matrixformat erfasst. Sobald wir diese Fehlerdeltas haben, müssen wir sie um ihr Aktivierungsprodukt bereinigen, da sie vor dem Erreichen dieser letzten Schicht aktiviert wurden. Diese Anpassung der Aktivierung erfolgt durch Multiplikation der Fehlerdeltas mit der Ableitung der Aktivierungsfunktion.

Denken Sie auch daran, dass dieser Vorgang für jeden Kernel wiederholt werden muss, auch wenn die Ausgangsfehler und Ausgangsgradienten in Matrixform vorliegen. Deshalb haben wir jede dieser Operationen in eine weitere übergreifende for-Schleife eingeschlossen, deren Index eine ganze Zahl 'f' ist und deren maximale Größe niemals die Kernelanzahl übersteigt. Unsere Ausgabematrizen für die CNN-Testklasse, die wir in diesem Artikel vorstellen, sind drei an der Zahl. Sie liefern die Feature-Maps für Auf-, Abwärts- und die Seitwärtsbewegung des Wertpapiers, dessen Kurslücken mit den verschiedenen gleitenden Durchschnitten als Eingaben im CNN angegeben wurden. Diese Preisunterschiede sind ebenfalls in Form einer Matrix dargestellt.

Da die Werte des Ausgangsfehlers und des Ausgangsgradienten in Form einer Matrix vorliegen und in einem vorangegangenen Schritt zusammengefasst wurden (siehe oben), stimmen ihre Größen nicht mit den Größen der Kernelmatrix überein. Dies stellt zunächst eine Herausforderung dar, wenn es darum geht, wie die Gradienten zur Anpassung der Kernelgewichte verwendet werden können. Die Lösung ist jedoch recht einfach, da sie dem Faltungsansatz folgt, den wir im Vorwärtsdurchgang angewandt haben, bei dem Kernel-Gewichtungsmatrizen unterschiedlicher Größe als die Eingabedatenmatrix (und deren Padding) zyklisch multipliziert wurden, sodass an jedem Punkt ein einziger Wert aus allen Kernelprodukten auf dem Fenster im Fokus summiert und in die Ausgabematrix eingefügt wurde.

Dies wird mit Schritten durchgeführt, und unser Schritt für diesen Test ist nur ein einziger, da er mit dem Schritt übereinstimmen sollte, der im Feed Forward verwendet wird. Die Aktualisierung der Biase ist allerdings etwas schwierig, da es sich nur um einen einzigen Wert handelt. Die Lösung besteht jedoch immer darin, die Gradienten in der Matrix zu summieren und diese Summe mit dem alten Bias zu multiplizieren (nach Anpassung mit einer Lernrate).

Einbindung in eine Signalklasse

Um unsere CNN-Klasse in einem nutzerdefinierten Signal zu verwenden, müssen wir im Wesentlichen 2 Dinge definieren. Erstens, welche Form von Eingabedaten wir verwenden werden, und zweitens, welche Art von Zieldaten wir in den Ausgabematrizen erwarten. Die Antworten auf diese beiden Fragen wurden oben bereits angedeutet, denn die Eingabedaten sind Kurslücken zwischen dem aktuellen Schlusskurs und vielen (standardmäßig 25) gleitenden Durchschnittskurswerten. Die vielen gleitenden Durchschnitte unterscheiden sich durch ihre eindeutige gleitende Durchschnittsperiode, die wir über die Funktion „GetOutput“ in die Eingabematrix einfügen (siehe unten):

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  int _index = 5;
   matrix _inputs;
   vector _ma, _h, _l, _c;
   _inputs.Init(m_input_size, m_input_size);
   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         for(int i = 0; i < m_input_size; i++)
         {  for(int j = 0; j < m_input_size; j++)
            {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, h, __KERNEL + 1))
               {  _inputs[i][j] = _c[0] - _ma[0];
                  _index++;
               }
            }
         }
         //
         
        ...

      }
   }

        ...
   
        ...

}

Was nicht so einfach ist, sind die Zieldaten in unseren Ausgabematrizen. Wie bereits erwähnt, wollen wir Feature-Maps für Auf- und Abwärtsbewegungen erstellen. Und der Einfachheit halber sollen es nur diese beiden sein (und kein Beurteilung, ob die Märkte stagnieren), aber der Leser kann den Quellcode ändern, um dies zu berücksichtigen. Wir messen dies, indem wir uns die Kursentwicklung nach jedem Input-Datenpunkt ansehen. Auch hier nimmt unser Datenpunkt Indikatorwerte auf, für die wir uns entschieden haben, Preislücken zu einer Reihe von gleitenden Durchschnittspreisen zu schließen, aber dies kann leicht an Ihre Präferenzen angepasst werden.

Das von uns gewählte Maß für die Aufwärtsbewegung, das wir in einer Matrix und nicht in einem einzelnen Wert erfassen wollen, sind die Veränderungen des Höchstkurses über verschiedene Zeiträume. Um eine eventuelle Abwärtsbewegung nach der Aufzeichnung eines Datenpunktes zu erfassen, werden die Veränderungen der Tiefs über verschiedene Zeiträume in einer Matrix aufgezeichnet. Die Kodierung ist wie unten dargestellt:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
   ...

   for(int g = 0; g < m_epochs; g++)
   {  for(int h = m_train_set - 1; h >= 0; h--)
      {  _inputs.Fill(0.0);
         _index = 0;
         
        ...

         //
         _h.CopyRates(m_symbol.Name(), m_period, 2, h, __KERNEL + 1);
         _l.CopyRates(m_symbol.Name(), m_period, 4, h, __KERNEL + 1);
         _c.CopyRates(m_symbol.Name(), m_period, 8, h, __KERNEL + 1);
         //Print(" inputs are: \n", _inputs);
         CNN.Set(_inputs);
         CNN.Pad();
         //Print(" padded inputs are: \n", CNN.inputs);
         CNN.Convolve();
         CNN.Activate();
         CNN.Pool();
         // targets as eventual price changes with each matrix a proxy for bullishness, bearishness, or whipsaw action
         // implying matrices for eventual:
         // high price changes
         // low price changes
         // close price changes,
         // respectively
         //
         // price changes in each column are over 1 bar, 2 bar and 3 bars respectively
         // & price changes in each row are over different weightings of the applied price with other applied prices
         // so high is: highs only(H); (Highs + Highs + Close)/3 (HHC); and (Highs + Close)/3 (HC)
         // while low is: lows only(L); (Lows + Lows + Close)/3 (LLC); and (Lows + Close)/3 (LC)
         // and close is: closes only(C); (Highs + Lows + Close + Close)/3 (HLCC); and (Highs + Lows + Close)/3 (HLC)
         //
         // assumptions here are:
         // large values in highs mean bullishness
         // large values in lows mean bearishness
         // and small magnitude in close imply a whipsaw market
         matrix _targets[];
         ArrayResize(_targets, __KERNEL_SIZES.Size());
         for(int i = 0; i < int(__KERNEL_SIZES.Size()); i++)
         {  _targets[i].Init(__KERNEL_SIZES[i], __KERNEL_SIZES[i]);
            //
            for(int j = 0; j < __KERNEL_SIZES[i]; j++)
            {  if(i == 0)// highs for 'bullishness'
               {  _targets[i][j][0] = _h[j] - _h[j + 1];
                  _targets[i][j][1] = ((_h[j] + _h[j] + _c[j]) / 3.0) - ((_h[j + 1] + _h[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _c[j]) / 2.0) - ((_h[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 1)// lows for 'bearishness'
               {  _targets[i][j][0] = _l[j] - _l[j + 1];
                  _targets[i][j][1] = ((_l[j] + _l[j] + _c[j]) / 3.0) - ((_l[j + 1] + _l[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_l[j] + _c[j]) / 2.0) - ((_l[j + 1] + _c[j + 1]) / 2.0);
               }
               else if(i == 2)// close for 'whipsaw'
               {  _targets[i][j][0] = _c[j] - _c[j + 1];
                  _targets[i][j][1] = ((_h[j] + _l[j] + _c[j] + _c[j]) / 3.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1] + _c[j + 1]) / 3.0);
                  _targets[i][j][2] = ((_h[j] + _l[j] + _c[j]) / 2.0) - ((_h[j + 1] + _l[j + 1] + _c[j + 1]) / 2.0);
               }
            }
            //
            //Print(" targets for: "+IntegerToString(i)+" are: \n", _targets[i]);
         }
         CNN.Get(_targets);
         CNN.Evolve(m_learning_rate);
      }
   }
   
        ...

}

Unsere dritte Ausgabematrix, die auch protokolliert, wie „flach“ die Märkte nach jedem Datenpunkt werden, wird dargestellt, indem wir uns wieder auf die Größe der Schlusskursänderungen über verschiedene Zeitspannen konzentrieren, und die verschiedenen Längen dieser Zeitspannen entsprechen den Größen, die bei der Messung der oben erwähnten Auf- oder Abwärtsbewegung verwendet werden. Die Erfassung dieser Zieldaten bei jedem neuen Balken bedeutet, dass unser Modell mit jedem neuen Balken trainiert wird, und auch dies ist nur ein Ansatz, denn man kann sich auch dafür entscheiden, dieses Training weniger häufig durchzuführen, z. B. monatlich oder vierteljährlich, wie oben erwähnt.

Nach jeder Trainingssitzung müssen wir jedoch eine Vorhersage darüber treffen, wie die Aussichten für Auf- und Abwärtsbewegungen angesichts des aktuellen Datenpunkts sein werden, und der Teil unseres Codes, der dies erledigt, wird weiter unten erläutert:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSignalCNN::GetOutput()
{  
        ...

        ...

   _index = 0;
   _h.CopyRates(m_symbol.Name(), m_period, 2, 0, __KERNEL + 1);
   _l.CopyRates(m_symbol.Name(), m_period, 4, 0, __KERNEL + 1);
   _c.CopyRates(m_symbol.Name(), m_period, 8, 0, __KERNEL + 1);
   for(int i = 0; i < m_input_size; i++)
   {  for(int j = 0; j < m_input_size; j++)
      {  if(_ma.CopyIndicatorBuffer(m_ma[_index].Handle(), 0, 0, __KERNEL + 1))
         {  _inputs[i][j] = _c[__KERNEL] - _ma[__KERNEL];
            _index++;
         }
      }
   }
   CNN.Set(_inputs);
   CNN.Pad();
   CNN.Convolve();
   CNN.Activate();
   CNN.Pool();
   double _long = 0.0, _short = 0.0;
   if(CNN.output[0].Median() > 0.0)
   {  _long = fabs(CNN.output[0].Median());
   }
   if(CNN.output[1].Median() < 0.0)
   {  _short = fabs(CNN.output[1].Median());
   }
   double _neutral = fabs(CNN.output[2].Median());
   if(_long+_short+_neutral == 0.0)
   {  return(0.0);
   }
   return((_long-_short)/(_long+_short+_neutral));
}

Da eine Matrix viele Datenpunkte enthält, ist es am besten, die jeweiligen Medianwerte der einzelnen Matrizen abzulesen, um ein Gefühl dafür zu bekommen, ob es sich um eine Auf- oder Abwärtsbewegung handelt. Für die Aufwärts-Matrix wünschen wir uns also einen großen positiven Wert, während wir für die Abwärts-Matrix uns einen sehr negativen Wert wünschen. Für unsere flache Marktmatrix benötigen wir die Größe dieses Medians, und je kleiner er ist, desto flacher werden die Märkte voraussichtlich sein.

Das Ergebnis der Funktion „GetOutput“ ist also ein Fließkommawert, der, wenn er unter 0,5 liegt, auf eine bevorstehende Abwärtsbewegung hindeutet, und wenn er über 0,5 liegt, auf eine Aufwärtsbewegung hinweist. Bei den Testläufen, die mit einem einschichtigen CNN mit einer 5 x 5-Eingabematrix und 3 3 x 3-Kernen durchgeführt wurden, das auch Padding verwendet, um Ausgabematrizen in der Größe von 3 x 3 für das Symbol EURJPY auf dem täglichen Zeitrahmen zu haben, hatten wir Ausgaben, die sehr nahe am 0,5-Wert plus oder minus lagen. Dies bedeutete, dass bei dieser Implementierung alles über 0,5 in der Bedingungsfunktion für einen Kauf der Wert 100 zugewiesen und alles unter 0,5 in der Bedingungsfunktion für einen Verkauf der Wert 100.

Berichte des Strategie-Testers

Die zusammengestellte Signalklasse wird über den MQL5-Assistenten zu einem Expert Advisor zusammengestellt, wobei die Richtlinien hier und hier umgesetzt werden. Beim Testen des EURJPY für das Jahr 2023 mit dem Tages-Zeitrahmen erhalten wir folgende Ergebnisse:

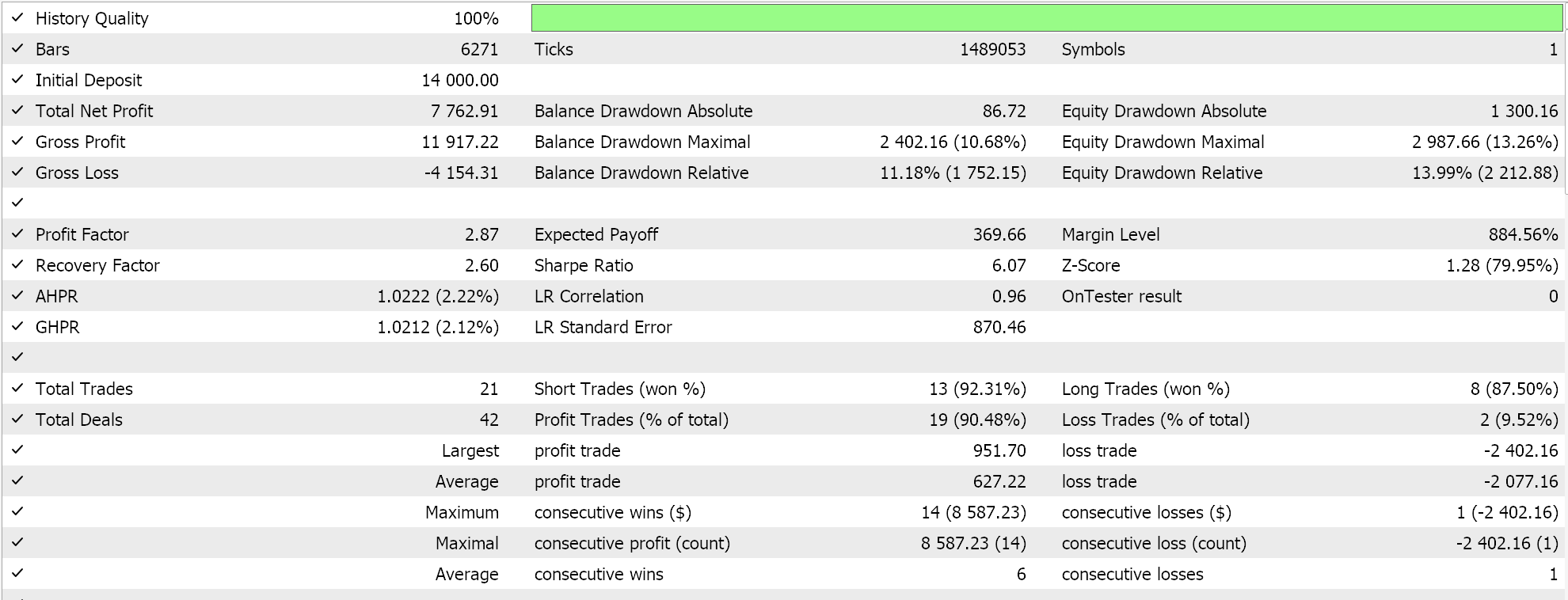
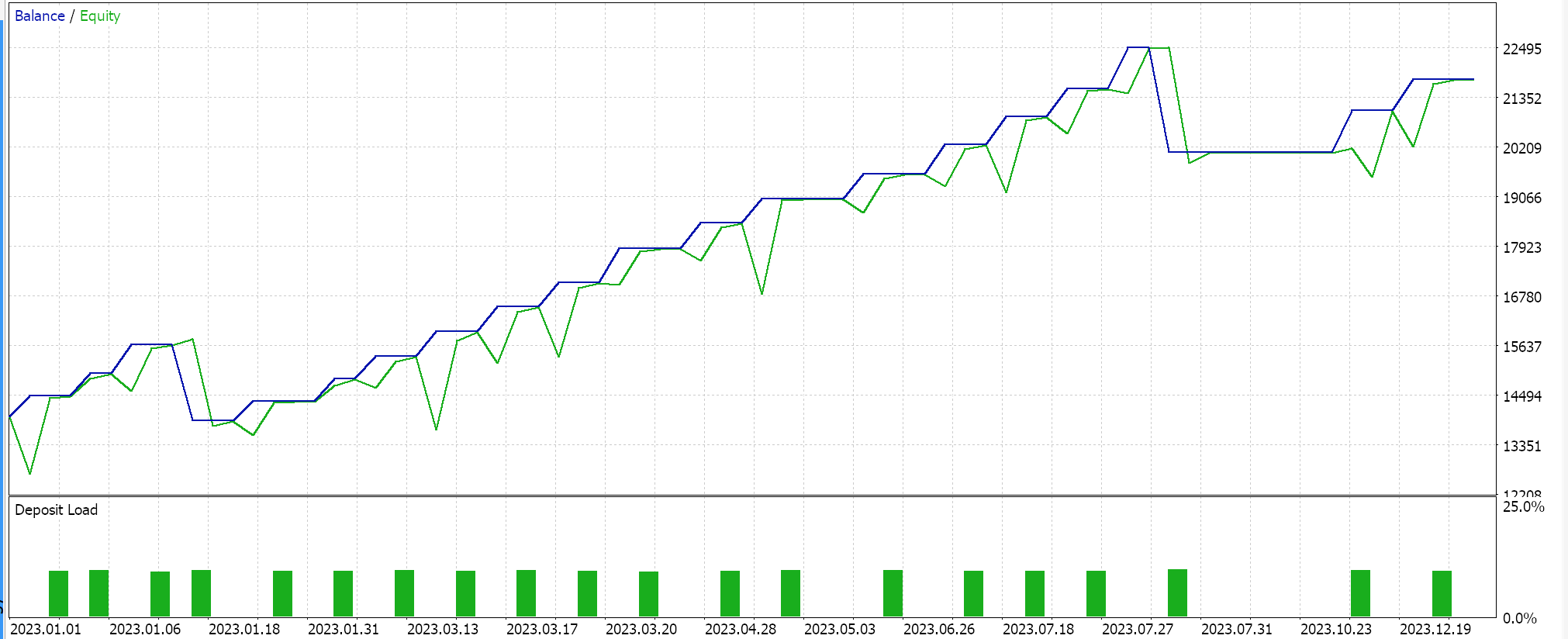
Diese Ergebnisse stammen aus den Bedingungen für Kauf und Verkauf, die entweder 0 oder 100 sind, da der Ausgangswert des Netzes nicht normalisiert ist. Der Versuch, die Netzwerkergebnisse zu normalisieren, sollte ein „empfindlicheres“ Ergebnis liefern, da die Schwellenwerte für das Öffnen und Schließen für eine Feinabstimmung offen sind.

Schlussfolgerung

Zusammenfassend lässt sich sagen, dass wir CNNs, einen maschinellen Lernalgorithmus, der häufig in der Bildverarbeitung eingesetzt wird, durch die Brille eines Händlers betrachtet haben. Wir haben die wichtigsten Schritte des Padding, des Vorwärtsdurchgangs, dem Aktivieren und Zusammenfassen in einer unabhängigen MQL5-Klassendatei untersucht und kodiert. Wir haben uns auch mit dem Trainingsprozess beschäftigt, indem wir uns mit der CNN-Rückwärtsfortpflanzung befasst und die Rolle der Faltung bei der Paarung ungleich großer Matrizen hervorgehoben haben. In diesem Artikel wurde ein einschichtiger CNN vorgestellt. Es gibt also eine Menge ungedecktes Land, den der Leser nicht nur durch das Stapeln dieser einschichtigen Klasse in einem Transformator (oder mehreren) erkunden kann, sondern auch durch die Betrachtung verschiedener Eingabedatentypen und Ziel-Ausgabedatensätze.