MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 18): Neuronale Architektursuche mit Eigenvektoren
Vorwort
Wir setzen die Serie über die Implementierung von MQL5-Assistenten fort, indem wir uns mit der Neurale Architektur-Suche befassen, wobei wir insbesondere auf die Rolle eingehen, die Eigenvektoren bei der Beschleunigung des Netzwerktrainings spielen können, um diesen Prozess effizienter zu gestalten. Neuronale Netze sind wohl die Anpassung einer Kurve an einen Datensatz, denn sie helfen dabei, einen formelhaften Ausdruck zu finden, der, wenn er auf Eingabedaten (x) angewendet wird, einen Zielwert (y) ergibt, genau wie eine quadratische Gleichung bei einer Kurve. Die x- und y-Datenpunkte können jedoch mehrdimensional sein und sind es oft auch, weshalb sich neuronale Netze einer großen Beliebtheit erfreuen. Das Prinzip, einen formelhaften Ausdruck zu finden, bleibt jedoch bestehen, weshalb neuronale Netze nur ein Mittel, aber nicht das einzige Mittel sind, um zu diesem Ziel zu gelangen.Einführung
Wenn wir uns dafür entscheiden, neuronale Netze zu verwenden, um die Beziehung zwischen einem Trainingsdatensatz und seinem Ziel zu definieren, wie es in diesem Artikel der Fall ist, dann müssen wir uns mit der Frage auseinandersetzen, welche Einstellungen dieses Netz verwenden wird. Es gibt verschiedene Arten von Netzen, und das bedeutet, dass auch die anwendbaren Designs und Einstellungen vielfältig sind. In diesem Artikel betrachten wir einen sehr einfachen Fall, der oft als mehrlagiges Perzeptron bezeichnet wird. Bei diesem Typ beschränken sich die Einstellungen auf die Anzahl der verborgenen Schichten und die Größe jeder verborgenen Schicht.
NAS kann in der Regel helfen, diese 2 Einstellungen und vieles mehr zu identifizieren. So sind beispielsweise selbst bei einfachen MLPs die Frage nach der zu verwendenden Aktivierungsart, die zu verwendenden Anfangsgewichte sowie die anfänglichen Verzerrungen allesamt Faktoren, die die Leistung und Genauigkeit des Netzes beeinflussen. Diese werden hier jedoch übergangen, da der Suchraum sehr umfangreich ist und die für die Vorwärts- und Rückwärtsdurchgang erforderlichen Rechenressourcen selbst bei einem mäßig großen Datensatz unerschwinglich wären.
Der Ansatz, der hier bei NAS verfolgt wird, ist jedoch insofern etwas neuartig, als er Eigenwerte und Eigenvektoren in einem Matrix-Suchraum verwendet, um die idealen Einstellungen zu ermitteln. Üblicherweise wird NAS entweder über verstärkendes Lernen, evolutionärer Algorithmus, Bayes’sche Optimierung oder zufällige Suche durchgeführt.
Jeder dieser herkömmlichen Ansätze beinhaltet das Training und die Kreuzvalidierung eines Netzes mit den gewählten Einstellungen (auch Architektur genannt), indem jede Leistung zu Vergleichszwecken mit dem Ziel verglichen wird. Was sie von anderen unterscheidet, ist, wie erschöpfend sie sind, oder ihr Ansatz, effizient zu sein, ohne im Suchraum erschöpfend zu sein. Das Verstärkungslernen beruht auf einem Algorithmus, der ein Netz im Suchraum auf der Grundlage seiner Einstellungen vorbewertet und diesen Algorithmus mit jeder Auswahl verbessert. Evolutionäre Algorithmen kreuzen oder kombinieren Netze innerhalb des Suchraums, um zu neuen Netzen zu gelangen, die sich zu Beginn nicht unbedingt im Suchraum befunden haben, indem sie ihre Leistung anhand eines Ziels bewerten. Die Bayes'sche Optimierung beruht wie die Zufallssuche darauf, dass der Suchraum in einem Array-Format sortiert ist oder dass die verschiedenen Netzeinstellungen als Koordinaten innerhalb des Suchraums aufgefasst werden können. Wenn beispielsweise ein zweidimensionaler Suchraum mit nur zwei Variablen, der Standardgröße einer verborgenen Schicht und der Anzahl der verborgenen Schichten, vorliegt, werden diese Optionen in dieser Matrix in aufsteigender (oder absteigender) Reihenfolge über die Diagonale in einem Format ähnlich dem nachstehenden Bild verteilt.
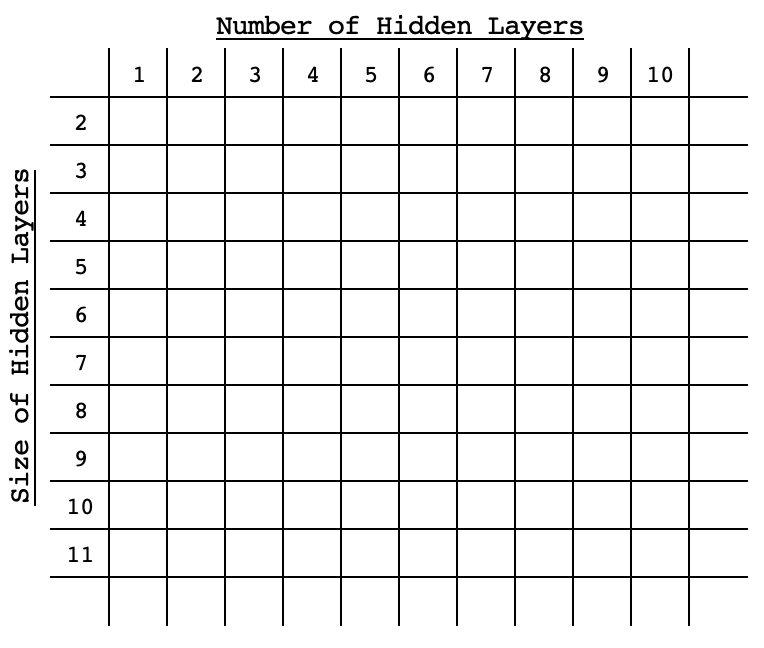
Auf diese Weise würde die Leistung eines jeden Netzes an seinen „Koordinaten“ im Raum festgemacht, sodass bei jeder weiteren Auswahl statistische Methoden angewandt würden, um die Wahl des Netzes zu verfeinern, das die beste Leistung erbringen würde. In diesem Artikel über Eigenvektoren und PCA, der vor ein paar Tagen geschrieben wurde, wurde ein Matrix-Suchraum verwendet, um einen idealen Wochentag und einen idealen Indikatorpreis für den Handel mit dem EURUSD im 4-Stunden-Zeitrahmen auszuwählen. Dies ergab sich aus einer Kreuzmatrix der Preisänderungen für jeden der 5-Wochen-Tage und in jedem der betrachteten angewandten Preise.
Wir werden für diesen Artikel einen ähnlichen Suchansatz wählen. Da das erschöpfende Training aller Netze ein Problem ist, das wir zu „lösen“ versuchen, werden unsere Benchmarks einfach die Werte des Vorwärtsdurchgangs von den Zielwerten der Netze sein, die mit Standardgewichten und Tendenzen initialisiert werden. Wir führen nur Vorwärtsläufe mit einer Datenstichprobe durch, und der Mittelwert für jede Einstellung dient als Benchmark in der Matrix.Die Rolle der Eigenvektoren im NAS
Die Eigenmatrix, die wir für NAS verwenden, ist der Einfachheit halber zweidimensional, wie oben bereits erwähnt. Wenn wir einen einfachen MLP betrachten, bei dem alle verborgenen Schichten die gleiche Größe haben, sind die einzigen beiden Fragen, die wir beantwortet haben wollen, wie viele verborgene Schichten der MLP haben sollte und wie groß jede versteckte Schicht ist.
Die möglichen Antworten auf diese Fragen lassen sich leicht in einer Matrix darstellen, in der die Standardleistung jedes Netzes für jede Kombination von Schichtgröße und Schichtnummer protokolliert wird. Die Netze unterscheiden sich in den Einstellungen, wie sie in der Matrixtabelle angegeben sind, ihre Eingangs- und Ausgangsschichten sind jedoch standardisiert. Für diesen Artikel werden wir eine Eingabeschicht der Größe 4 und eine Ausgabeschicht der Größe 1 verwenden. Wir betrachten ein gewöhnliches Szenario, bei dem wir den nächsten Schlusskurs auf der Grundlage der 4 letzten Schlusskurswerte prognostizieren.Das Testsymbol ist EURJPY für das Jahr 2022 auf dem 4-Stunden-Zeitrahmen. Das bedeutet, dass unsere Daten 4-Stunden-Schlusskurse für das Jahr 2022 sein werden. Beim „Training“ dieses Modells geht es lediglich darum, die mittlere Abweichung von den Zielwerten über das Jahr hinweg für alle Netzwerkeinstellungen zu protokollieren. Unsere Einstellungen reichen von einer verborgenen Schicht bis zu 10 verborgenen Schichten entlang der Matrixzeilen, während die Spalten die Größen der verborgenen Schichten von 2 bis 11 enthalten. Diese Testeinstellungen sind willkürlich, und da der vollständige Quellcode am Ende dieses Artikels beigefügt ist, kann der Leser ihn gerne nach seinen Wünschen anpassen.
Um es noch einmal zu wiederholen: Das „Training“ des Modells umfasst einen einzigen Vorwärtsdurchlauf von jedem der verfügbaren Netz, alle mit den standardmäßigen Standardgewichten und Tendenzen über das Jahr 2022, wobei jede Balkenprognose mit dem tatsächlichen Schlusskurs verglichen wird. Während dieses „Trainings“ findet kein Training durch Rückwärtsdurchgänge oder typisches Netztraining statt.
Wir verwenden eine Netzwerkklasse, die wir in diesem Artikel besprochen haben, um das MLP zu implementieren. Es wird einfach ein Integer-Array benötigt, dessen Größe die Gesamtzahl der Schichten definiert, wobei der Integer-Wert an jedem Index die Schichtgröße festlegt.
Obwohl dieser Artikel und diese Serie den MQL5-Assistenten hervorheben, wird das oben erwähnte „Training“ per Skript durchgeführt, wie es im letzten Artikel über Eigenvektoren der Fall war, und wir werden die Ergebnisse/Empfehlungen daraus verwenden, um eine Signalklasseninstanz zu kodieren, die mit einem aus dem Assistenten zusammengesetzten Expert Advisor getestet werden kann. Unser Test des zusammengestellten Expert Advisors wird das übliche Netztraining auf jedem Balken oder mit jedem neuen Datenpunkt haben. Das Ergebnis des Strategietesters für das empfohlene Netzwerk wird mit der schlechtesten Empfehlung als Kontrolle verglichen, sodass wir die These bewerten können, ob Eigenvektoren und Werte in NAS einfallsreich sein können.
Wenn wir jedoch rekapitulieren, was wir im letzten Artikel über Eigenvektoren und -werte behandelt haben, so liefert uns die verwendete Dimensionalitätsreduktion einen einzigen Vektor aus einer zu analysierenden Matrix. In unserem Fall wird also die protokollierte Leistung der einzelnen Netze, die wir in einer Matrix haben, auf einen Vektor reduziert. Im letzten Artikel wollten wir den Wochentag und den angewandten Kurs ermitteln, der den größten Teil der Varianz des Paares EURJPY über ein Jahr auf dem 4-Stunden-Zeitrahmen erfasst hat. Dies bedeutete, dass wir uns auf die Maximalwerte der Eigenvektoren innerhalb der projizierten Matrix konzentrierten, da diese am stärksten positiv mit unserem Ziel korrelierten.
In diesem Fall hat unsere Matrix jedoch Abweichungen von den Zielwerten aufgezeichnet, was bedeutet, dass wir in unserer Matrix den Fehlerfaktor jedes Netzes haben. Da wir zu Testzwecken das Netz mit dem geringsten Fehler verwenden wollen, wählen wir das Netz nach der Anzahl der Schichten und der Größe der einzelnen Schichten aus, und zwar nach den Minima der einzelnen Eigenvektoren, die aus der Projektionsmatrix ermittelt werden. Diese Vorverarbeitung wird, wie bereits erwähnt, per Skript abgewickelt und kann in 5 Abschnitte unterteilt werden, nämlich a) die Initialisierung der Netzwerke:
//initialise networks ArrayResize(__M.row, __SIZE); for(int r = 0; r < __SIZE; r++) { for(int c = 0; c < __SIZE; c++) { ArrayResize(__M.row[r].col, __SIZE); ArrayResize(__M.row[r].col[c].settings, 2 + __LEAST_LAYERS + r); ArrayFill(__M.row[r].col[c].settings, 0, __LEAST_LAYERS + r + 2, __LEAST_SIZE + c); __M.row[r].col[c].settings[0] = __INPUTS; __M.row[r].col[c].settings[__LEAST_LAYERS + r + 1] = __OUTPUTS; __M.row[r].col[c].n = new Cnetwork(__M.row[r].col[c].settings, __initial_weight, __initial_bias); } }
b) Benchmarking der Netze:
//benchmark networks int _buffer_size = (52*PeriodSeconds(PERIOD_W1))/PeriodSeconds(Period()); PrintFormat(__FUNCSIG__ + " buffered: %i", _buffer_size); if(_buffer_size >= __INPUTS) { for(int i = _buffer_size - 1; i >= 0; i--) { for(int r = 0; r < __SIZE; r++) { for(int c = 0; c < __SIZE; c++) { vector _in,_out; vector _in_new,_out_new,_in_old,_out_old; _in_new.CopyRates(Symbol(), Period(), 8, i + 1, __INPUTS); _in_old.CopyRates(Symbol(), Period(), 8, i + 1 + 1, __INPUTS); _out_new.CopyRates(Symbol(), Period(), 8, i, __OUTPUTS); _out_old.CopyRates(Symbol(), Period(), 8, i + 1, __OUTPUTS); _in = Norm(_in_new, _in_old); _out = Norm(_out_new, _out_old); __M.row[r].col[c].n.Set(_in); __M.row[r].col[c].n.Forward(); __M.row[r].col[c].benchmark += fabs(__M.row[r].col[c].n.output[0]-_out[0]); } } } }
c) Kopieren von Benchmarks in die Analysematrix:
//copy benchmarks to analysis matrix matrix _m; _m.Init(__SIZE, __SIZE); _m.Fill(0.0); for(int r = 0; r < __SIZE; r++) { for(int c = 0; c < __SIZE; c++) { _m[r][c] = __M.row[r].col[c].benchmark; } }
d) Normalisierung der Matrix und Generierung der Eigenvektoren und -werte:
//generating eigens PrintFormat(" for: %s, with: %s", Symbol(), EnumToString(Period())); matrix _z = ZNorm(_m); matrix _cov_col = _z.Cov(false); matrix _e_vectors; vector _e_values; _cov_col.Eig(_e_vectors, _e_values);
e) und schließlich die Interpretation der Eigenvektoren, um aus der Projektionsmatrix die ideale und die schlechteste Netzschichtenzahl und -größe zu ermitteln:
//interpreting the eigens from projection matrix _t = _e_vectors.Transpose(); matrix _p = _m * _t; vector _max_row = _p.Max(0); vector _max_col = _p.Max(1); string _layers[__SIZE]; for(int i=0;i<__SIZE;i++) { _layers[i] = IntegerToString(i + __LEAST_LAYERS)+" layer"; } double _nr_layers[]; _max_row.Swap(_nr_layers); //since network performance inversely relates to network deviation from target PrintFormat(" est. ideal nr. of layers is: %s", _layers[ArrayMinimum(_nr_layers)]); PrintFormat(" est. worst nr. of layers is: %s", _layers[ArrayMaximum(_nr_layers)]); string _sizes[__SIZE]; for(int i=0;i<__SIZE;i++) { _sizes[i] = "size "+IntegerToString(i + __LEAST_SIZE); } double _size_nr[]; _max_col.Swap(_size_nr); PrintFormat(" est. ideal size of layers is: %s", _sizes[ArrayMinimum(_size_nr)]); PrintFormat(" est. worst size of layers is: %s", _sizes[ArrayMaximum(_size_nr)]);Die Ausführung des obigen Skripts in einem Suchraum von 100 läuft einige Sekunden lang, was ein gutes Zeichen ist. Man könnte jedoch argumentieren, dass der Raum nicht umfassend genug ist, und das ist ein gültiges Argument, weshalb das beigefügte Skript die Größenattribute des Raums als globale Variable enthält, die der Nutzer ändern kann, um etwas sorgfältigeres zu erstellen. Außerdem brauchten wir eine Struktur für die Handhabung von Netzwerkinstanzen und deren Benchmarks. Dies ist in der Kopfzeile wie folgt definiert:
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ struct Scol { int settings[]; Cnetwork *n; double benchmark; Scol() { ArrayFree(settings); benchmark = 0.0; } ~Scol(){ delete n; }; }; struct Srow { Scol col[]; Srow(){}; ~Srow(){}; }; struct Smatrix { Srow row[]; Smatrix(){}; ~Smatrix(){}; }; Smatrix __M; //matrix of networks
Testen des Expert Advisors
Wenn wir das obige Skript ausführen, das bei der Suche nach den idealen Netzwerkeinstellungen hilft, erhalten wir die folgenden Protokolle, wenn sie mit EURJPY auf dem 4-Stunden-Zeitrahmen verbunden sind:
2024.05.03 18:22:39.336 nas_1_changes (EURJPY.ln,H4) void OnStart() buffered: 2184 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) for: EURJPY.ln, with: PERIOD_H4 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal nr. of layers is: 6 layer 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst nr. of layers is: 9 layer 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. ideal size of layers is: size 2 2024.05.03 18:22:42.209 nas_1_changes (EURJPY.ln,H4) est. worst size of layers is: size 4Die empfohlenen Netzwerkeinstellungen gelten für ein Netzwerk mit 6 Schichten, wobei jede Schicht die Größe 2 hat! Nebenbei bemerkt wurden die Zieldaten (y-Werte), die zum Benchmarking der Matrix verwendet wurden, auf einen Wert zwischen 0,0 und 1,0 normiert, wobei ein Wert von 0,5 bedeutet, dass die resultierende Preisänderung 0 war, während ein Wert unter 0,5 auf einen resultierenden Preisrückgang und ein Wert über 0,5 auf einen Preisanstieg hinweisen würde. Der Code für die Funktion, die diese Normalisierung vornimmt, ist unten aufgeführt:
//+------------------------------------------------------------------+ //| Normalization (0.0 - 1.0, with 0.5 for 0 | //+------------------------------------------------------------------+ vector Norm(vector &A, vector &B) { vector _n; _n.Init(A.Size()); if(A.Size() > 0 && B.Size() > 0 && A.Size() == B.Size() && A.Min() > 0.0 && B.Min() > 0.0) { int _size = int(A.Size()); _n.Fill(0.5); for(int i = 0; i < _size; i++) { if(A[i] > B[i]) { _n[i] += (0.5*((A[i] - B[i])/A[i])); } else if(A[i] < B[i]) { _n[i] -= (0.5*((B[i] - A[i])/B[i])); } } } return(_n); }Diese Normalisierung war notwendig, weil angesichts des kleinen Datensatzes, den wir in Betracht ziehen, das Training eines Netzwerks zur Entwicklung von Gewichten und Verzerrungen, die in der Lage sind, negative und positive Werte als Ausgaben zu verarbeiten, sehr große Datensätze, komplexere Netzwerkeinstellungen und sicherlich mehr Rechenressourcen erfordern würde. Beide Szenarien werden in diesem Artikel nicht untersucht, können aber in Erwägung gezogen werden, wenn sie für machbar gehalten werden. Mit unserer Normalisierung sind wir also in der Lage, mit bescheidenen Trainings- und Datensätzen sensible Ergebnisse aus unserem Netzwerk zu erhalten.
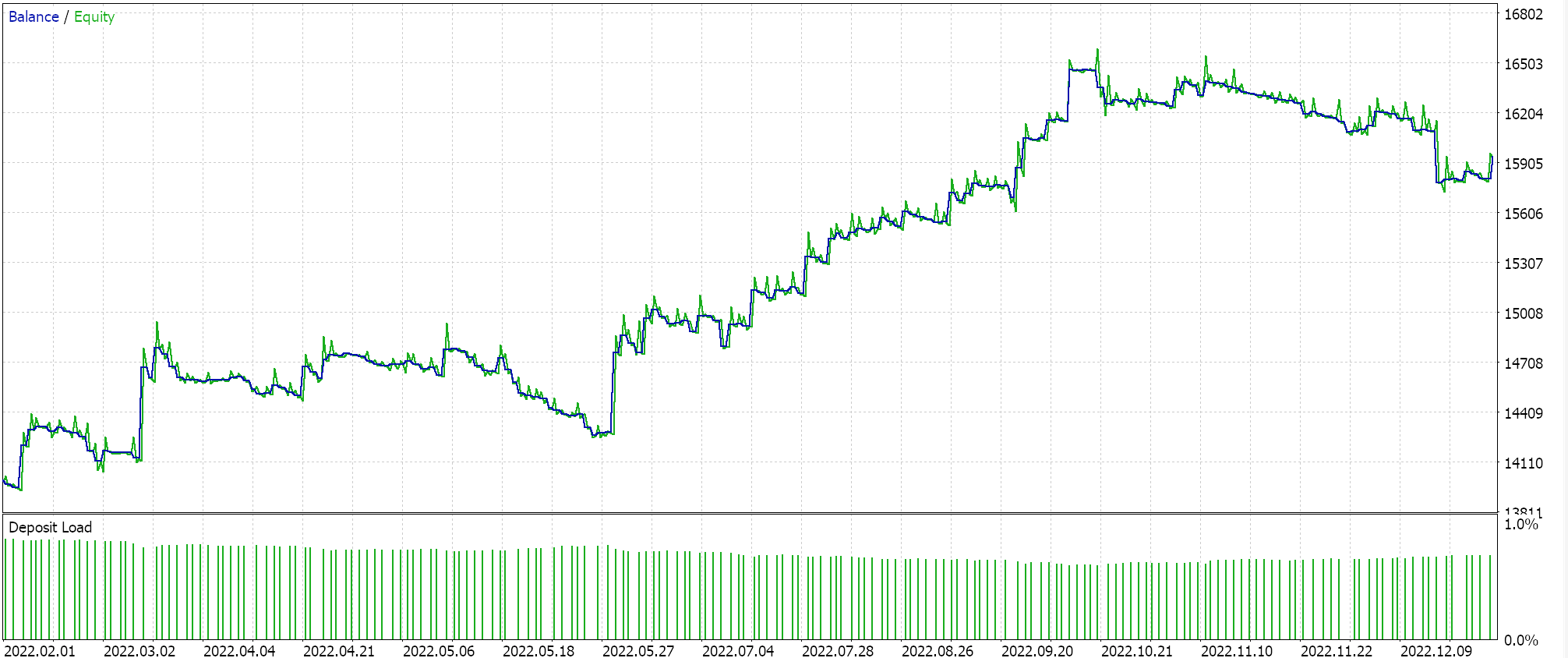
Wenn wir Tests mit der empfohlenen Netzwerkkonfiguration von 6 Schichten bei einer Größe von 2 durchführen, erhalten wir den unten dargestellten Bericht und die Equity-Kurve:
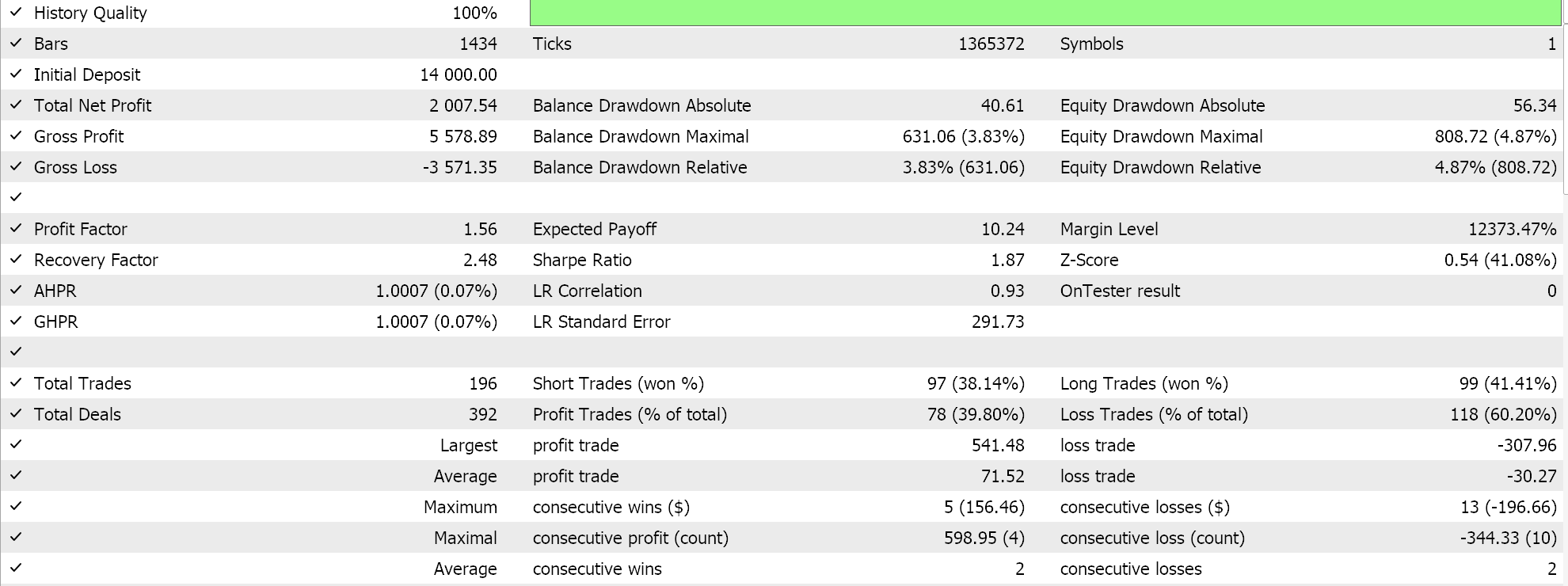
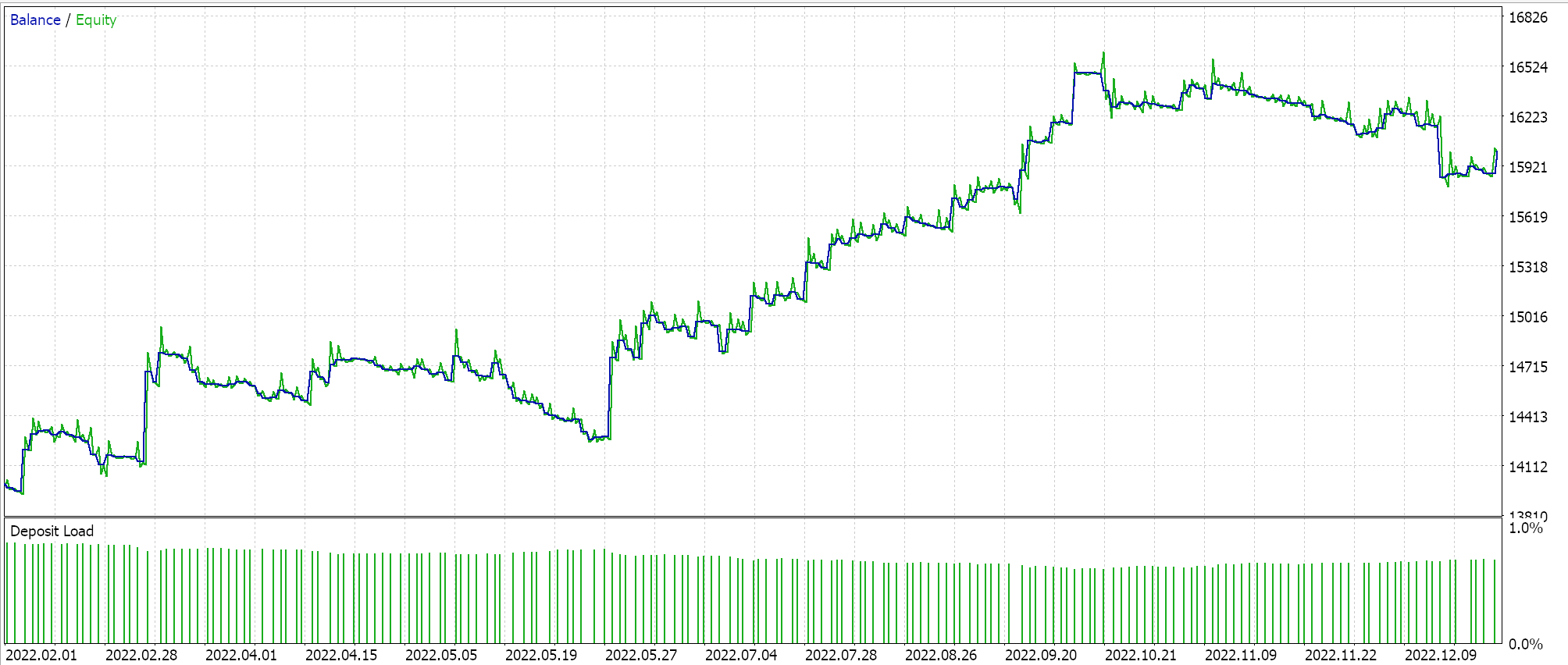
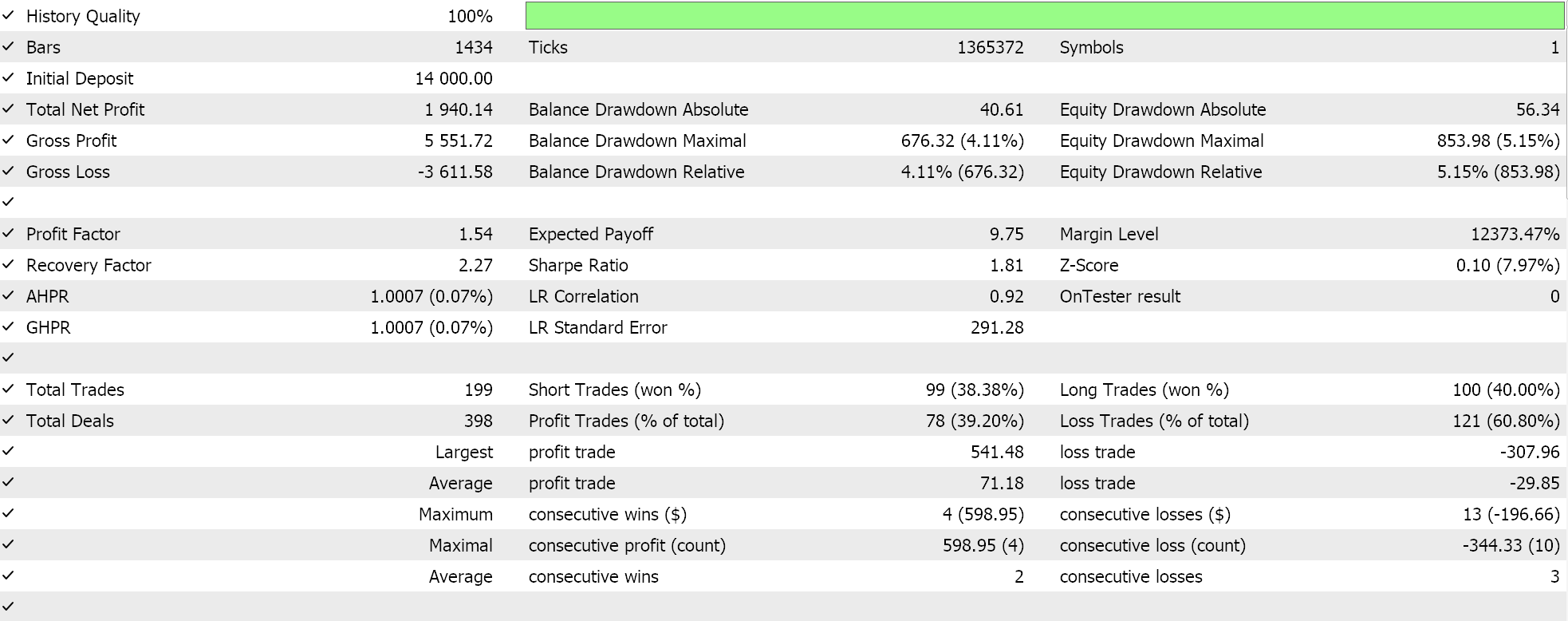
Neuronale Netze können durch Redundanz in ihrer Kapazität leiden, wobei verschiedene Einstellungen (oder Architekturen) die gleichen zugrunde liegenden Beziehungen in den Daten lernen, obwohl sie unterschiedliche Strukturen haben. Es sei daran erinnert, dass die Netze in beiden Durchgängen trainiert wurden, sodass sowohl die Gewichte als auch die Verzerrungen verbessert wurden. Während also die Eigenvektoren mit der größeren Varianz einen breiteren Satz von Merkmalen erfassen und die mit der geringeren Varianz sich auf Details konzentrieren, können beide Netzkonfigurationen die Grundlagen für eine gute Leistung erlernen.
Während die Anzahl der verborgenen Schichten und ihre Größe in dieser Situation ausschlaggebend für die Leistung des Netzes sind, könnten auch andere Faktoren eine Rolle spielen, wie die Wahl der Aktivierungsfunktion (wir verwenden Soft Plus) oder die verwendete Lernrate. Jeder einzelne oder alle diese Faktoren könnten einen unverhältnismäßig großen Einfluss auf die Leistung der Netze gehabt haben.
Eine andere mögliche Erklärung könnte in der Begrenzung des Suchraums liegen. Wir haben 10 verschiedene Schichtgrößen und 10 verschiedene Optionen für verborgene Schichten in Betracht gezogen, die sich alle zu einer rechteckigen Form entwickeln. Dies hätte bei der Abbildung dieses speziellen Datensatzes die möglichen Netzwerkkombinationen so einschränken können, dass eine dieser wenigen Optionen leicht zur gewünschten Lösung führen könnte.
Schlussfolgerung
Wir haben gesehen, wie NAS unorthodox mit Eigenvektoren und -werten durchgeführt werden kann, wenn nur eine bescheidene Anzahl von Konfigurationen für neuronale Netze zur Auswahl steht. Dieser Prozess kann skaliert und vielleicht sogar erweitert werden, um andere Faktoren einzubeziehen oder zu berücksichtigen, die nicht Teil der Analysematrix waren, indem die Form der verborgenen Schicht (wir haben nur Rechtecke betrachtet) oder sogar Aktivierungsarten hinzugefügt werden. Letzteres ist am einfachsten zu einer Matrix wie der in diesem Artikel betrachteten hinzuzufügen, da es nur 2 - 3 Haupttypen von Aktivierungen gibt und dies einfach bedeuten könnte, die Anzahl der Spalten zu verdreifachen und gleichzeitig die Anzahl der Zeilen zu erweitern, um sicherzustellen, dass eine quadratische Matrix erhalten bleibt, eine Voraussetzung für die Eigenvektoranalyse. Die Hinzufügung der Form der verborgenen Schicht könnte in ähnlicher Weise erfolgen, wenn die verschiedenen Formen, die berücksichtigt werden sollen, in klaren Typen aufgezählt werden. Anmerkungen:
Die beigefügten Dateien können verwendet werden, indem Sie die Anleitungen zum Bau des Expert Advisor dem Wizard befolgen, die Sie hier und hier finden.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/14845
 Aufbau eines Modells aus Kerzen, Trend und Nebenbedingungen (Teil 3): Erkennung von Trendänderungen bei der Verwendung dieses Systems
Aufbau eines Modells aus Kerzen, Trend und Nebenbedingungen (Teil 3): Erkennung von Trendänderungen bei der Verwendung dieses Systems
 Modifizierter Grid-Hedge EA in MQL5 (Teil IV): Optimierung der einfachen Grid-Strategie (I)
Modifizierter Grid-Hedge EA in MQL5 (Teil IV): Optimierung der einfachen Grid-Strategie (I)
 Klassische Strategien neu interpretieren: Rohöl
Klassische Strategien neu interpretieren: Rohöl
 Scheinkorrelationen in Python
Scheinkorrelationen in Python
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.