知っておくべきMQL5ウィザードのテクニック（第20回）：関数同定問題

はじめに

MQL5ウィザードには、コード化されたEAに付随する標準的な取引関数やクラスのライブラリがあるだけでなく、カスタムクラスの実装と並行して使用できる代替の取引シグナルやメソッドも用意されています。

関数同定問題は、回帰分析の変種で、その伝統的ないとこである古典的回帰よりも「白紙の状態」から始まります。これを説明するのに最も適した方法は、データ点の集合に最もよく合う直線の傾きとy切片を求める典型的な回帰問題を考えることでしょう。

source

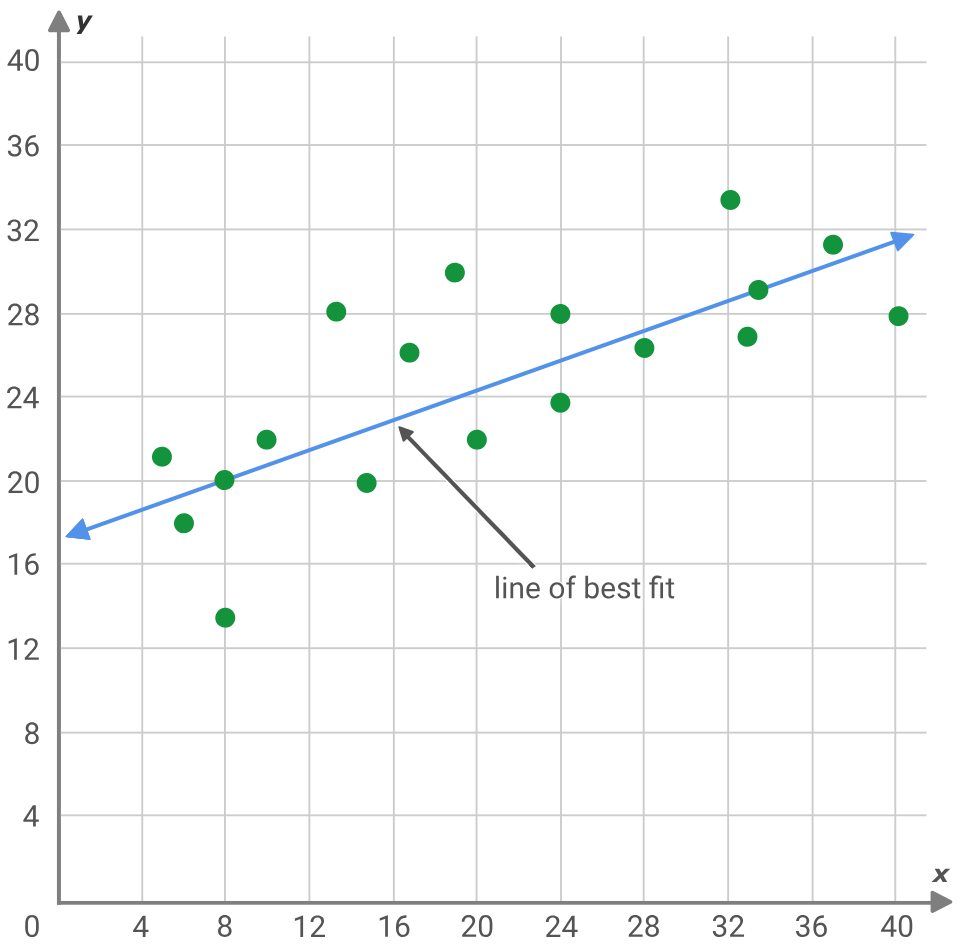
y = mx + c

ここで

• yは予測値と依存値
• mは最良の適合の直線の傾き
• cはy切片
• xは独立変数

上記の問題は、データ点が理想的には直線に合うことを前提としており、そのためにy切片と傾きの解を求めます。あるいは、ニューラルネットワークも同様に、要するに、あらかじめ設定されたアーキテクチャー（層の数、層のサイズ、活性化のタイプなど）を持つネットワークを想定して、2つのデータセット（別名モデル）を最もよく対応付ける二次方程式を見つけようとします。これらのアプローチや同様のアプローチにはすべて、最初からこのバイアスがあり、ディープラーニングや経験からこれが正当化される場合もありますが、関数同定問題では、無作為に割り当てられたノードから開始しながら、2 つのデータセットをマッピングする記述モデルを式木として構築できます。

これは理論的には、従来の方法では見過ごされてしまうような複雑な市場の関係を明らかにすることに長けています。関数同定問題（Symbolic Regression：SR）の他の推定的アプローチに対する利点は、まとめれば、新しい市場データや変化する状況に適応しやすくなることだと言えます。これは、各分析がバイアスなしで開始され、最適化によって訓練/改善される式木ノードの無作為割り当てがおこなわれるため可能です。また、これだけでなく、変数xのみがy値に影響を与えると想定されていた上記の線形回帰の例とは異なり、複数のデータソースを使用することもできます。適応性とは、yの値をよりよく定義する式木において、単独のx以外のより多くの変数が組み合わされることです。式木は、線形関係のみがとらえられる線形回帰（上記の通り）とは対照的に、より複雑な関係をとらえることができるように定義された係数を持つ一連のシーケンスでデータを処理する系統的なノードを開発することによって、訓練データに対してより多くの制御をおこなうため、より柔軟です。たとえyがxにのみ依存していたとしても、この関係は線形ではなく二次関数である可能性があり、SRでは遺伝的最適化からこれを確立できます。そして最後に、構築された式木は、入力データが実際に目標にどのようにマッピングされるかを本質的により正確な言葉で「説明」するため、説明可能性を導入することで、研究対象のデータセット間のブラックボックス モデルの関係を解明できます。説明可能性はほとんどの方程式に内在していますが、SRが追加するのは、より複雑な式から遺伝的進化をおこない、その最良適合スコアが優れていれば、より単純な式に向かって進化することによる「単純さ」でしょう。

定義

SRは、独立変数と従属（または予測）変数の間のマッピングモデルを式木（英語）として表現します。図式的な表現は下のようになります。

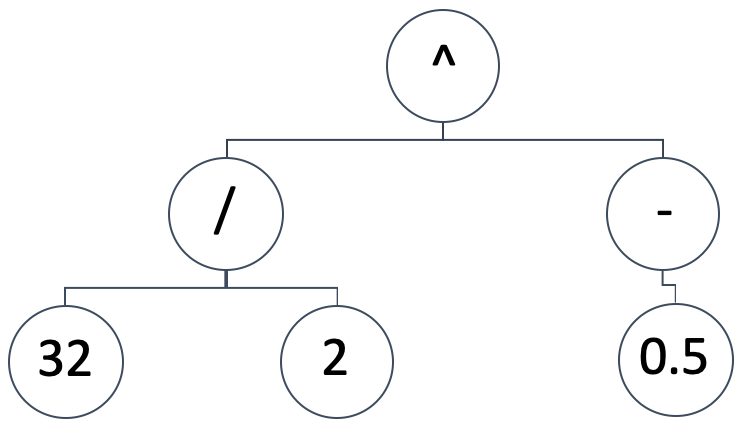
これは次の数式を意味します。

(32/2) ^ (-0.5)

これは0.25です。式木はさまざまな形やデザインを取ることができますが、無作為で偏りのない構成から始めるというSRの基本的な前提は守りたいものです。同時に、最初に生成されたどのようなサイズの式木に対しても遺伝的最適化を実行できるようにする必要があり、その結果（または最良の適合の指標）を異なるサイズの式木と比較できるようにする必要があります。

これを実現するために、遺伝的最適化を「エポック」単位で実行します。機械学習の用語では、ニューラルネットワークのように学習セッションをバッチ処理するときにエポックを使用するのが一般的ですが、ここでは、各実行が同じサイズの式木を使用する、異なる遺伝的最適化の反復を指す用語として使用します。なぜ各エポックでサイズを維持するのでしょうか。遺伝的最適化ではクロスオーバーを使用するため、式木の長さが異なると、プロセスが不必要に複雑になります。では、どのようにして初期式木を無作為に保つのでしょう。各エポックに特定の大きさの木を表現させることによってです。こうすることで、すべてのエポックにわたって最適化し、すべてのエポックを同じベンチマークまたは最良の適合指標と比較します。

MQL5のベクトル/行列データ型で使用可能な適応度関数測定オプションは回帰および 損失です。これらの組み込み関数は、訓練データセットからの理想的な出力を1つのベクトルとして、同じくベクトル形式でテストされた式木によって生成された出力と比較するため、適用可能です。つまり、テストデータセットが長ければ長いほど、あるいは大きければ大きいほど、比較するベクトルも大きくなります。このような大規模なデータセットは、理想的なゼロの最良の適合値を達成することが非常に困難であることを意味するため、各エポックにおいて十分な最適化世代を許容する必要があります。

最良の適合スコアに基づいて最良の式木に到達する際、最も長い（したがって最も複雑な）式木から、最も単純で、おそらく「説明」するのが最も簡単な式木まで評価します。式木の書式はさまざまですが、ここでは基本的なものにとどめます。

coeff, x-exponent, sign, coeff, x-exponent, sign, …

ここで

• coeffはxの係数
• x-exponentはxの冪乗
• signは式中の演算子で、-、+、*、/のいずれか

式の最後の値が演算子になることはありません。なぜなら、そのようなsignは何にもつながらないからです。つまり、どの式でもsignの数は常にx値の数よりも少なくなります。このような式のサイズは、1つのx係数と指数だけがある（演算子なし）1から、16までの範囲になります（ここでは厳密にテストする目的で16を使用）。前述したように、この最大サイズは遺伝的最適化で使用されるエポック数と直接相関しています。これは単純に、16単位の長さの式木で理想的な式の最適化を開始することを意味します。この16単位は、前述のように15のsignを意味し、「各単位」は単にのx係数と指数です。

そのため、最初の無作為な式木を選択する際、式木が1単位を超えた長さで、式を終了していない場合、つまり1単位に続く式木がある場合は、常に無作為な2つの数の「ノード」と無作為な演算子「ノード」の形式に従います。そのためのコードを下に示します。

//+------------------------------------------------------------------+
// Get Expression Tree
//+------------------------------------------------------------------+
void CSignalSR::GetExpressionTree(int Size, string &ExpressionTree[])
{  if(Size < 1)
   {  return;
   }
   ArrayFree(ExpressionTree);
   ArrayResize(ExpressionTree, (2 * Size) + Size - 1);
   int _digit[];
   GetDigitNode(2 * Size, _digit);
   string _sign[];
   if(Size >= 2)
   {  GetSignNode(Size - 1, _sign);
   }
   int _di = 0, _si = 0;
   for(int i = 0; i < (2 * Size) + Size - 1; i += 3)
   {  ExpressionTree[i] = IntegerToString(_digit[_di]);
      ExpressionTree[i + 1] = IntegerToString(_digit[_di + 1]);
      _di += 2;
      if(Size >= 2 && _si < Size - 1)
      {  ExpressionTree[i + 2] = _sign[_si];
         _si ++;
      }
   }
}

上記の関数は、式木のサイズが少なくとも1であることを確認することから始めます。このテストに合格したら、次に木の実際の配列サイズを決定する必要があります。以上から、木は係数、指数、そして必要に応じて演算子という形式をとることがわかりました。これは、サイズsが与えられると、各サイズ単位が係数と指数値を持たなければならないので、その木の桁ノードの総数は2×sになることを意味します。これらのノードは、getDigitNode関数によって無作為に選択されます。

//+------------------------------------------------------------------+
// Get Digit
//+------------------------------------------------------------------+
void CSignalSR::GetDigitNode(int Count, int &Digit[])
{  ArrayFree(Digit);
   ArrayResize(Digit, Count);
   for(int i = 0; i < Count; i++)
   {  Digit[i] = __DIGIT_NODE[MathRand() % __DIGITS];
   }
}

数字は静的なグローバル数字ノード配列から無作為に選択されます。演算子ノードは、木のサイズが1を超えるかどうかで変わります。もしサイズが1の木があれば、x係数とその指数しか入る余地がないため、演算子は適用されません。もし2以上ならば、演算子ノードの数は入力サイズから1を引いた数に相当します。式の演算子スロットを埋める演算子を無作為に選択する関数を以下に示します。

//+------------------------------------------------------------------+
// Get Sign
//+------------------------------------------------------------------+
void CSignalSR::GetSignNode(int Count, string &Sign[])
{  ArrayFree(Sign);
   ArrayResize(Sign, Count);
   for(int i = 0; i < Count; i++)
   {  Sign[i] = __SIGN_NODE[MathRand() % __SIGNS];
   }
}

演算子は、数字ノード配列と同様、演算子ノード配列から無作為に選択されます。この配列はいろいろなバリエーションがありますが、ここでは簡潔にするため、+と-演算子だけに対応するように短縮しています。これに「*」（乗算）記号を追加することができますが、ゼロ除算を扱わないため、特に「/」除算記号が省略されています。ゼロ除算は、遺伝的最適化を開始し、クロスなどをおこなわなければならなくなると、かなり厄介なことになります。ゼロ除算の問題が最適化の結果をゆがめる可能性があります。適切に対処できる限り、この問題はご自由に探求してください。

無作為な式木の初期集団ができたら、その特定のエポックについて遺伝的最適化プロセスを開始することができます。注目すべきは、式木情報の保存とアクセスに使用しているシンプルな構造体です。本質的には、サイズ変更の柔軟性が追加された文字列行列です（doubleを処理する行列などの標準データ型によって提供されるべき機能）。これも以下に掲載します。

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
struct Stree
{  string   tree[];

   Stree()
   {  ArrayFree(tree);
   };
   ~Stree() {};
};
struct Spopulation
{  Stree   population[];

   Spopulation() {};
   ~Spopulation() {};
};

この構造体を使用して、最適化世代ごとに個体群を作成し、追跡しています。各エポックは設定された世代数を用いて最適化をおこないます。すでに述べたように、テストデータセットが大きければ大きいほど、より多くの最適化世代が必要になります。反面、テストデータが少なすぎると、テストデータセットの根本的なパターンではなく、ほとんどがホワイトノイズに由来する式木になってしまう可能性があるため、バランスを取る必要があります。

各世代で最適化を開始したら、各木の適合度を得る必要があります。複数の木があるので、これらの適合度スコアはベクトルに記録されます。このベクトルを手に入れたら、次のステップは、この木が特定のエポック内の各世代ごとに洗練され、狭められていくと仮定し、この母集団を刈り込むための閾値を設定することです。この閾値「_fit」はパーセンタイルマーカーとして機能する整数入力パラメータに基づいています。パラメータの範囲は0から100までです。

この初期母集団から別のサンプル母集団を作成し、適合度が閾値以下の式木のみを選択します。上記で使用した適合度スコアを計算する関数は、以下のようなリストとなります。

//+------------------------------------------------------------------+
// Get Fitness
//+------------------------------------------------------------------+
double CSignalSR::GetFitness(matrix &XY, vector &Y, string &ExpressionTree[])
{  Y.Init(XY.Rows());
   for(int r = 0; r < int(XY.Rows()); r++)
   {  Y[r] = 0.0;
      string _sign = "";
      for(int i = 0; i < int(ExpressionTree.Size()); i += 3)
      {  double _yy = pow(XY[r][0], StringToDouble(ExpressionTree[i + 1]));
         _yy *= StringToDouble(ExpressionTree[i]);
         if(_sign == "+")
         {  Y[r] += _yy;
         }
         else if(_sign == "-")
         {  Y[r] -= _yy;
         }
         else if(_sign == "/" && _yy != 0.0)//un-handled
         {  Y[r] /= _yy;
         }
         else if(_sign == "*")
         {  Y[r] *= _yy;
         }
         else if(_sign == "")
         {  Y[r] = _yy;
         }
         if(i + 2 < int(ExpressionTree.Size()))
         {  _sign = ExpressionTree[i + 2];
         }
      }
   }
   return(Y.RegressionMetric(XY.Col(1), m_regressor));
   //return(_y.Loss(XY.Col(1),LOSS_MAE));
}

適合度取得関数は、入力データセット行列XY」を受け取り、行列のx列に着目して（入力と出力の両方に1次元データを使用しています）、入力式木の予測値を計算します。入力行列には複数行のデータがあるため、各行（最初の列）のx値に基づいて投影がおこなわれ、各行のすべての投影がベクトルYに格納されます。すべての行が処理された後、このベクトルYは、回帰内蔵関数または損失関数のいずれかを使用して、2列目の実際の値と比較されます。回帰を選択し、回帰指標として二乗平均平方根誤差を用います。

この値の大きさが、入力された式木の適合度値となります。小さければ小さいほど適合度が増します。各サンプル母集団についてこの値を得たら、まずサンプルサイズが偶数かどうかを確認する必要があります。次の段階ではこれらのツリーを交差し、生成された交差がペアで追加されるため、サイズは均等である必要があります。また、各世代でサンプリングするときにのみ集団が削減されるため、それらは親集団（サンプル）と一致する必要があります。サンプル内の式木の交差は、インデックス選択によって無作為におこなわれます。交差を担当する関数は以下の通りです。

//+------------------------------------------------------------------+
// Set Crossover
//+------------------------------------------------------------------+
void CSignalSR::SetCrossover(string &ParentA[], string &ParentB[], string &ChildA[], string &ChildB[])
{  if(ParentA.Size() != ParentB.Size() || ParentB.Size() == 0)
   {  return;
   }
   int _length = int(ParentA.Size());
   ArrayResize(ChildA, _length);
   ArrayResize(ChildB, _length);
   int _cross = 0;
   if(_length > 1)
   {  _cross = rand() % (_length - 1) + 1;
   }
   for(int c = 0; c < _cross; c++)
   {  ChildA[c] = ParentA[c];
      ChildB[c] = ParentB[c];
   }
   for(int l = _cross; l < _length; l++)
   {  ChildA[l] = ParentB[l];
      ChildB[l] = ParentA[l];
   }
}

この関数は、まず2つの式の親が同じサイズであること、そして親が0でないことを確認します。条件が満たされた場合、2つの出力子配列は親の長さに合わせてサイズ変更され、交差の点が選択されます。この交差も無作為であり、親のサイズが1以上の場合にのみ有効です。交差の点が設定されると、2つの親の値が入れ替わり、2つの子の配列に出力されます。ここで、長さのマッチングが便利です。例えば、もし長さが違っていたら、数字と演算子が入れ替わるケースを処理する（あるいは避ける）ために、余計なコードが必要になるからです。すべてのサイズをそれぞれのエポックで独立してテストし、最適な適合度を得ることができるのであれば、明らかに不必要な複雑さです。

交差を終えたら、子供たちに突然変異を起こすかもしれません。「かも」というのは、これらの突然変異を行うために5%の確率閾値を使用しているためです。突然変異は保証されていませんが、遺伝的最適化プロセスの一部です。次に、この新しい交差集団をコピーして、最初にサンプリングした集団に上書きし、マーカーとして、この新しい交差集団から得られた最良の式木の最良の適合スコアを記録します。記録されたスコアは、最適な木を決定するためだけでなく、まれに値がゼロになった場合に最適化を中止するためにも使用します。

カスタムシグナルクラス

シグナルクラスを開発する際の主なステップは、この連載を通じてこれまでのカスタムシグナルクラスでおこなってきたことと大きくは変わりません。まず、モデル用のデータセットを準備する必要があります。これは、上で見た適合度を求める関数のXY入力行列を埋めるデータです。これはまた、上で説明したすべてのステップを統合するGetBestTree関数の入力でもあります。この関数のソースコードを以下に示します。

//+------------------------------------------------------------------+
// Get Best Fit
//+------------------------------------------------------------------+
void CSignalSR::GetBestTree(matrix &XY, vector &Y, string &BestTree[])
{  double _best_fit = DBL_MAX;
   for(int e = 1 + m_epochs; e >= 1; e--)
   {  Spopulation _p;
      ArrayResize(_p.population, m_population);
      int _e_size = 2 * e;
      for(int p = 0; p < m_population; p++)
      {  string _tree[];
         GetExpressionTree(e, _tree);
         _e_size = int(_tree.Size());
         ArrayResize(_p.population[p].tree, _e_size);
         for(int ee = 0; ee < _e_size; ee++)
         {  _p.population[p].tree[ee] = _tree[ee];
         }
      }
      for(int g = 0; g < m_generations; g++)
      {  vector _fitness;
         _fitness.Init(int(_p.population.Size()));
         for(int p = 0; p < int(_p.population.Size()); p++)
         {  _fitness[p] = GetFitness(XY, Y, _p.population[p].tree);
         }
         double _fit = _fitness.Percentile(m_fitness);
         Spopulation _s;
         int _samples = 0;
         for(int p = 0; p < int(_p.population.Size()); p++)
         {  if(_fitness[p] <= _fit)
            {  _samples++;
               ArrayResize(_s.population, _samples);
               ArrayResize(_s.population[_samples - 1].tree, _e_size);
               for(int ee = 0; ee < _e_size; ee++)
               {  _s.population[_samples - 1].tree[ee] = _p.population[p].tree[ee];
               }
            }
         }
         if(_samples % 2 == 1)
         {  _samples--;
            ArrayResize(_s.population, _samples);
         }
         if(_samples == 0)
         {  break;
         }
         Spopulation _g;
         ArrayResize(_g.population, _samples);
         for(int s = 0; s < _samples - 1; s += 2)
         {  int _a  = rand() % _samples;
            int _b  = rand() % _samples;
            SetCrossover(_s.population[_a].tree, _s.population[_b].tree, _g.population[s].tree, _g.population[s + 1].tree);
            if (rand() % 100 < 5)   // 5% chance
            {  SetMutation(_g.population[s].tree);
            }
            if (rand() % 100 < 5)
            {  SetMutation(_g.population[s + 1].tree);
            }
         }
         // Replace old population
         ArrayResize(_p.population, _samples);
         for(int s = 0; s < _samples; s ++)
         {  for(int ee = 0; ee < _e_size; ee++)
            {  _p.population[s].tree[ee] = _g.population[s].tree[ee];
            }
         }
         // Print best individual
         for(int s = 0; s < _samples; s ++)
         {  _fit = GetFitness(XY, Y, _p.population[s].tree);
            if (_fit < _best_fit)
            {  _best_fit = _fit;
               ArrayCopy(BestTree,_p.population[s].tree);
            }
         }
      }
   }
}

入力行列は、1次元のx値と1次元のy値のペアです。独立変数と従属変数。Y入力ベクトルが行列に変換され、入力ベクトルの各x値、出力ベクトルの各y値に対する式木に変換されることで、多次元性にも対応できます。これらの式木は、行列や高次元の保存形式でなければなりません。

ただし、ここではは1次元を使用しており、データ行は単に連続した終値で構成されています。つまり、一番上、または直近のデータ行では、直近の終値をx値、現在の終値をy値とします。このデータの準備とXY行列への入力は、以下のソースコードで処理されます。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   matrix _xy;
   _xy.Init(m_data_set, 2);
   for(int i = 0; i < m_data_set; i++)
   {  _xy[i][0] = m_close.GetData(StartIndex()+i+1);
      _xy[i][1] = m_close.GetData(StartIndex()+i);
   }

...

   return(result);
}

データの準備が完了したら、モデルで使用する適合度評価方法を明確にしておくとよいです。損失ではなく回帰を選択しますが、回帰の中であっても、選択できるメトリクスはかなりあります。従って、最適な選択を可能にするために、使用する回帰尺度のタイプは入力パラメータであり、テストされたデータセットをより良く適合させるために最適化することができます。デフォルト値は一般的な二乗平均平方根誤差です。

遺伝的アルゴリズムの実装は、上記のソースコードにあるGetBestTree関数によって処理されます。これは、最適な式木を筆頭に、いくつかの出力を返します。この木では、現在の終値を入力（x値）として処理し、次の終値（y値）を求めることができます。入力Yベクトルには目標予測が含まれているため、GetFitness関数を使用すると、クエリされた式の適応度以上のものも返されます。これは以下のコードで処理されます。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{ 
        ...

   vector _y;
   string _best_fit[];
   GetBestTree(_xy, _y, _best_fit);

        ...

   return(result);
}

次の終値の目安が得られたので、次のステップでは、この終値をEAで使用可能なシグナルに変換します。予測値は上昇または下降を示すだけであることが多いが、その絶対値は直近の終値と比較すると範囲外です。つまり、使用する前に正規化する必要があります。正規化とシグナル生成は、以下のコードでおこなわれます。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{  int result = 0;
   
        ...

   double _cond = (_y[0]-m_close.GetData(StartIndex()))/fmax(fabs(_y[0]),m_close.GetData(StartIndex()));
   _cond *= 100.0;
   //printf(__FUNCSIG__ + " cond: %.2f", _cond);
   //return(result);
   if(_cond > 0.0)
   {  result = int(fabs(_cond));
   }
   return(result);
}

標準的なExpertSignalクラスのロングとショートの両条件の整数出力は、0～100の範囲でなければなりません。上記のコードも同じにしています。

LongCondition関数とShortCondition関数は互いにミラーです。EAへのシグナルクラスのアセンブリーについては、こちらと こちらの記事で取り上げています。

バックテストと最適化

組み立てたEAのいくつかの「最良の設定」でテスト実行をおこなうと、次のようなレポートとエクイティカーブが得られました。

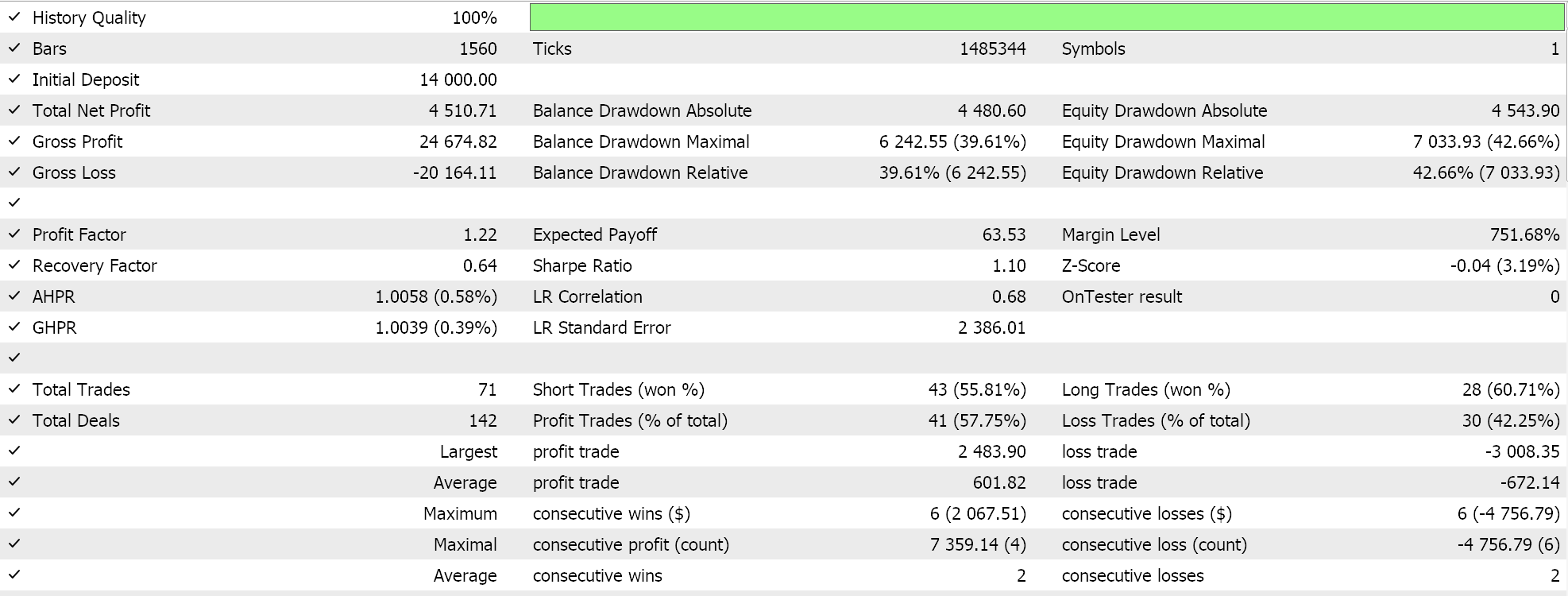
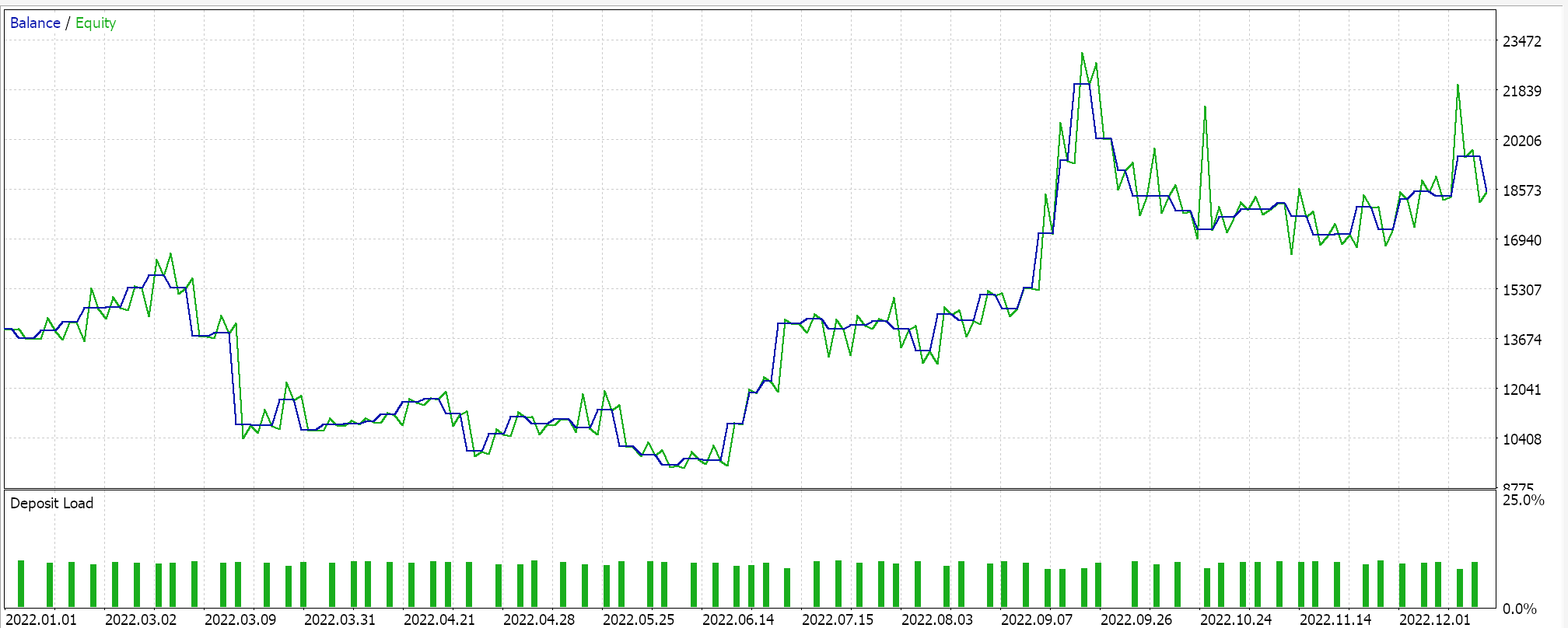
どのような設定であっても、式木は無作為に選択され、また無作為に交差され変異されるため、特定のテスト実行がその結果を正確に再現する可能性は低いですが、興味深いことに、あるテスト実行が有益であった場合、同じ設定でのその後の実行は、パフォーマンスの統計は異なるが、全体としては有益です。テストは2022年、4時間枠のペアEUR JPYでおこなわれます。いつものように、SLやTPに目標価格を設定せずにテストをおこないます。

結論

要約すると、ロングとショートのコンディションを計量するためにExpertSignalクラスのカスタムインスタンスで使用できるモデルとして、関数同定問題を紹介しました。この分析では、モデルの入力値も出力値も一次元であるため、非常に控えめなデータセットを使用しました。これは、多次元データセットに対応するためにモデルを拡張できないという意味ではありません。加えて、このモデルのアルゴリズムは遺伝的最適化であるため、各テスト実行から同一の結果を得るのは難しいです。つまり、このモデルに基づくEAは、かなり上位の時間枠で、他の取引シグナルと同時に使用されるべきであり、すでに独自に生成されたシグナルの確認として機能するようにしなければなりません。