Neuronales Netz in der Praxis: Die Sekante

Einführung

Herzlich willkommen, liebe Leserinnen und Leser, zu einem Thema, das nicht in Form einer Artikelserie behandelt wird.

Obwohl viele denken, dass es besser wäre, eine Reihe von Artikeln zum Thema künstliche Intelligenz zu veröffentlichen, kann ich mir nicht vorstellen, wie dies geschehen könnte. Die meisten Menschen haben keine Ahnung vom wahren Zweck neuronaler Netze und dementsprechend auch nicht von der so genannten künstlichen Intelligenz.

Daher werden wir dieses Thema hier nicht im Detail behandeln. Stattdessen werden wir uns auf andere Aspekte konzentrieren. Daher können Sie meine Artikel zu diesem Thema in beliebiger Reihenfolge lesen und sich auf das für Sie relevante Material konzentrieren. Wir werden das Thema neuronale Netze und künstliche Intelligenz so weit wie möglich fassen. Der Hauptzweck besteht nicht darin, ein System zu schaffen, das auf den Markt oder eine bestimmte Aufgabe ausgerichtet ist. Hier soll erklärt und gezeigt werden, wie ein Computerprogramm das tun kann, was in den Medien gezeigt wurde und was so viele Menschen fasziniert hat, dass sie glauben, dass neuronale Netze oder künstliche Intelligenz ein gewisses Maß an Bewusstsein haben können.

Ich sehe einen Unterschied zwischen neuronalen Netzen und künstlicher Intelligenz, aber das ist natürlich nur meine Meinung. In diesen Artikeln werden Sie sehen, dass künstliche Intelligenz und neuronale Netze nichts Besonderes sind. Es ist einfach ein gut durchdachtes Programm zur Erreichung eines bestimmten Ziels. Aber wir sollten nichts überstürzen. Zunächst müssen wir die verschiedenen Phasen durchlaufen, um zu verstehen, wie alles funktioniert. Wir werden nichts anderes als MQL5 verwenden.

Dies wird eine persönliche Herausforderung für mich sein. Ich möchte nur zeigen, dass man mit den richtigen Konzepten und dem Verständnis dafür, wie die Dinge tatsächlich funktionieren, jede Sprache verwenden kann, um das zu erstellen, was in diesem Artikel gezeigt wird. Ich wünsche Ihnen eine angenehme Lektüre und hoffe, dass diese Artikel für Sie interessant sind und Ihr Wissen über dieses Thema bereichern werden.

Lineare Regression

Wie bereits im theoretischen Teil erläutert, müssen wir bei der Arbeit mit neuronalen Netzen lineare Regressionen und Ableitungen verwenden. Warum? Der Grund dafür ist, dass die lineare Regression eine der einfachsten Formeln ist, die es gibt. In der Tat ist die lineare Regression nur eine affine Funktion. Wenn wir über neuronale Netze sprechen, sind wir jedoch nicht an den Auswirkungen der direkten linearen Regression interessiert. Wir interessieren uns für die Gleichung, die diese Linie erzeugt. Wir interessieren uns nicht für die erstellte Linie, sondern für die Formel.

Um dies zu verstehen, lassen Sie uns einen kleinen Indikator erstellen, wie im folgenden Code gezeigt.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. void Func_01(const int x, const int y)
11. {
12.     int A[] {
13.                 -100,  150,
14.                  -80,   50,
15.                   30,  -80,
16.                  100, -120
17.             };
18. 
19.     canvas.LineVertical(x, y - 200, y + 200, ColorToARGB(clrRoyalBlue, 255));
20.     canvas.LineHorizontal(x - 200, x + 200, y, ColorToARGB(clrRoyalBlue, 255));
21. 
22.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
23.         canvas.FillCircle(x + A[c1++], y + A[c1++], 5, ColorToARGB(clrRed, 255));
24. }
25. //+------------------------------------------------------------------+
26. int OnInit()
27. {    
28.     int px, py;
29.     
30.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
31.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
32. 
33.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
34.     canvas.Erase(ColorToARGB(clrWhite, 255));
35.         
36.     Func_01(px / 2, py / 2);
37. 
38.     canvas.Update(true);
39.     
40.     return INIT_SUCCEEDED;
41. }
42. //+------------------------------------------------------------------+
43. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
44. {
45.     return rates_total;
46. }
47. //+------------------------------------------------------------------+
48. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
49. {
50. }
51. //+------------------------------------------------------------------+
52. void OnDeinit(const int reason)
53. {
54.     canvas.Destroy();
55. }
56. //+------------------------------------------------------------------+

Bei der Ausführung dieses Codes wird folgendes auf dem Bildschirm angezeigt.

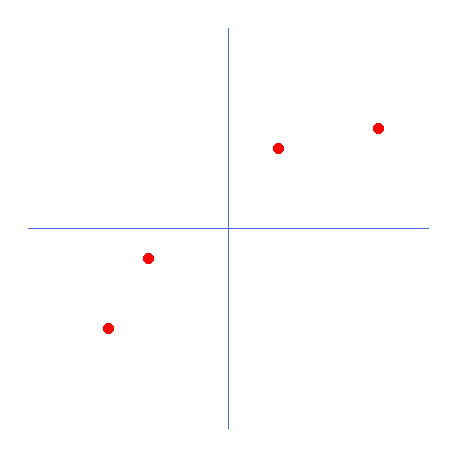
An dieser Stelle sollten wir beginnen zu verstehen, warum wir bei der Arbeit mit neuronalen Netzen lineare Regression und Ableitungen verwenden sollten. Die roten Punkte stellen die Informationen im neuronalen Netz dar, d. h. die KI wurde trainiert und enthält die Informationen, die als rote Punkte angezeigt werden. Die blauen Linien sind die Koordinatenachsen. Die Frage ist: Welche mathematische Gleichung beschreibt diesen Datensatz am besten? Mit anderen Worten, wenn wir die in der obigen Abbildung dargestellten Konzepte verallgemeinern würden, welche mathematische Formel würde dieses Bild am besten darstellen? Betrachtet man die Verteilung der Punkte, so kann man sagen, dass es sich um eine gerade Linie handelt. Dann könnten wir über eine Geradengleichung nachdenken, die eine affine Funktion ist. Diese Gleichung wird im Folgenden dargestellt.

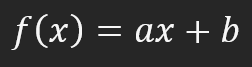
Diese Funktion wird also verwendet, um eine gerade Linie zu erstellen. Kommen wir nun zurück zur Hauptfrage. Welche Werte von A und B sollten wir verwenden, um die Gerade bestmöglich zu erstellen? Nun, viele mögen sagen, dass man sie durch Versuch und Irrtum finden muss. Aber lassen Sie uns die Dinge vereinfachen. Dazu nehmen wir an, dass B gleich Null ist. Das heißt, die gerade Linie geht durch den Ursprung der Koordinatenachse. Zunächst werden wir dies nur der Einfachheit halber tun, um die im neuronalen Netz verwendete Mathematik zu verstehen.

In diesem Fall müssen wir nur den Wert der Konstante A finden. Nun stellt sich eine weitere Frage: Wie finden wir diesen Wert für A? Sie können einen beliebigen Wert eingeben, aber je nach dem verwendeten Wert wird die Formel nicht wirklich optimiert sein. Selbst für eine so geringe Menge an Wissen, die in unserem neuronalen Netz gespeichert ist, würde es sich nicht lohnen, sie zu verlieren. Aus diesem Grund verwenden wir keine Bedeutung (oder können sie nicht verwenden). Wir müssen den Wert finden, bei dem A der bestmögliche Wert wäre.

An dieser Stelle beginnt die Maschine zu lernen. Hier kommt also der Begriff Machine Learning (ML) ins Spiel. Viele Menschen verwenden diesen Begriff, ohne seine Bedeutung zu verstehen. Die Idee ist genau das: Eine mathematische Gleichung erstellen, die die Wissenspunkte innerhalb des Netzes am besten darstellt. Dies manuell zu tun, ist eine der schwierigsten Aufgaben. Durch mathematische Manipulationen können wir die Maschine jedoch dazu zwingen, eine Gleichung für uns zu erstellen. Dies ist der Begriff für ein maschinelles Lernsystem. Die Idee ist, den Computer irgendwie dazu zu bringen, automatisch eine mathematische Gleichung zu erstellen.

Jetzt haben Sie angefangen zu verstehen, wie eine Maschine lernt. Dies ist nur eine Möglichkeit, aber es gibt auch andere. Jetzt wollen wir uns jedoch auf diese spezielle Methode konzentrieren. Wir haben bereits eine bestimmte Aufgabe, die wir erfüllen müssen. Wir müssen berechnen, wie wir den optimalen Wert der Konstante A in der oben dargestellten affinen Gleichung finden können.

Man könnte meinen, dass wir eine Schleife erstellen können, die über alle Werte in einem bestimmten Bereich iteriert. Das funktioniert zwar, ist aber nicht sehr rechenintensiv. Überlegen Sie sich Folgendes: In diesem Beispiel benötigen wir nur eine Variable, die Konstante A. Denn wir betrachten den Wert der Konstante B als gleich Null. In der Praxis wird die Konstante B jedoch höchstwahrscheinlich nicht Null sein. Daher funktioniert diese Methode, einen Wertebereich zu durchlaufen, nicht in allen Situationen. Wir müssen etwas konstruieren, das sich an alle Situationen anpassen kann, auch wenn wir den Wert der Konstante B ändern müssen.

Wie können wir also dieses Problem lösen? Um das Verständnis zu erleichtern, werden wir diesen Ansatz ein wenig abändern, um die verwendeten mathematischen Verfahren besser zu veranschaulichen. Der neue Code ist unten abgebildet:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. #define _ToRadians(A) (A * (M_PI / 180.0))
09. #define _SizeLine 200
10. //+------------------------------------------------------------------+
11. CCanvas canvas;
12. //+------------------------------------------------------------------+
13. struct st_00
14. {
15.     int     x,
16.             y;
17.     double  Angle;
18. }global;
19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                   -100,  150,
24.                    -80,   50,
25.                     30,  -80,
26.                    100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+
36. void NewAngle(const char direct, const double step = 1)
37. {
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.     Func_01();
40. 
41.     global.Angle = (MathAbs(global.Angle + (step * direct)) <= 90 ? global.Angle + (step * direct) : global.Angle);
42.     canvas.TextOut(global.x + 250, global.y, StringFormat("%.2f", global.Angle), ColorToARGB(clrBlack));
43.     canvas.Line(
44.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
45.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
46.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
47.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
48.                 ColorToARGB(clrForestGreen)
49.             );
50.     canvas.Update(true);
51. }
52. //+------------------------------------------------------------------+
53. int OnInit()
54. {    
55.     global.Angle = 0;
56.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
60.     global.x /= 2;
61.     global.y /= 2;
62.         
63.     NewAngle(0);
64. 
65.     canvas.Update(true);
66.     
67.     return INIT_SUCCEEDED;
68. }
69. //+------------------------------------------------------------------+
70. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
71. {
72.     return rates_total;
73. }
74. //+------------------------------------------------------------------+
75. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
76. {
77.     switch (id)
78.     {
79.         case CHARTEVENT_KEYDOWN:
80.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
81.                 NewAngle(-1);
82.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
83.                 NewAngle(1);
84.             break;
85.     }
86. }
87. //+------------------------------------------------------------------+
88. void OnDeinit(const int reason)
89. {
90.     canvas.Destroy();
91. }
92. //+------------------------------------------------------------------+

Das folgende Bild zeigt, was wir bekommen:

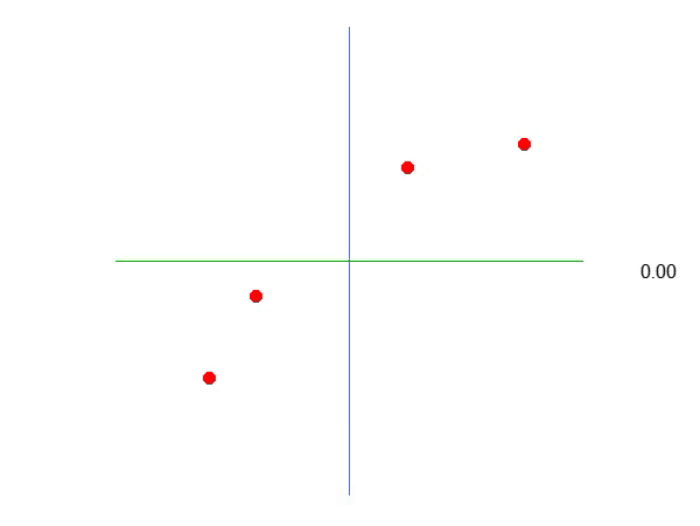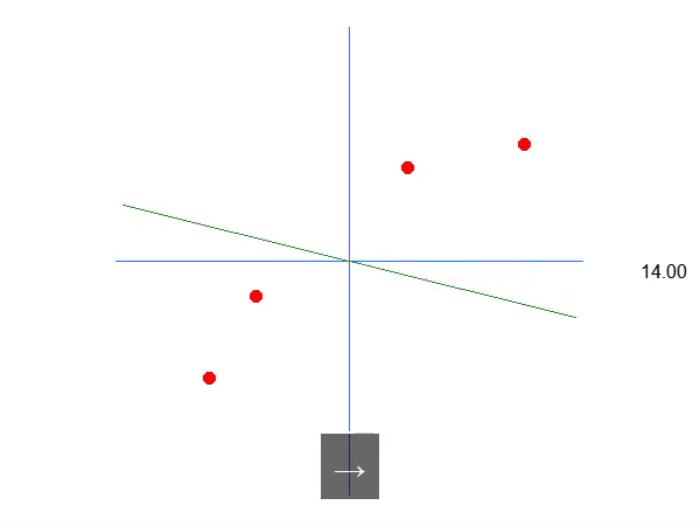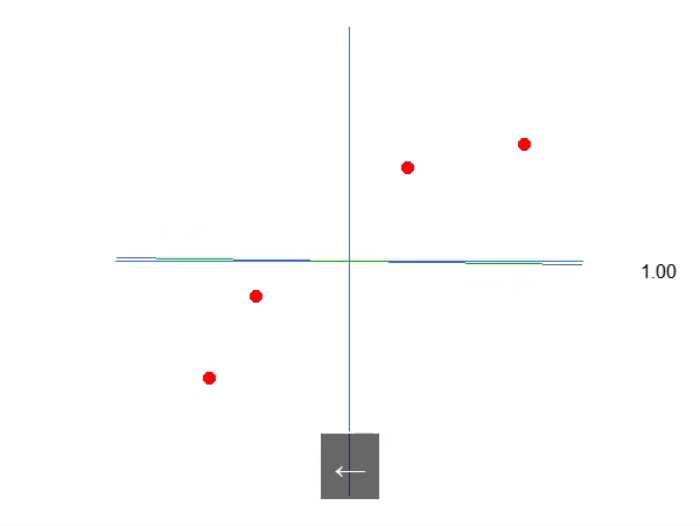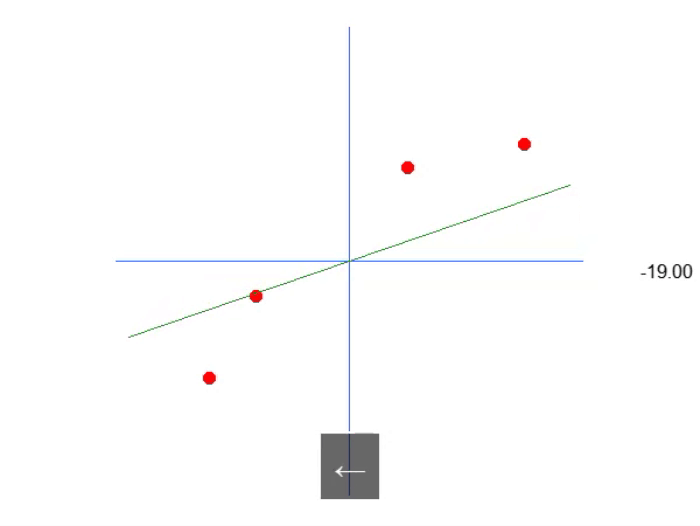
Das heißt, wir können eine affine Gleichung konstruieren, in der wir den Wert der Konstante A ändern können, um eine mögliche lineare Regressionsgleichung zu erstellen, wobei wir versuchen, das vorhandene Wissen, d. h. die roten Punkte, zu erhalten. In diesem Fall ist die korrekte Gleichung die untenstehende. Der angezeigte Winkel ist der Winkel, den man mit den Pfeilen nach links oder rechts erhält.

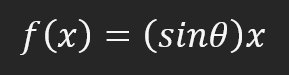
Wir können also davon ausgehen, dass die erforderliche Konstante der Sinus des Winkels ist, und so unsere Gleichung aufstellen. Dies ist jedoch nicht der Fall. Nicht, weil die Konstante nichts mit dem Winkel zu tun hat (das hat sie in der Tat), sondern weil man meinen könnte, man würde den Sinus oder Kosinus verwenden. Diese Methode ist nicht die beste allgemeine Methode, um die Idee auszudrücken. Normalerweise wird eine affine Gleichung nicht in trigonometrischen Funktionen ausgedrückt. Das ist nicht falsch, es ist nur ungewöhnlich. In diesem Artikel werden wir sehen, wie der Winkel verwendet werden kann, um diese Konstante zu erhalten. Zunächst muss ich jedoch etwas anderes erklären. Wenn Sie den Code ein wenig ändern, wie im folgenden Code gezeigt, können Sie sehen, dass es eher wie die korrekte Gleichung der Linie in der Animation aussieht. Denn die Konstante wird wissen, dass sie den richtigen Begriff verwendet.

35. //+------------------------------------------------------------------+
36. void NewAngle(const char direct, const double step = 1)
37. {
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.     Func_01();
40. 
41.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
42.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
43.     canvas.TextOut(global.x, global.y + _SizeLine + 50, StringFormat("f(x) = %.2fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
44.     canvas.Line(
45.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
46.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
47.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
48.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
49.                 ColorToARGB(clrForestGreen)
50.             );
51.     canvas.Update(true);
52. }
53. //+------------------------------------------------------------------+

Das Ergebnis der Code-Ausführung ist in der nachstehenden Grafik zu sehen.

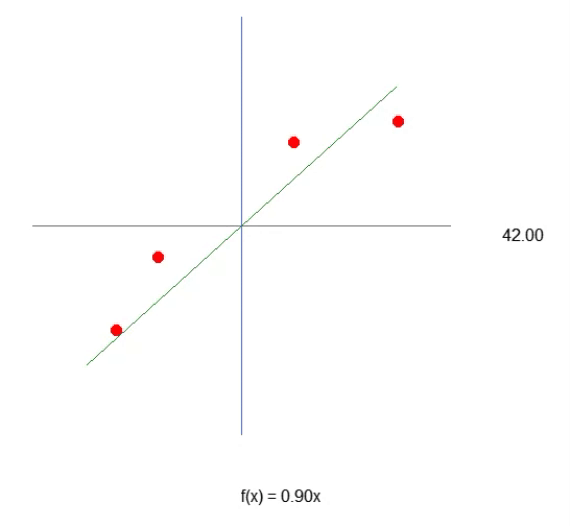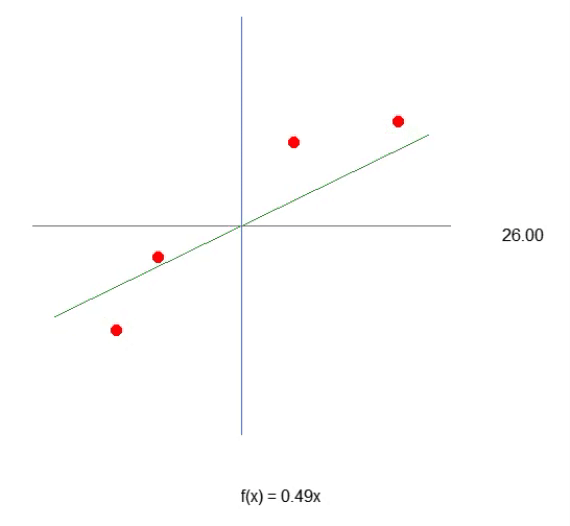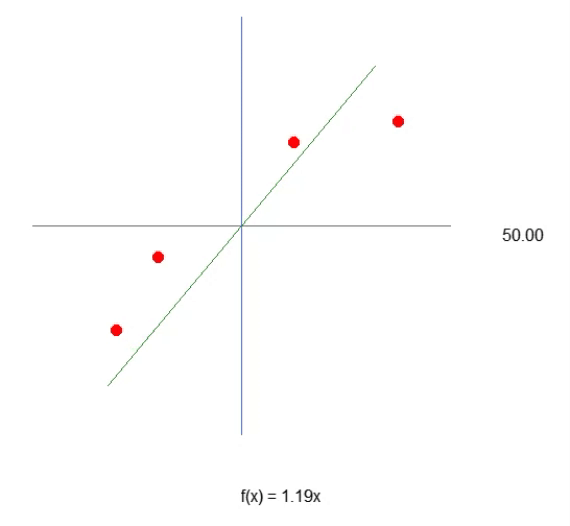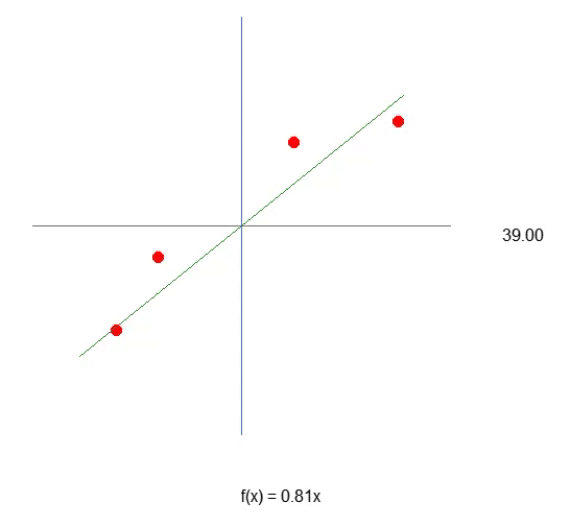
Beachten Sie, dass wir nun dank Zeile 43 eine Gleichung haben, die der einer Geraden sehr nahe kommt. Sie sehen, dass wir zur Erstellung der Formel den Tangens des Winkels und nicht den Sinus oder Kosinus verwenden werden. Dies ist lediglich ein Versuch, den am besten geeigneten Wert zu ermitteln. Obwohl es uns gelingt, die Gleichung zu formulieren, sehen wir, dass es nicht so einfach ist, den optimalen Wert für die Steigung der Linie, d. h. den Winkel des Systems, zu ermitteln. Wir können versuchen, es manuell zu tun, aber das ist eine sehr schwierige Aufgabe. Trotz aller Komplexität der Konstruktion der Gleichung, die eine lineare Regression ergibt, ist es wichtig, sich daran zu erinnern, dass wir an diesem Punkt nur mit einer Variablen in diesem System arbeiten. Dies ist der Wert, den wir finden müssen, wie in der obigen Animation gezeigt.

Wenn wir jedoch die Mathematik richtig anwenden, können wir den geeignetsten Wert für den Neigungswinkel finden. Zu diesem Zweck müssen wir in unserem System Derivate verwenden. Wir müssen auch verstehen, warum der Tangens die trigonometrische Funktion ist, die am besten die in der Gleichung zu verwendende Konstante angibt. Aber um das besser zu verstehen, lieber Leser, beginnen wir ein neues Thema.

Verwendung von Derivaten

An dieser Stelle wird die Mathematik für viele ein wenig verwirrend. Aber es ist kein Grund für Verzweiflung, Angst oder Kummer im Herzen. Wir müssen unserem Code mitteilen, wie er den optimalen Wert für den Winkel finden soll, damit die Gleichung uns erlaubt, auf bereits bekannte Werte zuzugreifen oder ihnen so nahe wie möglich zu kommen. Die Gleichung enthält also Konstanten mit Werten, die sehr nahe am Idealwert liegen. Auf diese Weise kann das im Diagramm vorhandene Wissen im Gleichungsformat erhalten werden, das in diesem Fall eine lineare Gleichung ist.

Die Tatsache, dass wir mit einer linearen Gleichung arbeiten, die oft einer linearen Regression ähnelt, liegt daran, dass diese Art von Gleichung am einfachsten für die Berechnung der erforderlichen Konstanten ist. Dies liegt nicht daran, dass sich die Werte besser in einem Diagramm darstellen lassen, sondern daran, dass sie leichter zu berechnen sind. In einigen Fällen kann die Bearbeitungszeit jedoch erheblich sein. Aber das ist eine andere Frage.

Um eine solche Gleichung zu berechnen, benötigen wir einige mathematische Hilfsmittel. Das liegt daran, dass eine affine Funktion eine geradlinige Funktion ist und keine Ableitung zulässt. Eine Ableitung ist eine gerade Linie, die durch einen bestimmten Punkt verläuft und aus einer beliebigen Gleichung abgeleitet werden kann. Viele Menschen werden durch diese Erklärungen verwirrt, aber eigentlich ist eine Ableitung nur eine Tangente an einen bestimmten Punkt der Funktion. Die Tangente wird an einem Punkt gezeichnet, der zu der Gleichung gehört, die normalerweise die Kurve im Diagramm erzeugt. Da es sich bei der affinen Funktion um eine Tangente handelt, spiegelt die Tangente den Wert der Konstante wider, mit der der unbekannte Teil multipliziert wird, was die Gleichung dieser spezifischen Linie ergibt. Aus diesem Grund kann die zweite Tangente nicht mit dieser ursprünglichen Gleichung gezeichnet werden. Hierfür brauchen wir etwas anderes. Es spielt also keine Rolle, welchen Punkt wir zur Ermittlung der Ableitung heranziehen wollen. Es ist nicht möglich, eine Ableitung in einer affinen Funktion zu erstellen.

Es gibt jedoch eine Möglichkeit, die Schaffung eines Derivats zu gewährleisten. Genau damit wollen wir uns heute beschäftigen. Um zu verstehen, wie wir dies tun werden, müssen Sie wissen, was ein Derivat ist. Dann müssen Sie die Methode verstehen, mit der Sie diese Ableitung erhalten und dementsprechend eine affine Funktion erstellen, die eine minimale Ideallinie beschreibt. Dazu verwenden wir eine Funktion, mit der wir die Ableitung ausgeben können. Die einfachste von ihnen ist die quadratische Funktion. Seine Formel lautet wie folgt:

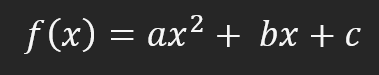
Beachten Sie, dass in dieser Gleichung eine Zweierpotenz enthalten ist. Allein dadurch lässt sich das Vorhandensein einer Ableitung im System erklären, aber wir können jede beliebige Funktion verwenden, um die Kurve zu konstruieren. Es könnte sich sogar um eine logarithmische Funktion handeln. Eine logarithmische Funktion macht jedoch keinen Sinn, wenn wir uns ansehen, was wir als Nächstes tun müssen. Aus diesem Grund und um das Verfahren so einfach wie möglich zu gestalten, werden wir eine quadratische Gleichung verwenden. Unter Verwendung der obigen Formel ergibt sich also das folgende Diagramm.

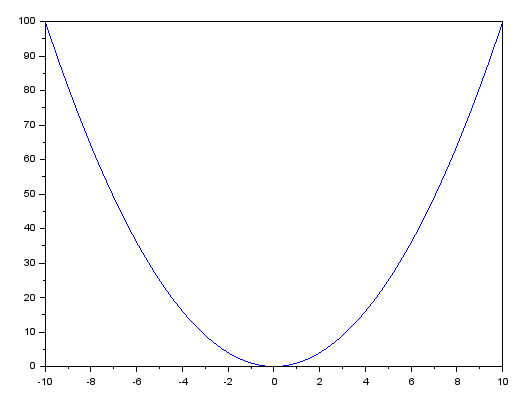
Dieses Diagramm wird erstellt, indem der Wert von A auf eins und die Werte von B und C auf null gesetzt werden. Wirklich wichtig für uns ist jedoch die Kurve, die in der Grafik zu sehen ist.

Passen Sie gut auf - diese Erklärung ist wichtig, um zu verstehen, was wir in unserem Programm implementieren werden, um die benötigte Gleichung zu finden.

Aus dem obigen Schaubild lassen sich einige Annahmen ableiten, und es ist wichtig, diese zu verstehen. Wir wollen den Wert der Ableitung an dem Punkt wissen, an dem X gleich vier ist. Dazu müssen Sie eine Tangente zeichnen, die genau durch den Punkt geht, an dem X gleich vier ist. Auf den ersten Blick ist das ganz einfach: Nehmen Sie ein Lineal und markieren Sie einen Punkt X auf der Koordinate, die gleich vier ist. Und dann werden wir versuchen, eine Linie zu konstruieren, die einen Punkt auf der Kurve tangiert. Aber können wir auf diese Weise tatsächlich eine Tangente zeichnen? Das ist unwahrscheinlich!

Es ist viel wahrscheinlicher, dass wir eine Linie erzeugen, die nicht tangential ist. Aus diesem Grund müssen wir einige Berechnungen anstellen. An dieser Stelle werden die Dinge kompliziert. Um die Situation aber nicht unnötig zu verkomplizieren, werde ich an dieser Stelle nicht auf die Berechnungen selbst eingehen. Ich gehe davon aus, dass der Leser die Formel für die Ableitung einer quadratischen Gleichung kennt. Für diejenigen, die es nicht wissen, werde ich später erklären, wie man diese Formel erhält. Wichtig für uns ist nun die Art und Weise, wie wir die Ableitungsgleichungen erhalten. Das Endergebnis ist nicht so wichtig, aber die Formel, die sich aus der Ableitung ergibt, ist wichtig. Lassen Sie uns also weitermachen.

Die Ableitung einer quadratischen Gleichung lässt sich mit der folgenden Formel ermitteln.

Als Nächstes werde ich zwei der gebräuchlichsten Schreibweisen zeigen. Sie können die rechte oder die linke Seite verwenden, das spielt keine Rolle. Jetzt interessiert uns die Formel selbst, sie ist gleich 2 mal X. Diese Formel gibt uns einen Wert von 8, der in unserem Beispiel der Wert der Tangente an dem Punkt ist, an dem X vier ist. Wenn Sie wissen, was der Wert acht bedeutet, können Sie eine Tangente an dem Punkt ziehen, an dem X gleich vier ist. Wenn Sie jedoch nicht wissen, was dieser Wert bedeutet, benötigen Sie eine zweite Formel, um den Tangens zu zeichnen. 

Wenn Sie nicht verstehen, warum der Wert acht ist, schauen Sie sich das Bild unten an, wo die Ableitung nach X vier sein soll. Dazu berechnen wir den Wert an dieser Position wie unten dargestellt.

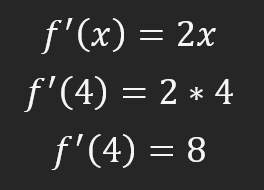
Doch bevor wir zu anderen Berechnungen übergehen, sollten wir herausfinden, was dieser Wert acht bedeutet. Das heißt, wenn wir eine Position auf der X-Achse verschieben, müssen wir acht Positionen auf der Y-Achse verschieben. Dies ermöglicht es uns, eine Tangente zu zeichnen. Sie werden es vielleicht nicht glauben, bis Sie es im wirklichen Leben sehen. Wenn dies der Fall ist, gibt es eine Formel, mit der Sie die Gleichung einer Tangente schreiben können. Diese Gleichung lautet:

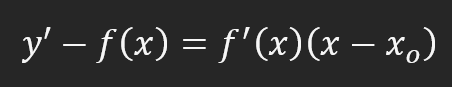
Ja, es ist ein bisschen beängstigend, aber es ist viel einfacher, als es scheint. Trotzdem ist diese Formel etwas ganz Besonderes. Damit können Sie eine Gleichung einer Tangente an eine Ableitung erstellen, obwohl die Ableitung letztendlich eine Tangente ist. Aber das ist nur eine Tatsache, die ich als etwas Interessantes erwähne, nichts, worüber man sich Sorgen machen müsste. Da wir also die meisten Werte bereits kennen, können wir die entsprechenden Substitutionen vornehmen, um die Formel für die Gleichung der Tangente zu finden. Dieser Moment ist unten zu sehen.

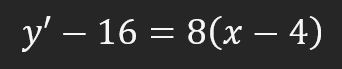
Dies ist der Punkt, an dem sich ein Großteil der Komplexität ergibt, aber lassen Sie uns herausfinden, woher diese Werte kommen. Der Wert 16 ist das Ergebnis der ursprünglichen Gleichung. Mit anderen Worten: Wir haben in die quadratische Gleichung den Wert von X eingesetzt, den wir in der Ableitung verwenden, also „4“. Der Wert 8 ergibt sich aus der Berechnung der Ableitung der Funktion. Auch hier ist X gleich 4, und dies gilt auch für die Ableitung der Funktion. Der Wert 4, den wir hier sehen, ist der Anfangswert von X, den wir in allen anderen Gleichungen verwenden. Nach den Berechnungen erhalten wir die folgende Formel für die Tangente.

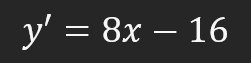
Großartig, jetzt können wir eine Tangente auf der Grundlage der obigen Gleichung zeichnen. Die gezeichnete Linie ist in der folgenden Abbildung zu sehen, sie ist rot hervorgehoben.

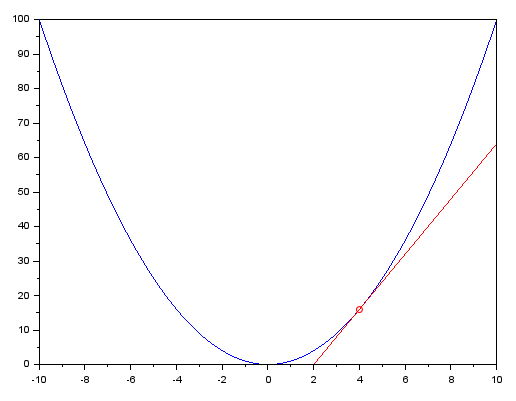
Dieses Diagramm wurde mit dem Programm SCILAB erstellt. Für diejenigen, die einen genaueren Blick darauf werfen wollen, finden Sie unten den Code, der in SCILAB verwendet wird, um ihn zu erzeugen.

x = [-10:.2:10];
y = x ^ 2;

plot(x, y, 'b-');
plot(4, 16, 'ro');

x = [2:.2:10];
y = 8 * x - 16;

plot(x, y, 'r-');

Ich füge dies hinzu, damit Sie verstehen können, dass es nicht nur darum geht, zu lernen, wie man dieses oder jenes Programm nutzt. Die Beherrschung einer bestimmten Sprache ist nicht das, was einen wirklich qualifiziert. Oft müssen wir auf verschiedene Programme zurückgreifen, um die Situation genau analysieren zu können. Aus diesem Grund ist die Weiterbildung von großer Bedeutung. Und egal, für wie gut Sie sich halten, es wird immer jemanden geben, der in dem einen oder anderen Bereich mehr Erfahrung hat als Sie. Also, hören Sie nicht auf zu lernen.

Jetzt haben wir alle notwendigen Kenntnisse, aber was bedeutet diese Tangente? Und warum ist sie so wichtig für diejenigen, die mit neuronalen Netzen arbeiten? Der Grund dafür ist, dass diese Linie uns zeigt, wohin wir uns bewegen sollten. Genauer gesagt, wohin sich unser Programm bewegen sollte, um eine lineare Regressionsgleichung zu erstellen.

Aber das ist noch nicht alles: In dieser Zeile wird erklärt, wie man die Abweichungen berechnet. In diesen Berechnungen liegt der „Zauber“ der neuronalen Netze. Siehst du das nicht? Vielleicht können Sie nicht verstehen, wie das möglich ist. Um dies zu verstehen, müssen wir wissen, wie die Berechnung der Ableitung erfolgt. Auch wenn wir am Ende die Tangente verwenden, ergeben sich die Berechnungen nicht aus der Tangente. Sie ergeben sich aus einer anderen trigonometrischen Funktion. Darin liegt der Zauber des Systems. Diese „Magie“ ermöglicht es uns, eine allgemeine Lösung für alle möglichen und akzeptablen Fälle zu finden, und das ist es, was das neuronale System funktionieren lässt. Wir werden das also für ein anderes Thema aufheben, um die Dinge getrennt zu halten.

Eine Sekante

Obwohl alle, die über neuronale Netze sprechen, nur Ableitungen erwähnen, liegt das Geheimnis nicht in der Ableitung oder der Tangente. Das Geheimnis liegt in einer anderen geraden Linie. Und dies ist die Sekante. Deshalb war ich auch etwas zurückhaltend, über das Thema neuronale Netze zu schreiben. Man hat mich sogar gebeten, über dieses Thema zu berichten. Die Wahrheit ist, dass viele Menschen über neuronale Netze sprechen, aber nur wenige wirklich verstehen, wie sie aus mathematischer Sicht funktionieren. Das Programmieren ist der einfache Teil, der schwierige Teil ist die Mathematik. Viele Menschen glauben, dass sie diese oder jene Bibliothek, diese oder jene Programmiersprache verwenden sollten. Aber in Wirklichkeit können wir jede Sprache verwenden, wenn wir verstehen, wie ihre mathematische Komponente funktioniert. Ich möchte mich nicht negativ über jemanden äußern oder behaupten, dass jemand mit seinen Erklärungen falsch liegt. Jeder hat das Recht, alles so zu verstehen, wie er will. Mein Wunsch ist es jedoch, wirklich zu erklären, wie alles funktioniert. Ich möchte nicht, dass Sie ein weiterer Sklave von Sprachen oder Bibliotheken werden. Ich möchte, dass Sie verstehen, wie alles von innen heraus funktioniert. Deshalb habe ich beschlossen, eine Reihe von Artikeln zu diesem Thema zu schreiben.

Bei der Ableitung geht es darum, den Wert der Tangente zu ermitteln. Dies geschieht, weil die Tangente die Steigung der Funktion angibt. Mit anderen Worten, es handelt sich um den Fehler der linearen Regression bei Verwendung in einem neuronalen Netz. Wenn die Tangente beginnt, einen Winkel von Null Grad zu erreichen, geht der Fehler daher gegen Null. Mit anderen Worten: Die Gleichung, die eine lineare Regression auf die bereits in der Datenbank vorhandenen Werte erzeugt, nähert sich den Idealwerten an. Dies geschieht in diesem speziellen Fall und mit diesen speziellen Werten.

Bei der Durchführung der Berechnungen wird jedoch nicht die Tangente verwendet. Wir verwenden eigentlich eine Sekante. Dabei spielt es keine Rolle, welche Art von neuronalem Netz eingesetzt wird. Wenn es eine Berechnung gibt, dann wird keine Tangente, sondern eine Sekante verwendet. Man könnte meinen, dass dies viel komplizierter ist, aber wenn man das denkt, dann weiß man nicht, wie die Tangente an die Ableitung tatsächlich ermittelt wird. Oder, noch schlimmer, wie man die Formel für die Ableitung erhält. Es hat keinen besonderen Sinn, Formeln auswendig zu lernen. Am besten ist es, zu verstehen, warum die Formel dieses und nicht ein anderes Format hat. Erinnern Sie sich an die Berechnungen aus dem vorherigen Thema? Wissen Sie, woher sie stammen? Falls nicht, schauen wir uns das folgende Diagramm an:

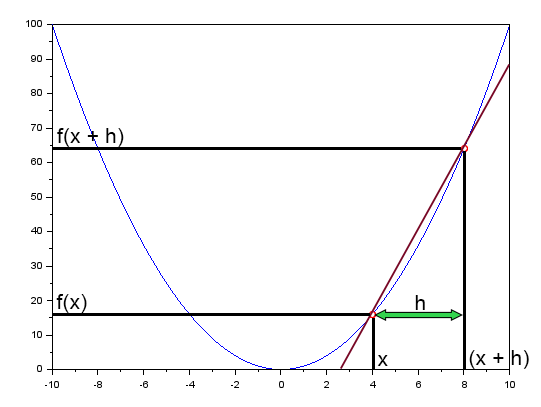
Die rote Linie in diesem Diagramm ist eine Sekante. Wenn Sie bis jetzt aufmerksam waren, möchte ich, dass Sie jetzt Ihre Aufmerksamkeit verdoppeln. Dies ist sogar noch wichtiger als alles, was Sie sonst über neuronale Netze lesen oder hören können.

Hier verwende ich denselben X-Punkt wie im vorherigen Thema, er ist gleich 4. Ich tue dies, damit Sie besser verstehen, was ich Ihnen erkläre.

Beachten Sie, dass es unmöglich ist, eine Tangente zu erzeugen, egal, was Sie denken oder sich vorstellen. Es ist nicht möglich, aus einer Kurve in einem Diagramm eine Tangente zu erzeugen.. Wenn Sie jedoch eine Sekante verwenden, können Sie eine Tangente erhalten. Wie? Es ist alles ganz einfach. Man beachte, dass f(x + h) f(x) ist, das um eine Strecke h verschoben ist. Wenn dann h gegen Null geht, wird die Sekante zur Tangente. Und wenn h genau Null ist, fällt die in der Abbildung gezeigte Sekante genau mit der Tangente zusammen. An diesem Punkt ergibt die Tangente also die Steigung der Ableitung der Funktion an dem gegebenen Punkt. Okay, aber ich verstehe es trotzdem nicht. Nun, mein lieber Leser, lassen Sie uns das, was Sie oben sehen, in eine weniger verwirrende Form bringen, vielleicht wird das die Situation klären.

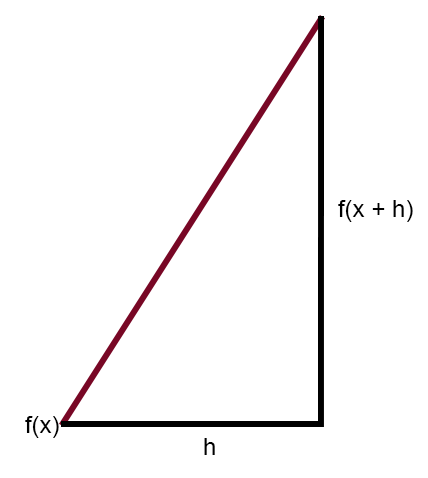
Das Bild oben zeigt dasselbe wie das vorherige. Ich denke, dies wird die Idee der Verwendung der Sekante klarer machen. Und warum wir, anders als von allen behauptet, bei der Verwendung eines neuronalen Netzes eine Tangente oder Ableitungen verwenden, in Wirklichkeit eine Sekante nutzen, damit der Computer die richtige Gleichung erstellen kann.

Wenn Sie den Wert von h verringern, nähern Sie sich f(x) an, aber dieses h wird nie gleich Null sein. Dies ist der Fall, wenn wir neuronale Netze verwenden. Dies kann ein sehr kleiner Wert sein; wie klein dieser Wert ist, hängt von einer Sache ab, die wir später sehen werden. Dieser Moment wird als neuronaler Netzwerkwahnsinn bezeichnet. Je kleiner dieser Wert h ist, desto weniger verrückt ist das neuronale Netz, aber je größer er ist, desto verrückter wird es sein. Warum? Der Grund dafür ist die Konvergenz. Bei den Berechnungen, die wir später betrachten werden, wird man feststellen können, dass diese Konvergenz gegen den Wert h tendiert. Dies führt dazu, dass die am Ende erhaltene Gleichung dazu neigt, innerhalb dieser Konvergenz zu schwanken. Aus diesem Grund ist h sehr wichtig. Die Erklärung scheint kompliziert, aber Sie werden sehen, dass in der Praxis alles viel einfacher ist. Wir sind jedoch noch nicht an dem Punkt angelangt, den wir zeigen wollen. Auf der Grundlage des obigen Bildes ergibt sich die folgende Formel.

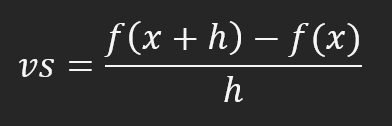
Diese Formel zeigt, wie weit die Sekante von der Tangente entfernt ist. In der tatsächlich verwendeten Berechnung wird jedoch die in der nachstehenden Abbildung dargestellte Methode verwendet.

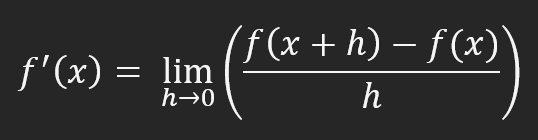
Diese Gleichung erklärt alles, was Sie über neuronale Netze wissen müssen. Deshalb sagt man, dass neuronale Netze Derivate verwenden. Aus dieser Gleichung ergeben sich die Berechnungen, die viele einfach auswendig lernen: Ableitungsformeln. Das war's. Es gibt nichts mehr zu erklären oder zu diskutieren. Alles, was wir brauchen, ist die oben dargestellte Gleichung. Damit kann ich den Artikel schließen und in aller Ruhe mein Leben leben.

Abschließende Überlegungen

Aber warten Sie einen Moment. Sie haben nicht erklärt, wie man diese Sekantengleichung verwendet oder warum sie alles erklärt. Was meinen Sie mit „nicht erklärt haben“? Wollen Sie mich auf den Arm nehmen? Liebe Leserin, lieber Leser, ich habe gerade damit begonnen, dieses Thema vorzustellen. Ich möchte, dass Sie dieses Material zunächst in Ruhe studieren. Im nächsten Artikel über neuronale Netze werden wir uns damit befassen, wie man das hier vorgestellte Wissen nutzen kann, um die richtige Gleichung zu formulieren.