Red neuronal en la práctica: Recta secante

Introducción

Bienvenidos, mis queridos lectores, a un tema que no trataré como una serie de artículos.

Aunque muchos podrían pensar que sería mejor tener una serie de artículos sobre el tema de la inteligencia artificial, no veo cómo hacerlo. La mayoría de las personas no tiene ni idea del verdadero objetivo de las redes neuronales y, por ende, de lo que se conoce como inteligencias artificiales.

Aquí no trataremos este tema en concreto. Nos centraremos en diferentes aspectos. Por lo tanto, podrás leer mis artículos sobre el tema en cualquier orden que desees, pudiendo centrarte en uno u otro. Abordaré el tema de las redes neuronales y la inteligencia artificial de la manera más amplia posible. El objetivo aquí no será crear un sistema orientado a operar en el mercado o para algún propósito específico. El objetivo será explicar y, principalmente, mostrar por qué y cómo un programa de ordenador puede hacer lo que los medios han mostrado y que tanto fascina a tanta gente, al punto de hacerles creer que las redes neuronales o la inteligencia artificial pueden tener algún nivel de conciencia.

Para mí, existe una diferencia entre redes neuronales e inteligencia artificial, pero esto es solo mi visión. A lo largo de los artículos, verás que ni la inteligencia artificial ni la red neuronal tienen nada de especial. Se trata simplemente de un programa bien elaborado y pensado para lograr un objetivo determinado. Pero no tengas prisa. Pasaremos por diversas etapas de desarrollo para que puedas comprender realmente cómo y por qué las cosas funcionan. No utilizaremos nada que no sea MQL5 puro.

Este será mi desafío personal. Pero verás que, si tenemos los conceptos correctos y conocemos el verdadero funcionamiento de las cosas, podrás usar cualquier lenguaje para producir lo que aquí se mostrará. Así que les deseo a todos una excelente lectura y que estos artículos sean divertidos y les aporten algún conocimiento sobre el tema.

La regresión lineal

Como se explicó en la parte teórica, necesitamos usar regresiones lineales y derivadas cuando trabajamos con redes neuronales. ¿Pero por qué? La razón es que la regresión lineal es una de las fórmulas más simples que existen. Básicamente, una regresión lineal es solo una función afín. Sin embargo, cuando hablamos de redes neuronales, no nos interesan los efectos de la recta de regresión lineal. Lo que nos interesa es la ecuación que genera dicha recta. La recta generada poco importa. Pero la fórmula es la parte que nos interesa.

Para entenderlo vamos a crear un pequeño indicador, como se muestra en el código a continuación.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. CCanvas canvas;
09. //+------------------------------------------------------------------+
10. void Func_01(const int x, const int y)
11. {
12.     int A[] {
13.                 -100,  150,
14.                  -80,   50,
15.                   30,  -80,
16.                  100, -120
17.             };
18. 
19.     canvas.LineVertical(x, y - 200, y + 200, ColorToARGB(clrRoyalBlue, 255));
20.     canvas.LineHorizontal(x - 200, x + 200, y, ColorToARGB(clrRoyalBlue, 255));
21. 
22.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
23.         canvas.FillCircle(x + A[c1++], y + A[c1++], 5, ColorToARGB(clrRed, 255));
24. }
25. //+------------------------------------------------------------------+
26. int OnInit()
27. {    
28.     int px, py;
29.     
30.     px = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
31.     py = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
32. 
33.     canvas.CreateBitmapLabel("BL", 0, 0, px, py, COLOR_FORMAT_ARGB_NORMALIZE);
34.     canvas.Erase(ColorToARGB(clrWhite, 255));
35.         
36.     Func_01(px / 2, py / 2);
37. 
38.     canvas.Update(true);
39.     
40.     return INIT_SUCCEEDED;
41. }
42. //+------------------------------------------------------------------+
43. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
44. {
45.     return rates_total;
46. }
47. //+------------------------------------------------------------------+
48. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
49. {
50. }
51. //+------------------------------------------------------------------+
52. void OnDeinit(const int reason)
53. {
54.     canvas.Destroy();
55. }
56. //+------------------------------------------------------------------+

Al ejecutar este código, se mostrará la siguiente imagen.

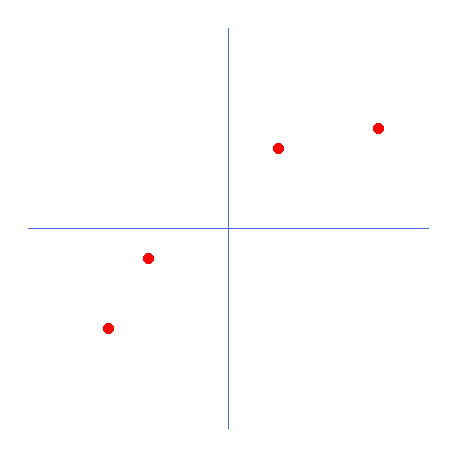
Muy bien, en este momento exacto, vamos a empezar a entender por qué usar la regresión lineal y las derivadas cuando se trata de redes neuronales. Los puntos rojos representan la información presente en la red neuronal. Es decir, la inteligencia artificial se ha entrenado y contiene la información que se ve como puntos rojos. Las líneas azules son los ejes de coordenadas. La pregunta es: ¿qué ecuación matemática describe mejor este conjunto de datos? O, dicho de otro modo, si tuviéramos que resumir el conocimiento mostrado en la imagen anterior, ¿qué fórmula matemática representaría mejor este mismo conocimiento? Al observar la distribución de los puntos, dirías que es una recta. Entonces, pensarías en la ecuación de una recta, que es una función afín. Esta tiene el formato mostrado en la imagen a continuación.

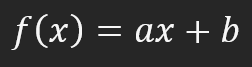
De acuerdo, esta función sirve para crear una recta. Entonces, volviendo a la cuestión principal. ¿Cuáles son los valores de A y B que debemos usar para crear la recta de la mejor manera posible? Bueno, muchos podrían decir que deberíamos buscarlos mediante prueba y error. De hecho, sin embargo, vamos a simplificar un poco las cosas. Para ello, asumiremos que B es igual a cero. Es decir, la recta pasará por el origen del eje de coordenadas. Haremos esto en un primer momento solo para simplificar las cosas, de modo que tú, mi querido lector, puedas comprender las matemáticas utilizadas en la red neuronal.

Así, todo lo que nos queda es encontrar un valor para la constante A. Ahora surge una nueva pregunta: ¿cómo pretendes encontrar este valor para A? Puedes poner cualquier valor. Sin embargo, dependiendo del valor utilizado, la fórmula no estará realmente optimizada. Incluso para una cantidad tan pequeña de conocimiento dentro de nuestra red neuronal, no es adecuado que este conocimiento se pierda. Por este motivo, no usamos, o no podemos usar, cualquier valor. Necesitamos encontrar un valor en el que A sea el mejor valor posible.

Y es en este punto donde la máquina comienza a aprender. O donde surge el término "aprendizaje automático" o, en inglés, Machine Learning (ML). Muchas personas utilizan este término sin realmente entender lo que significa. La idea aquí es precisamente esta. Crear una ecuación matemática que mejor represente los puntos de conocimiento dentro de la red. Hacer esto manualmente es una de las tareas más complicadas y difíciles que existen. Sin embargo, mediante manipulaciones matemáticas, podemos conseguir que la máquina genere una ecuación para nosotros. Y esto es el sistema de aprendizaje automático. Se trata de forzar de alguna manera al ordenador para que cree una ecuación matemática de forma automática.

Muy bien, ahora has comenzado a entender cómo una máquina aprende. Esta es una de las maneras de hacerlo. Existen otras. Sin embargo, en este momento, vamos a centrarnos en este método. Así que ya tenemos lo que tenemos que hacer. Calcular alguna forma de encontrar el mejor valor para la constante A en la ecuación afín mostrada arriba.

En este punto, podrías pensar lo siguiente: Podemos crear un bucle que recorra todos los valores dentro de un rango dado. Esto funcionaría en realidad, pero no sería eficiente en términos de computación. Para entenderlo, piensa en lo siguiente: En este ejemplo solo necesitamos una variable, la constante A. Esto se debe a que estamos considerando que el valor de la constante B es cero. Sin embargo, en la práctica, B probablemente no será cero. Por tanto, este método de recorrer un rango de valores no sirve para todas las situaciones posibles. Necesitamos construir algo que pueda adaptarse a todas las situaciones posibles, incluso cuando tengamos que ajustar el valor de la constante B.

Una vez entendido este punto, podemos comenzar a pensar en cómo resolver esta cuestión. Para que todo resulte más comprensible, vamos a modificarlo ligeramente para tener una mejor visualización de las matemáticas que se van a utilizar. A continuación, se muestra el nuevo código:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. #property indicator_chart_window
04. #property indicator_plots 0
05. //+------------------------------------------------------------------+
06. #include <Canvas\Canvas.mqh>
07. //+------------------------------------------------------------------+
08. #define _ToRadians(A) (A * (M_PI / 180.0))
09. #define _SizeLine 200
10. //+------------------------------------------------------------------+
11. CCanvas canvas;
12. //+------------------------------------------------------------------+
13. struct st_00
14. {
15.     int     x,
16.             y;
17.     double  Angle;
18. }global;
19. //+------------------------------------------------------------------+
20. void Func_01(void)
21. {
22.     int A[] {
23.                   -100,  150,
24.                    -80,   50,
25.                     30,  -80,
26.                    100, -120
27.             };
28. 
29.     canvas.LineVertical(global.x, global.y - _SizeLine, global.y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
30.     canvas.LineHorizontal(global.x - _SizeLine, global.x + _SizeLine, global.y, ColorToARGB(clrRoyalBlue, 255));
31. 
32.     for (uint c0 = 0, c1 = 0; c1 < A.Size(); c0++)
33.         canvas.FillCircle(global.x + A[c1++], global.y + A[c1++], 5, ColorToARGB(clrRed, 255));
34. }
35. //+------------------------------------------------------------------+
36. void NewAngle(const char direct, const double step = 1)
37. {
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.     Func_01();
40. 
41.     global.Angle = (MathAbs(global.Angle + (step * direct)) <= 90 ? global.Angle + (step * direct) : global.Angle);
42.     canvas.TextOut(global.x + 250, global.y, StringFormat("%.2f", global.Angle), ColorToARGB(clrBlack));
43.     canvas.Line(
44.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
45.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
46.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
47.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
48.                 ColorToARGB(clrForestGreen)
49.             );
50.     canvas.Update(true);
51. }
52. //+------------------------------------------------------------------+
53. int OnInit()
54. {    
55.     global.Angle = 0;
56.     global.x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
57.     global.y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
58. 
59.     canvas.CreateBitmapLabel("BL", 0, 0, global.x, global.y, COLOR_FORMAT_ARGB_NORMALIZE);
60.     global.x /= 2;
61.     global.y /= 2;
62.         
63.     NewAngle(0);
64. 
65.     canvas.Update(true);
66.     
67.     return INIT_SUCCEEDED;
68. }
69. //+------------------------------------------------------------------+
70. int OnCalculate(const int rates_total, const int prev_calculated, const int begin, const double &price[])
71. {
72.     return rates_total;
73. }
74. //+------------------------------------------------------------------+
75. void OnChartEvent(const int id, const long &lparam, const double &dparam, const string &sparam)
76. {
77.     switch (id)
78.     {
79.         case CHARTEVENT_KEYDOWN:
80.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_LEFT))
81.                 NewAngle(-1);
82.             if (TerminalInfoInteger(TERMINAL_KEYSTATE_RIGHT))
83.                 NewAngle(1);
84.             break;
85.     }
86. }
87. //+------------------------------------------------------------------+
88. void OnDeinit(const int reason)
89. {
90.     canvas.Destroy();
91. }
92. //+------------------------------------------------------------------+

Muy bien, lo que tenemos aquí se muestra en la animación a continuación:

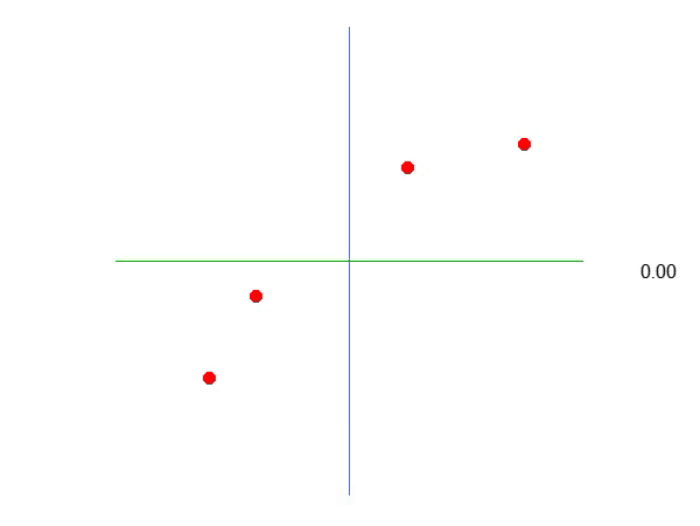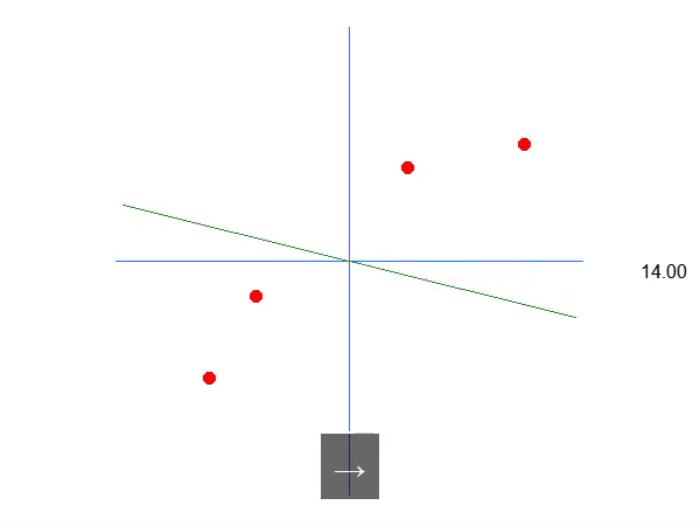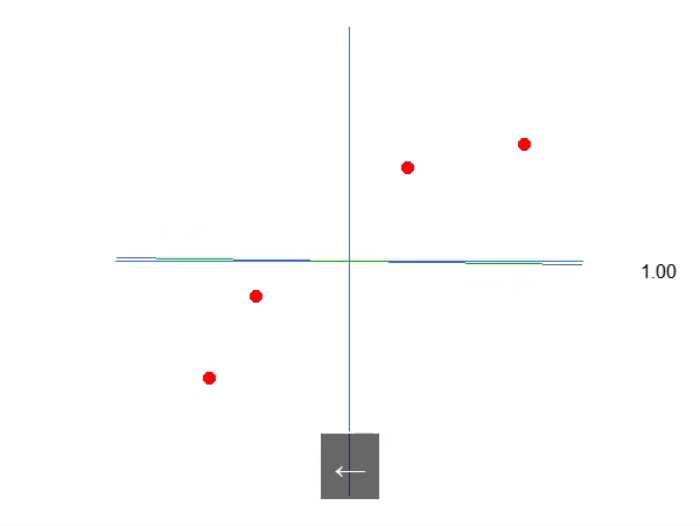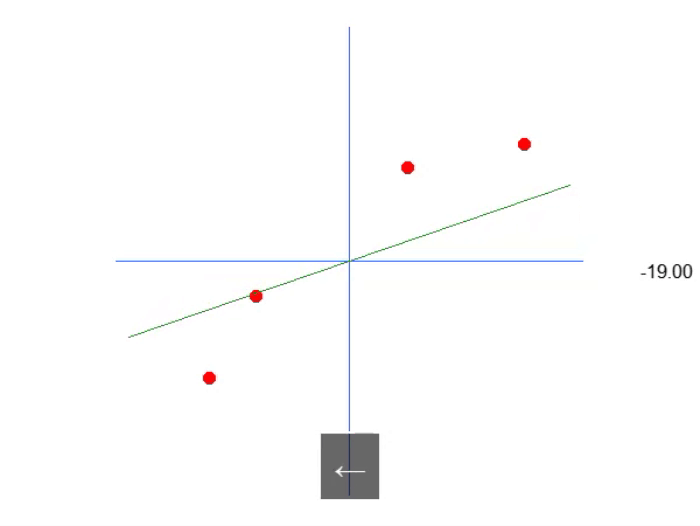
Es decir, podemos generar una ecuación afín en la que se puede ajustar el valor de la constante A para crear lo que sería una posible ecuación de regresión lineal, intentando conservar el conocimiento existente, es decir, los puntos en rojo. En este caso, la ecuación que consideraríamos correcta sería la mostrada en la imagen a continuación. El ángulo informado es exactamente el que se obtiene al usar las flechas hacia la izquierda o la derecha.

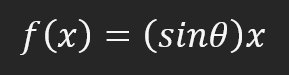
Es decir, imaginarías que la constante que estaríamos buscando podría ser el seno del ángulo, creando así nuestra ecuación. Sin embargo, estarías equivocado. No por imaginar que la constante no está relacionada con el ángulo, ya que en realidad lo está, sino porque pensarías que deberías usar el seno o el coseno. No obstante, este método no es la mejor forma general de expresar las cosas. Normalmente no verás una ecuación afín escrita utilizando funciones trigonométricas. No es que sea incorrecto, pero es inusual. Sin embargo, en este artículo veremos cómo podemos utilizar el ángulo para obtener dicha constante. Pero vamos despacio, porque antes aún tenemos que explicar otras cosas. Si cambiamos un poco más el código, como se muestra en el fragmento a continuación, podemos verificar algo que se parecería un poco más a la ecuación correcta de la recta mostrada en la animación. Es decir, ahora la constante utiliza el término correcto.

35. //+------------------------------------------------------------------+
36. void NewAngle(const char direct, const double step = 1)
37. {
38.     canvas.Erase(ColorToARGB(clrWhite, 255));
39.     Func_01();
40. 
41.     global.Angle = (MathAbs(global.Angle + (step * direct)) < 90 ? global.Angle + (step * direct) : global.Angle);
42.     canvas.TextOut(global.x + _SizeLine + 50, global.y, StringFormat("%.2f", MathAbs(global.Angle)), ColorToARGB(clrBlack));
43.     canvas.TextOut(global.x, global.y + _SizeLine + 50, StringFormat("f(x) = %.2fx", -MathTan(_ToRadians(global.Angle))), ColorToARGB(clrBlack));
44.     canvas.Line(
45.                 global.x - (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
46.                 global.y - (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
47.                 global.x + (int)(_SizeLine * cos(_ToRadians(global.Angle))), 
48.                 global.y + (int)(_SizeLine * sin(_ToRadians(global.Angle))), 
49.                 ColorToARGB(clrForestGreen)
50.             );
51.     canvas.Update(true);
52. }
53. //+------------------------------------------------------------------+

El resultado de la ejecución se puede ver en la animación inmediatamente a continuación.

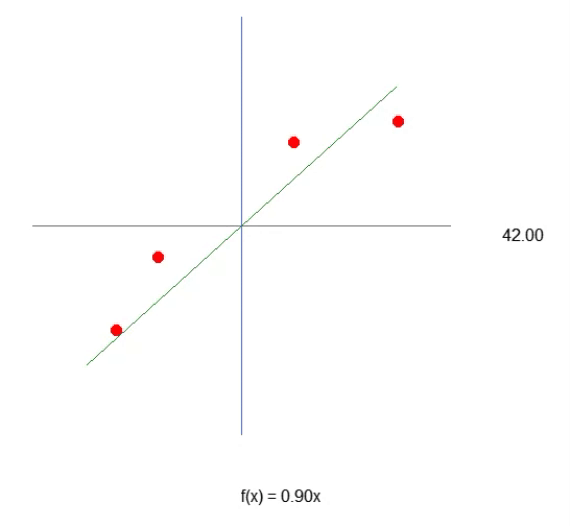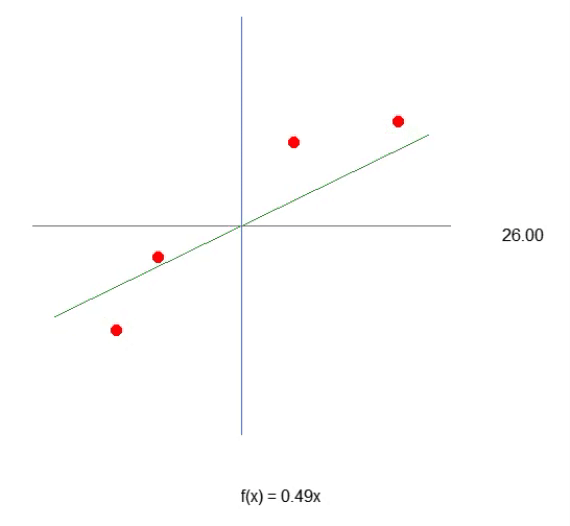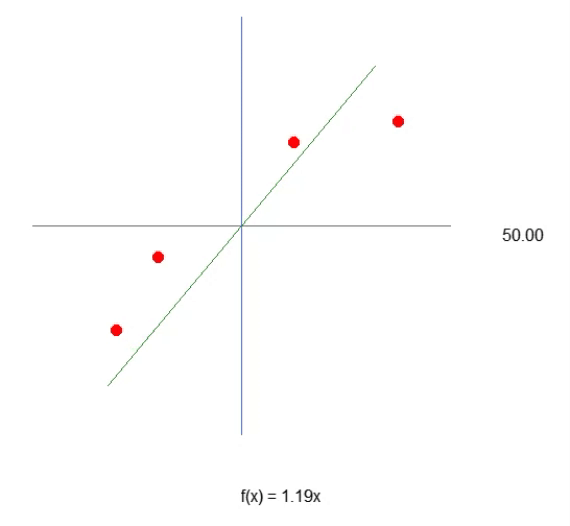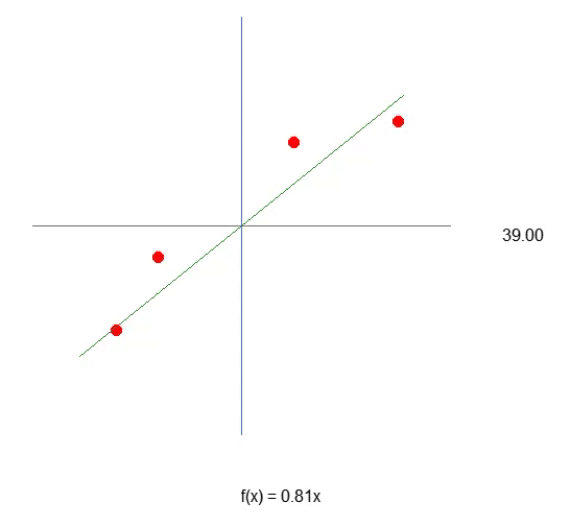
Observa que ahora, debido a la línea 43, tenemos algo muy cercano a lo que sería una ecuación de recta. Vemos que, para crear la fórmula, usaremos la tangente del ángulo, y no el seno o el coseno, como muchos podrían imaginar. Pero esto es solo un intento de generar el valor más adecuado. Sin embargo, aunque estamos consiguiendo generar una ecuación, puedes darte cuenta de que no es sencillo acertar el mejor valor de la inclinación de la recta, es decir, el ángulo del sistema. Puedes intentar hacerlo de manera manual, pero es una tarea extremadamente complicada. A pesar de toda la dificultad que supone generar una ecuación, que nos dé una regresión lineal, debes tener en cuenta que en este momento estamos trabajando con una sola variable en este sistema. Este es precisamente el valor que necesitamos encontrar, como se muestra en la animación anterior.

Pero si se utiliza adecuadamente la matemática, nos permitirá encontrar el valor más adecuado para el ángulo de inclinación. Para hacer esto, necesitaremos usar derivadas en nuestro sistema, así como para entender por qué la tangente es la función trigonométrica que mejor indica la constante que se debe usar en la ecuación. Pero para que tú, mi querido lector, puedas entender esto, vamos a abrir un nuevo tema a fin de no confundir las cosas.

Hacemos uso de derivadas

En este punto es donde la matemática empieza a volverse un tanto confusa para muchos. Sin embargo, no hay motivo para desesperarse, ni para tener miedo o aflicción en el corazón. Lo que debemos hacer es decirle a nuestro código, cómo encontrar el mejor valor para el ángulo, para que la ecuación nos permita acceder a los valores ya conocidos, o aproximarnos lo máximo posible a ellos. De esta forma, la ecuación tendrá como constantes los valores más cercanos posibles a los valores ideales. lo que hará que el conocimiento presente en el gráfico se conserve mínimamente en un formato de ecuación, que en este caso sería una ecuación lineal.

El hecho de que usemos y busquemos una ecuación lineal, que muchas veces se parece a una regresión lineal, se debe a que calcular las constantes necesarias es más sencillo en este tipo de ecuación. No es porque sea la mejor opción para representar los valores en el gráfico, sino simplemente porque es más fácil de calcular. Aun así, en algunos casos, el tiempo de procesamiento puede ser considerable. Pero este será un tema para otra ocasión.

Para calcular dicha ecuación, necesitaremos algunos recursos matemáticos. Esto se debe a que una función afín, que es una función de recta, no nos permite generar una derivada. Esto se debe a que una derivada es, precisamente, una recta que pasa por un punto dado y que se obtiene a partir de cualquier ecuación. Muchos se confunden al explicar esto, pero en esencia, una derivada no es más que una recta tangente en un punto cualquiera de una función. Esta recta tangente se traza en un punto perteneciente a una ecuación, que normalmente creará una curva en el gráfico. Es decir, como la función afín es una recta tangente, la tangente representa tan bien el valor de la constante que multiplica la parte desconocida que nos proporciona la ecuación de esa recta específica. Por esta razón, no se puede trazar una segunda recta tangente utilizando esta ecuación original. Para ello necesitamos algún tipo de artificio. En resumen, da igual qué punto intentemos utilizar para generar la derivada. NO ES POSIBLE CREAR UNA DERIVADA EN UNA FUNCIÓN AFÍN.

Sin embargo, existen algunas formas de hacer posible la creación de la derivada. Esto es lo que comenzaremos a ver en este tema. Para comprender cómo lo haremos, es necesario que tú, mi querido lector, entiendas definitivamente qué es esta derivada, así como el método que utilizaremos para generar dicha derivada y así conseguir crear la función afín que describiría la recta mínimamente ideal. Para hacer esto, utilizaremos una función que permita trazar una derivada. La más sencilla de ellas es la función cuadrática. Para quien no la conozca, esta función tiene la siguiente fórmula:

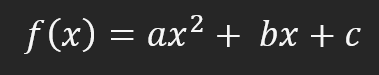
Observa que tenemos un exponente dos en esta ecuación. Este hecho ya nos permite explicar una derivada en el sistema. Sin embargo, podríamos usar cualquier función para generar la curva. Incluso podría ser una función logarítmica. Sin embargo, la función logarítmica no tendría sentido cuando visualicemos otra cosa que necesitaremos hacer después. Por esta razón y para simplificar las cosas al máximo, usaremos esta ecuación cuadrática. Así, cuando uses la fórmula mostrada arriba, conseguirás el gráfico visto a continuación.

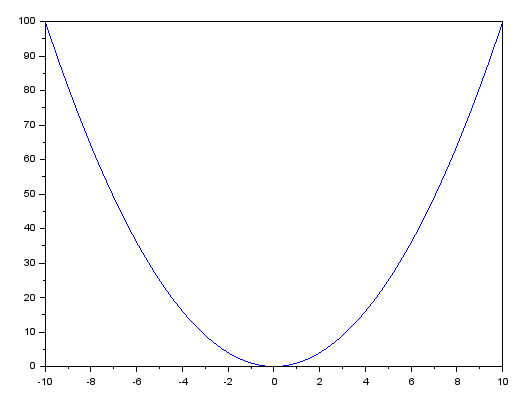
Este gráfico se obtiene al tomar el valor de A como uno y hacer los valores de B y C iguales a cero. Sin embargo, este hecho no importa mucho. Lo que realmente nos importa es la curva que se puede ver en el gráfico. Esa sí nos interesa.

Ahora presta mucha atención, pues lo que se explicará es importante para comprender lo que haremos en nuestro programa, para que logre encontrar la ecuación que tanto deseamos.

Partiendo del gráfico anterior, supongamos que, de ahora en adelante, es importante entender estas suposiciones. Quieres saber el valor de la derivada en el punto en el que X es igual a cuatro. Bien, para hacer esto, deberás trazar una recta tangente que deberá pasar obligatoria y exactamente por el punto donde X es igual a cuatro. Puede parecer fácil: solo hay que tomar una regla y marcar el punto igual a cuatro en la coordenada X. Y ahí intentas hacer una recta que tangente el punto en la curva. Mmm, pero ¿de verdad lograrás trazar la recta tangente haciendo esto? ¡Bien, esto es poco probable!

Es mucho más probable que crees una recta que no será la recta tangente. Por esta razón, es necesario realizar algunos cálculos. Y aquí es donde las cosas comienzan a complicarse. Pero, para no complicar las cosas innecesariamente, no entraré en los detalles del cálculo en sí en este momento. Supondré que sabes cuál es la fórmula de la derivada de una ecuación cuadrática. Luego explicaré cómo se obtiene esta fórmula, para aquellos que desconocen este hecho. La forma en que se consiguen las ecuaciones de derivadas es de suma importancia para nosotros. El resultado final, poco importa. Pero la fórmula que se obtiene de la derivada sí es importante. Así que continuemos.

La derivada de una ecuación cuadrática se obtiene usando la fórmula que se muestra a continuación.

A continuación, muestro ambas notaciones más comunes. Puedes usar la de la derecha o la de la izquierda. Eso no importa. Lo que nos interesa ahora es la fórmula en sí. Es precisamente dos por X. Esta fórmula nos da un valor de ocho, que, en nuestro ejemplo, es el valor de la recta tangente en el punto donde X vale cuatro. Si sabes qué significa este valor ocho, podrás trazar la recta tangente en el punto donde X vale cuatro. Sin embargo, si no sabes qué significa este valor ocho, necesitarás una segunda fórmula para trazar la recta tangente. 

Si no has entendido por qué el valor es ocho, mira la imagen siguiente, en la que queremos que la derivada en X sea igual a cuatro. Para ello, calculamos el valor en esta posición. Como se muestra a continuación.

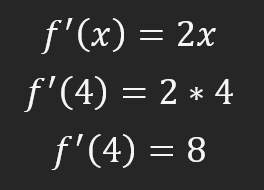
De acuerdo, pero antes de continuar con otros cálculos, comprendamos qué significa este ocho. Este valor significa que, si avanzamos una posición en el eje X, necesitaremos avanzar ocho en el eje Y. Esto nos permite trazar la recta tangente. Tal vez no lo creas y necesites ver esto suceder de hecho. Si este es tu caso, existe una fórmula que permite crear la ecuación de esta recta tangente. Dicha ecuación puede verse a continuación.

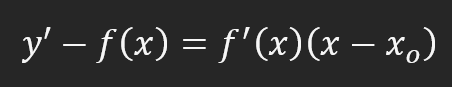
Puede parecer algo aterrador, pero es mucho más sencillo de lo que parece. Sin embargo, esta fórmula es bastante especial. Nos permite crear la ecuación de la recta tangente de la derivada. Aunque la derivada en última instancia será una recta tangente. Pero esto es solo un hecho que menciono como curiosidad. No es algo de lo que debas preocuparte. Muy bien, como ya conocemos gran parte de los valores que se van a utilizar, podemos hacer las sustituciones para encontrar la fórmula de la ecuación de la recta tangente. Esto puede verse a continuación.

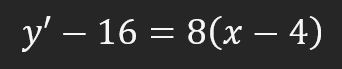
Este es el punto en el que muchos se complican. Pero vamos a comprender de dónde vienen los valores mostrados aquí. El valor 16 es el resultado de la ecuación original. Es decir, hemos colocado en la ecuación cuadrática el valor de "X" que estamos usando en la derivada, es decir, "cuatro". El valor ocho proviene del cálculo efectuado en la función derivada. Una vez más, "X" vale cuatro, y esto también se aplica a la función derivada. El valor cuatro que vemos aquí es el valor de X inicial, que estamos usando en todas las demás ecuaciones. Una vez realizados los cálculos, llegamos a la siguiente fórmula de la recta tangente.

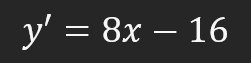
Genial, ahora podemos trazar finalmente la recta tangente basándonos en la ecuación vista arriba. La recta trazada puede verse en la imagen siguiente en rojo.

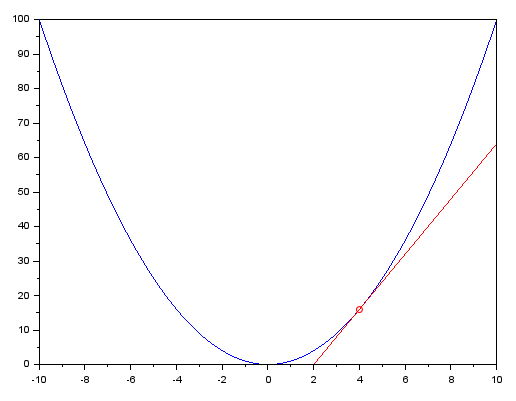
Este gráfico se ha creado con SCILAB. Para quien desee observar con más atención, a continuación se muestra el código utilizado en SCILAB para generar esta figura.

x = [-10:.2:10];
y = x ^ 2;

plot(x, y, 'b-');
plot(4, 16, 'ro');

x = [2:.2:10];
y = 8 * x - 16;

plot(x, y, 'r-');

Estoy añadiendo esto para que percibas, mi querido lector, que no se trata solo de aprender a usar uno u otro programa. El dominio de una u otra lengua no es lo que realmente te capacitará. Muchas veces necesitamos recurrir a diversos programas para poder analizar las cosas de forma clara. Por esta razón, es importante seguir formándose. No importa lo bueno que creas ser. Siempre habrá alguien un poco más capacitado que tú en alguna área concreta. Por esta razón, estudia siempre.

Muy bien, ahora ya tenemos todo el conocimiento que necesitaremos. Pero, ¿qué nos quiere decir esta recta tangente? ¿Y por qué es tan especial para quienes trabajan con redes neuronales? El motivo es que esta recta nos indica hacia dónde debemos ir. O, mejor dicho, hacia dónde debe ir nuestro programa para poder generar la ecuación de regresión lineal.

Pero no se trata solo de eso, esta recta nos explica cómo debemos calcular los desvíos. Y es en este cálculo donde reside la magia de las redes neuronales. ¿No lo ves? ¿O no entiendes cómo es posible hacerlo? Bueno, para entenderlo, es necesario comprender qué genera el cálculo de la derivada, del que te hablé hace poco. Pues, a pesar de que al final usamos una recta tangente, el cálculo no surge de una recta tangente. Surge de otra función trigonométrica. Y es allí donde reside la magia del sistema. Esta magia nos permite crear una solución genérica para todos los casos posibles e imaginables, lo que hace que el sistema neuronal funcione. Entonces, dejaremos esto para otro tema. Para dejar las cosas bien separadas.

La Recta Secante

Aunque todos, cuando hablan de redes neuronales, solo mencionan las derivadas, el secreto no está en la derivada o en la recta tangente. Está en otra recta. La recta secante. Por eso, había cierta resignación por mi parte en escribir sobre el tema de las redes neuronales. De hecho, algunas personas me han pedido que explique sobre el tema. La gran verdad es que, aunque mucha gente habla sobre redes neuronales, muy pocos realmente entienden cómo funcionan. Esto, desde el punto de vista matemático. La programación es la parte fácil; la parte complicada es la matemática. Muchos creen que es necesario usar esta o aquella biblioteca. Uno u otro lenguaje de programación. Pero, en realidad, podemos usar cualquier lenguaje, siempre y cuando entendamos cómo funciona la parte matemática. No estoy aquí para hablar mal de nadie ni para decir que están equivocados en la forma en que explican o dicen las cosas. Cada uno es libre de entender las cosas como desee. Sin embargo, mi deseo es realmente explicar cómo funcionan las cosas. No quiero que tú, mi querido lector, seas un esclavo más de un lenguaje o biblioteca. Quiero que aprendas y entiendas cómo funcionan las cosas por dentro. Por eso he decidido crear estos artículos para hablar sobre el tema.

La idea detrás de la derivada es precisamente buscar el valor de la recta tangente. Esto se debe a que la recta tangente nos indica cuál es la inclinación que está teniendo la función. O, dicho de otro modo, cuál es el error que se produce en la regresión lineal cuando se utiliza en una red neuronal. Por tanto, cuando la recta tangente comience a alcanzar el ángulo de cero grados, el error se acercará a cero. Es decir, la ecuación de la regresión lineal sobre los valores ya existentes en la base de datos se va acercando a los valores ideales. Esto ocurre en ese caso y con esos valores concretos.

Sin embargo, cuando vamos a hacer los cálculos, no usamos la recta tangente. De hecho, usamos la recta secante. Da igual el tipo de red neuronal que se implemente. Si se está realizando un cálculo, no se utiliza la recta tangente, sino la recta secante. Podrías pensar que esto parece mucho más complicado. Pero si has pensado eso, significa que no sabes cómo se obtiene realmente la recta tangente de la derivada. O peor, cómo se obtiene la fórmula de la derivada. Memorizar fórmulas no tiene sentido. Lo correcto es entender por qué la fórmula tiene ese y no otro formato. ¿Recuerdas los cálculos vistos en el tema anterior? ¿Sabes de dónde vinieron? Si no, observa el siguiente gráfico:

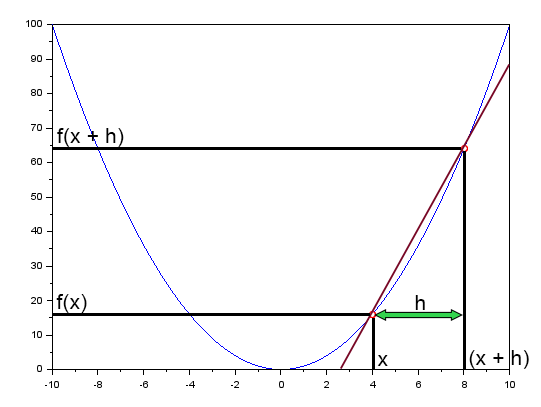
La línea roja en este gráfico es la recta secante. Si antes estabas prestando atención. Ahora quiero que redobles tu atención. Esto será aún más importante que cualquier otra cosa que puedas leer o escuchar sobre redes neuronales.

Aquí estoy utilizando el mismo punto X que en el tema anterior, es decir, el valor cuatro. Así podrás comprender realmente lo que deseo explicar.

Observa que es imposible generar la recta tangente, no importa lo que pienses o imagines. NO SE PUEDE GENERAR UNA RECTA TANGENTE A PARTIR DE UNA CURVA EN EL GRÁFICO. Sin embargo, si usamos la recta secante, podemos obtener la recta tangente. ¿Cómo? Es muy sencillo. Observa que f(x + h) es f(x) desplazado una distancia h. Entonces, si h tiende a cero, la recta secante se convertirá en la recta tangente. Y cuando h sea exactamente cero, la recta secante vista en la imagen será exactamente la recta tangente. Es decir, en este punto, la recta tangente nos dará la inclinación de la derivada de la función en ese punto. De acuerdo, pero aún no lo entiendo. Bien, mi querido lector, pongamos lo que se ve arriba de una forma que sea un poco menos confusa. Así quizá quede más claro.

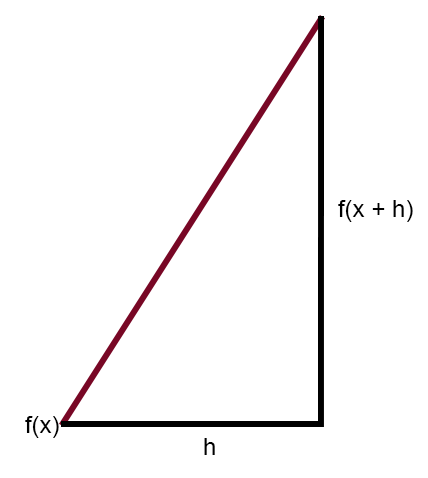
En esta imagen de arriba se ve exactamente lo mismo que en la imagen anterior. Así creo que quedará más clara la idea de usar la secante. Y, por qué, a diferencia de lo que todos afirman, que usamos la recta tangente o las derivadas cuando usamos una red neuronal, en realidad usamos la recta secante para que la máquina pueda generar la ecuación correcta.

Si reduces el valor de h, comenzarás a acercarte al f(x), pero este h nunca será realmente cero. Esto cuando estamos usando redes neuronales. Puede ser un valor muy pequeño. Cuánto más pequeño sea este valor dependerá de una cosa que veremos más adelante. Esa cosa se conoce como: La locura de la red neuronal. Cuanto más pequeño sea este h, menos loca será la red neuronal, pero cuanto mayor sea, más loca será. ¿Pero por qué? El motivo es la convergencia. Durante los cálculos que veremos después, notarás que esta convergencia tiende al valor de h. Esto hará que la ecuación generada al final tienda a variar dentro de esta convergencia. Por esta razón, este h es importante. Puede parecer complicado de explicar, pero verás que es mucho más sencillo en la práctica. Sin embargo, aún no he llegado al punto que quiero mostrar. Si aplicas esta imagen de arriba en una fórmula, obtendrás el siguiente cálculo.

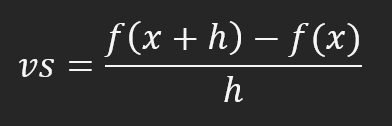
Esta fórmula nos indica cuánto está la recta secante de la recta tangente. Sin embargo, el cálculo que se utiliza realmente es el que se muestra en la imagen siguiente.

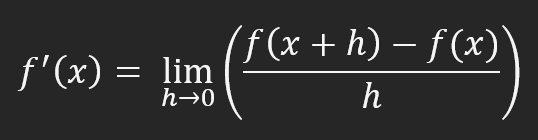
Esta ecuación explica todo lo que necesitas saber sobre redes neuronales. Esta es la razón por la que se dice que las redes neuronales usan derivadas. Porque esta ecuación es la que genera esos cálculos que muchos simplemente memorizan: las fórmulas de las derivadas. Listo. No hay más que explicar o decir. Todo lo que necesitamos es la ecuación mostrada arriba. Con esto puedo concluir y seguir con mi vida tranquilamente.

Consideraciones finales

Pero espera un momento. No has explicado cómo se usa esta ecuación de la recta secante ni has explicado por qué lo aclara todo. ¿Cómo que no hay más nada que explicar? ¡¿Estás bromeando?! De hecho, querido lector, solo he comenzado a introducir la cuestión. Sin embargo, quiero que estudies este artículo con calma. En el próximo artículo sobre redes neuronales, mostraré cómo usar el conocimiento presentado aquí para generar la ecuación correcta.