Datenwissenschaft und maschinelles Lernen (Teil 14): Mit Kohonenkarten den Weg in den Märkten finden

Einführung

Kohonenkarten oder Selbstorganisierende Karten (Self-Organizing Maps, SOM) oder Self-Organizing Feature Map (SOFM). Es ist eine nicht überwachte maschinelle Lerntechnik, die zur Erstellung einer niedrigdimensionalen (typischerweise zweidimensionalen) Darstellung eines höherdimensionalen Datensatzes verwendet wird, wobei die topologische Struktur der Daten erhalten bleibt. Zum Beispiel: Ein Datensatz mit p Variablen, gemessen in n Beobachtungen, könnte als Cluster von Beobachtungen mit ähnlichen Werten für die Variablen dargestellt werden. Diese Cluster können dann als „zweidimensionale Karte“ visualisiert werden, sodass die Beobachtungen in den proximalen Clustern mehr ähnliche Werte aufweisen als die Beobachtungen in den distalen Clustern. Dadurch können hochdimensionale Daten leichter visualisiert und analysiert werden.

Kohonen-Maps wurden von einem finnischen Mathematiker namens Teuvo Kohonen in den 1980er Jahren entwickelt.

Übersicht

Eine Kohonenkarte besteht aus einem Netz von Neuronen, die mit ihren Nachbarneuronen verbunden sind. Während des Trainings werden dem Netz die Eingabedaten präsentiert, und jedes Neuron berechnet seine Ähnlichkeit mit den Eingabedaten. Das Neuron mit der höchsten Ähnlichkeit wird als Gewinner bezeichnet, und seine Gewichte werden so angepasst, dass sie besser zu den Eingabedaten passen.

Mit der Zeit passen auch die benachbarten Neuronen ihre Gewichte an, um dem Gewinnerneuron ähnlicher zu werden, was zu einer topologischen Anordnung der Neuronen in der Karte führt. Dieser Prozess der Selbstorganisation ermöglicht es der Kohonenkarte, komplexe Beziehungen zwischen den Eingabedaten in einem niedrigdimensionalen Raum darzustellen. Das macht sie nützlich für die Datenvisualisierung und das Clustering.

Lernalgorithmus

Das Ziel dieses Algorithmus in der Selbstorganisierenden Karte ist es, verschiedene Teile des Netzes dazu zu bringen, auf bestimmte Eingabemuster ähnlich zu reagieren. Dies ist zum Teil dadurch begründet, wie visuelle, auditive und andere Informationen in einigen Teilen des menschlichen Gehirns verarbeitet werden.

Schauen wir uns an, wie dieser Algorithmus funktioniert, wenn es um mathematische Begriffe und MQL5-Code geht.

Am Algorithmus beteiligte Schritte

Beim Versuch, diesen Algorithmus zu kodieren, sind vier wichtige Schritte zu beachten:

Schritt 01: Initialisieren der Gewichte . Es können zufällige Werte angenommen werden. Andere Parameter wie die Lernrate und die Anzahl der Cluster werden in dieser Phase ebenfalls initialisiert.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters;
   
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
 }

Wie üblich werden die Parameter im Konstruktor der Klasse CKohonenMaps initialisiert.

Die Kohonenkarte ist eine Data-Mining-Technik. Nachdem alles gesagt und getan ist, müssen wir die verarbeiteten Daten erhalten, weshalb wir das boolesche Argument save_clusters=true sehen, mit dem wir die Cluster erhalten, die Kohonenkarte für uns erhalten hat.

Schritt 02: Berechnen des euklidischen Abstands zwischen den einzelnen Eingaben und ihren jeweiligen Gewichten

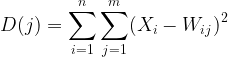
wobei:

  = Eingangsvektor

 = Vektor der Gewichte

double CKohonenMaps:: Euclidean_distance(const vector &v1, const vector &v2)
  {
   double dist = 0;

   if(v1.Size() != v2.Size())
      Print(__FUNCTION__, " v1 and v2 not matching in size");
   else
     {
      double c = 0;
      for(ulong i=0; i<v1.Size(); i++)
         c += MathPow(v1[i] - v2[i], 2);

      dist = MathSqrt(c);
     }

   return(dist);
  }

Um diese Formel anzuwenden und alles zu verdeutlichen, benötigen wir einen einfachen Datensatz, der uns bei der Kodierung und beim Testen der Dinge hilft.

   matrix Matrix = {
                     {1.2, 2.3},
                     {0.7, 1.8},
                     {3.6, 4.8},
                     {2.8, 3.9},
                     {5.2, 6.7},
                     {4.8, 5.6}
                   };
   
   maps = new CKohonenMaps(Matrix); //Giving our kohonen maps class data

Wenn der Konstruktor aufgerufen wird und die Gewichte generiert werden, sind die folgenden Ergebnisse zu sehen.

CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) w Matrix
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) [[0.005340739158299509,0.01220740379039888]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [0.5453352458265939,0.9172643208105716]]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) Matrix
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1) [[1.2,2.3]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [0.7,1.8]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [3.6,4.8]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [2.8,3.9]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [5.2,6.7]
CS      0       15:52:27.572    Self Organizing map (EURUSD,H1)  [4.8,5.6]]

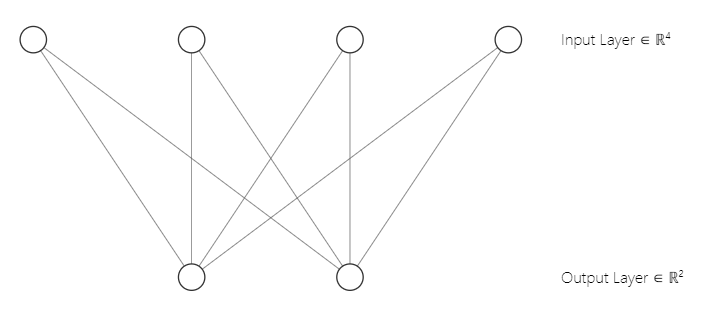
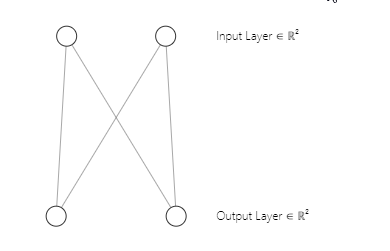
Sie haben vielleicht bemerkt, dass die Architektur unseres neuronalen Netzes ein [2 Eingänge und 2 Ausgänge] ist. Deshalb haben wir eine 2x2-Matrix von Gewichten. Diese Matrix wurde unter Berücksichtigung von [2 Spalten der Eingabematrix mit der Markierung n und 2 ausgewählten Clustern mit der Markierung m] aus der untenstehenden Codezeile, die wir im ersten Teil gesehen haben, erstellt.

   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 

Zur Verdeutlichung: So sieht die Architektur unseres neuronalen Netzes einer Kohonenkarte aus;

Schritt 03: Finden des Index i der gewinnenden Einheit, sodass D(j) minimal ist. Mit einfachen Worten: Finde den Einheitscluster. Dies bringt mich zu einem wichtigen Thema über Kohonenkarten, die wettbewerbsorientiertes Lernen ermöglichen.

Wettbewerbsorientiertes Lernen.

Eine Selbstorganisierende Karte ist eine Art von künstlichem neuronalem Netz, das im Gegensatz zu anderen Arten von künstlichen neuronalen Netzen, die mit Hilfe von Fehlerkorrektur-Lernen wie Backpropagation mit Gradientenabstieg trainiert werden, während Kohonenkarten mit Hilfe von kompetitivem Lernen trainiert werden.

Beim kompetitiven Lernen konkurrieren die Neuronen in der Kohonenkarte miteinander, um als das Neuron, das den Eingabedaten am ähnlichsten ist, zum „Gewinner“ zu werden.

Während der Trainingsphase wird jeder Eingabedatenpunkt der Kohonenkarte vorgelegt, und die Ähnlichkeit zwischen den Eingabedaten und dem Gewichtsvektor jedes Neurons wird berechnet. Das Neuron, dessen Gewichtsvektor den Eingabedaten am ähnlichsten ist, wird als Gewinner oder als „best-matching unit“ (BMU, beste, passende Einheit) bezeichnet.

Die BMU wird auf der Grundlage des kleinsten euklidischen Abstands zwischen den Eingabedaten und dem Gewichtsvektor des Neurons ausgewählt. Das Gewinnerneuron aktualisiert dann seinen Gewichtsvektor, um den Eingabedaten ähnlicher zu werden. Die verwendete Formel zur Aktualisierung der Gewichte ist als Kohonen-Lernregel bekannt, die den Gewichtsvektor des Gewinnerneurons und seiner Nachbarneuronen näher an die Eingabedaten heranführt.

Zur Codierung dieses Schritts 03. Es sind nur ein paar Zeilen Code erforderlich.

   vector D(m); //Euclidean distance btn clusters  | Remember m is the number of clusters selected

   for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 

Denken Sie immer daran, dass das Neuron, das die Klasse mit dem geringsten euklidischen Abstand von allen produziert, der Gewinnercluster ist.

Durch wettbewerbsorientiertes Lernen lernt die Kohonenkarte, eine topologische Darstellung der Eingabedaten in einem niedrigdimensionalen Raum zu erstellen, wobei die Beziehungen zwischen den Eingabedaten erhalten bleiben. 

Schritt 04: Aktualisierung der Gewichte.

Die Aktualisierung der Gewichte kann mit der nachstehenden Formel vorgenommen werden.

wobei:

 = Neuer Gewichtungsvektor

 = Vektor der alten Gewichte

 = Lernrate

 = Vektor der Eingaben

Im Folgenden finden Sie den Code für diese Formel:

//--- weights update
   
   ulong min = D.ArgMin(); //winning cluster
    
   vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
   
   w_matrix.Col(w_new, min);

Im Gegensatz zu anderen Arten von künstlichen neuronalen Netzen, bei denen alle Gewichte für eine bestimmte Schicht ineinandergreifen, berücksichtigen Kohonenkarten die Gewichte für ein bestimmtes Cluster und verwenden sie nur für die Suche nach diesem Cluster.

Wir sind mit den Schritten fertig und unser Algorithmus ist vollständig. Es ist an der Zeit, ihn auszuführen, um zu sehen, wie alles funktioniert.

Nachfolgend finden Sie den gesamten Code für den Algorithmus bis zu diesem Punkt.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters;
   
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
      
   vector D(m); //Euclidean distance btn clusters
   
   
   for (uint epoch=0; epoch<epochs; epoch++)
    {
      double epoch_start = GetMicrosecondCount()/(double)1e6, epoch_stop=0; 
      
      for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 
         
   //--- weights update
         
         ulong min = D.ArgMin();
          
         vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
         
         w_matrix.Col(w_new, min);
         
       }
  
      epoch_stop =GetMicrosecondCount()/(double)1e6;    
      
      printf("Epoch [%d/%d] | %sElapsed ",epoch+1,epochs, CalcTimeElapsed(epoch_stop-epoch_start));
      
    }  //end of training

//---

  #ifdef DEBUG_MODE
      Print("\nNew weights\n",w_matrix);
  #endif 
   
 }

Ausgaben:

CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [2.122748018266242,1.822857430002081] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [1.434132188481296,1.100846180984197] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [5.569896531530945,5.257391342266398] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [4.36622216533946,4.000958814345993] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [8.053842751911217,7.646959164093921] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Euc distance [6.966950064745546,6.499246789416081] Winning cluster 1
CS      0       04:13:26.617    Self Organizing map (EURUSD,H1) Epoch [1/100] | 0.000 Seconds Elapsed 
....
....
....
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [0.7271897806071723,4.027137175049654] Winning cluster 0
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [0.08133608432880858,4.734224801594559] Winning cluster 0
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [4.18281664576938,0.5635073709012016] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [2.979092473547668,1.758946102746018] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [6.664860479474853,1.952054507391296] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Euc distance [5.595867985957728,0.8907607121421737] Winning cluster 1
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) Epoch [100/100] | 0.000 Seconds Elapsed 
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) 
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) New weights
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1) [[0.75086979456201,4.028060179594681]
CS      0       04:13:26.622    Self Organizing map (EURUSD,H1)  [1.737580668068743,5.173650598091957]]

Großartig, alles funktioniert, unsere Kohonenkarten konnte unsere primäre Matrix ‚clustern‘.

   matrix Matrix = {
                     {1.2, 2.3}, //Into cluster 0
                     {0.7, 1.8}, //Into cluster 0
                     {3.6, 4.8}, //Into cluster 1
                     {2.8, 3.9}, //Into cluster 1
                     {5.2, 6.7}, //Into cluster 1
                     {4.8, 5.6}  //Into cluster 1
                   };

Das ist genau das, was es sein sollte, das ist großartig, aber diese Ergebnisse zu präsentieren und sie auf einem Diagramm zu visualisieren, ist nicht so einfach, wie es scheint. Wir haben zwei Cluster, einer ist eine 2x2-Matrix, der andere ist eine 4x2-Matrix. Der eine hat 4 Werte, der andere 8 Werte. Wenn Sie sich daran erinnern, dass ich in dem Artikel über K-Means-Clustering Schwierigkeiten hatte, die Cluster zu präsentieren, weil die Größe der Cluster so unterschiedlich ist, wurden diesmal extreme Maßnahmen ergriffen.

Tensoren im maschinellen Lernen

Ein Tensor ist eine Verallgemeinerung von Vektoren und Matrizen innerhalb eines mehrdimensionalen Feldes. Einfach ausgedrückt ist ein Tensor ein Array, das Matrizen und Vektoren enthält. In Python sieht das so aus;

# create tensor
from numpy import array

T = array([
  [[1,2,3],    [4,5,6],    [7,8,9]],
  [[11,12,13], [14,15,16], [17,18,19]],
  [[21,22,23], [24,25,26], [27,28,29]],
  ])

Tensoren sind die grundlegende Datenstruktur, die von Frameworks für maschinelles Lernen wie TensorFlow, PyTorch, and Keras.

Tensoren werden in Algorithmen für maschinelles Lernen für Operationen wie Matrixmultiplikation, Faltung und Pooling verwendet. Tensoren werden auch zum Speichern und Manipulieren der Gewichte und Verzerrungen neuronaler Netze während des Trainings und der Inferenz verwendet. Insgesamt sind Tensoren eine wichtige Datenstruktur beim maschinellen Lernen, die eine effiziente Berechnung und Darstellung komplexer Daten ermöglicht. 

Ich musste die Bibliothek Tensors.mqh importieren. Lesen Sie darüber in meinem GitHub wiki,

Ich habe Tensoren hinzugefügt, um uns bei der Sammlung von Clustern zu jedem Tensor zu helfen.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters;
   
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
   
   Print("w Matrix\n",w_matrix,"\nMatrix\n",Matrix);
   
   vector D(m); //Euclidean distance btn clusters
   
   
   for (uint epoch=0; epoch<epochs; epoch++)
    {
      double epoch_start = GetMicrosecondCount()/(double)1e6, epoch_stop=0; 
      
      for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 
         
   //--- weights update
         
         ulong min = D.ArgMin();
         
         if (epoch == epochs-1) //last iteration
            cluster_tensor.TensorAppend(Matrix.Row(i), min);
          
         vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
         
         w_matrix.Col(w_new, min);
         
         //Print("New w_Matrix\n ",w_matrix);
       }
  
      epoch_stop =GetMicrosecondCount()/(double)1e6;    
      
      printf("Epoch [%d/%d] | %sElapsed ",epoch+1,epochs, CalcTimeElapsed(epoch_stop-epoch_start));
      
    }  //end of the training

//---

  #ifdef DEBUG_MODE
      Print("\nNew weights\n",w_matrix);
  #endif 
  
//---

   Print("\nclusters");
   cluster_tensor.TensorPrint();
}

Ausgaben:

CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) clusters
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) TENSOR INDEX <<0>>
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) [[1.2,2.3]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [0.7,1.8]]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) TENSOR INDEX <<1>>
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1) [[3.6,4.8]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [2.8,3.9]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [5.2,6.7]
CS      0       04:13:26.624    Self Organizing map (EURUSD,H1)  [4.8,5.6]]

Toll, jetzt sind die Cluster in ihren jeweiligen Tensoren gespeichert, Zeit, etwas Nützliches daraus zu machen.

Extrahieren von Clustern

Extrahieren wir nun die Cluster, indem wir sie in CSV-Dateien speichern.

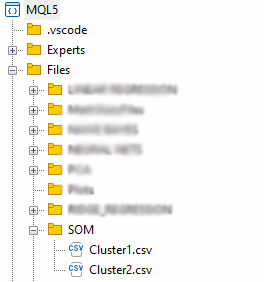
  matrix mat= {};
  
  if (save_clusters)
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
          mat = this.cluster_tensor.Tensor(i); //Obtain a matrix located at I index in a cluster tensor
         
         string header[]; ArrayResize(header, (int)mat.Cols());
         
         for (int k=0; k<ArraySize(header); k++) 
           header[k] = "col"+string(k);
         
         if (this.matrix_utils.WriteCsv("SOM\\Cluster"+string(i+1)+".csv",mat,header))
            Print("Clusters CSV files saved under the directory Files\\SOM");
       }

Die Dateien werden im Verzeichnis SOM innerhalb des übergeordneten Verzeichnisses Files gespeichert.

Wir sind mit der Extraktion der Daten fertig, aber der wesentliche Teil der Kohonenkarten besteht darin, die Cluster zu visualisieren und die Karten zu zeichnen, die der Algorithmus für uns vorbereitet hat. Python-Bibliotheken und andere Frameworks verwenden in der Regel Hit-Maps. Wir werden den Curve Plot für diese Bibliothek verwenden.

   vector v;  
   matrix plotmatrix(rows, m); 
   
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
          mat = this.cluster_tensor.Tensor(i);
          
          v  = this.matrix_utils.MatrixToVector(mat);
          
          plotmatrix.Col(v, i);
       }   
    
    this.plt.ScatterCurvePlotsMatrix("kom",plotmatrix,"Map","clusters","clusters");    

Ausgaben:

Cool, alles funktioniert und die Darstellung konnte die Daten wie beabsichtigt gut visualisieren, probieren wir den Algorithmus an etwas Nützlichem aus.

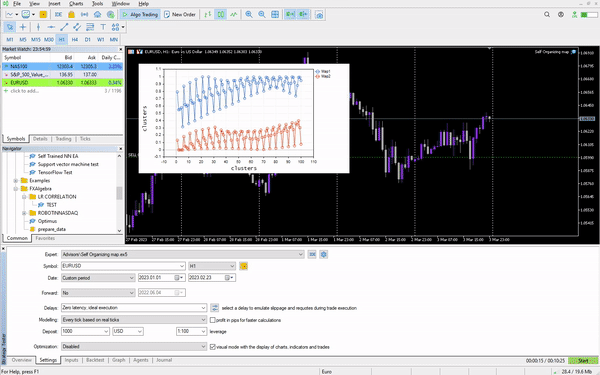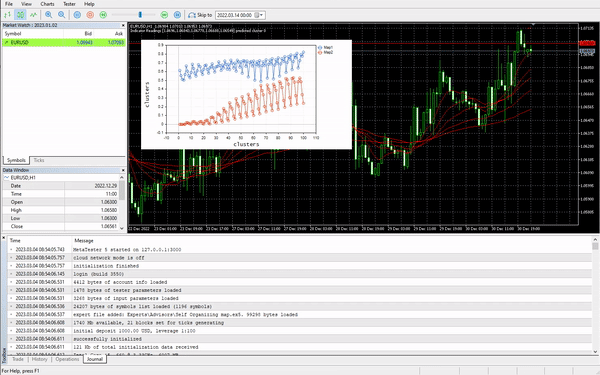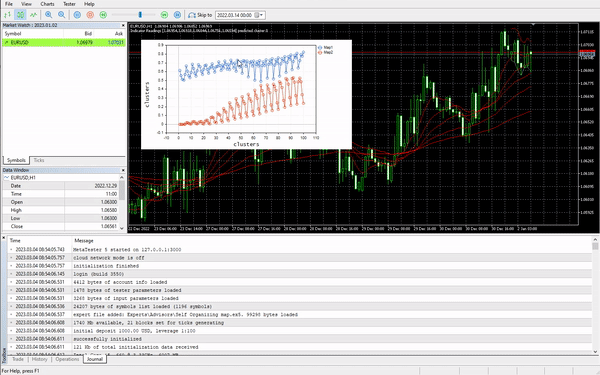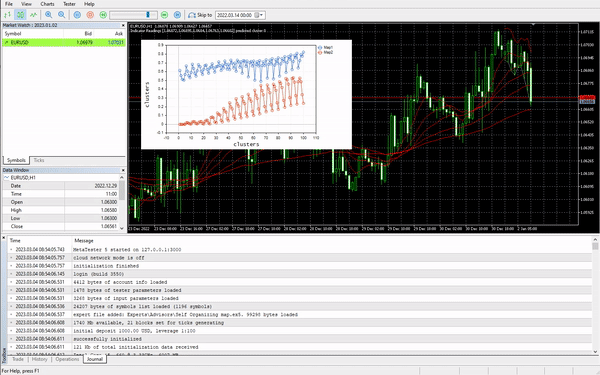
Clustering Indikatorwerte.

Sammeln wir 100 Balken für verschiedene Indikatoren mit 5 gleitenden Durchschnitten und versuchen wir, sie mithilfe von Kohonenkarten zu clustern. Diese Indikatoren beziehen sich auf dasselbe Chart, denselben Zeitrahmen und denselben Preis, mit Ausnahme der Zeitrahmen, die für jeden Indikator unterschiedlich sind.

#include <MALE5\Neural Networks\kohonen maps.mqh> 
#include <MALE5\matrix_utils.mqh>
 

CMatrixutils matrix_utils;
CKohonenMaps *maps;

input int bars = 100;

int handles[5];
int period[5] = {10,20,30,50,100};
matrix Matrix(bars,5);
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   
   vector v;
   
   for (int i=0; i<5; i++)
      {
         handles[i] = iMA(Symbol(),PERIOD_CURRENT,period[i],0,MODE_LWMA,PRICE_CLOSE);
         matrix_utils.CopyBufferVector(handles[i],0,0,bars, v);
         
         Matrix.Col(v, i); //store indicators into a matrix
      }
    
   
   maps = new CKohonenMaps(Matrix,true,2,0.01,1000);
      
//---
   return(INIT_SUCCEEDED);
  }

Ich habe die Lernrate/alpha = 0,01 und die Epochen = 1000 gewählt, unten sind die Kohonenkarten.

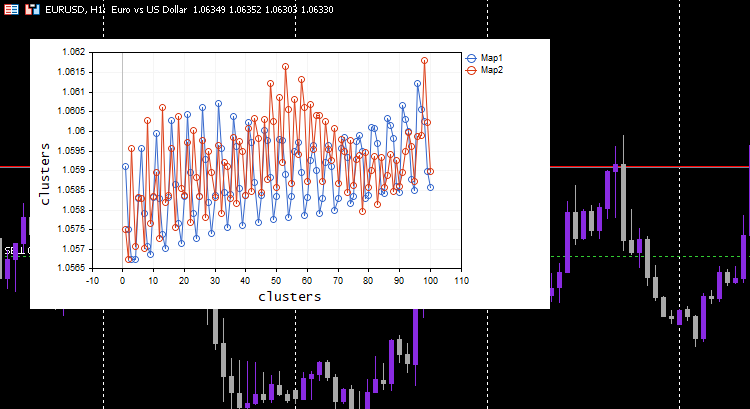
Sieht seltsam aus, ich musste die Protokolle auf dieses merkwürdige Verhalten untersuchen und fand es.

CS      0       06:19:59.911    Self Organizing map (EURUSD,H1) clusters
CS      0       06:19:59.911    Self Organizing map (EURUSD,H1) TENSOR INDEX <<0>>
CS      0       06:19:59.911    Self Organizing map (EURUSD,H1) [[1.059108363197969,1.057514381244092,1.056754472954214,1.056739184229631,1.058300613902105]
CS      0       06:19:59.911    Self Organizing map (EURUSD,H1)  [1.059578181379783,1.057915286006,1.057066064352063,1.056875795994335,1.05831249905062]
....
....
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1)  [1.063954363197777,1.061619428863266,1.061092386932678,1.060653270504107,1.059293304991227]
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1)  [1.065106545015954,1.062409714577555,1.061610946072463,1.06098919991587,1.059488318852614…]
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1) TENSOR INDEX <<1>>
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1) []
CS      0       06:19:59.912    Self Organizing map (EURUSD,H1) CMatrixutils::MatrixToVector Failed to turn the matrix to a vector rows 0 cols 0

Der Tensor für den zweiten Cluster war leer, d.h. der Algorithmus hat ihn nicht vorhergesagt, alle Daten wurden als zu Cluster 0 gehörig vorhergesagt.

Normalisieren Sie immer Ihre Variablen

Ich habe es schon ein paar Mal gesagt und werde es auch weiterhin sagen: Die Normalisierung Ihrer Eingabedaten ist für alle Modelle des maschinellen Lernens, die Sie kennen, unerlässlich. Schauen wir uns das Ergebnis an, nachdem die Daten normalisiert wurden.

Ich habe mich für die Normalisierungstechnik des Min-Max scaler entschieden.

#include <MALE5\Neural Networks\kohonen maps.mqh>
#include <MALE5\preprocessing.mqh>
#include <MALE5\matrix_utils.mqh>

CPreprocessing *pre_processing;
CMatrixutils matrix_utils;
CKohonenMaps *maps;

input int bars = 100;

int handles[5];
int period[5] = {10,20,30,50,100};
matrix Matrix(bars,5);
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   
   vector v;
   
   for (int i=0; i<5; i++)
      {
         handles[i] = iMA(Symbol(),PERIOD_CURRENT,period[i],0,MODE_LWMA,PRICE_CLOSE);
         matrix_utils.CopyBufferVector(handles[i],0,0,bars, v);
         
         Matrix.Col(v, i);
      }
   
   pre_processing = new CPreprocessing(Matrix, NORM_MIN_MAX_SCALER);
   
   maps = new CKohonenMaps(Matrix,true,2,0.01,1000);
    
   
//---
   return(INIT_SUCCEEDED);
  }

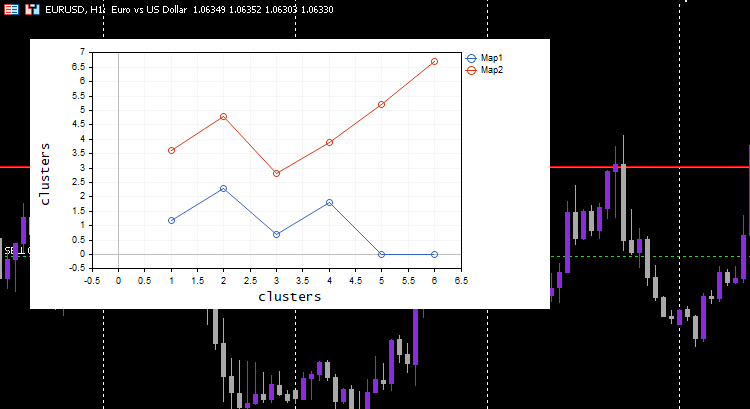
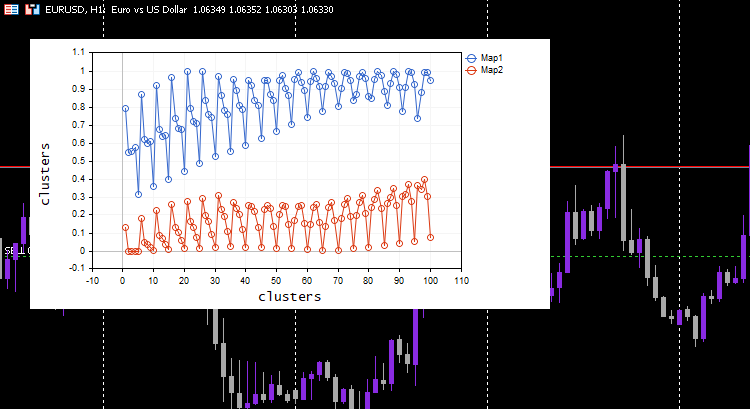
Dieses Mal wurden schöne Kohonenkarten auf der Chart angezeigt.

Großartig, aber die Normalisierung der Daten verwandelt die Daten in kleinere Werte, aber als jemand, der nur seine Daten clustern will, um die Muster zu verstehen und die extrahierten Daten in anderen Programmen zu verwenden, muss dieser Normalisierungsprozess in den Kern des Algorithmus integriert werden, Die Daten müssen normalisiert und umgekehrt normalisiert werden, sodass die erhaltenen Cluster in den ursprünglichen Werten sind, da die Clustertechniken die Daten nicht verändern, sondern sie nur gruppieren. Der Prozess der Normalisierung und der umgekehrten Normalisierung kann mit dieser Preprocessing-Klasse erfolgreich durchgeführt werden.

CKohonenMaps::CKohonenMaps(matrix &matrix_, bool save_clusters=true, uint clusters=2, double alpha=0.01, uint epochs=100, norm_technique NORM_TECHNIQUE=NORM_MIN_MAX_SCALER)
 {
   Matrix = matrix_;
   
   n = (uint)matrix_.Cols();
   rows = matrix_.Rows();
   m = clusters; 
   
   pre_processing = new CPreprocessing(Matrix, NORM_TECHNIQUE);
   cluster_tensor = new CTensors(m);
   
   w_matrix =matrix_utils.Random(0.0, 1.0, n, m, RANDOM_STATE); 
   
   #ifdef DEBUG_MODE
      Print("w Matrix\n",w_matrix,"\nMatrix\n",Matrix);
   #endif 
   
   vector D(m); //Euclidean distance btn clusters
   
   
   for (uint epoch=0; epoch<epochs; epoch++)
    {
    
      double epoch_start = GetMicrosecondCount()/(double)1e6, epoch_stop=0; 
      
      for (ulong i=0; i<rows; i++)
       {
         for (ulong j=0; j<m; j++)
           {
             D[j] = Euclidean_distance(Matrix.Row(i),w_matrix.Col(j));
           }
         
         #ifdef DEBUG_MODE  
            Print("Euc distance ",D," Winning cluster ",D.ArgMin());
         #endif 
         
   //--- weights update
         
         ulong min = D.ArgMin();
         
         if (epoch == epochs-1) //last iteration
            cluster_tensor.TensorAppend(Matrix.Row(i), min); 

          
         vector w_new =  w_matrix.Col(min) + (alpha * (Matrix.Row(i) - w_matrix.Col(min)));
         
         w_matrix.Col(w_new, min);
       }
  
      epoch_stop =GetMicrosecondCount()/(double)1e6;    
      
      printf("Epoch [%d/%d] | %sElapsed ",epoch+1,epochs, CalcTimeElapsed(epoch_stop-epoch_start));
      
    }  //end of the training

//---

  #ifdef DEBUG_MODE
      Print("\nNew weights\n",w_matrix);
  #endif 

//---
   
   matrix mat= {};

   vector v;  
   matrix plotmatrix(rows, m); 
   
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
          mat = this.cluster_tensor.Tensor(i);
          
          v  = this.matrix_utils.MatrixToVector(mat);
          
          plotmatrix.Col(v, i);
       }   
    
    this.plt.ScatterCurvePlotsMatrix("kom",plotmatrix,"Map","clusters","clusters");       

//---

  
  if (save_clusters)
     for (uint i=0; i<this.cluster_tensor.TENSOR_DIMENSION; i++)
       {
         mat = this.cluster_tensor.Tensor(i);
         pre_processing.ReverseNormalization(mat);
         cluster_tensor.TensorAdd(mat, i);
         
         string header[]; ArrayResize(header, (int)mat.Cols());
         
         for (int k=0; k<ArraySize(header); k++) 
           header[k] = "col"+string(k);
         
         if (this.matrix_utils.WriteCsv("SOM\\Cluster"+string(i+1)+".csv",mat,header))
            Print("Clusters CSV files saved under the directory Files\\SOM");
       }

//---

   Print("\nclusters");
   cluster_tensor.TensorPrint();

 }

Um Ihnen zu zeigen, wie das funktioniert, musste ich zu dem einfachen Datensatz zurückkehren, den wir am Anfang hatten.

   matrix Matrix = {
                     {1.2, 2.3},
                     {0.7, 1.8},
                     {3.6, 4.8},
                     {2.8, 3.9},
                     {5.2, 6.7},
                     {4.8, 5.6}
                   };
   
   maps = new CKohonenMaps(Matrix,true,2,0.01,1000);
    

Ausgaben:

CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) w Matrix
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) [[0.005340739158299509,0.01220740379039888]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.5453352458265939,0.9172643208105716]]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Matrix
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) [[0.1111111111111111,0.1020408163265306]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0,0]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.6444444444444445,0.6122448979591836]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.4666666666666666,0.4285714285714285]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [1,1]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1)  [0.911111111111111,0.7755102040816325]]
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Epoch [1/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Epoch [2/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.660    Self Organizing map (EURUSD,H1) Epoch [3/1000] | 0.000 Seconds Elapsed 
...
...
...
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) Epoch [999/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) Epoch [1000/1000] | 0.000 Seconds Elapsed 
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) 
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) New weights
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1) [[0.1937869656464888,0.8527427060068337]
CS      0       07:14:44.674    Self Organizing map (EURUSD,H1)  [0.1779676215121214,0.7964618795904062]]
CS      0       07:14:44.725    Self Organizing map (EURUSD,H1) Clusters CSV files saved under the directory Files\SOM
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) Clusters CSV files saved under the directory Files\SOM
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) 
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) clusters
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) TENSOR INDEX <<0>>
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1) [[1.2,2.3]
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1)  [0.7,1.8]
CS      0       07:14:44.726    Self Organizing map (EURUSD,H1)  [2.8,3.899999999999999]]
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1) TENSOR INDEX <<1>>
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1) [[3.600000000000001,4.8]
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1)  [5.2,6.7]
CS      0       07:14:44.727    Self Organizing map (EURUSD,H1)  [4.8,5.6]]

Dieser Prozess funktioniert wie Zauberei. Trotz eines maschinellen Lernmodells, das die normalisierten Daten verwendet, kann das Modell die Daten clustern und trotzdem die nicht normalisierten/ursprünglichen Daten ausgeben, obwohl nichts passiert ist. Beachten Sie, dass es sich bei den gezeichneten Clustern um normalisierte Daten handelt. Dies ist wichtig, da es schwierig ist, Daten mit unterschiedlichen Skalen zu zeichnen. Diesmal war das Diagramm für die Cluster auf dem einfachen Testdatensatz viel besser;

Erweitern der Kohonenkarten

Obwohl die Kohonenkarten und andere Data-Mining-Techniken nicht in erster Linie dazu gedacht sind, Vorhersagen zu treffen, da sie über die erlernten Parameter verfügen, die die Gewichte sind, können wir sie so erweitern, dass wir die Cluster erhalten, wenn wir ihnen neue Daten geben.

uint CKohonenMaps::KOMPredCluster(vector &v)
 {
  vector temp_v = v;
  pre_processing.Normalization(v);
  
  if (n != v.Size())
   {
     Print("Can't predict the cluster | the input vector size is not the same as the trained matrix cols");
     return(-1);
   }
   
   vector D(m); //Euclidean distance btn clusters
   
   for (ulong j=0; j<m; j++)
       D[j] = Euclidean_distance(v, w_matrix.Col(j));
   
   v.Copy(temp_v);
   return((uint)D.ArgMin());
 }

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+

vector CKohonenMaps::KOMPredCluster(matrix &matrix_)
 {   
   vector v(n);
   
   if (n != matrix_.Cols())
      {
         Print("Can't predict the cluster | the input matrix Cols is not the same size as the trained matrix cols");
         return (v);
      }
   
   for (ulong i=0; i<matrix_.Rows(); i++)
      v[i] = KOMPredCluster(matrix_.Row(i));
      
    return(v);
 }

Geben wir ihm die neuen Daten, die es noch nicht gesehen hat. Sie und ich wissen, welcher Cluster zu [0,5, 1,5] und [5,5, 6] gehört. Diese Daten gehören zu den Clustern 0 bzw. 1.

   maps = new CKohonenMaps(Matrix,true,2,0.01,1000); //Training
   
   matrix new_data = {
         {0.5,1.5},
         {5.5, 6.0}
      };
   
   Print("new data\n",new_data,"\nprediction clusters\n",maps.KOMPredCluster(new_data)); //using it for predictions

Ausgaben:

CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) new data
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) [[0.5,1.5]
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1)  [5.5,6]]
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) prediction clusters
CS      0       07:46:00.857    Self Organizing map (EURUSD,H1) [0,1]

Cool, die Kohonenkarten haben sie richtig vorhergesagt.

Kohonenkarten im Strategie-Tester

Der Algorithmus funktioniert perfekt und ich konnte feststellen, dass er Cluster 0 vorhersagt, wenn der Markt oben ist und umgekehrt, ich bin nicht sicher, ob die Implikation richtig ist, ich habe das Verhalten nicht gut analysiert, Ich überlasse das Ihnen.  Wenn das der Fall ist, können wir die Kohonenkarten sogar als Indikator verwenden, denn das tun die meisten Indikatoren.

Vorteile der Kohonenkarten

Kohonenkarten haben mehrere Vorteile, darunter:

1. Die Fähigkeit, nicht-lineare Beziehungen zwischen den Eingabedaten und der Ausgabekarte zu erfassen, bedeutet, dass sie mit komplexen Mustern und Strukturen in den Daten umgehen können, die mit linearen Methoden nicht so leicht zu erfassen sind.
2. Sie können Muster und Strukturen in den Daten finden, ohne dass Sie die Daten beschriften müssen. Dies kann in Situationen nützlich sein, in denen beschriftete Daten knapp oder teuer zu beschaffen sind.
3. Sie tragen dazu bei, die Dimensionalität der Eingabedaten zu reduzieren, indem sie diese auf einen niedriger-dimensionalen Raum abbilden. Dies kann dazu beitragen, die Rechenkomplexität einer nachgelagerten Aufgabe wie Regression und Klassifizierung zu verringern.
4. Beibehaltung der topologischen Beziehungen zwischen den Eingabedaten und der Ausgabekarte, d. h. benachbarte Neuronen in der Karte entsprechen ähnlichen Regionen im Eingaberaum, was bei der Datenexploration und -visualisierung hilfreich sein kann
5. Kann robust gegenüber Rauschen und Ausreißern in den Eingabedaten sein, solange das Rauschen zu groß ist.

Nachteile von Kohonenkarten

1. Die Qualität der endgültigen selbstorganisierenden Karten kann von der Initialisierung des Gewichtsvektors abhängen. Wenn die Initialisierung schlecht ist, kann die SOM zu einer suboptimalen Lösung konvergieren oder in einem lokalen Minimum stecken bleiben.
2. Empfindlich auf Parameterabstimmung: Die Leistung des SOM kann von der Wahl der Hyperparameter abhängen, z. B. von der Lernrate, der Nachbarschaftsfunktion und der Anzahl der Neuronen. Die Abstimmung dieser Parameter kann zeitaufwändig sein und erfordert Fachwissen.
3. Rechenintensiv und speicherintensiv für große Datenmengen. Die Größe der SOM skaliert mit der Anzahl der Eingabedatenpunkte, sodass große Datensätze eine große Anzahl von Neuronen und eine lange Trainingszeit erfordern können.
4. Fehlen von formalen Konvergenzkriterien: Im Gegensatz zu einigen Algorithmen des maschinellen Lernens, wie z. B. neuronalen Netzen, gibt es für SOMs keine formalen Konvergenzkriterien. Dies kann es schwierig machen, festzustellen, wann das Training konvergiert und wann es zu beenden ist.

Die Quintessenz

Kohonenkarten oder selbstorganisierende Maps (SOMs) sind ein innovativer Ansatz für den Handel, der Händlern helfen kann, sich auf den Märkten zurechtzufinden. Durch den Einsatz von unüberwachtem Lernen können Kohonenkarten Muster und Strukturen in Marktdaten erkennen, sodass die Händler fundierte Entscheidungen treffen können. Wie wir gesehen haben, waren Kohonenkarten in der Lage, nicht-lineare Beziehungen in den Daten zu erkennen und die Daten in ihre jeweiligen Gruppen einzuteilen. Allerdings sollten sich Händler der potenziellen Nachteile von Kohonenkarten bewusst sein, wie z. B. die Empfindlichkeit gegenüber der Initialisierung, die fehlende formale Konvergenz und andere oben genannte Nachteile. Insgesamt haben Kohonenkarten das Potenzial, eine wertvolle Ergänzung für das Instrumentarium eines Händlers zu sein, aber wie jedes Instrument sollten sie mit Sorgfalt und unter Berücksichtigung ihrer Stärken und Schwächen eingesetzt werden.

Passen Sie auf sich auf.

Verfolgen Sie die Entwicklung und Änderungen an diesem Algorithmus auf meinem GitHub-Repository https://github.com/MegaJoctan/MALE5.

Datei	Inhalt & Verwendung
Self Organizing map.mq5	EA-Datei zum Testen des in diesem Artikel beschriebenen Algorithmus.
kohonen maps.mqh	Eine Bibliothek, die den Algorithmus für die Kohonenkarten enthält.
plots.mqh	Eine Bibliothek mit Funktionen zum Zeichnen der Darstellung (plots) auf dem Chart in MT5.
preprocessing.mqh	Enthält Funktionen zur Normalisierung und Vorverarbeitung der Eingabedaten.
matrix_utils.mqh	Enthält zusätzliche Funktionen für Matrixoperationen in MQL5.
Tensoren.mqh	Eine Bibliothek mit Klassen zur Erstellung von Tensoren.

Referenzartikel:

• Matrix Utils, Erweiterung der Funktionalität der Standardbibliothek für Matrizen und Vektoren

• Datenwissenschaft und maschinelles Lernen — Neuronales Netzwerk (Teil 02): Entwurf von Feedforward-NN-Architekturen

• Datenwissenschaft und maschinelles Lernen — Neuronales Netzwerk (Teil 01): Feed Forward Neural Network entmystifiziert

• Datenwissenschaft und maschinelles Lernen (Teil 06): Gradientenverfahren

• Tensor ist ein einfacher Weg zu neuronalen Netzen

• Preprocessing Bibliothek