Rebuy-Algorithmus: Handelssimulation mit mehreren Währungen

Inhalt

• Einführung
• Erläuterung der Notwendigkeit einer Handelssimulation
• Mathematisches Modell der Preissimulation mit Diskretisierungslogik
• Modellprüfung
• Test-EA
• Schlussfolgerung

Einführung

Im vorigen Artikel habe ich Ihnen viele nützliche Funktionen gezeigt, die Sie wahrscheinlich noch nicht kannten, aber das Interessanteste liegt noch vor Ihnen - die Recherche oder Handelssimulation. Manchmal reicht ein Strategietester nicht aus. Dies ist zwar ein sehr praktisches Instrument, um den Markt kennen zu lernen, aber es ist nur der erste Schritt. Wenn Sie den vorangegangenen Artikel aufmerksam gelesen haben, kennen Sie den Grund wahrscheinlich schon.

Erläuterung der Notwendigkeit einer Handelssimulation

Der Grund für die Handelssimulation liegt direkt in der Tatsache, dass die Menge der historischen Daten für jedes Handelsinstrument begrenzt ist. Dieses Problem kann nur erkannt werden, wenn Sie das Material verstehen, das ich im vorherigen Artikel oder auf eine andere Art und Weise bereitgestellt habe.  

Der Kern des Problems besteht darin, dass eine einfache Geschichte der Kurse nicht immer ausreicht, da diese Geschichte aus einer Vielzahl von zufälligen und nicht zufälligen Weltereignissen entsteht und es unzählige Szenarien gibt, wie sich das Ereignis entwickeln könnte. Im Moment versuche ich, die Dinge so einfach wie möglich zu beschreiben, aber wenn wir zur Sprache der Wahrscheinlichkeitstheorie übergehen und gleichzeitig die Errungenschaften des vorherigen Artikels nutzen, verstehen wir, dass sich die Geschichte der Kurse aller uns bekannten Instrumente anders entwickeln könnte.

Diese Tatsache ist offensichtlich, wenn Sie den Film „Zurück in die Zukunft“ gesehen haben. Er enthält viele Fehler und komische Ungereimtheiten aus wissenschaftlicher Sicht, aber dennoch vermittelt dieser Film die Hauptidee der hier vermittelten Botschaft. Der Kern der Botschaft ist, dass eine Version der sich entfaltenden Ereignisse für uns nicht ausreicht, und wir sollten ihre maximale Anzahl in Betracht ziehen. In der Geschichte gibt es nur eine Version, deren Umfang für eine objektive Bewertung manchmal nicht ausreicht. Zum Beispiel haben vor nicht allzu langer Zeit viele Broker einige der beliebtesten Krypto-Symbole erworben. Das ist sehr gut für die Möglichkeit, diese Symbole zu testen und zu handeln. Der Nachteil ist jedoch, dass es nicht genügend historische Daten gibt, um nachhaltige Handelssysteme für EAs zu entwickeln, die mit Balken arbeiten.

Die Simulation wird es ermöglichen, künstliche Instrumente zu schaffen und ihre Kurse jedes Mal auf eine völlig andere Weise zu generieren. Dadurch erhalten wir den größtmöglichen Rahmen für die Untersuchung des mathematischen Rebuy-Modells und anderer wichtiger mathematischer Prinzipien, über die ich im vorherigen Artikel gesprochen habe. Ein weiterer wichtiger Vorteil ist, dass wir in der Lage sein werden, eine unbegrenzte Anzahl unabhängiger Instrumente für den Parallelhandel zu simulieren. Letztlich gibt es keine Beschränkung mehr für die Dauer der Prüfung und die Anzahl der unabhängig gehandelten Instrumente. Natürlich handelt es sich dabei nicht um reale Kurse, aber sie unterscheiden sich in keiner Weise von realen Kursen in Bezug auf die Preisgesetze.

Mathematisches Modell der Preissimulation mit Diskretisierungslogik

Im Zusammenhang mit unserer Aufgabe ist die Verwendung des Ansatzes der „willkürlichen Diskretisierung“ mehr als ausreichend, denn eine starke Diskretisierung wird die Effizienz unseres Algorithmus nur erhöhen, und sei es nur, weil solche Systeme sich automatisch besser gegen Streuungen wehren. Ich habe jedoch einen Algorithmus entwickelt, der auch die Simulation von Ticks ermöglicht. Schließlich ist ein Tick der kleinste Zeitrahmen. Die Zeit zwischen den Tick-Ankünften ist sehr unterschiedlich, aber wenn man die durchschnittliche Zeit zwischen den Ticks berechnet, kann man die Ticks in erster Näherung imitieren.

Unter einem Balken verstehen wir in diesem Fall eine feste Zeitspanne, die für uns visuell gut wahrnehmbar ist. Aber das ist nur bequem, weil man Ihnen gesagt hat, dass es bequem ist, und Sie können nicht davon wegkommen, weil alle Handelsterminals speziell auf dieses Paradigma zugeschnitten sind. Dies ist jedoch bei weitem nicht der beste Weg, um Preise zu diskretisieren. Ich denke, viele von Ihnen sind mit „Renko“ vertraut. Dieser Ansatz der Preisdiskretisierung ist nur für eines gedacht - um von der Zeit wegzukommen. Der Wert dieses Ansatzes kann bei verschiedenen Ansätzen und Händlern völlig unterschiedlich sein. Ich verwende dieses Beispiel jedoch nur, um eine der alternativen Möglichkeiten zur Diskretisierung von Preisreihen aufzuzeigen. Dieses Beispiel soll Ihnen meines Erachtens verdeutlichen, dass wir im Rahmen unserer Aufgabe eine völlig andere und ungewohnte Diskretisierungslogik verwenden werden, die es uns jedoch ermöglicht, die Preisbildung sehr einfach und effizient zu modellieren, ohne übermäßige Rechenkosten zu verursachen.

Für die korrekte Konstruktion eines effizienten und wirtschaftlichen Paradigmas in Bezug auf die Rechenleistung, schauen Sie sich das folgende Bild an:

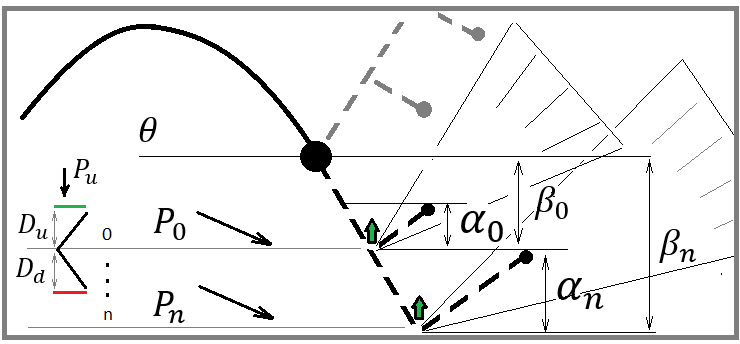
Die Abbildung zeigt einige mögliche Szenarien für einen Preisrückgang (rollback). Diese beiden Rückgänge stellen für mich zwei beliebige Punkte dar, die absolut beliebig gewählt werden können, und die Wahlmethode ist nicht von Bedeutung. Wichtig ist, dass wir jeden beliebigen Punkt wählen können, der als wahrscheinlicher Umkehrpunkt in Frage kommt.

Das Wort „wahrscheinlich“ sollte jedem Mathematiker sofort sagen, dass es an einem bestimmten Punkt eine gewisse Wahrscheinlichkeit für ein bestimmtes Ereignis gibt. In unserem Fall können wir sagen, dass ein bestimmtes Ereignis willkürlich sein kann. Das Ereignis eine Rückganges ist durch die Ober- und Untergrenze des Preise gekennzeichnet. Die Wahrscheinlichkeit dieses Ereignisses kann wie folgt berechnet werden:

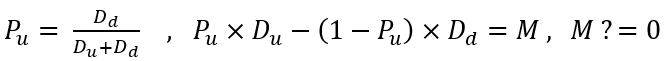
Hier ist die Wahrscheinlichkeit für das Erreichen der oberen Grenze und die Gleichung, aus der diese Formel abgeleitet ist. Die Gleichung beschreibt die mathematische Erwartung des Preisanstiegs, wenn es kein prädiktives Moment gibt. Das Fehlen eines prädiktiven Moments führt zu einer Nullerwartung, aber in unserer Simulation möchte ich in der Lage sein, die Parameter des prädiktiven Moments so anzupassen, dass wir die flachen Merkmale unserer simulierten Preisbildung bequem verstärken oder abschwächen können. Letztendlich werden Sie sehen, wie sich dies auf den Rebuy-Algorithmus auswirkt, und Sie werden ein funktionierendes mathematisches Modell für den diversifizierten Handel mit dem Rebuy-Algorithmus erhalten. Aber zuerst möchte ich Ihnen die ganze Mathematik dahinter erklären.

Derzeit können wir sehen, dass all diese Gleichungen schön und scheinbar nützlich sind, aber bisher gibt es keinen geeigneten Algorithmus für die Anpassung der Flachheit (Rückgang) des Instruments. Um einen solchen Algorithmus zu entwickeln, müssen wir die folgenden Werte eingeben:

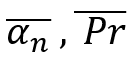
Der erste Wert ist eigentlich der durchschnittliche Wert „alpha“. Man kann es auch die mathematische Erwartung des Kursrückgangs nach einer willkürlichen Abwärtsbewegung nennen. Der zweite Wert ist der mathematische Erwartungswert des Rollback-Prozentsatzes, ausgedrückt als relativer Wert zu seiner vorherigen Bewegung. Das Wesen dieser Mengen ist das gleiche, mit der einzigen Ausnahme:

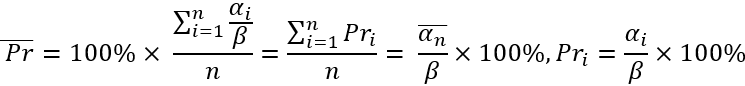
Hier zeige ich Ihnen nur, wie diese Größen zusammenhängen und wie sie berechnet werden. In unserem Modell werden wir den durchschnittlichen Rollback regulieren, indem wir seinen durchschnittlichen Prozentsatz festlegen, und wir werden die Logik umkehren, indem wir ihn zur Bestimmung des durchschnittlichen Preis-Rollbacks verwenden. Sie müssen zugeben, dass der durchschnittliche Rollback-Prozentsatz als Regulierungswert für den Parameter der Marktabflachung sehr geeignet ist. Wenn dieser Prozentsatz auf Null gesetzt wird, dann wird tatsächlich eine zufällige Preisgestaltung verlangt (dies ist nur ein Beispiel). Das Einzige, was ich anmerken möchte, ist, dass alle Kursrückgänge relativ zum Punkt „theta“ betrachtet werden. Ich hoffe, Sie verzeihen mir die Freiheiten, die ich mir bei der Notation genommen habe, denn dieses Material stammt vollständig von mir, und es gibt nicht einen Tropfen der Arbeit eines anderen hier. Diese Gleichungen sind notwendig, um zu verstehen, was ich als Nächstes tun werde.

Ein weiteres wichtiges Merkmal jeder Preisbildung ist die Volatilität (Preisänderungsrate). Dieser Parameter ist mit der Zeit verbunden, und wir müssen uns eine äußerst bequeme Methode ausdenken, um diesen Wert einzustellen. Dies sollte es uns ermöglichen, die Preisgestaltung einfach und effektiv zu kontrollieren und den Zeitpunkt der Handelszyklen korrekt zu berechnen. Im Moment mag das alles noch zu kompliziert erscheinen, aber es wird viel klarer werden, wenn ich in die Praxis gehe und Ihnen zeige, wie es funktioniert. Betrachten wir zunächst die Volatilität.

In der klassischen Interpretation ist die Volatilität etwas anders zu verstehen, nämlich als das Ausmaß der möglichen relativen Preisbewegung von einem Minimum zu einem Maximum und umgekehrt von einem Maximum zu einem Minimum. Dies ist eine sehr unbequeme Art, die Preisbewegungsrate festzulegen. Es gibt eine weitaus bequemere Methode, bei der die durchschnittliche Kursentwicklung über einen bestimmten Zeitraum gemessen wird. Wir haben solche Segmente. Sie werden Balken (bars) genannt. In der Tat haben wir das Verteilungsgesetz einer Zufallsvariablen des Preisänderungsmoduls pro Balken. Je größer dieser Wert ist, desto größer ist die Preisvolatilität (Änderungsrate). Wir geben die folgenden Einstellungen ein:

Zur Frage, ob die Zufallsverteilung von „S“ simuliert werden sollte, kann ich sagen, dass dies nicht notwendig ist. Das Einzige, was Sie wissen müssen, ist, dass die tatsächliche Preisgestaltung von der Methode, die wir im mathematischen Modell verwenden, abweichen wird. Ich schlage vor, den Wert von „S“ auf die Höhe seines Durchschnittswertes festzulegen. Da die Zeit jedes Schritts bereits festgelegt ist, erhalten wir sowohl die Größe des Schritts als auch seine Dauer in Zeit. So können wir anschließend die jährliche Rentabilität des Handelssystems bewerten und die durchschnittliche Dauer des Handelszyklus messen. Werfen wir nun einen Blick auf das folgende Bild, um weiterzukommen:

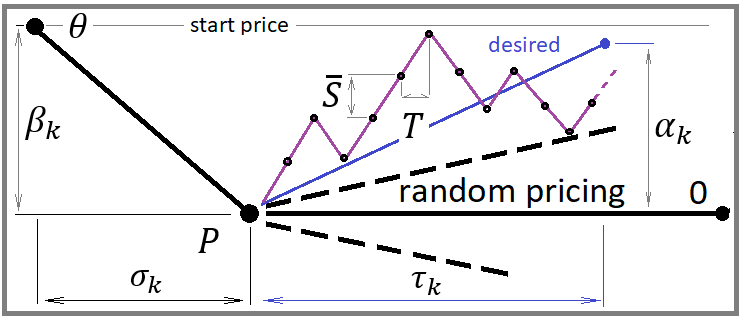
Da wir die Preisbildung für jeden Schritt simulieren müssen, ist es offensichtlich, dass der Schritt entweder nach unten oder nach oben gehen kann. Wenn wir einen gleichwertigen Schritt in beide Richtungen setzen, erhalten wir eine zufällige Preisbildung. Das bedeutet, dass wir diese Schrittwahrscheinlichkeiten ändern sollten, um die Flachheit zu regulieren. Dies wird die Bereitstellung einer Art von „Schwerkraft“, um den Ausgangspunkt des Preises, von dem der Preis begann, nach oben oder unten zu bewegen sein. In unserem Fall müssen wir Folgendes realisieren:  

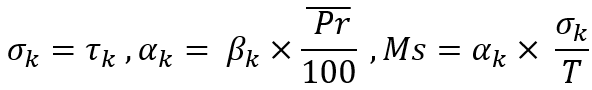
In diesem Fall habe ich zur Vereinfachung des Modells angenommen, dass die gewählte durchschnittliche Preisumkehr genau die gleiche Zeit benötigt, die für den vorherigen Preisanstieg oder -rückgang aufgewendet wurde. Der Zweck dieser Berechnungen ist es, die momentane Erwartung für einen einzelnen Schritt zu bestimmen, um die Wahrscheinlichkeit zu berechnen, dass der Schritt nach oben erfolgt. Mit dieser Wahrscheinlichkeit wird die Simulation des neuen Schrittes angepasst. Dieser Wert wird nach jedem Schritt für jedes einzelne Handelsinstrument neu errechnet.

Hier ist ein sehr wichtiger Punkt: Wenn wir jedes Instrument separat beschreiben, müssen wir ein Array mit Daten über die durchschnittliche Preisänderung für jedes Instrument erstellen. Aber im Rahmen meiner Aufgabe sind alle Instrumente gleich, und daher ist es möglich, ein allgemeines und bequemeres Merkmal für die Beschreibung einer Stufe in Form eines durchschnittlichen Prozentsatzes der Preisänderung einzuführen:

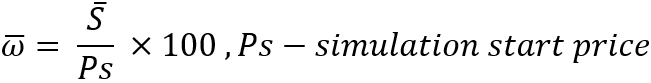
Der Vorteil dieses Merkmals ist, dass es relativ zu jedem aktuellen Preis unveränderlich ist. Wenn wir außerdem von idealen Instrumenten ausgehen, spielt es keine Rolle, zu welchem Preis die Simulation beginnt, da dies keinen Einfluss auf den Gewinn oder Verlust während des Tests hat. Nachdem wir dies verstanden haben, können wir den Parallelhandel für unseren Rebuy-Algorithmus sicher ab einem Preis von, sagen wir, 1 beginnen. Nach der Bestimmung dieses Wertes ist es bereits möglich, den Schrittwert selbst zu berechnen:

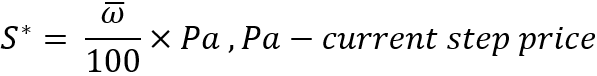
Nun, da wir die Stufe kennen, können wir feststellen, dass wir alle notwendigen Daten gesammelt haben, um die Wahrscheinlichkeit zu berechnen, dass es eine Stufe nach oben geben wird. Dazu verwenden wir unsere ursprüngliche Formel für die mathematische Erwartung eines Schrittes mit einigen Substitutionen:

Nach dieser Substitution können wir diese Gleichung für die Wahrscheinlichkeit eines Aufwärtsschritts lösen und erhalten schließlich die fehlende Wahrscheinlichkeit:

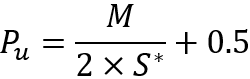
Zu beachten ist nur, dass diese Gleichungen für den Fall gelten, dass der Simulationspreis unter den Ausgangspunkt fällt. Aber was tun, wenn der Preis nach oben geht? Alles ist sehr einfach. Wir müssen nur das Spiegelchart betrachten. Dies ist möglich, da wir von perfekten Instrumenten ausgehen. Wenn wir uns vorstellen, dass das Preischart durch einen bestimmten Ausdruck „P = P(t)“ beschrieben werden kann, dann sieht die Umkehrung des Instruments wie folgt aus:

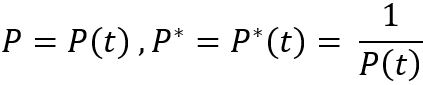
Diese Umkehrung sorgt dafür, dass die Gleichungen für die Situation funktionieren, in der der Preis über den Ausgangspunkt gestiegen ist. Das Einzige, was wir verstehen müssen, ist, dass alle Mengen in unseren Ausdrücken, die mit Preisen berechnet werden (z. B. Deltas), den bereits umgerechneten Preis hoch minus erste Potenz verwenden müssen.

Lassen Sie uns nun ein Handelsmodell erstellen. Ich habe es einseitig gemacht, da es ursprünglich für den Spot-Handel mit Kryptowährungen gedacht war. Dieses Handelsmodell eignet sich jedoch auch für Forex-Währungspaare. Wenn das Modell zum Beispiel nur bei einem Rebuy funktioniert, dann wird es auch bei einem Resell funktionieren. Das einzige Problem ist, dass wir während des Tests die oberen Halbwellen auslassen und nur an den unteren arbeiten werden. Um das Handelsmodell zu verwalten, habe ich die folgenden Merkmale eingegeben:

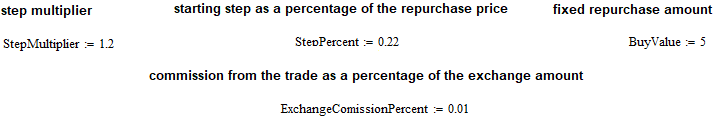
Der Startkauf beginnt mit dem Preis „1-Schritt-Prozent/100“, und der Rebuy-Schritt entspricht dem „Schritt-Prozent/100“. Eigentlich müsste immer noch mit dem Ausgangspreis multipliziert werden, aber da wir diesen Preis mit eins gleichsetzen, wird die Berechnung der Stufe stark vereinfacht. Darüber hinaus wurde die Möglichkeit einer wiederkehrenden Erhöhung der Schrittweite eingeführt. So kann beispielsweise jeder nächste Rebuy-Schritt im Vergleich zum vorhergehenden entweder um das N-fache erhöht oder in gleicher Weise verringert werden. All dies hängt vom Wert des entsprechenden Koeffizienten ab. Der Rebuy-Schritt wird in der unteren Währung des Instruments gemessen (nicht in der Basiswährung). Diese Regel gilt auch für Kryptowährungen.

Zur Vereinfachung des Modells wird davon ausgegangen, dass die verwendeten Handelsinstrumente in diesem Fall in etwa wie folgt aussehen: EURUSD, GBPUSD, NZDUSD usw., d. h. die untere Währung des gehandelten Instruments muss bei allen gehandelten Instrumenten dieselbe sein. Dies vereinfacht ein bereits sehr komplexes Modell, aber es reicht völlig aus, um die mathematischen Prinzipien aus dem letzten Artikel zu testen und die Rebuy-Algorithmen zu optimieren. Der Spread wird in unserem Fall in Form einer Provision berücksichtigt, was dasselbe ist. Im Allgemeinen sind die Parameter für den Prototyp des mathematischen Modells ausreichend. Werfen wir einen Blick auf den Rebuy-Prozess:

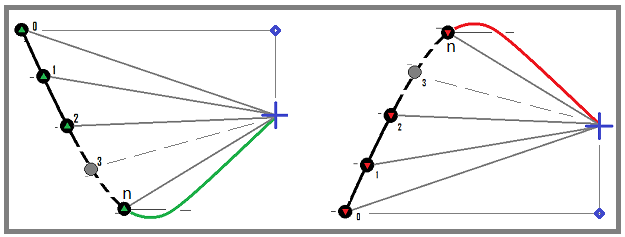
Wir werden die erste Option (mit dem grünen Rückwärtsgang) verwenden. Das heißt, Sie kaufen die Basiswährung und verkaufen sie dann zum blauen Punkt. Mit diesem Ansatz wird jeder abgeschlossene Handelszyklus profitabel sein. Das Gleiche gilt für den Verkaufszyklus mit einer roten Rückkehrbewegung, aber wir werden sie, wie gesagt, auslassen, damit das Modell so vielseitig wie möglich ist und sich sowohl für den Handel auf dem Devisenmarkt als auch für den Spot-Handel an Kryptowährungsbörsen eignet.

Das Modell ist so angelegt, dass die Handelshebelwirkung keine Rolle spielt. Ich denke, dass ich Ihnen genügend theoretische Informationen gegeben habe, damit Sie den praktischen Teil besser verstehen können, und es kann jemandem helfen, sein eigenes Modell auf der Grundlage meiner Ergebnisse zu bauen.

Modellprüfung

Beginnen wir unsere Tests mit verschiedenen Varianten der Kurserzeugung. Um Ihnen den Unterschied bei der Erstellung von Kursen zu verdeutlichen, stellen wir das Modell zunächst auf die folgende Position ein:

Mit dieser Einstellung erreichen wir eine zufällige Preisbildung. Schauen wir uns einige Kurse an, die unter diesem Gesichtspunkt erstellt wurden:

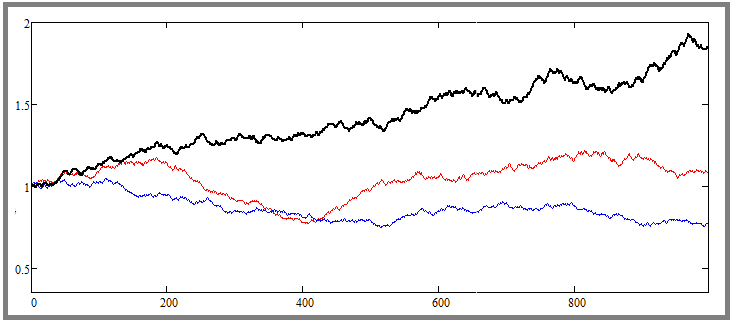
Dies ist ein Chart eines mathematischen Modells, das zwei zufällig aus dem Deck entnommene Kurse und eine weitere zusätzliche Kurve zeigt, die die größte Abweichung vom Ausgangskurs aufweist. Im mathematischen Modell kann die erforderliche Anzahl der parallel zu simulierenden Instrumente festgelegt werden, und es ist natürlich, dass es viele davon gibt, und es wird immer eines geben, das am wenigsten symmetrisch und am volatilsten ist. Aber ich hoffe, Sie verstehen, dass dies nur das Ergebnis probabilistischer Prozesse ist. Setzen wir nun den Parameter an eine andere Stelle:

Wie Sie vielleicht schon verstanden haben, erzeugt dieser Schritt eine Rückkehr der Schwerkraft des Preises zum Ausgangspunkt. Das Ergebnis sieht wie folgt aus:

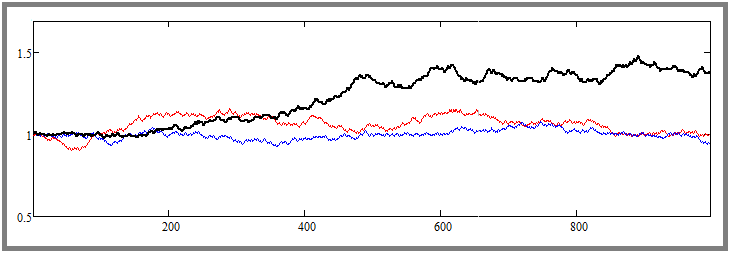
Beachten Sie den Unterschied zwischen dem vorherigen und dem aktuellen Bild. Hier haben wir bereits die flache Einstellung in die gewünschte Richtung erzwungen. Wir können sehen, dass die Kurven stark gegen den Startpreis gedrückt werden - dasselbe geschah mit dem schwarz gefärbten volatilsten Kurs. In beiden Beispielen werden für jedes Werkzeug genau eintausend Schritte simuliert. Später werde ich diese Zahlen erhöhen und mit ihnen herumspielen, um zu verstehen, wie das Ganze funktioniert und welche Parameter genau betroffen sind.

Nun muss festgelegt werden, welche Parameter für die Prüfung des künstlichen Handels verwendet werden sollen und wie diese Prüfung erfolgen soll. Erinnern wir uns kurz an die Fragen, die ich im vorherigen Artikel beantwortet habe. Einfacher und verständlicher ausgedrückt, lauteten sie wie folgt:

1. Die Bedingung für die Rentabilität von Handelssystemen mit Rebuy.
2. Nähert sich die Gewinnlinie einer perfekten Geraden an, wenn endlos mit idealen Handelsinstrumenten gehandelt wird?
3. Nähert sich die Gewinnlinie einer perfekten Geraden an, wenn die Anzahl der Instrumente bei einem festen Handelszeitraum ins Unendliche steigt?

Lassen Sie uns herausfinden, wie es um die Rentabilität bestellt ist. Dazu führen wir zunächst einen Parallelhandel mit Zufallspreisen durch und betrachten das Ergebnis. Sie wird ungefähr wie folgt aussehen:

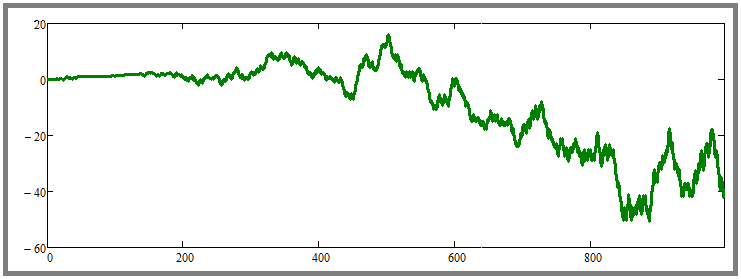
In verschiedenen Generationen wurden entweder rentable oder unrentable Kurven ermittelt. Es ist noch nicht klar, aber die Bestätigung für die Sinnlosigkeit von Rebuys im Falle einer zufälligen Preisfestsetzung könnte ein extremer Anstieg der Anzahl der parallel gehandelten Instrumente sein. Schauen wir uns an, was passiert, wenn wir ihre Anzahl auf, sagen wir, hundert erhöhen und gleichzeitig die Anzahl der Simulationsschritte für jedes Werkzeug auf 10.000 erhöhen:

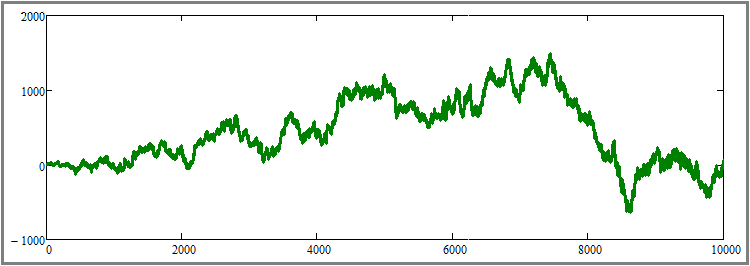
Wie Sie sehen können, hatte weder die Erhöhung der Anzahl der parallel gehandelten Instrumente noch die Verlängerung der Testdauer sichtbare Auswirkungen. Wahrscheinlich bestätigt dies die mathematisch bewiesene Tatsache aus dem vorangegangenen Artikel, dass jedes Handelssystem, einschließlich des Rebuy-Algorithmus, das Konto bei völlig zufälliger Preisbildung und ohne ein vorhersehbares Moment leert. In diesem Stadium betrachte ich Punkt 1 als theoretisch und praktisch bewiesen. Gehen wir nun zum zweiten Punkt über und nehmen die folgende Einstellung vor:

Nach meinen Tests erwies sich das Ausmaß des Rückgangs als völlig ausreichend für die Möglichkeit einer visuellen Beurteilung der Wirkung für jeden Leser. Natürlich können wir auch einen niedrigeren Prozentsatz einstellen, aber die Wirkung wird nicht so ausgeprägt sein. Ich habe die Anzahl der Simulationsschritte auf den ursprünglichen Wert von tausend Schritten zurückgesetzt. Schauen wir uns nun das Ergebnis an:

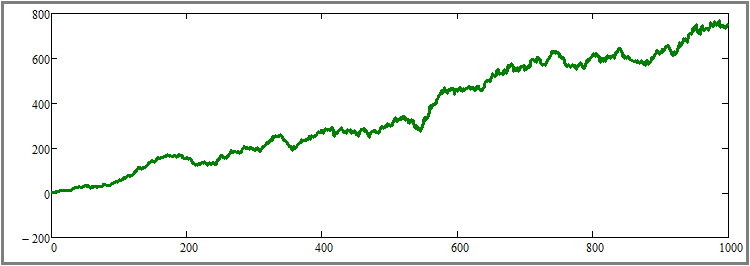
Es dürfte nicht schwer zu verstehen sein, dass dieses Schaubild unter anderem eine Ergänzung zum Beweis des vorangegangenen Absatzes darstellt, gleichzeitig aber auch ein Ausgangspunkt für den Beweis des nächsten Unterabsatzes ist. Als Nächstes plane ich, die Dauer aller Testabschnitte zu erhöhen, ohne andere Parameter zu ändern. Zur Verdeutlichung habe ich die Anzahl der Simulationsschritte für jedes Werkzeug um das Fünfzigfache erhöht - von 1000 auf 50.000. Dies ist ein ziemlich großer Anstieg, aber dies ist die einzige Möglichkeit, diesen Effekt visuell zu spüren, ohne mehrere Tests durchzuführen und die Ergebnisse zu mitteln. Werfen wir einen Blick auf das Ergebnis:

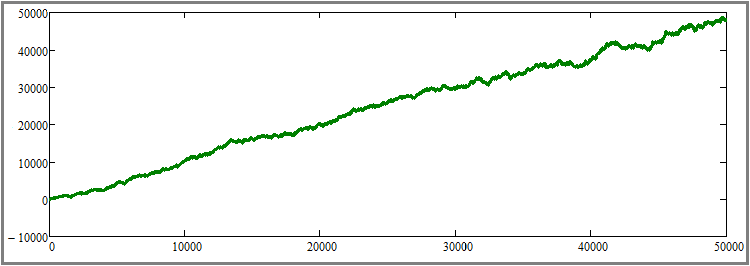
Wie wir sehen können, ist die Kurve viel glatter geworden und nähert sich einer Geraden, was bedeutet, dass das zweite Prinzip der Erhöhung des Linearitätsfaktors (Schönheit der Grafik) mit zunehmender Testdauer genau wie vorhergesagt funktioniert. Dies gilt natürlich nur unter der Annahme, dass bekannt ist, dass die gewählte Strategie rentabel ist. Zum jetzigen Zeitpunkt betrachte ich den zweiten Unterabsatz als theoretisch und praktisch bewiesen.

Setzen wir nun die Anzahl der Simulationsschritte wieder auf das Ausgangsniveau von tausend Schritten zurück und erhöhen wir umgekehrt die Anzahl der parallel gehandelten Instrumente um das Zehnfache auf den Wert 1000. Laut der Legende sollte die Schönheit der Grafik sichtbar zunehmen. Mal sehen, ob das wahr ist:

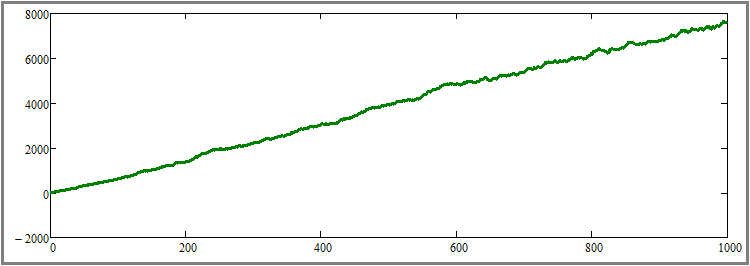
Wie wir sehen, hat sich diese Hypothese bestätigt, und der Effekt ist extrem ausgeprägt. Zum jetzigen Zeitpunkt glaube ich, dass alle drei Hypothesen theoretisch und praktisch bewiesen sind. Die Ergebnisse sind wie folgt:

1. Die Voraussetzung für die Rentabilität eines jeden Handelssystems ist das Vorhandensein eines prädiktiven Moments.
2. Mit zunehmender Dauer des Handels oder Backtestings wird jede Kurve eines profitablen Handelssystems schöner und gerader (ohne Auto-Lot) + [vorausgesetzt, Punkt 1 ist erfüllt].
3. Mit einer Erhöhung der Anzahl der gehandelten Währungspaare für ein Multiwährungshandelssystem oder einer Erhöhung der Anzahl der gleichzeitig gehandelten Systeme wird die Rentabilitätskurve des Handelssystems schöner und gerader + [vorausgesetzt, dass der Punkt 1 für jedes dieser Systeme erfüllt ist].

Test-EA

Wir haben herausgefunden, wie man Handelssysteme, einschließlich des Rebuy-Algorithmus, richtig einsetzt, um sowohl beim automatischen als auch beim manuellen Handel so effizient und sicher wie möglich Geld zu verdienen. Die Berechnung der Geldverwaltung und andere verschiedene Situationen für die richtige Kombination von Handelssystemen verdienen einen separaten Artikel, den ich ein wenig später schreiben werde.

Ich habe diesen Abschnitt hinzugefügt, damit Sie deutlich sehen können, dass der Rebuy-Algorithmus eine funktionierende Strategie ist. Zu diesem Zweck habe ich einen Test-EA erstellt, der unser mathematisches Modell wiederholt, mit dem einzigen Unterschied, dass er auch die oberen Halbwellen (Verkaufs-Handelszyklen) verarbeitet. Ich habe einige Einstellungen gefunden, die beweisen, dass es möglich ist, ein ähnliches Handelssystem für MetaTrader 5 zu erstellen. Hier ist einer von ihnen:

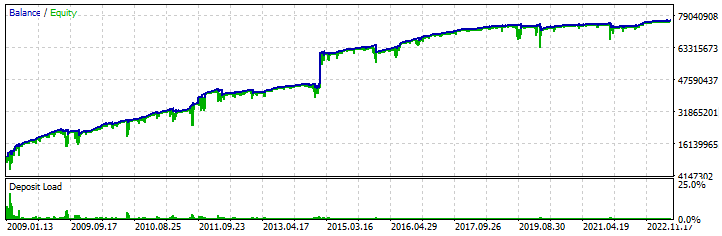
Die Tests wurden für den Zeitraum von 2009 bis 2023 durchgeführt, wobei alle „28“ Währungspaare parallel getestet wurden, die unserem mathematischen Modell entsprechen. Ich habe die Multibot-Vorlage verwendet, die ich in einem der vorherigen Artikel beschrieben habe, um den Testalgorithmus zu erstellen. Natürlich ist die Gewinnkurve bei weitem nicht ideal, und die Ersteinlage für einen solchen Handel sollte riesig sein, aber dennoch, meine Aufgabe in diesem Artikel ist es nicht, Ihnen einen fertigen Roboter zu geben, sondern die Nähe zum mathematischen Modell zu demonstrieren. Das Wichtigste, was Sie verstehen sollten, ist, dass dieser Algorithmus mit bestimmten Änderungen viel sicherer, effizienter und praktikabler sein wird. Ich schlage vor, dass Sie das Wesentliche der Verbesserungen selbst entdecken. Ich denke, es wird fair sein, da ich Dinge zeige, die normalerweise verborgen sind.

Der Expert Advisor und das Set sowie das mathematische Modell selbst sind als Datei an den Artikel angehängt, und Sie können, wenn Sie möchten, ihre Struktur genauer studieren und die Idee vielleicht noch weiter entwickeln. Mein mathematisches Modell ist in der Tat viel nützlicher als ich hier beschrieben habe. Es berechnet viele wichtige Handelscharakteristika dank einer eigenen Reihe von Ausgabeparametern nach dem Backtest. Natürlich ist seine Funktionsweise sehr eingeschränkt, aber für den Nachweis und die annähernden Schätzungen ist es ausreichend.

Schlussfolgerung

In diesem Artikel habe ich den praktischen Teil des Nachweises, dass das Prinzip der Diversifizierung funktioniert und angewendet werden sollte, abgeschlossen. Am wichtigsten ist, dass ich in Kombination mit dem vorherigen Artikel sowohl theoretisch als auch praktisch viele wichtige Dinge bewiesen habe, die es Ihnen zumindest ermöglichen, die Effizienz Ihres Handels zu erhöhen. Darüber hinaus wurde die Überlebensfähigkeit des Rebuy-Algorithmus für mehr als ein Jahrzehnt mit Hilfe des erstellten EA bewiesen.

In Anbetracht dessen haben wir eine Bestätigung für die Wellentheorie der Preisbildung bzw. für die Flachheit des Marktes. Ich empfehle Ihnen, diesen Artikel als zusätzliche Bestätigung zu lesen. Darin schenkt der Autor genau demselben Algorithmus, den ich in meinem Artikel beschrieben habe, größte Aufmerksamkeit. Von dort aus können Sie zusätzliches Wissen darüber erhalten, wie Sie diese Effekte nutzen können, um meinen Test-EA zu verbessern oder Ihren eigenen zu entwickeln.