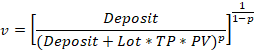Erwartungsnutzen im Handel

In diesem Artikel werde ich den Dukaten als Währungseinheit verwenden, um die historische Kontinuität zu wahren. Sie können den Dukaten jederzeit durch eine andere Währung ersetzen, die Sie gewohnt sind.

Mathematische Erwartung

Die mathematische Erwartung im Handel ist einer der Indikatoren, die zur Bewertung der Effizienz einer Handelsstrategie verwendet werden. Ein solcher Nutzer der mathematischen Erwartung (und vieles mehr) wird detailliert betrachtet in dem Artikel "Mathematics in Trading Wie schätzt man Handelsergebnisse ein“.

Wir interessieren uns jetzt aber für die probabilistische Definition der mathematischen Erwartung. Ich biete Ihnen zum Beispiel ein Spiel an, bei dem Sie eine 10%ige Chance haben, 100 Dukaten zu gewinnen und eine 90%ige Chance, 10 Dukaten zu verlieren. Dann sieht die mathematische Erwartung eines solchen Spiels wie folgt aus: E = 0,1 * 100 + 0,9 * (-10) = 1 Dukaten. Wir können also die erwartete Rendite anhand der mathematischen Erwartung beurteilen. Wenn wir dieses Spiel zum Beispiel 100 Mal spielen, können wir davon ausgehen, dass sich unsere ursprüngliche Einlage um 100 Dukaten erhöhen kann.

Die Intuition legt nahe, dass die Teilnahme an einem solchen Spiel umso interessanter ist, je höher die mathematische Erwartung ist. Wenn wir zum Beispiel die Gewinne im Spiel auf 200 Dukaten erhöhen, dann steigt die mathematische Erwartung auf 11, während der erwartete Gewinn aus 100 Spielen auf 1100 Dukaten steigt. Und was ist, wenn die mathematische Erwartung bei +100.500 liegt? Das klingt wie ein Traum! Sind Sie mit dieser Aussage einverstanden?

Wenn ja, dann ist heute einer der glücklichsten Tage Ihres Lebens. Denn ich schlage vor, dass wir das Spiel der unendlichen Erwartung spielen. Stellen Sie sich vor, Sie werden in einer Stunde (oder noch schneller) ein Hyper-Mega-Multi-Super-Milliardär sein.

Aber dieses Spiel hat eine kleine Unannehmlichkeit. Um daran teilzunehmen, muss man eine geringe Startgebühr zahlen, etwa 100 Dukaten. Okay, das klingt ein bisschen gemein. Na gut, es seien 50 Dukaten. Außerdem möchte ich Ihnen einen besonderen Rabatt anbieten: Sie zahlen nur 25 Dukaten, und wir beginnen sofort mit diesem wunderbaren Spiel.

Während Sie das Startgeld überweisen, möchte ich Ihnen die Regeln dieses Spiels erklären. Zuerst erraten Sie das Ergebnis des Münzwurfs: Kopf oder Zahl. Dann werfe ich eine Münze und wenn Sie richtig geraten hast, zahle ich Ihnen 1 Dukaten. Der zweite richtige Tipp bringt Ihnen 2 Dukaten. Nach dem dritten Tipp erhalten Sie 4 Dukaten, usw. - Bei jedem weiteren Tipp verdoppeln Sie Ihren vorherigen Gewinn. Stellen Sie sich vor, wie viele Dukaten ich Ihnen nach fünfzig Mal Raten zahlen muss. Und nach hundert? Solche Zahlen sind noch gar nicht erfunden worden, und der ganze Reichtum der Welt wird im Vergleich zu Ihren Gewinnen eine Kleinigkeit sein.

Wenn Sie einen Fehler machen, endet das Spiel. Sie können erneut eine Teilnahmegebühr entrichten und wir beginnen das Spiel von vorne.

Irgendetwas sagt mir, dass niemand ein solches Spiel mit mir spielen will. Warum? Auf der einen Seite haben wir eine unendliche mathematische Erwartung:

Andererseits sagt eine innere Stimme, dass selbst 25 Dukaten ein zu hoher Preis für diese Unendlichkeit sind. Dieser Widerspruch wird als „Petersburger Paradoxon" bezeichnet.

Erwartungsnutzen

Im Jahr 1738 veröffentlichte Daniel Bernoulli sein Werk „Specimen theoriae novae de mensura sortis" (Darstellung einer neuen Theorie zur Messung des Risikos). In dieser Arbeit schlug er vor, dass in jedem Spiel nicht die erwartete Auszahlung, sondern der Nutzen für den Spieler maximiert werden muss.

Diese Annahme lässt sich anhand des folgenden Beispiels veranschaulichen. Es soll zwei verschiedene Spieler geben. Die eine hat ein Kapital von 100 Dukaten, die andere von 1000 Dukaten. Beiden wird ein Spiel mit einer erwarteten Auszahlung von 10 Dukaten angeboten. Natürlich ist ein solches Spiel für den ersten Spieler von größerem Interesse, denn wenn er gewinnt, erhöht sich sein Kapital um 10 %, während der zweite Spieler sein Kapital nur um 1 % erhöht. Mit anderen Worten, derselbe Gewinn wird für den ersten Spieler nützlicher sein als für den zweiten.

Auf der Grundlage dieser Annahme leitete Daniel Bernoulli die Gleichung eines Erwartungsnutzen ab. Gehen wir davon aus, dass Einlage das verfügbare Kapital eines Spielers ist, Gewinn die erwartete Auszahlung und Verlust ist ein möglicher Verlust, während p die Gewinnwahrscheinlichkeit ist. In diesem Fall sieht die Gleichung des Erwartungsnutzens wie folgt aus:

Der Hauptunterschied zwischen dem Erwartungsnutzen und der mathematischen Erwartung besteht darin, dass der Erwartungsnutzen vom Kapital des Spielers abhängt und implizit das Risiko des Spiels mit einbezieht.

Nehmen Sie zum Beispiel eines der Spiele, die ich vorhin vorgeschlagen habe - mit einer 10%igen Chance können Sie 200 Dukaten gewinnen, und mit einer 90%igen Chance können Sie 10 Dukaten verlieren. Die mathematische Erwartung bei diesem Spiel ist für alle Spieler gleich: 0,1*200 + 0,9*(-10) = 11 Dukaten. Aber der Erwartungsnutzen wird eine anderer sein und ein wenig mehr Informationen liefern.

Legen Sie zunächst Ihre Dukaten auf den Tisch und zählen Sie sie. Wägen Sie nun die Vor- und Nachteile ab und entscheiden Sie, ob Sie dieses Spiel spielen wollen? 

• Wenn Sie zugestimmt haben zu spielen und mehr als 73,74 Dukaten haben, dann ist alles in Ordnung - Sie haben die Risiken und Chancen richtig berechnet.
• Wenn Sie genau 73,74 Dukaten haben, dann bewegen Sie sich auf dünnem Eis. Auf sehr dünnem Eis.
• Wenn Sie weniger als 73,74 Dukaten haben, dann ... sollten Sie vielleicht nach anderen Möglichkeiten suchen, mit der Adrenalinsucht umzugehen. Sie können zum Beispiel versuchen, hungrige menschenfressende Haie auf hoher See zu füttern.
• Wenn Sie dieses Spiel aufgegeben haben und mehr als 73,74 Dukaten haben, dann ist es gut möglich, dass Sie die interessantesten Momente in Ihrem Leben verpassen.

Sie fragen sich vielleicht, woher diese mysteriöse Summe von 73,74 Dukaten stammt. Das liegt an dem Erwartungsnutzen, die mit diesem Spiel verbunden ist:

Für einen rationalen Spieler sollte der Erwartungsnutzen strikt positiv sein:

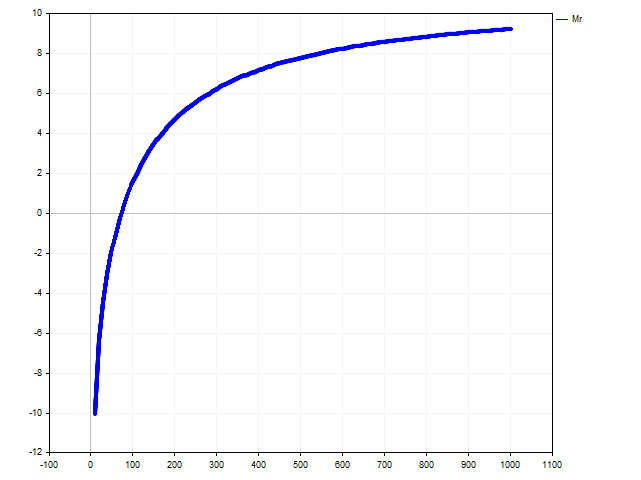
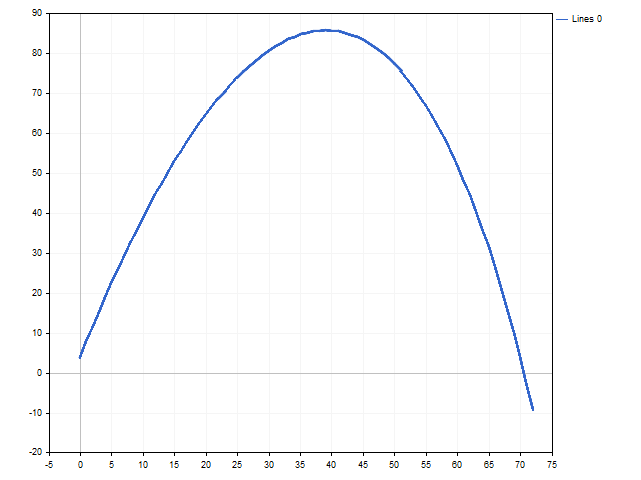
Es ist leicht, eine Lösung aus der Ungleichung zu finden Einlage > 73,74. Die folgende Abbildung zeigt, wie sich der Erwartungsnutzen in Abhängigkeit vom Kapital des Spielers verändert.

Erwartungsnutzen im Handel

Einige Handelsstrategien beinhalten die Festlegung eines Stop-Loss und eines Take-Profits. Bei solchen Handelsstrategien ist es möglich, den Erwartungsnutzen zu nutzen. In diesem Fall sind mehrere Optionen für die Anwendung des Erwartungsnutzen möglich.

Wenn ein Händler eine Position eröffnet, kennt er den genauen Stand seines Handelskontos. Außerdem kann er die Gewinnwahrscheinlichkeit abschätzen (wir werden dies weiter unten besprechen). Alle anderen Positionsparameter werden als Variablen dargestellt:

• SL – Differenz zwischen dem Eröffnungskurs der Position und ihrem Stop-Loss in Punkten (positive ganze Zahl);
• TP – Differenz zwischen dem Eröffnungskurs der Position und ihrem Take-Profit in Punkten;
• PV – Kosten für einen Punkt in der Einlagenwährung.
• Lot – Volumen der Position.

Dann wäre der Erwartungsnutzen für diese Position:

Die erste Art, die Erwartungsnutzen anzuwenden, ist nur möglich, wenn die Werte von zwei der drei Variablen im Voraus festgelegt werden – SL, TP und Lot.

Wenn wir zum Beispiel eine Position eröffnen, legen wir das Positionsvolumen und den Take-Profit fest. Dann können wir das Stop-Loss-Niveau für diesen Handel schätzen. Ihr Wert sollte so hoch sein, dass der Erwartungsnutzen positiv wird. Mit anderen Worten: Wir finden den maximal möglichen Stop-Loss-Wert. 

Schauen wir uns an, wie dies symbolisch geschehen kann. Zunächst müssen wir den Wert der Hilfsvariablen ermitteln:

Dann wird der Stop-Loss durch die Ungleichheit begrenzt:

Wenn wir ein Lot und einen Stop-Loss festgelegt haben, können wir das Take-Profit-Niveau schätzen.

Der Take-Profit für diesen Handel wird dann wie folgt sein:

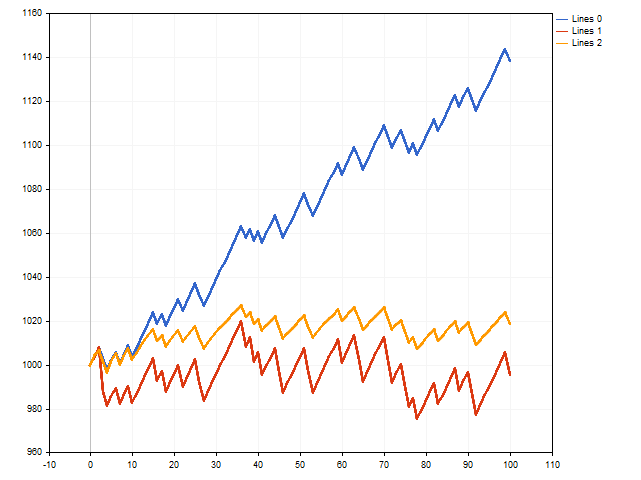
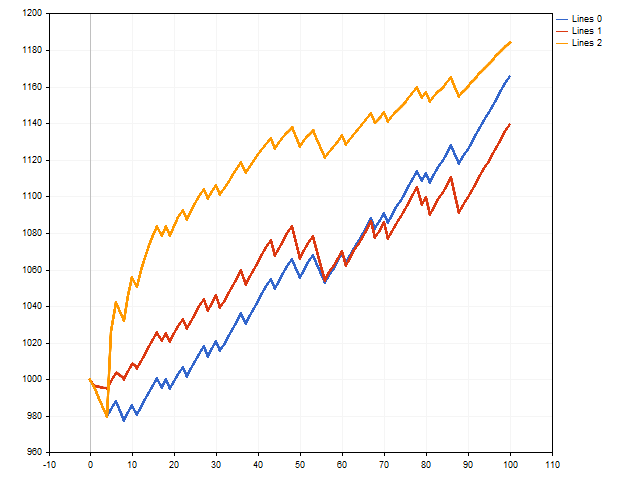
Dies war eine Theorie. Nun wollen wir sehen, was wir in der Praxis tun können. Dazu schreiben wir ein Skript, das den Handel simuliert. Wir werden drei Optionen gleichzeitig prüfen - mit festem Stop-Loss und Take-Profit, mit variablem Stop-Loss und mit variablem Take-Profit.

Auf den ersten Blick gewinnt die Option mit dem festen Stop-Loss und Take-Profit (blaue Linie).

Es sei jedoch daran erinnert, dass wir den maximal möglichen Stop-Loss und den minimal möglichen Take-Profit verwendet haben. Was wird passieren, wenn wir uns von diesen Grenzen entfernen, indem wir den Stop-Loss leicht reduzieren und den Take-Profit erhöhen? Dann kann sich die Situation ändern.

Die rote Linie zeigt die Handelsergebnisse mit einem variablen Stop-Loss, und die orangefarbene Linie zeigt die Handelsergebnisse mit einem variablen Take-Profit. Wie wir sehen, kann sich der gleitende Take-Profit positiv auf die Handelsergebnisse auswirken.

Erwartungsnutzen und Geldmanagement

Zerlegen wir die Gleichung des Erwartungsnutzen in zwei Teile. Nennen wir den ersten Teil bedingt rentabel:

Der zweite Teil wird als unrentabel bezeichnet:

Wenn wir uns den gewinnbringenden Teil genau ansehen, werden wir feststellen, dass eine Vergrößerung der Losgröße zu dessen Wachstum führt. Die gleiche Erhöhung der Menge führt jedoch zu einem Rückgang des unrentablen Teils. Infolgedessen kann der unrentable Teil einen Wert von Null (oder sogar einen negativen Wert) annehmen. In diesem Fall wird der Erwartungsnutzen eines solchen Geschäfts negativ. Wie wir uns erinnern, ist dies nicht die beste Wahl und wird von rationalen Händlern nicht befürwortet.

Unsere nächste Idee ist die Suche eine bestimmte Losgröße zu finden, sodass sowohl der gewinn- als auch der verlustbringende Teil der Gleichung gleichzeitig die maximal möglichen Werte annehmen. Dann ist der Erwartungsnutzen maximal für gegebene SL und TP. In der Abbildung können Sie sehen, wie sich der Erwartungsnutzen mit zunehmender Losgröße verändert.

Das numerische Experiment ergab ein positives Ergebnis. Lassen Sie uns nun die Gleichung für die optimale Positionsgröße herleiten. Dazu müssen wir die Ableitung des Erwartungsnutzen nach der Losgrößenvariablen lot finden, sie mit Null gleichsetzen und die resultierende Gleichung lösen. Daraus ergibt sich der folgende Ausdruck:

Achten wir auf den Teil des Ausdrucks, der in eckigen Klammern steht. Hier sehen wir die mathematische Erwartung geteilt durch Stop-Loss und Take-Profit. Bitte beachten Sie, dass für die korrekte Berechnung der Losgröße die mathematische Erwartung für die Transaktion streng positiv sein sollte. Mit anderen Worten: Die folgende Bedingung sollte immer erfüllt sein:

Übrigens, wenn wir den Bruch in eckigen Klammern erweitern, erhalten wir die Kelly-Formel:

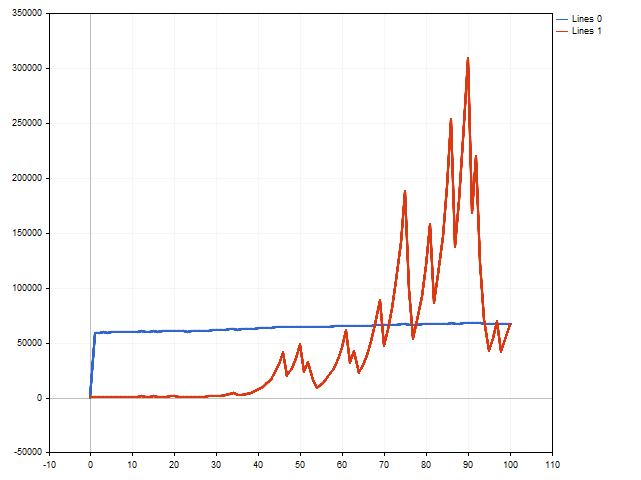
Lassen Sie uns nun versuchen, eine Reihe von Handelsgeschäften zu simulieren, bei denen die Losgröße mit Hilfe des Erwartungsnutzens verwaltet wird. Hier werden wir eine Vielzahl von Ergebnissen sehen. So kann sich beispielsweise die Ersteinlage um das über 160-fache erhöhen.

Allerdings können mehrere Verlustgeschäfte hintereinander das Ergebnis nicht gerade positiv beeinflussen. In der folgenden Abbildung ist zu sehen, dass die ursprüngliche Einlage um etwa das Fünfzigfache gestiegen ist. Das ist ziemlich gut. Wenn man die Tatsache außer Acht lässt, dass in der Nähe des 90. Schritts die ursprüngliche Einlage um etwa das Dreihundertfache erhöht wurde.

Risikomanagement

Wie wir sehen, kann die Verwaltung von Geld durch Erwartungsnutzen sowohl zu beeindruckenden Gewinnen als auch zu sehr greifbaren Verlusten führen. Dies wirft die Frage nach dem Risikomanagement auf.

Hier gibt es zwei Möglichkeiten. Die erste (offensichtlichste) besteht darin, nicht die gesamte verfügbare Einlage für die Berechnungen zu verwenden, sondern nur einen Teil davon. Sie können zum Beispiel einen festen Betrag festlegen. Sie können auch einen Prozentsatz des aktuellen Saldos festlegen. In jedem Fall wird es Ihnen helfen, das Risiko beim Handel zu verringern.

Die zweite Möglichkeit des Risikomanagements besteht darin, die Berechnung der Wahrscheinlichkeit eines profitablen Handels zu ändern. Schauen wir uns diese Option genauer an.

Angenommen, dass n eine Gesamtzahl von Handelsgeschäften ist, während m die Anzahl der Handelsgeschäfte mit Gewinn ist. Dann können wir die Gewinnwahrscheinlichkeit wie folgt berechnen:

Dieser Ansatz ist jedoch nicht ganz korrekt. Denn auf diese Weise können wir die Häufigkeit von Ereignissen, die bereits eingetreten sind, abschätzen. Stattdessen müssen wir die Wahrscheinlichkeit eines Gewinns bei einem zukünftigen Handel ermitteln.

Nehmen wir an, Sie haben bereits 15 Handelsgeschäfte getätigt, von denen 10 profitable waren. Sie sind dabei, die nächste Position zu öffnen. Dann erhöht sich die Gesamtzahl der Handelsgeschäfte um 1, aber die Anzahl der gewinnbringenden Handelsgeschäfte kann entweder steigen oder gleich bleiben.

Nehmen wir den Durchschnitt dieser Optionen, so ergibt sich eine Gewinnwahrscheinlichkeit für die eröffnete Position:

Auf diese Weise erhalten wir Krichevsky–Trofimov Estimator, der in symbolischer Form wie folgt aussieht:

Die Hinzufügung einer Schicht ermöglichte eine etwas geringere Gewinnwahrscheinlichkeit, was zu einem geringeren Risiko führte.

Verallgemeinern wir die Wahrscheinlichkeitsschätzung wie folgt: Wir führen eine beliebige Verschiebung ein s >= 1. Dann beträgt die Gewinnwahrscheinlichkeit:

Durch die Einstellung skönnen wir das Risiko in einem ziemlich breiten Bereich regulieren - je größer der Wert s, desto geringer das Risiko.

Leider wirkt sich die Risikominderung auch auf die Höhe des Gewinns aus. Daher steht jeder Händler vor der Wahl: Ein hohes Risiko ermöglicht große Gewinne, aber auch sehr hohe Verluste. Ein geringes Risiko ermöglicht es Ihnen, Verluste zu reduzieren, aber der Gewinn ist dann gering.

Werfen wir einen Blick darauf, wie sich das Risiko auf den Handel auswirken kann. Ich werde den einfachsten Expert Advisor am Schnittpunkt von zwei gleitenden Durchschnitten verwenden. Der EA wurde mit den folgenden Parametern getestet:

Währungspaar: EURUSD,

Zeitrahmen: H1,

Testzeitraum: 2021.01.01 – 2022.12.31

Alle anderen Parameter sind voreingestellt.

Während des Testzeitraums wurden 419 Handelsgeschäfte getätigt. Die Saldenkurve sieht wie folgt aus:

Für verschiedene Risikowerte wurden die folgenden Ergebnisse erzielt.

Risiko	Nettogewinn, $	Absoluter Drawdown vom Saldo	Profit-Faktor	Erwartetes Ergebnis	Erholungsfaktor	Marge Level
0	42 961.51	2 699.05	1.18	102.53	1.72	89.20%
25	28 932.51	570.27	1.21	69.05	1.89	260.70%
50	16 836.83	230.64	1.21	40.18	1.92	309.53%

Wie wir sehen, verringert die Risikominderung die Gewinne, kann aber andere Parameter einer Handelsstrategie verbessern.

Schlussfolgerung

Die folgenden Programme wurden bei der Erstellung dieses Artikels verwendet:

Name	Typ	Beschreibung
ME SL-TP	Skript	Das Skript zeigt, wie sich die Handelsrentabilität ändern kann, wenn die Stop-Loss- und Take-Profit-Werte entsprechend der Handelsmoral-Erwartung gewählt werden. Die Skriptparameter: ProbabilityWin - Gewinnwahrscheinlichkeit Deposit - Ersteinlage NumberTrades - Anzahl der simulierten Handelsgeschäfte SL - fester Stop-Loss in Punkten TP - fester Take-Profit in Punkten Shift - Verschiebung für gleitenden Stop-Loss und Take-Profit Width - Linienbreite ViewDuration - Dauer der Anzeige der Ergebnisse ScreenShot - wenn aktiviert, speichert das Bild im Ordner Files
ME Lot	Skript	Das Skript zeigt, wie die Positionsgröße den Erwartungsnutzen eines Handels beeinflusst.
ME MM	Skript	Das Skript vergleicht das Geldmanagement des Erwartungsnutzens mit dem Handel mit fester Losgröße. Am Ende der Arbeit wird eine Meldung mit dem Ergebnis des Handels für beide Optionen angezeigt, sowie die Größe eines rationalen festen Lots.
Two_Moving_Averages_System	Expert Advisor	Der EA ermöglicht die Bewertung der Auswirkungen des Risikos auf die Handelsleistung. Seine Parameter: Risk - je höher der Wert, desto geringer das Risiko. Gültiger Bereich 0 - 255 SL - Stop-Loss TP - Take-Profit. Beide Werte sollten ungleich Null sein. PeriodMA1, PeriodMA2 - Periodenlängen der gleitenden Durchschnitte.