Händlerfreundliche Stop-Loss und Take-Profit

Einführung

Wenn der größte Dramatiker einen Nachsatz zu diesem Artikel schreiben könnte, würde er ihn vielleicht so formulieren:

Sein oder nicht sein? Das ist die Frage:

Ob mit Stop-Loss im rasenden Markt,

Oder mit Take-Profit auf Trefferjagt?

Stop-Loss und Take-Profit sind Stop-Orders, die eine Position schließen, wenn der Kurs ihren Wert erreicht. Mit dem Stop-Loss können die Händler ihre Verluste begrenzen, während sie mit Take-Profit ihre Gewinne sichern können. Der Hauptvorteil der Verwendung von Stop-Loss und Take-Profit liegt in der Möglichkeit, finanzielle Risiken zu kontrollieren und Geldmanagement zu betreiben.

Einige Händler ziehen es jedoch vor, auf Stop-Orders zu verzichten. Ihre Argumentation ist ganz einfach. Es gibt Situationen, in denen der Kurs den Stop-Loss erreicht und sich dann umkehrt. Hätte es keinen Stop-Loss gegeben, hätte die Position im positiven Bereich schließen können. Das gleiche Argument gilt für die Gewinnmitnahme. Nach Erreichen des Niveaus wird die Position geschlossen. Aber der Kurs bewegt sich weiter in dieselbe Richtung, und wenn Take-Profit nicht gesetzt worden wäre, hätten weitere Gewinne erzielt werden können.

Dieser Ansatz hängt eher mit den subjektiven Einschätzungen des Händlers zusammen. Diese Subjektivität kann zu großen Problemen führen. Wenn ein Händler zum Beispiel keinen Stop-Loss setzt, wird der Broker dies für ihn tun. Um Begriffsverwirrungen zu vermeiden, bezeichnet der Broker sein Niveau als „stop out“. Das Stop-Loss-Niveau des Brokers können Sie jederzeit mit der Funktion AccountInfoDouble mit der Kennung ACCOUNT_MARGIN_SO_SO herausfinden. Dasselbe gilt für die Gewinnmitnahme. Ist es möglich, dass der Händler selbst das falsche Niveau gewählt hat und daher nicht in der Lage war, den gesamten möglichen Gewinn zu erzielen?

Versuchen wir, bei der Wahl der Stop-Loss- und Take-Profit-Niveaus rational vorzugehen.

Aufbereitung der Daten

Machen wir uns also mit dem Gegenstand unserer Forschung vertraut. Zunächst müssen wir herausfinden, welche Niveaus der Preis erreichen kann, wenn er sich nach oben oder unten bewegt. Außerdem interessiert uns, wie oft ein bestimmtes Niveau in der Geschichte auftritt.

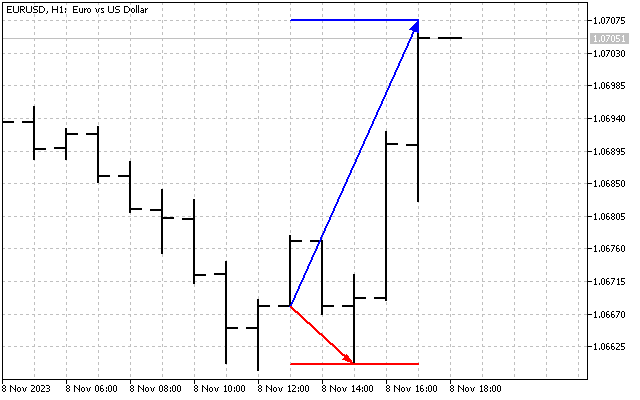
Wir werden ein recht einfaches Modell verwenden. Gehen wir davon aus, dass jede Position zum Preis „open“ eröffnet wird. Wir bestimmen auch die Dauer des Haltens der Position in N Balken. Wir interessieren uns für die maximalen Kursabweichungen nach oben und nach unten. Diese Werte werden für die Statistik erfasst. Ich habe zum Beispiel eine Haltezeit der Positionen von 5 Balken verwendet. Grafisch sieht es so aus.

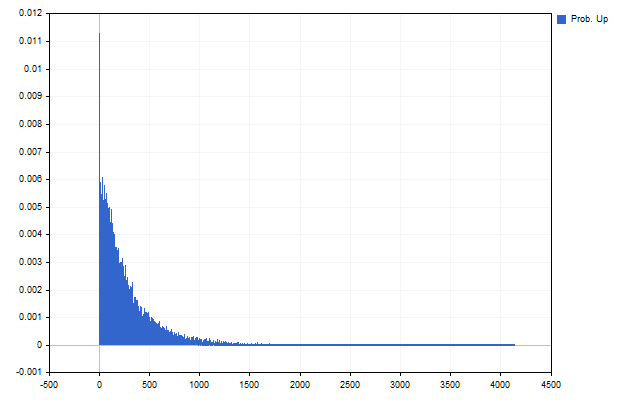
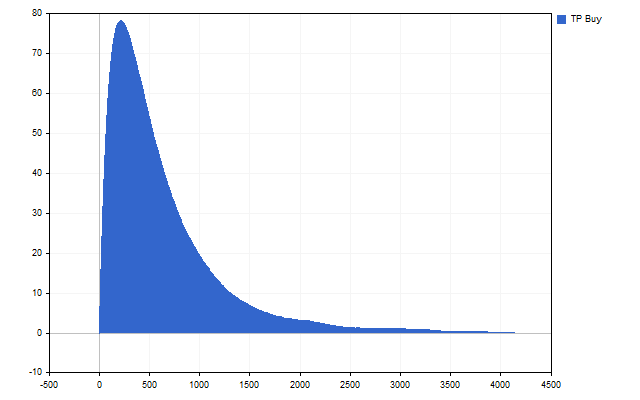
Als Ergebnis erhalten wir die Anzahl, wie oft eine bestimmte Preisabweichung in den historischen Daten aufgetreten ist. Mit anderen Worten, wir erhalten eine Schätzung der Wahrscheinlichkeit, dass der Preis ein bestimmtes Niveau erreichen wird. So sieht zum Beispiel die Statistik für die Aufwärtsbewegung der Kurse aus.

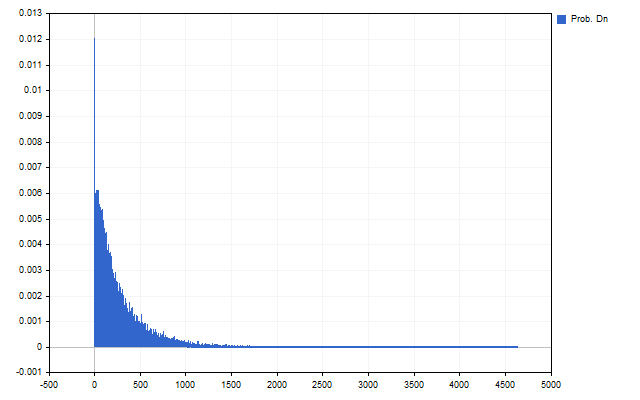
Und hier die Abwärtsbewegungen.

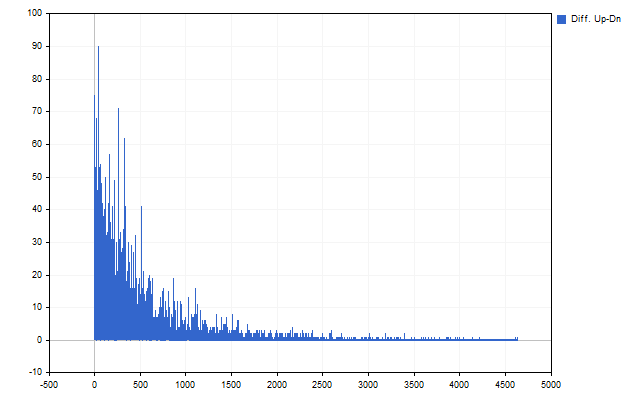
Das erste, was uns auffällt, sind große Abweichungen - sie sind weniger häufig. Das zweite wichtige Ergebnis ist der Unterschied zwischen Aufwärts- und Abwärtsbewegungen der Preise.

Dieser Unterschied bedeutet, dass die Werte von Stop-Loss und Take-Profit für Kauf- und Verkaufspositionen voneinander abweichen können.

Jetzt müssen wir einen weiteren Schritt tun. Die Bedingung für das Auslösen von Stop-Loss und Take-Profit kann wie folgt formuliert werden: Der Kurs wird ein bestimmtes Niveau erreichen und vielleicht noch weiter steigen.

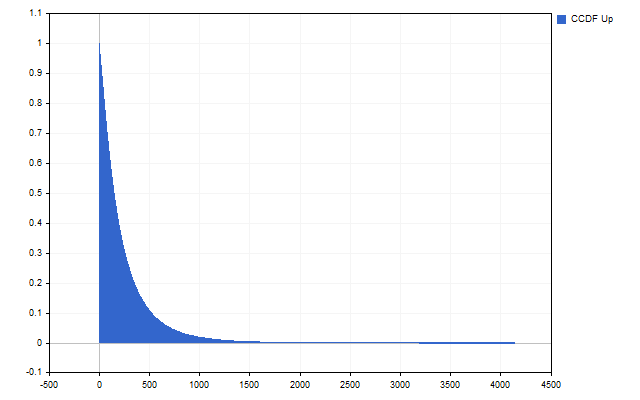
Wir benötigen zusätzliche kumulative Funktionen, um die Wahrscheinlichkeit zu schätzen, dass Stop-Loss oder Take-Profit bei einem bestimmten Niveau ausgelöst wird. Das Wesen der zusätzlichen kumulativen Funktion ist sehr einfach - wir müssen die Wahrscheinlichkeit eines bestimmten Niveaus mit den Wahrscheinlichkeiten aller nachfolgenden Niveaus addieren.

In der Praxis können wir die Funktion auf folgende Weise finden. Nehmen wir die Wahrscheinlichkeitsschätzung, die wir zu Beginn erhalten haben. Ausgehend von der vorletzten Stufe in Bezug auf ihren Wert, müssen wir Summen der Form finden:

Als Ergebnis sollten wir ein Bild wie dieses erhalten.

Ich möchte Sie noch einmal daran erinnern. Zunächst erhalten wir die Wahrscheinlichkeit, dass der Kurs genau dieses Niveau erreicht. Jetzt haben wir die Wahrscheinlichkeit, dass der Preis dieses Niveau erreicht und möglicherweise noch weiter steigt.

Jetzt können wir mit dem Hauptteil unserer Forschung beginnen.

Unabhängige SL & TP

Wir kennen also die Wahrscheinlichkeit, dass der Kurs ein bestimmtes Niveau erreicht. Jetzt sollten wir dieses Wissen zu Geld machen. Und wir beginnen mit... Übrigens, ist Ihnen aufgefallen, dass MetaQuotes bei allen seinen Produkten zuerst einen Stop-Loss und dann einen Take-Profit vorschlägt? Das liegt daran, dass dort nur Pessimisten arbeiten. Wir hingegen sind Optimisten, also beginnen wir mit Gewinnmitnahmen.

Jeder Händler ist daran interessiert, einen großen Take-Profit zu erzielen. Je größer Take-Profit, desto größer ist der Gewinn. Aber wie wir bereits gesehen haben, führt eine Erhöhung der Gewinnmitnahme zu einer Verringerung der Wahrscheinlichkeit ihrer Ausführung. Wir müssen den maximalen Take-Profit mit der höchstmöglichen Ausführungswahrscheinlichkeit finden:

Wir wollen sehen, ob diese Bedingung erfüllt werden kann.

In der Tat haben wir ein klar definiertes Maximum, und wir können diesen Take-Profit-Wert als optimal akzeptieren.

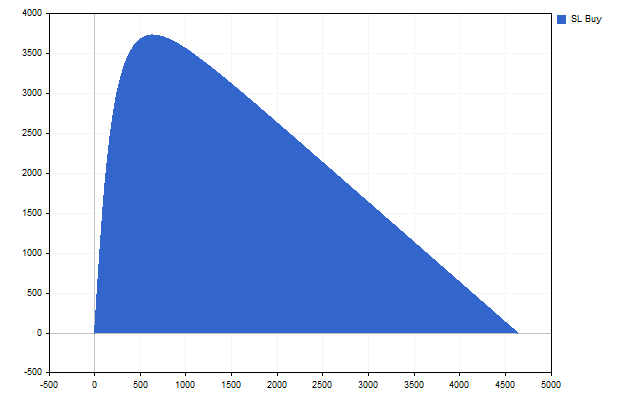
Jetzt können wir damit beginnen, den optimalen Stop-Loss zu finden. Auf den ersten Blick ist alles ganz einfach - wir brauchen einen Mindeststopp-Loss mit einer Mindestwahrscheinlichkeit für seine Ausführung. Doch diese Einfachheit ist trügerisch. Im Gegenteil, wir müssen das Gegenteil tun.

Als wir Statistiken über Preisabweichungen erhoben, erhielten wir auch den Höchstwert. Bei der Bewertung der Optimalität können wir nun die Differenz zwischen diesem Maximum und dem Stop-Loss-Wert heranziehen. Je größer dieser Unterschied ist, desto besser. Das Gleiche gilt für die Bewertung der Vollstreckungswahrscheinlichkeit. Eine geringe Wahrscheinlichkeit der Ausführung ist gleichbedeutend mit einer hohen Wahrscheinlichkeit der Nichtausführung. Mit anderen Worten, wir wollen, dass die folgende Bedingung erfüllt ist:

Schauen wir nach. Tatsächlich, ein solches Maximum existiert. Der optimale Stop-Loss ist gefunden.

Für EURUSD H1 beträgt die Haltedauer der Position 5 Balken. Ich habe die folgenden Werte erhalten.

	SL/Wahrscheinlichkeit	TP/Wahrscheinlichkeit
Kaufen (buy)	622 / 6.90%	210 / 37.28%
Verkaufen (sell)	603 / 7.28%	220 / 35.31%

Prüfen wir nun, wie optimal diese Werte sind. Ich werde eine einfache Strategie verwenden - Positionen werden bei jedem neuen Balken eröffnet, wenn es keine offenen Positionen gibt. Der Positionstyp wird nach dem Zufallsprinzip ausgewählt. Wir prüfen drei Optionen:

• optimale Stop-Orders;
• Stopp-Loss um 10 Punkte reduziert;
• Die Take-Profits stiegen um 10 Punkte.

So sieht die Saldenkurve bei der Verwendung von optimalen Stop-Orders aus.

Die Testergebnisse für alle Optionen sind in der Tabelle aufgeführt.

Nettogewinn, $	Bruttogewinn	Bruttoverlust	Profit-Faktor	Expected Payoff
303.02	1 870.84	-1 567.82	1.19	0.27
100.79	1 817.04	-1 716.25	1.06	0.09
135.07	1 773.24	-1 638.17	1.08	0.13

Betrachten wir nun kurz die praktische Anwendung dieses Ansatzes.

Erstens können wir es so verwenden, wie es ist, und es als Indikator einsetzen. Dann werden wir einzigartige Unterstützungs- und Widerstandsniveaus erhalten.

Zweitens: Nehmen wir an, wir haben eine Handelsstrategie, die Signale zum Öffnen und Schließen von Positionen erzeugt. Dann können wir Folgendes tun. Erfassen wir zunächst Statistiken für Kauf- und Verkaufssignale getrennt. In diesem Fall wird die Positionshaltezeit vom Eröffnungssignal bis zum Schließsignal gezählt.

Natürlich können wir auch nur Take-Profit oder nur Stop-Loss verwenden. Sie hängen nicht voneinander ab, sodass ihre getrennte Verwendung durchaus akzeptabel ist.

Expected Payoff

Das Konzept des Expected Payoffs (erwartete Auszahlung) oder der mathematischen Erwartung ist seit langem bekannt und wird im Handel häufig verwendet. Der SMA-Indikator zeigt zum Beispiel den Expected Payoff an. In dem Artikel „Mathematik im Trading: Wie man Handelsergebnisse schätzt“ zeigt im Detail, wie Handelsstrategien mit Hilfe der mathematischen Erwartung bewertet werden können.

Versuchen wir, die mathematische Erwartung auf die Berechnung von Stop-Orders anzuwenden. Wir haben bereits alle notwendigen Statistiken. Wir müssen nur wissen, was und wie wir zählen werden.

Wir können der Expected Payoff für eine Position mit der folgenden Gleichung berechnen:

wobei p die Wahrscheinlichkeit ist, dass die Position mit Gewinnmitnahme geschlossen wird. Das ist die Wahrscheinlichkeit, die wir finden müssen.

Jede Position wird entweder durch Take-Profit oder Stop-Loss geschlossen. Es gibt keine anderen Möglichkeiten. Das bedeutet, dass die Gesamtwahrscheinlichkeit für diese beiden Ereignisse gleich 1 sein muss. Die Wahrscheinlichkeit, dass eine Position zum Take-Profit geschlossen wird, setzt sich aus zwei Komponenten zusammen: der Wahrscheinlichkeit, dass der Kurs das Take-Profit-Niveau erreicht, und der Wahrscheinlichkeit, dass der Kurs das Stop-Loss-Niveau nicht erreicht. Die Schließung einer Position durch einen Stop-Loss wird auf die gleiche Weise geschätzt. In diesem Fall sieht die Gleichung des Expected Payoff wie folgt aus:

Wir müssen lediglich die Werte von Stop-Loss und Take-Profit so bestimmen, dass der Expected Payoff positiv ist. Die maximale Auszahlung kann zum Beispiel mit den folgenden Stop-Order-Werten erreicht werden.

	SL/Wahrscheinlichkeit	TP/Wahrscheinlichkeit	Erwarteter Wert
Kaufen (buy)	4611 / 7.69%	3690 / 92.31%	3051.53
Verkaufen (sell)	4071 / 14.29%	3950 / 85.71%	2804.19

In der Praxis kann der mathematische Erwartungswert wie folgt verwendet werden. Zunächst müssen wir einen bestimmten Stop-Loss- oder Take-Profit-Wert auswählen. Dann müssen wir den optimalen Wert einer anderen Stop-Order finden. Ich habe zum Beispiel die Stop-Loss-Werte aus dem vorherigen Beispiel genommen und für sie Take-Profits mit dem höchsten Expected Payoff gefunden. Ich habe die folgenden Werte erhalten:

	SL/Wahrscheinlichkeit	TP/Wahrscheinlichkeit	Erwarteter Wert
Kaufen (buy)	622 / 19.24%	310 / 80.76%	130.68
Verkaufen (sell)	603 / 19.25%	300 / 80.75%	126.13

So sieht die Veränderung des Saldos aus.

Neben dem Expected Payoff können auch andere Kriterien herangezogen werden. Zum Beispiel, das Kriterium

ermöglicht es uns, Stop-Order-Werte zu erhalten, die das optimale Verhältnis zwischen durchschnittlichem Gewinn und durchschnittlichem Verlust bieten.

Zeit und Gewinn

Jeder kennt den Aphorismus „Zeit ist Geld“. Schauen wir uns an, ob (und wie) dieser Aphorismus beim Handel funktioniert.

Jeder vernünftige Händler ist daran interessiert, einen Gewinn zu erzielen. Je größer der Gewinn, desto besser. Ich biete Ihnen eine Auswahl von 3 Handelsstrategien: die erste bringt 1440 Punkte Gewinn, die zweite 600, und die dritte 20. Welche Strategie würden Sie wählen?

Hier möchte ich eine kleine Klarstellung vornehmen. Die erste Strategie bringt Gewinn in einem Tag, die zweite in einer Stunde und die dritte in einer Minute. Um die Rentabilität dieser Strategien zu beurteilen, müssen wir sie natürlich auf denselben Zeitraum bringen. Zum Beispiel, M1. Dann erhalten wir die folgenden Werte:

• 1440/1440 = 1;

• 600/60 = 10;

• 20/1 = 20.

Mit anderen Worten: Wir haben die Strategien anhand des folgenden Kriteriums bewertet:

Versuchen wir, den gleichen Ansatz bei der Berechnung von Stop-Orders anzuwenden. Es liegt auf der Hand, dass die Händler daran interessiert sind, in möglichst kurzer Zeit den größtmöglichen Gewinn zu erzielen. Ebenso streben sie nach minimalen Verlusten, und der Zeitpunkt dieser Verluste wird so weit wie möglich hinausgeschoben.

Bei der Auswahl von Stopp-Aufträgen kann man sich das so vorstellen. Nehmen wir an, wir erwarten, dass wir innerhalb von 5 Balken einen Gewinn erzielen. Dann können wir den Stop-Loss um die Ausführungszeit auf eine längere Zeit verschieben. Die Ausführungszeit für den Stop-Loss kann z.B. auf 7 oder 10 Balken festgelegt werden. In diesem Fall erhöht sich der Umfang des Stop-Losses, aber die Wahrscheinlichkeit seiner Ausführung sinkt.

Dieser Ansatz kann in Strategien verwendet werden, die Signale zum Öffnen von Positionen haben, aber keine Signale zum Schließen von Positionen. Positionen sollten erst geschlossen werden, wenn Stop-Loss oder Take-Profit erreicht ist.

Zum Beispiel habe ich die Ausführungszeit von Take-Profit auf 5 Balken festgelegt. Die Ausführungszeit für den Stop-Loss beträgt 5, 10 und 15 Balken. Eine der Optionen zur Änderung der Handelssaldo sieht wie folgt aus.

Die wichtigsten Testergebnisse sind in der Tabelle aufgeführt.

Nettogewinn, $	Bruttogewinn	Bruttoverlust	Profit-Faktor	Expected Payoff
-1 462.31	45 593.97	-47 056.28	0.97	-0.13
3 177.61	59 307.98	-56 130.37	1.06	0.28
1 833.58	59 963.97	-58 130.39	1.03	0.16

Wie wir sehen, kann sich eine Änderung der Stop-Loss-Ausführungszeit positiv auf die Handelsergebnisse auswirken.

Schlussfolgerung

Die folgenden Programme wurden bei der Erstellung dieses Artikels verwendet.

Name	Typ	Beschreibung
Lvl SL & TP	Skript	Das Skript ermöglicht die Berechnung des optimalen Stop-Loss und Take-Profit. Duration legt die erwartete Zeit für das Halten einer Position in Balken fest. Sie bestimmt die Größe von SL und TP. Die Berechnungsergebnisse werden auf der Registerkarte Experten angezeigt. Verifiable SL und Verifiable TP um einen Stop-Loss oder Take-Profit zu setzen, müssen wir den besten Expected Payoff für auswählen. Die Berechnungsergebnisse werden im Verzeichnis Files gesichert.
EA SL&TP	EA	Er ermöglicht die Überprüfung der Stop-Loss- und Take-Profit-Niveaus. Seed - Anfangsnummer, die die Reihenfolge der Positionen bestimmt. Ist der Wert ungleich 0, so werden die Positionen wiederholt. Dies hilft beim Vergleich verschiedener Stop-Losses und Take-Profits. SLBuy, TPBuy, SLSell, TPSell - Stop-Losses und Take-Profits positionieren. Ihre Werte können dem Skript Lvl SL & TP entnommen werden.
EA TIM	EA	Ermöglicht das Testen der Hypothese über unterschiedliche Zeiten für SL und TP. Seed - Anfangsnummer, die die Reihenfolge der Positionen bestimmt. DurationTP - erwarteter Zeitpunkt des Auftretens von Take-Profit. ShiftSL - wie viele Balken länger SL zu erwarten ist.