
您应当知道的 MQL5 向导技术(第 20 部分):符号回归
概述
我们继续这些系列,在其中我们看到能够快速编码、测试、或许能部署的算法,这一切都归功于 MQL5 向导,它不仅拥有标准交易函数和类库,能贴合智能系统编码,而且还有能与任何自定义类实现并行运行的替代交易信号和方法。
符号回归是回归分析的一种变体,与它的传统表亲经典回归相比,它更多是从“白纸”开始。概括这一点的最好方法是,如果我们研究典型回归问题,即搜寻与一组数据点最佳拟合的一条直线斜率、和 y 截距。
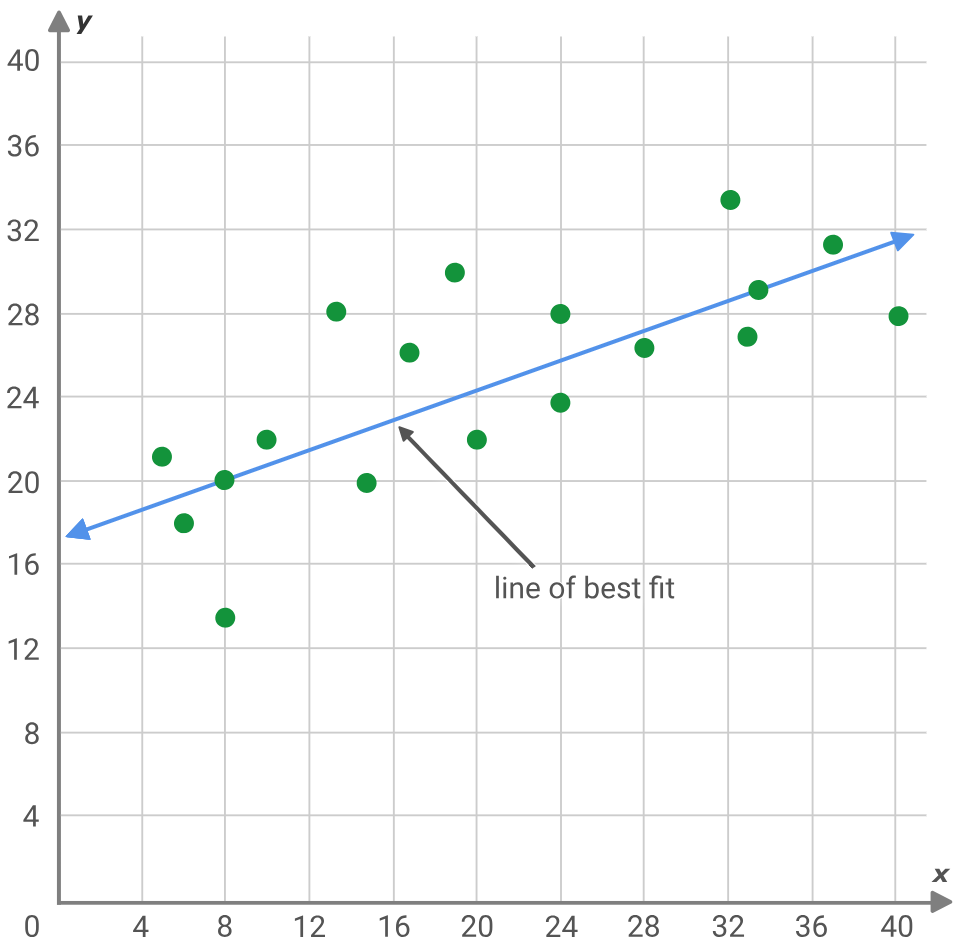
y = mx + c
其中:
- y 是预测 & 依赖值
- m 是最佳拟合直线的斜率
- c 是 y 截距
- 而 x 是自变量
上述问题假设,数据点理想情况下应拟合一条直线,这就是为何要寻求 y 截距和斜率的解。再者,神经网络亦然,本质上,通过假设具有预设架构(层编号、层大小、激活类型、等等)的网络,来搜寻最能映射 2 个数据集(又名模型)的波浪线、或二次方程。这些方式和其它同类在一开始就存在这种乖离,在某些情况下,从深度学习和(或)经验来看,这是合理的,不过符号回归允许描述性模型将两个欲构造的数据集映射为树型表达式,同时从随机分配的节点开始。
理论上,这可能更擅长揭示被传统手段掩盖的复杂市场关系。符号回归(SR)具有若干优势,盖过传统方式。它更能适应新的市场数据,和不断变化的条件,在于每次分析都从无乖离开始,使用随机分配的树型表达式节点,然后经优化。此外,SR 可以利用多个数据源,不像线性回归,其假设单一变量 'x' 影响 'y' 值。这种灵活性令 SR 能为复杂数据场景提供更准确、更全面的模型。适应性看到除了单一的 'x' 之外,更多的变量被组装在一个树型表达式之中,更好地定义了 'y' 的数值;更灵活,因为树型表达式通过开发系统节点来对训练数据进行更多控制,以定义的系数按设定的顺序处理数据,从而令其捕获更复杂的关系,相较线性回归而言(如上所述),其中仅能捕获线性关系。即使 'y' 仅依赖于 'x',这种关系或许也不是线性的,如它可能是二次方,而 SR 允许从遗传优化中建立这一点;最后,通过引入可解释性来揭开研究数据集之间黑盒模型关系的神秘面纱,因为所构造树型表达式本身就以更精确的术语“解释”输入数据实际上是如何映射到目标的。可解释性是大多数方程式所固有的,然而 SR 或许可通过从更复杂的表达中进行遗传进化来增加“简单性”,并朝更简单进化,前提是它们的最佳拟合分数更高。
定义
SR 将自变量和因(或预测)变量之间的映射模型表示为树型表达式。如此,图解表示如下所示:
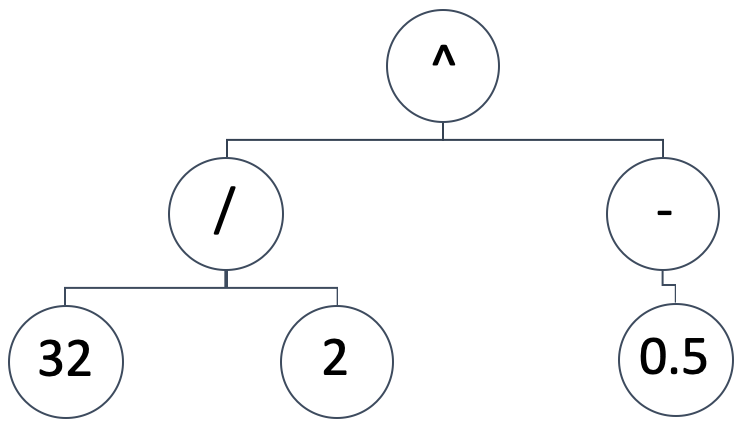
将暗示数学表达式:
(32/2) ^ (-0.5)
这相当于:0.25。树型表达式可以采用多种形式和设计,我们希望保持 SR 的基本前提,即从随机和非乖离配置开始。同时,我们需要能够在任何规模的初生树型表达式上运行遗传优化,同时能够将其结果(或最佳拟合衡量值)与不同规模的树型表达式进行比较。
为了达成这一点,我们将按'局次'运行我们的遗传优化。当如同神经网络一样批量训练区段时,尽管“局次”在机器学习术语中很常见,但于此,我们使用该术语来指代不同的遗传优化迭代,其中每次运行都采用相同规模的树型表达式。为什么我们在每个局次中都维持规模?因为遗传优化使用跨越式交叉,并且如果树型表达式的长度不同,那么就会令过程不必要地复杂化。那我们如何保持初始树型表达式的随机性呢?通过让每个局次表示特定规模的树。以这种方式,我们可以在所有局次中跨越优化,并将所有局次与相同的基准、或最佳拟合衡量值进行比较。
在 MQL5 内的向量/矩阵数据类型中提供了适应度函数测量选项,我们能用的是 regression 和 loss。这些内置函数都很适用,因为我们将把训练数据集的理想输出作为一个向量,相较已测试树型表达式所生成输出的向量格式进行比较。故此,测试数据集越长/越大,我们比较的向量就越大。这些大型数据集往往意味着达成理想的零差距最佳拟合值将非常困难,因此需要在每个局次中允许足够的优化代次。
基于最佳拟合分数到达最佳树型表达式,我们将从最长(因此最复杂)到最简单(想必也是最容易“解释”)的树型表达式进行评估。我们的树型表达式格式可以采取多种形式,不过我们将诉诸最基本的:
coeff, x-exponent, sign, coeff, x-exponent, sign, …
其中:
- Coeff 表示 x 的系数
- x-exponent 是 x 的幂
- sign 是表达式中的运算符,可以是 -、+、* 或 /
任何表达式的最后一个值都不能是运算符号,因为这样的符号不会连接到任何内容,而这意味着符号将始终少于任何表达式中的 x 值。这种表达式的大小范围从 1,其中我们只提供一个 x 系数及指数,没有符号,至 16 项(对于测试目的,于此严格约束到 16)。如上所述,这个最大规模与遗传优化中所用的局次直接相关。这简单地意味着我们开始优化树型表达式的理想表达式时,采用的单位长度是 16。如上所述,这 16 个单位意味着 15 个符号,而“每个单位”只是一个 x 系数、及其指数。
故此,在选择第一个随机树型表达式时,如果树型表达式的长度超过一个单位,我们将始终遵循 2 个随机数字“节点”后跟一个随机符号“节点”的格式,并且我们不会终止表达式,即我们有一个后随单位。帮助我们达成这一点的清单给出如下:
//+------------------------------------------------------------------+ // Get Expression Tree //+------------------------------------------------------------------+ void CSignalSR::GetExpressionTree(int Size, string &ExpressionTree[]) { if(Size < 1) { return; } ArrayFree(ExpressionTree); ArrayResize(ExpressionTree, (2 * Size) + Size - 1); int _digit[]; GetDigitNode(2 * Size, _digit); string _sign[]; if(Size >= 2) { GetSignNode(Size - 1, _sign); } int _di = 0, _si = 0; for(int i = 0; i < (2 * Size) + Size - 1; i += 3) { ExpressionTree[i] = IntegerToString(_digit[_di]); ExpressionTree[i + 1] = IntegerToString(_digit[_di + 1]); _di += 2; if(Size >= 2 && _si < Size - 1) { ExpressionTree[i + 2] = _sign[_si]; _si ++; } } }
上面的函数里,我们首先检查树型表达式的大小,以确保至少为 1。如果测试通过,则我们需要判定树的实际数组大小。据上,我们已经看到树遵循格式 coefficient、exponent,然后是 sign(如果用到的话)。这意味着给定大小 s,该树中的数字节点总数将为 2 x s,因为每个大小单位必须带有一个系数和指数值。这些节点是通过 GetDigitNode 函数随机选择的,其清单分享如下:
//+------------------------------------------------------------------+ // Get Digit //+------------------------------------------------------------------+ void CSignalSR::GetDigitNode(int Count, int &Digit[]) { ArrayFree(Digit); ArrayResize(Digit, Count); for(int i = 0; i < Count; i++) { Digit[i] = __DIGIT_NODE[MathRand() % __DIGITS]; } }
数字是从静态全局数字节点数组中随机选取的。虽然,符号节点会有所不同,取决于树的大小是否超过 1。如果我们有一个大小为一的树,那么不应有符号,因为这样留下的空间,只能容纳 x 系数及其指数。如果我们有多于一个的单元,那么符号节点的数量将等于输入大小减一。我们的函数如下,随机选择一个符号来填充表达式中的符号位:
//+------------------------------------------------------------------+ // Get Sign //+------------------------------------------------------------------+ void CSignalSR::GetSignNode(int Count, string &Sign[]) { ArrayFree(Sign); ArrayResize(Sign, Count); for(int i = 0; i < Count; i++) { Sign[i] = __SIGN_NODE[MathRand() % __SIGNS]; } }
与数字节点数组一样,符号是从符号节点数组中随机选择的。虽然这个数组可以取各种数量,但为了简洁起见,我们将其缩短,仅容纳 '+' 和 '-' 符号。可以添加 '*'(乘法)符号,不过 '/' 除法符号被特别省略,因为我们未处理除零,一旦我们开始遗传优化、且必须进行跨越等,这可能会非常棘手。读者可自行探索这个问题,前提是除零问题得到妥善解决,因为它可能会扭曲优化结果。
一旦我们得到随机树型表达式的初始群体,我们就能针对特定局次开启遗传优化过程。值得注意的还有我们存储和访问树型表达式信息的简单结构。它本质上是一个字符串矩阵,增加了调整大小的灵活性(这些功能应该由标准数据类型提供,就像处理双精度的矩阵?)。这些也列出如下:
//+------------------------------------------------------------------+ //| //+------------------------------------------------------------------+ struct Stree { string tree[]; Stree() { ArrayFree(tree); }; ~Stree() {}; }; struct Spopulation { Stree population[]; Spopulation() {}; ~Spopulation() {}; };
我们用此结构来创建和跟踪每个优化世代中的群体。每个局次使用一组世代数量进行优化。如前所述,测试数据集越大,需要的优化代次就越多。另一方面,如果测试数据太小,则也许会导致树型表达式主要来自白噪声,而非测试数据集中的底层形态,故此需要进行平衡。
一旦我们开始依据每一代进行优化,我们就需要获得每棵树的适应度,且因为我们有多棵树,这些适应度分数被记录在一个向量之中。一旦我们得到这个向量,下一步就变成了建立阈值来裁剪这个群体,给定树在给定局次内的每个后代中得以细化并收窄。我们将该阈值称为 “_fit”,它基于一个整数输入参数,充当百分位数标记。参数范围为 0 到 100。
我们继续自这个初始群体中创建另一个样本群体,其中我们只选择适应度低于、或等于阈值的树型表达式。上面所使用的计算我们的适应度分数的函数,给出清单如下:
//+------------------------------------------------------------------+ // Get Fitness //+------------------------------------------------------------------+ double CSignalSR::GetFitness(matrix &XY, vector &Y, string &ExpressionTree[]) { Y.Init(XY.Rows()); for(int r = 0; r < int(XY.Rows()); r++) { Y[r] = 0.0; string _sign = ""; for(int i = 0; i < int(ExpressionTree.Size()); i += 3) { double _yy = pow(XY[r][0], StringToDouble(ExpressionTree[i + 1])); _yy *= StringToDouble(ExpressionTree[i]); if(_sign == "+") { Y[r] += _yy; } else if(_sign == "-") { Y[r] -= _yy; } else if(_sign == "/" && _yy != 0.0)//un-handled { Y[r] /= _yy; } else if(_sign == "*") { Y[r] *= _yy; } else if(_sign == "") { Y[r] = _yy; } if(i + 2 < int(ExpressionTree.Size())) { _sign = ExpressionTree[i + 2]; } } } return(Y.RegressionMetric(XY.Col(1), m_regressor)); //return(_y.Loss(XY.Col(1),LOSS_MAE)); }
获取适应度函数采用输入数据集矩阵 'XY',并专注于矩阵的 x 列(我们对输入和输出两者都使用单维数据),来计算输入树型表达式的预测值。输入矩阵有多行数据,故此基于每行(第一列)的 x 值,每行进行投影,并将所有这些投影都存储在向量 'Y' 之中。所有行处理完毕之后,与向量 'Y' 第二列中调用内置回归函数、或损失函数得到的实际值比较。我们选择回归,以均方根误差作为回归衡量值。
该值的级量是输入树型表达式的适应度值。它越小,拟合越好。获得每个样本群体的该值之后,我们需要首先检查样本规模是否偶数,如果不是,则我们将样本规模减一。规模需要偶数,因为在下一阶段我们将在这些树之间交叉,并且世代的交叉是成对添加的,并且它们应与亲本群体(样本)匹配,因为我们只在每一代采样时减少群体。样本内树型表达式的交叉是按照随机选择索引完成的。负责交叉的函数清单如下:
//+------------------------------------------------------------------+ // Set Crossover //+------------------------------------------------------------------+ void CSignalSR::SetCrossover(string &ParentA[], string &ParentB[], string &ChildA[], string &ChildB[]) { if(ParentA.Size() != ParentB.Size() || ParentB.Size() == 0) { return; } int _length = int(ParentA.Size()); ArrayResize(ChildA, _length); ArrayResize(ChildB, _length); int _cross = 0; if(_length > 1) { _cross = rand() % (_length - 1) + 1; } for(int c = 0; c < _cross; c++) { ChildA[c] = ParentA[c]; ChildB[c] = ParentB[c]; } for(int l = _cross; l < _length; l++) { ChildA[l] = ParentB[l]; ChildB[l] = ParentA[l]; } }
该函数首先检查两个表达式亲本的大小是否相同,并且它们都不为零。如果这步通过,则调整两个输出子代数组的大小,以便匹配亲本数组的长度,然后选择交叉点。该交叉也是随机的,仅当亲本大小大于 一时才相关。一旦设置了交叉点,两个亲本数组的值将互换,并输出到两个子代数组之中。其中匹配长度就派上用场了,因为,举例,如果它们不同,则需要额外的代码来处理(或避免)数字与符号互换的情况。显然无需如此复杂,因为所有规模都能独立测试,按自己的局次,从而获得最佳拟合。
一旦我们完成了交叉,我们或许会令子节点变异。“或许”是因为我们使用 5% 的概率阈值来做这些突变,如此它们不能得到保证,但这是遗传优化过程的典型部分。然后,我们复制这个新的交叉群体,覆盖我们在开始时从中采样的起始群体,并作为标记,我们记录了这个新交叉群体中最佳树型表达式的最佳拟合分数。我们不仅使用记录的分数来判定最佳拟合树,而且在极少数情况下,即使我们得到零值,我们也会停止优化。
自定义信号类
在开发信号类时,我们的主要步骤与贯穿本系列之前我们所做的自定义信号类并无太大区别。首先,我们需要为我们的模型准备数据集。就是由上面看到的获取适应度函数填充 'XY' 输入矩阵的数据。它也是函数的输入,该函数集成了我们上面概述的所有步骤,称为 'GetBestTree'。该函数的源代码给出如下:
//+------------------------------------------------------------------+ // Get Best Fit //+------------------------------------------------------------------+ void CSignalSR::GetBestTree(matrix &XY, vector &Y, string &BestTree[]) { double _best_fit = DBL_MAX; for(int e = 1 + m_epochs; e >= 1; e--) { Spopulation _p; ArrayResize(_p.population, m_population); int _e_size = 2 * e; for(int p = 0; p < m_population; p++) { string _tree[]; GetExpressionTree(e, _tree); _e_size = int(_tree.Size()); ArrayResize(_p.population[p].tree, _e_size); for(int ee = 0; ee < _e_size; ee++) { _p.population[p].tree[ee] = _tree[ee]; } } for(int g = 0; g < m_generations; g++) { vector _fitness; _fitness.Init(int(_p.population.Size())); for(int p = 0; p < int(_p.population.Size()); p++) { _fitness[p] = GetFitness(XY, Y, _p.population[p].tree); } double _fit = _fitness.Percentile(m_fitness); Spopulation _s; int _samples = 0; for(int p = 0; p < int(_p.population.Size()); p++) { if(_fitness[p] <= _fit) { _samples++; ArrayResize(_s.population, _samples); ArrayResize(_s.population[_samples - 1].tree, _e_size); for(int ee = 0; ee < _e_size; ee++) { _s.population[_samples - 1].tree[ee] = _p.population[p].tree[ee]; } } } if(_samples % 2 == 1) { _samples--; ArrayResize(_s.population, _samples); } if(_samples == 0) { break; } Spopulation _g; ArrayResize(_g.population, _samples); for(int s = 0; s < _samples - 1; s += 2) { int _a = rand() % _samples; int _b = rand() % _samples; SetCrossover(_s.population[_a].tree, _s.population[_b].tree, _g.population[s].tree, _g.population[s + 1].tree); if (rand() % 100 < 5) // 5% chance { SetMutation(_g.population[s].tree); } if (rand() % 100 < 5) { SetMutation(_g.population[s + 1].tree); } } // Replace old population ArrayResize(_p.population, _samples); for(int s = 0; s < _samples; s ++) { for(int ee = 0; ee < _e_size; ee++) { _p.population[s].tree[ee] = _g.population[s].tree[ee]; } } // Print best individual for(int s = 0; s < _samples; s ++) { _fit = GetFitness(XY, Y, _p.population[s].tree); if (_fit < _best_fit) { _best_fit = _fit; ArrayCopy(BestTree,_p.population[s].tree); } } } } }
输入矩阵将单一维度的 x 值和单一维度的 y 值配对。自变量和因变量。多维性亦可容纳 “Y” 输入向量转换为矩阵和树型表达式,对应输入向量中的每个 x 值、输出向量中的每个 y 值。这些树型表达树还必须以矩阵、或更高维度的格式存储。
尽管,我们使用的是单一维度,且我们的数据行仅包含连续的收盘价。故此,在顶部或最近的数据行中,我们将倒数第二个收盘价作为我们的 x 值,并将当前收盘价当作我们的 y。准备工作和用这些数据填充我们的 'XY' 矩阵由下面的源代码处理:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalSR::LongCondition(void) { int result = 0; m_close.Refresh(-1); matrix _xy; _xy.Init(m_data_set, 2); for(int i = 0; i < m_data_set; i++) { _xy[i][0] = m_close.GetData(StartIndex()+i+1); _xy[i][1] = m_close.GetData(StartIndex()+i); } ... return(result); }
一旦我们的数据准备完毕,明确我们的模型中所的适应度评估方法是个好主意。相较损失,我们选择了回归,但即使在回归中,也有少量衡量值可供选择。因此,为了能够优选,被选用的回归衡量值类型是一个输入参数,可以对其进行优化,从而更好地适应经过测试的数据集。尽然,我们的默认值是常见的均方根误差。
遗传算法的实现由 GetBestTree 函数处理,其源代码已在上面列出。它返回一定数量的领头输出,其是最好的树型表达式树。配以该树,我们可将当前收盘价作为输入(x 值),调用 GetFitness 函数来处理,从而获得我们的下一个收盘价(y 值),不仅所查询表达式的适应度,它还返回更多内容,因为输入 'Y' 向量包含我们的目标预测。这项处理在下面的代码中:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalSR::LongCondition(void) { ... vector _y; string _best_fit[]; GetBestTree(_xy, _y, _best_fit); ... return(result); }
获得指示性的下一个收盘价后,下一步是将此价格转换为智能交易系统的可用信号。预测值往往仅指示性上涨或下跌,但与最近的收盘价值相比,它们的绝对值超出了范围。这意味着在使用它们之前,我们需要先对它们归一化。归一化和信号生成在下面的代码中完成:
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalSR::LongCondition(void) { int result = 0; ... double _cond = (_y[0]-m_close.GetData(StartIndex()))/fmax(fabs(_y[0]),m_close.GetData(StartIndex())); _cond *= 100.0; //printf(__FUNCSIG__ + " cond: %.2f", _cond); //return(result); if(_cond > 0.0) { result = int(fabs(_cond)); } return(result); }
在一个标准智能信号类中,多头和空头条件的整数输出必须在 0 – 100 范围内,这就是我们在上述代码中所做的信号转换。
多头条件函数和空头条件函数是彼此的镜像,将信号类组装成智能系统的内容在此处和 此处的文章中涵盖。
回测和优化
按组装的智能系统的一些 “最佳设置” 执行测试运行时,我们得到以下报告和净值曲线:
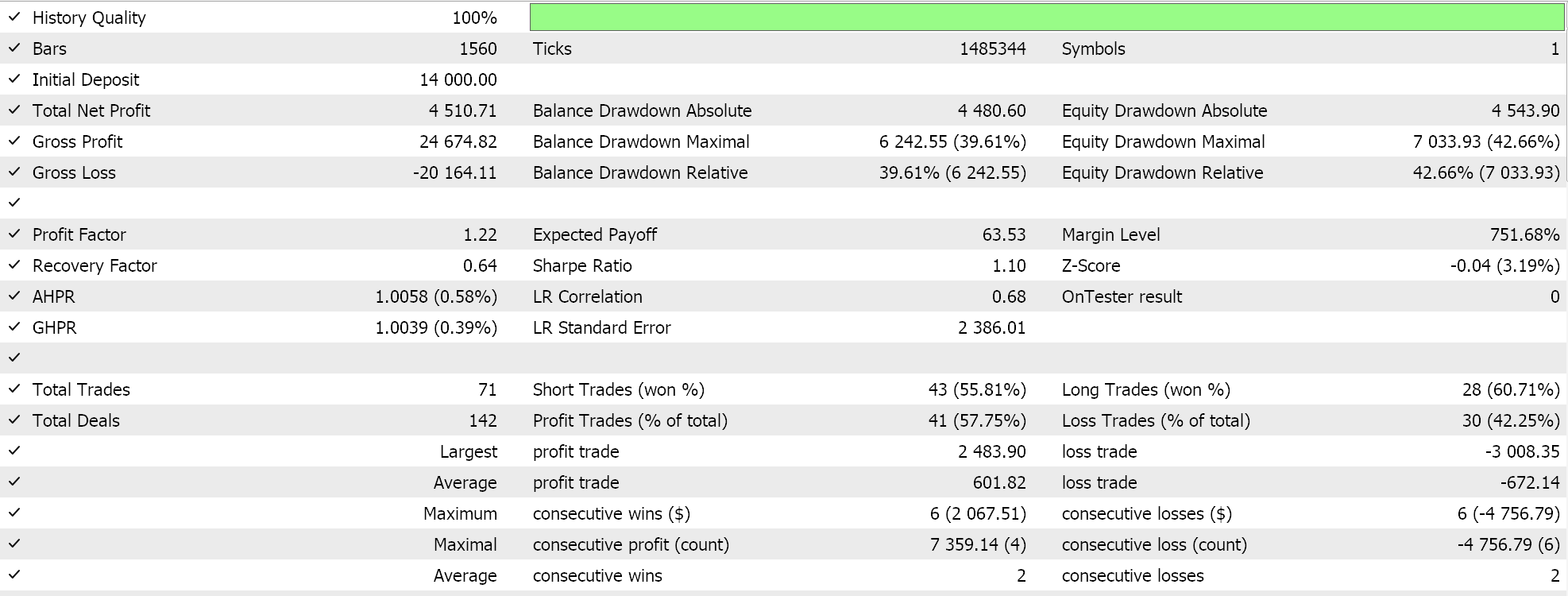
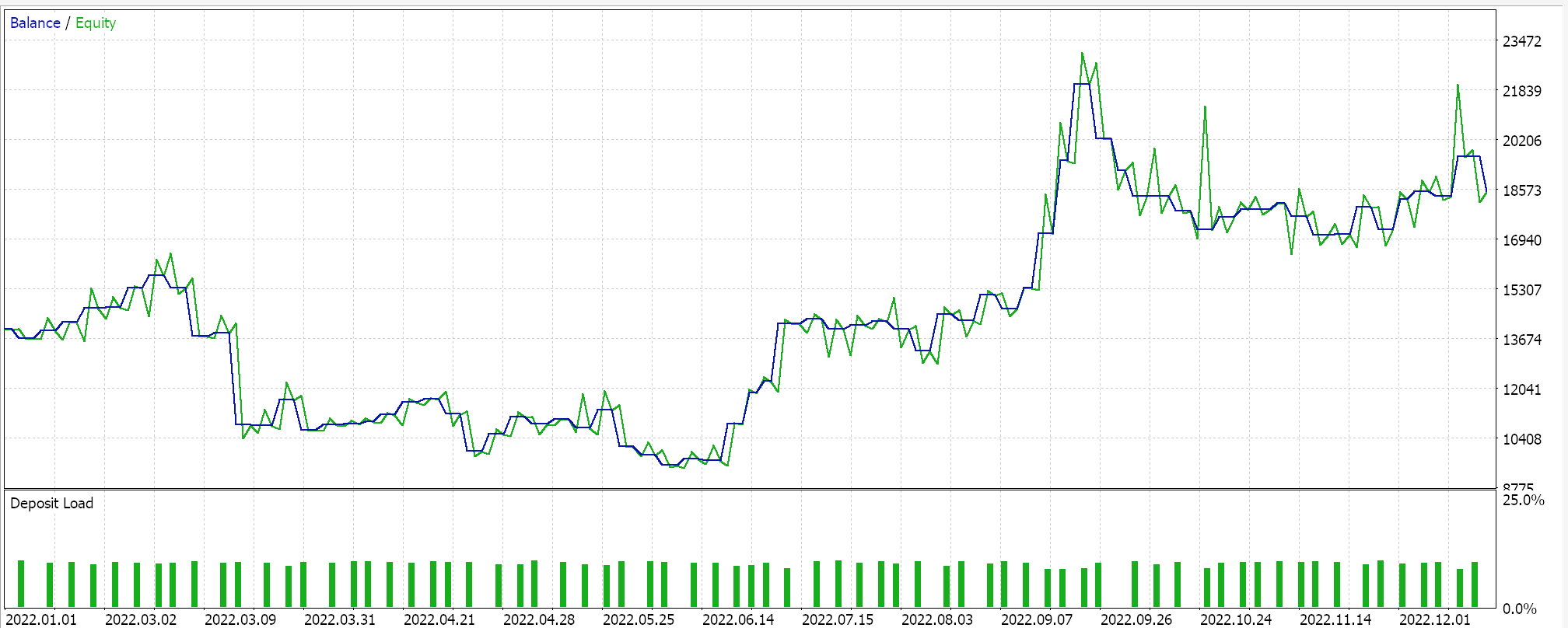
对于任何给定的设置,由于树型表达式来自随机选择,且交叉和突变也是随机的,因此任何特定的测试运行都不太可能完全复现其结果,有趣的是,如果测试运行是可盈利的,那么采用相同设置的后续运行将得到不同的性能统计信息,但总的来说,也将有利可图。我们的测试是针对 2022 年的,在 H4 时间帧内对欧元日元对进行。如常,我们运行的测试没有 SL 或 TP 的价格目标,因为这有助于更好地判定理想的智能系统设置。
结束语
回头看,我们阐述了符号回归作为模型,可用在一个智能信号类的自定义实例当中,以便权衡多头和空头条件。在此分析中,我们用到了十分适度的数据集,因为模型的输入和输出值都是一维的。这并不意味着模型无法扩展,以便容纳多维数据集。此外,模型算法的遗传优化性质,如此这般每次测试运行中获得相同结果变得很棘手。这意味着基于该模型的智能系统理应在相当大的时间帧内使用,并与其它交易信号结合使用,以便它们可作为已独立生成信号的确认。
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/14943
 您应当知道的 MQL5 向导技术(第 19 部分):贝叶斯(Bayesian)推理
您应当知道的 MQL5 向导技术(第 19 部分):贝叶斯(Bayesian)推理


