随机优化和最优控制示例

随机建模与控制优化简介

随机建模和控制优化是数学方法，有助于解决不确定性问题。它们被应用于金融、工程、人工智能以及许多其他领域。

随机建模用于描述具有随机元素的系统，例如股票市场价格波动或餐厅的排队情况。它基于随机变量、概率分布以及随机过程。蒙特卡洛（Monte Carlo）方法和马尔可夫链（Markov chains）等方法可以对这些过程进行建模并预测其行为。
控制优化有助于您为控制系统找到更好的解决方案。其被用于自动化并改进各种运行流程，从驾驶汽车到运营化工厂。基本方法包括线性二次控制器、模型预测控制以及强化学习。随机控制优化结合了上述两种方法，应用于那些必须在对未来的不完全信息下做出决策的问题，例如在投资或供应链管理中。

这些方法使我们能够在复杂环境中对不确定系统进行建模并做出明智决策，使它们成为当今世界中重要的工具。

EA

SMOC（智能资金最优控制）EA使用技术指标、数学模型和风险管理方法的组合，在外汇市场中做出交易决策，作为一个简单的示例来展示其能力。

主要特点：

1. 预测管理模型： 该EA使用最优管理算法来预测未来价格走势并做出交易决策。
2. 自适应参数： 系统根据市场波动和账户回撤调整预测范围和手数。
3. 多种技术指标： 包括简单移动平均线（SMA）、抛物线转向系统（SAR）、相对强弱指数（RSI）和平均真实范围（ATR），用于趋势和波动分析。
4. 动态止损和获利： 该EA根据市场波动计算并更新止损（SL）和获利（TP）水平。
5. 风险管理： 包括根据账户余额和回撤调整仓位规模的功能。

可能的应用领域：

• 中期和长期交易策略
• 具有明显趋势的市场
• 需要复杂风险管理的投资组合

优点：

1. 自适应方法： 系统适应不断变化的市场条件，可能增强其韧性。
2. 复杂分析： 通过结合多种指标和数学模型，旨在反映市场行为的各个方面。
3. 考虑风险： 该EA包括防止回撤和动态确定仓位规模的保护机制。
4. 详细的日志记录： 维护一个日志文件，用于性能分析和调试。

缺点：

1. 复杂性： 复杂的算法可能使系统难以理解和优化。
2. 计算密集型： 最优控制计算属于计算密集型，可能限制其在较不强大的系统上的使用。
3. 潜在的过拟合： 由于有大量的参数和指标，存在对历史数据过拟合的风险。
4. 市场假设： 该策略的有效性基于假设过去的价格行为可以预测未来的走势，但这在金融市场中并不总是成立。

SMOC EA的主要特点：

模型预测控制（MPC）： 该EA使用最优控制算法来预测未来价格走势并做出交易决策。这一点在OptimalControl()函数中实现。

//+------------------------------------------------------------------+
//| Function for optimal control using Model Predictive Control      |
//+------------------------------------------------------------------+
int OptimalControl( double currentPrice)
  {
   int predictionHorizon = CalculateAdaptiveHorizon();
   double mu = EstimateDrift();
   double sigma = EstimateVolatility();
   double baseThreshold = 0.001 ;
   double decisionThreshold = baseThreshold * ( 1 + ( 1 - successRate));
   double dt = 1.0 / 1440.0 ;

   double bestExpectedReturn = - DBL_MAX ;
   int bestDecision = 0 ;
   double bestU1 = 0 , bestU2 = 0 ;

// Optimize the search space
   double u1Start = 0.01 , u1End = 0.99 , u1Step = 0.01 ;
   double u2Start = 0.01 , u2End = 0.99 , u2Step = 0.01 ;

// Calculate historical average price
   int lookbackPeriod = 20 ; // You can adjust this
   double historicalPrices[];
   ArraySetAsSeries (historicalPrices, true );
   CopyClose ( Symbol (), PERIOD_CURRENT , 0 , lookbackPeriod, historicalPrices);
   double avgHistoricalPrice = ArraySum(historicalPrices) / lookbackPeriod;

   for ( double u1 = u1Start; u1 <= u1End; u1 += u1Step)
     {
       for ( double u2 = u2Start; u2 <= u2End; u2 += u2Step)
        {
         double expectedReturn = CalculateExpectedReturn(currentPrice, mu, sigma, dt, predictionHorizon, u1, u2);

         // Compare with historical average
         if (currentPrice > avgHistoricalPrice)
           {
            expectedReturn *= - 1 ; // Invert expected return to favor selling when price is high
           }

         if (expectedReturn > bestExpectedReturn)
           {
            bestExpectedReturn = expectedReturn;
            bestU1 = u1;
            bestU2 = u2;
           }
        }
     }

   LogMessage( StringFormat ( "OptimalControl - Best u1: %f, Best u2: %f, Best Expected Return: %f, Decision Threshold %f" ,
                           bestU1, bestU2, bestExpectedReturn, decisionThreshold));

   if (bestExpectedReturn > decisionThreshold)
       return 1 ; // Buy
   if (bestExpectedReturn < decisionThreshold)
       return - 1 ; // Sell
   return 0 ; // Hold
  }

该系统使用模型预测控制（MPC）来做出最优的交易决策。OptimalControl函数是该算法的核心，用于根据当前市场条件和预测来确定是购买、出售还是持有。

OptimalControl函数以当前价格作为输入，并返回一个整数来表示交易决策：

• 1代表买入
• -1代表卖出
• 0代表持有

关键组成部分

1. 自适应预测范围：该函数计算自适应预测范围，允许算法根据市场条件调整预测范围。
2. 市场参数评估：评估关键市场参数：
   • 漂移（μ）：资产的预期回报
   • 波动性（σ）：资产价格变化的速率。
3. 决策阈值：动态阈值基于基础阈值和算法的成功率计算得出。这使得算法对市场变化的感度的适应性更强。
4. 优化过程：在定义的搜索空间中，该函数使用网格搜索来优化两个控制参数（u1和u2）。
5. 历史价格比较：将当前价格与历史平均值进行比较，根据当前价格是相对高还是低来调整策略。
6. 计算预期回报：对于每组控制参数，使用一个单独的函数（在本代码段中未显示）来计算预期回报。
7. 决策制定：基于最佳预期回报和决策阈值，决定是购买、出售还是持有该资产。

详情回顾

1. 该函数首先初始化变量并计算所需参数。
2. 然后进入嵌套循环以找到最优的控制参数（u1和u2）。
3. 对于每组u1和u2的组合，计算预期回报。
4. 如果当前价格高于历史平均值，它将反转预期回报。在价格高时创建偏向于卖出的建议，在价格低时创建偏向于买入的建议。
5. 它跟踪最佳预期回报和相应的基准。
6. 优化后，记录最优参数和预期盈利性。
7. 最后，它将最佳预期回报与阈值进行比较，以做出交易决策。

核心理念：

• 该算法使用自适应范围和动态阈值来适应市场条件。
• 它既包括短期优化（使用MPC方法），也包括对趋势的长期理解（使用历史价格比较）。
• 使用网格搜索进行优化，允许对参数空间进行彻底的探索，可能会带来更稳健的决策。

可能的改进

1. 可以将网格搜索替换为更高效的优化算法以提高性能。
2. 历史价格的比较可以更复杂，例如包括多个时间框架。
3. 可以添加风险管理功能，以平衡回报优化与风险最小化。

 /+------------------------------------------------------------------+
//| Calculate expected return for given parameters                   |
//+------------------------------------------------------------------+
double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)
  {
   double tempPrice = currentPrice;
   double totalReturn = 0 ;

   for ( int i = 0 ; i < horizon; i++)
     {
       double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);
       double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);
      totalReturn += nextPrice - tempPrice;
      tempPrice = nextPrice;
     }

   return totalReturn / horizon;
  }

它是金融模型和算法交易系统中的关键组成部分。该函数使用一种称为几何布朗运动（GBM）的随机过程，来评估资产在指定时间范围内的预期回报。

 double CalculateExpectedReturn( double currentPrice, double mu, double sigma, double dt, int horizon, double u1, double u2)

参数

1. currentPrice：资产的当前价格
2. mu：漂移参数（预期回报）
3. sigma：波动率参数
4. dt：时间步长（通常是每年步数的倒数）
5. Horizon：要模拟的时间步数。
6. u1, u2：用于生成正态分布随机变量的随机数。

函数概述：

该函数使用几何布朗运动模型来模拟资产的价格路径，这种模型在金融数学中被广泛用于模拟股票价格。还用于计算沿模拟路径的平均回报。

详情说明

1. 初始化：
   • 将tempPrice初始化为当前价格。
   • 将totalReturn设置为0，用于累积回报。
2. 模拟循环： 函数进入循环，循环次数为horizon。在每次迭代中：生成随机正态变量 ：

 double Z = MathSqrt (- 2.0 * MathLog (u1)) * MathCos ( 2.0 * M_PI * u2);

此行代码实现了Box-Muller变换，用于生成标准正态随机变量。这是模拟资产价格随机变化的关键组成部分。

计算下一个价格：

 double nextPrice = tempPrice * MathExp ((mu - 0.5 * sigma * sigma) * dt + sigma * MathSqrt (dt) * Z);

此行代码实现了几何布朗运动的公式：

• (mu - 0.5 * sigma * sigma) * dt代表漂移部分
• sigma * MathSqrt(dt) * Z代表随机冲击部分

累积回报：

totalReturn += nextPrice - tempPrice;

该函数计算并累积每一步的回报。

价格更新：

tempPrice = nextPrice;

将当前价格更新为下一个迭代的价格。

计算平均回报：

 return totalReturn / horizon;

该函数返回模拟范围内的平均回报。

在金融建模中的重要性

1. 风险评估：模拟多条价格路径，此功能有助于评估与资产相关的潜在风险。
2. 期权定价：这种类型的建模是期权定价模型的基础，尤其是在蒙特卡洛方法中。
3. 投资组合优化：预期回报是投资组合优化算法的关键输入。
4. 交易策略：算法交易策略通常使用预期回报来做出买入/卖出决策。

局限性和注意事项

1. 模型假设：GBM模型假设回报呈正态分布且相互独立，但这在实际市场中并不总是成立。
2. 参数估计：该函数的准确性在很大程度上取决于对mu和sigma的正确估计。
3. 单一模拟：该函数仅运行一次模拟操作。在实践中，通常需要运行多次模拟以获得更可靠的估计。
4. 时间范围：选择horizon和dt会显著影响结果，应根据具体用例谨慎选择。

该函数是量化金融中的基本构建块，提供了一种基于当前市场参数估计未来回报的方法。其在交易算法中的实现，使处于复杂的金融环境中能够进行数据驱动的决策。

自适应参数：系统根据市场波动和账户回撤调整其预测范围和手数。通过CalculateAdaptiveHorizon()和AdjustLotSizeForDrawdown()等函数实现。

//+------------------------------------------------------------------+
//| Calculate adaptive horizon                                       |
//+------------------------------------------------------------------+
int CalculateAdaptiveHorizon()
  {
   double currentVolatility = EstimateVolatility();
   int baseHorizon = 5 ;
   return MathMax (baseHorizon, MathMin ( 20 , ( int )(baseHorizon * ( 1 + currentVolatility))));
  }

 // Función para ajustar el tamaño del lote basado en drawdown
double AdjustLotSizeForDrawdown()
  {
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   double drawdown = (maxBalance - currentEquity) / maxBalance;

   double baseLotSize = CalculateDynamicLotSize();

   if (drawdown > 0.1 ) // 10% drawdown
     {
       return baseLotSize * 0.5 ; // Reducir el tamaño del lote a la mitad
     }
   else
       if (consecutiveLosses > 3 )
        {
         return baseLotSize * 0.75 ; // Reducir el tamaño del lote en un 25%
        }

   return baseLotSize;
  }

这是交易风险管理中的一个重要组成部分。该功能根据当前账户的回撤和连续亏损的次数来调整交易的手数。

函数概述：

AdjustLotSizeForDrawdown函数旨在动态调整交易手数，以管理在波动的市场条件下的风险。它考虑了两个主要因素：

1. 当前交易账户的回撤
2. 连续亏损的次数

关键组成部分

1. 静态变量：
   • consecutiveLosses：跟踪连续亏损交易的数量
   • maxBalance：维护账户达到的最大余额
2. 账户信息：
   • currentBalance：当前交易账户的余额
   • currentEquity：当前交易账户的净值
3. 回撤计算：回撤是通过从最大余额到当前净值的百分比下降来计算的。
4. 基础手数：该函数调用CalculateDynamicLotSize()（在本段中未显示）来确定基础手数。
5. 手数调整：该函数根据两个条件调整手数：
• 如果回撤超过10%
• 如果连续亏损超过3次

详情说明

最大余额更新：

 if (currentBalance > maxBalance)
   maxBalance = currentBalance;

使您能够跟踪达到的最大余额，这对于计算回撤至关重要。

回撤计算：

 double drawdown = (maxBalance - currentEquity) / maxBalance;

计算当前回撤作为最大余额的百分比。

获取基础手数：

 double baseLotSize = CalculateDynamicLotSize();

调用一个单独的函数来计算初始手数。

高回撤情况下的调整：

 if (drawdown > 0.1 ) // 10% drawdown
  {
   return baseLotSize * 0.5 ; // Reduce lot size by half
  }

如果回撤超过10%，该函数会将手数减少一半，以降低风险。

连续亏损调整：

 else if (consecutiveLosses > 3 )
  {
   return baseLotSize * 0.75 ; // Reduce lot size by 25%
  }

如果出现超过3次的连续亏损，该函数会将手数减少25%。

返回默认值： 如果没有满足任何条件，该函数将返回未经调整的基础手数。

在风险管理中的重要性：

1. 回撤保护：在显著回撤期间减少手数，这一功能有助于在不利的市场条件下保护账户免受进一步损失。
2. 管理连败：调整连续亏损有助于减轻连败的影响，对于投资者而言这种影响在心理和财务上都可能是毁灭性的。
3. 动态风险调整： 这一功能使您能够通过根据当前市场条件和交易结果进行调整，从而动态地管理风险。

注意事项和潜在改进

1. 逐步调整：可以修改这一功能，根据不同程度的回撤实施对手数的更逐步调整。
2. 恢复机制：可以添加一个额外的机制，在账户从回撤中恢复时逐步增加手数。
3. 最大手数限制：引入最大手数限制可以提供额外的风险管理保障。
4. 连胜跟踪：可以扩展这一功能，跟踪连续获胜，并在有利时期可能增加手数。

这一功能是交易系统中风险管理的一个重要方面，有助于在艰难的市场条件下保护资本并减轻连败的影响。

多个技术指标：该EA包含多个技术指标用于分析。

• 简单移动平均线（SMA）
• 抛物线转向（Parabolic SAR）
• 相对强弱指数（RSI）
• 平均真实范围（ATR）

 // Initialize indicator handles
   smaHandle = iMA ( Symbol (), PERIOD_CURRENT , 50 , 0 , MODE_SMA , PRICE_CLOSE );
   psarHandle = iSAR ( Symbol (), PERIOD_CURRENT , 0.02 , 0.2 );
   rsiHandle = iRSI ( Symbol (), PERIOD_CURRENT , 14 , PRICE_CLOSE );
   atrHandle = iATR ( Symbol (), PERIOD_CURRENT , 14 );

动态止损和获利： 该EA使用CalculateDynamicSL()和CalculateDynamicTP()函数，根据市场波动计算并更新止损（SL）和获利（TP）水平。

 double CalculateDynamicSL( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

   return NormalizeDouble (dynamicSL, _Digits );
  }


double CalculateDynamicTP( double price, int decision)
  {
   double atrValue[];
   if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
     {
      LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
       return 0.0 ;
     }
   double volatility = atrValue[ 0 ];
   double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

   return NormalizeDouble (dynamicTP, _Digits );
  }

该功能根据当前市场波动计算动态止损（SL）和获利（TP）水平，从而改善风险管理并可能提升交易成果。

功能回顾

这两个函数均使用平均真实范围（ATR）指标来衡量市场波动，并据此相应调整止损（SL）和获利（TP）水平。它们会考虑交易是买入（1）还是卖出（-1）决策。

 double CalculateDynamicSL( double price, int decision)

该函数根据当前价格、交易方向和市场波动计算动态止损水平。

 double CalculateDynamicTP( double price, int decision)

该函数根据当前价格、交易方向和市场波动计算动态获利水平。

关键组成部分

1. ATR指标：这两个函数都使用ATR指标来衡量市场波动。
2. 价格：资产的当前市场价格。
3. 决策：一个整数（1代表买入，推测-1代表卖出），表示交易方向。
4. 乘数：全局变量multi用于调整波动率的影响。

详情说明

CalculateDynamicsSL函数

获取ATR值：

 double atrValue[];
if ( CopyBuffer (atrHandle, 0 , 0 , 1 , atrValue) <= 0 )
{
   LogMessage( StringFormat ( "Error getting ATR values: %d" , GetLastError ()));
   return 0.0 ;
}
double volatility = atrValue[ 0 ];

此段代码用于获取最新的ATR值，反映了市场的波动性。

计算动态止损（SL） ：

 double dynamicSL = (decision == 1 ) ? price - (volatility * multi * 1.2 ) : price + (volatility * multi * 0.8 );

对于买入交易（decision == 1），止损设置在当前价格下方。

对于卖出交易，止损设置在当前价格上方。

距离是通过ATR的倍数来计算的，使用multi变量和一个系数进行调整（买入时为1.2，卖出时为0.8，我这样做是为了在文章中展示差异）。

归一化并返回：

 return NormalizeDouble (dynamicSL, _Digits );

将止损值归一化到所交易工具的适当小数位数。

CalculateDynamicTP函数：

获取ATR值： 这部分与止损函数相同。

计算动态获利（TP）：

 double dynamicTP = (decision == 1 ) ? price + (volatility * multi * 1.8 ) : price - (volatility * multi * 2.2 );

对于买入交易，获利（TP）设置在当前价格上方。

对于卖出交易，获利（TP）设置在当前价格下方。

距离是通过ATR的倍数计算的，使用multi变量和一个系数进行调整（买入时为1.8，卖出时为2.2，我这样做是为了展示差异，您可以根据需要使用其他值）。

归一化并返回： 与止损（SL）函数类似。

交易中的重要性

1. 基于波动率的风险管理：使用ATR，这些功能根据当前市场条件调整止损（SL）和获利（TP）水平，从而提供更合适的风险管理。
2. 不对称的风险/回报比率：获利（TP）水平设置得比止损（SL）水平更远离入场价格，可能会创造出更有利的风险/回报比率。
3. 动态调整 ：随着市场波动率的变化，这些功能会自动为新的交易调整止损（SL）和获利（TP）水平。

注意事项和潜在改进

1. 错误处理 ：这两个函数在获取ATR时都有基本的错误处理，但可以进一步扩展。
2. 设置 ：乘数（1.2、0.8、1.8、2.2）可以转换为参数，以便更加容易设置。
3. 最小距离 ：为止损（SL）和获利（TP）设置最小距离，可以防止在极低波动率的条件下出现问题。
4. 最大距离 ：同样地，可以设置最大距离，以限制在高度不稳定条件下的风险。

这些功能代表了一种设置止损（SL）和获利（TP）水平的方法，该方法根据市场条件进行调整，以潜在地改善交易结果，同时有效地管理风险。

风险管理：包括根据账户余额和回撤调整仓位规模的函数，在AdjustLotSizeForDrawdown()和CalculateDynamicLotSize()中实现。

 // Function to adjust the lot size based on drawdown
double AdjustLotSizeForDrawdown()
{
   // Static variables to keep track of consecutive losses and maximum balance
   static int consecutiveLosses = 0 ;
   static double maxBalance = 0 ;

   // Get current account balance and equity
   double currentBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double currentEquity = AccountInfoDouble ( ACCOUNT_EQUITY );

   // Update the maximum balance if current balance is higher
   if (currentBalance > maxBalance)
      maxBalance = currentBalance;

   // Calculate the current drawdown as a percentage
   double drawdown = (maxBalance - currentEquity) / maxBalance;

   // Calculate the base lot size using a separate function
   double baseLotSize = CalculateDynamicLotSize();

   // If drawdown is greater than 10%, reduce lot size by half
   if (drawdown > 0.1 ) // 10% drawdown
   {
       return baseLotSize * 0.5 ; // Reduce lot size by half
   }
   else if (consecutiveLosses > 3 )
   {
       return baseLotSize * 0.75 ; // Reduce lot size by 25% after 3 consecutive losses
   }

   // Return the base lot size if no adjustments are needed
   return baseLotSize;
}

AdjustLotSizeForDrawdown() 函数旨在根据账户回撤和近期表现动态调整交易手数。以下是其主要功能分解：

1. 其使用静态变量来跟踪连续亏损次数以及达到的最大余额。
2. 通过将最大余额与当前净值进行比较，计算当前回撤。
3. 该函数实施了两种风险管理策略：
   • 如果回撤超过10%，手数将减半。
   • 如果出现超过3次的连续亏损，手数将减少25%。
4. 基础手数是通过另一个名为CalculateDynamicLotSize()的函数计算得出的，这在此代码段中未显示。
5. 如果未满足任何风险条件，函数将返回未经调整的基础手数。

这种方法通过减少影响，在市场表现不佳或高波动时期帮助保护您的交易账户。这是一种简单但有效的方法，用于在算法交易中实现自适应仓位调整。

 // Function to dynamically calculate the lot size
double CalculateDynamicLotSize()
{
   // Get current account balance and equity
   double accountBalance = AccountInfoDouble ( ACCOUNT_BALANCE );
   double equity = AccountInfoDouble ( ACCOUNT_EQUITY );
   double riskPercentage = 0.01 ; // 1% risk per trade

   // Use the lower value between balance and equity to be conservative
   double baseAmount = MathMin (accountBalance, equity);

   // Calculate the value of a pip for the current symbol
   double tickSize = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_SIZE );
   double tickValue = SymbolInfoDouble ( _Symbol , SYMBOL_TRADE_TICK_VALUE );
   double pipValue = (tickValue / tickSize) * 10 ; // Assuming a pip is 10 ticks

   // Calculate lot size based on desired risk
   double riskAmount = baseAmount * riskPercentage;
   double stopLossPips = 50 ; // Adjust according to your strategy

   double lotSize1 = NormalizeDouble (riskAmount / (stopLossPips * pipValue), 2 );

   // Ensure the lotSize is within the allowed limits
   double minLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MIN );
   double maxLot = SymbolInfoDouble ( _Symbol , SYMBOL_VOLUME_MAX );
   double lotSize2 = MathMax (minLot, MathMin (maxLot, lotSize1));

   return lotSize2;
}

CalculateDynamicLotSize() 函数旨在根据你的账户余额、风险承受能力以及当前市场条件计算合适的交易手数。以下是其主要功能分解：

1. 它通过取两者中的较低值来提取当前账户余额和净值，以采取更保守的方法。
2. 该函数使用固定的每笔交易风险比例，在此情况下设置为1%。
3. 它计算当前交易品种的点值，假设一个点相当于10个ticks。
4. 然后基于以下因素计算手数：
   • 风险金额（基础金额的1%）
   • 预定义的止损点数（在本例中设置为50点）
   • 计算出的项目价值
5. 该函数确保计算出的手数在交易品种允许的最小和最大手数范围内。
6. 最终返回的手数已归一化到两位小数。

这种对手数的动态方法有助于在交易中保持一致的风险水平，无论账户规模或市场条件如何。它是风险管理策略的重要组成部分，并与我们之前讨论的AdjustLotSizeForDrawdown() 函数协同工作。

这两个函数的结合提供了一个强大的风险管理系统，能够：

1. 根据账户表现和回撤调整仓位大小
2. 保持每笔交易的固定风险比例
3. 适应变化的账户余额和市场条件

这种方法可以帮助交易者在有利和不利的市场条件下保持自律，并保全自己的资本。

重要特征：

1. OptimalControl(double currentPrice)：这是EA的核心决策函数。它使用模型预测控制来确定是买入、卖出还是持有。它计算预测范围内的预期回报，并将其与决策阈值进行比较。
2. CalculateExpectedReturn(...)：该函数计算在OptimalControl 函数中使用的给定参数集的预期回报。
3. ManageOpenOrder(int decision)：管理现有未平仓订单，根据已开仓的K线数量或当前决策是否与未平仓头寸冲突，来决定是否平仓。
4. ExecuteTrade(int decision)：根据OptimalControl 的决策执行新交易，并设置适当的止损和获利水平。
5. UpdateSLTP(ulong ticket, int decision)：根据当前市场条件更新现有仓位的止损和获利水平。
6. EstimateDrift() 和 EstimateVolatility()：这些函数估计用于最优控制计算的价格漂移和波动性。
7. IsTrendFavorable(int decision) 和 IsLongTermTrendFavorable(int decision)：这些函数使用移动平均线和RSI检查当前市场趋势是否与交易决策一致。
8. AdjustLotSizeForDrawdown() 和 CalculateDynamicLotSize()：这些函数根据当前回撤和账户余额调整交易量，实施动态风险管理。
9. LogMessage(string message)：将重要事件和决策记录到文件中，以便后续分析和调试。

结果

1天时间周期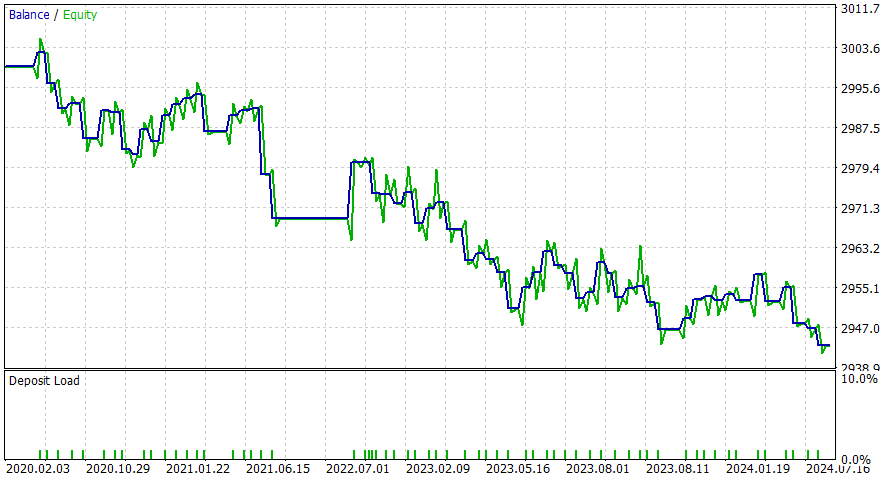

1小时时间周期

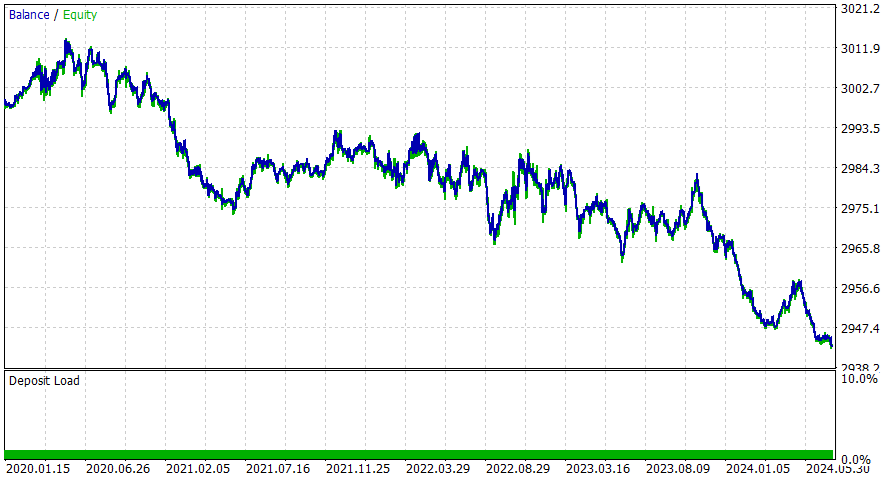
4小时时间周期

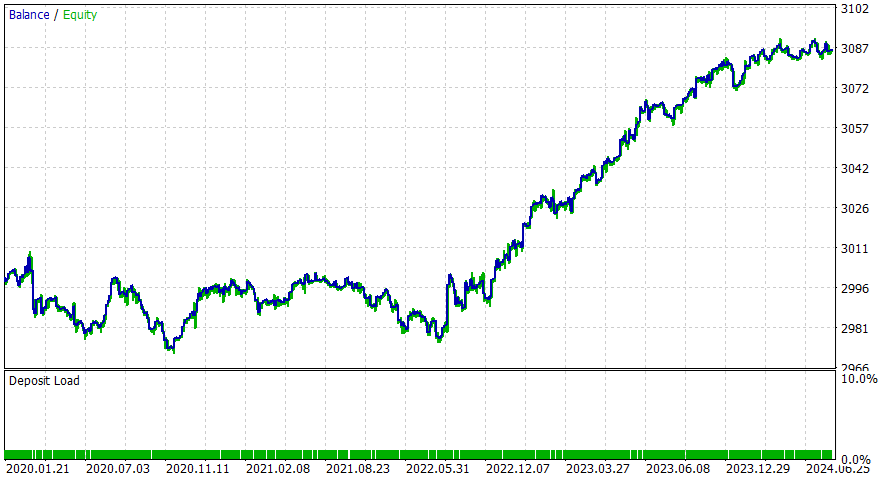
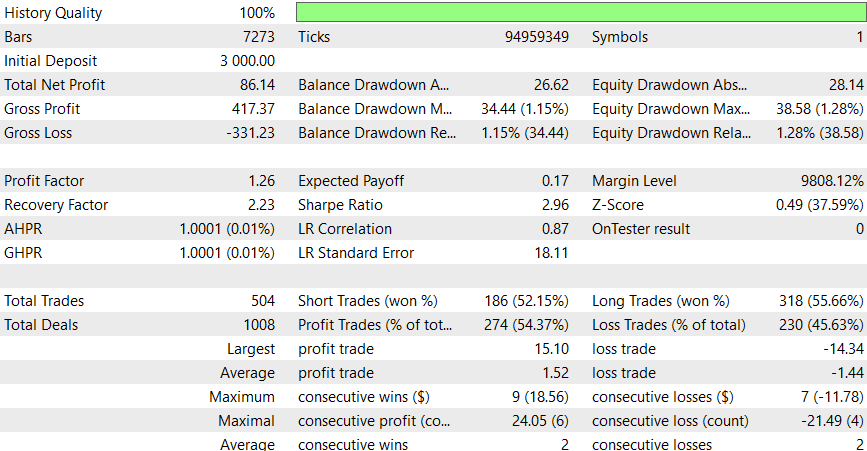
6小时时间周期

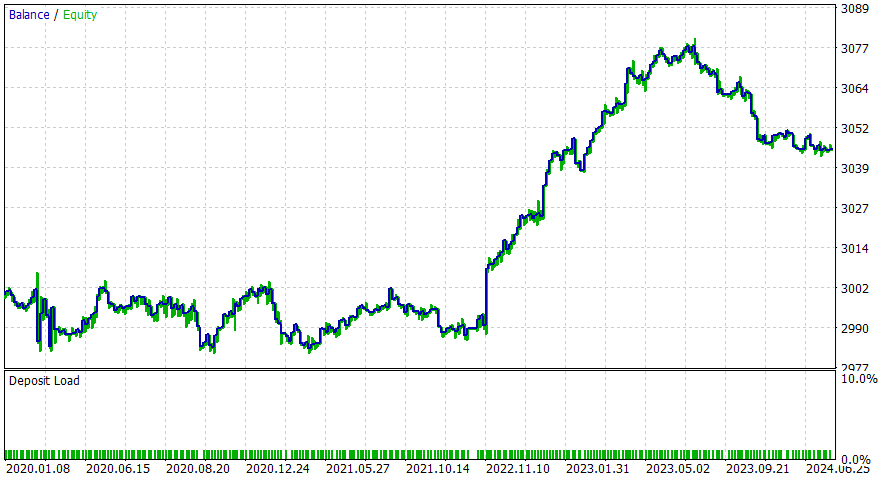
该EA似乎在日内交易时段表现得更好，但我相信通过添加止损（SL）或应用潜在改进措施，您可以获得更好的结果。

结论

SMOC EA是自动化交易中结合随机建模和控制优化的复杂方法的简化版本。结合了包括移动平均线、RSI、ATR和自定义最优控制算法在内的多种分析方法，旨在做出明智的交易决策。该系统具有适应性，例如动态手数调整和基于回撤的风险调整，这表明其注重长期的可持续性。然而，与任何其它交易系统一样，通过充分的回测和前瞻性测试，对于评估其实际表现和可靠性至关重要。

到此为止： 这只是一个高级EA的简单示例。