Técnicas do MQL5 Wizard que você deve conhecer (Parte 20): Regressão Simbólica

Introdução

Continuamos esta série onde analisamos algoritmos que podem ser rapidamente codificados, testados e talvez até implantados, tudo graças ao MQL5 Wizard, que não apenas tem uma biblioteca de funções e classes de trading padrão que acompanham um Expert Advisor codificado, mas também possui sinais de trade alternativos e métodos que podem ser usados em paralelo com qualquer implementação de classe personalizada.

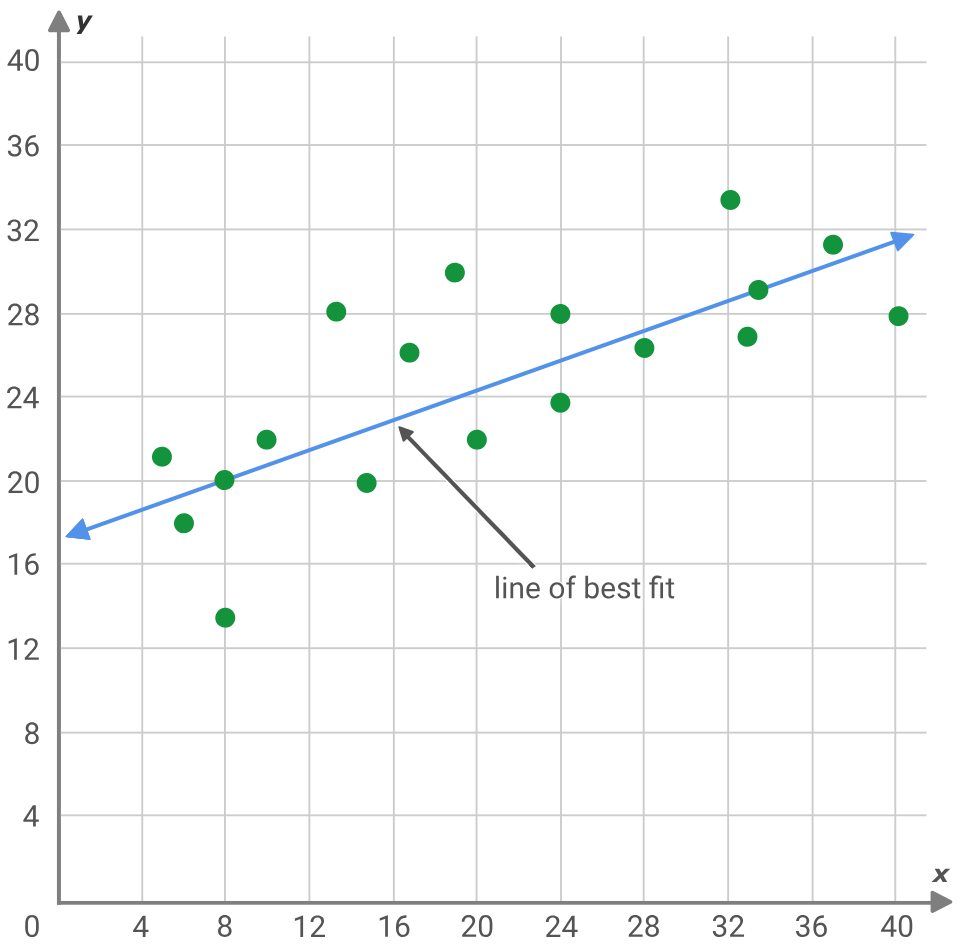
Regressão simbólica é uma variante da análise de regressão que começa com mais de uma 'tela em branco' do que sua prima tradicional, regressão clássica. A melhor maneira de ilustrar isso seria se considerássemos o problema típico de regressão que busca a inclinação e a interseção no eixo y de uma linha que melhor se ajusta a um conjunto de pontos de dados.

fonte

y = mx + c

onde:

• y é o valor previsto e dependente
• m é a inclinação da linha de melhor ajuste
• c é a interseção no eixo y
• e x é a variável independente

O problema acima assume que os pontos de dados idealmente devem se ajustar a uma linha reta, e é por isso que as soluções são buscadas para a interseção no eixo y e a inclinação. Alternativamente, as redes neurais, em essência, buscam encontrar a curva ou equação quadrática que melhor mapeia dois conjuntos de dados (também conhecido como o modelo), assumindo uma rede com uma arquitetura predefinida (número de camadas, tamanhos de camadas, tipos de ativação, etc.). Essas abordagens e outras semelhantes possuem esse viés desde o início, e há casos em que, a partir de aprendizado profundo e (ou) experiência, isso é justificado. No entanto, a regressão simbólica permite que o modelo descritivo que mapeia dois conjuntos de dados seja construído como uma árvore de expressões, começando com nós atribuídos aleatoriamente.

Isso poderia, em teoria, ser mais apto a descobrir relações complexas de mercado que podem ser negligenciadas por meios convencionais. A Regressão Simbólica (RS) tem várias vantagens sobre as abordagens tradicionais. Ela é mais adaptável a novos dados de mercado e condições em mudança, pois cada análise começa sem viéses, usando uma alocação aleatória de nós de árvore de expressões que são então otimizados. Além disso, a RS pode utilizar várias fontes de dados, ao contrário da regressão linear, que assume que uma única variável 'x' influencia o valor de 'y'. Essa flexibilidade permite que a RS forneça modelos mais precisos e abrangentes para cenários de dados complexos. A adaptabilidade vê mais variáveis além da simples ‘x’ sendo montadas em uma árvore de expressões que define melhor o valor de ‘y’; sendo mais flexível, já que a árvore de expressões exerce mais controle sobre os dados de treinamento, desenvolvendo nós sistemáticos que processam os dados em uma sequência definida com coeficientes que permitem capturar relações mais complexas, em oposição à regressão linear (como acima), onde apenas relações lineares seriam capturadas. Mesmo que ‘y’ dependesse apenas de ‘x’, essa relação pode não ser linear, podendo ser quadrática, e a RS permite que isso seja estabelecido a partir da otimização genética; e, finalmente, desmistificando o modelo de caixa preta entre os conjuntos de dados estudados, ao introduzir explicabilidade, já que as árvores de expressões construídas ‘explicam’ de forma mais precisa como os dados de entrada realmente mapeiam para o alvo. A explicabilidade está presente na maioria das equações, mas o que a RS adiciona é talvez a ‘simplicidade’, ao realizar evoluções genéticas a partir de expressões mais complexas e evoluindo em direção às mais simples, desde que suas pontuações de melhor ajuste sejam superiores.

Definição

A RS representa o modelo de mapeamento entre as variáveis independentes e a variável dependente (ou prevista) como uma árvore de expressões. Então, uma representação diagramática como a seguinte:

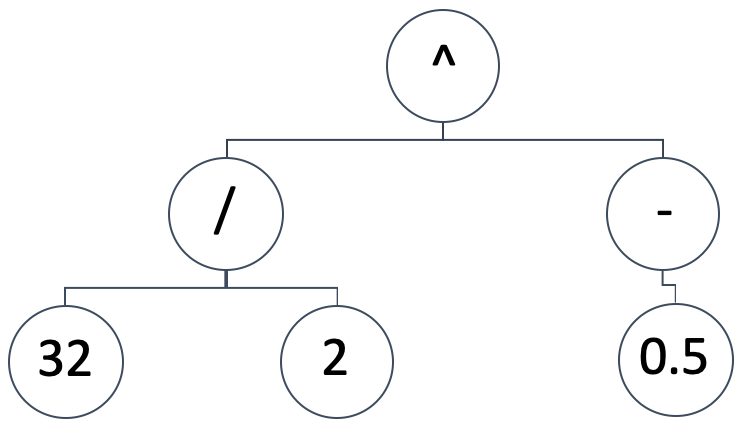
Implicaria na expressão matemática:

(32/2) ^ (-0.5)

Que seria equivalente a: 0.25. Árvores de expressões podem assumir uma variedade de formas e designs, mas queremos manter o princípio fundamental da RS, que é começar com uma configuração aleatória e não tendenciosa. Ao mesmo tempo, precisamos ser capazes de executar otimizações genéticas em qualquer tamanho de árvore de expressões gerada inicialmente, enquanto comparamos seu resultado (ou métrica de melhor ajuste) a árvores de expressões de diferentes tamanhos.

Para alcançar isso, vamos executar nossas otimizações genéticas em ‘épocas’. Embora épocas sejam comuns no jargão de aprendizado de máquina ao agrupar sessões de treinamento, como com redes neurais, aqui usamos o termo para nos referirmos a diferentes iterações de otimização genética, onde cada execução usa árvores de expressões do mesmo tamanho. Por que mantemos o tamanho dentro de cada época? Porque a otimização genética usa cruzamentos, e se as árvores de expressões tiverem comprimentos diferentes, isso complicaria desnecessariamente o processo. Como, então, mantemos as árvores de expressões iniciais aleatórias? Fazendo com que cada época represente um tamanho particular de árvores. Dessa forma, otimizamos em todas as épocas e comparamos todas ao mesmo benchmark ou métrica de melhor ajuste.

As opções de função de aptidão disponíveis nos tipos de dados de vetor/matriz do MQL5 que podemos usar são regressão e perda. Essas funções internas serão aplicáveis porque estaremos comparando o resultado ideal do conjunto de dados de treinamento como um vetor contra as saídas produzidas pela árvore de expressões testada, também em formato de vetor. Então, quanto mais longo/maior for o conjunto de dados de teste, maiores serão os vetores comparados. Esses grandes conjuntos de dados tendem a sugerir que atingir o valor de melhor ajuste ideal zero será muito difícil e, portanto, gerações suficientes de otimização precisam ser permitidas em cada época.

Ao chegar na melhor árvore de expressões com base na melhor pontuação de ajuste, avaliaremos as árvores de expressões das mais longas (e, portanto, mais complexas) para as mais simples e, presumivelmente, mais fáceis de ‘explicar’. Os formatos das nossas árvores de expressões podem assumir uma infinidade de formas, porém recorreremos ao básico:

coeficiente, expoente de x, sinal, coeficiente, expoente de x, sinal, …

onde:

• O Coeff representa o coeficiente de x
• O expoente de x é a potência de x
• O sinal é um operador na expressão que pode ser -, +, * ou /

O último valor de qualquer expressão não será um sinal, porque tal sinal não estará conectando a nada, o que significa que os sinais sempre serão em menor número que os valores de x em qualquer expressão. O tamanho de tal expressão variará de 1, onde fornecemos apenas um coeficiente e expoente de x sem sinal, até 16 (16 é usado aqui estritamente para fins de teste). Como mencionado acima, esse tamanho máximo está diretamente correlacionado com o número de épocas a serem utilizadas na otimização genética. Isso simplesmente implica que começamos a otimizar para a expressão ideal com uma árvore de expressão de 16 unidades de comprimento. Essas 16 unidades implicam 15 sinais, conforme mencionado acima, e ‘cada unidade’ é simplesmente um coeficiente de x e o expoente de x.

Então, ao selecionar as primeiras árvores de expressão aleatórias, sempre seguiremos o formato de 2 ‘nós’ dígitos aleatórios seguidos por um nó de sinal aleatório, se a árvore de expressão tiver mais de uma unidade de comprimento, e não estivermos encerrando a expressão, ou seja, temos uma unidade a seguir. A listagem que nos ajuda a alcançar isso está dada abaixo:

//+------------------------------------------------------------------+
// Get Expression Tree
//+------------------------------------------------------------------+
void CSignalSR::GetExpressionTree(int Size, string &ExpressionTree[])
{  if(Size < 1)
   {  return;
   }
   ArrayFree(ExpressionTree);
   ArrayResize(ExpressionTree, (2 * Size) + Size - 1);
   int _digit[];
   GetDigitNode(2 * Size, _digit);
   string _sign[];
   if(Size >= 2)
   {  GetSignNode(Size - 1, _sign);
   }
   int _di = 0, _si = 0;
   for(int i = 0; i < (2 * Size) + Size - 1; i += 3)
   {  ExpressionTree[i] = IntegerToString(_digit[_di]);
      ExpressionTree[i + 1] = IntegerToString(_digit[_di + 1]);
      _di += 2;
      if(Size >= 2 && _si < Size - 1)
      {  ExpressionTree[i + 2] = _sign[_si];
         _si ++;
      }
   }
}

Nossa função acima começa verificando para garantir que o tamanho da árvore de expressão seja pelo menos um. Se esse teste for aprovado, então precisamos determinar o tamanho real do array da árvore. Como visto acima, as árvores seguem o formato coeficiente, expoente e, então, o sinal, se aplicável. Isso implica que, dado um tamanho s, o número total de nós de dígitos nessa árvore será 2 x s, já que cada unidade de tamanho deve carregar um valor de coeficiente e expoente. Esses nós são selecionados aleatoriamente por meio da função get digit node, cuja listagem é compartilhada abaixo:

//+------------------------------------------------------------------+
// Get Digit
//+------------------------------------------------------------------+
void CSignalSR::GetDigitNode(int Count, int &Digit[])
{  ArrayFree(Digit);
   ArrayResize(Digit, Count);
   for(int i = 0; i < Count; i++)
   {  Digit[i] = __DIGIT_NODE[MathRand() % __DIGITS];
   }
}

Os números são escolhidos aleatoriamente do array estático global de nós de dígitos. Os nós de sinal, no entanto, variarão dependendo se o tamanho da árvore excede um. Se tivermos uma árvore de tamanho um, então nenhum sinal será aplicável, pois isso só deixaria espaço para um coeficiente de x e seu expoente. Se tivermos mais de um, então o número de nós de sinal será equivalente ao tamanho da entrada menos um. Nossa função para selecionar aleatoriamente um sinal para preencher o espaço do sinal na expressão está dada abaixo:

//+------------------------------------------------------------------+
// Get Sign
//+------------------------------------------------------------------+
void CSignalSR::GetSignNode(int Count, string &Sign[])
{  ArrayFree(Sign);
   ArrayResize(Sign, Count);
   for(int i = 0; i < Count; i++)
   {  Sign[i] = __SIGN_NODE[MathRand() % __SIGNS];
   }
}

Os sinais, assim como o array de nós de dígitos, são escolhidos aleatoriamente do array de nós de sinais. Este array, no entanto, pode assumir uma série de variantes, mas, por brevidade, estamos encurtando para acomodar apenas os sinais ‘+’ e ‘-’. O sinal de ‘*’ (multiplicação) poderia ser adicionado a isso, no entanto, o sinal de divisão ‘/’ foi especificamente omitido porque não estamos lidando com divisões por zero, que podem ser bastante complicadas uma vez que começamos a otimização genética e temos que fazer cruzamentos, etc. O leitor é livre para explorar isso, desde que o problema da divisão por zero seja devidamente abordado, pois isso pode distorcer os resultados da otimização.

Uma vez que tenhamos uma população inicial de árvores de expressão aleatórias, podemos começar o processo de otimização genética para aquela época particular. Também vale a pena notar a estrutura simples que estamos usando para armazenar e acessar as informações da árvore de expressão. Essencialmente, é uma matriz de strings com flexibilidade adicional de redimensionamento (recursos que deveriam ser fornecidos por um tipo de dado padrão como o matrix que lida com doubles?). Isso também está listado abaixo:

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
struct Stree
{  string   tree[];

   Stree()
   {  ArrayFree(tree);
   };
   ~Stree() {};
};
struct Spopulation
{  Stree   population[];

   Spopulation() {};
   ~Spopulation() {};
};

Usamos essa estrutura para criar e rastrear populações em cada geração de otimização. Cada época usa um número definido de gerações para fazer sua otimização. Como já mencionado, quanto maior o conjunto de dados de teste, mais gerações de otimização seriam necessárias. Por outro lado, se o conjunto de dados de teste for muito pequeno, isso pode levar a árvores de expressão derivadas principalmente de ruído branco em vez dos padrões subjacentes nos conjuntos de dados testados, então é preciso equilibrar isso.

Uma vez que começamos nossa otimização em cada geração, precisamos obter a aptidão de cada árvore e, como temos várias árvores, essas pontuações de aptidão são registradas em um vetor. Uma vez que temos esse vetor, o próximo passo é estabelecer um limite para a poda dessa população, dado que essa árvore é refinada e reduzida a cada geração subsequente dentro de uma determinada época. Chamamos esse limite de ‘_fit’ e ele é baseado em um parâmetro de entrada inteiro que atua como um marcador de percentil. O parâmetro varia de 0 a 100.

Prosseguimos para criar outra população de amostra a partir dessa população inicial, onde selecionamos apenas as árvores de expressão cuja aptidão esteja abaixo ou igual ao limite. A função para calcular nossa pontuação de aptidão usada acima teria a listagem dada abaixo:

//+------------------------------------------------------------------+
// Get Fitness
//+------------------------------------------------------------------+
double CSignalSR::GetFitness(matrix &XY, vector &Y, string &ExpressionTree[])
{  Y.Init(XY.Rows());
   for(int r = 0; r < int(XY.Rows()); r++)
   {  Y[r] = 0.0;
      string _sign = "";
      for(int i = 0; i < int(ExpressionTree.Size()); i += 3)
      {  double _yy = pow(XY[r][0], StringToDouble(ExpressionTree[i + 1]));
         _yy *= StringToDouble(ExpressionTree[i]);
         if(_sign == "+")
         {  Y[r] += _yy;
         }
         else if(_sign == "-")
         {  Y[r] -= _yy;
         }
         else if(_sign == "/" && _yy != 0.0)//un-handled
         {  Y[r] /= _yy;
         }
         else if(_sign == "*")
         {  Y[r] *= _yy;
         }
         else if(_sign == "")
         {  Y[r] = _yy;
         }
         if(i + 2 < int(ExpressionTree.Size()))
         {  _sign = ExpressionTree[i + 2];
         }
      }
   }
   return(Y.RegressionMetric(XY.Col(1), m_regressor));
   //return(_y.Loss(XY.Col(1),LOSS_MAE));
}

A função get fitness pega a matriz de dados de entrada 'XY' e se concentra na coluna x da matriz (estamos usando dados unidimensionais para entradas e saídas) para calcular o valor previsto da árvore de expressão de entrada. A matriz de entrada tem várias linhas de dados, então, com base no valor de x em cada linha (a primeira coluna), uma projeção é feita e todas essas projeções, para cada linha, são armazenadas em um vetor 'Y'. Depois que todas as linhas são processadas, esse vetor 'Y' é comparado aos valores reais na segunda coluna usando ou a função de regressão incorporada ou a função de perda. Optamos pela regressão, com o erro quadrático médio como métrica de regressão.

A magnitude desse valor é o valor de aptidão da árvore de expressão de entrada. Quanto menor for, melhor será o ajuste. Obtendo esse valor para cada uma das populações amostradas, precisamos primeiro verificar se o tamanho da amostra é par; caso contrário, reduzimos o tamanho em um. O tamanho precisa ser par porque, na próxima etapa, estamos cruzando essas árvores e os cruzamentos gerados são adicionados em pares, devendo corresponder à população original (as amostras), uma vez que apenas reduzimos a população ao amostrar em cada geração. O cruzamento de árvores de expressão dentro das amostras é feito aleatoriamente por seleção de índice. A função responsável pelo cruzamento está listada abaixo:

//+------------------------------------------------------------------+
// Set Crossover
//+------------------------------------------------------------------+
void CSignalSR::SetCrossover(string &ParentA[], string &ParentB[], string &ChildA[], string &ChildB[])
{  if(ParentA.Size() != ParentB.Size() || ParentB.Size() == 0)
   {  return;
   }
   int _length = int(ParentA.Size());
   ArrayResize(ChildA, _length);
   ArrayResize(ChildB, _length);
   int _cross = 0;
   if(_length > 1)
   {  _cross = rand() % (_length - 1) + 1;
   }
   for(int c = 0; c < _cross; c++)
   {  ChildA[c] = ParentA[c];
      ChildB[c] = ParentB[c];
   }
   for(int l = _cross; l < _length; l++)
   {  ChildA[l] = ParentB[l];
      ChildB[l] = ParentA[l];
   }
}

Esta função começa verificando se os dois pais da expressão têm o mesmo tamanho e nenhum deles é zero. Se esse critério for atendido, os dois arrays de saída dos filhos são redimensionados para corresponder ao comprimento dos pais e, em seguida, o ponto de cruzamento é selecionado. Esse cruzamento também é aleatório e só é relevante quando o tamanho do pai é maior que um. Depois que o ponto de cruzamento é definido, os dois pais têm seus valores trocados e inseridos nos dois arrays dos filhos. É aqui que os comprimentos correspondentes são úteis, porque, por exemplo, se fossem diferentes, seria necessário código extra para lidar (ou evitar) casos em que dígitos fossem trocados por sinais. Complicações desnecessárias quando todos os tamanhos podem ser testados independentemente, em sua própria época, para o melhor ajuste.

Depois que terminamos o cruzamento, podemos mutar os filhos. 'Podemos', porque usamos um limite de probabilidade de 5% para realizar essas mutações, pois elas não são garantidas, mas geralmente fazem parte do processo de otimização genética. Em seguida, copiamos essa nova população cruzada para sobrescrever nossa população inicial, da qual amostramos no início, e como marcador registramos a melhor pontuação de ajuste da melhor árvore de expressão dessa nova população cruzada. Usamos a pontuação registrada não apenas para determinar a melhor árvore, mas também, em alguns casos raros, para interromper a otimização caso obtenhamos um valor zero.

Classe de Sinal Personalizada

No desenvolvimento da classe de sinal, nossos principais passos não diferem muito do que fizemos em classes de sinal personalizadas anteriores nesta série. Primeiramente, precisamos preparar o conjunto de dados para nosso modelo. Este é o dado que preenche nossa matriz de entrada 'XY' para a função discutida acima, get fitness. É também uma entrada para a função que integra todas as etapas que mencionamos acima, chamada get best tree. O código-fonte desta função é dado abaixo:

//+------------------------------------------------------------------+
// Get Best Fit
//+------------------------------------------------------------------+
void CSignalSR::GetBestTree(matrix &XY, vector &Y, string &BestTree[])
{  double _best_fit = DBL_MAX;
   for(int e = 1 + m_epochs; e >= 1; e--)
   {  Spopulation _p;
      ArrayResize(_p.population, m_population);
      int _e_size = 2 * e;
      for(int p = 0; p < m_population; p++)
      {  string _tree[];
         GetExpressionTree(e, _tree);
         _e_size = int(_tree.Size());
         ArrayResize(_p.population[p].tree, _e_size);
         for(int ee = 0; ee < _e_size; ee++)
         {  _p.population[p].tree[ee] = _tree[ee];
         }
      }
      for(int g = 0; g < m_generations; g++)
      {  vector _fitness;
         _fitness.Init(int(_p.population.Size()));
         for(int p = 0; p < int(_p.population.Size()); p++)
         {  _fitness[p] = GetFitness(XY, Y, _p.population[p].tree);
         }
         double _fit = _fitness.Percentile(m_fitness);
         Spopulation _s;
         int _samples = 0;
         for(int p = 0; p < int(_p.population.Size()); p++)
         {  if(_fitness[p] <= _fit)
            {  _samples++;
               ArrayResize(_s.population, _samples);
               ArrayResize(_s.population[_samples - 1].tree, _e_size);
               for(int ee = 0; ee < _e_size; ee++)
               {  _s.population[_samples - 1].tree[ee] = _p.population[p].tree[ee];
               }
            }
         }
         if(_samples % 2 == 1)
         {  _samples--;
            ArrayResize(_s.population, _samples);
         }
         if(_samples == 0)
         {  break;
         }
         Spopulation _g;
         ArrayResize(_g.population, _samples);
         for(int s = 0; s < _samples - 1; s += 2)
         {  int _a  = rand() % _samples;
            int _b  = rand() % _samples;
            SetCrossover(_s.population[_a].tree, _s.population[_b].tree, _g.population[s].tree, _g.population[s + 1].tree);
            if (rand() % 100 < 5)   // 5% chance
            {  SetMutation(_g.population[s].tree);
            }
            if (rand() % 100 < 5)
            {  SetMutation(_g.population[s + 1].tree);
            }
         }
         // Replace old population
         ArrayResize(_p.population, _samples);
         for(int s = 0; s < _samples; s ++)
         {  for(int ee = 0; ee < _e_size; ee++)
            {  _p.population[s].tree[ee] = _g.population[s].tree[ee];
            }
         }
         // Print best individual
         for(int s = 0; s < _samples; s ++)
         {  _fit = GetFitness(XY, Y, _p.population[s].tree);
            if (_fit < _best_fit)
            {  _best_fit = _fit;
               ArrayCopy(BestTree,_p.population[s].tree);
            }
         }
      }
   }
}

A matriz de entrada pareia valores x unidimensionais e valores y unidimensionais. Variáveis independentes e variáveis dependentes. A multidimensionalidade também pode ser acomodada com o vetor de entrada 'Y' sendo transformado em uma matriz e uma árvore de expressão para cada valor x no vetor de entrada, para cada valor y no vetor de saída. Essas árvores de expressão também teriam que estar em uma matriz ou formato de armazenamento de dimensão superior.

Estamos usando dimensões únicas, porém, e nossa linha de dados simplesmente consiste em preços de fechamento consecutivos. Então, na linha de dados mais recente, temos o penúltimo preço de fechamento como nosso valor x e o preço de fechamento atual como nosso y. Os preparativos e o preenchimento de nossa matriz 'XY' com esses dados são tratados pelo código-fonte abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   matrix _xy;
   _xy.Init(m_data_set, 2);
   for(int i = 0; i < m_data_set; i++)
   {  _xy[i][0] = m_close.GetData(StartIndex()+i+1);
      _xy[i][1] = m_close.GetData(StartIndex()+i);
   }

...

   return(result);
}

Uma vez que nossa preparação de dados está concluída, é uma boa ideia esclarecer o método de avaliação de aptidão a ser usado em nosso modelo. Estamos optando por regressão em vez de perda, mas mesmo dentro da regressão há algumas métricas para selecionar. Portanto, para permitir uma seleção ideal, o tipo de métrica de regressão a ser usada é um parâmetro de entrada, que pode ser otimizado para melhor atender aos conjuntos de dados testados. Nosso valor padrão, no entanto, é o erro quadrático médio.

A implementação do algoritmo genético é tratada pela função get best tree, cujo código-fonte já foi listado acima. Ela retorna vários resultados, dos quais o principal é a melhor árvore de expressão. Com essa árvore, podemos processar o preço de fechamento atual como uma entrada (valor x) para obter nosso próximo fechamento (valor y), usando a função get fitness, pois ela também retorna mais do que apenas a aptidão de uma expressão consultada, já que o vetor de entrada 'Y' contém nossa previsão de destino. Isso é tratado no código abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{ 
        ...

   vector _y;
   string _best_fit[];
   GetBestTree(_xy, _y, _best_fit);

        ...

   return(result);
}

Com um preço de fechamento indicativo obtido, o próximo passo é converter esse preço em um sinal utilizável para o Expert Advisor. Os valores previstos geralmente indicam apenas uma alta ou queda, mas seu valor absoluto está fora de alcance quando comparado aos valores recentes de preços de fechamento. Isso significa que precisaríamos normalizá-los antes que possam ser usados. A normalização e a geração de sinais são feitas em nosso código abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalSR::LongCondition(void)
{  int result = 0;
   
        ...

   double _cond = (_y[0]-m_close.GetData(StartIndex()))/fmax(fabs(_y[0]),m_close.GetData(StartIndex()));
   _cond *= 100.0;
   //printf(__FUNCSIG__ + " cond: %.2f", _cond);
   //return(result);
   if(_cond > 0.0)
   {  result = int(fabs(_cond));
   }
   return(result);
}

A saída inteira de condições longas e curtas em uma classe de sinal Expert padrão tem que estar na faixa de 0 a 100, e é isso que estamos convertendo nosso sinal no código acima.

A função de condição longa e a função de condição curta são espelhos uma da outra, e a montagem das classes de sinal em Expert Advisors é abordada nos artigos aqui e aqui.

Teste de Retrocesso e Otimização

Ao realizar um teste com algumas das "melhores configurações" do Expert Advisor montado, obtemos o seguinte relatório e curva de capital:

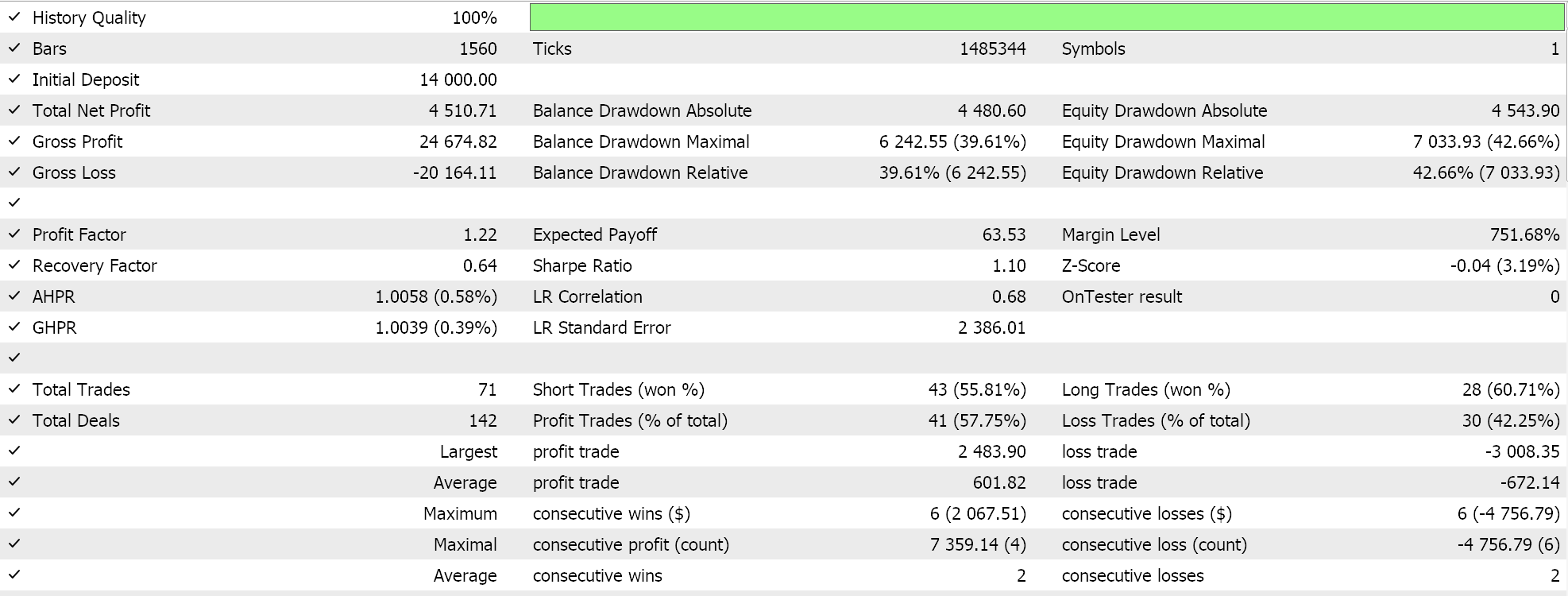
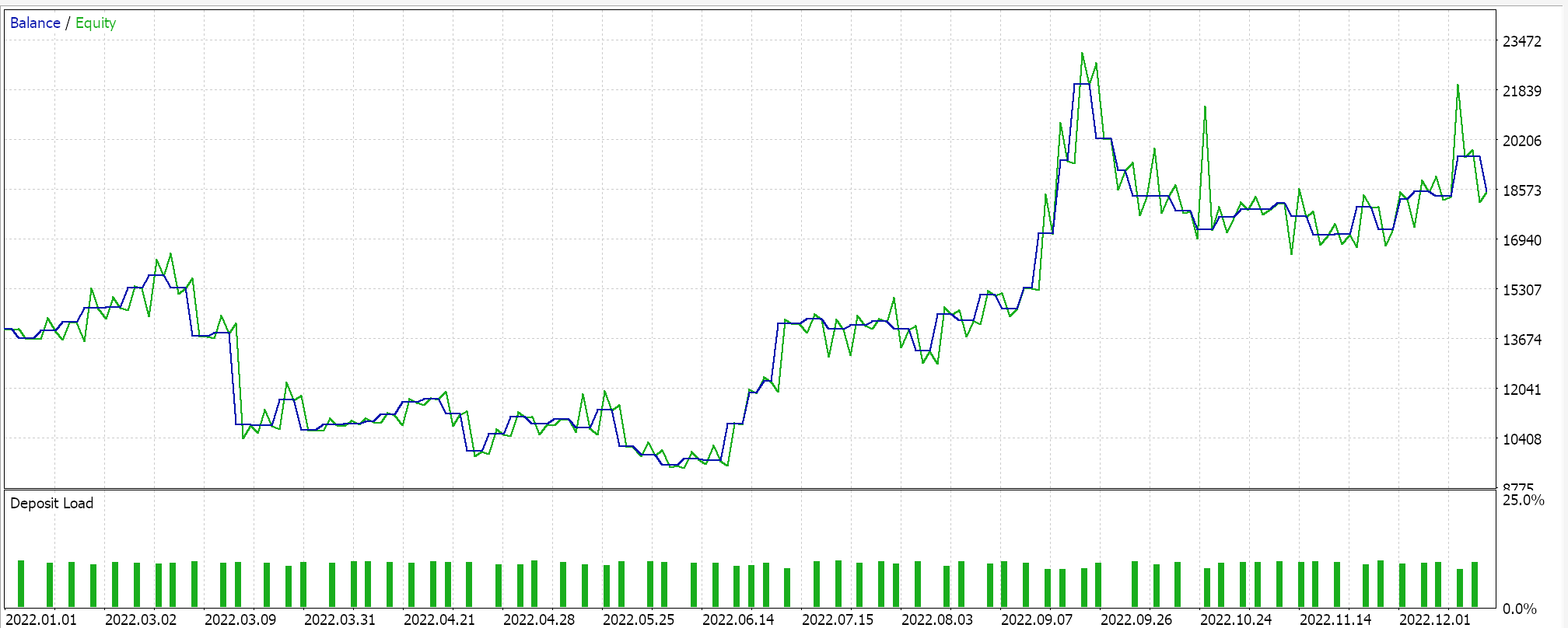
Para qualquer configuração, como as árvores de expressão são obtidas por seleção aleatória e são cruzadas e mutadas também aleatoriamente, é improvável que um teste produza exatamente os mesmos resultados. No entanto, e de forma interessante, se um teste for lucrativo, as execuções subsequentes com as mesmas configurações terão estatísticas de desempenho diferentes, mas, no geral, também serão lucrativas. Nosso teste foi realizado para o ano de 2022, no par EUR/JPY, no período de 4 horas. Como sempre, executamos os testes sem metas de preço para SL (Stop Loss) ou TP (Take Profit), pois isso pode ajudar a identificar melhor as configurações ideais do Expert.

Conclusão

Para recapitular, introduzimos a regressão simbólica como um modelo que pode ser usado em uma instância personalizada de uma classe de sinal Expert para avaliar condições longas e curtas. Usamos um conjunto de dados bastante modesto nesta análise, uma vez que tanto os valores de entrada quanto os de saída do modelo eram unidimensionais. Isso não significa que o modelo não possa ser expandido para acomodar conjuntos de dados multidimensionais. Além disso, a natureza da otimização genética do algoritmo do modelo torna complicado obter resultados idênticos em cada execução de teste. Isso implica que Expert Advisors baseados neste modelo devem ser usados em períodos de tempo bastante longos e em conjunto com outros sinais de negociação, para que possam atuar como uma confirmação para sinais já gerados de forma independente.