交易中的混沌理论（第一部分）：简介、在金融市场中的应用和李亚普诺夫指数

混沌理论简介及其与金融市场的关系

什么是混沌理论？如何将其应用于金融市场？我们将在文章中讨论这个问题。

我将撰写一系列文章，回答什么是混沌理论，以及比尔·威廉姆斯提出的市场混沌概念与传统的、以科学为基础的理论有何不同等问题。该理论如何描述市场？如何以及在哪些交易领域可以应用它？ 

我们将分析理论基础，并创建一些可以帮助交易者进行交易的工具。

混沌理论的基本概念：吸引子、分形和蝴蝶效应

混沌理论是一个有趣的数学和物理学领域，它帮助我们更好地理解复杂的系统，如金融市场。让我们来看看这个理论的三个主要观点：

1. 吸引子：这些就像系统状态的磁铁 — 随着时间的推移，系统会向它们靠拢。在金融市场中，这些可能是特定的价格或市场一次又一次回归的重复模式。混沌系统中的奇异吸引子尤其引人关注。它们看起来很复杂，可以揭示市场随机行为中隐藏的秩序。

2. 分形：这些几何形状在任何放大倍数下看起来都是一样的。在金融市场中，分形可以在价格图表中看到 — 在短期和长期内都可以看到相同的模式。这允许在不同的时间间隔内应用相同的分析方法，有助于分析价格变化和评估风险。

3. 蝴蝶效应：这种影响表明，即使是开始时最小的变化也会导致巨大而意想不到的后果。在金融领域，这意味着数据或模型的微小变化可能会极大地改变预测。这使得金融市场的长期预测具有挑战性，并强调了不断更新和调整我们的模型以适应新条件的重要性。

理解这些想法有助于分析师和交易员以一种新的方式看待市场，发现隐藏的模式和可能的交易入场或出场点。混沌理论为分析和预测开辟了超越传统模型的新途径。

金融市场背景下的混沌系统

金融市场具有混沌系统的特征，这对其分析和预测具有重要意义。

• 非线性：微小的变化会导致不成比例的波动。
• 对初始条件的敏感性：小事件可能导致大运动。
• 自组织：在没有外部控制的情况下形成趋势和模式。
• 分形结构：价格图表显示出分形特性。
• 可预测性有限：预测精度随着时间的增加而降低。
• 奇异吸引子：围绕某些水平或状态的波动。
• 状态之间的过渡：从稳定到波动的突然转变。

理解这一点有助于开发复杂的分析方法、风险管理和交易算法。

交易中的波动性

波动性是交易和金融中的一个关键概念，与混沌理论有关。它衡量资产价格在给定时间内的变化程度。在交易中，波动性有助于评估风险、定价期权和制定交易策略。

金融市场往往表现得像混沌系统，它们会对微小的变化做出出乎意料的反应，类似于蝴蝶效应。市场也可以自组织，在没有外部干预的情况下创造趋势和模式，价格图表显示了不同时间框架的相似性，这被称为分形属性。

混沌理论为波动性分析提供了独特的工具，如相空间重构和李雅普诺夫（Lyapunov）指数，这有助于发现隐藏的模式并评估可预测性。这些混沌模型可以补充 GARCH 模型（Generalized Autoregressive Conditional Heteroskedasticity，广义自回归条件异方差模型）等传统方法，特别是在识别市场机制和预测波动性突变方面。

了解波动性的混沌性质为更准确地分析和预测市场动态开辟了新的机会，从而制定了有效的交易策略和风险管理方法。

传统混沌理论与比尔·威廉姆斯的方法

传统的混沌理论和比尔·威廉姆斯（Bill Williams）的“混沌”概念有很大不同。前者依赖于严格的数学原理，并使用复杂的工具来分析系统。而后者使用直观的方法和技术指标，如鳄鱼和分形，它们与混沌的数学理论没有直接联系。

传统的混沌理论基于严格的数学原理和非线性动力学领域的科学研究。它使用严格的数学方法，并认为混沌表现出确定性但不可预测的行为。威廉姆斯更宽泛地使用了“混沌”一词，指的是市场的普遍不可预测性。他的方法旨在实际应用于交易，而不是深入分析市场的混沌性质。

尽管威廉姆斯采用了混沌理论中的一些术语，但他的方法更多地基于技术分析和对市场走势的个人解释。这引起了混沌理论学家的批评，他们认为在这种情况下使用“混沌”一词具有误导性。

市场分析中的混沌理论

混沌理论认识到金融市场的复杂性和不可预测性，为分析市场动态提供了新的视角。与传统方法不同，混沌理论考虑到了市场过程的非线性和复杂性。

这种方法有助于解释为什么小事件会导致大的市场波动，以及为什么长期预测往往不准确。混沌理论使我们能够分析市场崩溃和泡沫等现象，为更准确、更具适应性的市场分析提供了新的工具。

李亚普诺夫指数及其在金融时间序列分析中的应用

李雅普诺夫指数是混沌理论中的一种工具，它帮助我们理解系统对初始条件的敏感性。在金融市场中，这很重要，因为它允许人们估计市场条件的小幅变化会带来多少价格变化。

如果李雅普诺夫指数为正，则意味着系统现为混沌状态：微小的变化可能会导致未来的大幅波动。如果指数为负，则系统更稳定，价格变化较小。

使用此指数，您可以确定市场何时变得更加波动和可预测。高值可能表明价格可能发生剧烈变化，这对评估风险和调整交易策略很有用。

为了计算金融数据中的李雅普诺夫指数，有必要通过分析该空间中的闭合点如何发散来创建相空间。这个过程需要选择正确的参数，如维度和时间延迟。

使用李雅普诺夫指数的一个重要方面是估计预测准确的时间。指数值越高，预测保持可靠的时间越短。这对短期交易和风险管理特别有用。

现在我们可以开始在 MQL5 中实现李雅普诺夫指数了。

使用 MQL5 实现李雅普诺夫指数

该指标实现了用于分析金融时间序列的李雅普诺夫指数计算。它可以评估市场的混乱程度和价格变动的潜在可预测性。

输入：

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag - 相空间重构的时间延迟。
• InpEmbedDim - 相空间重构的嵌入维度。
• InpDataLength - 用于计算指标的烛形数量。

有一个全局变量：

double LyapunovBuffer[];

初始化：

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

在 OnInit() 函数中，我们配置了指标缓冲区，将显示精度设为小数点后 5 位，并为指标设置了一个短名称。

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

OnCalculate() 函数在每个分时上调用，并从 InpDataLength 开始计算每根烛形的李亚普诺夫指数。

李亚普诺夫指数计算：

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

CalculateLyapunovExponent() 函数实现了计算本地李亚普诺夫指数的算法。它使用最近邻方法来估计重建相空间中轨迹的散度。

搜索最近邻：

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

FindNearestNeighbor() 函数利用欧氏距离在重构的相空间中找到最近的点。

结果解释

• 该指标的正值表明存在混沌的市场行为。
• 负值表示价格动态更稳定，更有可能预测。
• 指标的绝对值越高，相应的特征（混沌或稳定）就越明显。

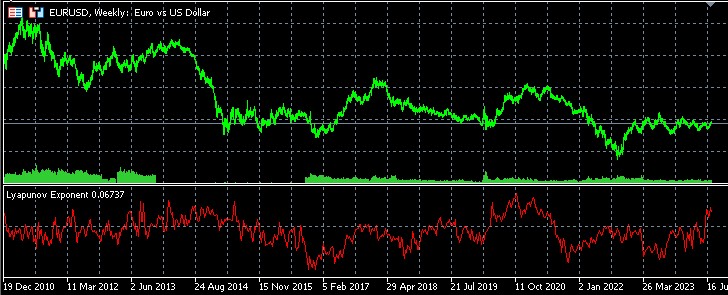
利用李雅普诺夫指数对趋势反转和延续进行统计分析

我用 MQL5 语言开发了一个专门的脚本，用于深入研究李雅普诺夫指数与金融市场动态之间的关系。该工具允许在李雅普诺夫指数值的背景下对趋势逆转和延续进行详细的统计分析，为交易者和分析师提供有关市场行为的宝贵见解。

该脚本使用所选金融工具的历史数据，分析指定数量的柱形。对于每个柱形，采用相空间重构和近邻搜索法计算局部李亚普诺夫指数。通过这种方法，我们可以评估系统在每个特定时间点的混沌程度。

同时，脚本分析价格动态，识别反转和趋势延续。反转是指当前收盘价高于前一个收盘价，而下一个收盘价低于当前收盘价（反之亦然）。所有其他情况都被视为趋势的延续。

该脚本的关键特征是它能够将趋势反转和延续的时刻与李雅普诺夫指数的值进行比较。这使我们能够识别市场混沌行为与其价格动态之间的统计模式。该脚本计算李雅普诺夫指数为正值和负值时发生的趋势逆转和延续的次数。

分析完成后，脚本将显示详细的统计数据，包括李雅普诺夫指数正值和负值的趋势逆转和延续的绝对值和百分比。这些信息使交易者能够评估趋势逆转与市场波动加剧的时期重合的频率，反之，趋势延续与更稳定的时期对应的频率。

解释统计分析结果

使用李雅普诺夫指数对趋势逆转和延续进行统计分析的结果为 EURUSD 市场在每小时的动态提供了有趣的数据。

首先，我们注意到李雅普诺夫指数的正负值之间的事件分布几乎相等。在李雅普诺夫指数为正和负的情况下，大约有一半的情况下观察到反转和趋势延续。这可能表明，EURUSD H1 市场在相对稳定期和混沌期之间保持平衡。

正李雅普诺夫指数值通常与更混乱、不可预测的行为有关，在所有情况下，只有一半以上的情况下观察到（反转为50.61%，连续为51.09%）。这可能表明市场波动性或不确定性增加的时期略有优势。

李雅普诺夫指数的负值通常被解释为系统更有序、更少混沌行为的标志，在 49.39% 的反转和 48.91% 的趋势延续中观察到。这些时期的特点可能是价格走势更可预测，遵循某些模式。

有趣的是，正和负李雅普诺夫值的趋势逆转和延续的百分比几乎相同。在这两种情况下，差异都小于 0.5%。这可能表明李雅普诺夫指数本身不是预测趋势逆转或延续的决定因素。

正和负李雅普诺夫值之间事件的均匀分布可能表明了 EURUSD 市场的复杂性，其中稳定和混乱的周期以大致相等的频率交替。 

结论

混沌理论为分析金融市场提供了一种创新的方法，可以更深入地理解其复杂和非线性的本质。在这篇文章中，我们研究了混沌理论的关键概念（吸引子、分形和蝴蝶效应）及其在金融时间序列中的应用。李雅普诺夫指数作为评估市场动态混乱程度的工具受到了特别关注。