
Нейросети — это просто (Часть 18): Ассоциативные правила
Содержание
Введение
С ростом объёмов анализируемой информации растет и интерес к методом обучения без учителя. В нескольких последних статьях этой серии мы уже познакомились с алгоритмами кластеризации и понижения размерности, которые относятся к методам обучения без учителя. В этой статье мы продолжаем изучение методов обучения без учителя. И я предлагаю Вам познакомиться ещё с одним типом решаемых задач — анализ ассоциативных правил. Впервые данный тип задач был сформулирован в ритейле для анализа покупательских корзин, как поиск наиболее часто встречающихся наборов продуктов. В настоящее время, алгоритмы решения данного типа задач широко используются в различных областях. Давайте посмотрим на возможности использования подобных алгоритмом в трейдинге.
1. Ассоциативные правила
Задача анализа ассоциативных правил относится к прикладным задачам Data Mining и является одной из основных, так как позволяет выявлять корреляцию между данными в объёмных базах данных.
Данный тип задач впервые был сформулирована и определен в ритейле. Когда перед маркетологами возник вопрос, какую пользу для бизнеса можно извлечь из анализа большой базы транзакций кассовых операций. Если ранее анализировались только общие объёмы продаж, то анализ кассовых чеков покупателей открывал новые горизонты. Так как позволял анализировать отдельные наборы продуктов, приобретаемых покупателями.
Первый алгоритм был создан группой разработчиков из IBM в 1993 году. Тогда же были сформулированы основные постулаты, которые легли в основу целой группы алгоритмов.
Прежде всего, найденные с помощью алгоритмов правила должны быть часто встречаемые. То есть они должны быть не случайны и в анализируемой базе данных должны повторяться как минимум определенное количество раз. Так сказать, подтверждаться на практике. И с точки зрения статистики выборка транзакций, содержащая такое правило, должна быть репрезентативной. Для соблюдения этого требования во всех алгоритмах поиска ассоциативных правил присутствует параметр минимальной поддержки (MinSup - minimal support), указывающий в долях "1" соотношение частоты появления правила к общему числу транзакций в анализируемой выборке.
И тут надо понимать, что имея набор из 3-х признаков A, B и C по правилам комбинаторики без учета позиции элементов мы можем получить 7 различных наборов, содержащих от 1-го до 3-х этих признаков. С ростом числа признаков в разы растет и количество возможных комбинаций. А с учетом объемов баз данных, прямой пересчет частоты появления каждого набора признаков становится довольно трудоёмкой задачей. Часто даже не реальной. Поэтому, авторы воспользовались свойством анти-монотонности.
Если с признаком А в базе встречается только какой-то один набор из всех возможных, то его частота будет равна частоте появления самого признака А. Если же количество встречаемых наборов больше, то их частота может быть только меньше. Так как суммарное количество появлений их в анализируемой выборке будет равняться количеству появлений признака А. Таким образом, если частота появления какого-либо признака меньше минимальной поддержки, то, как следствие, и частота всех возможных вариантов наборов, содержащих этот признак, будет меньше минимальной поддержки. А значит, нам достаточно вычислить частоту появления каждого признака, чтобы отсеять значительную часть случайных наборов. Которые не представляют для нас практическую ценность.
Как можно заметить, здесь алгоритмы поиска ассоциативных правил сильно отличаются от всех рассмотренных ранее алгоритмов. Если раньше мы старались максимально использовать все доступные данные. То алгоритмы поиска ассоциативных правил сразу отсеивают случайные (шумовые) признаки.
Второй параметр, используемый во всех алгоритмах поиска ассоциативных правил — минимальная степень доверия правилу (MinConf - minimal confidence). Который также указывается в долях единицы. Для объяснения данного параметра надо сказать, что каждое правило состоит из 2-х частей: посыл и следствие. И посыл, и следствие могут состоять как из одного признака, так и из целого набора признаков. В общем случае правило звучит как если верен посыл, то довольно часто будет и следствие.
Здесь надо обратить внимание, что вероятность появления "следствия" при появлении "посыла" не 100%. А вот минимальная вероятность появления "следствия" и задаётся параметром MinConf. Именно при соблюдении данного параметра правило считается действительным и сохраняется в массив правил. Определяется как отношения частоты выполнения правила к частоте появления посыла.
2. Алгоритм Apriori
Наверное, один из самых известных алгоритмов поиска ассоциативных правил является алгоритм Apriori, который предложили Ракеш Агравал и Рамакришнан Срикант в 1994 году. В основе алгоритма лежит итерационный процесс поиска наиболее частых паттернов в базе данных. С последующим извлечением правил из отобранных паттернов.
Чтобы лучше его понять, давайте рассмотрим действие алгоритма на небольшом примере из 10 транзакций с 5-ю признаками.
| ID транзакции | Содержимое |
|---|---|
| T1 | BCDE |
| T2 | BCD |
| T3 | B |
| T4 | BCD |
| T5 | D |
| T6 | ACD |
| T7 | BCDE |
| T8 | BCE |
| T9 | CDE |
| T10 | AD |
Введем в задачу константы минимальной поддержки 0.3 и минимальной степени доверия 0.7 (30% и 70% соответственно).
Надо понимать, что все алгоритмы поиска ассоциативных правил работают с бинарными массивами. Поэтому, для начала работы представим, приведенные выше данные, в виде бинарной таблицы.
| ID транзакции | A | B | C | D | E |
|---|---|---|---|---|---|
| T1 | 0 | 1 | 1 | 1 | 1 |
| T2 | 0 | 1 | 1 | 1 | 0 |
| T3 | 0 | 1 | 0 | 0 | 0 |
| T4 | 0 | 1 | 1 | 1 | 0 |
| T5 | 0 | 0 | 0 | 1 | 0 |
| T6 | 1 | 0 | 1 | 1 | 0 |
| T7 | 0 | 1 | 1 | 1 | 1 |
| T8 | 0 | 1 | 1 | 1 | 0 |
| T9 | 0 | 0 | 1 | 1 | 1 |
| T10 | 1 | 0 | 0 | 1 | 0 |
Из данной таблицы легко посчитать, что признак A встречается всего 2 раза и его поддержка составляет 0.2 или 20%. Аналогично посчитаем поддержки для остальных признаков: B — 0.6, C — 0.7, D — 0.8, E — 0.4. Как можно заметить, только признак А не удовлетворяет требованию минимальной поддержки, и мы его исключаем из дальнейшей обработки по свойству анти-монотонности.
Из оставшихся элементов составляем кандидатов в часто встречающиеся паттерны. На предыдущем шаге мы определили часто встречающиеся признаки. И согласно алгоритму мы определяем в кандидаты наборы из 2-х признаков: BC, BD, BE, CD, CE, DE.
Теперь нам необходимо повторно пройтись по всей базе данных и определить поддержку для каждого из отобранных кандидатов.
| ID транзакции | BC | BD | BE | CD | CE | DE |
|---|---|---|---|---|---|---|
| T1 | 1 | 1 | 1 | 1 | 1 | 1 |
| T2 | 1 | 1 | 0 | 1 | 0 | 0 |
| T3 | 0 | 0 | 0 | 0 | 0 | 0 |
| T4 | 1 | 1 | 0 | 1 | 0 | 0 |
| T5 | 0 | 0 | 0 | 0 | 0 | 0 |
| T6 | 0 | 0 | 0 | 1 | 0 | 0 |
| T7 | 1 | 1 | 1 | 1 | 1 | 1 |
| T8 | 1 | 0 | 1 | 0 | 1 | 0 |
| T9 | 0 | 0 | 0 | 1 | 1 | 1 |
| T10 | 0 | 0 | 0 | 0 | 0 | 0 |
Как можно заметить, поддержки всех наших кандидатов удовлетворяют условия минимальной поддержки: BC — 0.5, BD — 0.4, BE — 0.3, CD — 0.6, CE — 0.4, DE — 0.3. Но такое положение возможно не всегда. При решение практических задач с большей вероятностью некоторые кандидаты будут отсеяны.
Далее мы продолжаем итерационный процесс и на это раз составляем наборы-кандидаты из 3-х признаков. Для этого мы берем отобранные на предыдущей итерации частые паттерны и объединяем пары, отличающиеся только одним элементом. Таким образом мы определяем 4 кандидата: BCD, BCE, BDE, CDE.
И согласно алгоритму Apriori нам опять предстоит пройтись по всей базе данных и определить поддержки для всех новых кандидатов.
| ID транзакции | BCD | BCE | BDE | CDE |
|---|---|---|---|---|
| T1 | 1 | 1 | 1 | 1 |
| T2 | 1 | 0 | 0 | 0 |
| T3 | 0 | 0 | 0 | 0 |
| T4 | 1 | 0 | 0 | 0 |
| T5 | 0 | 0 | 0 | 0 |
| T6 | 0 | 0 | 0 | 0 |
| T7 | 1 | 1 | 1 | 1 |
| T8 | 0 | 1 | 0 | 0 |
| T9 | 0 | 0 | 0 | 1 |
| T10 | 0 | 0 | 0 | 0 |
В результате мы получим следующие поддержки для наших кандидатов: BCD — 0.4, BCE — 0.3, BDE — 0.2, CDE — 0.3. На этой итерации поддержка набора BDE не удовлетворяет требованию минимально поддержки и его мы исключаем. Остальные кандидаты переходят в статус частых паттернов.
На следующей итерации мы составляем наборы-кандидаты из 4-х признаков. В данном случае, из отобранных на предыдущей итерации паттернов, мы можем составить только один кандидат BCDE. Но прежде, чем еще раз пройтись по всей базе данных для подсчета поддержки данного кандидата, давайте обратим внимание на его составную часть BDE. На прошлой итерации мы отсеяли этого кандидата, так как его поддержка составила 0.2, что ниже требования минимальной поддержки 0.3. Следовательно, по свойству анти-монотонности и у кандидата BCDE поддержка не может превышать 0.2. А это ниже уровня минимальной поддержки.
Так как у нас больше нет кандидатов, то мы останавливаем процесс поиска частых паттернов и переходим ко второму подпроцессу — определению правил из отобранных частых паттернов. Для этого мы разделим отобранные паттерны на посыл и следствие. После чего определим степень доверия каждому правилу и сравним с минимальным требуемым уровнем доверия.
Правила мы будем строить последовательно для каждого товара и набора. Так как на самом первом этапе мы отсеяли все паттерны с признаком A (его поддержка ниже минимального требования), то определение правил мы начинаем с признака B.
Из отобранных паттернов выделим все, содержащие анализируемый товар. Из паттернов извлечем признак B для следствия, а оставшаяся часть будет посылом. И определим степень доверия для каждого созданного правила.
Степень доверия правила демонстрирует с какой вероятностью появляется следствие при формировании посыла. Для её определения нам не нужно заново перебирать всю базу данных. Нам достаточно разделить поддержку полного паттерна на поддержку посыла, которые мы уже посчитали на этапе отбора частых паттернов.
| Паттерн | Посыл | Поддержка | Правило |
|---|---|---|---|
| BC (0.5) | C (0.7) | 0.71 | C -> B |
| BD (0.4) | D (0.8) | 0.50 | D -> B |
| BE (0.3) | E (0.4) | 0.75 | E -> B |
| BCD (0.4) | CD (0.6) | 0.67 | CD -> B |
| BCE (0.3) | CE (0.4) | 0.75 | CE -> B |
Правила D -> B и CD -> B не удовлетворяют требованию минимальной поддержки 0.7 и мы их исключаем.
Аналогичным образом определяем другие правила.
| Паттерн | Посыл | Поддержка | Правило |
|---|---|---|---|
| BC (0.5) | B (0.6) | 0.83 | B -> C |
| CD (0.6) | D (0.8) | 0.75 | D -> C |
| CE (0.4) | E (0.4) | 1.00 | E -> C |
| BCD (0.4) | BD (0.4) | 1.00 | BD -> C |
| BCE (0.3) | BE (0.3) | 1.00 | BE -> C |
| CDE (0.3) | DE (0.3) | 1.00 | DE -> C |
| CD (0.6) | C (0.7) | 0.86 | C -> D |
| DE (0.3) | E (0.4) | 0.75 | E -> D |
| BCD (0.4) | BC (0.5) | 0.80 | BC -> D |
| CDE (0.3) | CE (0.4) | 0.75 | CE -> D |
Мы с вами рассмотрели один из наиболее известных алгоритмов поиска ассоциативных правил Apriori. Но надо сказать, что несмотря на его простоту и известность, сейчас его мало кто использует на практике. Дело в том, что, как можно заметить, наиболее узким местом рассмотренного метода является многократный проход по базе данных для оценки поддержек кандидатов в частые паттерны. С ростом объема анализируемых баз данных это становится все большей и большей проблемой. Она практически решена в следующем алгоритме. Который требует только 2 прохода по базе данных не зависимо от её объема и количества анализируемых признаков.
3. Алгоритм FP-Growth
Вариант решения выше описанных проблем я предлагаю рассмотреть на примере одного из наиболее быстрых алгоритмов поиска ассоциативных правил FP-Growth (Frequent Pattern - Growth). Благодаря особенностям построения алгоритма, в процессе его выполнения полный перебор всех элементов обучающей выборки осуществляется только 2 раза. Других обращений к обучающей выборке алгоритмом не предусмотрено.
Как и выше рассмотренный алгоритм поиска ассоциативных правил, алгоритм FP-Growth условно можно разделить на 2 подзадачи:
- Нахождение часто встречающихся паттернов. В рассматриваемом алгоритме называется построением FP-дерева.
- Определение правил.
Начинается работа алгоритма с отсеивания случайных признаков. Для этого, аналогично предыдущему алгоритму, мы осуществляем первый проход по всей обучающей выборке и подсчитываем поддержку каждого признака. После чего мы удаляем все признаки, частота появления которых меньше минимальной поддержки.
Оставшиеся признаки выстраиваются в порядке убывания их поддержек. Для приведенного выше примера получим ряд:
D (0.8) -> C (0.7) -> B (0.6) -> E(0.4)
Далее осуществляется построение (выращивание) FP-дерева. Для этого мы осуществляем второй проход по обучающей выборке. При этом в каждой транзакции мы берем только часто встречающиеся признаки выстроенные в порядке убывания поддержек и выстраиваем путь в нашем дереве. Таким образом, узел с максимальной поддержкой будет в корне дерева, а с минимальной поддержкой — будет его листом. При этом для каждого узла создаем счетчик. И на первой итерации присваиваем значения счетчика равное 1 (или 1/N, где N - размер обучающей выборки).
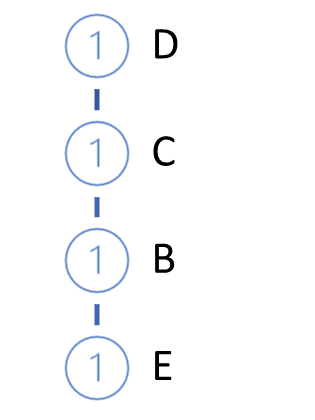
Затем мы берем из базы следующую транзакцию. Аналогичным образом строим для неё путь. И добавляем его к нашему дереву. Для этого начиная от корня дерева мы проверяем путь с уже существующими ветвями. В части повторения пути от корня мы просто увеличиваем счетчик существующих узлов. Для новой части создаем ответвление.
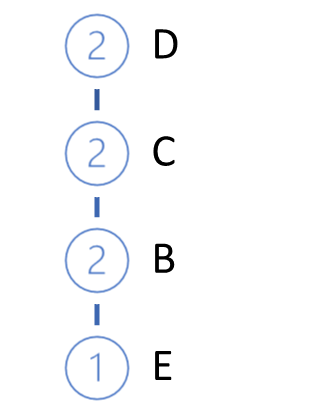
Цикл итераций повторяется до полного перебора всей обучающей выборки. Для приведенного выше примера мы получим нижеследующее FP-дерево.
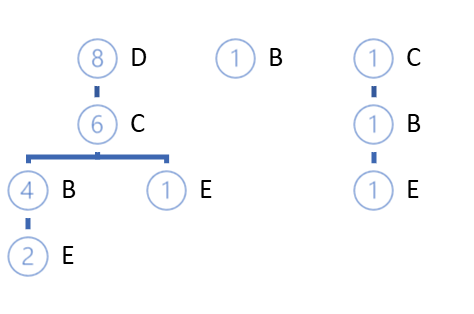
Надо сказать, с большой долей вероятности могут быть найдены пути, которые будут отличаться от самого корня. И здесь возможно 2 варианта:
- построения леса,
- создание некоего корневого узла, который будет объединять всю выборку.
Вполне очевидно, что вначале процесса выращивания FP-дерева в большей части будут создаваться новые узлы. Но в процессе продвижения по обучающей выборке мы будем приходить ко все большему увеличению счетчиков существующих узлов без создания новых ответвлений. Изюминка данного алгоритма в том, что в процессе построения дерева мы сможем сжать обучающую выборку до таких размеров, с которыми мы легко сможем оперировать в рамках оперативной памяти компьютера без обращения к базе данных.
Дальнейшая работа по определению правил осуществляется с FP-деревом, без обращения к исходной базе данных.
Построение правил осуществляется для всех признаков в порядке возрастания их поддержек.
Напомню, что на первом этапе мы удалили все признаки с частотой менее заданной, и теперь в нашем дереве содержатся только часто встречающиеся признаки. Кроме того, при построении дерева мы сортировали признаки в порядке убывания. А значит, признаки с минимальной поддержкой у нас являются листьями.
Начиная определение правил с признаков с наименьшей поддержкой, мы будем двигаться от листьев к корню дерева. И здесь прослеживается ещё не явная установка причинно-следственной связи. Алгоритмом предполагается, что признаки с меньшей поддержкой появляются вследствие комбинации признаков с большей поддержкой.
Но вернемся к нашему алгоритму определения правил. Мы берем признак с наименьшей поддержкой и определяем все пути в FP-дереве, ведущие к данному признаку. Первое, на что мы обращаем внимание при отборе путей, это частота появления искомого признака при формировании паттерна из признаков пути. Критерием отбора пути является отношение поддержки признака в пути к поддержки предшествующего узла. Данное отношение должно быть не менее минимальной степени доверия правила.
В приведенном выше примере, наименьшей поддержкой обладает признак E. До него в наших FP-деревьях ведут 3 пути: DCBE (0.2), DCE (0.1), CBE(0.1). Ни один из этих путей не удовлетворяет требованию минимальной поддержки. И 2 из них не удовлетворяют требованию минимального доверия. Поэтому, ни одного правила мы не можем создать для признака E. Надо сказать, что это подтверждается результатами, полученными в результате работы алгоритма Apriori.
Мы удаляем листья E из нашего дерева и получаем ниже следующий вид нашего FP-дерева.
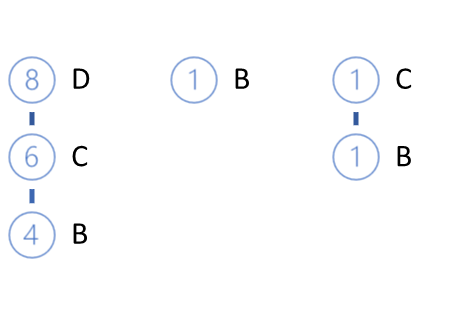
Следующим анализируемым элементом будет признак В. У него наименьшая поддержка из оставшихся. Для него есть 3 пути: DCB (0.4), B (0.1), CB (0.1).
В отобранных путях поддержка каждому признаку, предшествующего анализируемому, присваивается поддержка анализируемого признака в данном пути.
Из отобранных путей формируется список участвующих признаков и определяется поддержка каждого из них. Обратите внимание, что поддержка определяется как отношение количества появления признака в отобранных путях к общему числу записей в исходной обучающей выборке. Таким образом, новая поддержка каждого признака не может превышать ни начальную поддержку признака, ни поддержку анализируемого признака (для которого определяются правила).
Здесь мы также удаляем признаки с поддержкой менее минимальной. И выстраиваем оставшиеся признаки в порядке убывания поддержки.
В нашем примере мы получаем С (0.5), D (0.4).
Обратите внимание, так как мы посчитали поддержки для признаков исходя только из отобранных путей, то полученные значения могут сильно отличаться от первоначальных. Вследствие этого фактора часть признаков может быть отсеяна и изменится их порядок в новой иерархии.
Далее, в соответствии с новой иерархией из отобранных путей мы строим новое частное дерево. Алгоритм построения дерева не отличается от описанного выше алгоритма построения FP-дерева.
Ветви построенного частного дерева будут посылами правил, следствием которых будет наш анализируемый признак.
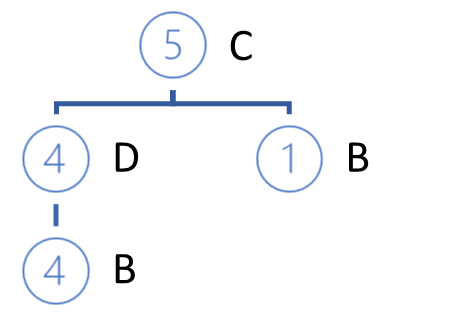
После построения частного дерева мы удаляем узлы проанализированного признака из первоначального FP-дерева. Фокус заключается в том, что мы проанализировали признак с минимальной поддержкой. А значит, все узлы, содержащие этот признак являются листьями FP-дерева. Следовательно, их удаления ни как не повлияет на пути других признаков (чуть выше мы говорили о причинно-следственной связи).
Кроме того, постепенно удаляя проанализированные признаки мы постепенно уменьшаем наше FP-дерево. Тем самым уменьшая объем для последующего поиска путей при анализе следующих признаков. И это сказывается на общей производительности алгоритма.
Аналогичным образом мы строим правила для каждого признака в первоначальной иерархии FP-дерева.
Обратите внимание, что мы можем построить правила только для признаков, которым в FP-дереве предшествует хотя бы один корневой признак. Для корневых признаков мы не можем построить правил, так как нам нечего отнести в посыл. Разумеется кроме визита потенциального покупателя в магазин. Если он пришел в магазин, значит он что-то купит. И вероятнее всего это что-то будет из числа наиболее продаваемых товаров в магазине. Но это уже выходит за рамки рассматриваемого алгоритма.
Заключение
В данной статье мы познакомились с еще один типом задач, решаемых методами обучения без учителя — поиск ассоциативных правил. Мы рассмотрели 2 алгоритма поиска ассоциативных правил: Apriori и FP-Growth. Но их существует гораздо больше. К сожалению, я не могу уместить всю тему в рамках одной статьи. И в ней даны лишь теоретические аспекты. В следующей статье мы рассмотрим практическое построение одного алгоритма поиска ассоциативных правил средствами MQL5. И оценим результаты его работы в решении практической задачи трейдинга.
Ссылки
- Нейросети — это просто (Часть 14): Кластеризация данных
- Нейросети — это просто (Часть 15): Кластеризации данных средствами MQL5
- Нейросети — это просто (Часть 16): Практическое использование кластеризации
- Нейросети — это просто (Часть 17): Понижение размерности
- Fast Algorithms for Mining Association Rules
- Mining Frequent Patterns without Candidate Generation
 Разработка торгового советника с нуля (Часть 13): Время и торговля (II)
Разработка торгового советника с нуля (Часть 13): Время и торговля (II)
 Разработка торговой системы на основе индикатора MACD
Разработка торговой системы на основе индикатора MACD
 Биржевая сеточная торговля лимитными ордерами на полном автомате на Московской бирже MOEX
Биржевая сеточная торговля лимитными ордерами на полном автомате на Московской бирже MOEX
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования